Identity-Based Proxy Signature with Message Recovery over NTRU Lattice
Abstract
1. Introduction
2. Preliminary Knowledge
2.1. Notations
2.2. NTRU Lattice
2.3. Gaussian on Lattice
| Algorithm 1 GaussianSampler |
|
2.4. Rejection Sampling Technique
| Algorithm 2 Rejection sampling technique |
Input: Message u, a matrix A randomly sampled from , (signature key) sampled from , , where , and , is constant and . Then there exists a constant . Output: Vector and 1: Obtain randomly from 2: 3: return with probability |
2.5. Hardness Assumption
2.6. Message Recovery
3. Syntax and Security Model for Identity-Based Proxy Signature Scheme with Message Recovery
3.1. Syntax
- Original signer with ;
- Proxy signer ;
- Verifier;
- Key generation center (KGC) in the system.
- Setup: The algorithm Setup takes a security parameters N as input, and then it outputs the system’s public parameters , KGC’s public and secret key , that is .
- KeyExtract: The algorithm KeyExtract takes the system’s public parameters , KGC’s secret key and public key , user’s identity (i.e., user’s public key ) as input, and then it outputs the user ’s secret key , that is, .
- DelGen: The algorithmDelGen’s input consists of the system’s public parameters , KGC’s public key , a warrant W where , T is valid time period of W, original signer’s secret and public key , original signer computes the delegation, it outputs the delegation information , that is, .
- DelVer: On input the system’s public parameters , KGC’s public key , original signer’s public key , warrant W and its delegation , he verifies the legality of delegation information , If delegation satisfied, the output is 1, and the delegation is accepted; otherwise, the output is 0, and the delegation is rejected, that is, .
- Psign: Given the system’s public parameters , KGC’s public key , original signer’s public key , proxy signer’s secret and public key , delegation key , warrant W and delegation information , and the message m to be signed, the algorithmPsignoutputs the identity-based proxy signature(IB-PS) on behalf of the original signer, that is, .
- Pver: For a verifier in our IB-PSSMR system, he first recovers the message m embedded in the signature sig. Then, the algorithmPvertakes the public key of the original signer, the public key of the proxy signer, and the public delegation key as input. if the proxy signature is valid, output 1, or output 0 if it is invalid, that is .
3.2. Security Model for IB-PSSMR
- Initial Phase: the challenger runs the algorithm to generate the system public parameters and then sends them to the adversary .
- Query Phase: in the Query Phase, the adversary can adaptively issue some query (also known as query the oracles). The number of queries is polynomial bounded.
- -query: given an , the adversary can issue a query to obtain the corresponding secret key. The challenger runs the algorithm , and returns with .
- -query: for some interested delegation information , the adversary issues query with two secret key corresponding to the identity and as input. Once upon receiving the query, the challenger runs . Additionally, returns to .
- -query: if is interested in the proxy signature of message m under , he issues such a query to the challenger. runs the algorithm , and delivers sig to .
- Forgery Phase: through the query phase above, the adversary tries to forge a proxy signature to win the game. Given a message m and an identity as the proxy signer, needs to generate a valid sig to make it pass the verification. The following conditions should naturally be satisfied:
- (a)
- .
- (b)
- In the -query phase, m has never been signed.
- (c)
- In the -query phase, the secret key of has not been queried.
4. Our Identity-Based Proxy Signature Scheme with Message Recovery
- A trusted third party KGC,
- An original signer with ,
- A proxy signer with ,
- A verifier.
- : the algorithm run by KGC. It takes a system security parameter as the algorithms’ input. Assume , be positive integers. The algorithm will do the following steps:
- Choose hash functions , , , , , , are seen as a random oracle.
- Select two encoding functions , .
- KGC starts the algorithm to output the system’s master key , which is described in Algorithm 3.
- Finally, KGC publishes as public parameters of our IB-PSSMR system.
- : KGC takes the public parameters and system’s master secret key as the algorithm’s input, then KGC works as follows:
- The system’s participants original signer and proxy signer request their secret key from KGC, and offer their identity and , respectively.
- KGC first checks whether these identities exist in the identity list . If so, request can be terminated, otherwise, KGC runs to obtain ’s secret key and runs to obtain ’s secret key , where and .
- KGC sends to the proxy signer and to the original signer by a a secure authenticated channel.
- : original signer generates the delegation on warrant W where , T is the valid time period of W, and delegation information on W is described as Algorithm 4.
- : when the proxy signer receives the warrant W and its delegation , he first checks if and both are true. If the conditions hold, then proxy signer can take the warrant as his lawful authority from the original signer; otherwise, he should reject it.
- : after confirming the legitimacy of the signer, given a message u, the proxy signer with can generate a proxy signature for it by Algorithm 4.
- : given the public parameters , for a a user in the system who wants to verify the legitimacy of the proxy signature, he performs the steps described in Algorithm 5.
| Algorithm 3 Master Keygen |
|
| Algorithm 4 Message recovery |
|
| Algorithm 5 Pver |
|
5. Security Analysis
- -query: to make use of the oracle response, the challenger builds a list to store the query response information. It is initialized as an empty set. Given the adversary’s query with , first check if it is in the list . If there is a value corresponding to , then return it to the adversary. Otherwise the challenger randomly chooses , then updates the list as , and finally outputs as the response.
- -query: the challenger maintains the list which is a list of tuples , and the initial value is null, when the adversary issues a query on a vector , the challenger looks it up in the list, if the challenger finds a matched tuple , he returns to adversary as the query response. If not, randomly selects string , then updates the list as , and finally outputs as the response.
- -query: the challenger maintains a list , and set it empty in the beginning. When there is a query for from the adversary , the challenger first checks if it is in the list. If there is a corresponding pair in list , then send back to as the query response. Otherwise, randomly picks , then updates the list , and finally outputs as the response.
- -query: the challenger maintains a list , and set it empty in the beginning. When there is a query for from adversary , the challenger firstly checks if it is in the list. If there is a corresponding pair , return , otherwise, challenger randomly chooses , then updates the list , and finally outputs as the response.
- -query: the challenger maintains a list , and also sets the list as an empty set in the initial phase. When there is a query for , the challenger firstly checks if it is in the list. If it exists, then return the corresponding array to . Otherwise, randomly selects vector , then updates the list , and finally outputs as the response.
- -query: the challenger maintains a list , and makes the list an empty set in the beginning. Now if the adversary initiates a request for the private key associated with an identity , the challenger checks if it is already in the list. If there exists the corresponding pair , then the challenger returns . Otherwise recovers the corresponding from the list, then runs to obtain , then updates the list .
- -query: the challenger maintains a list where warrant , When the adversary issues a query for delegation of warrant , the challenger searches it in list first, if there exist corresponding tuple , return , otherwise, the adversary executes to obtain a valid delegation signature, then updates the list .
- -query: the challenger maintains a list where message , when the adversary issues a query for the proxy signature of message U, the challenger searches it in the list first, if there exists a corresponding tuple , return . Otherwise, the adversary executes to obtain a valid proxy signature, then updates the list .
6. Efficiency Analysis
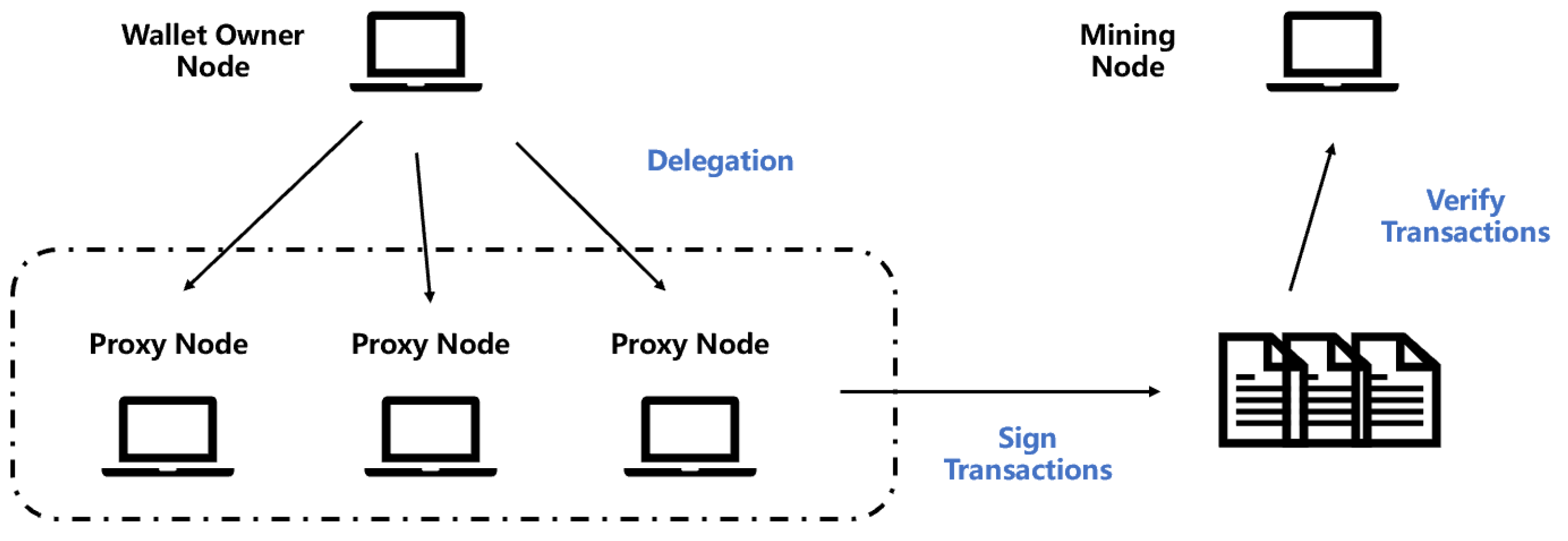
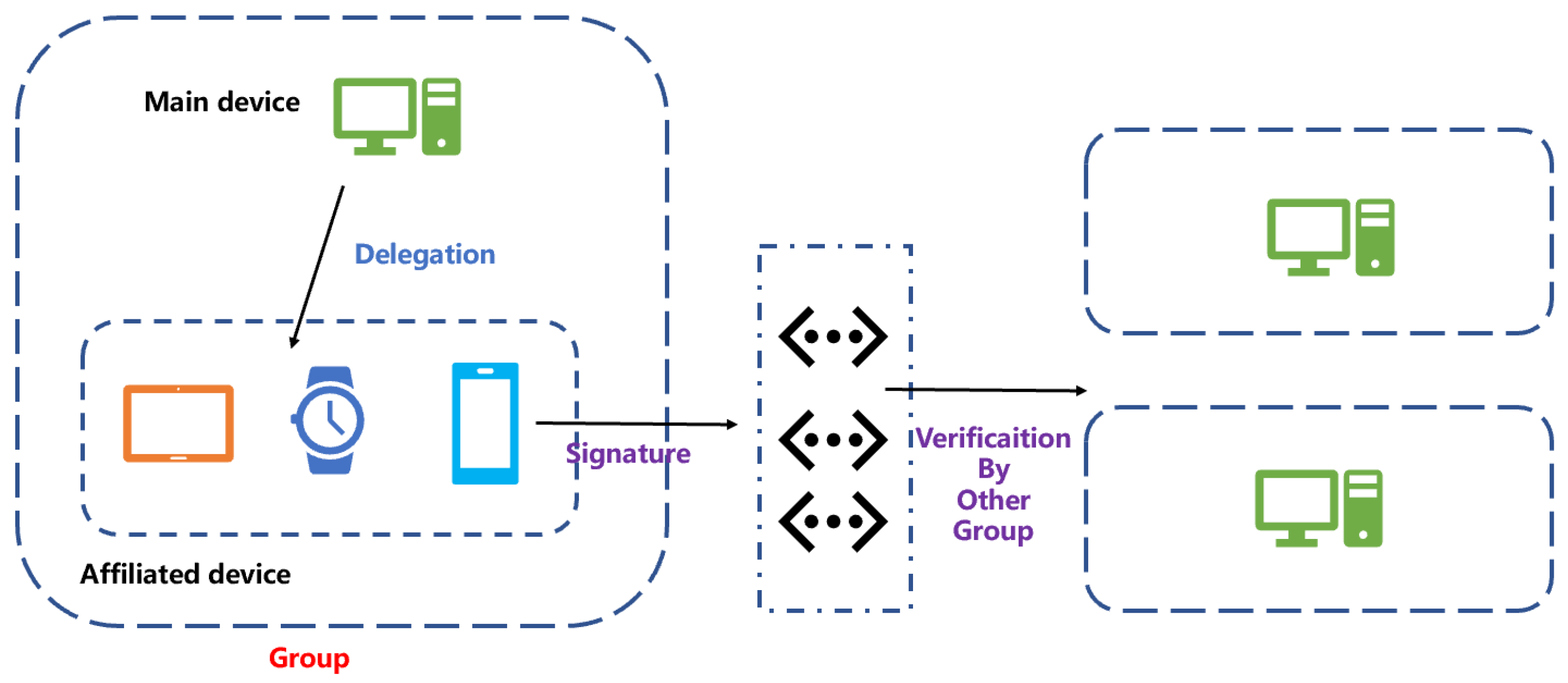
7. Application of The IB-PSSMR
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mambo, M.; Usuda, K.; Okamoto, E. Proxy Signatures: Delegation of the Power to Sign Messages. IEICE Trans. Fundam. A 1996, 79, 1338–1354. [Google Scholar]
- Yang, X.; Gao, G.; Li, Y.; Wang, C. On-line/off-line threshold proxy re-signature scheme through the simulation approach. Appl. Math. Inf. Sci. 2015, 9, 3251–3261. [Google Scholar]
- Kumar, R.; Verma, H.K.; Dhir, R. Analysis and Design of Protocol for Enhanced Threshold Proxy Signature Scheme Based on RSA for Known Signers. Wirel. Pers. Commun. 2015, 80, 1281–1345. [Google Scholar] [CrossRef]
- Shor, P. Algorithms for quantum computation: Discrete logarithms and factoring. In Proceedings of the 35th Annual Symposium On Foundations Of Computer Science, Santa Fe, NM, USA, 20–22 November 1994; pp. 124–134. [Google Scholar]
- Tang, S.; Xu, L. Towards Provably Secure Proxy Signature Scheme Based on Isomorphisms of Polynomials; Springer: Berlin/Heidelberg, Germany, 2012; pp. 91–97. [Google Scholar]
- Yang, C.; Qiu, P.; Zheng, S.; Wang, L. An Efficient Lattice-Based Proxy Signature Scheme without Trapdoor. In Proceedings of the International Conference on Intelligent Information Hiding and Multimedia Signal Processing, Adelaide, Australia, 25 February 2016; pp. 189–194. [Google Scholar]
- Chen, Y.Z.; Liu, Y.; Wen, X.J. A quantum proxy weak blind signature scheme. Chin. J. Quantum Electron. 2011, 54, 1325–1333. [Google Scholar]
- Zhang, L.; Ma, Y. A Lattice-Based Identity-Based Proxy Blind Signature Scheme in the Standard Model. Math. Probl. Eng. 2014, 2014, 307637. [Google Scholar] [CrossRef]
- Wang, T.Y.; Wei, Z.L. Analysis of Forgery Attack on One-Time Proxy Signature and the Improvement. Int. J. Theor. Phys. 2015, 55, 1–3. [Google Scholar] [CrossRef]
- Micciancio, D.; Regev, O. Worst-Case to Average-Case Reductions Based on Gaussian Measures. In Proceedings of the IEEE Symposium on Foundations of Computer Science, Philadelphia, PA, USA, 18–21 October 2014; pp. 372–381. [Google Scholar]
- Simoens, P.; Vankeirsbilck, B.; Deboosere, L.; Ali, F.A.; Turck, F.D.; Dhoedt, B.; Demeester, P. Upstream bandwidth optimization of thin client protocols through latency-aware adaptive user event buffering. Int. J. Commun. Syst. 2011, 24, 666–690. [Google Scholar] [CrossRef]
- Liu, C.X.; Liu, Y.; Zhang, Z.J.; Cheng, Z.Y. High energy-efficient and privacy-preserving secure data aggregation for wireless sensor networks. Int. J. Commun. Syst. 2013, 26, 380–394. [Google Scholar] [CrossRef]
- Nyberg, K.; Rueppel, R.A. A new signature scheme based on the DSA giving message recovery. In Proceedings of the CCS′93: Proceedings of the ACM Conference on Computer and Communications Security, Fairfax, VA, USA, 3–5 November 1993; pp. 58–61. [Google Scholar]
- Lyubashevsky, V. Lattice signatures without trapdoors. In Proceedings of the Advances In Cryptology–EUROCRYPT 2012: 31st Annual International Conference on the Theory and Applications of Cryptographic Techniques, Cambridge, UK, 15–19 April 2012; pp. 738–755. [Google Scholar]
- Tian, M.; Huang, L. Lattice-based message recovery signature schemes. Int. J. Electron. Secur. Digit. Forensics 2013, 5, 257–269. [Google Scholar] [CrossRef]
- Wu, F.; Yao, W.; Zhang, X.; Zheng, Z. An Efficient Lattice-Based Proxy Signature with Message Recovery. In Proceedings of the International Conference on Security, Privacy and Anonymity in Computation, Communication and Storage, Guangzhou, China, 12–15 December 2017; Springer: Berlin/Heidelberg, Germany, 2017; pp. 321–331. [Google Scholar]
- Lu, X.; Wen, Q.; Yin, W.; Liang, K.; Jin, Z.; Panaousis, E.; Chen, J. Quantum-Resistant Identity-Based Signature with Message Recovery and Proxy Delegation. Symmetry 2019, 11, 272. [Google Scholar] [CrossRef]
- Feng, Y.; Zhou, J.; Li, J.; Zhao, W.; Shi, J.; Shi, R.; Li, W. SKC-CCCO: An encryption algorithm for quantum group signature. Quantum Inf. Process. 2022, 21, 328. [Google Scholar] [CrossRef]
- Lu, D.; Li, Z.; Yu, J.; Han, Z. A verifiable arbitrated quantum signature scheme based on controlled quantum teleportation. Entropy 2022, 24, 111. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.J.; You, F.C.; Li, Z.Z. Quantum multi-proxy blind signature based on cluster state. Quantum Inf. Process. 2022, 21, 104. [Google Scholar] [CrossRef]
- Feng, Y.; Shi, R.; Shi, J.; Zhao, W.; Lu, Y.; Tang, Y. Arbitrated quantum signature protocol with boson sampling-based random unitary encryption. J. Phys. A Math. Theor. 2020, 53, 135301. [Google Scholar] [CrossRef]
- Feng, Y.; Shi, R.; Shi, J.; Zhou, J.; Guo, Y. Arbitrated quantum signature scheme with quantum walk-based teleportation. Quantum Inf. Process. 2019, 18, 154. [Google Scholar] [CrossRef]
- Fang, W.; Chen, W.; Zhang, W.; Pei, J.; Gao, W.; Wang, G. Digital signature scheme for information non-repudiation in blockchain: A state of the art review. EURASIP J. Wirel. Commun. Netw. 2020, 2020, 2643546. [Google Scholar] [CrossRef]
- Verma, G.K.; Singh, B.; Kumar, N.; Obaidat, M.S.; He, D.; Singh, H. An efficient and provable certificate-based proxy signature scheme for IIoT environment. Inf. Sci. 2020, 518, 142–156. [Google Scholar] [CrossRef]
- Zhang, J.; Bai, W.; Wang, Y. Non-interactive ID-based proxy re-signature scheme for IoT based on mobile edge computing. IEEE Access 2019, 7, 37865–37875. [Google Scholar] [CrossRef]
- Verma, G.K.; Singh, B.; Kumar, N.; He, D. CB-PS: An efficient short-certificate-based proxy signature scheme for UAVs. IEEE Syst. J. 2019, 14, 621–632. [Google Scholar] [CrossRef]
- Xie, J.; Hu, Y.p.; Gao, J.t.; Gao, W. Efficient identity-based signature over NTRU lattice. Front. Inf. Technol. Electron. Eng. 2016, 17, 135–142. [Google Scholar] [CrossRef]
- Lyubashevsky, V. Lattice Signatures without Trapdoors. In Proceedings of the 31st Annual international conference on Theory and Applications of Cryptographic Techniques, Athens, Greece, 26–30 May 2013; pp. 738–755. [Google Scholar]
- Barr, K.C. Energy-aware lossless data compression. Acm Trans. Comput. Syst. 2006, 24, 250–291. [Google Scholar] [CrossRef]
- Peikert, C. An efficient and parallel Gaussian sampler for lattices. In Proceedings of the Annual Cryptology Conference, Santa Barbara, CA, USA, 15–19 August 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 80–97. [Google Scholar]
- Sinha Roy, S.; Vercauteren, F.; Verbauwhede, I. High precision discrete Gaussian sampling on FPGAs. In Proceedings of the International Conference on Selected Areas in Cryptography, Burnaby, BC, Canada, 14–16 August 2013; Springer: Berlin/Heidelberg, Germany, 2013; pp. 383–401. [Google Scholar]
- Ducas, L.; Nguyen, P.Q. Faster Gaussian lattice sampling using lazy floating-point arithmetic. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security, Bengaluru, India, 1–5 December 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 415–432. [Google Scholar]
- Buchmann, J.; Cabarcas, D.; Göpfert, F.; Hülsing, A.; Weiden, P. Discrete Ziggurat: A time-memory trade-off for sampling from a Gaussian distribution over the integers. In Proceedings of the International Conference on Selected Areas in Cryptography, Burnaby, BC, Canada, 14–16 August 2013; Springer: Berlin/Heidelberg, Germany, 2013; pp. 402–417. [Google Scholar]
- Cai, J.Y.; Nerurkar, A. Approximating the SVP to within a factor (1-1/dim/sup/spl epsiv//) is NP-hard under randomized conditions. In Proceedings of the Thirteenth Annual IEEE Conference on Computational Complexity (Formerly: Structure in Complexity Theory Conference) (Cat. No. 98CB36247), Buffalo, NY, USA, 18 June 1998; IEEE: New York, NY, USA, 1998; pp. 46–55. [Google Scholar]
- Zhang, J.; Yu, Y. Short computational Diffie–Hellman-based proxy signature scheme in the standard model. Int. J. Commun. Syst. 2014, 27, 1894–1907. [Google Scholar] [CrossRef]
- Apostol, T.M. Resultants of cyclotomic polynomials. Proc. Am. Math. Soc. 1970, 24, 457–462. [Google Scholar] [CrossRef]
- Bellare, M.; Neven, G. Multi-signatures in the plain public-Key model and a general forking lemma. In Proceedings of the ACM Conference on Computer and Communications Security, CCS 2006, Alexandria, VA, USA, 30 October–3 November 2006; pp. 390–399. [Google Scholar]
- Agrawal, S.; Boyen, X. Identity-Based Encryption from Lattices in the Standard Model. Manuscript 2009, 3. Available online: http://www.cs.stanford.edu/xb/ab09/ (accessed on 5 February 2023).
- Wu, F.; Yao, W.; Zhang, X.; Wang, W.; Zheng, Z. Identity-based proxy signature over NTRU lattice. Int. J. Commun. Syst. 2019, 32, e3867. [Google Scholar] [CrossRef]
- Ducas, L.; Lyubashevsky, V.; Prest, T. Efficient identity-based encryption over NTRU lattices. In Proceedings of the Advances in Cryptology–ASIACRYPT 2014: 20th International Conference on the Theory and Application of Cryptology and Information Security, Part II 20. Kaoshiung, Taiwan, 7–11 December 2014; Springer: Berlin/Heidelberg, Germany, 2014; pp. 22–41. [Google Scholar]
- Wang, Y.; Qiu, W.; Dong, L.; Zhou, W.; Pei, Y.; Yang, L.; Nian, H.; Lin, Z. Proxy signature-based management model of sharing energy storage in blockchain environment. Appl. Sci. 2020, 10, 7502. [Google Scholar] [CrossRef]
- Qiao, Z.; Zhou, Y.; Yang, B.; Zhang, M.; Wang, T.; Xia, Z. Secure and efficient certificate-based proxy signature schemes for industrial internet of things. IEEE Syst. J. 2021, 16, 4719–4730. [Google Scholar] [CrossRef]
- Hussain, S.; Ullah, I.; Khattak, H.; Khan, M.A.; Chen, C.M.; Kumari, S. A lightweight and provable secure identity-based generalized proxy signcryption (IBGPS) scheme for Industrial Internet of Things (IIoT). J. Inf. Secur. Appl. 2021, 58, 102625. [Google Scholar] [CrossRef]
- Gentry, C.; Peikert, C.; Vaikuntanathan, V. Trapdoors for hard lattices and new cryptographic constructions. In Proceedings of the Fortieth Annual ACM Symposium on Theory of Computing, Victoria, BC, Canada, 17–20 May 2008; pp. 197–206. [Google Scholar]

| Message Recovery | Delegation | Signature’s Size | |
|---|---|---|---|
| [39] | No | Yes | ++4Nlog(12)+2N(log+1) |
| [40] | No | No | |
| Ours | Yes | Yes | +4Nlog(12) |
| Parameter Size (N, Instance, q, k, , ) | Communication Overhead Reduction (Bits) |
|---|---|
| (512, 1, 227, 80, 28, 100) | 2305 |
| (512, 2, 225, 512, 14, 100) | 1997 |
| (512, 3, 233, 512, 14, 200) | 1777 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, F.; Zhou, B.; Zhang, X. Identity-Based Proxy Signature with Message Recovery over NTRU Lattice. Entropy 2023, 25, 454. https://doi.org/10.3390/e25030454
Wu F, Zhou B, Zhang X. Identity-Based Proxy Signature with Message Recovery over NTRU Lattice. Entropy. 2023; 25(3):454. https://doi.org/10.3390/e25030454
Chicago/Turabian StyleWu, Faguo, Bo Zhou, and Xiao Zhang. 2023. "Identity-Based Proxy Signature with Message Recovery over NTRU Lattice" Entropy 25, no. 3: 454. https://doi.org/10.3390/e25030454
APA StyleWu, F., Zhou, B., & Zhang, X. (2023). Identity-Based Proxy Signature with Message Recovery over NTRU Lattice. Entropy, 25(3), 454. https://doi.org/10.3390/e25030454





