Nested Variational Chain and Its Application in Massive MIMO Detection for High-Order Constellations
Abstract
:1. Introduction
- Firstly, the basic idea of the nested variational chain is proposed, and an algorithm is then proposed to establish a general framework. By referring to ’general’, it means this framework is able to combine ’exclusive’ and ’inclusive’ KL divergences, or it degrades to either one as a special case.
- Secondly, providing several examples, we show that existing algorithms, such as MMSE, GTA, and EC, can be regarded as special cases of the variational chain.
- Finally, to provide an initial application of the variational chain into massive MIMO detection, a GTA-embedded Expecatation Consistency (GTA-EC) algorithm is proposed which proves to provide better detection performance, especially for high-order constellations. The complexity of GTA-EC is analyzed as well along with comparisons.
2. Preliminary
2.1. Signal Model
2.2. MIMO Detection
3. Nested Variational Chain
3.1. A Generic Framework for Nested Variational Chain
| Algorithm 1 An algorithm for nested variational chain |
|
3.2. MMSE, GTA and EC MIMO Detectors as Special Cases
4. Applications into MIMO High-Order Detection
4.1. The GTA-EC Algorithm
| Algorithm 2 The GTA-EC Algorithm |
|
4.2. Complexity Analysis
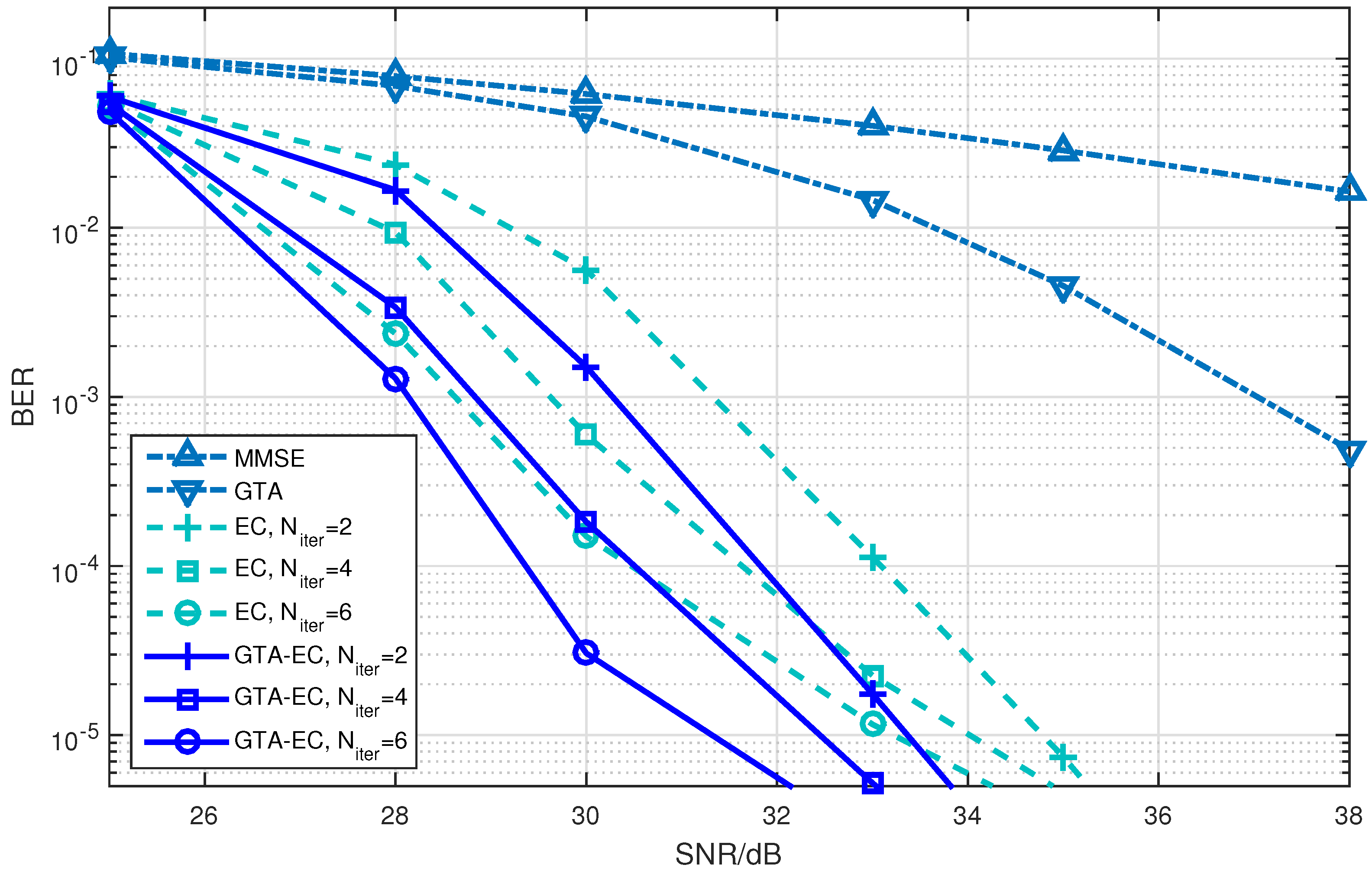
5. Numerical Results
5.1. Simulation Parameters
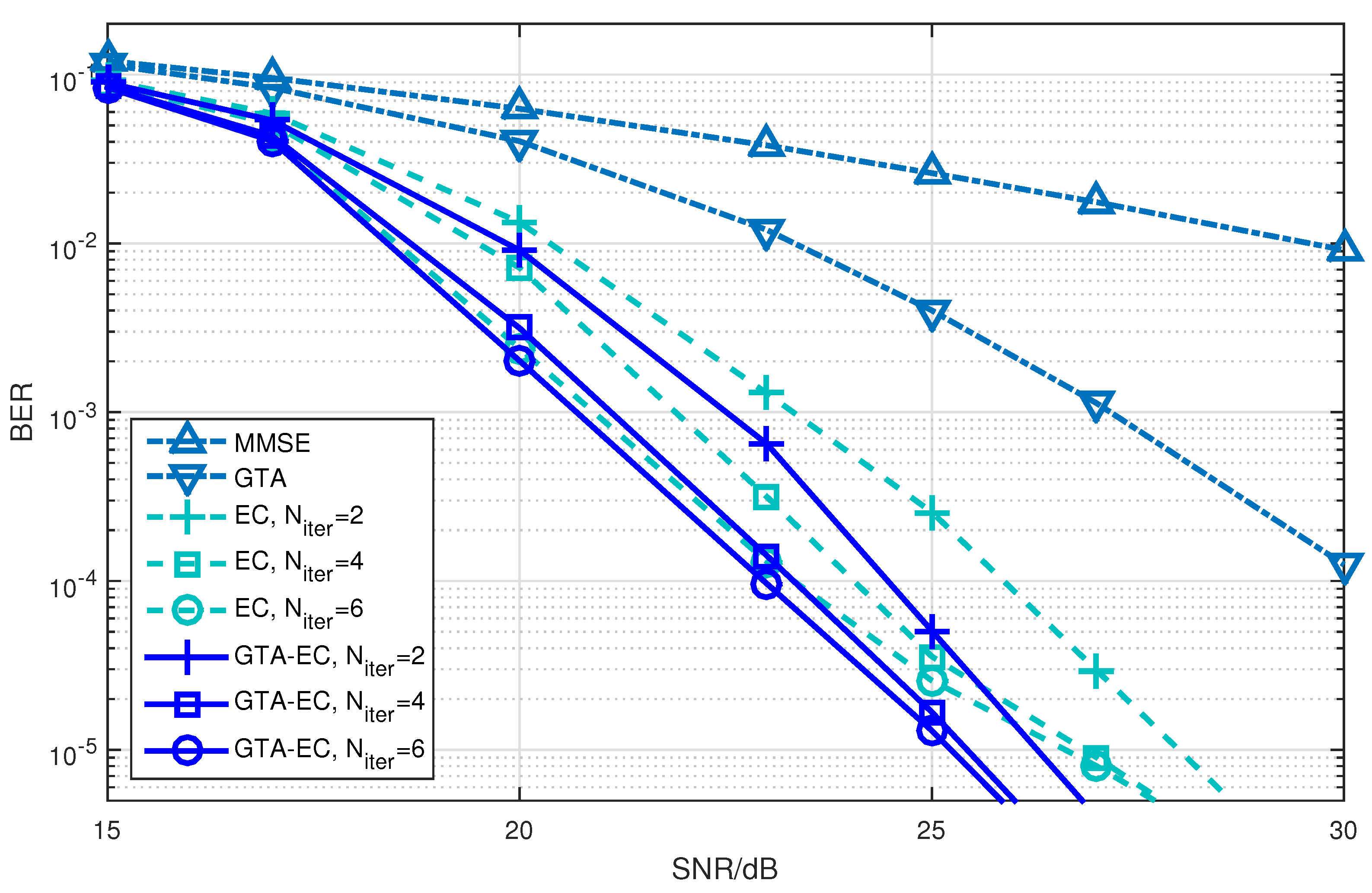
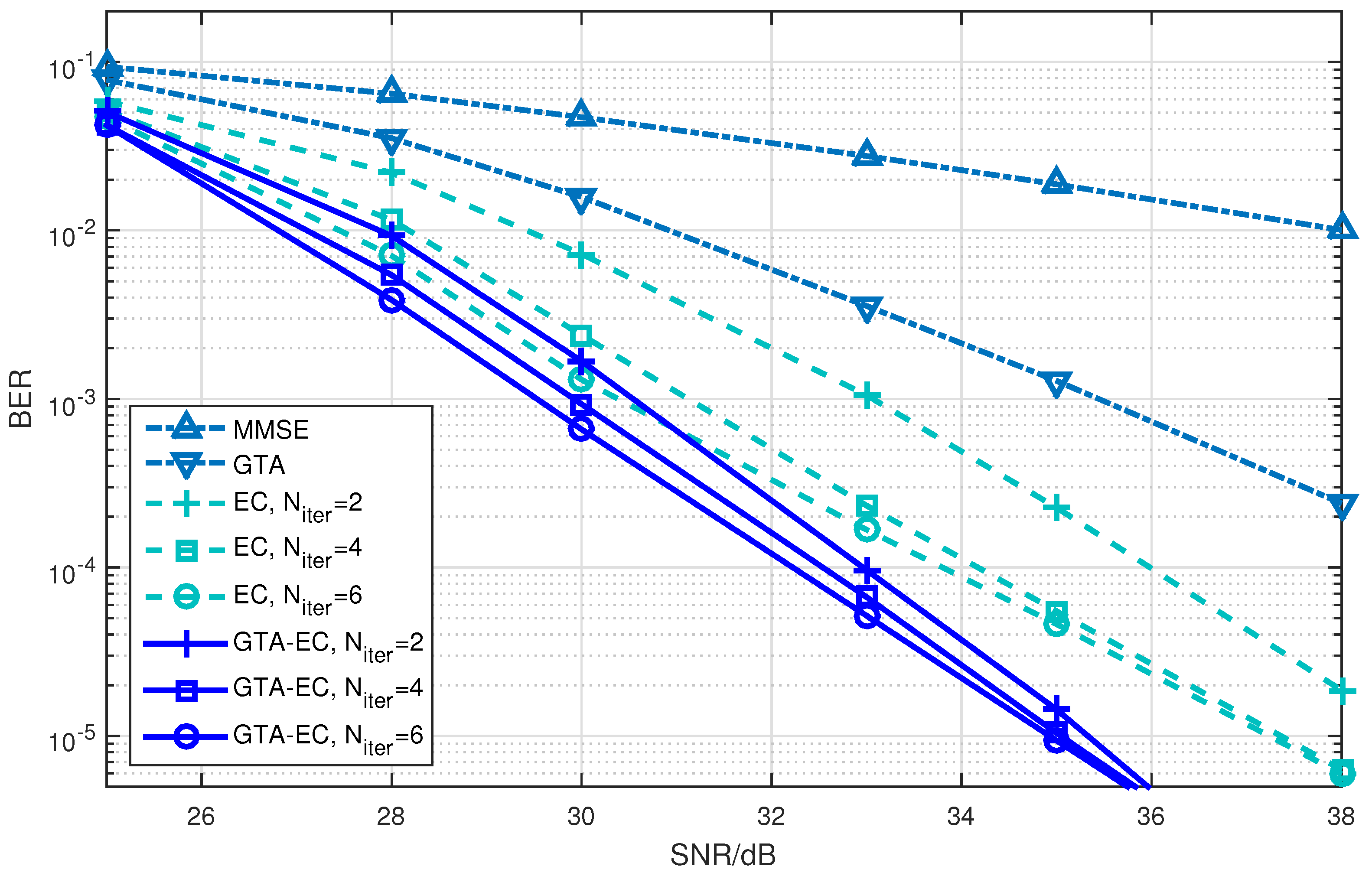
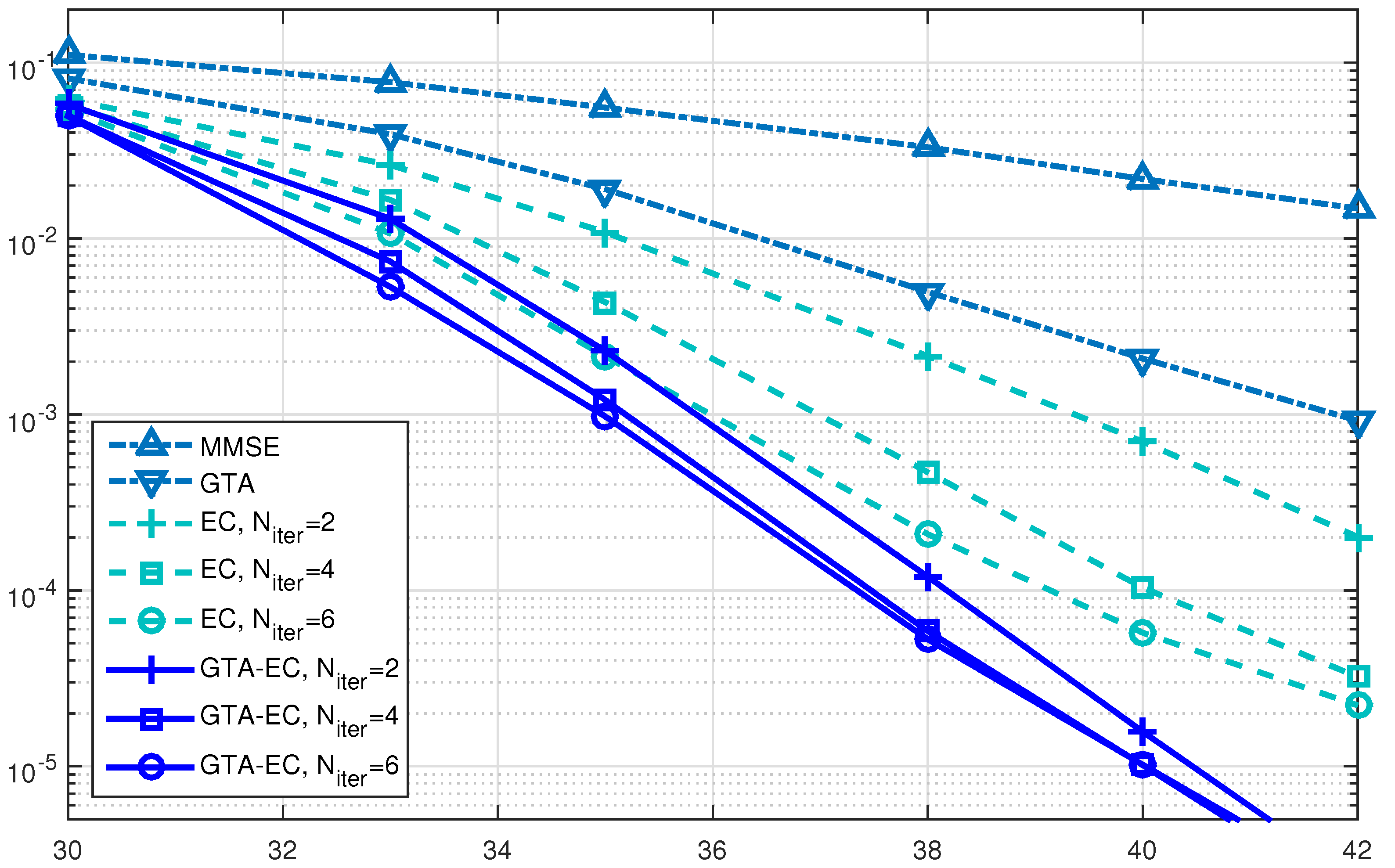
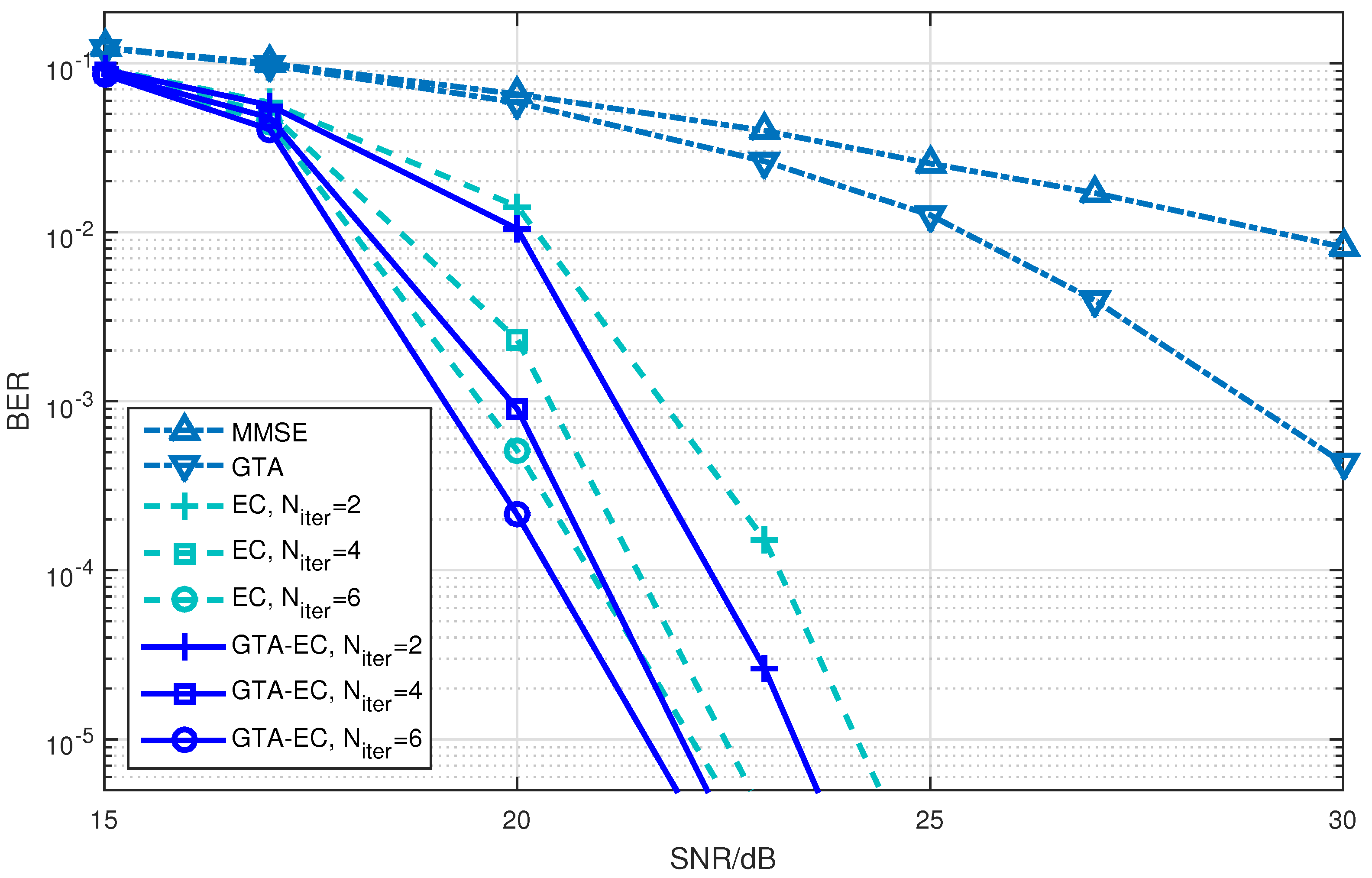
5.2. Performance Evaluation
- On one hand, both EC and GTA-EC significantly outperform existing algorithms such as MMSE and GTA. In most scenarios, GTA-EC can obviously outperform EC with either 16-QAM, 64-QAM, or 256-QAM employed. The performance gain of GTA-EC becomes larger when high-order constellation is employed. For example, both the 64-QAM and 256-QAM cases exhibit larger gain than the 16-QAM case when employing 16 or 64 antennas. This indicates that GTA-EC has superior performance gain and is especially suitable for high-order constellations. We believe that the performance gain comes from exploiting additonal relations (correlation) among symbols rather than treating them independently.
- On the other hand, as for the complexity issue, GTA-EC with iterations may outperform or have comparable performance to EC with iterations, suggesting that GTA-EC requires less complexity than EC by recalling that their computational burdens are dominated by the number of iterations needed. As a result, iterations are recommended for GTA-EC according to the simulation results, and hence the complexity of GTA-EC is approximately times more than MMSE, indicating that it is a practical method for massive MIMO systems.
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, S.; Hanzo, L. Fifty Years of MIMO Detection: The Road to Large-Scale MIMOs. IEEE Commun. Surv. Tutor. 2015, 17, 1941–1988. [Google Scholar] [CrossRef]
- Albreem, M.A.; Juntti, M.; Shahabuddin, S. Massive MIMO Detection Techniques: A Survey. IEEE Commun. Surv. Tutorials 2019, 21, 3109–3132. [Google Scholar] [CrossRef]
- Chen, J.-C. A low complexity data detection algorithm for uplink multiuser massive MIMO systems. IEEE J. Selecive Areas Commun. 2017, 35, 1701–1714. [Google Scholar] [CrossRef]
- Caire, G.; Muller, R.; Tanaka, T. Iterative multiuser joint decoding: Optimal power allocation and low-complexity implementation. IEEE Trans. Inf. Theory 2004, 50, 1950–1973. [Google Scholar] [CrossRef]
- Liu, T.; Liu, Y.-L. Modified fast recursive algorithm for efficient MMSE-SIC detection of the V-BLAST system. IEEE Trans. Wirel. Commun. 2008, 7, 3713–3717. [Google Scholar]
- Albreem, M.A.M.; Salleh, M.F.M. Radius selection for lattice sphere decoder-based block data transmission systems. Wirel. Netw. 2016, 22, 655–662. [Google Scholar] [CrossRef]
- Cui, T.; Han, S.; Tellambura, C. Probability-distribution-based node pruning for sphere decoding. IEEE Trans. Veh. Technol. 2013, 62, 1586–1596. [Google Scholar] [CrossRef]
- Chockalingam, A. Low-complexity algorithms for large-MIMO detection. In Proceedings of the 2010 4th International Symposium on Communications, Control and Signal Processing (ISCCSP), Limassol, Cyprus, 3–5 March 2010; pp. 1–6. [Google Scholar]
- Pereira, A.A., Jr.; Sampaio-Neto, R. A random-list based LAS algorithm for near-optimal detection in large-scale uplink multiuser MIMO systems. In Proceedings of the 19th International ITG Workshop on Smart Antennas, Ilmenau, Germany, 3–5 March 2015; pp. 1–5. [Google Scholar]
- Datta, T.; Srinidhi, N.; Chockalingam, A.; Rajan, B.S. Random restart reactive Tabu search algorithm for detection in large-MIMO systems. IEEE Commun. Lett. 2010, 14, 1107–1109. [Google Scholar] [CrossRef]
- Srinidhi, N.; Datta, T.; Chockalingam, A.; Rajan, B.S. Layered Tabu search algorithm for large-MIMO detection and a lower bound on ML performance. IEEE Trans. Commun. 2010, 59, 2955–2963. [Google Scholar] [CrossRef]
- Bai, L.; Li, T.; Liu, J.; Yu, Q.; Choi, J. Large-scale MIMO detection using MCMC approach with blockwise sampling. IEEE Trans. Commun. 2016, 64, 3697–3707. [Google Scholar] [CrossRef]
- Goldberger, J.; Leshem, A. MIMO detection for high-order QAM based on a Gaussian tree approximation. IEEE Trans. Inf. Theory 2011, 57, 4973–4982. [Google Scholar] [CrossRef]
- Goldberger, J. Improved MIMO detection based on successive tree approximations. In Proceedings of the 2013 IEEE International Symposium on Information Theory, Istanbul, Turkey, 7–12 July 2013; pp. 2004–2008. [Google Scholar]
- Céspedes, J.; Olmos, P.M.; Sánchez-Fernández, M.; Perez-Cruz, F. Expectation propagation detection for high-order high-dimensional MIMO systems. IEEE Trans. Commun. 2014, 62, 2840–2849. [Google Scholar] [CrossRef]
- Céspedes, J.; Olmos, P.M.; Sánchez-Fernández, M.; Perez-Cruz, F. Probabilistic MIMO Symbol Detection With Expectation Consistency Approximate Inference. IEEE Trans. Veh. Technol. 2018, 67, 3481–3494. [Google Scholar] [CrossRef]
- Tan, X.; Ueng, Y.; Zhang, Z.; You, X.; Zhang, C. A Low-Complexity Massive MIMO Detection Based on Approximate Expectation Propagation. IEEE Trans. Veh. Technol. 2019, 68, 7260–7272. [Google Scholar] [CrossRef]
- Ge, Y.; Tan, X.; Ji, Z.; Zhang, Z.; You, X.; Zhang, C. Improving Approximate Expectation Propagation Massive MIMO Detector With Deep Learning. IEEE Wirel. Commun. Lett. 2021, 10, 2145–2149. [Google Scholar] [CrossRef]
- Fuentes, J.J.; Santos, I.; Aradillas, J.C.; Sánchez-Fernández, M. A Low-Complexity Double EP-based Detector for Iterative Detection and Decoding in MIMO. IEEE Trans. Commun. 2021, 69, 1538–1547. [Google Scholar] [CrossRef]
- Wataru, T.; Keigo, T. Pilot Decontamination in Spatially Correlated Massive MIMO Uplink via Expectation Propagation. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2021, E104/A, 723–733. [Google Scholar]
- Rashid, M.; Naraghi-Pour, M. Clustered Sparse Channel Estimation for Massive MIMO Systems by Expectation Maximization-Propagation (EM-EP). IEEE Trans. Veh. Technol. 2023, 72, 9145–9159. [Google Scholar] [CrossRef]

| Algorithm | Factor Substitution | Inner Approximation | Detection and Factor Updating | Total Complexity |
|---|---|---|---|---|
| MMSE | ||||
| GTA | ||||
| EC | ||||
| GTA-EC |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q. Nested Variational Chain and Its Application in Massive MIMO Detection for High-Order Constellations. Entropy 2023, 25, 1621. https://doi.org/10.3390/e25121621
Wang Q. Nested Variational Chain and Its Application in Massive MIMO Detection for High-Order Constellations. Entropy. 2023; 25(12):1621. https://doi.org/10.3390/e25121621
Chicago/Turabian StyleWang, Qiwei. 2023. "Nested Variational Chain and Its Application in Massive MIMO Detection for High-Order Constellations" Entropy 25, no. 12: 1621. https://doi.org/10.3390/e25121621
APA StyleWang, Q. (2023). Nested Variational Chain and Its Application in Massive MIMO Detection for High-Order Constellations. Entropy, 25(12), 1621. https://doi.org/10.3390/e25121621







