Bridging Extremes: The Invertible Bimodal Gumbel Distribution
Abstract
:1. Introduction
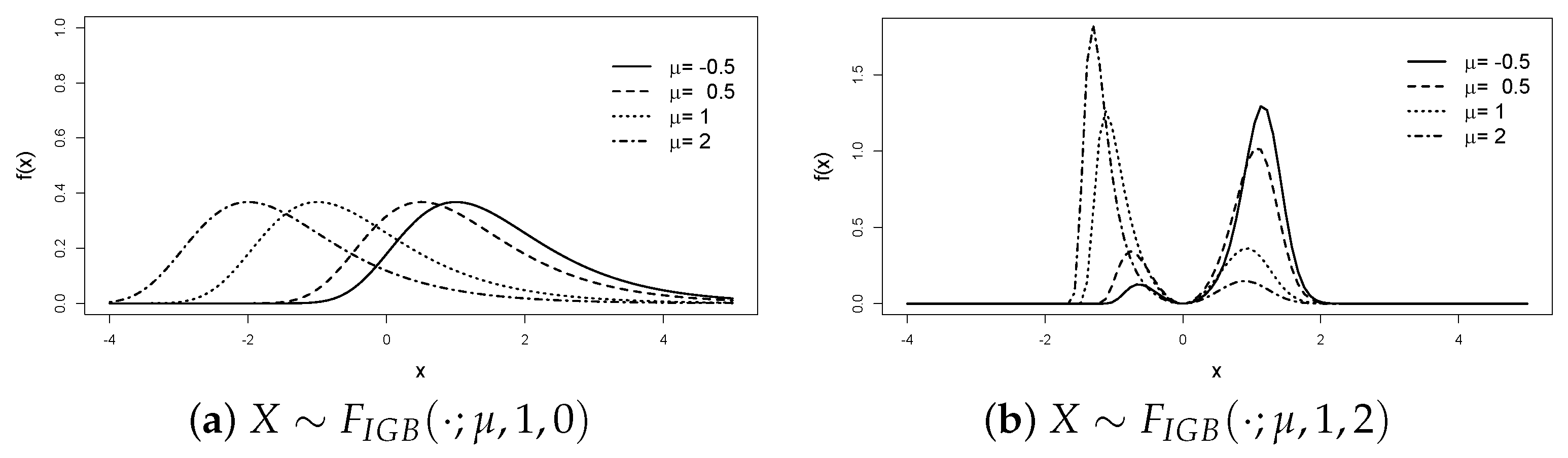
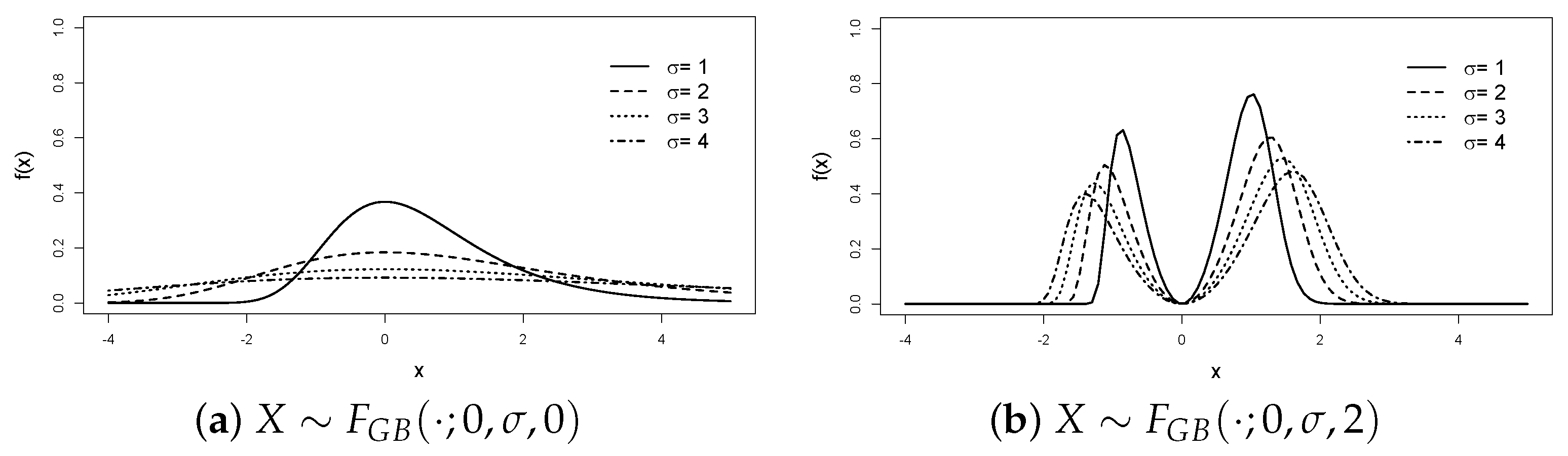
2. Main Results
Some Distributional Characteristics
3. Parameter Estimation
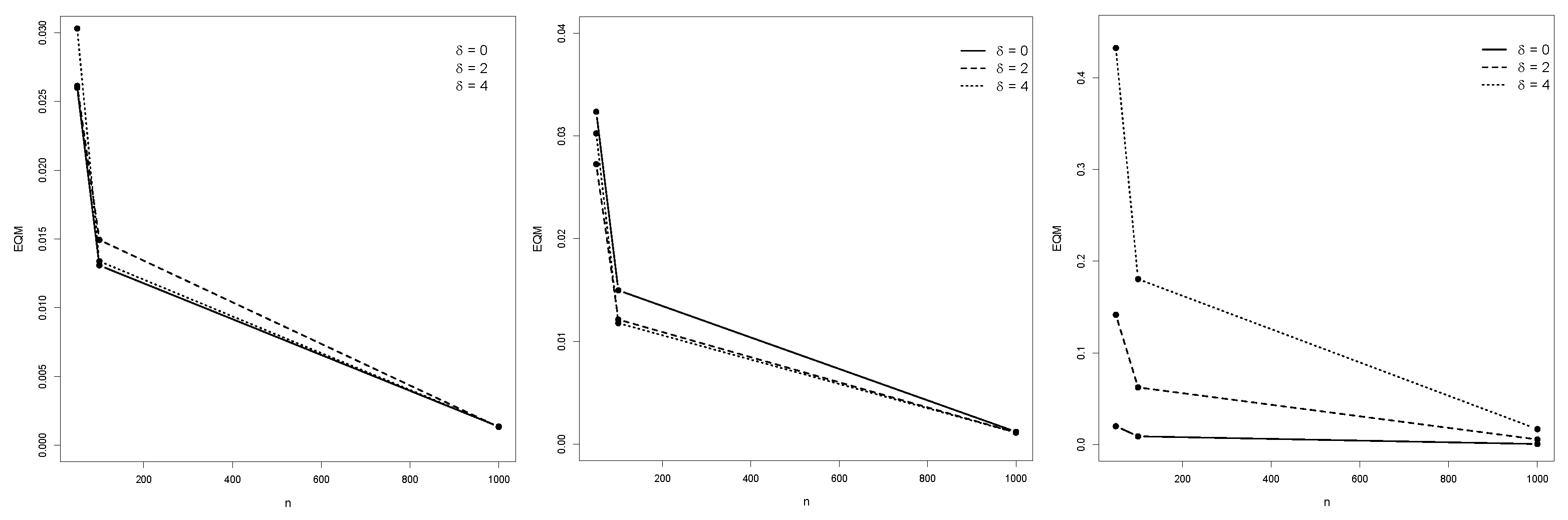
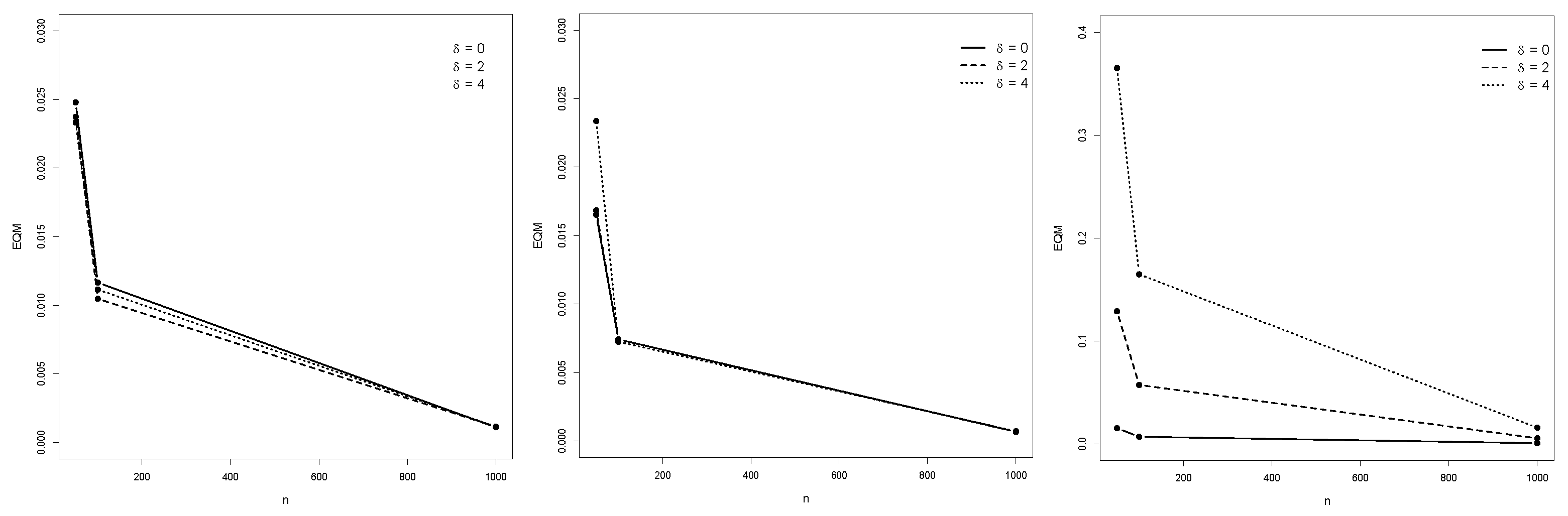
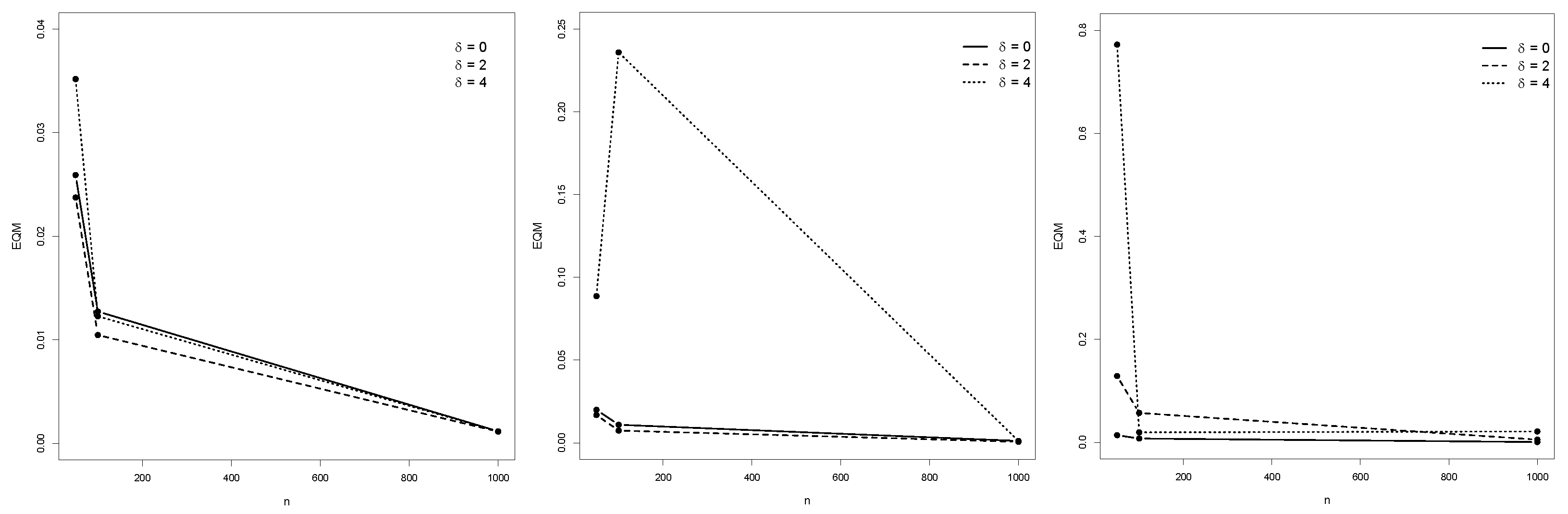
Numerical Performance of ML Estimates
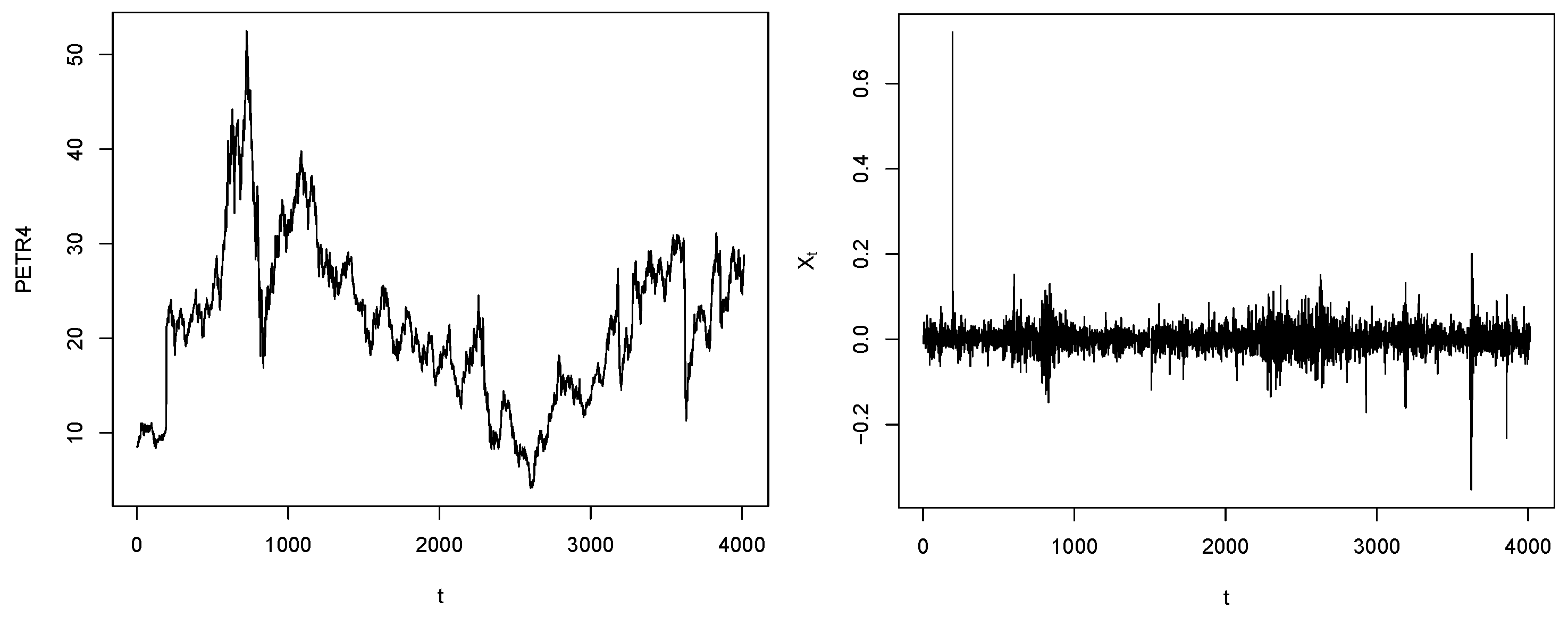
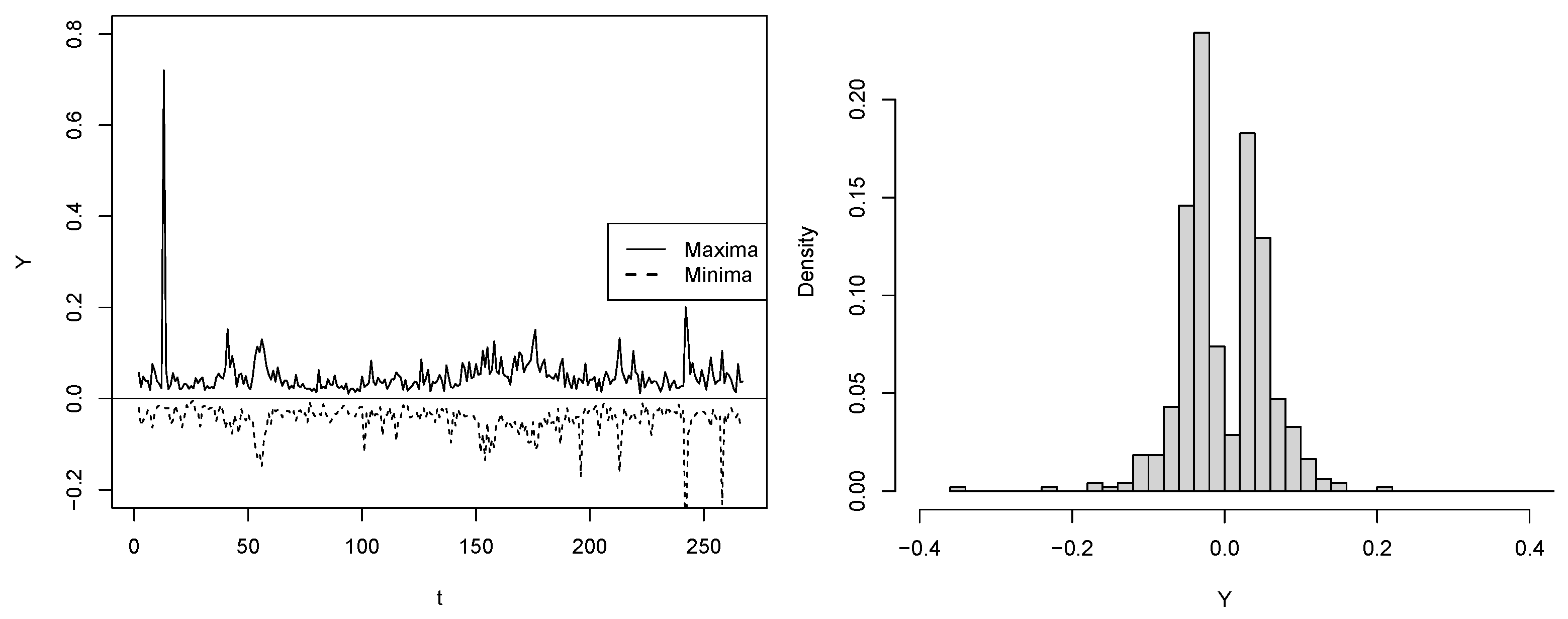
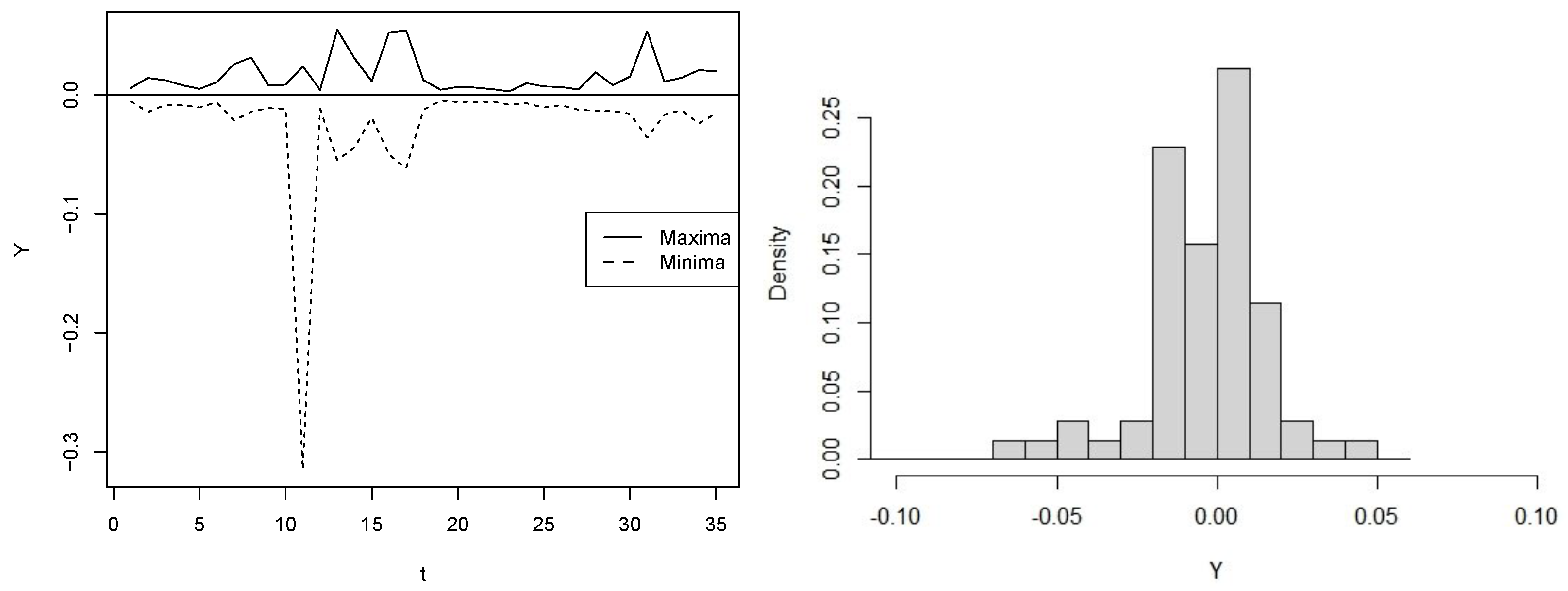
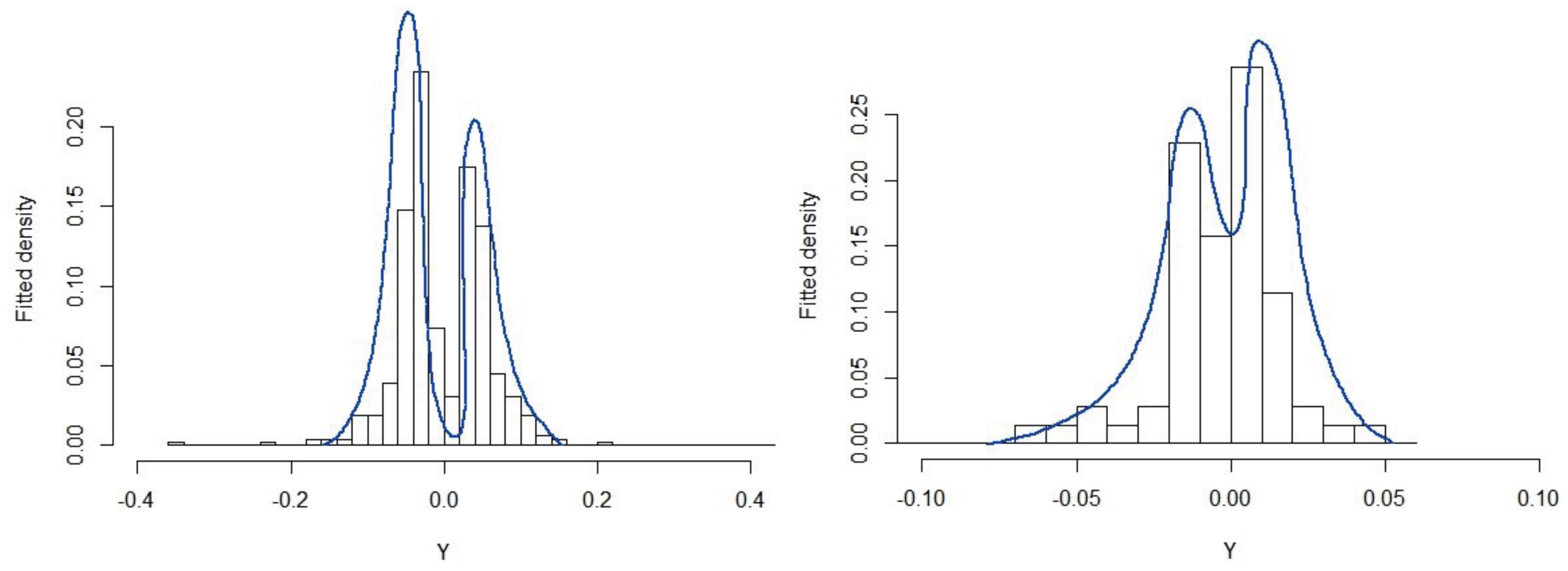
4. Application
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Aubin, D. Forms of explanation in the catastrophe theory of René Thom: Topology, morphogenesis, and structuralism. In Growing Explanations: Historical Perspectives on Recent Science; Wise, M.N., Smith, B.H., Weintraub, E.R., Eds.; Duke University Press: New York, NY, USA, 2004; pp. 95–130. [Google Scholar]
- Ebeling, W.; Schimansky-Geier, L. Stochastic dynamics of a bistable reaction system. Phys. A Stat. Mech. Its Appl. 1979, 98, 587–600. [Google Scholar] [CrossRef]
- Smirnov, V.; Ma, Z.; Volchenkov, D. Invited article by M. Gidea Extreme events and emergency scales. Commun. Nonlinear Sci. Numer. Simul. 2020, 90, 105350. [Google Scholar] [CrossRef] [PubMed]
- Rossi, F.; Fiorentino, M.; Versace, P. Two-component extreme value distribution for flood frequency analysis. Water Resour. Res. 1984, 20, 847–856. [Google Scholar] [CrossRef]
- Nadarajah, S. The exponentiated Gumbel distribution with climate application. Environmetrics 2006, 17, 13–23. [Google Scholar] [CrossRef]
- Aryal, G.R.; Tsokos, C.P. On the transmuted extreme value distribution with application. Nonlinear Anal. Theory Methods Appl. 2009, 71, 401–407. [Google Scholar] [CrossRef]
- Cooray, K. Generalized Gumbel distribution. J. Appl. Stat. 2010, 37, 171–179. [Google Scholar] [CrossRef]
- Jeong, B.Y.; Murshed, M.S.; Am Seo, Y.; Park, J.S. A three-parameter kappa distribution with hydrologic application: A generalized Gumbel distribution. Stoch. Environ. Res. Isk Assess. 2014, 8, 2063–2074. [Google Scholar] [CrossRef]
- Nadarajah, S.; Kotz, S. The beta Gumbel distribution. Math. Probl. Eng. 2004, 4, 323–332. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; Nadarajah, S.; Ortega, E.M.M. The Kumaraswamy Gumbel distribution. Stat. Methods Appl. 2012, 21, 139–168. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; Ortega, E.M.M.; Da Cunha, D.C.C. The exponentiated generalized class of distributions. J. Data Sci. 2013, 11, 1–27. [Google Scholar] [CrossRef]
- Pinheiro, E.C.; Ferrari, S.L.P. A comparative review of generalizations of the Gumbel extreme value distribution with an application to wind speed data. J. Stat. Comput. Simul. 2016, 86, 2241–2261. [Google Scholar] [CrossRef]
- Okorie, I.E.; Akpanta, A.C.; Ohakwe, J. The Exponentiated Gumbel Type-2 Distribution: Properties and Application. Int. J. Math. Math. Sci. 2016, 2016, 5898356. [Google Scholar] [CrossRef]
- Okorie, I.E.; Akpanta, A.C.; Ohakwe, J.; Chikezie, D.C.; Obi, E.O. The Kumaraswamy G Exponentiated Gumbel type-2 distribution. Afr. Stat. 2017, 12, 1367–1396. [Google Scholar]
- Otiniano, C.E.G.; Sousa, B.; Vila, R.; Bourguignon, M. A Bimodal Model for Extremes Data. Environ. Ecol. Stat. 2023, 30, 261–288. [Google Scholar] [CrossRef]
- Otiniano, C.E.G.; Vila, R.; Brom, P.C.; Bourguignon, M. On the bimodal Gumbel model with application to environmental data. Austrian J. Stat. 2023, 52, 45–65. [Google Scholar] [CrossRef]
- Maia, A.; Matsushita, R.; Da Silva, S. Earnings distributions of scalable vs. non-scalable occupations. Phys. A 2020, 560, 125192. [Google Scholar]
- Newman, M.E.J. Power laws, Pareto distributions and Zipf’s law. Contemp. Phys. 2005, 46, 323–351. [Google Scholar] [CrossRef]
- Gumbel, E.J. Les valeurs extremes des distributions statistiques. Ann. L’Institut Henri Poincaré 1935, 5, 115–158. [Google Scholar]
- Jenkinson, A.F. The frequency distribution of the annual maximum (or minimum) values of meteorological elements. Q. J. R. Meteorol. Soc. 1995, 81, 158–171. [Google Scholar] [CrossRef]
- Ahmad, K.E.; Jaheen, Z.; Modhesh, A.A. Estimation of a Discriminant Function Based on Small Sample Size from a Mixture of Two Gumbel Distributions. Commun. Stat. Simul. Comput. 2010, 39, 713–725. [Google Scholar] [CrossRef]
- Longin, F.M. From value at risk to stress testing: The extreme value approach. J. Bank. Financ. 2000, 24, 1097–1130. [Google Scholar] [CrossRef]


| True | Mean | Bias | MSE | SE | ||
|---|---|---|---|---|---|---|
| −1 | −1.00952 | −0.00952 | 0.02163 | 0.1475 | ||
| 1 | 0.97492 | −0.02507 | 0.02765 | 0.1653 | ||
| 0 | 0.01114 | 0.01114 | 0.01554 | 0.1248 | ||
| −1 | −1.03142 | −0.03142 | 0.03419 | 0.1831 | ||
| 1 | 1.02366 | 0.02366 | 0.02592 | 0.1600 | ||
| 2 | 2.05863 | 0.05863 | 0.12062 | 0.3440 | ||
| −1 | −0.99788 | 0.00211 | 0.02748 | 0.1666 | ||
| 1 | 0.96513 | −0.03486 | 0.02763 | 0.1634 | ||
| 4 | 3.91971 | −0.08028 | 0.34339 | 0.5834 | ||
| 0 | 0.00145 | 0.00145 | 0.02113 | 0.1461 | ||
| 1 | 0.99965 | −0.00034 | 0.01646 | 0.1289 | ||
| 0 | 0.03047 | 0.03047 | 0.01316 | 0.1111 | ||
| 0 | 0.00339 | 0.00339 | 0.02363 | 0.1544 | ||
| 1 | 1.00572 | 0.00572 | 0.01401 | 0.1188 | ||
| 2 | 2.14749 | 0.14749 | 0.14933 | 0.3589 | ||
| 0 | −0.02841 | −0.02841 | 0.02129 | 0.1438 | ||
| 1 | 0.97091 | −0.02908 | 0.01374 | 0.1141 | ||
| 4 | 4.00093 | 0.00093 | 0.26488 | 0.5172 | ||
| 1 | 0.95417 | −0.04582 | 0.02859 | 0.1636 | ||
| 1 | 0.98530 | −0.01469 | 0.01918 | 0.1384 | ||
| 0 | 0.00560 | 0.00560 | 0.01242 | 0.1118 | ||
| 1 | 0.96207 | −0.03792 | 0.02218 | 0.1447 | ||
| 1 | 1.04081 | 0.04081 | 0.02338 | 0.1481 | ||
| 2 | 2.10659 | 0.10659 | 0.17084 | 0.4013 | ||
| 1 | 0.93990 | −0.06009 | 0.05954 | 0.2376 | ||
| 1 | 0.97762 | −0.02237 | 0.12103 | 0.3489 | ||
| 4 | 3.96419 | −0.03580 | 0.91265 | 0.9594 |
| True | Mean | Bias | MSE | SE | ||
|---|---|---|---|---|---|---|
| −1 | −0.98025 | 0.01974 | 0.01280 | 0.1120 | ||
| 1 | 0.98180 | −0.01819 | 0.01146 | 0.1060 | ||
| 0 | −0.00898 | −0.00898 | 0.00780 | 0.0883 | ||
| −1 | −0.99734 | 0.00265 | 0.01532 | 0.1243 | ||
| 1 | 0.99027 | −0.00972 | 0.01188 | 0.1091 | ||
| 2 | 2.01504 | 0.01504 | 0.06759 | 0.2608 | ||
| −1 | −0.99937 | 0.00062 | 0.01558 | 0.1254 | ||
| 1 | 0.97695 | −0.02304 | 0.01185 | 0.1069 | ||
| 4 | 3.9113 | −0.08860 | 0.13284 | 0.3553 | ||
| 0 | −0.02087 | −0.02087 | 0.01232 | 0.1095 | ||
| 1 | 0.99485 | −0.00514 | 0.00724 | 0.0854 | ||
| 0 | 0.02235 | 0.02235 | 0.00722 | 0.0824 | ||
| 0 | −0.01413 | −0.01413 | 0.01182 | 0.1083 | ||
| 1 | 0.98941 | −0.01058 | 0.00694 | 0.0830 | ||
| 2 | 2.06691 | 0.06691 | 0.07194 | 0.2610 | ||
| 0 | −0.00765 | −0.00765 | 0.01211 | 0.1103 | ||
| 1 | 0.99801 | −0.00198 | 0.00713 | 0.0848 | ||
| 4 | 4.05904 | 0.05904 | 0.16391 | 0.4025 | ||
| 1 | 0.94706 | −0.05293 | 0.01350 | 0.1039 | ||
| 1 | 0.98666 | −0.01333 | 0.00964 | 0.0977 | ||
| 0 | −0.02825 | −0.0282 | 0.00588 | 0.0717 | ||
| 1 | 0.96052 | −0.03947 | 0.014831 | 0.1157 | ||
| 1 | 1.01628 | 0.01628 | 0.01126 | 0.1053 | ||
| 2 | 1.99650 | −0.00349 | 0.06319 | 0.2526 | ||
| 1 | 0.98981 | −0.01018 | 0.01102 | 0.1050 | ||
| 1 | 0.99397 | −0.00602 | 0.00709 | 0.0844 | ||
| 4 | 4.02093 | 0.02093 | 0.11929 | 0.3464 |
| True | Mean | Bias | MSE | SE | ||
|---|---|---|---|---|---|---|
| −1 | −0.99837 | 0.00162 | 0.00149 | 0.0388 | ||
| 1 | 0.99413 | −0.00586 | 0.00104 | 0.0319 | ||
| 0 | −0.00209 | −0.00209 | 0.00072 | 0.0269 | ||
| −1 | −0.99906 | 0.00093 | 0.00130 | 0.0362 | ||
| 1 | 1.00507 | 0.00507 | 0.00088 | 0.0293 | ||
| 2 | 2.01457 | 0.01457 | 0.00540 | 0.0724 | ||
| −1 | −0.99417 | 0.00582 | 0.00110 | 0.0328 | ||
| 1 | 0.99574 | −0.00425 | 0.00091 | 0.03016 | ||
| 4 | 3.99378 | −0.00621 | 0.01433 | 0.1201 | ||
| 0 | −0.00232 | −0.00232 | 0.00134 | 0.0367 | ||
| 1 | 1.00226 | 0.00226 | 0.00069 | 0.02643 | ||
| 0 | 0.00303 | 0.00303 | 0.00076 | 0.0277 | ||
| 0 | −0.00322 | −0.00322 | 0.00094 | 0.0307 | ||
| 1 | 0.99633 | −0.00366 | 0.00062 | 0.0248 | ||
| 2 | 2.01715 | 0.01715 | 0.00587 | 0.0751 | ||
| 0 | −0.00824 | −0.00824 | 0.00114 | 0.0330 | ||
| 1 | 1.00379 | 0.00379 | 0.00065 | 0.0254 | ||
| 4 | 4.01962 | 0.01962 | 0.01519 | 0.1223 | ||
| 1 | 0.99310 | −0.00689 | 0.00136 | 0.0365 | ||
| 1 | 0.99649 | −0.00350 | 0.00107 | 0.0327 | ||
| 0 | −0.00116 | −0.00116 | 0.00080 | 0.0284 | ||
| 1 | 0.95857 | −0.04142 | 0.00253 | 0.0286 | ||
| 1 | 0.99516 | −0.00483 | 0.00104 | 0.0320 | ||
| 2 | 1.96530 | −0.03469 | 0.00929 | 0.0904 | ||
| 1 | 0.99638 | −0.00361 | 0.00133 | 0.0365 | ||
| 1 | 1.00135 | 0.00135 | 0.00108 | 0.0330 | ||
| 4 | 4.00819 | 0.00819 | 0.01701 | 0.1308 |
| Stock | Minimum | 1st Quartile | Median | Mean | 3rd Quartile | Maximum |
|---|---|---|---|---|---|---|
| PETR4 | −0.3523667 | −0.0137843 | 0.0000000 | 0.0003036 | 0.0138190 | 0.7203695 |
| USD/BRL | −0.3148314 | −0.0056746 | 0.0000000 | 0.0001515 | 0.0060800 | 0.0966945 |
| Stock | |||
|---|---|---|---|
| PETR4 | 0.000009962 | 0.000089877 | 1.246255323 |
| SE | 0.0000071 | 0.0000003 | 0.0000083 |
| USD/BRL | 0.000016486 | 0.000099908 | 1.31295954 |
| SE | 0.0000007 | 0.0000001 | 0.0000027 |
| Stock | 10% | 5% | 1% |
|---|---|---|---|
| PETR4 | 0.07166153 | 0.07835825 | 0.09003984 |
| USD/BRL | 0.02594245 | 0.0295429 | 0.03612925 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Otiniano, C.G.; Silva, E.B.; Matsushita, R.Y.; Silva, A. Bridging Extremes: The Invertible Bimodal Gumbel Distribution. Entropy 2023, 25, 1598. https://doi.org/10.3390/e25121598
Otiniano CG, Silva EB, Matsushita RY, Silva A. Bridging Extremes: The Invertible Bimodal Gumbel Distribution. Entropy. 2023; 25(12):1598. https://doi.org/10.3390/e25121598
Chicago/Turabian StyleOtiniano, Cira G., Eduarda B. Silva, Raul Y. Matsushita, and Alan Silva. 2023. "Bridging Extremes: The Invertible Bimodal Gumbel Distribution" Entropy 25, no. 12: 1598. https://doi.org/10.3390/e25121598
APA StyleOtiniano, C. G., Silva, E. B., Matsushita, R. Y., & Silva, A. (2023). Bridging Extremes: The Invertible Bimodal Gumbel Distribution. Entropy, 25(12), 1598. https://doi.org/10.3390/e25121598







