Design of DNA Storage Coding with Enhanced Constraints
Abstract
:1. Introduction
2. Constraints on DNA Codes
2.1. Traditional Constraints
2.1.1. GC-Content Constraint
2.1.2. Hamming Distance Constraint
2.1.3. No-Runlength Constraint
2.2. Enhanced Constraints
2.2.1. Repeated Tandem Sequence Constraint
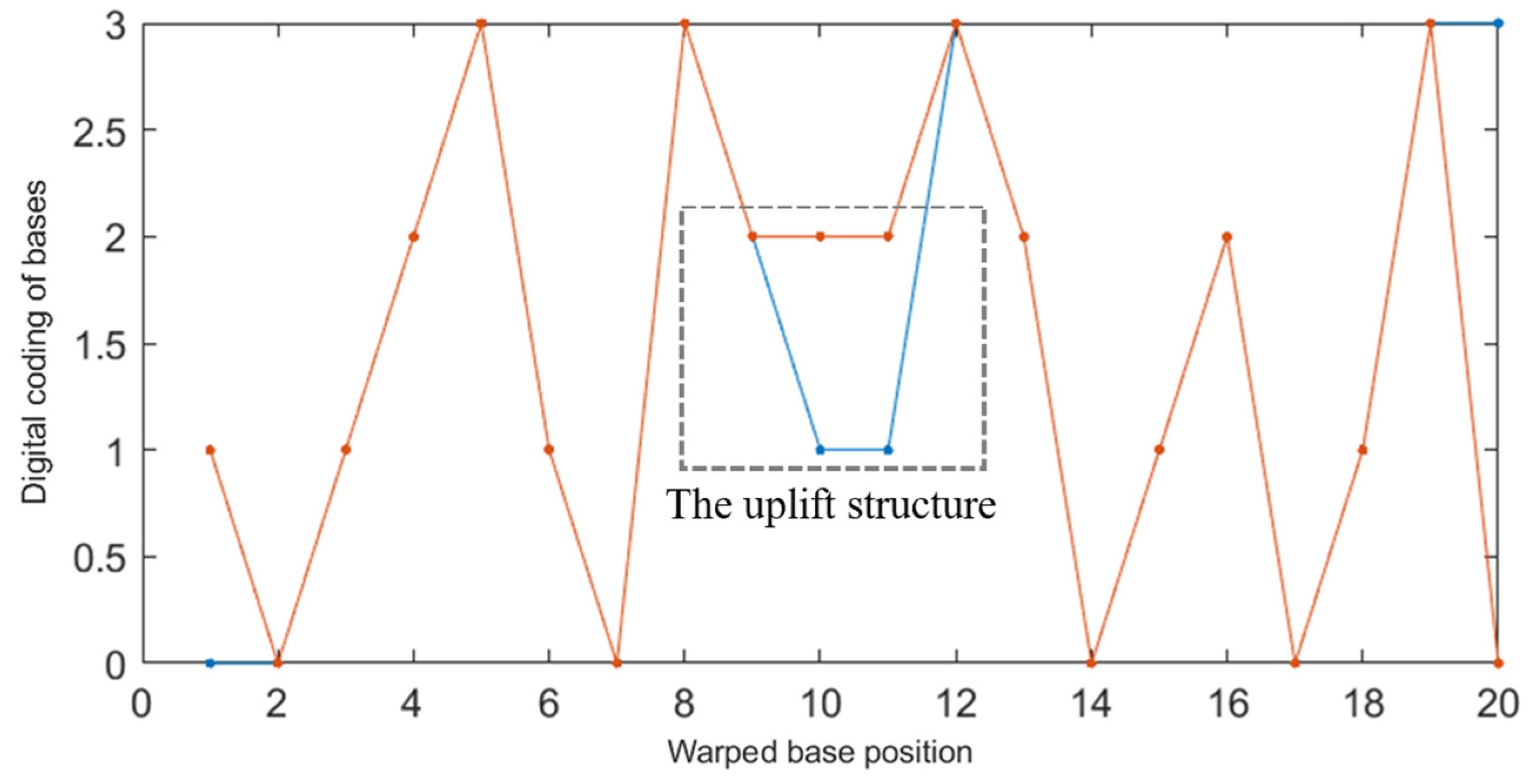
2.2.2. Improved DTW Distance Constraint
2.3. Fitness Function
3. Algorithm Description
3.1. Aquila Optimizer
3.2. The Improved Algorithm
3.2.1. Random Opposition-Based Learning
3.2.2. Eddy Jump
3.2.3. ROEAO Algorithm Description
| Algorithm 1 ROEAO algorithm pseudo code. |
| Set a series of initial parameters |
| Randomly set the initial individual Xi(i = 1,2,…,N) |
| While (t T) Compute the fitness value and update Xbest |
| for I from 1 to N update parameters and XM(t) |
| if if rand 0.5 update the position with Equation (11) and Xbest else update the position with Equation (12) and Xbest end if else if rand 0.5 update the position with Equation (13) and Xbest else update the position with Equation (14) and Xbest end if end if end for Execute Random Opposition-Based Learning based on Equation (15) Execute Eddy Jump based on Equation (16) end while Return the best solution Xbest |
3.3. Experiment Environment and Symbol
3.4. Benchmark Function Comparison
4. Experimental Results and Analysis
4.1. Lower Bound of Coding Set with Traditional Constraints
4.2. Lower Bound of Coding Set with Enhanced Constraints
4.3. Comparison Results of Set Quality
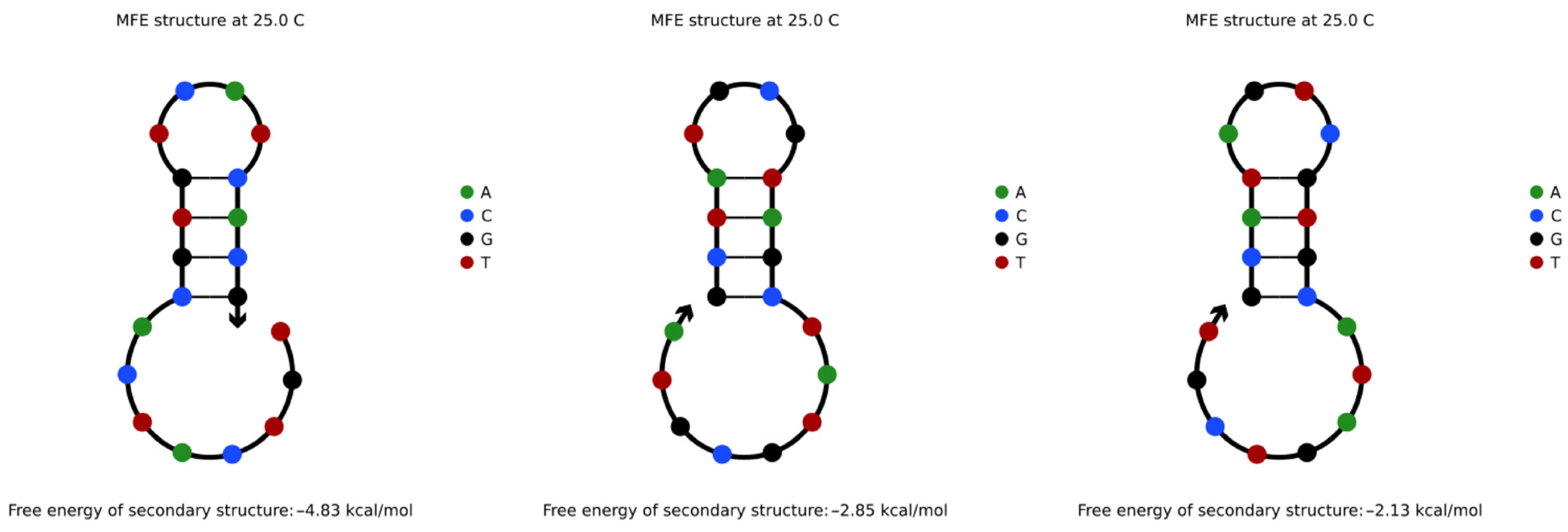
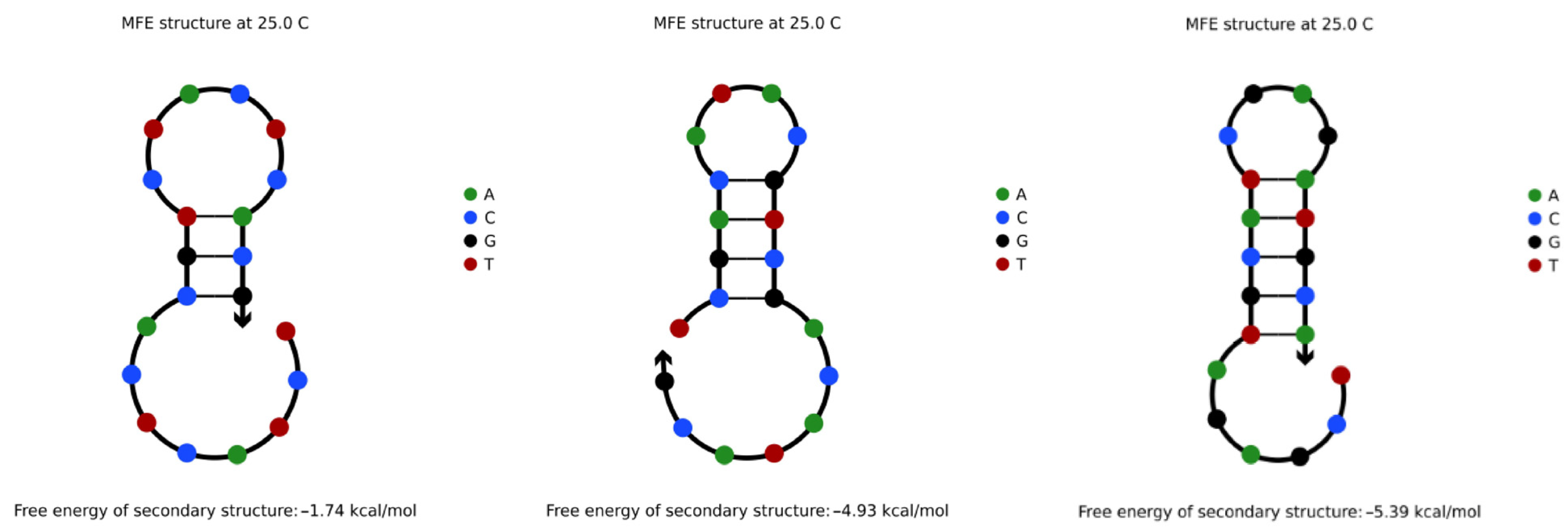
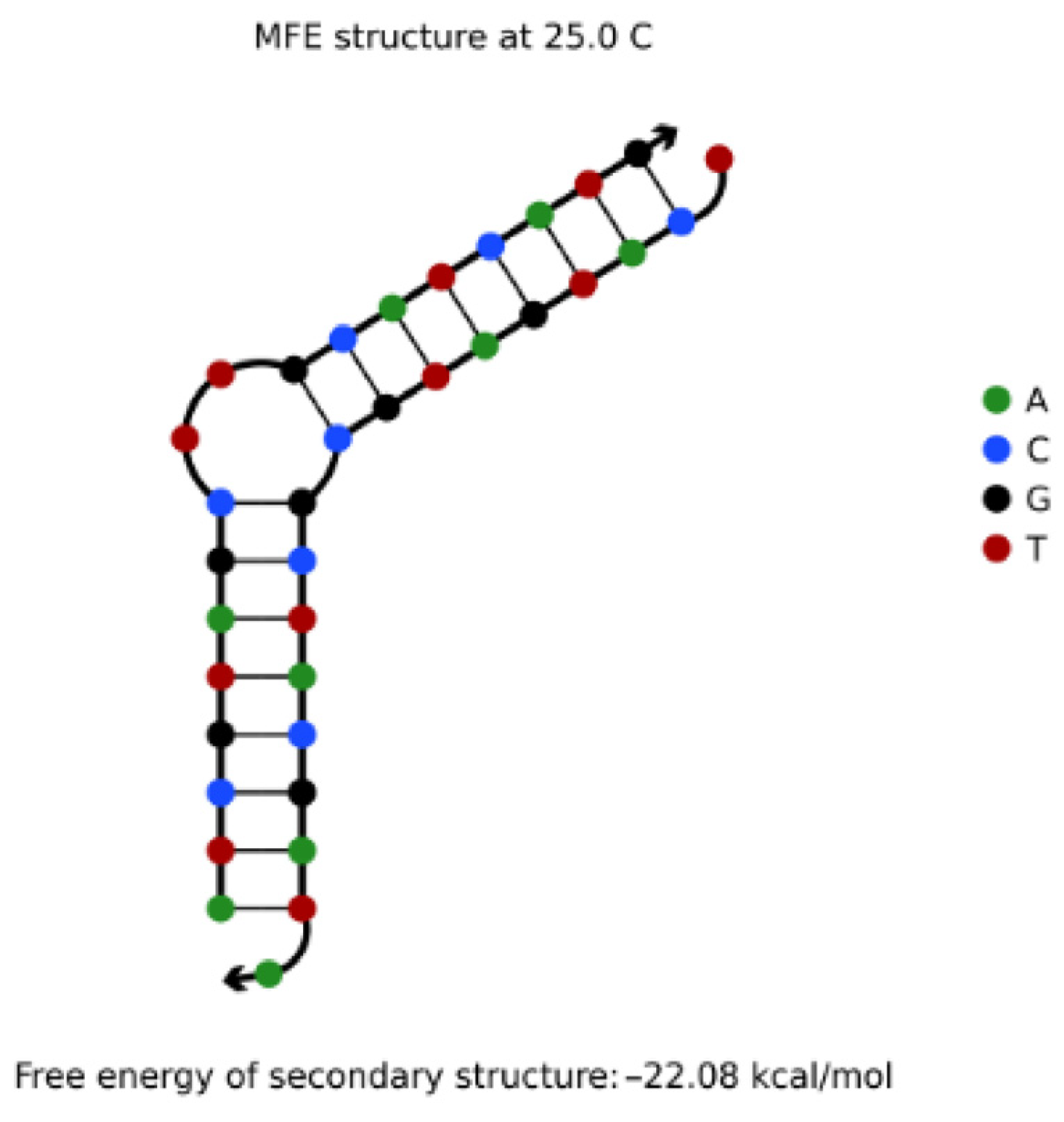
4.3.1. Hairpin Structures
4.3.2. Melting Temperature
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- De Silva, P.Y.; Ganegoda, G.U. New Trends of Digital Data Storage in DNA. BioMed Res. Int. 2016, 2016, 8072463. [Google Scholar] [CrossRef] [PubMed]
- Neiman, M.S. On the molecular memory systems and the directed mutations. Radiotekhnika 1965, 6, 1–8. [Google Scholar]
- Davis, J. Microvenus. Art J. 1996, 55, 70–74. [Google Scholar] [CrossRef]
- Garzon, M.H.; Bobba, K.V.; Hyde, B.P. Digital information encoding on DNA. In Aspects of Molecular Computing; Jonoska, N., Paun, G., Rozenberg, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 152–166. [Google Scholar]
- Ailenberg, M.; Rotstein, O.D. An improved Huffman coding method for archiving text, images, and music characters in DNA. Biotechniques 2009, 47, 747–751. [Google Scholar] [CrossRef]
- Church, G.M.; Gao, Y.; Kosuri, S. Next-Generation Digital Information Storage in DNA. Science 2012, 337, 1628. [Google Scholar] [CrossRef]
- Goldman, N.; Bertone, P.; Chen, S. Towards practical, high-capacity, low-maintenance information storage in synthesized DNA. Nature 2013, 494, 77–80. [Google Scholar] [CrossRef]
- Grass, R.N.; Heckel, R.; Puddu, M. Robust Chemical Preservation of Digital Information on DNA in Silica with Error-Correcting Codes. Angew. Chem.-Int. Ed. 2015, 54, 2552–2555. [Google Scholar] [CrossRef]
- Hong, H.; Wang, L.; Ahmad, H. Construction of DNA codes by using algebraic number theory. Finite Fields Appl. 2016, 37, 328–343. [Google Scholar] [CrossRef]
- Blawat, M.; Gaedke, K.; Huetter, I. Forward Error Correction for DNA Data Storage. Procedia Comput. Sci. 2016, 80, 1011–1022. [Google Scholar] [CrossRef]
- Bornhol, J.; Lopez, R.; Carmean, D.M. A DNA-Based Archival Storage System. In Proceedings of the Twenty-First International Conference on Architectural Support for Programming Languages and Operating Systems, Atlanta, GA, USA, 2–6 April 2016. [Google Scholar]
- Gabrys, R.; Kiah, H.M.; Milenkovic, O. Asymmetric Lee Distance Codes for DNA-Based Storage. IEEE Trans. Inf. Theory 2017, 63, 4982–4995. [Google Scholar] [CrossRef]
- Erlich, Y.; Zielinski, D. DNA Fountain enables a robust and efficient storage architecture. Science 2017, 355, 950–953. [Google Scholar] [CrossRef] [PubMed]
- Yazdi, S.M.H.T.; Kiah, H.M.; Gabrys, R. Mutually Uncorrelated Primers for DNA-Based Data Storage. IEEE Trans. Inf. Theory 2018, 64, 6283–6296. [Google Scholar] [CrossRef]
- Organick, L.; Ang, S.D.; Chen, Y.-J. Random access in large-scale DNA data storage. Nat. Biotechnol. 2018, 36, 242–248. [Google Scholar] [CrossRef]
- Nguyen, H.H.; Park, J.; Park, S.J. Long-Term Stability and Integrity of Plasmid-Based DNA Data Storage. Polymers 2018, 10, 28. [Google Scholar] [CrossRef]
- Limbachiya, D.; Gupta, M.K.; Aggarwal, V. Family of Constrained Codes for Archival DNA Data Storage. IEEE Commun. Lett. 2018, 22, 1972–1975. [Google Scholar] [CrossRef]
- Song, W.; Cai, K.; Zhang, M. Codes With Run-Length and GC-Content Constraints for DNA-Based Data Storage. IEEE Commun. Lett. 2018, 22, 2004–2007. [Google Scholar] [CrossRef]
- Choi, Y.; Ryu, T.; Lee, A.C. High information capacity DNA-based data storage with augmented encoding characters using degenerate bases. Sci. Rep. 2019, 9, 6582. [Google Scholar] [CrossRef]
- Zhang, S.; Huang, B.; Song, X. A high storage density strategy for digital information based on synthetic DNA. 3 Biotech. 2019, 9, 342. [Google Scholar] [CrossRef]
- Anavy, L.; Vaknin, I.; Atar, O. Data storage in DNA with fewer synthesis cycles using composite DNA letters. Nat. Biotechnol. 2019, 37, 1229–1236. [Google Scholar] [CrossRef]
- Wang, Y.; Noor-A-Rahim, M.; Gunawan, E. Construction of Bio-Constrained Code for DNA Data Storage. IEEE Commun. Lett. 2019, 23, 963–966. [Google Scholar] [CrossRef]
- Heckel, R.; Mikutis, G.; Grass, R.N. A Characterization of the DNA Data Storage Channel. Sci. Rep. 2019, 9, 9663. [Google Scholar] [CrossRef] [PubMed]
- Press, W.H.; Hawkins, J.A.; Jones, S.K. HEDGES error-correcting code for DNA storage corrects indels and allows sequence constraints. Proc. Natl. Acad. Sci. USA 2020, 117, 18489–18496. [Google Scholar] [CrossRef] [PubMed]
- Yin, Q.; Zheng, Y.; Wang, B. Design of Constraint Coding Sets for Archive DNA Storage. IEEE/ACM Trans. Comput. Biol. Bioinform. 2021. [Google Scholar] [CrossRef] [PubMed]
- Organick, L.; Nguyen, B.H.; McAmis, R. An Empirical Comparison of Preservation Methods for Synthetic DNA Data Storage. Small Methods 2021, 5, 2001094. [Google Scholar] [CrossRef] [PubMed]
- Ren, Y.; Zhang, Y.; Liu, Y. DNA-Based Concatenated Encoding System for High-Reliability and High-Density Data Storage. Small Methods 2022, 6, 2101335. [Google Scholar] [CrossRef]
- Cao, B.; Li, X.; Zhang, X. Designing Uncorrelated Address Constrain for DNA Storage by DMVO Algorithm. IEEE/ACM Trans. Comput. Biol. Bioinform. 2020, 19, 866–877. [Google Scholar] [CrossRef]
- Tabor, S.; Richardson, C.C. DNA sequence analysis with a modified bacteriophage T7 DNA polymerase. Proc. Natl. Acad. Sci. USA 1987, 84, 4767–4771. [Google Scholar] [CrossRef]
- Tabatabaei Yazdi, S.M.H.; Yuan, Y.; Ma, J. A Rewritable, Random-Access DNA-Based Storage System. Sci. Rep. 2015, 5, 14138. [Google Scholar] [CrossRef]
- Li, J.K.; Wang, Y.Z. Early Abandon to Accelerate Exact Dynamic Time Warping. Int. Arab. J. Inf. Technol. 2009, 6, 144–152. [Google Scholar]
- Abualigah, L.; Yousri, D.; Abd Elaziz, M. Aquila Optimizer: A novel meta-heuristic optimization algorithm. Comput. Ind. Eng. 2021, 157, 107250. [Google Scholar] [CrossRef]
- Tizhoosh, H.R. Opposition-Based Learning: A New Scheme for Machine Intelligence. In Proceedings of the International Conference on Computational Intelligence for Modelling, Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce (CIMCA-IAWTIC’06), Vienna, Austria, 28–30 November 2005. [Google Scholar]
- Yan, W. Computational Methods for Deep Learning: Theoretic, Practice and Applications; Springer: Berlin/Heidelberg, Germany, 2021; pp. XVII, 134. [Google Scholar]
- Faramarzi, A.; Heidarinejad, M.; Mirjalili, S. Marine Predators Algorithm: A Nature-inspired Metaheuristic. Expert Syst. Appl. 2020, 152, 113377. [Google Scholar] [CrossRef]
- Chen, P.; Zhou, S.; Zhang, Q. A meta-inspired termite queen algorithm for global optimization and engineering design problems. Eng. Appl. Artif. Intell. 2022, 111, 104805. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995. [Google Scholar]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst.-Int. J. Esci. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Khishe, M.; Mosavi, M.R. Chimp optimization algorithm. Expert Syst. Appl. 2020, 149, 113338. [Google Scholar] [CrossRef]
- Derrac, J.; García, S.; Molina, D. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]
- Li, X.; Guo, L. Combinatorial constraint coding based on the EORS algorithm in DNA storage. PLoS ONE 2021, 16, e0255376. [Google Scholar]
- Wu, J.; Zheng, Y.; Wang, B. Enhancing Physical and Thermodynamic Properties of DNA Storage Sets With End-Constraint. IEEE Trans. NanoBiosci. 2022, 21, 184–193. [Google Scholar] [CrossRef]


| Superscript | Meaning |
|---|---|
| R | The result from ROEAO |
| EO | The result from EORS |
| A | The result from Altruistic |
| T | The result from ROEAO with Traditional constraints |
| E | The result from ROEAO with Enhanced constraints |
| ID | Metric | ROEAO | AO | GWO | WOA | HHO | MPA | PSO | DE |
|---|---|---|---|---|---|---|---|---|---|
| F1 | AVG | 0.00 × 100 | 2.32 × 10−112 | 1.25 × 10−28 | 5.67 × 10−75 | 1.88 × 10−98 | 3.45 × 10−23 | 1.43 × 104 | 1.26 × 10−4 |
| STD | 0.00 × 100 | 1.48 × 10−114 | 2.01 × 10−28 | 1.67 × 10−74 | 1.98 × 10−98 | 4.54 × 10−23 | 2.01 × 103 | 2.92 × 10−5 | |
| F2 | AVG | 0.00 × 100 | 6.44 × 10−54 | 6.71 × 10−17 | 4.78 × 10−49 | 3.44 × 10−48 | 2.646 × 10−13 | 3.38 × 102 | 4.83 × 10−4 |
| STD | 0.00 × 100 | 4.13 × 10−53 | 4.63 × 10−17 | 3.56 × 10−48 | 2.63 × 10−48 | 2.36 × 10−13 | 1.33 × 103 | 6.06 × 10−4 | |
| F3 | AVG | 0.00 × 100 | 4.35 × 10−101 | 5.23 × 10−06 | 4.57 × 104 | 3.36 × 10−68 | 1.74 × 10−4 | 3.25 × 104 | 3.46 × 104 |
| STD | 0.00 × 100 | 9.90 × 10−101 | 1.58 × 10−6 | 2.02 × 104 | 2.41 × 10−67 | 1.26 × 10−4 | 8.91 × 103 | 5.57 × 103 | |
| F4 | AVG | 0.00 × 100 | 1.06 × 10−53 | 1.23 × 10−6 | 3.72 × 101 | 2.23 × 10−47 | 2.84 × 10−9 | 5.31 × 101 | 1.33 × 101 |
| STD | 0.00 × 100 | 3.90 × 10−52 | 8.32 × 10−7 | 3.38 × 101 | 5.24 × 10−47 | 2.27 × 10−9 | 2.75 × 100 | 2.65 × 100 | |
| F5 | AVG | 2.63 × 10−15 | 4.45 × 10−3 | 2.64 × 101 | 3.01 × 101 | 1.01 × 10−2 | 25.32 × 100 | 2.96 × 107 | 1.44 × 102 |
| STD | 1.41 × 10−14 | 5.58 × 10−3 | 7.53 × 10−1 | 2.97 × 10−1 | 1.19 × 10−2 | 6.74 × 10−1 | 6.83 × 106 | 1.78 × 102 | |
| F6 | AVG | 1.72 × 10−29 | 1.62 × 10−4 | 7.42 × 10−1 | 2.41 × 10−1 | 1.48 × 10−4 | 2.81 × 10−8 | 1.88 × 104 | 7.24 × 10−4 |
| STD | 5.84 × 10−29 | 1.53 × 10−4 | 3.48 × 10−1 | 1.74 × 10−1 | 1.42 × 10−4 | 1.66 × 10−8 | 2.89 × 103 | 5.36 × 10−4 | |
| F7 | AVG | 1.55 × 10−4 | 9.67 × 10−5 | 1.68 × 10−3 | 1.75 × 10−3 | 1.31 × 10−4 | 1.33 × 10−3 | 1.27 × 101 | 5.56 × 10−2 |
| STD | 4.24 × 10−4 | 1.57 × 10−4 | 1.16 × 10−3 | 1.52 × 10−3 | 1.62 × 10−4 | 5.36 × 10−4 | 3.45 × 100 | 1.84 × 10−2 |
| ID | Metric | ROEAO | AO | GWO | WOA | HHO | MPA | PSO | DE |
|---|---|---|---|---|---|---|---|---|---|
| F8 | AVG | −1.29 × 104 | −6.69 × 103 | −5.58 × 103 | −1.23 × 104 | −1.26 × 104 | −8.34 × 103 | −2.86 × 103 | −5.47 × 103 |
| STD | 6.27 × 103 | 3.53 × 103 | 7.10 × 102 | 1.67 × 103 | 1.83 × 102 | 5.38 × 102 | 2.79 × 102 | 2.73 × 102 | |
| F9 | AVG | 0.00 × 100 | 0.00 × 100 | 2.12 × 100 | 1.36 × 10−15 | 0.00 × 100 | 0.00 × 100 | 1.87 × 102 | 1.92 × 102 |
| STD | 0.00 × 100 | 0.00 × 100 | 3.09 × 100 | 1.01 × 10−14 | 0.00 × 100 | 0.00 × 100 | 1.15 × 101 | 1.94 × 101 | |
| F10 | AVG | 8.88 × 10−16 | 8.88 × 10−16 | 1.23 × 10−13 | 3.57 × 10−15 | 8.88 × 10−16 | 2.95 × 10−12 | 1.71 × 101 | 1.41 × 10−2 |
| STD | 0.00 × 100 | 0.00 × 100 | 1.82 × 10−14 | 2.32 × 10−15 | 3.41 × 10−31 | 1.57 × 10−12 | 3.62 × 10−1 | 3.45 × 10−3 | |
| F11 | AVG | 0.00 × 100 | 0.00 × 100 | 2.56 × 10−3 | 5.56 × 10−3 | 0.00 × 100 | 0.00 × 100 | 1.72 × 102 | 4.58 × 10−2 |
| STD | 0.00 × 100 | 0.00 × 100 | 8.77 × 10−3 | 3.74 × 10−2 | 0.00 × 100 | 0.00 × 100 | 3.27 × 101 | 7.12 × 10−2 | |
| F12 | AVG | 1.41 × 10−30 | 5.31 × 10−6 | 3.84 × 10−2 | 2.36 × 10−2 | 8.23 × 10−6 | 1.26 × 10−5 | 1.54 × 107 | 1.35 × 10−3 |
| STD | 6.08 × 10−30 | 7.26 × 10−6 | 1.92 × 10−2 | 2.65 × 10−2 | 1.72 × 10−5 | 6.68 × 10−5 | 9.78 × 106 | 2.72 × 10−3 | |
| F13 | AVG | 2.76 × 10−29 | 2.53 × 10−5 | 6.16 × 10−1 | 5.76 × 10−1 | 2.11 × 10−4 | 1.66− × 10−2 | 5.53 × 107 | 8.12 × 10−3 |
| STD | 1.13 × 10−28 | 4.66 × 10−5 | 2.73 × 10−1 | 2.15 × 10−1 | 2.27 × 10−4 | 5.46 × 10−2 | 3.08 × 107 | 2.74 × 10−2 |
| Comparison | s/e/w | p-Value |
|---|---|---|
| AO vs. ROEAO | 9/3/1 | 3.6658 × 10−2 |
| GWO vs. ROEAO | 13/0/0 | 1.4740 × 10−3 |
| WOA vs. ROEAO | 13/0/0 | 1.4740 × 10−3 |
| HHO vs. ROEAO | 9/3/1 | 2.8417 × 10−2 |
| MPA vs. ROEAO | 11/2/0 | 3.3460 × 10−3 |
| PSO vs. ROEAO | 13/0/0 | 1.4740 × 10−3 |
| DE vs. ROEAO | 13/0/0 | 1.4740 × 10−3 |
| n\d | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|
| 4 | 11 A | ||||||
| 12 EO | |||||||
| 12 R | |||||||
| 5 | 17 A | 7 A | |||||
| 20 EO | 8 EO | ||||||
| 20 R | 8 R | ||||||
| 6 | 44 A | 16 A | 6 A | ||||
| 55 EO | 21 EO | 8 EO | |||||
| 60 R | 27 R | 8 R | |||||
| 7 | 110 A | 36 A | 11A | 4 A | |||
| 125 EO | 46 EO | 16 EO | 6 EO | ||||
| 127 R | 47 R | 17 R | 7 R | ||||
| 8 | 289 A | 86 A | 29 A | 9 A | 4 A | ||
| 326 EO | 110 EO | 38 EO | 15 EO | 5 EO | |||
| 327 R | 110 R | 36 R | 14 R | 5 R | |||
| 9 | 662 A | 199 A | 59 A | 15 A | 8 A | ||
| 737 EO | 226 EO | 71 EO | 26 EO | 11 EO | 5 EO | ||
| 786R | 228R | 71R | 27 R | 11R | 5 R | ||
| 10 | 1810 A | 525 A | 141 A | 43 A | 7 A | 5 A | 4 A |
| 1856 EO | 546 EO | 153 EO | 53 EO | 22 EO | 9 EO | 5 EO | |
| 1964 R | 581R | 157 R | 57 R | 21R | 10 R | 5 R |
| n/dDTW | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|
| 8 | 170 E | 40 E | 14 E | 5 E | 3 E | ||
| 9 | 314 E | 83 E | 21 E | 8 E | 4 E | 2 E | |
| 10 | 607 E | 155 E | 34 E | 11 E | 6 E | 3 E | 1 E |
| n/d | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|
| 8 | 170 T | 40 T | 14 T | 5 T | 3 T | ||
| 67 E | 16 E | 5 E | 2 E | 1 E | |||
| 9 | 403 T | 112 T | 32 T | 11 T | 6 T | 4 T | |
| 314 E | 83 E | 21 E | 8 E | 4 E | 2 E | ||
| 10 | 1776 T | 442 T | 100 T | 33 T | 14 T | 8 T | 2 T |
| 607 E | 155 E | 34 E | 11 E | 6 E | 3 E | 1E |
| n/d | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|
| 8 | 0.4709 T | 0.4273 T | 0.3611 T | 0.5714 T | 0.4000 T | ||
| 0.3941 E | 0.4000 E | 0.3571 E | 0.3333 E | 0.3333 E | |||
| 9 | 1.4389 T | 1.4430 T | 1.5775 T | 1.4074 T | 1.5455 T | 2.6000 T | |
| 1.2834 E | 1.3494 E | 1.5238 E | 1.3750 E | 1.5000 E | 2.0000 E | ||
| 10 | 3.0351 T | 3.0637 T | 3.1210 T | 3.2807 T | 2.4762 T | 2.8000 T | 2.0000 T |
| 2.9259 E | 2.8516 E | 2.9412 E | 3.0000 E | 2.3333 E | 2.6667 E | 2.0000 E |
| n/d | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|
| 8 | 5.913 T | 6.5933 T | 6.1047 T | 3.7399 T | 3.0728 T | ||
| 5.6656 E | 6.4030 E | 4.5663 E | 3.5999 E | 2.3000 E | |||
| 9 | 5.1303 T | 5.0506 T | 5.1692 T | 6.2964 T | 2.9481 T | 3.5663 T | |
| 4.8113 E | 4.4362 E | 4.3375 E | 4.0537 E | 2.5743 E | 2.3743 E | ||
| 10 | 4.7194 T | 4.5276 T | 5.1658 T | 4.7232 T | 3.5348 T | 3.3421 T | 1.6232 T |
| 4.5559 E | 4.3101 E | 4.3337 E | 3.5932 E | 2.8485 E | 2.9237 E | 0.5121 E |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Zhou, S.; Zou, L. Design of DNA Storage Coding with Enhanced Constraints. Entropy 2022, 24, 1151. https://doi.org/10.3390/e24081151
Li X, Zhou S, Zou L. Design of DNA Storage Coding with Enhanced Constraints. Entropy. 2022; 24(8):1151. https://doi.org/10.3390/e24081151
Chicago/Turabian StyleLi, Xiangjun, Shihua Zhou, and Lewang Zou. 2022. "Design of DNA Storage Coding with Enhanced Constraints" Entropy 24, no. 8: 1151. https://doi.org/10.3390/e24081151
APA StyleLi, X., Zhou, S., & Zou, L. (2022). Design of DNA Storage Coding with Enhanced Constraints. Entropy, 24(8), 1151. https://doi.org/10.3390/e24081151





