Contrarian Voter Model under the Influence of an Oscillating Propaganda: Consensus, Bimodal Behavior and Stochastic Resonance
Abstract
1. Introduction
2. Methods
2.1. The Model
2.2. Topology of Interactions
- Complete graph (CG): This is the simplest topology in which every agent is connected to every other agent in the population (all-to-all interactions).
- Lattices: Agents are located at the sites of a lattice with periodic boundary conditions, and interact with their first nearest-neighbors (NNs). The number of neighbors depends on the lattice: one-dimensional () lattice or ring (two NNs), two-dimensional () square lattice (four NNs), triangular lattice (six NNs) and hexagonal lattice (three NNs).
2.3. Magnetization and Signal-to-Noise Ratio
3. Results
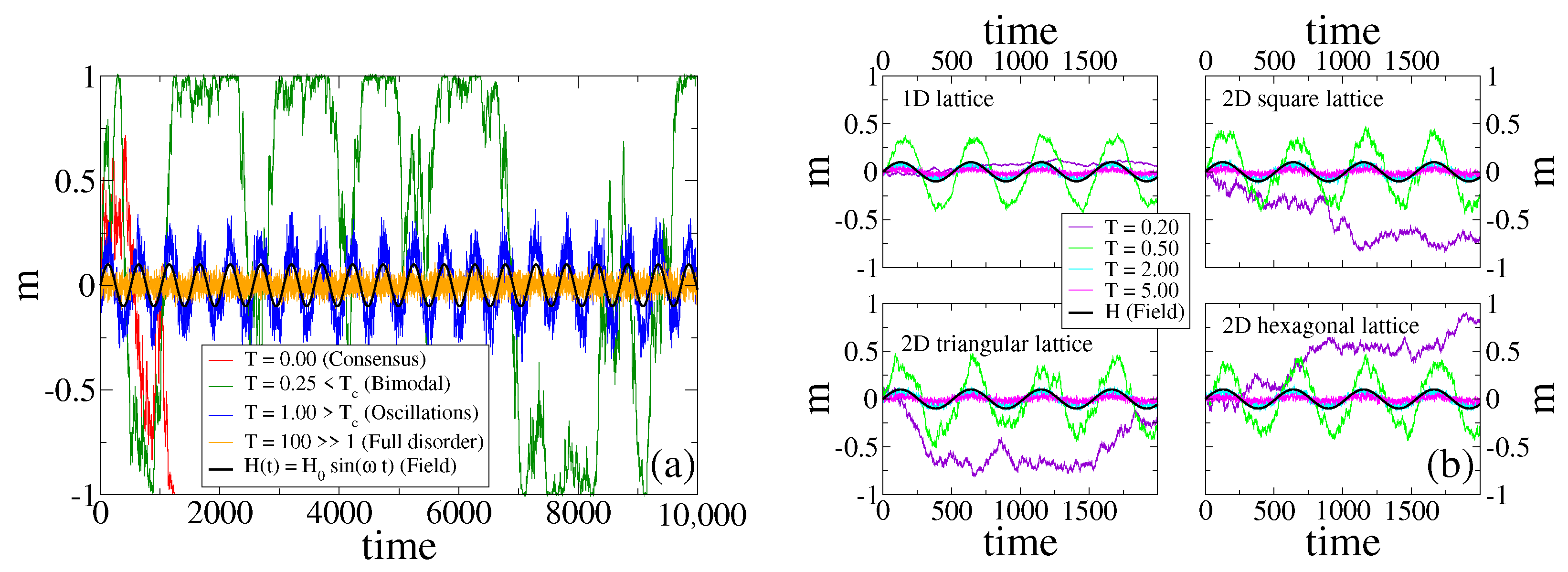
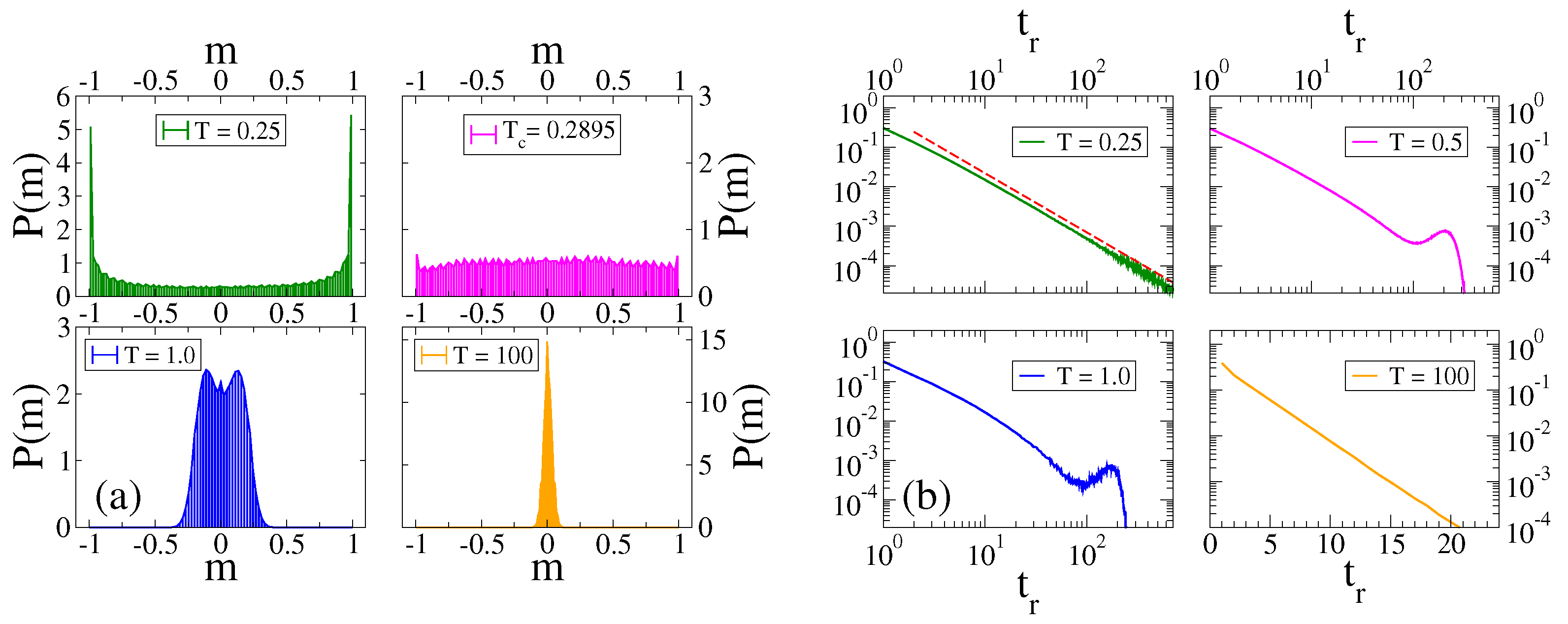
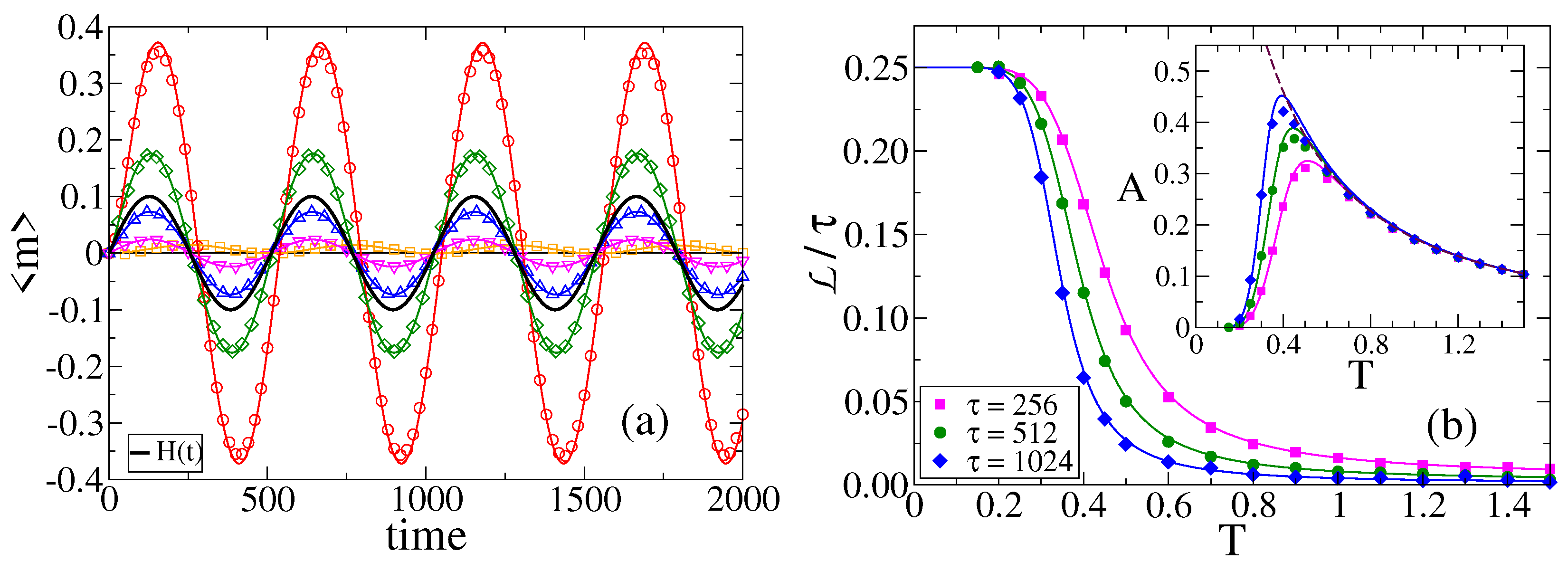
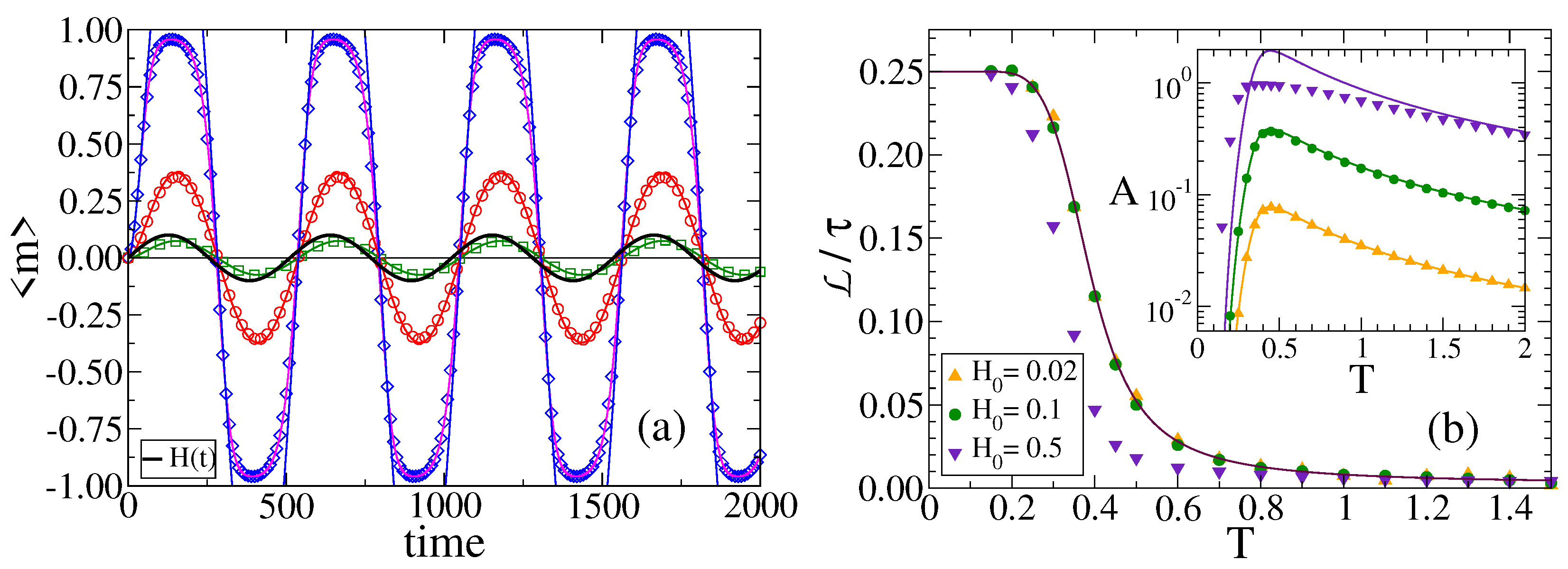
3.1. Evolution of the Magnetization
3.2. Transition Temperature
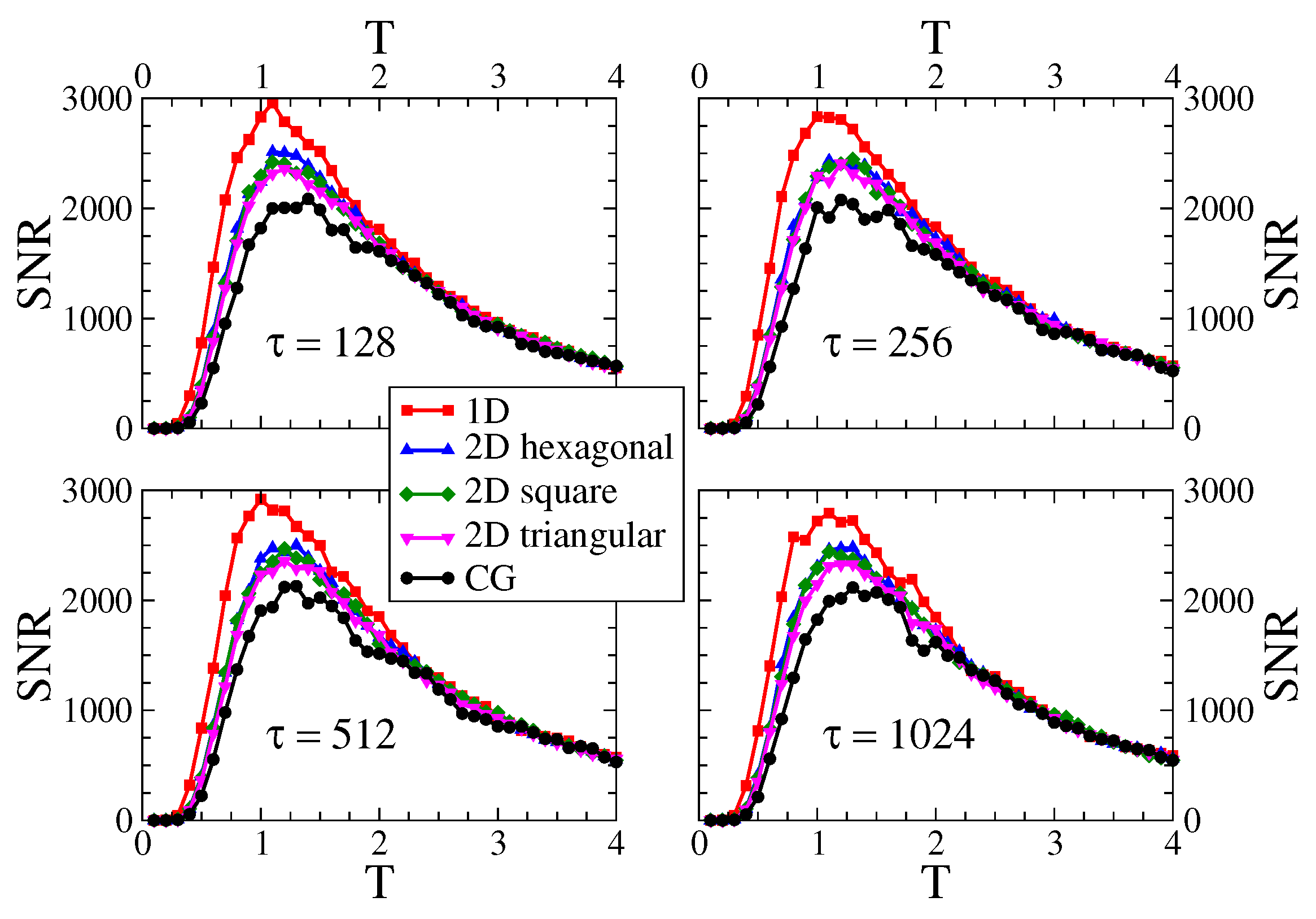
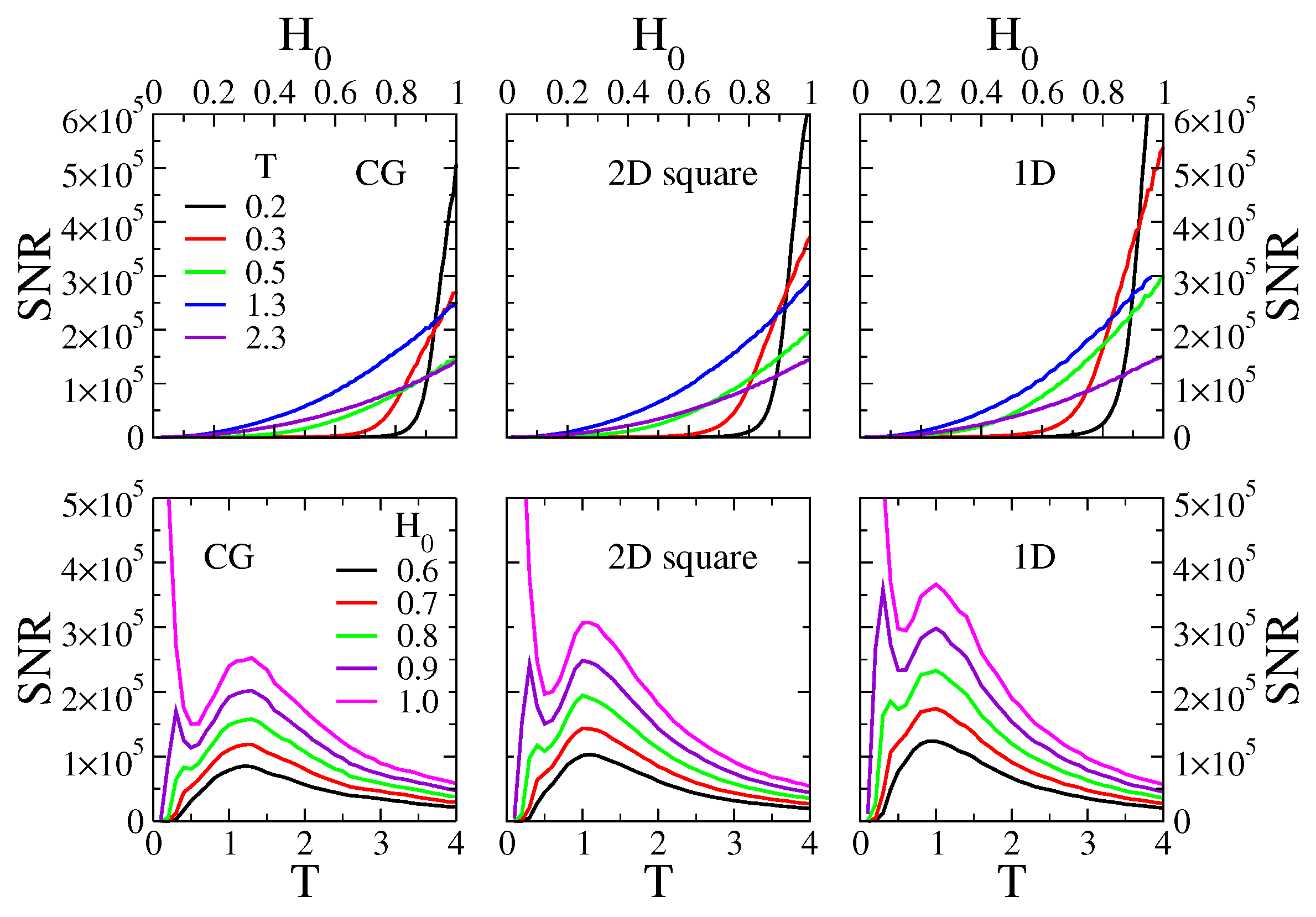
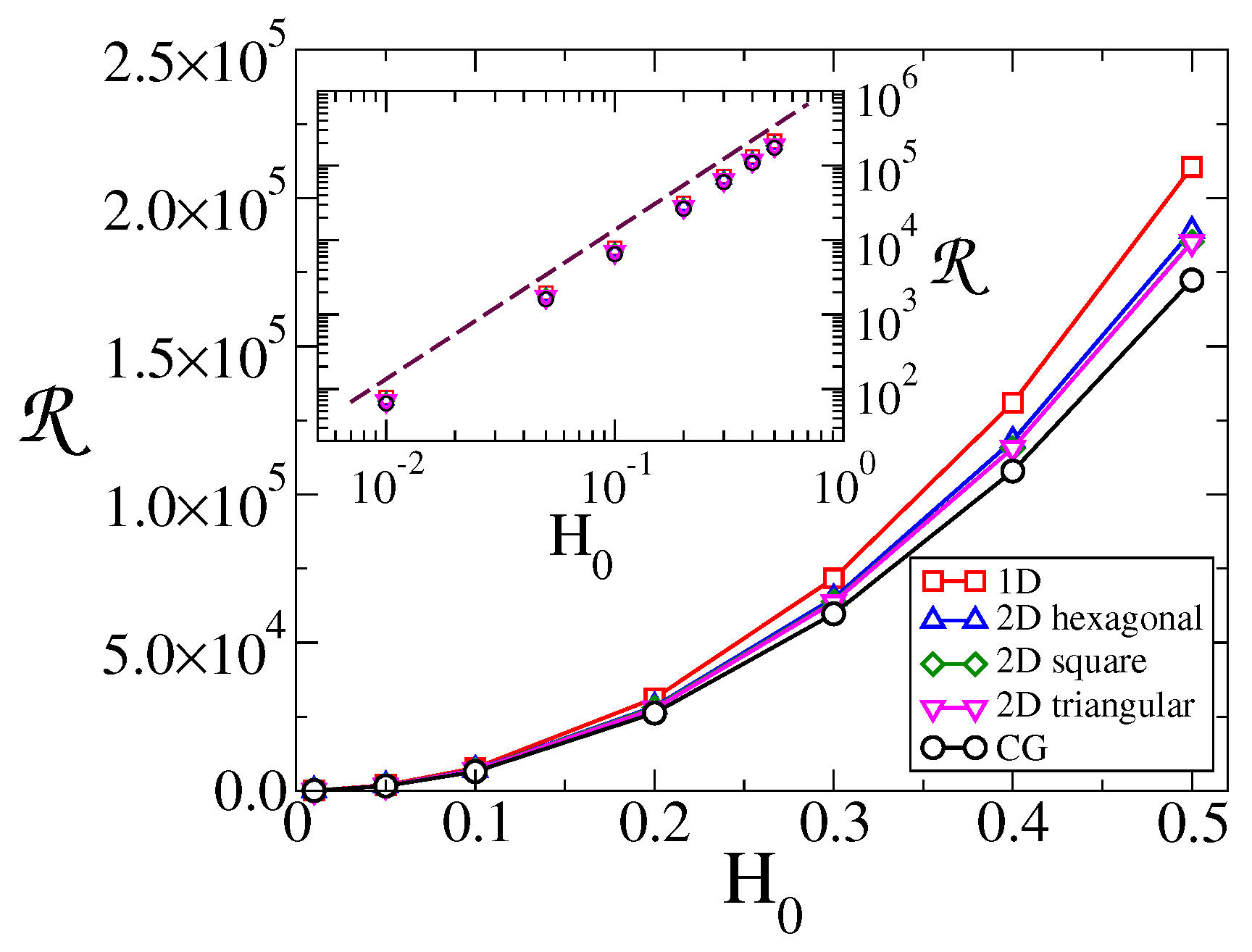
3.3. Signal-to-Noise Ratio
3.4. Amplitude and Lag of Mean Opinion Oscillations
3.5. Mean-Field Approach
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Solution of the Rate Equation for m
References
- Clifford, P.; Sudbury, A. A model for spatial conflict. Biometrika 1973, 60, 581. [Google Scholar] [CrossRef]
- Holley, R.; Ligget, T.M. Ergodic Theorem for Weakly Interacting Infinite Systems and the voter model. Ann. Probab. 1975, 3, 643–663. [Google Scholar] [CrossRef]
- Castellano, C.; Fortunato, S.; Loreto, V. Statistical physics of social dynamics. Rev. Mod. Phys. 2009, 81, 591. [Google Scholar] [CrossRef]
- Redner, S. Reality-inspired voter models: A mini-review. Comptes Rendus Phys. 2019, 20, 275–292. [Google Scholar] [CrossRef]
- Jedrzejewski, A.; Sznajd-Weron, K. Statistical physics of opinion formation: Is it a SPOOF? Comptes Rendus Phys. 2019, 20, 244–261. [Google Scholar] [CrossRef]
- Vazquez, F.; Kaprivsky, P.L.; Redner, S. Constrained Opinion Dynamics: Freezing and Slow Evolution. J. Phys. A 2003, 36, L61. [Google Scholar] [CrossRef]
- Vazquez, F.; Redner, S. Ultimate Fate of Constrained Voters. J. Phys. A 2004, 37, 8479. [Google Scholar] [CrossRef]
- Gimenez, M.C.; García, A.P.P.; Paci, M.A.B.; Reinaudi, L. Range of interaction in an opinion evolution model of ideological self-positioning: Contagion, hesitance and polarization. Physica A 2016, 447, 320–330. [Google Scholar] [CrossRef]
- Masuda, N.; Gibert, N.; Redner, S. Heterogeneous voter models. Phys. Rev. E 2010, 82, 010103. [Google Scholar] [CrossRef]
- Mobilia, M.; Petersen, A.; Redner, S. On the role of zealotry in the voter model. J. Stat. Mech. Theory Exp. 2007, 2007, P08029. [Google Scholar] [CrossRef]
- Suchecki, K.; Eguíluz, V.M.; Miguel, M.S. Conservation laws for the voter model in complex networks. EPL 2005, 69, 228. [Google Scholar] [CrossRef]
- Sood, V.; Redner, S. Voter Model on Heterogeneous Graphs. Phys. Rev. Lett. 2005, 94, 178701. [Google Scholar] [CrossRef] [PubMed]
- Vazquez, F.; Eguíluz, V.M. Analytical solution of the voter model on uncorrelated networks. New J. Phys. 2008, 10, 063011. [Google Scholar] [CrossRef]
- Vazquez, F.; Eguíluz, V.M.; Miguel, M.S. Generic Absorbing Transition in Coevolution Dynamics. Phys. Rev. Lett. 2008, 100, 108702. [Google Scholar] [CrossRef] [PubMed]
- Demirel, G.; Vazquez, F.; Böhme, G.A.; Gross, T. Moment-closure approximations for discrete adaptive networks. Physica D 2014, 267, 68–80. [Google Scholar] [CrossRef]
- Vazquez, F. Opinion dynamics on coevolving networks. In Dynamics on and of Complex Networks, Volume 2; Modeling and Simulation in Science, Engineering and Technology; Springer: New York, NY, USA, 2013; pp. 89–107. [Google Scholar]
- Galam, S. Contrarian deterministic effects on opinion dynamics: The hung elections scenario. Physica A 2004, 333, 453–460. [Google Scholar] [CrossRef]
- Stauffer, D.; Sa Martins, J.S. Simulation of Galam’s contrarian opinions on percolative lattices. Physica A 2004, 334, 558. [Google Scholar] [CrossRef]
- Schneider, J.J. The influence of contrarians and opportunists on the stability of a democracy in the Sznajd model. Int. J. Mod. Phys. C 2004, 15, 659. [Google Scholar] [CrossRef]
- De la Lama, M.S.; López, J.M.; Wio, H.S. Spontaneous emergence of contrarian-like behaviour in an opinion spreading model. Europhys. Lett. 2005, 72, 851. [Google Scholar] [CrossRef]
- Wio, H.S.; de la Lama, M.S.; López, J.M. Contrarian-like behaviour and system size stochastic resonance in an opinion spreading model. Physica A 2006, 371, 108–111. [Google Scholar] [CrossRef]
- Sznajd-Weron, K.; Tabiszewski, M.; Timpanaro, A.M. Phase transition in the sznajd model with independence. Europhys. Lett. 2011, 96, 48002. [Google Scholar] [CrossRef]
- Nyczka, P.; Sznajd-Weron, K.; Cislo, J. Phase transitions in the q-voter model with two types of stochastic driving. Phys. Rev. E 2012, 86, 011105. [Google Scholar] [CrossRef]
- Cecilia Gimenez, M.; Revelli, J.A.; Wio, H.S. Non Local Effects in the Sznajd Model: Stochastic resonance aspects. ICST Trans. Complex Syst. 2012, 12, e3. [Google Scholar] [CrossRef][Green Version]
- Gimenez, M.C.; Revelli, J.A.; de la Lama, M.S.; Lopez, J.M.; Wio, H.S. Interplay between social debate and propaganda in an opinion formation model. Physica A 2013, 392, 278–286. [Google Scholar] [CrossRef]
- Masuda, N. Voter models with contrarian agents. Phys. Rev. E 2013, 88, 052803. [Google Scholar] [CrossRef] [PubMed]
- Banisch, S. From microscopic heterogeneity to macroscopic complexity in the contrarian voter model. Adv. Complex Syst. 2014, 17, 1450025. [Google Scholar] [CrossRef]
- Banisch, S. Markov Chain Aggregation for Agent-Based Models; Understanding Complex Systems; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar] [CrossRef]
- Khalil, N.; Toral, R. The noisy voter model under the influence of contrarians. Physica A 2019, 515, 81–92. [Google Scholar] [CrossRef]
- Martins, A.C.R.; Kuba, C.D. The importance of disagreeing: Contrarians and extremism in the coda model. Adv. Complex Syst. 2010, 13, 621–634. [Google Scholar] [CrossRef]
- Li, Q.; Braunstein, L.A.; Havlin, S.; Stanley, H.E. Strategy of competition between two groups based on an inflexible contrarian opinion model. Phys. Rev. E 2011, 84, 066101. [Google Scholar] [CrossRef]
- Tanabe, S.; Masuda, N. Complex dynamics of a nonlinear voter model with contrarian agents. Chaos 2013, 23, 043136. [Google Scholar] [CrossRef]
- Yi, S.D.; Baek, S.K.; Zhu, C.; Kim, B.J. Phase transition in a coevolving network of conformist and contrarian voters. Phys. Rev. E 2013, 87, 012806. [Google Scholar] [CrossRef] [PubMed]
- Crokidakis, N.; Blanco, V.H.; Anteneodo, C. Impact of contrarians and intransigents in a kinetic model of opinion dynamics. Phys. Rev. E 2014, 89, 013310. [Google Scholar] [CrossRef] [PubMed]
- Guo, L.; Cheng, Y.; Luo, Z. Opinion dynamics with the contrarian deterministic effect and human mobility on lattice. Complexity 2014, 20, 5. [Google Scholar] [CrossRef]
- Gambaro, J.P.; Crokidakis, N. The influence of contrarians in the dynamics of opinion formation. Physica A 2017, 486, 465–472. [Google Scholar] [CrossRef]
- Crokidakis, N. Effects of mass media on opinion spreading in the Sznajd sociophysics model. Physica A 2012, 391, 1729–1734. [Google Scholar] [CrossRef]
- Pineda, M.; Buendía, G.M. Mass media and heterogeneous bounds of confidence in continuous opinion dynamics. Physica A 2015, 420, 73–84. [Google Scholar] [CrossRef]
- Pinto, S.; Albanese, F.; Dorso, C.O.; Balenzuela, P. Quantifying time-dependent Media Agenda and public opinion by topic modeling. Physica A 2019, 524, 614–624. [Google Scholar] [CrossRef]
- Albanese, F.; Pinto, S.; Semeshenko, V.; Balenzuela, P. Analyzing mass media influence using natural language processing and time series analysis. J. Phys. Complex. 2020, 1, 025005. [Google Scholar] [CrossRef]
- Gimenez, M.C.; Reinaudi, L.; Paz-García, A.P.; Centres, P.M.; Ramirez-Pastor, A.J. Opinion evolution in the presence of constant propaganda: Homogeneous and localized cases. Eur. Phys. J. B 2021, 94, 35. [Google Scholar] [CrossRef]
- Kuperman, M.; Zanette, D. Stochastic resonance in a model of opinion formation on small-world networks. Eur. Phys. J. B 2002, 26, 387–391. [Google Scholar] [CrossRef]
- Tessone, C.J.; Toral, R. System size stochastic resonance in a model for opinion formation. Physica A 2005, 351, 106–116. [Google Scholar] [CrossRef]
- Tessone, C.J.; Mirasso, C.R.; Toral, R.; Gunton, J.D. Diversity-induced resonance. Phys. Rev. Lett. 2006, 97, 194101. [Google Scholar] [CrossRef] [PubMed]
- Tessone, C.J.; Toral, R. Diversity-induced resonance in a model for opinion formation. Eur. Phys. J. B 2009, 71, 549–555. [Google Scholar] [CrossRef]
- Martins, T.V.; Toral, R.; Santos, M.A. Divide and conquer: Resonance induced by competitive interactions. Eur. Phy. J. B 2009, 67, 329–336. [Google Scholar] [CrossRef]
- Gammaitoni, L.; Hänggi, P.; Jung, P.; Marchesoni, F. Stochastic resonance. Rev. Mod. Phys. 1998, 70, 223–287. [Google Scholar] [CrossRef]
- Gammaitoni, L.; Hänggi, P.; Jung, P.; Marchesoni, F. Stochastic resonance: A remarkable idea that changed our perception of noise. Eur. Phys. J. B 2009, 69, 1–3. [Google Scholar] [CrossRef]
- Vazquez, F.; López, C. Systems with two symmetric absorbing states: Relating the microscopic dynamics with the macroscopic behavior. Phys. Rev. E 2008, 78, 061127. [Google Scholar] [CrossRef]
- Kirman, A. Ants, Rationality, and Recruitment. Q. J. Econ. 1993, 108, 137. [Google Scholar] [CrossRef]
- Carro, A.; Toral, R.; San Miguel, M. The noisy voter model on complex networks. Sci. Rep. 2016, 6, 24775. [Google Scholar] [CrossRef]
- Vazquez, F.; Loscar, E.S.; Baglietto, G. Multistate voter model with imperfect copying. Phys. Rev. E 2019, 100, 042301. [Google Scholar] [CrossRef]
- Herrerías-Azcué, F.; Galla, T. Consensus and diversity in multistate noisy voter models. Phys. Rev. E 2019, 100, 022304. [Google Scholar] [CrossRef] [PubMed]
- Loscar, E.S.; Baglietto, G.; Vazquez, F. Noisy multistate voter model for flocking in finite dimensions. Phys. Rev. E 2021, 104, 034111. [Google Scholar] [CrossRef] [PubMed]
- Nowak, B.; Stón, B.; Sznajd-Weron, K. Discontinuous phase transitions in the multi-state noisy q-voter model: Quenched vs. annealed disorder. Sci. Rep. 2021, 11, 6098. [Google Scholar] [CrossRef]
- Redner, S. A Guide to First Passage Processes; Cambridge University Press: New York, NY, USA, 2001. [Google Scholar]
- Torrico Terán, M.A.; Solís Delgadillo, D. Voto ideológico, por qué los latinoamericanos votan por la izquierda o la derecha? Foro Int. 2020, 60, 175–226. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gimenez, M.C.; Reinaudi, L.; Vazquez, F. Contrarian Voter Model under the Influence of an Oscillating Propaganda: Consensus, Bimodal Behavior and Stochastic Resonance. Entropy 2022, 24, 1140. https://doi.org/10.3390/e24081140
Gimenez MC, Reinaudi L, Vazquez F. Contrarian Voter Model under the Influence of an Oscillating Propaganda: Consensus, Bimodal Behavior and Stochastic Resonance. Entropy. 2022; 24(8):1140. https://doi.org/10.3390/e24081140
Chicago/Turabian StyleGimenez, Maria Cecilia, Luis Reinaudi, and Federico Vazquez. 2022. "Contrarian Voter Model under the Influence of an Oscillating Propaganda: Consensus, Bimodal Behavior and Stochastic Resonance" Entropy 24, no. 8: 1140. https://doi.org/10.3390/e24081140
APA StyleGimenez, M. C., Reinaudi, L., & Vazquez, F. (2022). Contrarian Voter Model under the Influence of an Oscillating Propaganda: Consensus, Bimodal Behavior and Stochastic Resonance. Entropy, 24(8), 1140. https://doi.org/10.3390/e24081140






