Quantum Teleportation and Dense Coding in Multiple Bosonic Reservoirs
Abstract
1. Introduction
2. Preliminaries
3. Solution of the Model
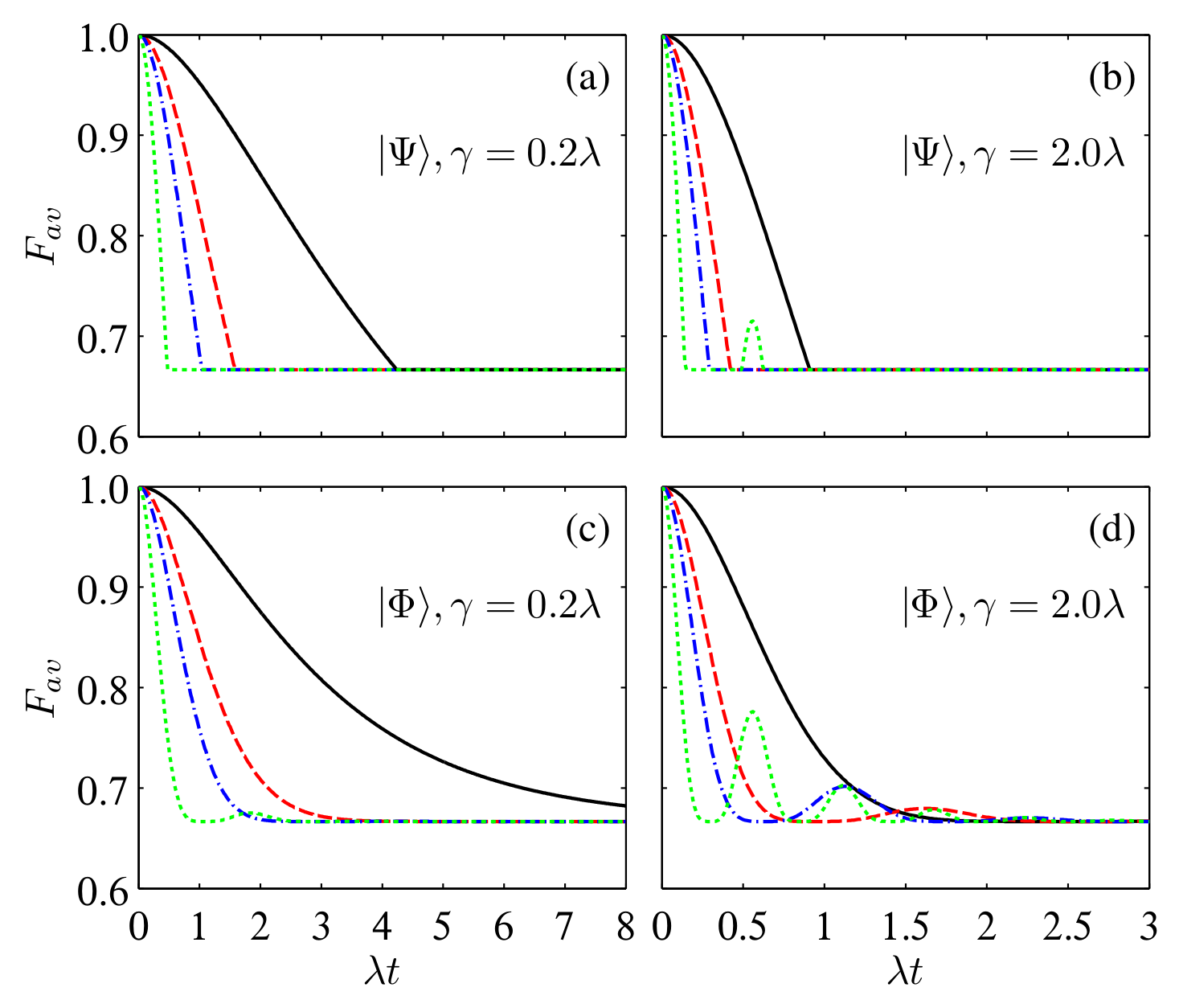
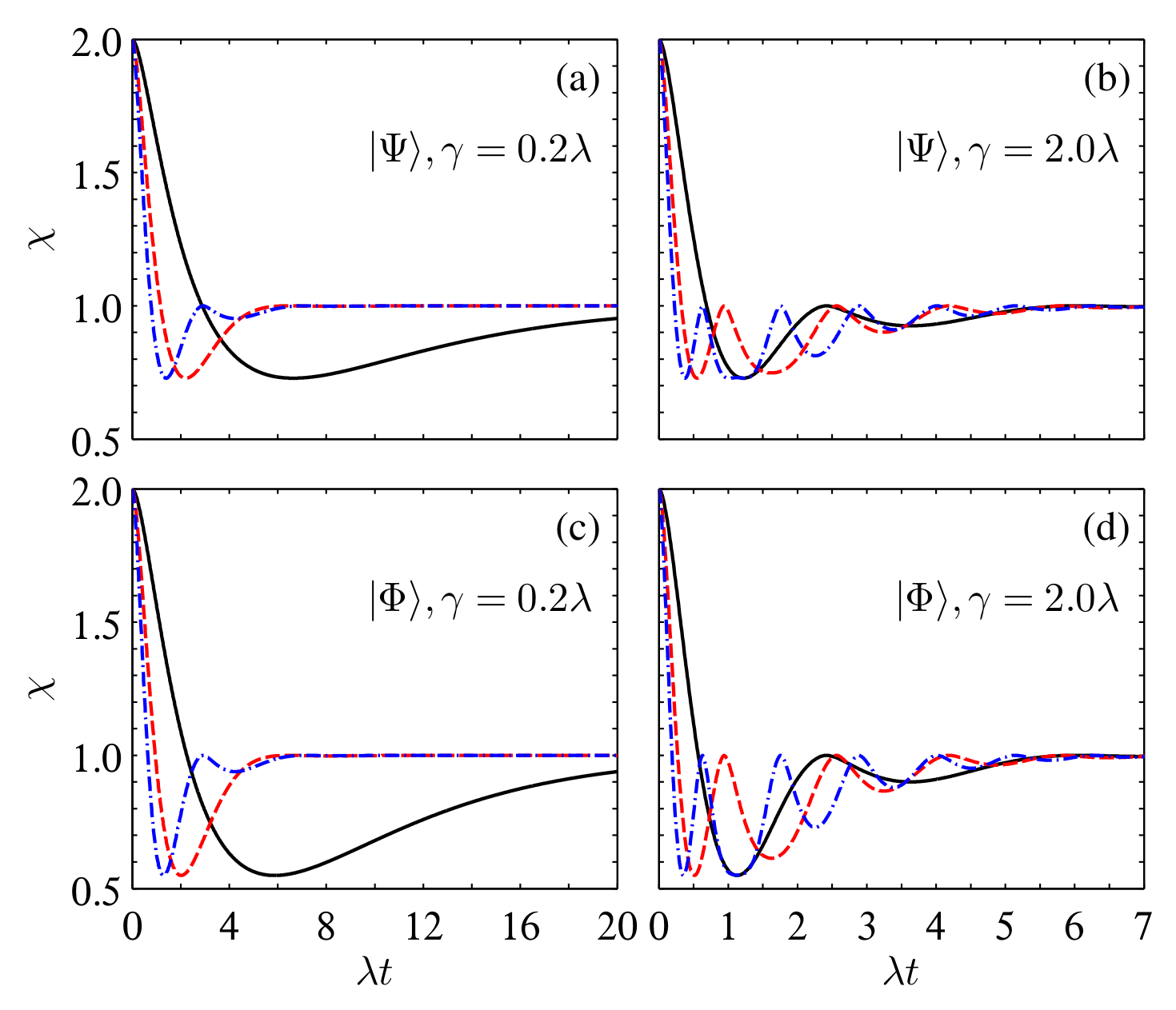
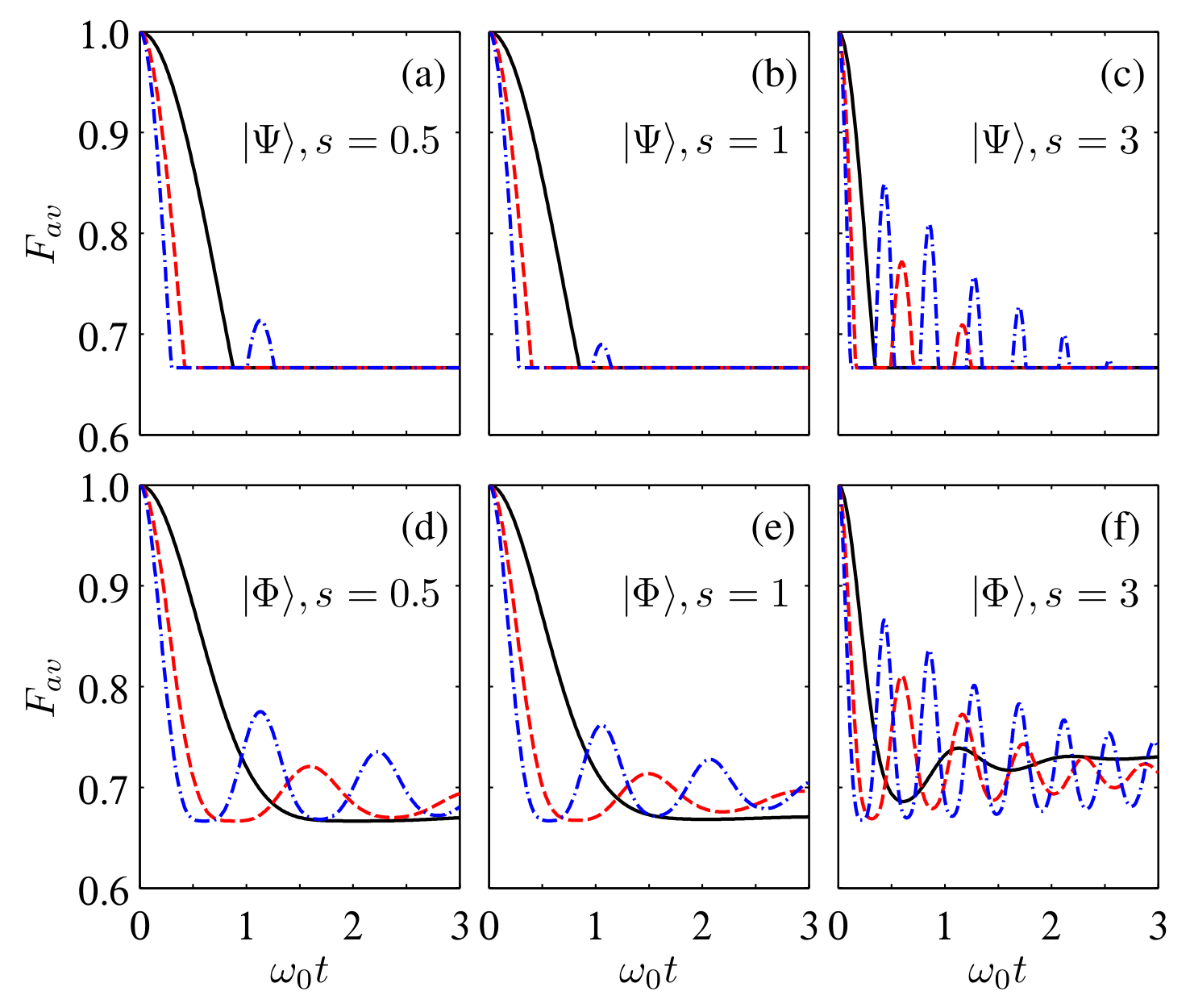
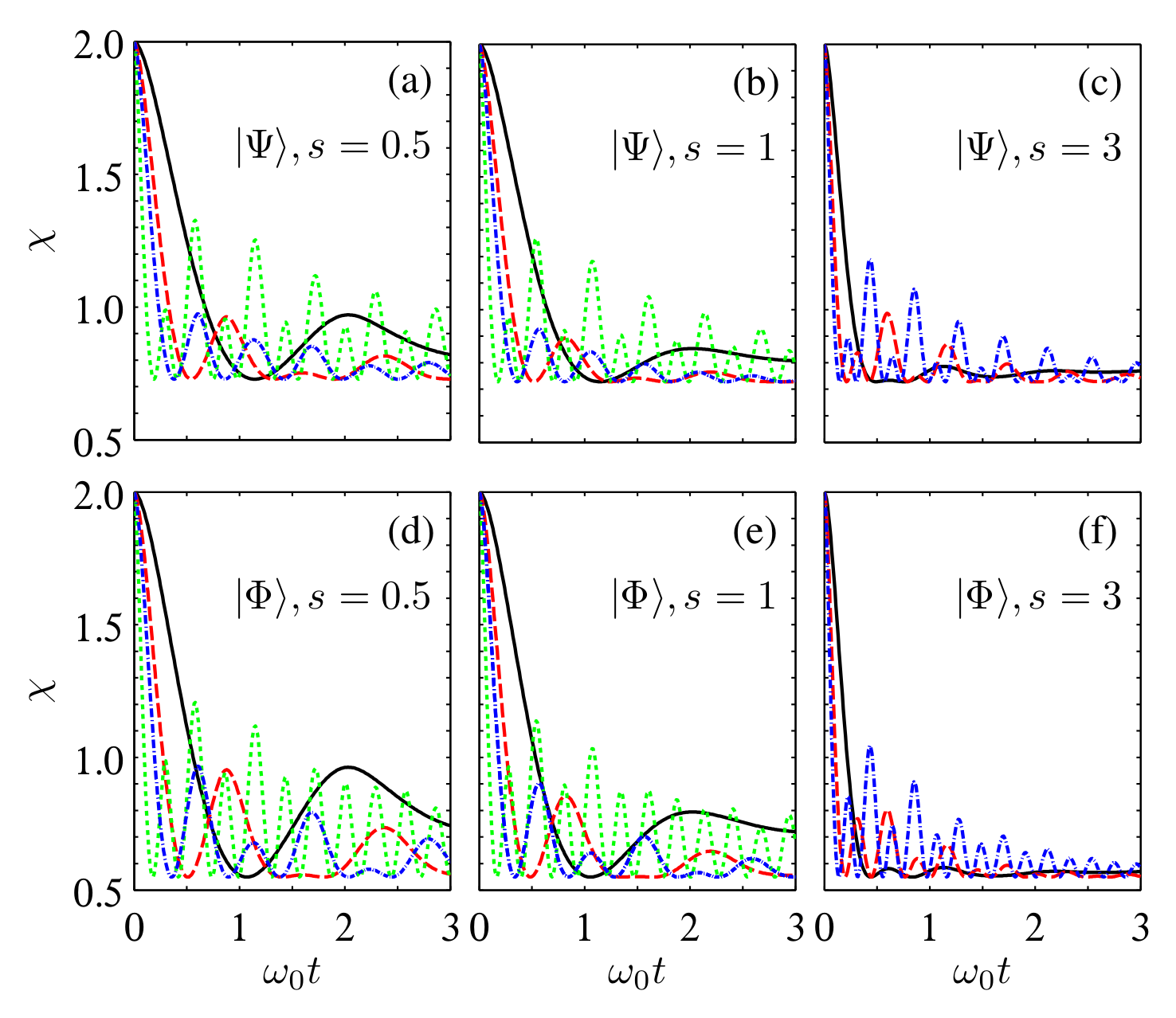
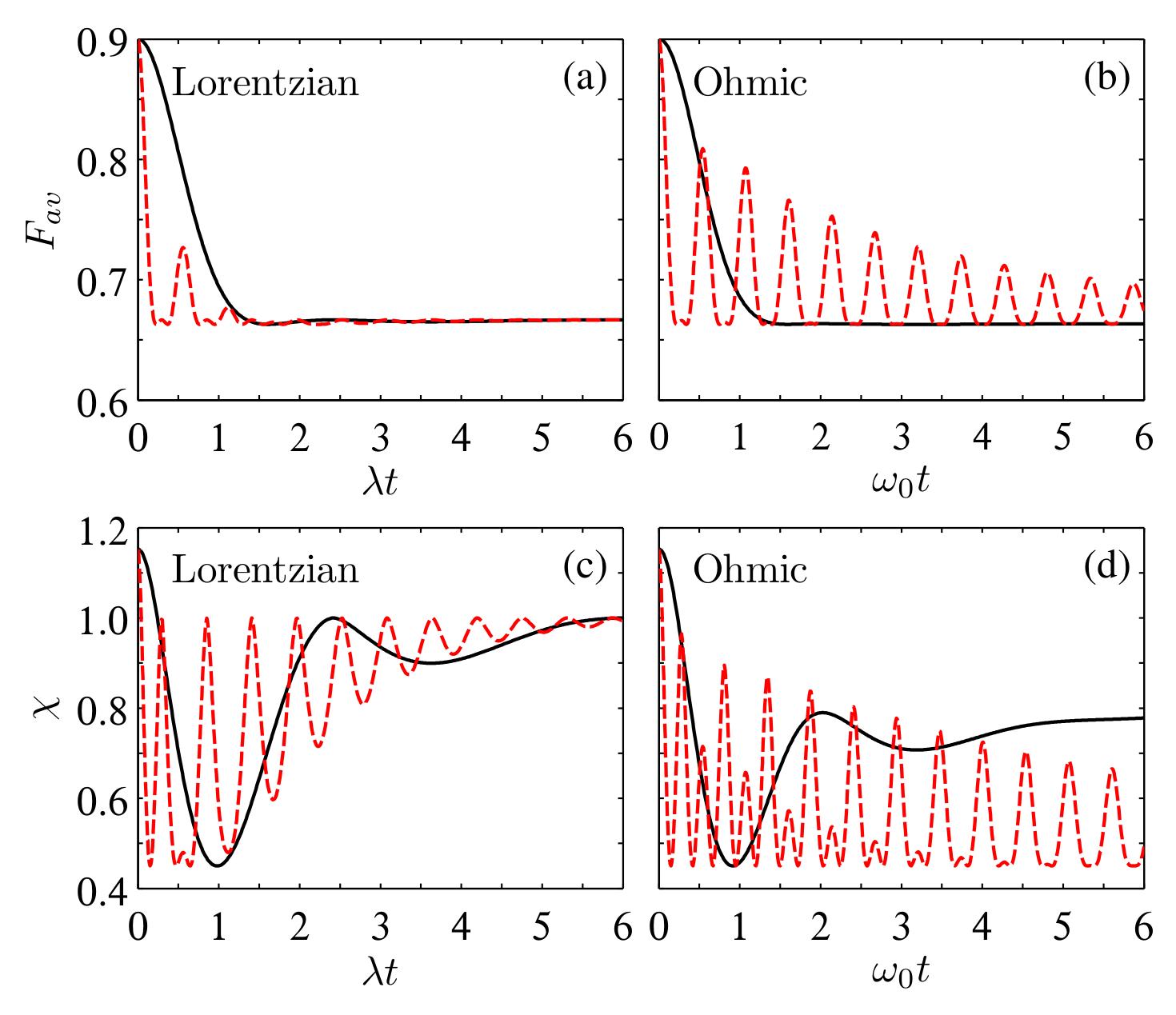
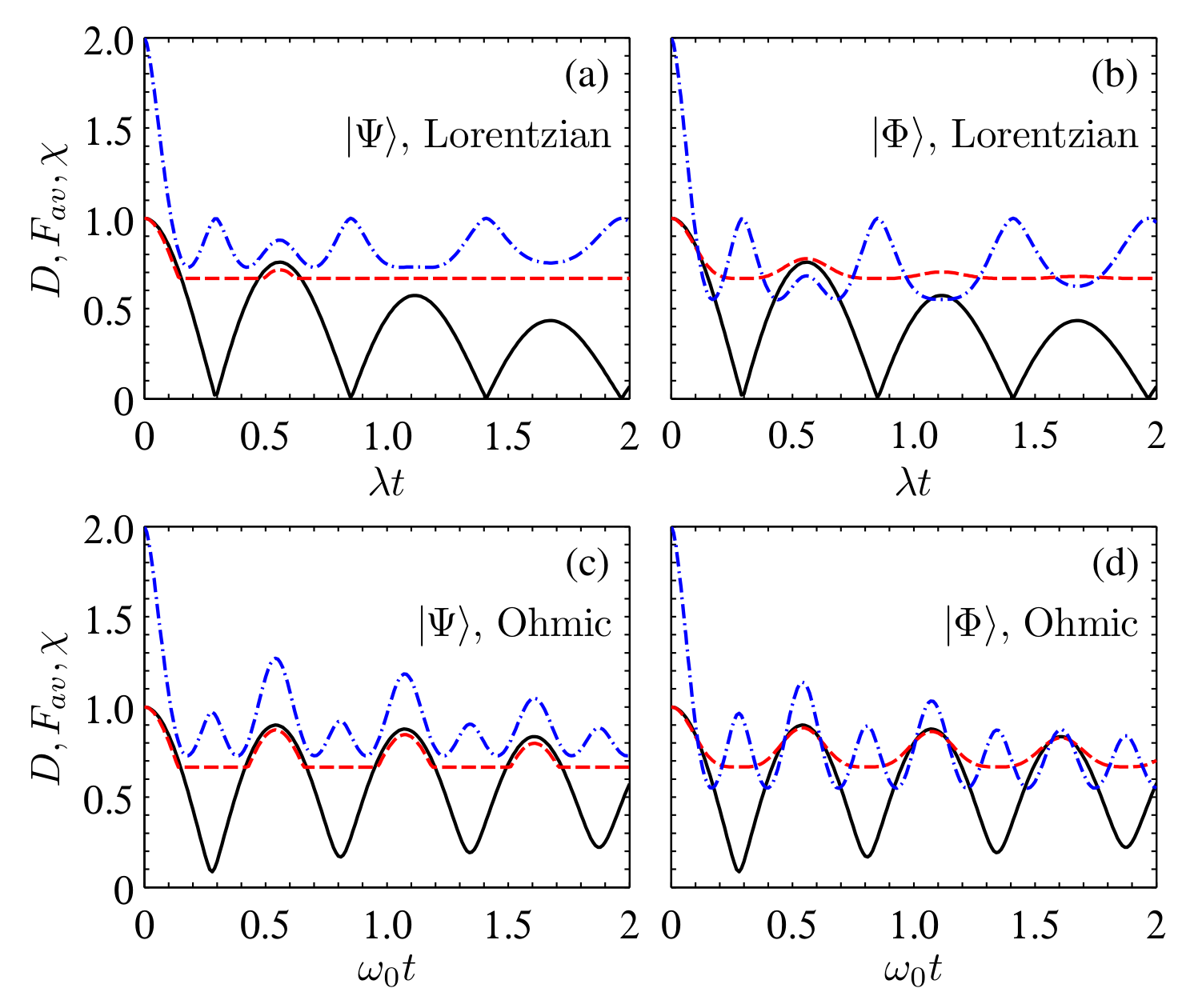
4. Behaviors of Average Fidelity and Dense Coding Capacity
4.1. Lorentzian Spectrum
4.2. Sub-Ohmic, Ohmic, and Super-Ohmic Spectra
5. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Bennett, C.H.; Brassard, G.; Crépeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 1993, 70, 1895. [Google Scholar] [CrossRef] [PubMed]
- Horodecki, R.; Horodecki, M.; Horodecki, P. Teleportation, Bell’s inequalities and inseparability. Phys. Lett. A 1996, 222, 21. [Google Scholar] [CrossRef]
- Popescu, S. Bell’s inequalities versus teleportation: What is nonlocality. Phys. Rev. Lett. 1994, 72, 797. [Google Scholar] [CrossRef] [PubMed]
- Bennett, C.H.; Wiesner, S.J. Communication via one- and two-particle operators on Einstein-Podolsky-Rosen states. Phys. Rev. Lett. 1992, 69, 2881. [Google Scholar] [CrossRef]
- Bareno, A.; Ekert, A. Dense coding based on quantum entanglement. J. Mod. Opt. 1995, 42, 1253. [Google Scholar] [CrossRef]
- Mattle, K.; Weinfurter, H.; Kwiat, P.G.; Zeilinger, A. Dense coding in experimental quantum communication. Phys. Rev. Lett. 1996, 76, 4656. [Google Scholar] [CrossRef]
- Hiroshima, T. Optimal dense coding with mixed state entanglement. J. Phys. A Math. Gen. 2001, 34, 6907. [Google Scholar] [CrossRef]
- Bowen, G.; Bose, S. Teleportation as a depolarizing quantum channel, relative entropy, and classical capacity. Phys. Rev. Lett. 2001, 87, 267901. [Google Scholar] [CrossRef]
- Albeverio, S.; Fei, S.M.; Yang, W.L. Optimal teleportation based on bell measurements. Phys. Rev. A 2002, 66, 012301. [Google Scholar] [CrossRef]
- Hu, M.L. Relations between entanglement, Bell-inequality violation and teleportation fidelity for the two-qubit X states. Quantum Inf. Process. 2013, 12, 229. [Google Scholar] [CrossRef]
- Horodecki, M.; Piani, M. On quantum advantage in dense coding. J. Phys. A Math. Theor. 2012, 45, 105306. [Google Scholar] [CrossRef]
- Hu, M.L.; Hu, X.; Wang, J.C.; Peng, Y.; Zhang, Y.R.; Fan, H. Quantum coherence and geometric quantum discord. Phys. Rep. 2018, 762–764, 1–100. [Google Scholar] [CrossRef]
- Lee, J.; Kim, M.S. Entanglement teleportation via Werner states. Phys. Rev. Lett. 2000, 84, 4236. [Google Scholar] [CrossRef] [PubMed]
- Oh, S.; Lee, S.; Lee, H.W. Fidelity of quantum teleportation through noisy channels. Phys. Rev. A 2002, 66, 022316. [Google Scholar] [CrossRef]
- Jung, E.; Hwang, M.R.; Ju, Y.H.; Kim, M.S.; Yoo, S.K.; Kim, H.; Park, D.; Son, J.W.; Tamaryan, S.; Cha, S.K. Greenberger-Horne-Zeilinger versus W states: Quantum teleportation through noisy channels. Phys. Rev. A 2008, 78, 012312. [Google Scholar] [CrossRef]
- Bhaktavatsala Rao, D.D.; Panigrahi, P.K.; Mitra, C. Teleportation in the presence of common bath decoherence at the transmitting station. Phys. Rev. A 2008, 78, 022336. [Google Scholar]
- Yeo, Y.; Kho, Z.W.; Wang, L. Effects of Pauli channels and noisy quantum operations on standard teleportation. Europhys. Lett. 2009, 86, 40009. [Google Scholar] [CrossRef]
- Shadman, Z.; Kampermann, H.; Macchiavello, C.; Bruß, D. Optimal super dense coding over noisy quantum channels. New J. Phys. 2010, 12, 073042. [Google Scholar] [CrossRef]
- Quek, S.; Li, Z. Effects of quantum noises and noisy quantum operations on entanglement and special dense coding. Phys. Rev. A 2010, 81, 024302. [Google Scholar] [CrossRef]
- Li, J.K.; Xu, K.; Zhang, G.F. Dense coding capacity in correlated noisy channels with weak measurement. Chin. Phys. B 2021, 30, 110302. [Google Scholar] [CrossRef]
- Haddadi, S.; Hu, M.L.; Knedif, Y.; Dolatkhah, H.; Pourkarimi, M.R.; Daoud, M. Measurement uncertainty and dense coding in a two-qubit system: Combined effects of bosonic reservoir and dipole-dipole interaction. Results Phys. 2022, 32, 105041. [Google Scholar] [CrossRef]
- Sun, Y.H.; Xie, Y.X. Memory effect of a dephasing channel on measurement uncertainty, dense coding, teleportation, and quantum Fisher information. Results Phys. 2022, 37, 105526. [Google Scholar] [CrossRef]
- Yeo, Y. Teleportation with a mixed state of four qubits and the generalized singlet fraction. Phys. Rev. A 2006, 74, 052305. [Google Scholar] [CrossRef]
- Yeo, Y. Local noise can enhance two-qubit teleportation. Phys. Rev. A 2008, 78, 022334. [Google Scholar] [CrossRef]
- Laine, E.M.; Breuer, H.P.; Piilo, J. Nonlocal memory effects allow perfect teleportation with mixed states. Sci. Rep. 2014, 4, 4620. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.N.; Tian, Q.L.; Zeng, K.; Chen, P.X. Fidelity of quantum teleportation in correlated quantum channels. Quantum Inf. Process. 2020, 19, 182. [Google Scholar] [CrossRef]
- Hu, M.L.; Zhang, Y.H.; Fan, H. Nonlocal advantage of quantum coherence in a dephasing channel with memory. Chin. Phys. B 2021, 30, 030308. [Google Scholar] [CrossRef]
- Li, Y.L.; Zu, C.J.; Wei, D.M. Enhance quantum teleportation under correlated amplitude damping decoherence by weak measurement and quantum measurement reversal. Quantum Inf. Process. 2019, 18, 2. [Google Scholar] [CrossRef]
- Tian, M.B.; Zhang, G.F. Improving the capacity of quantum dense coding by weak measurement and reversal measurement. Quantum Inf. Process. 2018, 17, 19. [Google Scholar] [CrossRef]
- Bellomo, B.; Franco, R.L.; Compagno, G. Non-Markovian effects on the dynamics of entanglement. Phys. Rev. Lett. 2007, 99, 160502. [Google Scholar] [CrossRef]
- Bellomo, B.; Franco, R.L.; Maniscalco, S.; Compagno, G. Entanglement trapping in structured environments. Phys. Rev. A 2008, 78, 060302. [Google Scholar] [CrossRef]
- Maniscalco, S.; Francica, F.; Zaffino, R.L.; Gullo, N.L.; Plastina, F. Protecting entanglement via the quantum Zeno effect. Phys. Rev. Lett. 2008, 100, 090503. [Google Scholar] [CrossRef] [PubMed]
- Bellomo, B.; Franco, R.L.; Compagno, G. Dynamics of non-classically-reproducible entanglement. Phys. Rev. A 2008, 78, 062309. [Google Scholar] [CrossRef]
- Mazzola, L.; Maniscalco, S.; Piilo, J.; Suominen, K.A.; Garraway, B.M. Sudden death and sudden birth of entanglement in common structured reservoirs. Phys. Rev. A 2009, 79, 042302. [Google Scholar] [CrossRef]
- Mazzola, L.; Maniscalco, S.; Piilo, J.; Suominen, K.A. Interplay between entanglement and entropy in two-qubit systems. J. Phys. B At. Mol. Opt. Phys. 2010, 43, 085505. [Google Scholar] [CrossRef]
- Wang, B.; Xu, Z.Y.; Chen, Z.Q.; Feng, M. Non-Markovian effect on the quantum discord. Phys. Rev. A 2010, 81, 014101. [Google Scholar] [CrossRef]
- Fanchini, F.F.; Werlang, T.; Brasil, C.A.; Arruda, L.G.E.; Caldeira, A.O. Non-Markovian dynamics of quantum discord. Phys. Rev. A 2010, 81, 052107. [Google Scholar] [CrossRef]
- Hu, M.L.; Fan, H. Dynamics of entropic measurement-induced nonlocality in structured reservoirs. Ann. Phys. (N. Y.) 2012, 327, 2343. [Google Scholar] [CrossRef][Green Version]
- Hu, M.L.; Lian, H.L. Geometric quantum discord and non-Markovianity of structured reservoirs. Ann. Phys. (N. Y.) 2015, 362, 795. [Google Scholar] [CrossRef]
- Man, Z.X.; An, N.B.; Xia, Y.J. Non-Markovianity of a two-level system transversally coupled to multiple bosonic reservoirs. Phys. Rev. A 2014, 90, 062104. [Google Scholar] [CrossRef]
- Horodecki, M.; Horodecki, P.; Horodecki, R. General teleportation channel, singlet fraction, and quasidistillation. Phys. Rev. A 1999, 60, 1888. [Google Scholar] [CrossRef]
- Schumacher, B.; Westmoreland, M.D. Sending classical information via noisy quantum channels. Phys. Rev. A 1997, 56, 131. [Google Scholar] [CrossRef]
- Holevo, A.S. The capacity of the quantum channel with general signal states. IEEE Trans. Inf. Theory 1998, 44, 269. [Google Scholar] [CrossRef]
- Kuhr, S.; Gleyzes, S.; Guerlin, C.; Bernu, J.; Hoff, U.B.; Deléglise, S.; Osnaghi, S.; Brune, M.; Raimondb, J.M. Ultrahigh finesse Fabry-Pérot superconducting resonator. Appl. Phys. Lett. 2007, 90, 164101. [Google Scholar] [CrossRef]
- Xu, X.X.; Hu, M.L. Maximal steered coherence and its conversion to entanglement in multiple bosonic reservoirs. Ann. Phys. (Berl.) 2022, 534, 2100412. [Google Scholar] [CrossRef]
- Breuer, H.P.; Petruccione, F. The Theory of Open Quantum Systems; Oxford University Press: Oxford, NY, USA, 2002. [Google Scholar]
- Leggett, A.J.; Chakravarty, S.; Dorsey, A.T.; Fisher, M.P.A.; Garg, A.; Zwerger, W. Dynamics of the dissipative two-state system. Rev. Mod. Phys. 1987, 59, 1. [Google Scholar] [CrossRef]
- Tong, Q.J.; An, J.H.; Luo, H.G.; Oh, C.H. Decoherence suppression of a dissipative qubit by the non-Markovian effect. J. Phys. B At. Mol. Opt. Phys. 2010, 43, 155501. [Google Scholar] [CrossRef]
- Hu, M.L.; Fan, H. Quantum-memory-assisted entropic uncertainty principle, teleportation, and entanglement witness in structured reservoirs. Phys. Rev. A 2012, 86, 032338. [Google Scholar] [CrossRef]
- Breuer, H.P.; Laine, E.-M.; Piilo, J. Measure for the degree of non-Markovian behavior of quantum processes in open systems. Phys. Rev. Lett. 2009, 103, 210401. [Google Scholar] [CrossRef]
- Myatt, C.J.; King, B.E.; Turchette, Q.A.; Sackett, C.A.; Kielpinski, D.; Itano, W.M.; Monroe, C.; Wineland, D.J. Decoherence of quantum superpositions through coupling to engineered reservoirs. Nature 2000, 403, 269273. [Google Scholar] [CrossRef]
- Kienzler, D.; Lo, H.Y.; Keitch, B.; De Clercq, L.; Leupold, F.; Lindenfelser, F.; Marinelli, M.; Negnevitsky, V.; Home, J.P. Quantum harmonic oscillator state synthesis by reservoir engineering. Science 2015, 347, 53. [Google Scholar] [CrossRef] [PubMed]
- Yanay, Y.; Clerk, A.A. Reservoir engineering with localized dissipation: Dynamics and prethermalization. Phys. Rev. Res. 2020, 2, 023177. [Google Scholar] [CrossRef]
- Bai, S.Y.; An, J.H. Generating stable spin squeezing by squeezed-reservoir engineering. Phys. Rev. Lett. 2021, 127, 083602. [Google Scholar] [CrossRef] [PubMed]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Hu, M.-L. Quantum Teleportation and Dense Coding in Multiple Bosonic Reservoirs. Entropy 2022, 24, 1114. https://doi.org/10.3390/e24081114
Wang Y, Hu M-L. Quantum Teleportation and Dense Coding in Multiple Bosonic Reservoirs. Entropy. 2022; 24(8):1114. https://doi.org/10.3390/e24081114
Chicago/Turabian StyleWang, Yu, and Ming-Liang Hu. 2022. "Quantum Teleportation and Dense Coding in Multiple Bosonic Reservoirs" Entropy 24, no. 8: 1114. https://doi.org/10.3390/e24081114
APA StyleWang, Y., & Hu, M.-L. (2022). Quantum Teleportation and Dense Coding in Multiple Bosonic Reservoirs. Entropy, 24(8), 1114. https://doi.org/10.3390/e24081114





