Abstract
The fractional generalized cumulative residual entropy (FGCRE) has been introduced recently as a novel uncertainty measure which can be compared with the fractional Shannon entropy. Various properties of the FGCRE have been studied in the literature. In this paper, further results for this measure are obtained. The results include new representations of the FGCRE and a derivation of some bounds for it. We conduct a number of stochastic comparisons using this measure and detect the connections it has with some well-known stochastic orders and other reliability measures. We also show that the FGCRE is the Bayesian risk of a mean residual lifetime (MRL) under a suitable prior distribution function. A normalized version of the FGCRE is considered and its properties and connections with the Lorenz curve ordering are studied. The dynamic version of the measure is considered in the context of the residual lifetime and appropriate aging paths.
1. Introduction
The classical Shannon entropy (see Shannon [1]) associated with a random variable (RV) X has a crucial role in many branches of science to measure the uncertainty contained in Throughout the paper, X denotes a non-negative RV with an absolutely continuous cumulative distribution function (CDF) with corresponding probability density function (PDF) The Shannon differential entropy is
Possible alternative measures of information have been introduced in the literature.
The cumulative residual entropy (CRE) initiated by Rao et al. [2] as a counterpart to (1), obtained by substituting the survival function (SF) in place of the PDF as
where
is the cumulative the hazard rate (HR) function and is the HR function. Dynamic versions of the CRE were considered in Asadi and Zohrevand [3] and also in Navarro et al. [4] where the CRE of the residual lifetime was measured as
For related results, one can see Baratpour [5], Baratpour and Habibi Rad [6] and also Toomaj et al. [7] and the references therein. In a recent work by Di Crescenzo et al. [8], the CRE measure was extended to FGCRE as
where . The notation is used across the paper. Note that The properties of fractional cumulative entropy, such as its alteration under linear transformations, its bounds, its connection to stochastic orders along with its empirical estimation, and various relations to other functions have been argued and discussed by Xiong et al. [9]. We note that, as pointed out by [8], if is a positive integer, say, then is identical to the generalized cumulative residual entropy (GCRE) introduced by Psarrakos and Navarro [10]. It is noticeable that is considered a dispersion measure. The measure is also connected to the relevance transformation and interepoch intervals of a nonhomogeneous Poisson process (see, e.g., Toomaj and Di Crescenzo [11]). This paper aims to continue this line of research. In this context, we present new findings on the FGRCE and its dynamic version. The FGCRE is in particular a suitable quantity to be applied in the proportional HR model.
The subsequent materials of this article are organized in the following order. In Section 2, we first give an overview of the concept of generalized cumulative residual entropy and present a similar representation for fractional generalized residual cumulative entropy. We then give some expressions for the FGCRE, one of which is related to the MRL function. We also consider the connection of the FGCRE with the excess wealth order and the Bayesian risk of the FGCRE. A normalized version of the FGCRE is given and its connection with the Lorenz curve order is studied. Section 3 examines some bounds and stochastic ordering properties of FGCRE. In Section 4, properties of the dynamic FGCRE are discussed.
The reader can be referred to [12] for the definitions of stochastic orders and and for the definitions of (increasing) decreasing MRL (IMRL(DMRL)), (decreasing) increasing failure rate (DFR (IFR)) and new better (worse) than used in expectation (NBUE (NWUE)) classes.
2. Basic Properties
As mentioned earlier, the FGCRE in (4) reduces to the GCRE when In this case,
for all . As pointed out by Psarrakos and Navarro [10], the GCRE fulfills the following property:
where and denotes the epoch times of a Poisson process which is nonhomogeneous having intensity function . Note that and X are equally distributed. Signifying by the SF of one has (see Baxter [13])
and the PDF of is
In the following, we show that the same results can be obtained for the FGCRE. It is worth noting that our results are extensions of the results obtained using the GCRE. To this end, we define the RV with the PDF as
for all where is defined in (3). Denoting by the SF of it can be represented as where
is increasing in t for all If is an integer, say, then (9) reduces to (8). Notice that from (4), the FGCRE can be rewritten as
for all From (9), the ratio
is increasing in t and, therefore, for any In particular, this implies that . That is, for all . Hence, if X is IFR (DFR), then, from (10) and Equation (1.A.7) in [12], we have
for all . In Table 1, we give FGCREs for a number of distributions.

Table 1.
FGCREs for a number of distributions.
Now, we obtain an analogue representation for the FGCRE which is a generalization of relation (6) with FGCRE in place of GCRE.
Proposition 1.
Let X have FGCRE Then, for all
Proof.
Note that is the areas surrounded between and for all . In particular, is the area under . In Figure 1, we depict these areas for the exponential distribution and various values of .
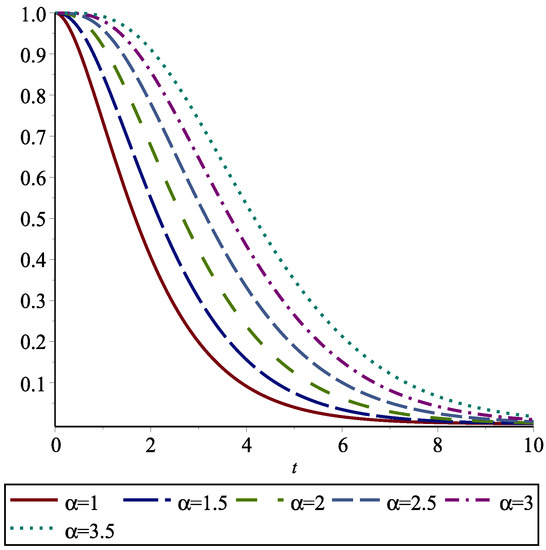
Figure 1.
for an exponential distribution for . The area under is and the areas among them give the amounts of the FGCRE for .
Theorem 1.
(i) If, for some then for all .
(ii) If, for some then for all .
Proof.
(i) It is not difficult to see whether for each and one can obtain
By taking for we obtain
Thus, one concludes
where the third inequality is obtained by virtue of the Markov inequality. The last expression is finite if and this completes the proof. In the case when the results apply to □
Note that does not guarantee equality in the distributions of X and Y, but the converse holds. If where is strictly increasing and differentiable, then
for all Below, the connection between the FGCRE and the cumulative HR function of X given by (3) is realized.
Theorem 2.
Let X fulfill for all . Then,
where
Proof.
We note that in (16) is increasing and convex in This immediately generates the following property.
Theorem 3.
Let X have a finite mean μ. Then,
for all
Another useful application of Theorem 2 is given here.
Theorem 4.
If X and Y are non-negative RVs in the way , it holds that
where the function is given in (16). In particular, implies
Proof.
Since is a convex function and also since it is an increasing function for all , thus (see Theorem 4.A.8 in [12]), . Now, using relation 4.A.2 in [12], we derive . □
Clearly, is increasing and also convex and Hence, for the RVs X and Y satisfying we obtain that
for all This relation is immediately obtained from Theorem 2 and Shaked and Shantikumar [12] (see page 24). It is worth pointing out that Equation (17) leads us to define the normalized FGCRE by
Under the condition Equation (17) can be rewritten as for Moreover, if X is a non-negative RV having IFR (DFR) property, from relation (11), one can conclude that
From this, we derive that For , the normalized cumulative residual entropy is generated (see Rao [2]). This is an analogue for the coefficient of variation of an RV. In Table 2, we give the normalized FGCREs for some distributions.

Table 2.
FGCREs for several distributions.
To continue our results, consider the following observation.
Theorem 5.
Let for all . Then
where
Proof.
Recalling Proposition 1 and the change of , we have
where
for all In (20), let and Then and Integrating by parts gives
and this gives the proof. □
When the De Vergottini index of inequality of an income distribution X is reached, given by (see Rao et al. [2] for more details). The index (19) belongs to the class of linear measures of income inequality defined by Mehran [14]. It can be obtained by weighting the Lorenz differences together with the income distribution.
Theorem 6.
Let and be non-negative RVs with survival functions and respectively. If then for all
Proof.
Assumption implies that due to Theorem 3.A.10 in [12]. From relation (19), we obtain
where the inequality is obtained by noting that is a non-negative function for all The result is obtained by reversing. □
The Bayes Risk of MRL
The PDF of is given by for Denote by the MRL function of X. In the decision theoretic framework, the MRL function is the optimal prediction of under the conditional quadratic loss function as the mean of the PDF In other words, we have
for all The function is a local risk measure, given the value the threshold t takes. Its global risk of the MRL function of X is the Bayes risk
where denotes the average based on the prior PDF for the threshold t (see Ardakani et al. [15] and Asadi et al. [16] for more details). The following theorem provides expressions for under different priors.
Theorem 7.
Let X have the MRL function and let Then, the Bayes risk of is given by the FGCRE functional of the baseline CDF, i.e.,
Proof.
By substituting for all we have
The second equality follows by observing that
and the proof is completed. □
From Theorem 7, it is obvious that
for all We point out that the representation in (23) is very useful since in many statistical models one may gather information about the behaviour of MRL. The following example illustrates a well-known situation in this context.
Example 1.
Let us suppose , , with , and Oakes and Dasu [17] observed that the corresponding SF is
It is a well-known property for the generalized Pareto distribution (GPD) as a fundamental aspect of this family of distributions. The exponential distribution is reached whenever , the Pareto distribution is resulted for and the power distribution is achieved for Hence, from (23), the FGCRE of the GPD distribution is derived as
where the identity for all , has been applied.
The Bayes risk of under the prior is given by for all
3. Bounds and Stochastic Ordering
In this section, we aim to derive several results on bounds for the FGCRE and provide results based on stochastic comparisons.
3.1. Some Bounds
It is well known that the cumulative residual entropy of the sum of two non-negative independent RVs is greater than the maximum of their original entropies (see, for example, Rao et al. [2]). By a similar approach, we can verify that the same result also holds true for the FGCRE. We omit the proof.
Theorem 8.
If and are non-negative independent RVs, then
for all
The following theorem establishes a bound for the FGCRE in terms of the cumulative residual entropy (2).
Theorem 9.
Let X have a finite mean μ and finite . Then
Proof.
Let follow the equilibrium distribution with PDF The FGCRE can be rewritten as
in which is a concave (convex) function for Therefore, Jensen’s inequality implies
and this provides the proof in the spirit of (2). If , the result is obtained analogously. □
In the setting of Theorem 9, the properties given below hold for the normalized FGCRE.
Theorem 10.
If X has a finite then, for all
- (i)
- such that and given by (1).
- (ii)
Proof.
Part (i) is easily obtained by applying the log-sum inequality (see, e.g., Rao et al. [2]). By using the identity for , then part (ii) can be obtained. □
We end this subsection by providing two upper bounds for the FGCRE of The first one is based on standard deviation of The second one is based on the risk-adjusted premium introduced by Wang [18] which is defined by
for all The risk-adjusted premium is additive when the risk is divided into layers, which makes it very attractive for pricing insurance layers. For a detailed discussion, the reader is referred to Wang [18].
Theorem 11.
Consider X with standard deviation and FGCRE function Then
- (i)
- for all
- (ii)
- where for and for
Proof.
(i) For all by the Cauchy–Schwarz inequality, from (23) we obtain
Applying Theorem 21 of Toomaj and Di Crescenzo [11], it holds that Further,
which is positive for all Therefore, the proof is then completed. Part (ii) is easily obtained from relation (13) by substituting for and for □
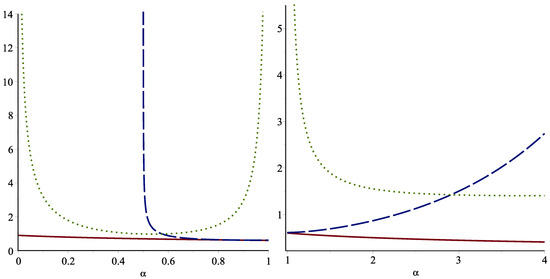
The standard deviation (SD) bound in Theorem 11 is decreasing in and increasing in , but it is applicable when However, the risk-adjustment (RA) bound is applicable for all Therefore, this bound can be a useful alternative for the case of The following example illustrates these points.
Example 2.
Consider X with SF Then,
for all The variance and the FGCRE of the Weibull distribution as given in Table 1 are
respectively. Therefore, part (i) of Theorem 11 gives
Moreover, by taking for all and for all , part (ii) of Theorem 11 gives
The left panel of Figure 2 indicates the plots of the SD and the RA bounds given in Theorem 11 along with the plot of for , and the right panel is for . The standard deviation bound is not valid for For , the standard deviation bound is outperformed.

Figure 2.
The SD (dashed line) and the RA (dotted line) bounds as well as the exact value of FGCRE (solid line) for the Weibull model with scale parameter when (left) and (right).
3.2. Stochastic Comparisons
In this subsection, ordering distributions according to the FGCRE is considered. We provide a counterexample to show that the usual stochastic ordering does not provide ordered distributions in accordance with their FGCREs.
Example 3.

Let us consider two RVs and coming from the Weibull distribution with the survival functions and for all and It is not hard to see that for we have However, numerical computations illustrate that for some choices of and and for some choices of the condition is not fulfilled as shown in Table 3.

Table 3.
Numerical values of and described in Example 3.
Before stating our main results, let us consider the following lemma.
Lemma 1.
If then for all
Proof.
The SF of is Since we have
in which the inequality follows since is increasing in Hence, the proof is completed. □
Theorem 12.
Let . Then, for all
- (i)
- If and either or is IMRL, then
- (ii)
- If and either or is DMRL, then
Proof.
We assume that the SF of is given by Let be IMRL. From (22), we obtain
The first inequality is due to and the last inequality follows since implies for due to Lemma 1 and this is equivalent to for all functions with increasing behaviour. Suppose is IMRL. Then,
and hence the result stated in (i) is obtained. The proof for assertion (ii) is quite similar. □
Hereafter, we show that the FGCRE is connected with the excess wealth order as another concept of variability. The excess wealth transform function has some links with the MRL function as
Recently, Toomaj and Di Crescenzo [11] have shown that a similar result also holds for the GCRE. The FGCRE can be calculated from the excess wealth transform employing (22).
Theorem 13.
For a non-negative RV X, we have, for all
It has been established by Fernández-Ponce et al. [19] that the variance of X can be measured by excess wealth as
Notice that implies (cf. [12]). From (28), the following result is reached.
Theorem 14.
If then for any .
Consequently,
for any
4. Dynamic FGRCE
The study of the times for events or the age of units is of interest in many fields. The FGCRE of is
for all . It is clear that . The HR of is for Hence, if X is IFR(DFR), then is also IFR(DFR) and, therefore,
for all . On the other hand, by using the generalized binomial expansion, for all ,
In analogy with Theorem 1, the next result is procured:
The dynamic version of identity (22) follows from the following identity,
which is the PDF of the conditional RV , . This is the generalization of expression given in (33) of Toomaj and Di Crescenzo [11] when is a positive integer. The result in Theorem 10 of Toomaj and Di Crescenzo [11] is generalized as follows:
Theorem 15.
In the setting of Theorem 7, for non-negative α and t,
Theorem 16.
For any and for all it holds that
Proof.
Let us denote . We obtain
The result now follows from (31). □
For Theorem 16 is reduced to the next achievement:
Corollary 1.
For all
In a similar manner as in Theorem 9, the following bounds for the dynamic measure (4) are derived for :
The following theorem with the same arguments as in the proof of Theorem 10 gives the dynamic version of the FGCRE.
Theorem 17.
For X with a finite MRL function and finite for all we have:
- (i)
- in which is as before. denotes the dynamic Shannon entropy introduced in [20].
- (ii)
Moreover, following the proof of Theorem 11, a couple of upper bounds for the dynamic FGCRE are acquired. The definition and properties of the variance residual lifetime (VRL) function in the context of lifetime data analysis have been studied in Gupta [21], Gupta et al. [22] and Gupta and Kirmani [23], among others.
Theorem 18.
Let X have a VRL function and finite dynamic FGCRE for all Then,
- (i)
- for all
- (ii)
- , where for and for and
Now, we give an expression for the derivative of
Theorem 19.
We have
for all
Proof.
The relation (33) gives
By differentiating, we obtain
The preceding theorem can be applied to present the following theorem:
Theorem 20.
If X is IFR (DFR), then is decreasing (increasing) for all
Proof.
The result is immediate for since and since the IFR (DFR) property is stronger than the DMRL (IMRL) property. For all using relation (30), we have
which validates the theorem by using Theorem 19. □
Let us define a new aging notion based on the FGCRE.
Definition 1.
The RV X has an increasing (decreasing) dynamic FGCRE of order α, and denote it by if is increasing (decreasing) in
We note that the and classes correspond to the IMRL (increasing MRL) and DMRL (decreasing MRL) classes, respectively. In the next theorem, we prove is a subclass of for all .
Lemma 2.
Let for a fixed Then
Under the assumptions of Lemma 2, is an absolutely continuous function. Furthermore, for then is also absolutely continuous under the hypothesis that Moreover, we have the following result.
Theorem 21.
If X is then X is for all .
Proof.
From Theorem 21, we can conclude that
and
for all An immediate consequence of the above relation is that
for all We remark that Navarro et al. (2010) provided some examples showing that an RV X is but it is not IMRL (DMRL). However, Navarro and Psarrakos [24] by some counterexamples showed that X is neither IMRL (DMRL) nor but it is included in the class when is an integer value. Hence, the result holds for all
This section is closed by introducing the dynamic normalized version of the FGCRE as follows:
for all
Theorem 22.
Let X have a finite normalized FGCRE If X is IMRL (DMRL), then for all
Proof.
Since X is IMRL (DMRL) based on the assumption, we have
In Table 4, we give the dynamically normalized FGCREs for some distributions. For example, we present the dynamically normalized FGCRE of the Weibull distribution in Figure 3. We note that X is IMRL when and X is DMRL when

Table 4.
FGCREs, MRLs and normalized FGCREs for some distributions.
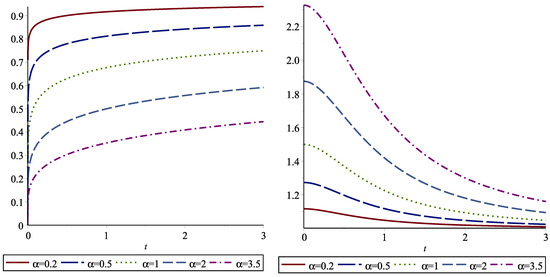
Figure 3.
The dynamic normalized FGCRE for the Weibull distribution given in case (ii) of Table 4, with (left panel) and (right panel) as a function of t for various values of .
Eventually, the inequalities given in (25) can be developed as
The inequalities given above are very useful when the dynamic FGCRE has a complicated form.
Author Contributions
Formal analysis, M.K.; Investigation, G.A.; Methodology, G.A. and M.K.; Project administration, G.A.; Resources, M.K.; Supervision, M.K.; Visualization, M.K.; Writing—original draft, G.A.; Writing—review & editing, M.K. All authors have read and agreed to the published version of the manuscript.
Funding
Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2022R226), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Rao, M.; Chen, Y.; Vemuri, B.C.; Wang, F. Cumulative residual entropy: A new measure of information. IEEE Trans. Inf. Theory 2004, 50, 1220–1228. [Google Scholar] [CrossRef]
- Asadi, M.; Zohrevand, Y. On the dynamic cumulative residual entropy. J. Stat. Plan. Inference 2007, 137, 1931–1941. [Google Scholar] [CrossRef]
- Navarro, J.; del Aguila, Y.; Asadi, M. Some new results on the cumulative residual entropy. J. Stat. Plan. Inference 2010, 140, 310–322. [Google Scholar] [CrossRef]
- Baratpour, S. Characterizations based on cumulative residual entropy of first-order statistics. Commun. Stat. Methods 2010, 39, 3645–3651. [Google Scholar] [CrossRef]
- Baratpour, S.; Rad, A.H. Testing goodness-of-fit for exponential distribution based on cumulative residual entropy. Biometrika 2012, 41, 1387–1396. [Google Scholar]
- Toomaj, A.; Sunoj, S.M.; Navarro, J. Some properties of the cumulative residual entropy of coherent and mixed systems. J. Appl. Probab. 2017, 54, 379–393. [Google Scholar] [CrossRef]
- Di Crescenzo, A.; Kayal, S.; Meoli, A. Fractional generalized cumulative entropy and its dynamic version. Commun. Nonlinear Sci. Numer. Simul. 2021, 102, 105899. [Google Scholar] [CrossRef]
- Xiong, H.; Shang, P.; Zhang, Y. Fractional cumulative residual entropy. Commun. Nonlinear Sci. Numer. Simul. 2019, 78, 104879. [Google Scholar] [CrossRef]
- Psarrakos, G.; Economou, P. On the generalized cumulative residual entropy weighted distributions. Commun. -Stat.-Theory Methods 2017, 46, 10914–10925. [Google Scholar] [CrossRef]
- Toomaj, A.; Di Crescenzo, A. Connections between weighted generalized cumulative residual entropy and variance. Mathematics 2020, 8, 1072. [Google Scholar] [CrossRef]
- Shaked, M.; Shanthikumar, J.G. Stochastic Orders; Springer Science and Business Media: New York, NY, USA, 2007. [Google Scholar]
- Baxter, L.A. Reliability applications of the relevation transform. Nav. Res. Logist. 1982, 29, 323–330. [Google Scholar] [CrossRef]
- Mehran, F. Linear measures of income inequality. Econom. J. Econom. Soc. 1976, 805–809. [Google Scholar] [CrossRef]
- Ardakani, O.M.; Ebrahimi, N.; Soofi, E.S. Ranking forecasts by stochastic error distance, information and reliability measures. Int. Stat. Rev. 2018, 86, 442–468. [Google Scholar] [CrossRef]
- Asadi, M.; Ebrahimi, N.; Soofi, E.S. Connections of Gini, Fisher, and Shannon by Bayes risk under proportional hazards. J. Appl. Probab. 2017, 54, 10–27. [Google Scholar] [CrossRef]
- Oakes, D.; Dasu, T. A note on residual life. Biometrika 1990, 77, 409–410. [Google Scholar] [CrossRef]
- Wang, S. Insurance pricing and increased limits ratemaking by proportional hazards transforms. Insur. Math. Econ. 1995, 17, 43–54. [Google Scholar] [CrossRef]
- Fernandez-Ponce, J.M.; Kochar, S.C.; Muñoz-Perez, J. Partial orderings of distributions based on right-spread functions. J. Appl. Probab. 1998, 35, 221–228. [Google Scholar] [CrossRef]
- Ebrahimi, N. How to measure uncertainty in the residual life time distribution. Sankhyā Indian J. Stat. Ser. A 1996, 58, 48–56. [Google Scholar]
- Gupta, R.C. On the monotonic properties of the residual variance and their applications in reliability. J. Stat. Plan. Inference 1987, 16, 329–335. [Google Scholar] [CrossRef]
- Gupta, R.C.; Kirmani, S.N.U.A.; Launer, R.L. On life distributions having monotone residual variance. Probab. Eng. Informational Sci. 1987, 1, 299–307. [Google Scholar] [CrossRef]
- Gupta, R.C.; Kirmani, S.N.U.A. Closure and monotonicity properties of nonhomogeneous poisson processes and record values. Probab. Eng. Inform. Sci. 1988, 2, 475–484. [Google Scholar] [CrossRef]
- Navarro, J.; Psarrakos, G. Characterizations based on generalized cumulative residual entropy functions. Commun. -Stat.-Theory Methods 2017, 46, 1247–1260. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).