Forecasting COVID-19 Epidemic Trends by Combining a Neural Network with Rt Estimation
Abstract
:1. Introduction
2. Background
- lag order (p): the number of lag observations included in the model;
- degree of differencing (d): the number of times that the raw observations are differenced;
- order of moving average (q): the size of the moving average window.
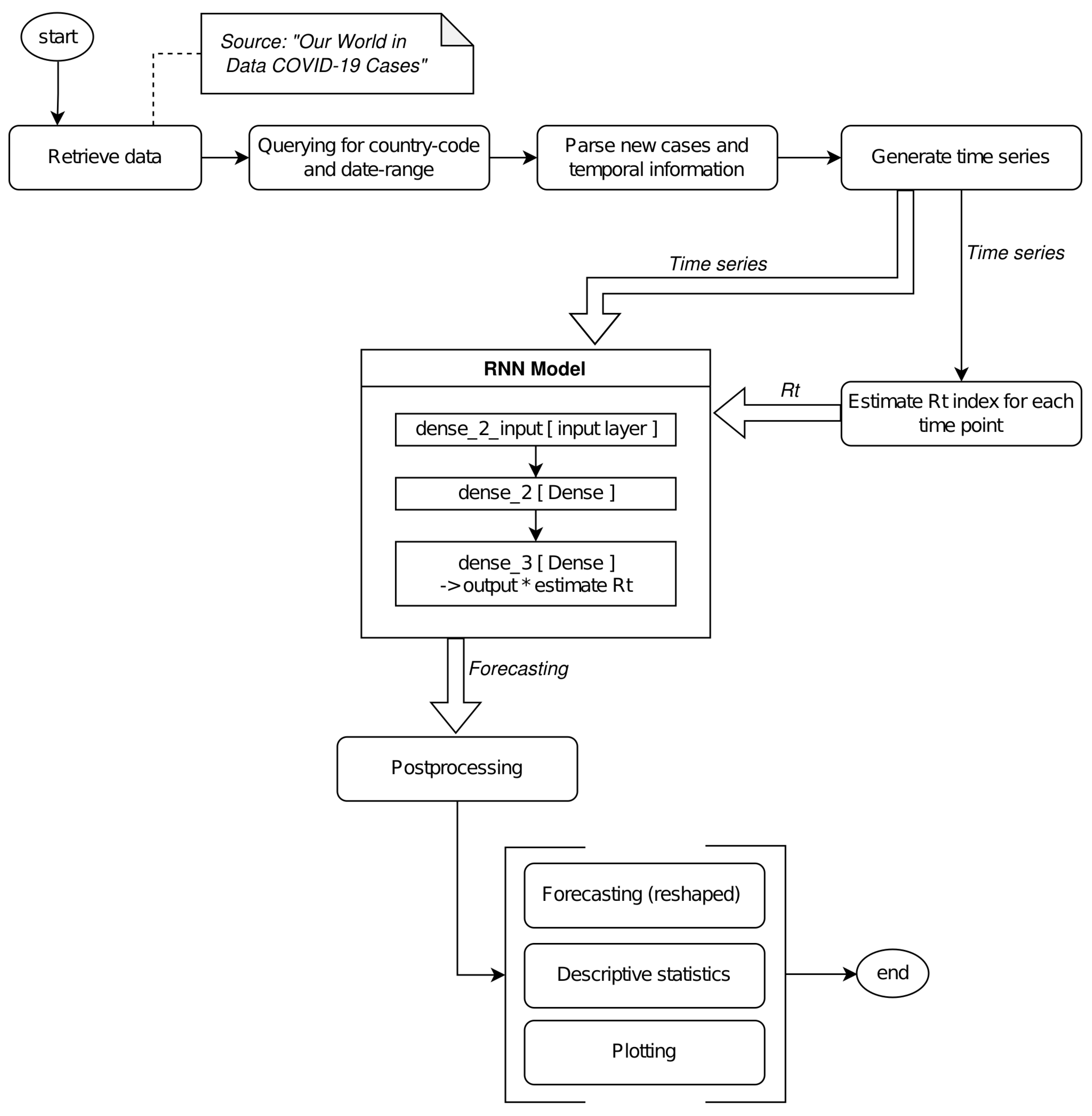
3. Materials and Methods
3.1. Dataset
3.2. Preprocessing
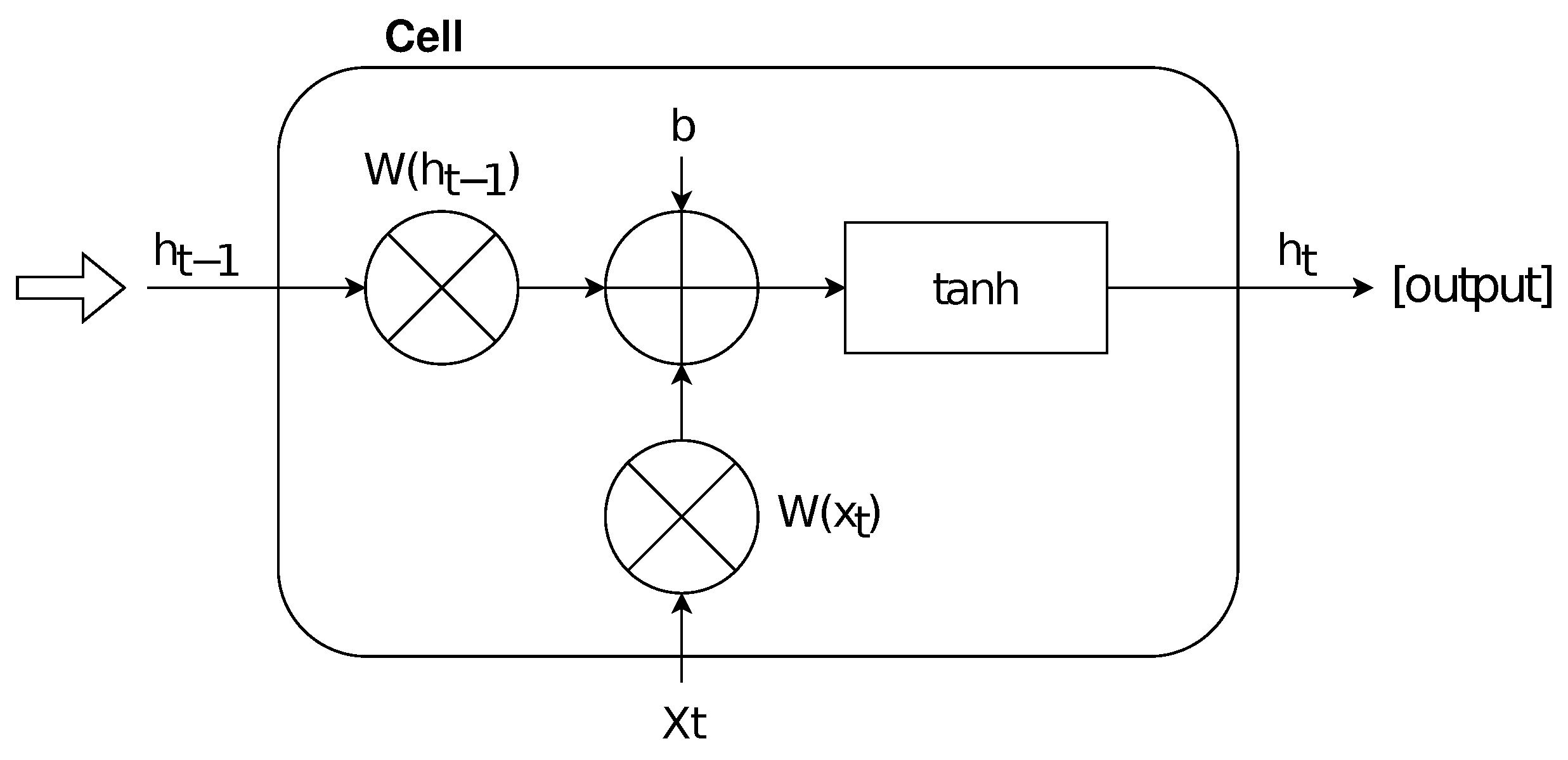
3.3. Model
3.4. Postprocessing
3.5. Implementation
- pandas [53]. This package is a software library for data analysis and manipulation. It includes a data structure to handle data frames efficiently. Furthermore, time-series are supported; for instance, it allows date range generation and frequency conversion, statistics, date shifting, and lagging.
- numpy [54]. This package provides support for large, multidimensional arrays and matrices, as well as a collection of high-level mathematical functions to manipulate these data structures.
- tensorflow [55]. This package is one of the most widely used end-to-end open source platforms for ML/DL.
- scikit-learn [56]. This package is a collection of tools for predictive data analysis, classification, regressions, and clustering. It supports the interoperability with other packages (e.g., numpy).
- epyestim [45]. This package is able to estimate time-varying reproduction numbers (i.e., ) from epidemic curves. It is provided in both software tool and package form. The latter also supports the Python languages.
3.6. Key Performance Indicators
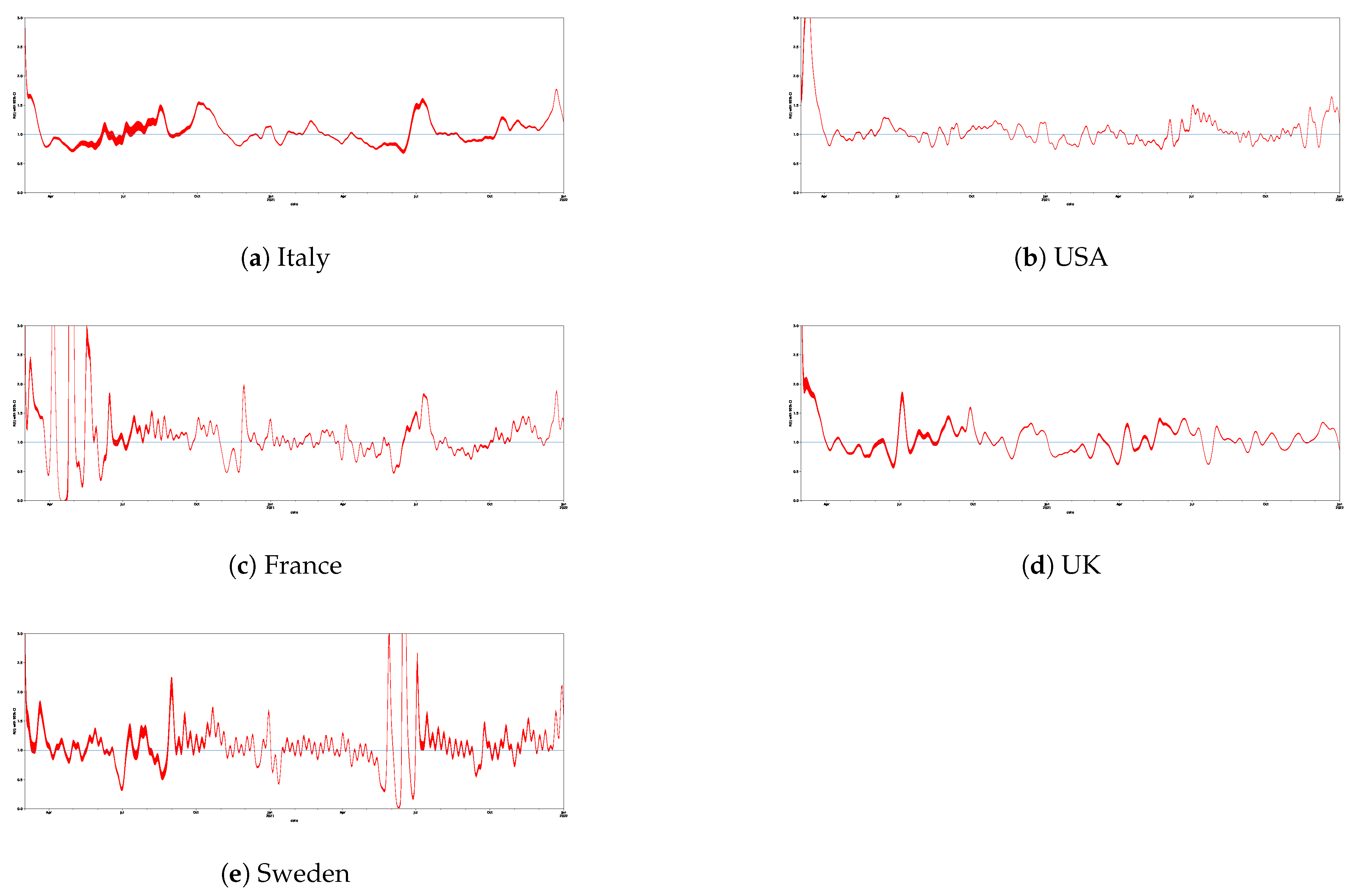
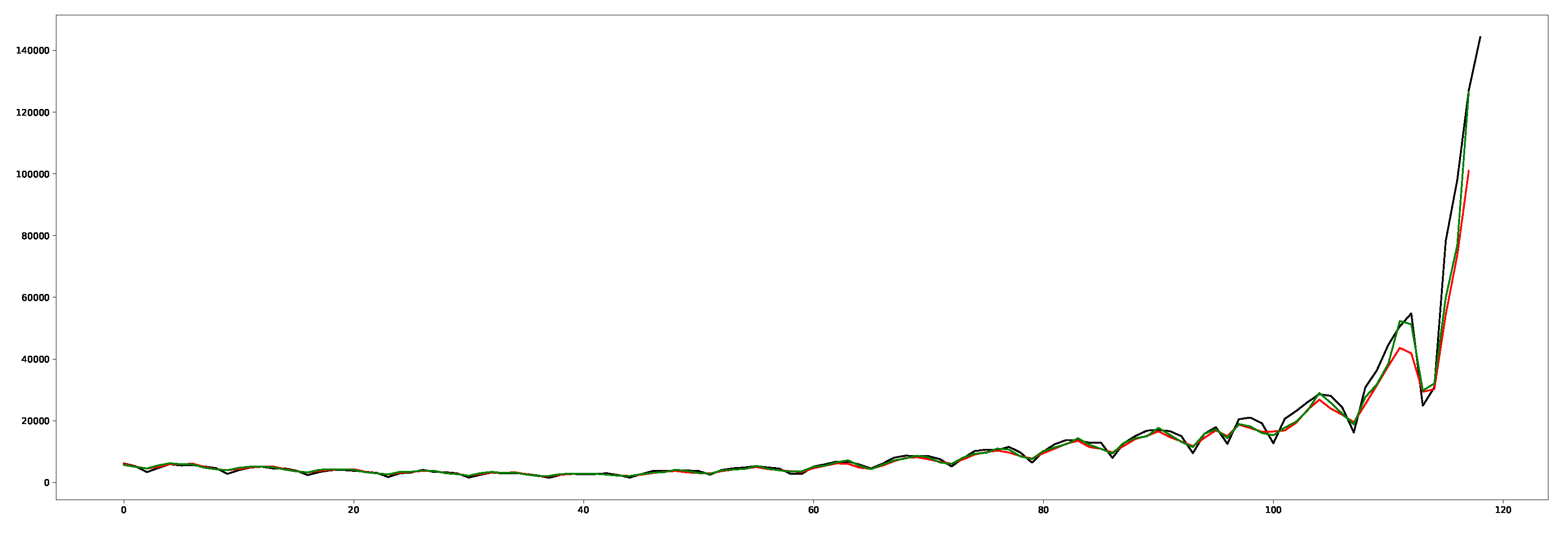
4. Results
- Type: n1-highmem-2 instance;
- CPU: 2vCPU @ 2.2 GHz;
- RAM: 13 GB;
- Backend: GCE, Python 3.
5. Discussion
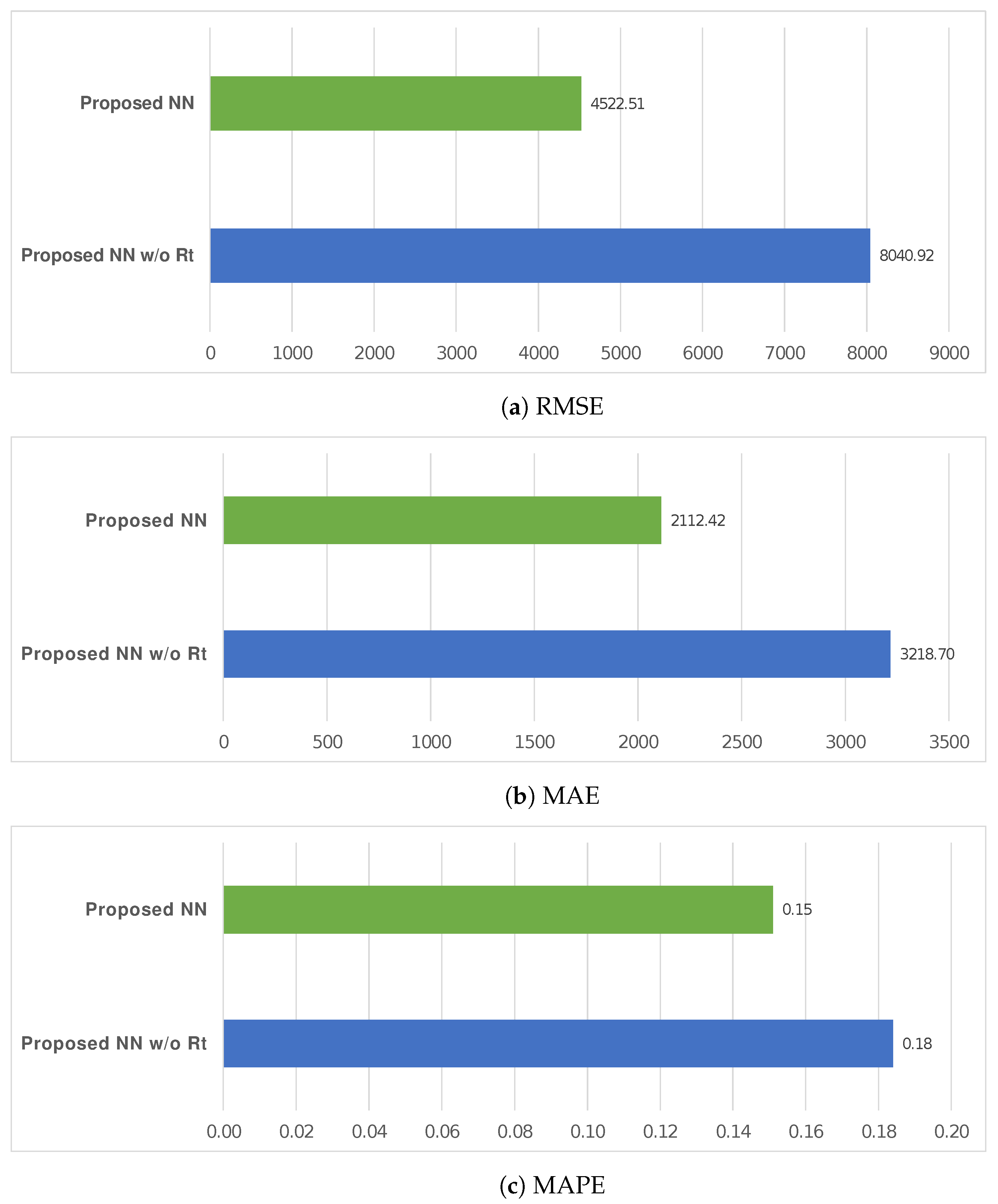
- vs. proposed without : 5.38%, 53.13%, 10.00%, and 14.63%;
- vs. LSTM: −10.00%, 68.75%, 18.18%, and 7.89%;
- vs. Simple RNN: 2.94%, 70.00%, 25.00%, and 20.45%;
- vs. GRU: 13.16%, 60.53%, 18.18%, and 16.67%,
6. Conclusions
Key Points
- We combined an NN with the estimation of time-varying reproduction numbers during epidemics (i.e., using as a corrective index).
- We developed a solution that was able to handle the frequent restrictions adopted by a country (e.g., lockdowns and limitations) that could destabilize the evolution of a time series.
- We provided an effective methodology to forecast COVID-19 epidemic trends on a dataset consisting of a limited amount of information (e.g., Italy).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Zhao, S.; Lin, Q.; Ran, J.; Musa, S.S.; Yang, G.; Wang, W.; Lou, Y.; Gao, D.; Yang, L.; He, D.; et al. Preliminary estimation of the basic reproduction number of novel coronavirus (2019-nCoV) in China, from 2019 to 2020: A data-driven analysis in the early phase of the outbreak. Int. J. Infect. Dis. 2020, 92, 214–217. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Knight, G.M.; Dharan, N.J.; Fox, G.J.; Stennis, N.; Zwerling, A.; Khurana, R.; Dowdy, D.W. Bridging the gap between evidence and policy for infectious diseases: How models can aid public health decision-making. Int. J. Infect. Dis. 2016, 42, 17–23. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lotfi, M.; Hamblin, M.R.; Rezaei, N. COVID-19: Transmission, prevention, and potential therapeutic opportunities. Clin. Chim. Acta 2020, 508, 254–266. [Google Scholar] [CrossRef]
- Kermack, W.O.; McKendrick, A.G.; Kermack, W.O.; McKendrick, A.G. Contributions to the mathematical theory of epidemics–I. 1927. Bull. Math. Biol. 1991, 53, 33–55. [Google Scholar]
- Singh, R.K.; Rani, M.; Bhagavathula, A.S.; Sah, R.; Rodriguez-Morales, A.J.; Kalita, H.; Nanda, C.; Sharma, S.; Sharma, Y.D.; Rabaan, A.A.; et al. Prediction of the COVID-19 Pandemic for the Top 15 Affected Countries: Advanced Autoregressive Integrated Moving Average (ARIMA) Model. JMIR Public Health Surveill. 2020, 6, e19115. [Google Scholar] [CrossRef] [PubMed]
- Meibalan, E.; Marti, M. Biology of Malaria Transmission. Cold Spring Harb. Perspect. Med. 2017, 7, a025452. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sharomi, O.; Podder, C.N.; Gumel, A.B.; Song, B. Mathematical analysis of the transmission dynamics of HIV/TB coinfection in the presence of treatment. Math. Biosci. Eng. 2008, 5, 145–174. [Google Scholar] [PubMed]
- Ding, Y.; Huang, R.; Shao, N. Time Series Forecasting of US COVID-19 Transmission. Altern. Ther. Health Med. 2021, 27, 4–11. [Google Scholar]
- Abenavoli, L.; Cinaglia, P.; Luzza, F.; Gentile, I.; Boccuto, L. Epidemiology of Coronavirus disease outbreak: The Italian trends. Rev. Recent Clin. Trials 2020, 15, 87–92. [Google Scholar] [CrossRef]
- Abenavoli, L.; Cinaglia, P.; Procopio, A.C.; Serra, R.; Aquila, I.; Zanza, C.; Longhitano, Y.; Artico, M.; Larussa, T.; Boccuto, L.; et al. SARS-CoV-2 spread dynamics in Italy: The Calabria experience. Rev. Recent Clin. Trials 2021, 16, 309–315. [Google Scholar] [CrossRef] [PubMed]
- Nelson, B.K. Statistical methodology: V. Time series analysis using autoregressive integrated moving average (ARIMA) models. Acad. Emerg. Med. 1998, 5, 739–744. [Google Scholar] [CrossRef] [PubMed]
- Sadia, F.; Boyd, S.; Keith, J.M. Bayesian change-point modeling with segmented ARMA model. PLoS ONE 2018, 13, e0208927. [Google Scholar] [CrossRef] [PubMed]
- Shahid, F.; Zameer, A.; Muneeb, M. Predictions for COVID-19 with deep learning models of LSTM, GRU and Bi-LSTM. Chaos Solitons Fractals 2020, 140, 110212. [Google Scholar] [CrossRef] [PubMed]
- Wiwanitkit, V. SARIMA for predicting the cases numbers of dengue. Rev. Soc. Bras. Med. Trop. 2012, 45, 140. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, Z.; Li, Y. A comparative study on the prediction of the BP artificial neural network model and the ARIMA model in the incidence of AIDS. BMC Med. Inf. Decis. Mak. 2020, 20, 143. [Google Scholar] [CrossRef]
- Chaurasia, V.; Pal, S. COVID-19 Pandemic: ARIMA and Regression Model-Based Worldwide Death Cases Predictions. SN Comput. Sci. 2020, 1, 288. [Google Scholar] [CrossRef] [PubMed]
- Qi, C.; Zhang, D.; Zhu, Y.; Liu, L.; Li, C.; Wang, Z.; Li, X. SARFIMA model prediction for infectious diseases: Application to hemorrhagic fever with renal syndrome and comparing with SARIMA. BMC Med. Res. Methodol. 2020, 20, 243. [Google Scholar] [CrossRef]
- Friedman, L.S.; Barach, P.; Richter, E.D. Raised speed limits, case fatality and road deaths: A six year follow-up using ARIMA models. Inj. Prev. 2007, 13, 156–161. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alabdulrazzaq, H.; Alenezi, M.N.; Rawajfih, Y.; Alghannam, B.A.; Al-Hassan, A.A.; Al-Anzi, F.S. On the accuracy of ARIMA based prediction of COVID-19 spread. Results Phys. 2021, 27, 104509. [Google Scholar] [CrossRef] [PubMed]
- Hernandez-Matamoros, A.; Fujita, H.; Hayashi, T.; Perez-Meana, H. Forecasting of COVID19 per regions using ARIMA models and polynomial functions. Appl. Soft Comput. 2020, 96, 106610. [Google Scholar] [CrossRef]
- ArunKumar, K.; Kalaga, D.V.; Sai Kumar, C.M.; Chilkoor, G.; Kawaji, M.; Brenza, T.M. Forecasting the dynamics of cumulative COVID-19 cases (confirmed, recovered and deaths) for top-16 countries using statistical machine learning models: Auto-Regressive Integrated Moving Average (ARIMA) and Seasonal Auto-Regressive Integrated Moving Average (SARIMA). Appl. Soft Comput. 2021, 103, 107161. [Google Scholar]
- Ngiam, K.Y.; Khor, I.W. Big data and machine learning algorithms for health-care delivery. Lancet Oncol. 2019, 20, e262–e273. [Google Scholar] [CrossRef]
- Esteva, A.; Robicquet, A.; Ramsundar, B.; Kuleshov, V.; DePristo, M.; Chou, K.; Cui, C.; Corrado, G.; Thrun, S.; Dean, J. A guide to deep learning in healthcare. Nat. Med. 2019, 25, 24–29. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Yao, H.; Lin, K. An overview of neural networks for drug discovery and the inputs used. Expert Opin. Drug Discov. 2018, 13, 1091–1102. [Google Scholar] [CrossRef] [PubMed]
- Alassafi, M.O.; Jarrah, M.; Alotaibi, R. Time series predicting of COVID-19 based on deep learning. Neurocomputing 2022, 468, 335–344. [Google Scholar] [CrossRef]
- Ramesh, A.N.; Kambhampati, C.; Monson, J.R.; Drew, P.J. Artificial intelligence in medicine. Ann. R Coll Surg. Engl. 2004, 86, 334–338. [Google Scholar] [CrossRef] [Green Version]
- Werner, F.M. Neural Networks in Neurological and Psychiatric Diseases. Curr. Pharm. Des. 2019, 25, 374–375. [Google Scholar] [CrossRef]
- Hessler, G.; Baringhaus, K.H. Artificial Intelligence in Drug Design. Molecules 2018, 23, 2520. [Google Scholar] [CrossRef] [Green Version]
- Alzubaidi, M.; Zubaydi, H.D.; Bin-Salem, A.A.; Abd-Alrazaq, A.A.; Ahmed, A.; Househ, M. Role of deep learning in early detection of COVID-19: Scoping review. Comput. Methods Programs Biomed. Update 2021, 1, 100025. [Google Scholar] [CrossRef]
- Barrett, D.G.; Morcos, A.S.; Macke, J.H. Analyzing biological and artificial neural networks: Challenges with opportunities for synergy? Curr. Opin. Neurobiol. 2019, 55, 55–64. [Google Scholar] [CrossRef]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to forget: Continual prediction with LSTM. Neural Comput. 2000, 12, 2451–2471. [Google Scholar] [CrossRef] [PubMed]
- Ghany, K.K.A.; Zawbaa, H.M.; Sabri, H.M. COVID-19 prediction using LSTM algorithm: GCC case study. Inf. Med. Unlocked 2021, 23, 100566. [Google Scholar] [CrossRef] [PubMed]
- Chimmula, V.K.R.; Zhang, L. Time series forecasting of COVID-19 transmission in Canada using LSTM networks. Chaos Solitons Fractals 2020, 135, 109864. [Google Scholar] [CrossRef] [PubMed]
- Ayoobi, N.; Sharifrazi, D.; Alizadehsani, R.; Shoeibi, A.; Gorriz, J.M.; Moosaei, H.; Khosravi, A.; Nahavandi, S.; Gholamzadeh Chofreh, A.; Goni, F.A.; et al. Time series forecasting of new cases and new deaths rate for COVID-19 using deep learning methods. Results Phys. 2021, 27, 104495. [Google Scholar] [CrossRef]
- Wilkosz, M.; Szczesna, A. Multi-Headed Conv-LSTM Network for Heart Rate Estimation during Daily Living Activities. Sensors 2021, 21, 5212. [Google Scholar] [CrossRef]
- Zhang, B.; Xiong, D.; Xie, J.; Su, J. Neural Machine Translation With GRU-Gated Attention Model. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 4688–4698. [Google Scholar] [CrossRef]
- Zhao, C.; You, J.; Wen, X.; Li, X. Deep Bi-LSTM Networks for Sequential Recommendation. Entropy 2020, 22, 870. [Google Scholar] [CrossRef]
- Zeroual, A.; Harrou, F.; Dairi, A.; Sun, Y. Deep learning methods for forecasting COVID-19 time-Series data: A Comparative study. Chaos Solitons Fractals 2020, 140, 110121. [Google Scholar] [CrossRef]
- Shastri, S.; Singh, K.; Kumar, S.; Kour, P.; Mansotra, V. Time series forecasting of Covid-19 using deep learning models: India-USA comparative case study. Chaos Solitons Fractals 2020, 140, 110227. [Google Scholar] [CrossRef]
- Ma, R.; Zheng, X.; Wang, P.; Liu, H.; Zhang, C. The prediction and analysis of COVID-19 epidemic trend by combining LSTM and Markov method. Sci. Rep. 2021, 11, 17421. [Google Scholar] [CrossRef]
- Chandra, R.; Jain, A.; Chauhan, D.S. Deep learning via LSTM models for COVID-19 infection forecasting in India. CoRR 2021, 2101, 11881. [Google Scholar] [CrossRef] [PubMed]
- Ritchie, H.; Mathieu, E.; Rodés-Guirao, L.; Appel, C.; Giattino, C.; Ortiz-Ospina, E.; Hasell, J.; Macdonald, B.; Beltekian, D.; Roser, M. Coronavirus Pandemic (COVID-19). Our World in Data. 2020. Available online: https://ourworldindata.org/coronavirus (accessed on 18 May 2022).
- Jung, S.M.; Endo, A.; Akhmetzhanov, A.R.; Nishiura, H. Predicting the effective reproduction number of COVID-19: Inference using human mobility, temperature, and risk awareness. Int. J. Infect. Dis. 2021, 113, 47–54. [Google Scholar] [CrossRef] [PubMed]
- Huisman, J.S.; Scire, J.; Angst, D.C.; Li, J.; Neher, R.A.; Maathuis, M.H.; Bonhoeffer, S.; Stadler, T. Estimation and worldwide monitoring of the effective reproductive number of SARS-CoV-2. medRxiv 2021. [Google Scholar] [CrossRef]
- Cori, A.; Ferguson, N.M.; Fraser, C.; Cauchemez, S. A New Framework and Software to Estimate Time-Varying Reproduction Numbers During Epidemics. Am. J. Epidemiol. 2013, 178, 1505–1512. [Google Scholar] [CrossRef] [Green Version]
- Lv, B.; Jiang, Y. Prediction of Short-Term Stock Price Trend Based on Multiview RBF Neural Network. Comput. Intell. Neurosci. 2021, 2021, 8495288. [Google Scholar] [CrossRef] [PubMed]
- Nabipour, M.; Nayyeri, P.; Jabani, H.; Mosavi, A.; Salwana, E.; S, S. Deep Learning for Stock Market Prediction. Entropy 2020, 22, 840. [Google Scholar] [CrossRef]
- Chandra, R.; He, Y. Bayesian neural networks for stock price forecasting before and during COVID-19 pandemic. PLoS ONE 2021, 16, e0253217. [Google Scholar] [CrossRef] [PubMed]
- Reid, D.; Hussain, A.J.; Tawfik, H. Financial time series prediction using spiking neural networks. PLoS ONE 2014, 9, e103656. [Google Scholar]
- Kriegeskorte, N.; Golan, T. Neural network models and deep learning. Curr. Biol. 2019, 29, R231–R236. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Van Rossum, G.; Drake, F.L. Python 3 Reference Manual; CreateSpace: Scotts Valley, CA, USA, 2009. [Google Scholar]
- McKinney, W. Data Structures for Statistical Computing in Python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010; pp. 56–61. [Google Scholar]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef] [PubMed]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems. arXiv 2016, arXiv:1603.04467. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Bisong, E. Google Colaboratory. In Building Machine Learning and Deep Learning Models on Google Cloud Platform: A Comprehensive Guide for Beginners; Apress: Berkeley, CA, USA, 2019; pp. 59–64. [Google Scholar]
- Dairi, A.; Harrou, F.; Zeroual, A.; Hittawe, M.M.; Sun, Y. Comparative study of machine learning methods for COVID-19 transmission forecasting. J. Biomed. Inf. 2021, 118, 103791. [Google Scholar] [CrossRef]
- Khalid, S.; Goldenberg, M.; Grantcharov, T.; Taati, B.; Rudzicz, F. Evaluation of Deep Learning Models for Identifying Surgical Actions and Measuring Performance. JAMA Netw. Open 2020, 3, e201664. [Google Scholar] [CrossRef]
- Chicco, D.; Warrens, M.J.; Jurman, G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. PeerJ Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef]
- de Myttenaere, A.; Golden, B.; Le Grand, B.; Rossi, F. Mean Absolute Percentage Error for regression models. Neurocomputing 2016, 192, 38–48. [Google Scholar] [CrossRef] [Green Version]
- Nevitt, J.; Hancock, G.R. Improving the Root Mean Square Error of Approximation for Nonnormal Conditions in Structural Equation Modeling. J. Exp. Educ. 2000, 68, 251–268. [Google Scholar] [CrossRef]
- Applegate, R.A.; Ballentine, C.; Gross, H.; Sarver, E.J.; Sarver, C.A. Visual acuity as a function of Zernike mode and level of root mean square error. Optom. Vis. Sci. 2003, 80, 97–105. [Google Scholar] [CrossRef]
- Benvenuto, D.; Giovanetti, M.; Vassallo, L.; Angeletti, S.; Ciccozzi, M. Application of the ARIMA model on the COVID-2019 epidemic dataset. Data Brief 2020, 29, 105340. [Google Scholar] [CrossRef]
- Mishra, P.; Singh, U.; Pandey, C.M.; Mishra, P.; Pandey, G. -test, analysis of variance, and covariance. Ann. Card Anaesth 2019, 22, 407–411. [Google Scholar] [CrossRef] [PubMed]



| Country | Organization | Data Source |
|---|---|---|
| Italy | Italian Civil Protection Department | github.com/pcm-dpc/COVID-19 |
| USA | Center for Systems Science and Engineering, Johns Hopkins University | systems.jhu.edu |
| France | French Ministry of Solidarity and Health and Public Health | data.gouv.fr/fr/datasets |
| UK | Government of the UK | coronavirus.data.gov.uk |
| Sweden | The Swedish Public Health Agency | experience.arcgis.com |
| N | Mean | Std. Deviation | Std. Error | 95% Confidence Interval for Mean | Minimum | Maximum | |||
|---|---|---|---|---|---|---|---|---|---|
| Lower Bound | Upper Bound | ||||||||
| Total Cases | Italy | 688 | 2,496,779.68 | 2,007,837.429 | 76,548.084 | 2,346,483.41 | 2,647,075.95 | 229 | 7,774,863 |
| USA | 688 | 22,722,404.82 | 17,313,142.593 | 660,057.373 | 21,426,432.95 | 24,018,376.69 | 16 | 62,588,935 | |
| France | 688 | 3,581,853.14 | 3,034,266.023 | 115,680.308 | 3,354,723.75 | 3,808,982.52 | 12 | 12,620,080 | |
| UK | 688 | 3,729,463.11 | 3,563,954.756 | 135,874.501 | 3,462,683.98 | 3,996,242.24 | 30 | 14,766,757 | |
| Sweden | 688 | 588,621.05 | 487,097.434 | 18,570.416 | 552,159.46 | 625,082.63 | 1 | 1,487,291 | |
| New Cases | Italy | 688 | 11,317.11 | 22,531.009 | 859.612 | 9629.33 | 13,004.90 | 74 | 220,519 |
| USA | 688 | 90,972.27 | 115,946.169 | 4420.406 | 82,293.14 | 99,651.39 | 0 | 1,383,898 | |
| France | 688 | 19,238.68 | 38,431.340 | 1475.947 | 16,340.70 | 22,136.67 | 0 | 368,379 | |
| UK | 688 | 21,536.37 | 29,864.863 | 1140.246 | 19,297.58 | 23,775.17 | 2 | 219,290 | |
| Sweden | 688 | 2161.76 | 5199.062 | 198.212 | 1772.58 | 2550.93 | 0 | 70,641 | |
| N | Mean | Std. Deviation | Minimum | 25% | 50% | 75% | Maximum | |
|---|---|---|---|---|---|---|---|---|
| Italy | 688 | 1.05 | 0.23 | 0.70 | 0.89 | 1.00 | 1.14 | 2.98 |
| USA | 688 | 1.08 | 0.33 | 0.74 | 0.91 | 1.03 | 1.13 | 3.74 |
| France | 688 | 1.32 | 2.99 | 0 | 0.91 | 1.06 | 1.24 | 56.87 |
| UK | 688 | 1.07 | 0.32 | 0.59 | 0.90 | 1.04 | 1.18 | 5.95 |
| Sweden | 688 | 1.11 | 0.622 | 0.02 | 0.93 | 1.06 | 1.20 | 10.04 |
| 95% Confidence Interval for Mean | ||||||||
|---|---|---|---|---|---|---|---|---|
| N | Mean | Std. Deviation | Std. Error | Lower Bound | Upper Bound | Minimum | Maximum | |
| LSTM | 10 | 0.2110 | 0.03281 | 0.01038 | 0.1875 | 0.2345 | 0.18 | 0.28 |
| GRU | 10 | 0.2490 | 0.04533 | 0.01433 | 0.2166 | 0.2814 | 0.20 | 0.31 |
| Simple RNN | 10 | 0.1960 | 0.05125 | 0.01621 | 0.1593 | 0.2327 | 0.16 | 0.33 |
| Proposed NN w/o | 10 | 0.1840 | 0.01713 | 0.00542 | 0.1717 | 0.1963 | 0.16 | 0.21 |
| Proposed NN | 10 | 0.1510 | 0.01101 | 0.00348 | 0.1431 | 0.1589 | 0.14 | 0.17 |
| 95% Confidence Interval for Mean | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| N | Mean | Std. Deviation | Std. Error | Lower Bound | Upper Bound | Minimum | Maximum | ||
| RMSE | |||||||||
| Proposed NN w/o | 10 | 8040.9180 | 1181.94026 | 373.76233 | 7195.4089 | 8886.4271 | 6224.14 | 9763.09 | |
| Proposed NN | 10 | 4522.5080 | 2645.23581 | 836.49701 | 2630.2203 | 6414.7957 | 1407.01 | 7123.64 | |
| MAE | |||||||||
| Proposed NN w/o | 10 | 3218.7000 | 922.85482 | 291.83232 | 2558.5294 | 3878.8706 | 2122.75 | 4813.67 | |
| Proposed NN | 10 | 2112.4220 | 1169.72987 | 369.90106 | 1275.6477 | 2949.1963 | 918.19 | 4010.12 | |
| MAPE | |||||||||
| Proposed NN w/o | 10 | 0.1840 | 0.01713 | 0.00542 | 0.1717 | 0.1963 | 0.16 | 0.21 | |
| Proposed NN | 10 | 0.1510 | 0.01101 | 0.00348 | 0.1431 | 0.1589 | 0.14 | 0.17 | |
| Proposed NN | Proposed NN w/o | LSTM | Simple RNN | GRU | |
|---|---|---|---|---|---|
| USA | 0.33 | 0.39 | 0.30 | 0.34 | 0.38 |
| France | 0.30 | 0.64 | 0.96 | 1.00 | 0.76 |
| UK | 0.09 | 0.10 | 0.11 | 0.12 | 0.11 |
| Sweden | 0.35 | 0.41 | 0.38 | 0.44 | 0.42 |
| Mean | Std. Deviation | Std. Error Mean | 95% Confidence Interval of the Difference | p-Value | |
|---|---|---|---|---|---|
| Lower | Upper | ||||
| −646.23 | 2690.34 | 247.67 | −1136.72 | −155.74 | 0.01 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cinaglia, P.; Cannataro, M. Forecasting COVID-19 Epidemic Trends by Combining a Neural Network with Rt Estimation. Entropy 2022, 24, 929. https://doi.org/10.3390/e24070929
Cinaglia P, Cannataro M. Forecasting COVID-19 Epidemic Trends by Combining a Neural Network with Rt Estimation. Entropy. 2022; 24(7):929. https://doi.org/10.3390/e24070929
Chicago/Turabian StyleCinaglia, Pietro, and Mario Cannataro. 2022. "Forecasting COVID-19 Epidemic Trends by Combining a Neural Network with Rt Estimation" Entropy 24, no. 7: 929. https://doi.org/10.3390/e24070929
APA StyleCinaglia, P., & Cannataro, M. (2022). Forecasting COVID-19 Epidemic Trends by Combining a Neural Network with Rt Estimation. Entropy, 24(7), 929. https://doi.org/10.3390/e24070929







