Causal Inference in Time Series in Terms of Rényi Transfer Entropy
Abstract
1. Introduction
2. Rényi Entropy
2.1. Definition
- RE is symmetric, i.e., ;
- RE is non-negative, i.e., ;
- , where is the Shannon entropy;
- is the Hartley entropy and is the Collision entropy;
- ;
- is a positive, decreasing the function of .
2.2. Multifractals, Chaotic Systems, and Rényi Entropy
2.3. Shannon Transfer Entropy
2.4. Rényi Transfer Entropy
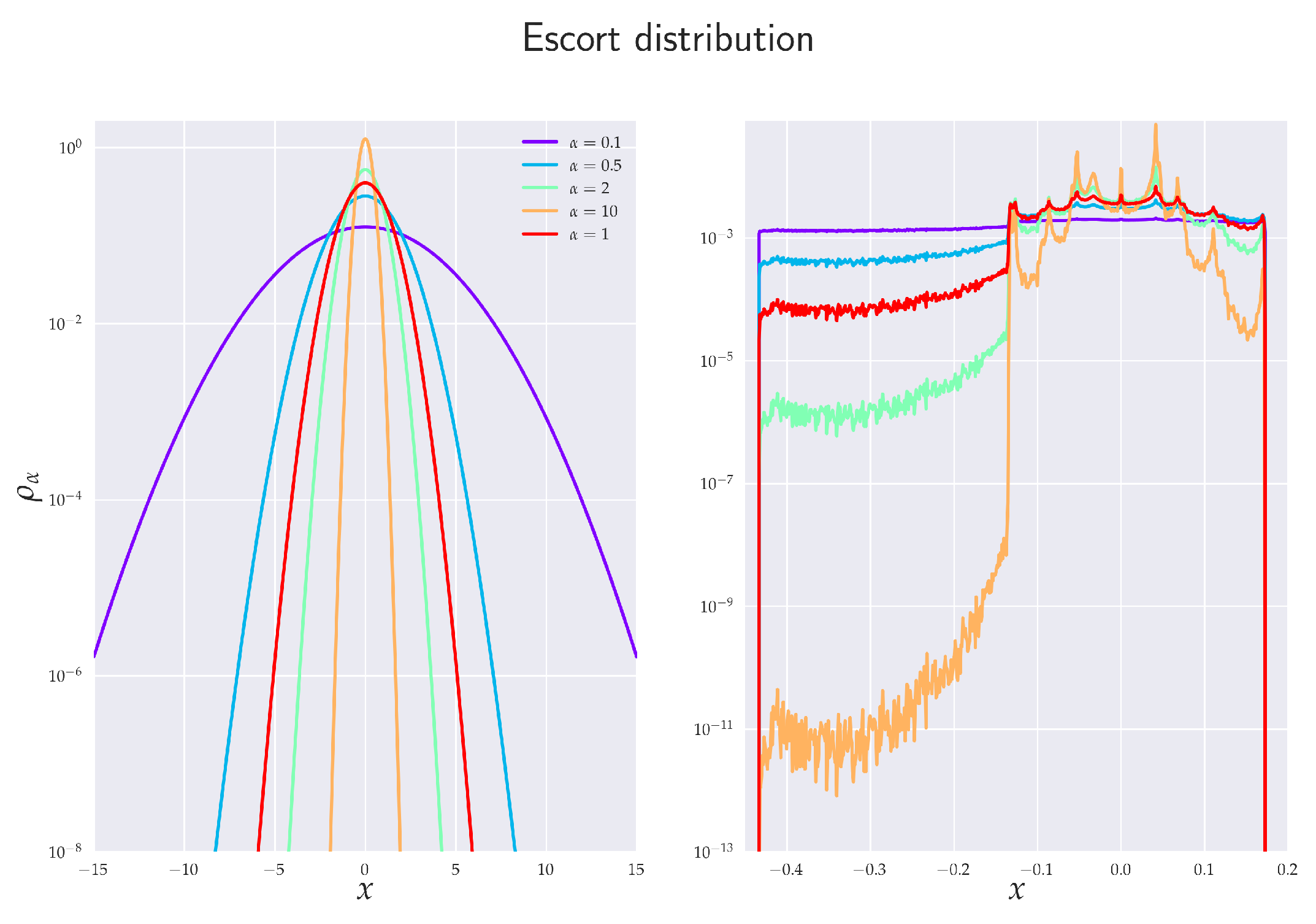
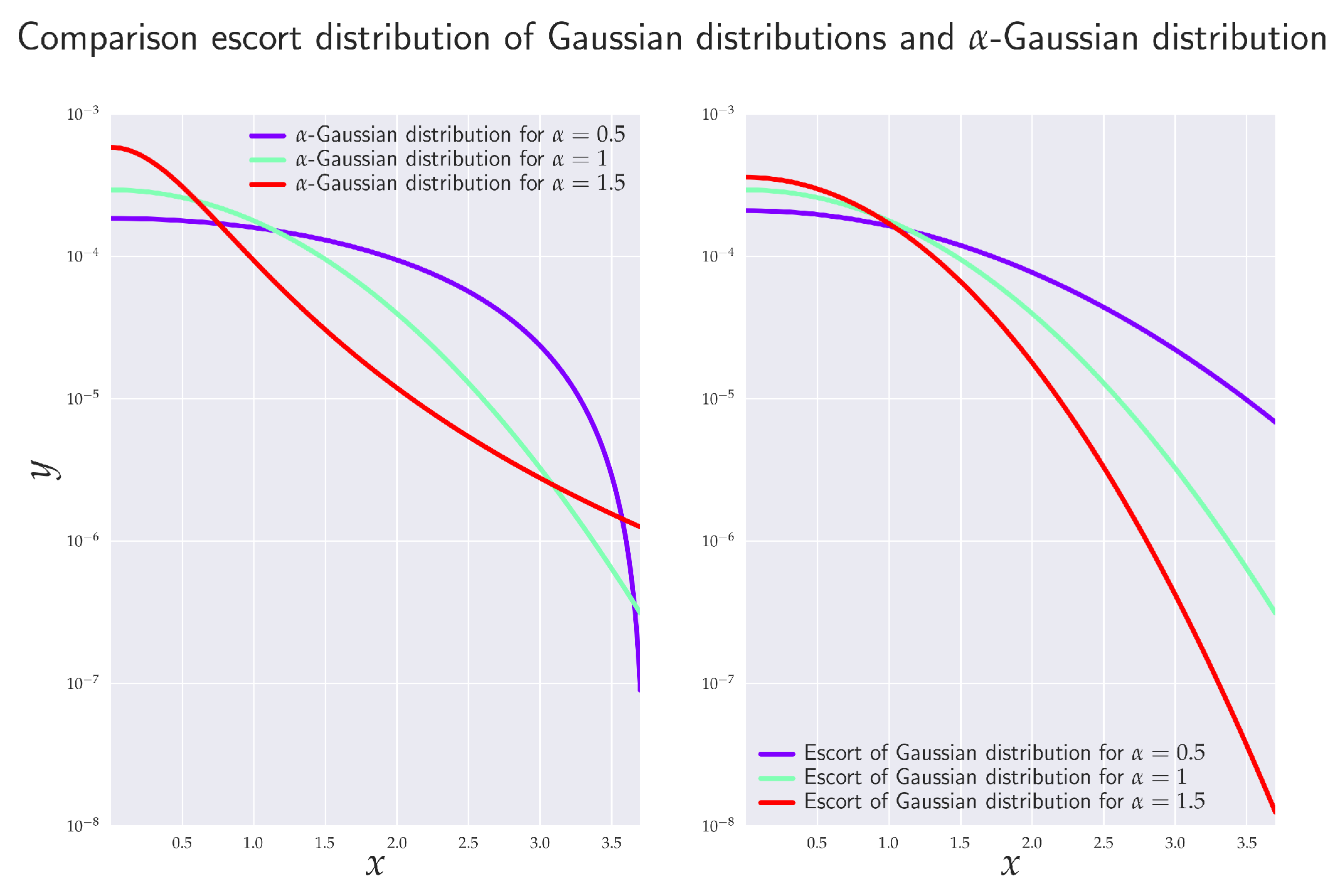
2.5. Escort Distribution
3. Rényi Transfer Entropy and Causality
3.1. Granger Causality—Gaussian Variables
3.2. Granger Causality—Heavy-Tailed Variables
4. Estimation of Rényi Entropy
4.1. RTE and Derived Concepts
4.1.1. Balance of Transfer Entropy
4.1.2. Effective Transfer Entropy
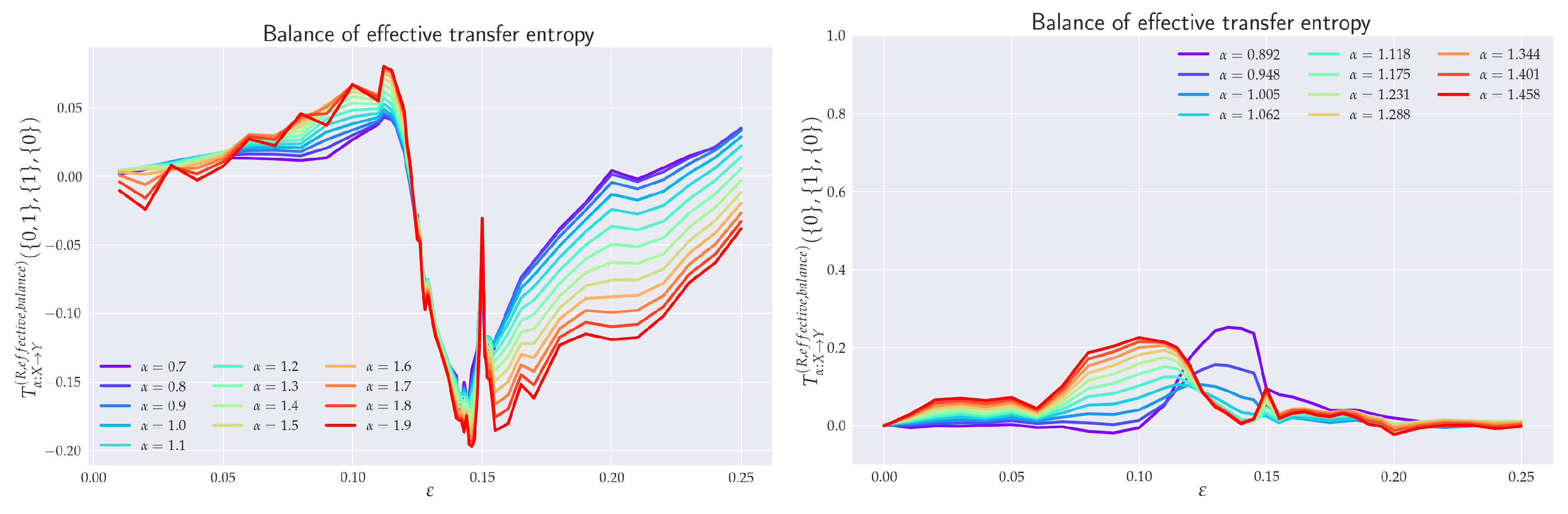
4.1.3. Balance of Effective Transfer Entropy
4.1.4. Choice of Parameters k and l
5. Rössler System
5.1. Equations for Master System
5.2. Equations for the Slave System
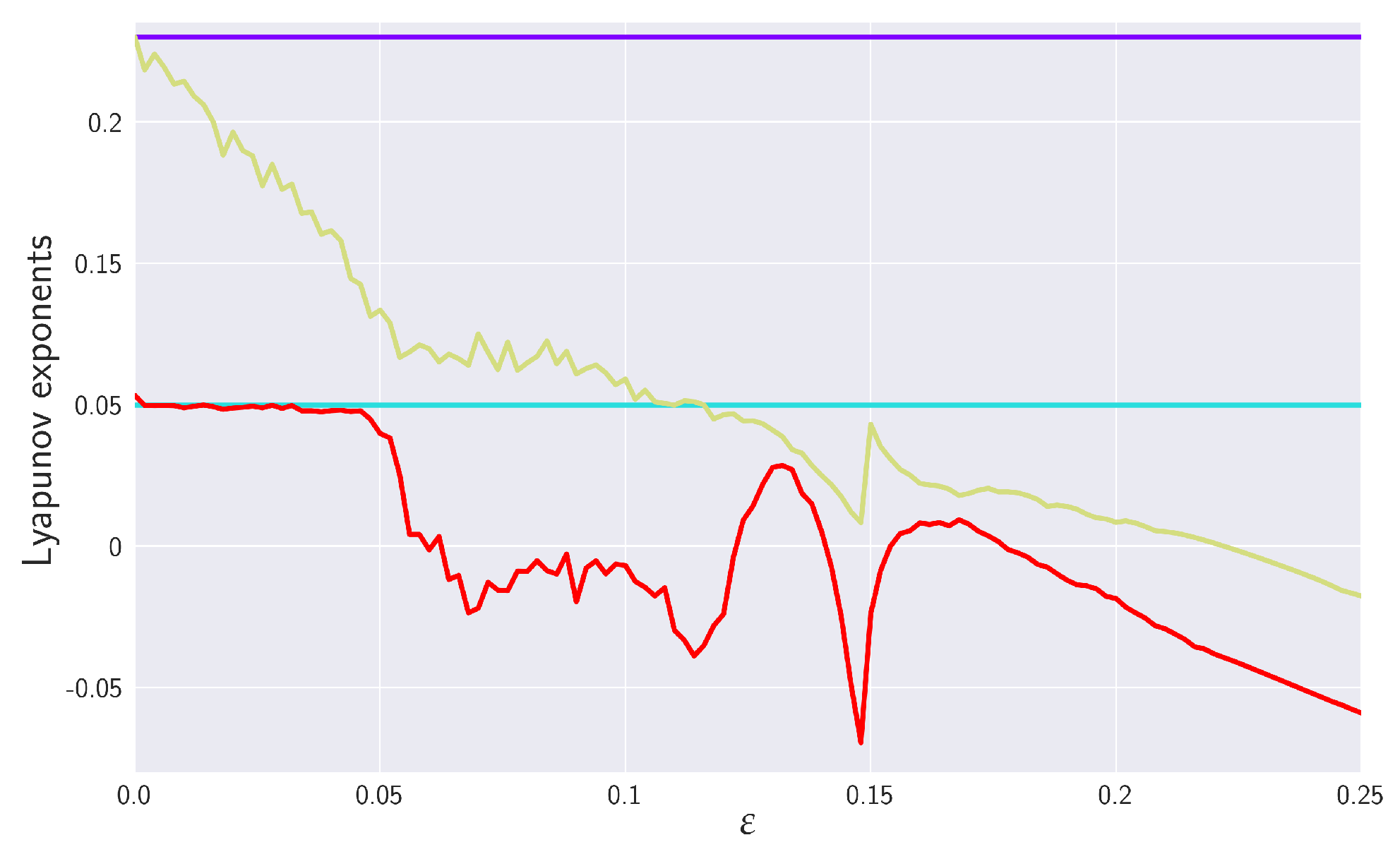
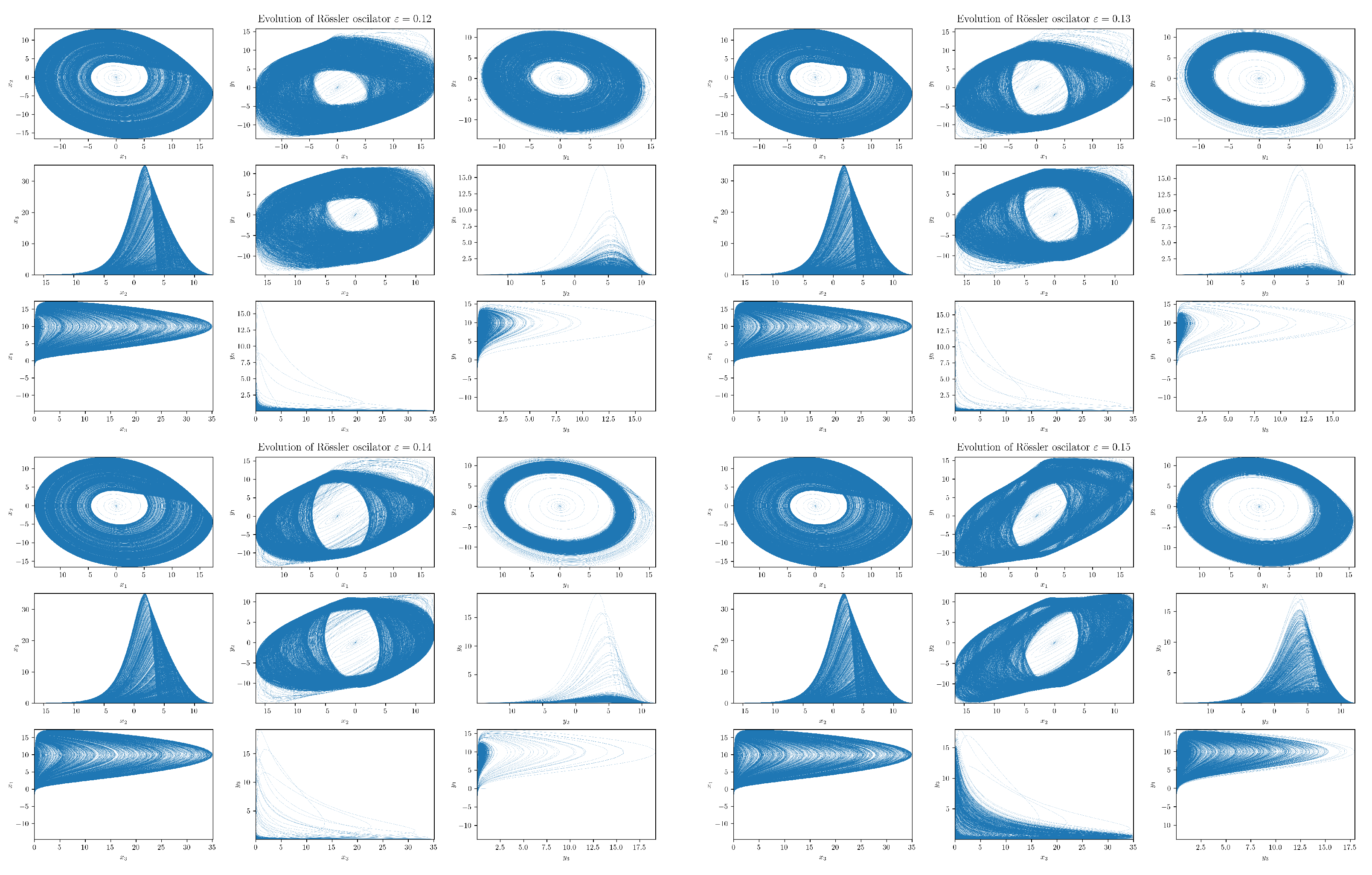
5.3. Numerical Experiments with Coupled RSs
Projections
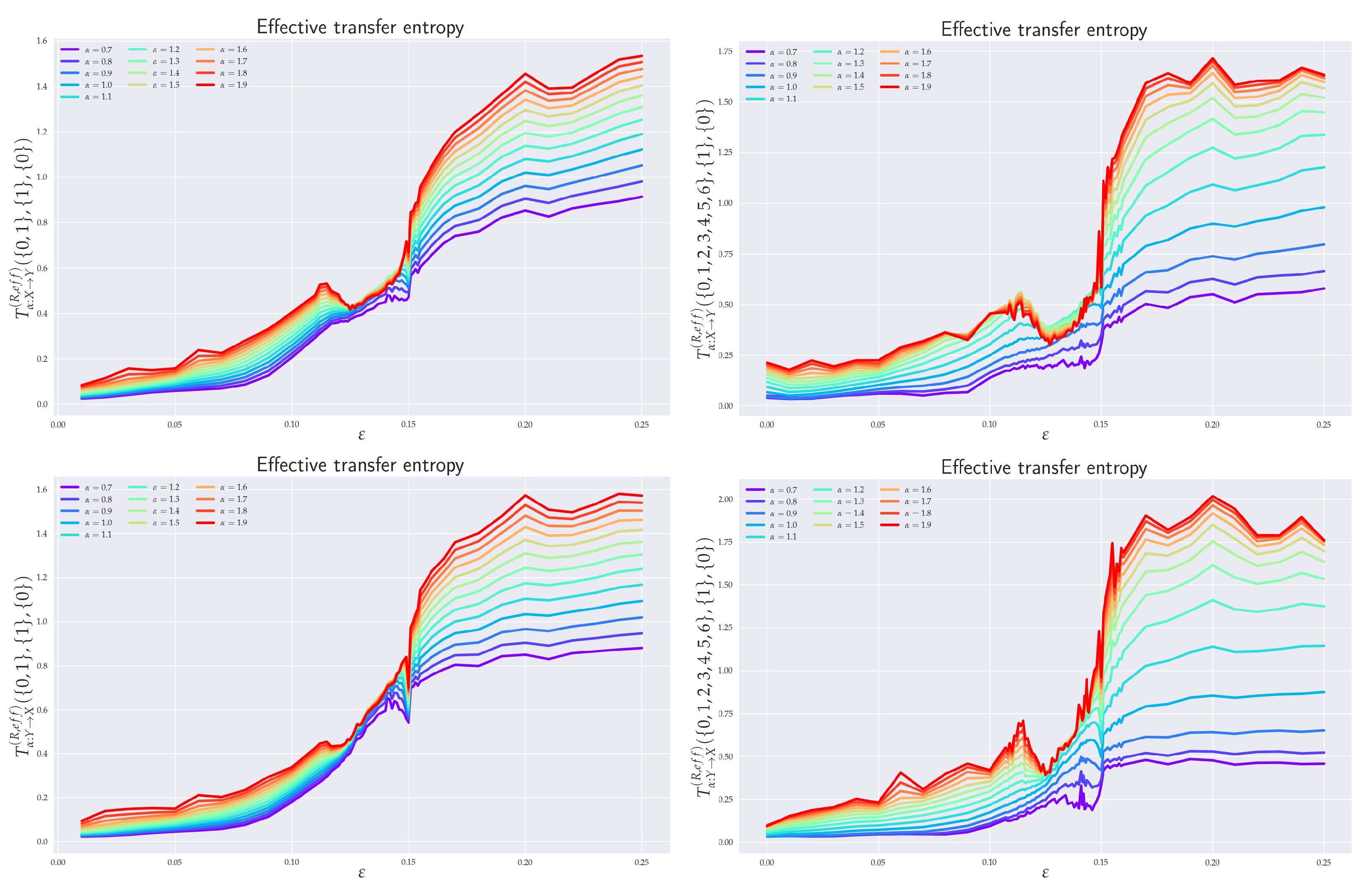
6. Numerical Analysis of RTE for Coupled RSs
6.1. Effective RTE between x1 and y1 Directions
6.2. Effective RTE between x3 and y3 Directions
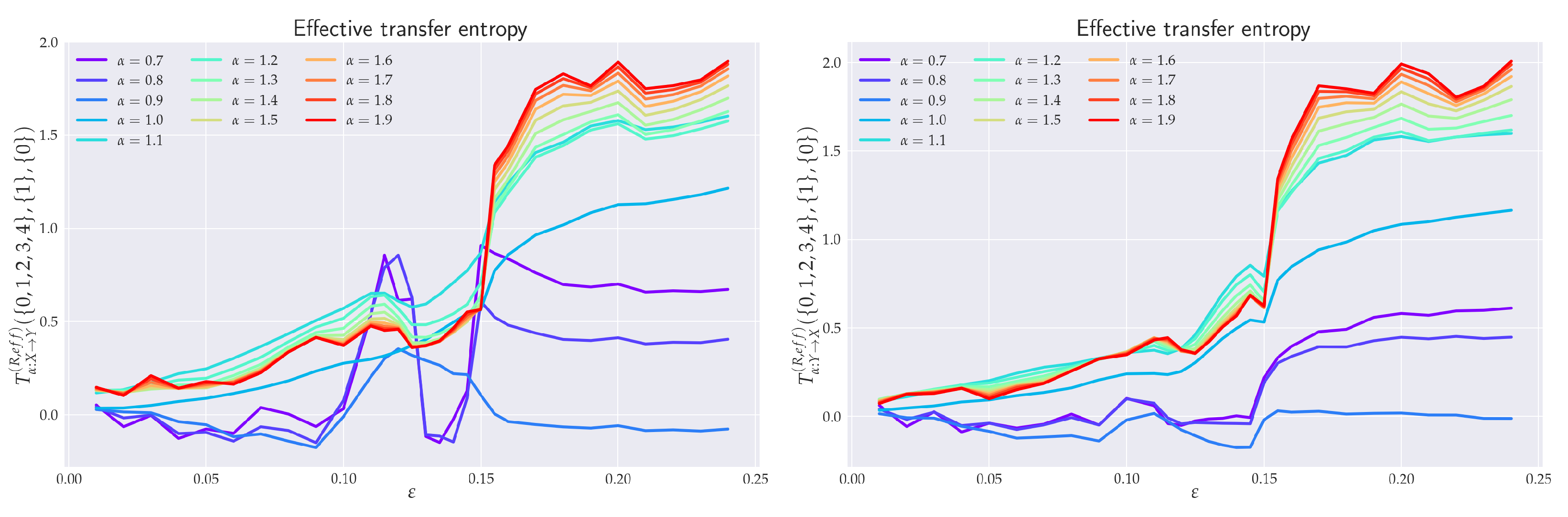
6.3. Effective RTE for the Full System
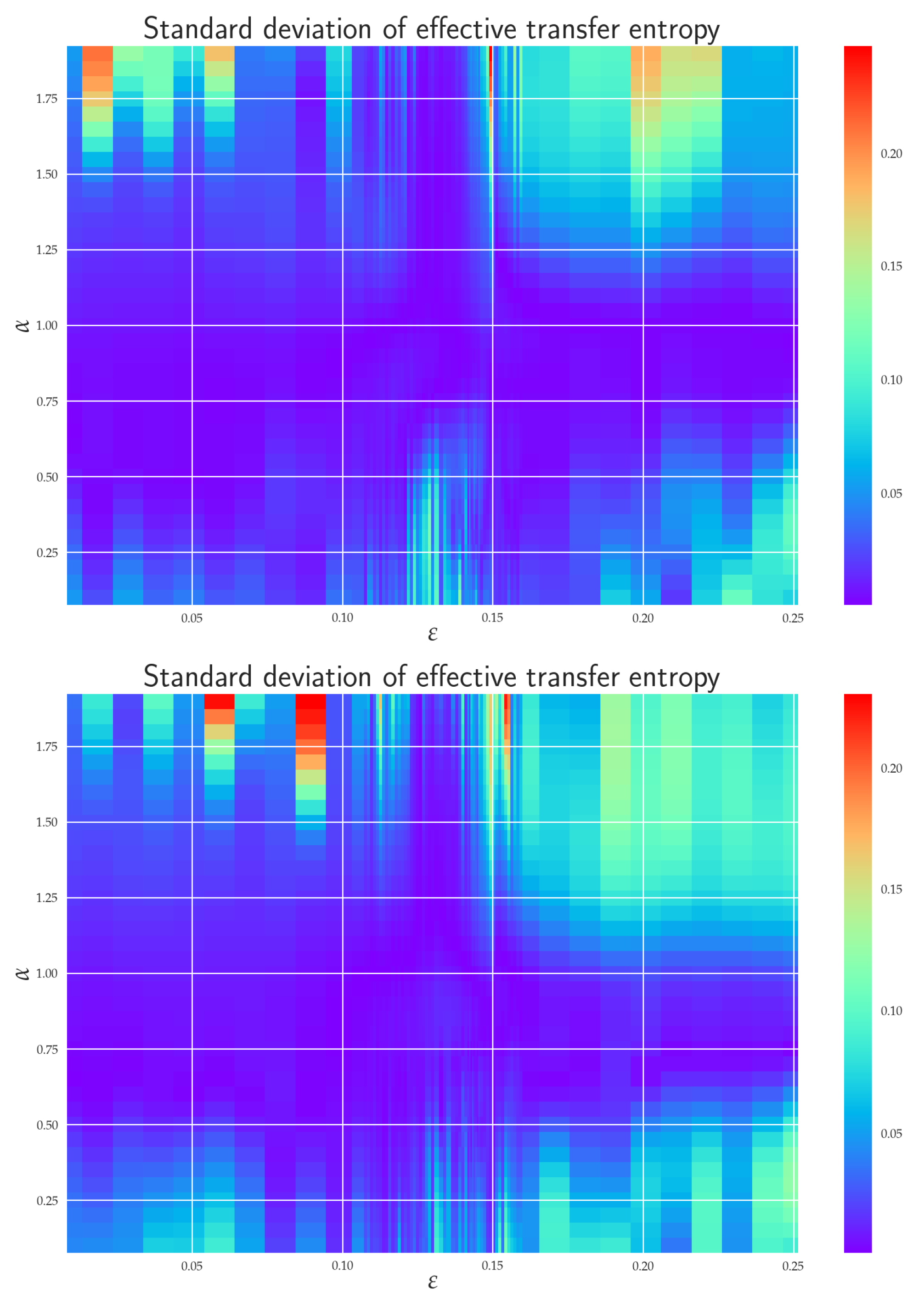
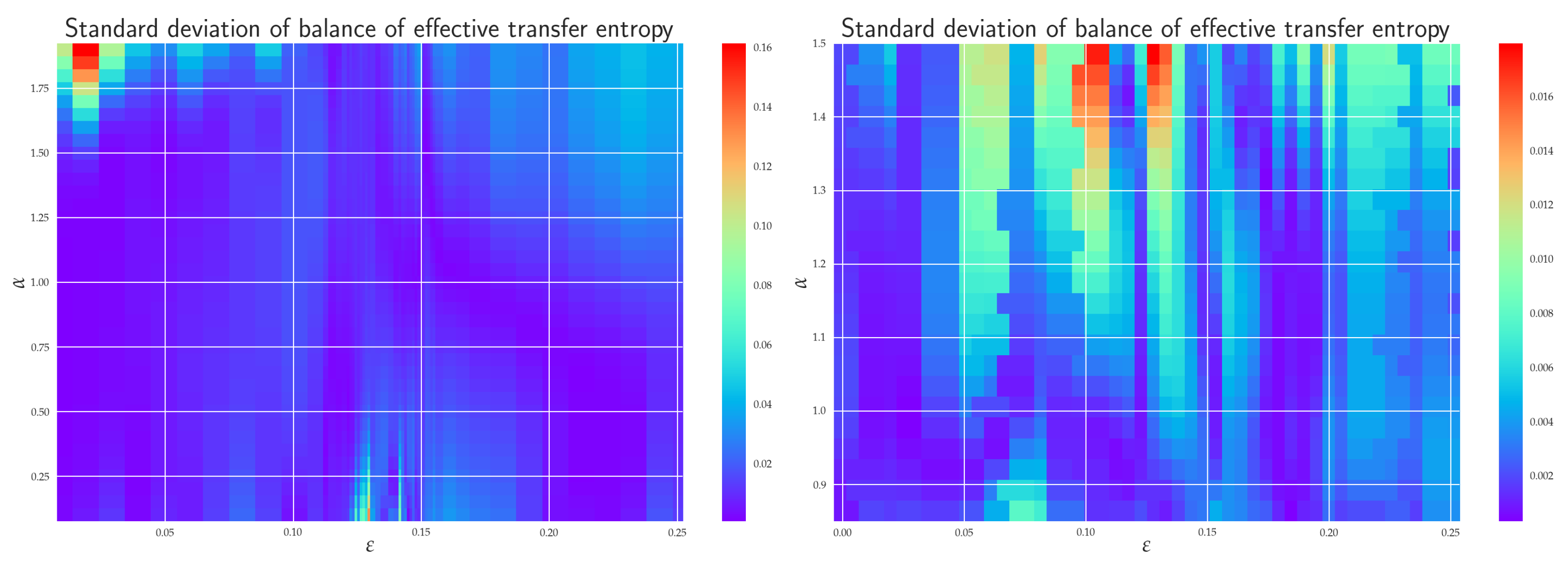
6.4. Balance of Effective RTE
7. Discussion and Conclusions
7.1. Theoretical Results
7.2. Numerical Analysis of RTE for Rössler Systems
7.3. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| RE | Rényi entropy |
| TE | transfer entropy |
| RTE | Rényi transfer entropy |
| probability density function | |
| ITE | information-theoretic entropy |
| RS | Rössler system |
| KSE | Kolmogorov–Sinai entropy rate |
| LE | Lyapunov exponent |
Appendix A
- It has relative accuracy for a small data set;
- It has applicability for high-dimensional data;
- The set estimators provide statistics for the estimation.
Appendix B

References
- Schreiber, T. Interdisciplinary application of nonlinear time series methods. Phys. Rep. 1999, 308, 1–64. [Google Scholar] [CrossRef]
- Kantz, H.; Schreiber, T. Nonlinear Time Series Analysis; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Pecora, L.M.; Carroll, T.L. Synchronization in chaotic systems. Phys. Rev. Lett. 1990, 64, 821–824. [Google Scholar] [CrossRef] [PubMed]
- Boccaletti, S.; Kurths, J.; Osipov, G.; Valladares, D.L.; Zhou, C.S. The synchronization of chaotic systems. Phys. Rep. 2002, 366, 1–101. [Google Scholar] [CrossRef]
- Quiroga, R.Q.; Arnhold, J.; Grassberger, P. Learning driver-response relationships from synchronization patterns. Phys. Rev. 2000, E61, 5142–5148. [Google Scholar] [CrossRef]
- Nawrath, J.; Romano, M.C.; Thiel, M.; Kiss, I.Z.; Wickramasinghe, M.; Timmer, J.; Kurths, J.; Schelter, B. Distinguishing Direct from Indirect Interactions in Oscillatory Networks with Multiple Time Scales. Phys. Rev. Lett. 2010, 104, 038701. [Google Scholar] [CrossRef] [PubMed]
- Sugihara, G.; May, R.; Ye, H.; Hsieh, C.; Deyle, E.; Fogarty, M.; Munch, S. Detecting causality in complex ecosystems. Science 2012, 338, 496–500. [Google Scholar] [CrossRef] [PubMed]
- Feldhoff, J.H.; Donner, R.V.; Donges, J.F.; Marwan, N.; Kurths, J. Geometric detection of coupling directions by means of inter-system recurrence networks. Phys. Lett. 2012, A376, 3504–3513. [Google Scholar] [CrossRef]
- Wiener, N. Modern Mathematics for Engineers; Beckenbach, E.F., Ed.; McGraw-Hill: New York, NY, USA, 1956. [Google Scholar]
- Granger, C.W.J. Investigating Causal Relations by Econometric Models and Cross-spectral Methods. Econometrica 1969, 37, 424–438. [Google Scholar] [CrossRef]
- Ancona, N.; Marinazzo, D.; Stramaglia, S. Radial basis function approach to nonlinear Granger causality of time series. Phys. Rev. 2004, R70, 056221. [Google Scholar] [CrossRef]
- Chen, Y.; Rangarajan, G.; Feng, J.; Ding, M. Analyzing multiple nonlinear time series with extended Granger causality. Phys. Lett. 2004, A324, 26–35. [Google Scholar] [CrossRef]
- Wismüller, A.; Souza, A.M.D.; Vosoughi, M.A.; Abidin, A.Z. Large-scale nonlinear Granger causality for inferring directed dependence from short multivariate time-series data. Sci. Rep. 2021, 11, 7817. [Google Scholar] [CrossRef]
- Zou, Y.; Romano, M.; Thiel, M.; Marwan, N.; Kurths, J. Inferring indirect coupling by means of recurrences. Int. J. Bifurc. Chaos 2011, 21, 1099–1111. [Google Scholar] [CrossRef]
- Donner, R.V.; Small, M.; Donges, J.F.; Marwan, N.; Zou, Y.; Xiang, R.; Kurths, J. Recurrence-based time series analysis by means of complex network methods. Int. J. Bifurc. Chaos 2011, 21, 1019–1046. [Google Scholar] [CrossRef]
- Romano, M.; Thiel, M.; Kurths, J.; Grebogi, C. Estimation of the direction of the coupling by conditional probabilities of recurrence. Phys. Rev. 2007, E76, 036211. [Google Scholar] [CrossRef] [PubMed]
- Vejmelka, M.; Paluš, M. Inferring the directionality of coupling with conditional mutual information. Phys. Rev. 2008, 77, 026214. [Google Scholar] [CrossRef] [PubMed]
- Paluš, M.; Krakovská, A.; Jakubík, J.; Chvosteková, M. Causality, dynamical systems and the arrow of time. Chaos 2018, 28, 075307. [Google Scholar] [CrossRef]
- Schreiber, T. Measuring Information Transfer. Phys. Rev. Lett. 2000, 85, 461–464. [Google Scholar] [CrossRef]
- Marschinski, R.; Kantz, H. Analysing the Information Flow Between Financial Time Series. Eur. Phys. J. B 2002, 30, 275–281. [Google Scholar] [CrossRef]
- Jizba, P.; Kleinert, H.; Shefaat, M. Rényi’s information transfer between financial time series. Physica A 2012, 391, 2971–2989. [Google Scholar] [CrossRef]
- Paluš, M.; Vejmelka, M. Directionality of coupling from bivariate time series: How to avoid false causalities and missed connections. Phys. Rev. 2007, 75, 056211. [Google Scholar] [CrossRef]
- Runge, J.; Heitzig, J.; Petoukhov, V.; Kurths, J. Escaping the Curse of Dimensionality in Estimating Multivariate Transfer Entropy. Phys. Rev. Lett. 2012, 108, 258701. [Google Scholar] [CrossRef] [PubMed]
- Faes, L.; Kugiumtzis, D.; Nollo, G.; Jurysta, F.; Marinazzo, D. Estimating the decomposition of predictive information in multivariate systems. Phys. Rev. 2015, 91, 032904. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Taylor, D.; Bollt, E.M. Causal Network Inference by Optimal Causation Entropy. SIAM J. Appl. Dyn. Syst. 2015, 14, 73–106. [Google Scholar] [CrossRef]
- Leonenko, N.; Pronzato, L.; Savani, V. A class of Rényi information estimators for multidimensional densities. Ann. Stat. 2008, 36, 2153–2182, Correction in Ann. Stat. 2008, 36, 3837–3838. [Google Scholar] [CrossRef]
- Lungarella, M.; Pitti, A.; Kuniyoshi, Y. Information transfer at multiple scales. Phys. Rev. 2007, 76, 056117. [Google Scholar] [CrossRef]
- Faes, L.; Nollo, G.; Stramaglia, S.; Marinazzo, D. Multiscale Granger causality. Phys. Rev. 2017, 76, 042150. [Google Scholar] [CrossRef]
- Paluš, M. Multiscale Atmospheric Dynamics: Cross-Frequency Phase-Amplitude Coupling in the Air Temperature. Phys. Rev. Lett. 2014, 112, 078702. [Google Scholar] [CrossRef]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics: Approaching a Complex World; Springer: New York, NY, USA, 2009. [Google Scholar]
- Thurner, S.; Hanel, R.; Klimek, P. Introduction to the Theory of Complex Systems; Oxford University Press: London, UK, 2018. [Google Scholar]
- Rössler, O.E. An equation for continuous chaos. Phys. Lett. 1976, 57, 397–398. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 5, 379–423, 623–656. [Google Scholar] [CrossRef]
- Jizba, P.; Arimitsu, T. The world according to Rényi: Thermodynamics of multifractal systems. Ann. Phys. 2004, 312, 17–59. [Google Scholar] [CrossRef]
- Burg, J.P. The Relationship Between Maximum Entropy Spectra In addition, Maximum Likelihood Spectra. Geophysics 1972, 37, 375–376. [Google Scholar] [CrossRef]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Havrda, J.; Charvát, F. Quantification Method of Classification Processes: Concept of Structural α-Entropy. Kybernetika 1967, 3, 30–35. [Google Scholar]
- Frank, T.; Daffertshofer, A. Exact time-dependent solutions of the Rényi Fokker–Planck equation and the Fokker–Planck equations related to the entropies proposed by Sharma and Mittal. Physica A 2000, 285, 352–366. [Google Scholar] [CrossRef]
- Sharma, B.D.; Mitter, J.; Mohan, M. On measures of “useful” information. Inf. Control 1978, 39, 323–336. [Google Scholar] [CrossRef][Green Version]
- Jizba, P.; Korbel, J. On q-non-extensive statistics with non-Tsallisian entropy. Physica A 2016, 444, 808–827. [Google Scholar] [CrossRef]
- Vos, G. Generalized additivity in unitary conformal field theories. Nucl. Phys. B 2015, 899, 91–111. [Google Scholar] [CrossRef]
- Rényi, A. Probability Theory; North-Holland: Amsterdam, The Netherlands, 1970. [Google Scholar]
- Rényi, A. Selected Papers of Alfréd Rényi, 2nd ed.; Akademia Kiado: Budapest, Hungary, 1976. [Google Scholar]
- Campbell, L.L. A coding theorem and Rényi’s entropy. Inf. Control 1965, 8, 423–429. [Google Scholar] [CrossRef]
- Csiszár, I. Generalized cutoff rates and Rényi’s information measures. IEEE Trans. Inform. Theory 1995, 26, 26–34. [Google Scholar] [CrossRef]
- Csiszár, I.; Shields, P.C. Information and Statistics: A Tutorial; Publishers Inc.: Boston, MA, USA, 2004. [Google Scholar]
- Aczél, J.; Darótzy, Z. Measure of Information and Their Characterizations; Academic Press: New York, NY, USA, 1975. [Google Scholar]
- Halsey, T.C.; Jensen, M.H.; Kadanoff, L.P.; Procaccia, I.; Schraiman, B.I. Fractal measures and their singularities: The characterization of strange sets. Phys. Rev. 1986, A33, 1141–1151. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Fractals: Form, Chance and Dimension; W. H. Freeman: San Francisco, CA, USA, 1977. [Google Scholar]
- Bengtsson, I.; Życzkowski, K. Geometry of Quantum States. An Introduction to Quantum Entanglement; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Jizba, P.; Korbel, J. Maximum Entropy Principle in Statistical Inference: Case for Non-Shannonian Entropies. Phys. Rev. Lett. 2019, 122, 120601. [Google Scholar] [CrossRef] [PubMed]
- Jizba, P.; Korbel, J. When Shannon and Khinchin meet Shore and Johnson: Equivalence of information theory and statistical inference axiomatics. Phys. Rev. 2020, E101, 042126. [Google Scholar] [CrossRef] [PubMed]
- Lesche, B. Instabilities of Rényi entropies. J. Stat. Phys. 1982, 27, 419–422. [Google Scholar] [CrossRef]
- Rényi, A. On measures of entropy and information. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 20–30 June 1961; pp. 547–561. [Google Scholar]
- Jizba, P.; Ma, Y.; Hayes, A.; Dunningham, J.A. One-parameter class of uncertainty relations based on entropy power. Phys. Rev. E 2016, 93, 060104(R). [Google Scholar] [CrossRef]
- Hentschel, H.G.E.; Procaccia, I. The infinite number of generalized dimensions of fractals and strange attractors. Physica D 1983, 8, 435–444. [Google Scholar] [CrossRef]
- Harte, D. Multifractals Theory and Applications; Chapman and Hall: New York, NY, USA, 2019. [Google Scholar]
- Latora, V.; Baranger, M. Kolmogorov–Sinai Entropy Rate versus Physical Entropy. Phys. Rev. Lett. 1999, 82, 520–523. [Google Scholar] [CrossRef]
- Jizba, P.; Korbel, J. On the Uniqueness Theorem for Pseudo-Additive Entropies. Entropy 2017, 19, 605. [Google Scholar] [CrossRef]
- Geweke, J. Measurement of Linear Dependence and Feedback between Multiple Time Series. J. Am. Stat. Assoc. 1982, 77, 304–313. [Google Scholar] [CrossRef]
- Barnett, L.; Barrett, A.B.; Seth, A.K. Granger Causality and Transfer Entropy are Equivalent for Gaussian Variables. Phys. Rev. Lett. 2009, 103, 238701. [Google Scholar] [CrossRef]
- Jizba, P.; Dunningham, J.A.; Joo, J. Role of information theoretic uncertainty relations in quantum theory. Ann. Phys. 2015, 355, 87–114. [Google Scholar] [CrossRef]
- Seth, A.K. A MATLAB toolbox for Granger causal connectivity analysis. J. Neurosci. Methods 2010, 186, 262–273. [Google Scholar] [CrossRef] [PubMed]
- Jizba, P.; Korbel, J. Multifractal Diffusion Entropy Analysis: Optimal Bin Width of Probability Histograms. Physica A 2014, 413, 438–458. [Google Scholar] [CrossRef]
- Kečkić, J.D.; Vasić, P.M. Some inequalities for the gamma function. Publ. De L’Institut Mathématique 1971, 11, 107–114. [Google Scholar]
- Fisher, R.A.; Yates, F. Statistical Tables for Biological, Agricultural and Medical Research, 3rd ed.; Oliver & Boyd: Edinburgh, UK, 1963. [Google Scholar]
- Matsumoto, M.; Nishimura, T. Mersenne Twister: A 623-Dimensionally Equidistributed Uniform Pseudo-Random Number Generator. ACM Trans. Model. Comput. Simul. 1998, 8, 3–30. [Google Scholar] [CrossRef]
- Theiler, J.; Eubank, S.; Longtin, A.; Galdrikian, B.; Farmer, J.D. Testing for nonlinearity in time series: The method of surrogate data. Physica D 1992, 58, 77–94. [Google Scholar] [CrossRef]
- Schreiber, T.; Schmitz, A. Improved Surrogate Data for Nonlinearity Tests. Phys. Rev. Lett. 1996, 77, 635–638. [Google Scholar] [CrossRef]
- Schreiber, T.; Schmitz, A. Surrogate time series. Physica D 2000, 142, 346–382. [Google Scholar] [CrossRef]
- Paluš, M. Linked by Dynamics: Wavelet-Based Mutual Information Rate as a Connectivity Measure and Scale-Specific Networks. In Advances in Nonlinear Geosciences; Springer International Publishing: Cham, Switzerland, 2018; pp. 427–463. [Google Scholar]
- Rosenblum, M.G.; Pikovsky, A.; Kurths, J. Phase Synchronization of Chaotic Oscillators. Phys. Rev. Lett. 1996, 76, 1804–1807. [Google Scholar] [CrossRef]
- Cheng, A.L.; Chen, Y.Y. Analyzing the synchronization of Rössler systems—When trigger-and-reinject is equally important as the spiral motion. Phys. Lett. 2017, 381, 3641–3651. [Google Scholar] [CrossRef]
- Rössler, O.E. Different Types of Chaos in Two Simple Differential Equations. Z. Naturforsch. 1976, 31, 1664–1670. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.; Travis, E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]
- Hunter, J.D. Matplotlib: A 2D Graphics Environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef] [PubMed]
- Use Branch tranfer_entropy. Available online: https://github.com/jajcayn/pyclits (accessed on 16 March 2022).
- Dobrushin, R.L. A simplified method of experimentally evaluating the entropy of a stationary sequence. Teor. Veroyatnostei I Ee Primen. 1958, 3, 462–464. [Google Scholar] [CrossRef]
- Vašíček, O. A test for normality based on sample entropy. J. Roy. Stat. Soc. Ser. B Methodol. 1976, 38, 54–59. [Google Scholar]
- Kaiser, A.; Schreiber, T. Information transfer in continuous processes. Physica D 2002, 166, 43–62. [Google Scholar] [CrossRef]
- Silverman, B.W. Density Estimation for Statistics and Data Analysis; Chapman & Hall: London, UK, 1986. [Google Scholar]
- Kraskov, A.; Stögbauer, H.; Grassberger, P. Estimating mutual information. Phys. Rev. 2004, 69, 066138. [Google Scholar] [CrossRef]
- Frenzel, S.; Pompe, B. Partial Mutual Information for Coupling Analysis of Multivariate Time Series. Phys. Rev. Lett. 2007, 99, 204101. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jizba, P.; Lavička, H.; Tabachová, Z. Causal Inference in Time Series in Terms of Rényi Transfer Entropy. Entropy 2022, 24, 855. https://doi.org/10.3390/e24070855
Jizba P, Lavička H, Tabachová Z. Causal Inference in Time Series in Terms of Rényi Transfer Entropy. Entropy. 2022; 24(7):855. https://doi.org/10.3390/e24070855
Chicago/Turabian StyleJizba, Petr, Hynek Lavička, and Zlata Tabachová. 2022. "Causal Inference in Time Series in Terms of Rényi Transfer Entropy" Entropy 24, no. 7: 855. https://doi.org/10.3390/e24070855
APA StyleJizba, P., Lavička, H., & Tabachová, Z. (2022). Causal Inference in Time Series in Terms of Rényi Transfer Entropy. Entropy, 24(7), 855. https://doi.org/10.3390/e24070855






