Replication in Energy Markets: Use and Misuse of Chaos Tools
Abstract
:1. Introduction
2. The “Core” of Chaos: Its Definition
3. Methodologies
3.1. Phase Space Reconstruction
3.2. Modified Correlation Entropy
3.3. Noise Level
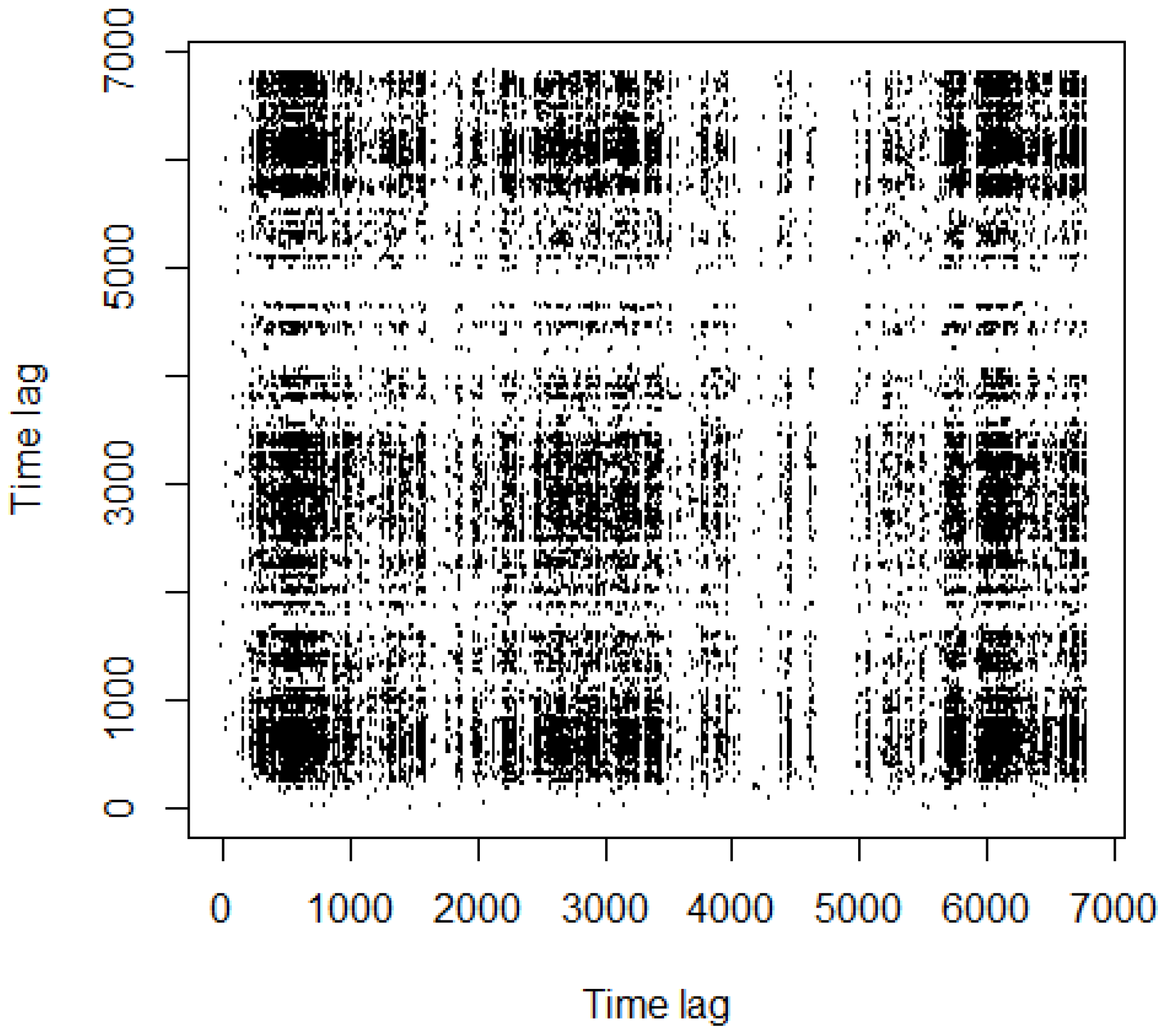
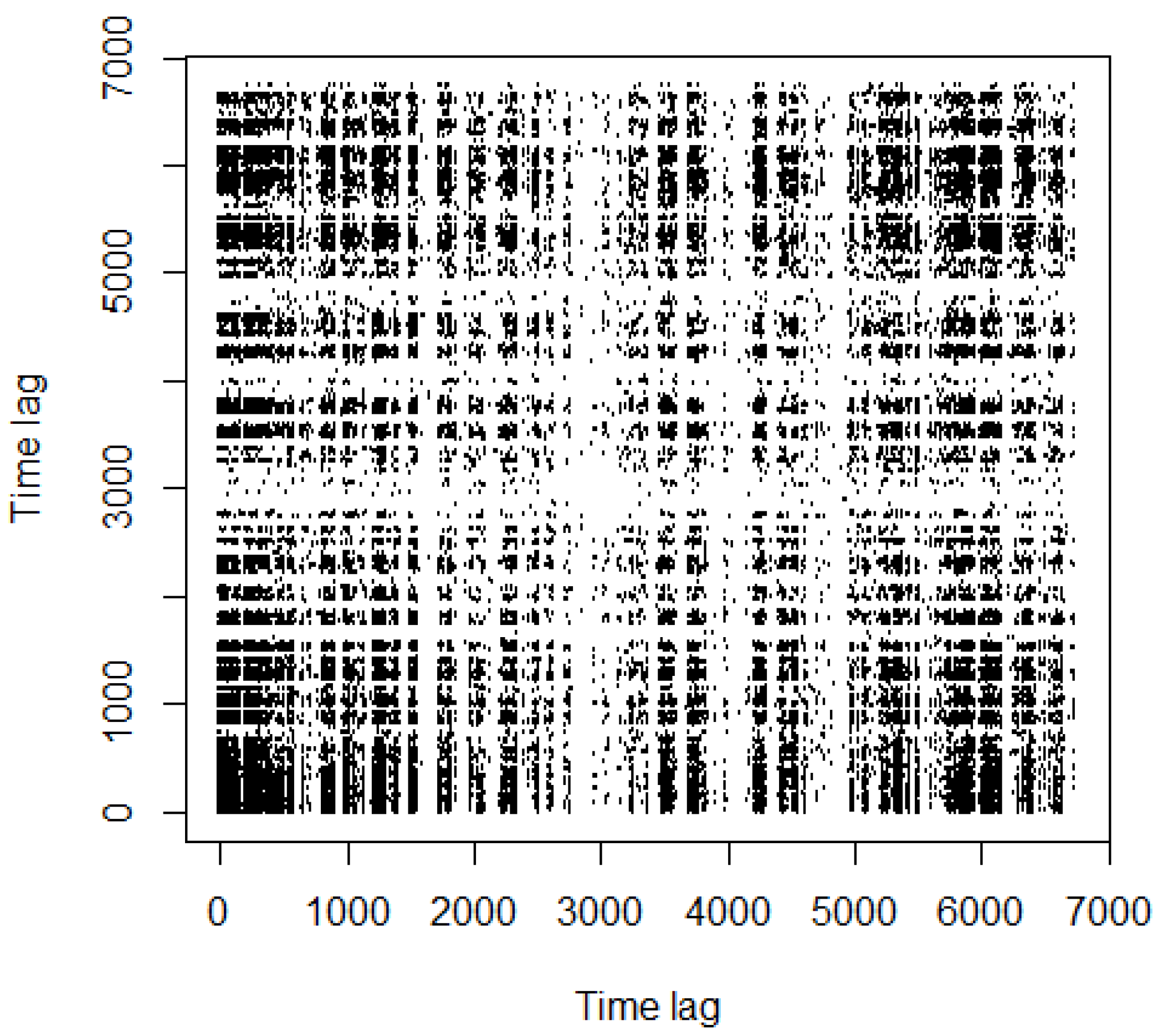
3.4. Recurrence Analysis
4. Implications of the New Approach
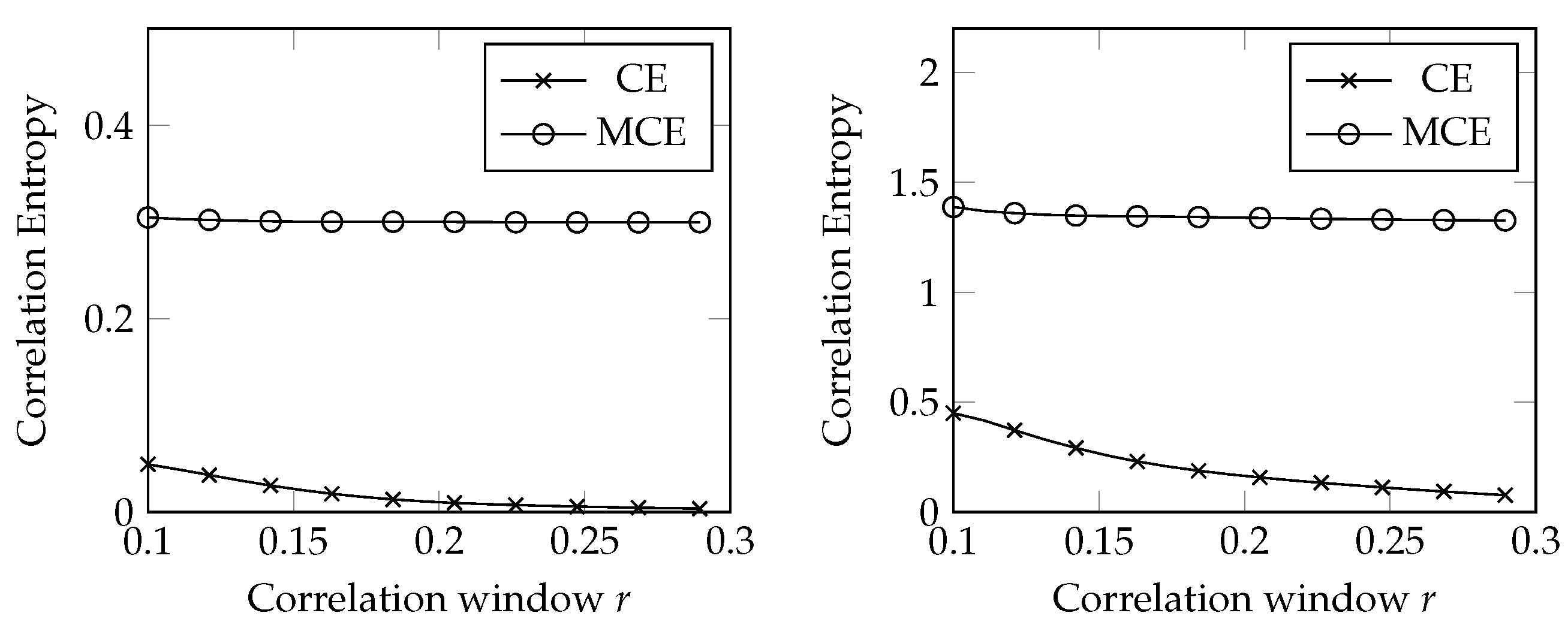
- The KS entropy estimated with a noise-oblivious approach is much smaller than the MCE;
- The CE decays as the size of the correlation window increases, whereas the MCE is rather steady.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tol, R.S. Special issue on replication. Energy Econ. 2018, 82, 1–3. [Google Scholar] [CrossRef]
- Mastroeni, L.; Vellucci, P. Chaos Versus Stochastic Paradigm in Energy Markets. In Handbook of Energy Finance: Theories, Practices and Simulations; World Scientific: Singapore, 2019; pp. 765–786. [Google Scholar]
- Mastroeni, L.; Vellucci, P.; Naldi, M. Co-existence of stochastic and chaotic behaviour in the copper price time series. Resour. Policy 2018, 58, 295–302. [Google Scholar] [CrossRef]
- Mastroeni, L.; Vellucci, P.; Naldi, M. A reappraisal of the chaotic paradigm for energy commodity prices. Energy Econ. 2019, 82, 167–178. [Google Scholar] [CrossRef]
- Orlando, G.; Bufalo, M.; Stoop, R. Financial markets’ deterministic aspects modeled by a low-dimensional equation. Sci. Rep. 2022, 12, 1693. [Google Scholar] [CrossRef] [PubMed]
- Hirata, Y. Recurrence plots for characterizing random dynamical systems. Commun. Nonlinear Sci. Numer. Simul. 2021, 94, 105552. [Google Scholar] [CrossRef]
- Adrangi, B.; Chatrath, A.; Dhanda, K.K.; Raffiee, K. Chaos in oil prices? Evidence from futures markets. Energ. Econ. 2001, 23, 405–425. [Google Scholar] [CrossRef] [Green Version]
- Barkoulas, J.T.; Chakraborty, A.; Ouandlous, A. A metric and topological analysis of determinism in the crude oil spot market. Energ. Econ. 2012, 34, 584–591. [Google Scholar] [CrossRef]
- Carrasco, R.; Vargas, M.; Alfaro, M.; Soto, I.; Fuertes, G. Copper Metal Price Using Chaotic Time Series Forecasting. IEEE Lat. Am. Trans. 2015, 13, 1961–1965. [Google Scholar] [CrossRef]
- Chwee, V. Chaos in Natural Gas Futures? Energy J. 1998, 19, 149–164. [Google Scholar] [CrossRef]
- Cortez, C.A.T.; Hitch, M.; Sammut, C.; Coulton, J.; Shishko, R.; Saydam, S. Determining the embedding parameters governing long-term dynamics of copper prices. Chaos Solitons Fractals 2018, 111, 186–197. [Google Scholar] [CrossRef]
- Kyrtsou, C.; Malliaris, A.G.; Serletis, A. Energy sector pricing: On the role of neglected nonlinearity. Energ. Econ. 2009, 31, 492–502. [Google Scholar] [CrossRef]
- Matilla-García, M. Nonlinear Dynamics in Energy Futures. Energy J. 2007, 28, 7–29. [Google Scholar] [CrossRef]
- Moshiri, S.; Foroutan, F. Forecasting nonlinear crude oil futures prices. Energy J. 2006, 27, 81–95. [Google Scholar] [CrossRef]
- Panas, E. Long memory and chaotic models of prices on the London Metal Exchange. Resour. Policy 2001, 27, 235–246. [Google Scholar] [CrossRef]
- Panas, E.; Ninni, V. Are oil markets chaotic? A non-linear dynamic analysis. Energ. Econ. 2000, 22, 549–568. [Google Scholar] [CrossRef]
- Serletis, A.; Gogas, P. The North American Natural Gas Liquids Markets are Chaotic. Energy J. 1999, 20, 83–103. [Google Scholar] [CrossRef] [Green Version]
- Devaney, R.L. An Introduction to Chaotic Dynamical Systems; Addison-Wesley Reading: Reading, MA, USA, 1989; Volume 13046. [Google Scholar]
- Martelli, M.; Dang, M.; Seph, T. Defining chaos. Math. Mag. 1998, 71, 112–122. [Google Scholar] [CrossRef]
- Ikeguchi, T.; Aihara, K. Lyapunov spectral analysis on random data. Int. J. Bifurcat. Chaos 1997, 7, 1267–1282. [Google Scholar] [CrossRef]
- Tanaka, T.; Aihara, K.; Taki, M. Lyapunov exponents of random time series. Phys. Rev. E 1996, 54, 2122. [Google Scholar] [CrossRef]
- Tanaka, T.; Aihara, K.; Taki, M. Analysis of positive Lyapunov exponents from random time series. Phys. D 1998, 111, 42–50. [Google Scholar] [CrossRef]
- Yousefpoor, P.; Esfahani, M.; Nojumi, H. Looking for systematic approach to select chaos tests. Appl. Math. Comput. 2008, 198, 73–91. [Google Scholar] [CrossRef]
- Packard, N.H.; Crutchfield, J.P.; Farmer, J.D.; Shaw, R.S. Geometry from a time series. Phys. Rev. Lett. 1980, 45, 712. [Google Scholar] [CrossRef]
- Takens, F. Detecting Strange Attractors in Turbulence. In Dynamical Systems and Turbulence, Warwick 1980; Springer: Berlin/Heidelberg, Germany, 1981; pp. 366–381. [Google Scholar]
- Ruelle, D. Chaotic Evolution and Strange Attractors; Cambridge University Press: Cambridge, UK, 1989; Volume 1. [Google Scholar]
- Mayfield, E.S.; Mizrach, B. On Determining the Dimension of Real-Time Stock-Price Data. J. Bus. Econ. Stat. 1992, 10, 367–374. [Google Scholar] [CrossRef]
- Kennel, M.B.; Brown, R.; Abarbanel, H.D.I. Determining embedding dimension for phase-space reconstruction using a geometrical construction. Phys. Rev. A 1992, 45, 3403–3411. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grassberger, P.; Procaccia, I. Estimation of the Kolmogorov entropy from a chaotic signal. Phys. Rev. A 1983, 28, 2591. [Google Scholar] [CrossRef] [Green Version]
- Frank, M.; Blank, H.R.; Heindl, J.; Kaltenhäuser, M.; Köchner, H.; Kreische, W.; Müller, N.; Poscher, S.; Sporer, R.; Wagner, T. Improvement of K2-entropy calculations by means of dimension scaled distances. Phys. D Nonlinear Phenom. 1993, 65, 359–364. [Google Scholar] [CrossRef]
- Jayawardena, A.W.; Xu, P.; Li, W.K. Modified correlation entropy estimation for a noisy chaotic time series. Chaos Interdiscip. J. Nonlinear Sci. 2010, 20, 023104. [Google Scholar] [CrossRef] [Green Version]
- Diks, C. Nonlinear Time Series Analysis: Methods and Applications; World Scientific: Singapore, 1999. [Google Scholar]
- Jayawardena, A.W.; Xu, P.; Li, W.K. A method of estimating the noise level in a chaotic time series. Chaos Interdiscip. J. Nonlinear Sci. 2008, 18, 023115. [Google Scholar] [CrossRef] [Green Version]
- Marwan, N.; Romano, M.C.; Thiel, M.; Kurths, J. Recurrence plots for the analysis of complex systems. Phys. Rep. 2007, 438, 237–329. [Google Scholar] [CrossRef]
- Orlando, G.; Zimatore, G. Recurrence quantification analysis of business cycles. Chaos Solitons Fractals 2018, 110, 82–94. [Google Scholar] [CrossRef]
- Eckmann, J.P.; Kamphorst, S.O.; Ruelle, D. Recurrence Plots of Dynamical Systems. EPL Europhys. Lett. 1987, 4, 973. [Google Scholar] [CrossRef] [Green Version]
- Mindlin, G.M.; Gilmore, R. Topological analysis and synthesis of chaotic time series. Phys. D Nonlinear Phenom. 1992, 58, 229–242. [Google Scholar] [CrossRef]
- Koebbe, M.; Mayer-Kress, G. Use of recurrence plots in the analysis of time-series data. In Santa Fe Institute Studies in Sciences of Complexity; Addison-Wesley Publishing Co.: Boston, MA, USA, 1992; Volume 12, p. 361. [Google Scholar]
- Zbilut, J.P.; Webber, C.L. Embeddings and delays as derived from quantification of recurrence plots. Phys. Lett. A 1992, 171, 199–203. [Google Scholar] [CrossRef]
- Kantz, H.; Schreiber, T. Nonlinear Time Series Analysis; Cambridge University Press: Cambridge, UK, 2004; Volume 7. [Google Scholar]
- Bianchi, F.M.; Livi, L.; Alippi, C. Investigating Echo-State Networks Dynamics by Means of Recurrence Analysis. IEEE Trans. Neural Netw. Learn. Syst. 2016, 29, 427–439. [Google Scholar] [CrossRef] [PubMed]
- Pomeau, Y.; Manneville, P. Intermittent transition to turbulence in dissipative dynamical systems. Commun. Math. Phys. 1980, 74, 189–197. [Google Scholar] [CrossRef]
- Bergé, P.; Dubois, M.; Mannevillel, P.; Pomeau, Y. Intermittency in Rayleigh-Bénard convection. J. Phys. Lett. 1980, 41, 341–345. [Google Scholar] [CrossRef]
- Bersini, H.; Sener, P. The connections between the frustrated chaos and the intermittency chaos in small Hopfield networks. Neural Netw. 2002, 15, 1197–1204. [Google Scholar] [CrossRef]
- Peterka, F.; Kotera, T.; Čipera, S. Explanation of appearance and characteristics of intermittency chaos of the impact oscillator. Chaos Solitons Fractals 2004, 19, 1251–1259. [Google Scholar] [CrossRef]
- Reinhart, C.M.; Rogoff, K.S. This Time Is Different: Eight Centuries of Financial Folly; Princeton University Press: Princeton, NJ, USA, 2009. [Google Scholar]
- Chen, P. Economic Complexity and Equilibrium Illusion: Essays on Market Instability and Macro Vitality; Routledge: London, UK, 2010. [Google Scholar]
- Chian, A.C.L.; Rempel, E.L.; Rogers, C. Crisis-induced intermittency in non-linear economic cycles. Appl. Econ. Lett. 2007, 14, 211–218. [Google Scholar] [CrossRef]
- Bornholdt, S. Expectation bubbles in a spin model of markets: Intermittency from frustration across scales. Int. J. Mod. Phys. C 2001, 12, 667–674. [Google Scholar] [CrossRef] [Green Version]
- Orlando, G.; Zimatore, G. Business cycle modeling between financial crises and black swans: Ornstein–Uhlenbeck stochastic process vs Kaldor deterministic chaotic model. Chaos Interdiscip. J. Nonlinear Sci. 2020, 30, 083129. [Google Scholar] [CrossRef] [PubMed]
- Ott, E. Chaos in Dynamical Systems; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Klimaszewska, K.; Żebrowski, J.J. Detection of the type of intermittency using characteristic patterns in recurrence plots. Phys. Rev. E 2009, 80, 026214. [Google Scholar] [CrossRef] [PubMed]
- Barnett, W.A.; Serletis, A. Martingales, nonlinearity, and chaos. J. Econ. Dyn. Control 2000, 24, 703–724. [Google Scholar] [CrossRef] [Green Version]
- Antonopoulos, I.; Robu, V.; Couraud, B.; Kirli, D.; Norbu, S.; Kiprakis, A.; Flynn, D.; Elizondo-Gonzalez, S.; Wattam, S. Artificial intelligence and machine learning approaches to energy demand-side response: A systematic review. Renew. Sustain. Energy Rev. 2020, 130, 109899. [Google Scholar] [CrossRef]
- Crespo-Vazquez, J.L.; Carrillo, C.; Diaz-Dorado, E.; Martinez-Lorenzo, J.A.; Noor-E-Alam, M. A machine learning based stochastic optimization framework for a wind and storage power plant participating in energy pool market. Appl. Energy 2018, 232, 341–357. [Google Scholar] [CrossRef]
- Ghoddusi, H.; Creamer, G.G.; Rafizadeh, N. Machine learning in energy economics and finance: A review. Energy Econ. 2019, 81, 709–727. [Google Scholar] [CrossRef]
- Herrera, G.P.; Constantino, M.; Tabak, B.M.; Pistori, H.; Su, J.J.; Naranpanawa, A. Long-term forecast of energy commodities price using machine learning. Energy 2019, 179, 214–221. [Google Scholar] [CrossRef]
| Futures Contract | Time Delay | Embedding Dimension |
|---|---|---|
| Crude oil Contract 1 | 4 | 11 |
| Crude oil Contract 3 | 4 | 10 |
| Heating oil Contract 1 | 1 | 13 |
| Heating oil Contract 3 | 1 | 11 |
| Natural gas | 1 | 14 |
| Commodity Contract | Noise Level % | |
|---|---|---|
| Crude oil C1 | ||
| Crude oil C3 | ||
| Heating oil C1 | ||
| Heating oil C3 | ||
| Natural gas |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mastroeni, L.; Vellucci, P. Replication in Energy Markets: Use and Misuse of Chaos Tools. Entropy 2022, 24, 701. https://doi.org/10.3390/e24050701
Mastroeni L, Vellucci P. Replication in Energy Markets: Use and Misuse of Chaos Tools. Entropy. 2022; 24(5):701. https://doi.org/10.3390/e24050701
Chicago/Turabian StyleMastroeni, Loretta, and Pierluigi Vellucci. 2022. "Replication in Energy Markets: Use and Misuse of Chaos Tools" Entropy 24, no. 5: 701. https://doi.org/10.3390/e24050701
APA StyleMastroeni, L., & Vellucci, P. (2022). Replication in Energy Markets: Use and Misuse of Chaos Tools. Entropy, 24(5), 701. https://doi.org/10.3390/e24050701







