Emergence of Integrated Information at Macro Timescales in Real Neural Recordings
Abstract
1. Introduction
2. Results
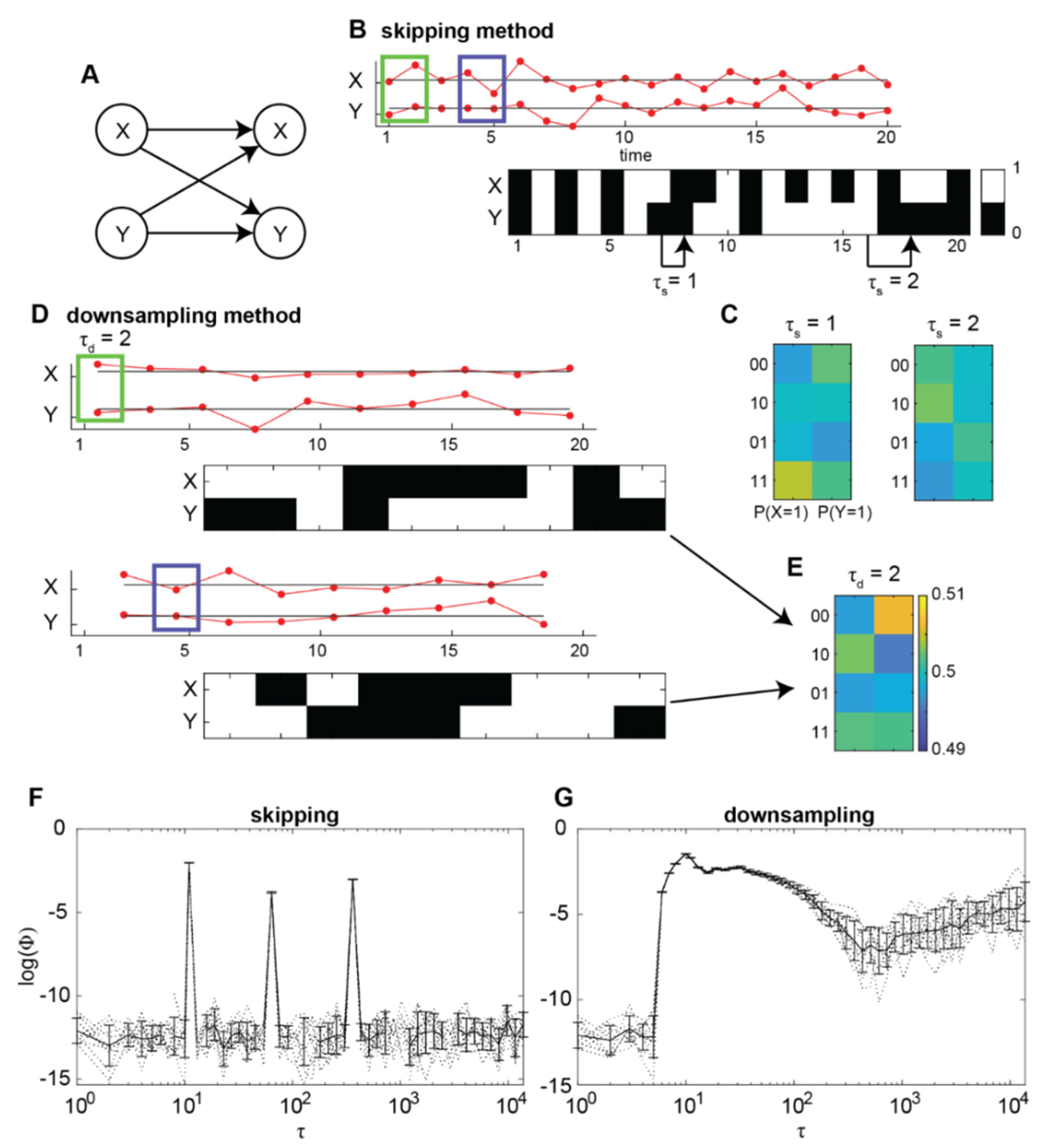
2.1. Integrated Information Identifies the Timescale of Interactions in a Nonlinear Autoregressive Process
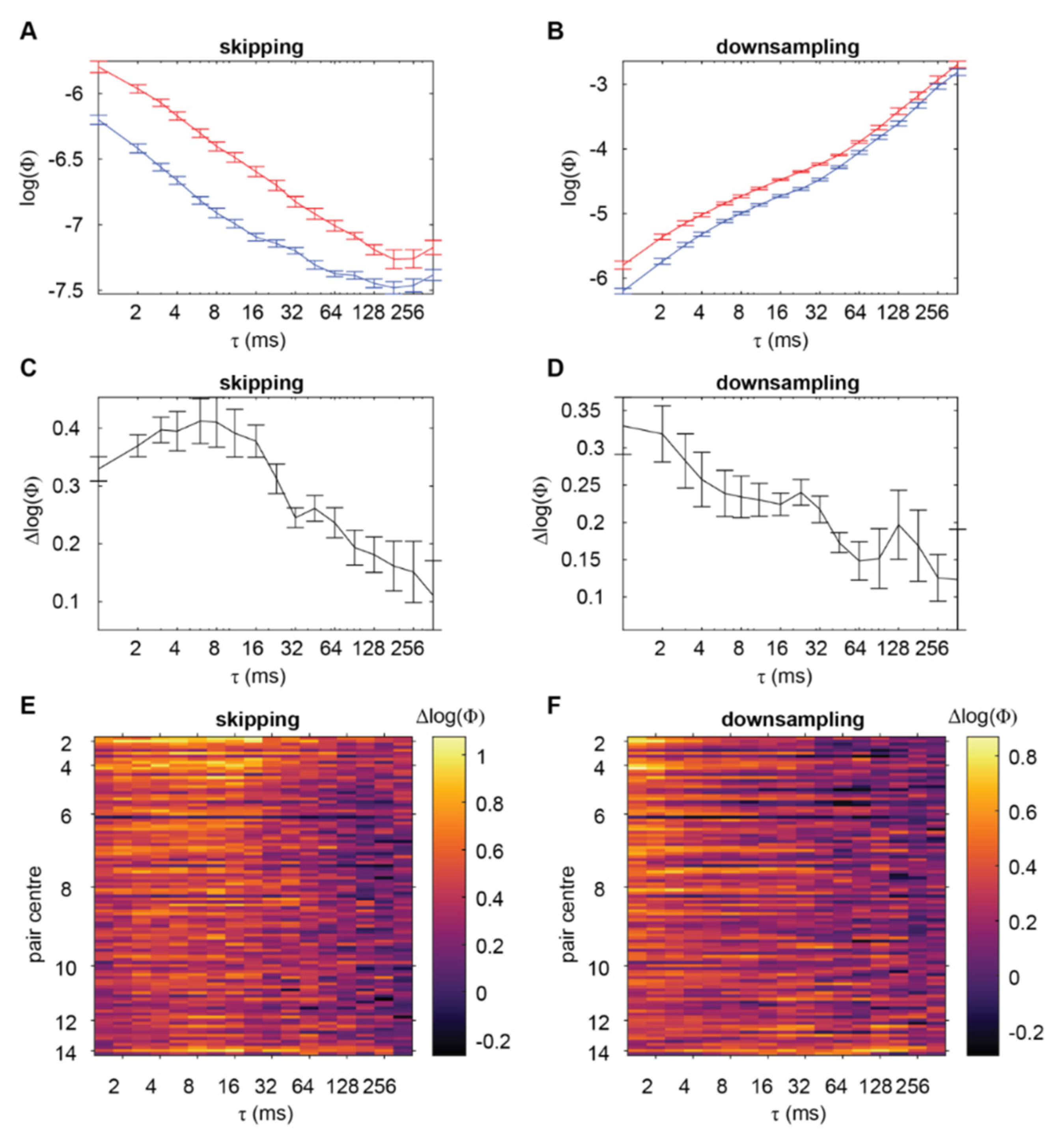
2.2. Normalised Empirical Integrated Information Identifies a Timescale of Interactions
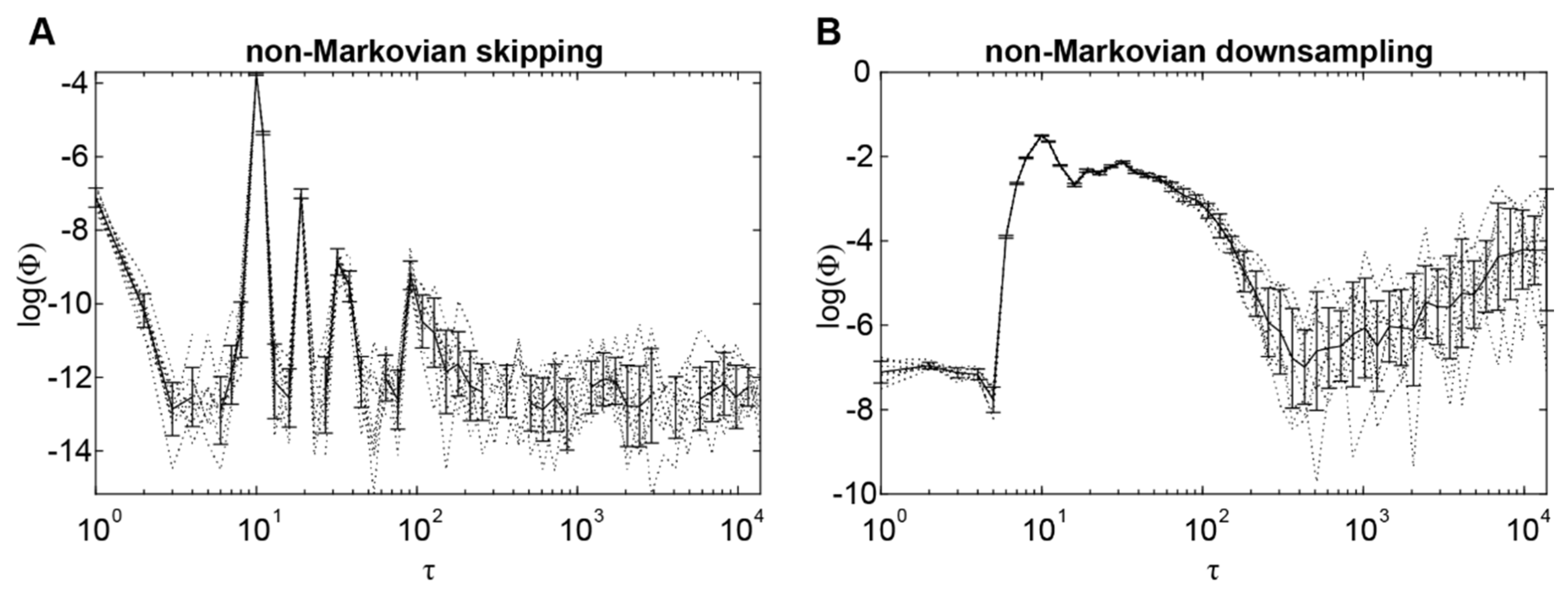
2.3. Integrated Information Identifies the Timescale of Interactions under Non-Markovianity
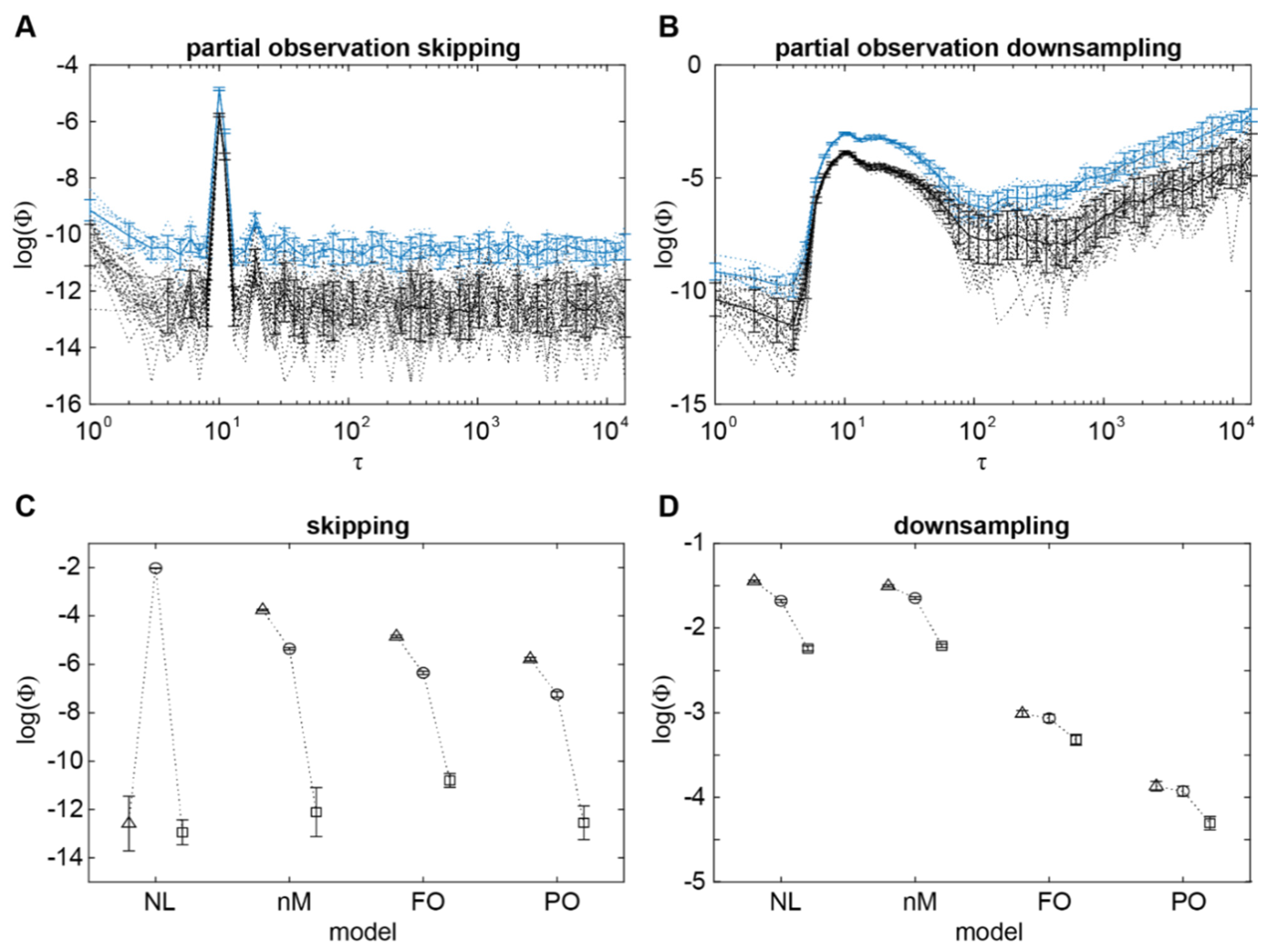
2.4. Integrated Information Identifies the Timescale of Interactions under Partial Observation
3. Discussion
3.1. Why Is There a Peak in Normalised Φ but Not Directly in Φ?
3.2. Why Do Skipping and Downsampling Methods Give Different Peaks?
4. Conclusions and Future Directions
5. Methods
5.1. Autoregressive Simulation
5.2. Φ Computation
5.3. Statistical Analyses
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| β2 b | β1 c | β0 d | χ2(1) e | τTP f | |
|---|---|---|---|---|---|
| ΦSW | 8.56 × 10−3 | −0.260 | −5.717 | 394.51 | 37,983 |
| ΦSA | 1.77 × 10−2 | −0.305 | −6.151 | 1795.09 | 384 |
| ΦSΔ | −9.18 × 10−3 | 4.441 × 10−2 | 0.433 | 308.79 | 5 |
| ΦDW | 1.16 × 10−2 | 0.237 | −5.63 | 853.28 | 0 |
| ΦDA | 1.05 × 10−2 | 0.279 | −6.026 | 663.99 | 0 |
| ΦDΔ | 1.10 × 10−3 | −4.26 × 10−2 | 0.399 | 5.20 (p = 0.022) | 655,125 |
| R2 | SD | ||
|---|---|---|---|
| Random Effect | + (1|f) # | + (1|f:n) ^ | |
| ΦSW~τ + τ2 | 0.827 | 0.502 | 0.445 |
| ΦSA~τ + τ2 | 0.756 | 0.278 | 0.415 |
| ΦDW~τ + τ2 | 0.880 | 0.233 | 0.295 |
| ΦDA~τ + τ2 | 0.891 | 0.209 | 0.329 |
| ΦSΔ~τ + τ2 | 0.601 | 0.415 | 0.367 |
| ΦDΔ~τ + τ2 | 0.327 | 0.164 | 0.247 |
References
- Tononi, G. Consciousness as Integrated Information: A Provisional Manifesto. Biol. Bull. 2008, 215, 216–242. [Google Scholar] [CrossRef] [PubMed]
- Oizumi, M.; Albantakis, L.; Tononi, G. From the Phenomenology to the Mechanisms of Consciousness: Integrated Information Theory 3.0. PLoS Comput. Biol. 2014, 10, e1003588. [Google Scholar] [CrossRef] [PubMed]
- Leung, A.; Cohen, D.; van Swinderen, B.; Tsuchiya, N. Integrated Information Structure Collapses with Anesthetic Loss of Conscious Arousal in Drosophila melanogaster. PLoS Comput. Biol. 2021, 17, e1008722. [Google Scholar] [CrossRef] [PubMed]
- Buzsáki, G.; Anastassiou, C.A.; Koch, C. The Origin of Extracellular Fields and Currents—EEG, ECoG, LFP and Spikes. Nat. Rev. Neurosci. 2012, 13, 407–420. [Google Scholar] [CrossRef] [PubMed]
- Holcombe, A.O. Seeing Slow and Seeing Fast: Two Limits on Perception. Trends Cogn. Sci. 2009, 13, 216–221. [Google Scholar] [CrossRef] [PubMed]
- Hoel, E.P.; Albantakis, L.; Marshall, W.; Tononi, G. Can the Macro Beat the Micro? Integrated Information across Spatiotemporal Scales. Neurosci. Conscious 2016, 2016, niw012. [Google Scholar] [CrossRef]
- Marshall, W.; Albantakis, L.; Tononi, G. Black-Boxing and Cause-Effect Power. PLoS Comput. Biol. 2018, 14, e1006114. [Google Scholar] [CrossRef] [PubMed]
- Gomez, J.D.; Mayner, W.G.P.; Beheler-Amass, M.; Tononi, G.; Albantakis, L. Computing Integrated Information (Φ) in Discrete Dynamical Systems with Multi-Valued Elements. Entropy 2021, 23, 6. [Google Scholar] [CrossRef]
- Cohen, D.; Sasai, S.; Tsuchiya, N.; Oizumi, M. A General Spectral Decomposition of Causal Influences Applied to Integrated Information. J. Neurosci. Methods 2020, 330, 108443. [Google Scholar] [CrossRef]
- Lütkepohl, H. New Introduction to Multiple Time Series Analysis; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2005; ISBN 978-3-540-27752-1. [Google Scholar]
- Zeldenrust, F.; Wadman, W.J.; Englitz, B. Neural Coding with Bursts—Current State and Future Perspectives. Front. Comput. Neurosci. 2018, 12, 48. [Google Scholar] [CrossRef]
- Constantinou, M.; Elijah, D.H.; Squirrell, D.; Gigg, J.; Montemurro, M.A. Phase-Locking of Bursting Neuronal Firing to Dominant LFP Frequency Components. Biosystems 2015, 136, 73–79. [Google Scholar] [CrossRef] [PubMed]
- Barrett, A.B.; Seth, A.K. Practical Measures of Integrated Information for Time-Series Data. PLoS Comput. Biol. 2011, 7, e1001052. [Google Scholar] [CrossRef] [PubMed]
- Oizumi, M.; Amari, S.; Yanagawa, T.; Fujii, N.; Tsuchiya, N. Measuring Integrated Information from the Decoding Perspective. PLoS Comput. Biol. 2016, 12, e1004654. [Google Scholar] [CrossRef]
- Kim, H.; Hudetz, A.G.; Lee, J.; Mashour, G.A.; Lee, U.; The ReCCognition Study Group. Estimating the Integrated Information Measure Phi from High-Density Electroencephalography during States of Consciousness in Humans. Front. Hum. Neurosci. 2018, 12, 42. [Google Scholar] [CrossRef] [PubMed]
- Cohen, D.; van Swinderen, B.; Tsuchiya, N. Isoflurane Impairs Low Frequency Feedback but Leaves High Frequency Feedforward Connectivity Intact in the Fly Brain. eNeuro 2018, 5. [Google Scholar] [CrossRef]
- Cousineau, D. Confidence Intervals in Within-Subject Designs: A Simpler Solution to Loftus and Masson’s Method. Tutor. Quant. Methods Psychol. 2005, 1, 42–45. [Google Scholar] [CrossRef]
- O’Brien, F.; Cousineau, D. Representing Error Bars in Within-Subject Designs in Typical Software Packages. Tutor. Quant. Methods Psychol. 2014, 10, 56–67. [Google Scholar] [CrossRef]
- Kepecs, A.; Lisman, J. Information Encoding and Computation with Spikes and Bursts. Network 2003, 14, 103–118. [Google Scholar] [CrossRef]
- Rauske, P.L.; Chi, Z.; Dave, A.S.; Margoliash, D. Neuronal Stability and Drift across Periods of Sleep: Premotor Activity Patterns in a Vocal Control Nucleus of Adult Zebra Finches. J. Neurosci. 2010, 30, 2783–2794. [Google Scholar] [CrossRef]
- Mediano, P.A.M.; Seth, A.K.; Barrett, A.B. Measuring Integrated Information: Comparison of Candidate Measures in Theory and Simulation. Entropy 2019, 21, 17. [Google Scholar] [CrossRef]
- Sarasso, S.; Rosanova, M.; Casali, A.G.; Casarotto, S.; Fecchio, M.; Boly, M.; Gosseries, O.; Tononi, G.; Laureys, S.; Massimini, M. Quantifying Cortical EEG Responses to TMS in (Un)Consciousness. Clin. EEG Neurosci. 2014, 45, 40–49. [Google Scholar] [CrossRef]
- Grasso, M.; Albantakis, L.; Lang, J.P.; Tononi, G. Causal Reductionism and Causal Structures. Nat. Neurosci. 2021, 24, 1348–1355. [Google Scholar] [CrossRef] [PubMed]
- Brovelli, A.; Ding, M.; Ledberg, A.; Chen, Y.; Nakamura, R.; Bressler, S.L. Beta Oscillations in a Large-Scale Sensorimotor Cortical Network: Directional Influences Revealed by Granger Causality. Proc. Natl. Acad. Sci. USA 2004, 101, 9849–9854. [Google Scholar] [CrossRef] [PubMed]
- Hoerzer, G.; Liebe, S.; Schloegl, A.; Logothetis, N.; Rainer, G. Directed Coupling in Local Field Potentials of Macaque V4 during Visual Short-Term Memory Revealed by Multivariate Autoregressive Models. Front. Comput. Neurosci. 2010, 4, 14. [Google Scholar] [CrossRef] [PubMed]
- Gaudry, Q.; Hong, E.J.; Kain, J.; de Bivort, B.L.; Wilson, R.I. Asymmetric Neurotransmitter Release Enables Rapid Odour Lateralization in Drosophila. Nature 2013, 493, 424–428. [Google Scholar] [CrossRef] [PubMed]
- Buschbeck, E.K.; Ehmer, B.; Hoy, R.R. The Unusual Visual System of the Strepsiptera: External Eye and Neuropils. J. Comp. Physiol. A 2003, 189, 617–630. [Google Scholar] [CrossRef]
- Hecht, S.; Shlaer, S. Intermittent Stimulation by Light: V. The Relation between Intensity and Critical Frequency for Different Parts of the Spectrum. J. Gen. Physiol. 1936, 19, 965–977. [Google Scholar] [CrossRef]
- Carmel, D.; Saker, P.; Rees, G.; Lavie, N. Perceptual Load Modulates Conscious Flicker Perception. J. Vis. 2007, 7, 14. [Google Scholar] [CrossRef][Green Version]
- Isler, J.R.; Stark, R.I.; Grieve, P.G.; Welch, M.G.; Myers, M.M. Integrated Information in the EEG of Preterm Infants Increases with Family Nurture Intervention, Age, and Conscious State. PLoS ONE 2018, 13, e0206237. [Google Scholar] [CrossRef]
- Mayner, W.G.P.; Marshall, W.; Albantakis, L.; Findlay, G.; Marchman, R.; Tononi, G. PyPhi: A Toolbox for Integrated Information Theory. PLoS Comput. Biol. 2018, 14, e1006343. [Google Scholar] [CrossRef]
- Bates, D.; Mächler, M.; Bolker, B.; Walker, S. Fitting Linear Mixed-Effects Models Using Lme4. J. Stat. Softw. 2015, 67, 1–48. [Google Scholar] [CrossRef]
- Harrison, X.A.; Donaldson, L.; Correa-Cano, M.E.; Evans, J.; Fisher, D.N.; Goodwin, C.E.; Robinson, B.S.; Hodgson, D.J.; Inger, R. A Brief Introduction to Mixed Effects Modelling and Multi-Model Inference in Ecology. PeerJ 2018, 6, e4794. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leung, A.; Tsuchiya, N. Emergence of Integrated Information at Macro Timescales in Real Neural Recordings. Entropy 2022, 24, 625. https://doi.org/10.3390/e24050625
Leung A, Tsuchiya N. Emergence of Integrated Information at Macro Timescales in Real Neural Recordings. Entropy. 2022; 24(5):625. https://doi.org/10.3390/e24050625
Chicago/Turabian StyleLeung, Angus, and Naotsugu Tsuchiya. 2022. "Emergence of Integrated Information at Macro Timescales in Real Neural Recordings" Entropy 24, no. 5: 625. https://doi.org/10.3390/e24050625
APA StyleLeung, A., & Tsuchiya, N. (2022). Emergence of Integrated Information at Macro Timescales in Real Neural Recordings. Entropy, 24(5), 625. https://doi.org/10.3390/e24050625






