Passive Light Source Monitoring for Sending or Not Sending Twin-Field Quantum Key Distribution
Abstract
:1. Introduction
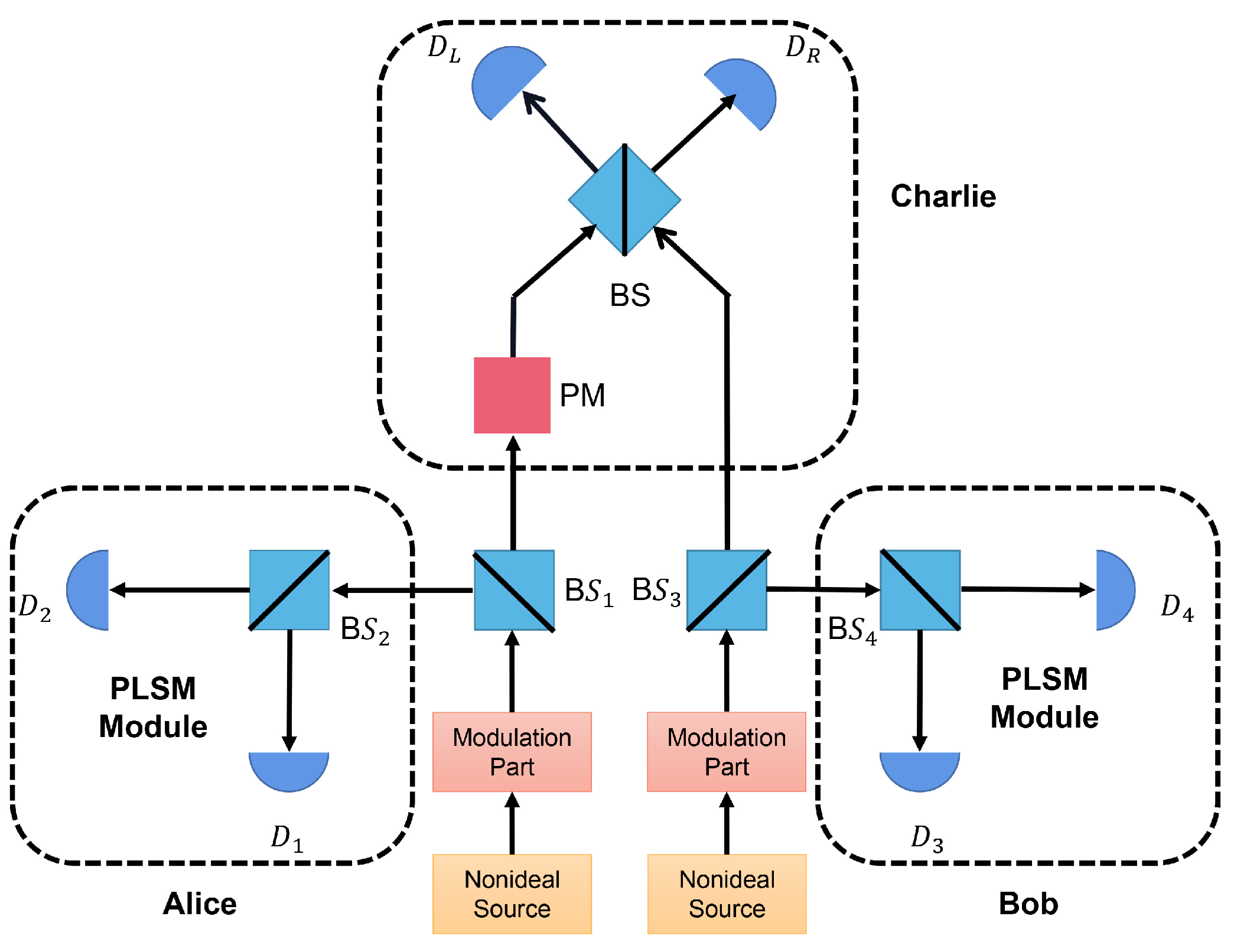
2. PLSM Scheme in SNS−TFQKD
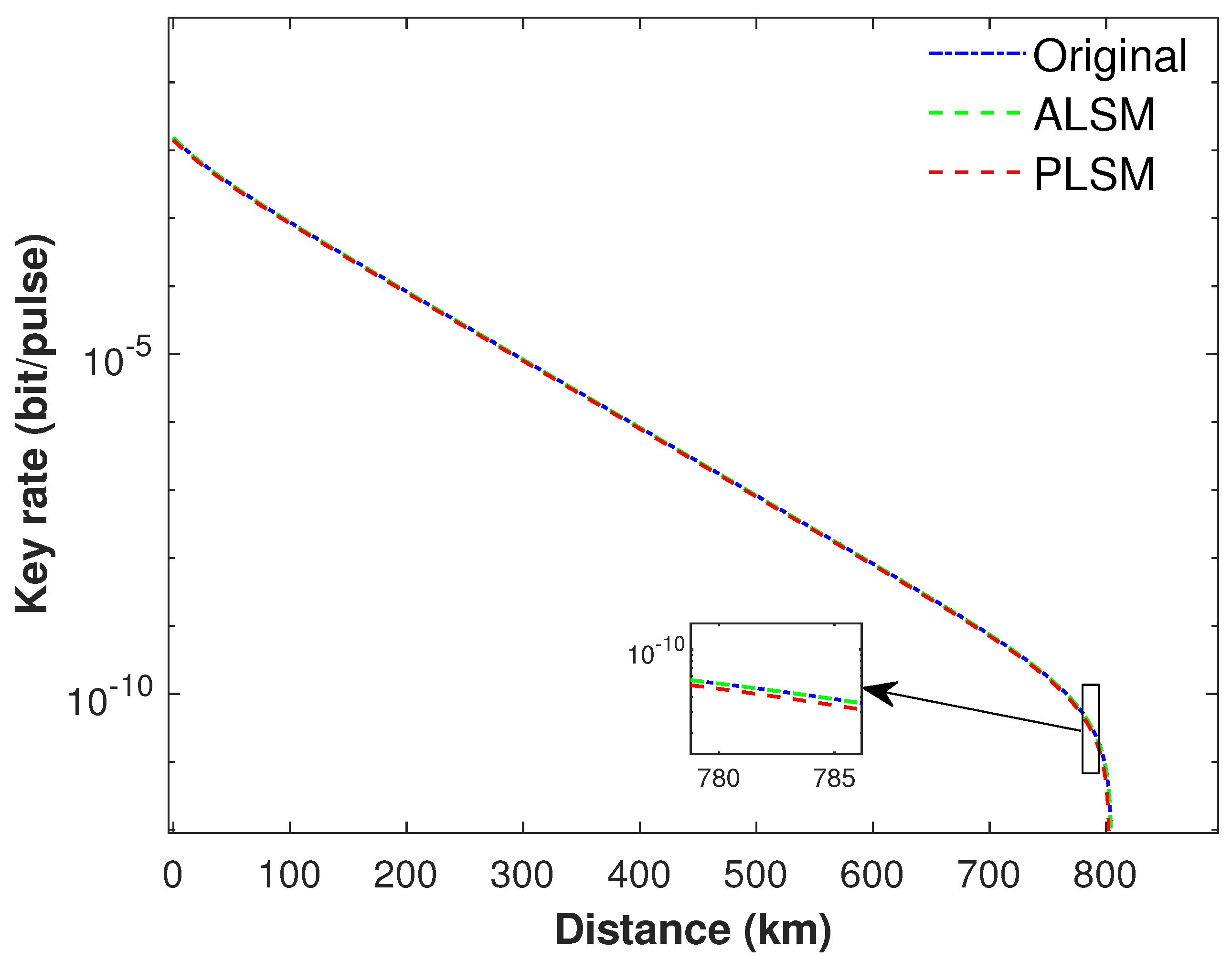
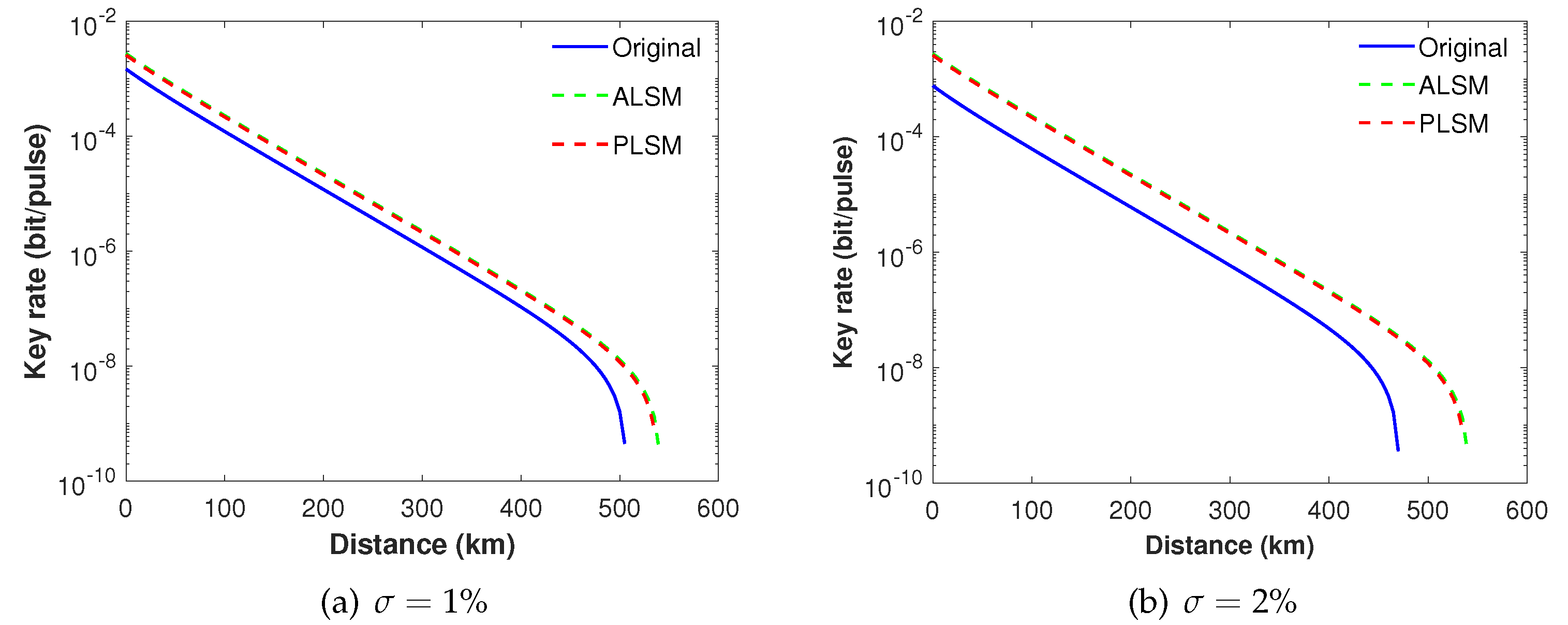
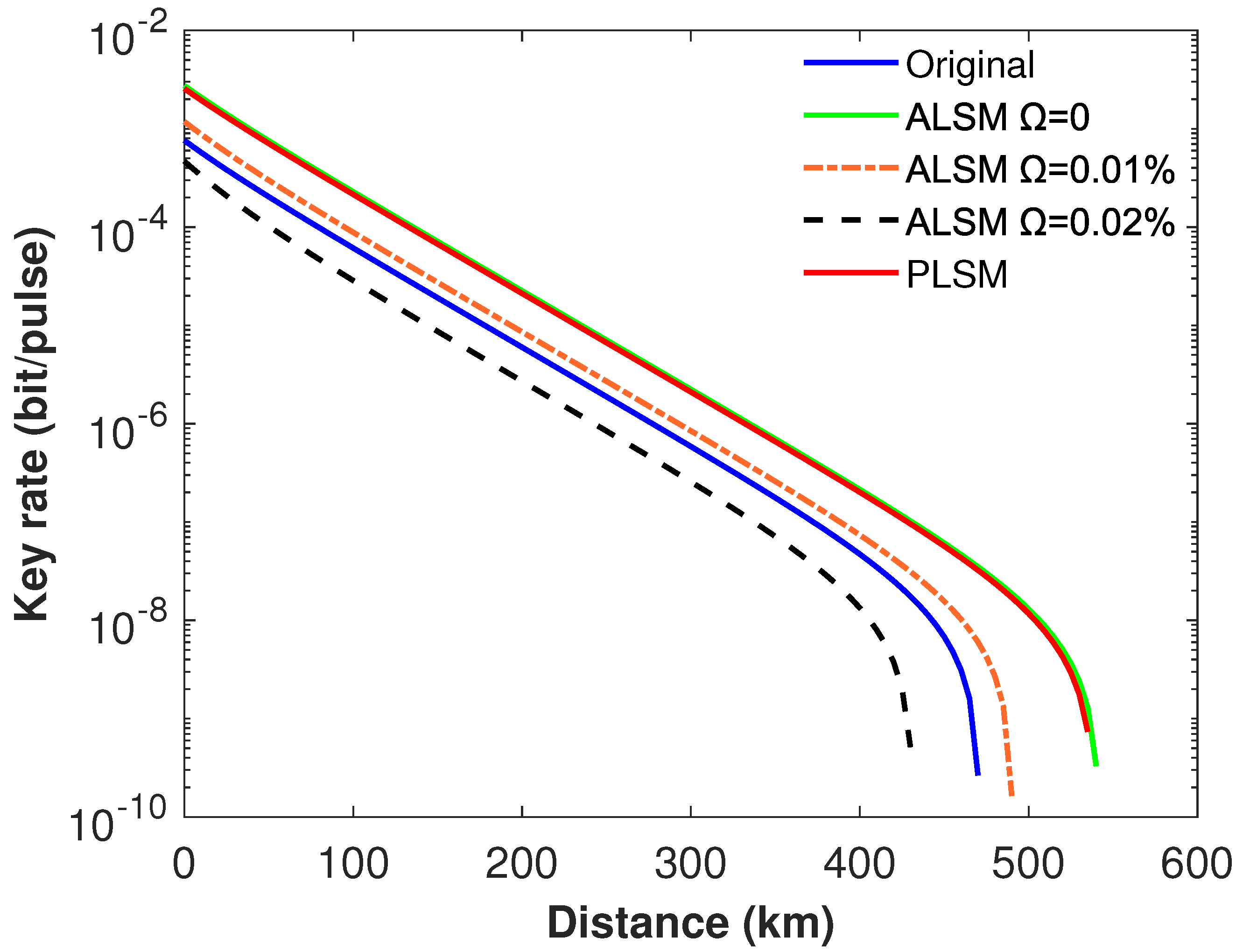
3. Numerical Simulations and Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Upper Bound and Lower Bound of Pn (μ) in PLSM
Appendix B. Upper Bound and Lower Bound of Pn (μ) in ALSM
References
- Bennett, C.H.; Brassard, G. Quantum cryptography: Public key distribution and coin tossing. Theor. Comput. Sci. 2014, 560, 7–11. [Google Scholar] [CrossRef]
- Ekert, A.K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 1991, 67, 661–663. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shor, P.W.; Preskill, J. Simple proof of security of the BB84 quantum key distribution protocol. Phys. Rev. Lett. 2000, 85, 441. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mayers, D. Unconditional security in quantum cryptography. JACM 2001, 48, 351–406. [Google Scholar] [CrossRef]
- Lo, H.-K.; Chau, H.-F. Unconditional security of quantum key distribution over arbitrarily long distances. Science 1999, 283, 2050. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bennett, C.H.; Bessette, F.; Brassard, G.; Salvail, L.; Smolin, J. Experimental quantum cryptography. J. Cryptol. 1992, 5, 3. [Google Scholar] [CrossRef]
- Wang, X.-B. Beating the photon-number-splitting attack in practical quantum cryptography. Phys. Rev. Lett. 2005, 94, 230503. [Google Scholar] [CrossRef] [Green Version]
- Lo, H.-K.; Curty, M.; Qi, B. Measurement-device-independent quantum key distribution. Phys. Rev. Lett. 2012, 108, 130503. [Google Scholar] [CrossRef] [Green Version]
- Xu, F.; Xu, H.; Lo, H.-K. Protocol choice and parameter optimization in decoy-state measurement-device-independent quantum key distribution. Phys. Rev. A 2014, 89, 052333. [Google Scholar] [CrossRef] [Green Version]
- Curty, M.; Xu, F.; Cui, W.; Lim, C.C.W.; Tamaki, K.; Lo, H.-K. Finite-key analysis for measurement-device-independent quantum key distribution. Nat. Commun. 2014, 5, 3732. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yu, Z.-W.; Zhou, Y.-H.; Wang, X.-B. Statistical fluctuation analysis for measurement-device-independent quantum key distribution with three-intensity decoy-state method. Phys. Rev. A 2015, 91, 032318. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.-H.; Yu, Z.-W.; Wang, X.-B. Making the decoy-state measurement-device independent quantum key distribution practically useful. Phys. Rev. A 2016, 93, 042324. [Google Scholar] [CrossRef] [Green Version]
- Jiang, C.; Yu, Z.-W.; Hu, X.-L.; Wang, X.-B. Higher key rate of measurement-device-independent quantum key distribution through joint data processing. Phys. Rev. A 2021, 103, 012402. [Google Scholar] [CrossRef]
- Tamaki, K.; Lo, H.-K.; Wang, W.-Y.; Lucamarini, M. Information theoretic security of quantum key distribution overcoming the repeaterless secret key capacity bound. arXiv 2018, arXiv:1805.05511. [Google Scholar]
- Pirandola, S.; Laurenza, R.; Ottaviani, C.; Banchi, L. Fundamental limits of repeaterless quantum communications. Nat. Commun. 2017, 8, 15043. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lucamarini, M.; Yuan, Z.-L.; Dynes, J.F.; Shields, A.J. Overcoming the rate–distance limit of quantum key distribution without quantum repeaters. Nature 2018, 557, 400. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.; Zeng, P.; Zhou, H. Phase-matching quantum key distribution. Phys. Rev. X 2018, 8, 031043. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.-B.; Yu, Z.-W.; Hu, X.-L.T. Twin-field quantum key distribution with large misalignment error. Phys. Rev. A 2018, 98, 062323. [Google Scholar] [CrossRef] [Green Version]
- Cui, C.; Yin, Z.Q.; Wang, R.; Chen, W.; Wang, S.; Guo, G.-C.; Han, Z.-F. Twin-field quantum key distribution without phase postselection. Phys. Rev. Appl. 2019, 11, 034053. [Google Scholar] [CrossRef] [Green Version]
- Curty, M.; Azuma, K.; Lo, H.-K. Simple security proof of twin-field type quantum key distribution protocol. Npj Quantum Inf. 2019, 5, 64. [Google Scholar] [CrossRef]
- Lin, J.; Lütkenhaus, N. Simple security analysis of phase-matching measurement-device-independent quantum key distribution. Phys. Rev. A 2018, 98, 042332. [Google Scholar] [CrossRef] [Green Version]
- Maeda, K.; Sasaki, T.; Koashi, M. Repeaterless quantum key distribution with efficient finite-key analysis overcoming the rate-distance limit. Nat. Commun. 2019, 10, 3140. [Google Scholar] [CrossRef] [Green Version]
- Minder, M.; Pittaluga, M.; Roberts, G.L.; Lucamarini, M.; Dynes, J.F.; Yuan, Z.L.; Shields, A.J. Experimental quantum key distribution beyond the repeaterless secret key capacity. Nat. Photonics 2019, 13, 334. [Google Scholar] [CrossRef]
- Liu, Y.; Yu, Z.-W.; Zhang, W.; Guan, J.Y.; Chen, J.-P.; Zhang, C.; Hu, X.-L.; Li, H.; Chen, T.-Y.; You, L.; et al. Experimental twin-field quantum key distribution through sending or not sending. Phys. Rev. Lett. 2019, 123, 100505. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, S.; He, D.-Y.; Yin, Z.-Q.; Lu, F.-Y.; Cui, C.-H.; Chen, W.; Zhou, Z.; Guo, G.-C.; Han, Z.-F. Beating the fundamental rate-distance limit in a proof-of-principle quantum key distribution system. Phys. Rev. X 2019, 9, 021046. [Google Scholar] [CrossRef] [Green Version]
- Zhong, X.; Hu, J.; Curty, M.; Qian, L.; Lo, H.-K. Proof-of-principle experimental demonstration of twin-field type quantum key distribution. Phys. Rev. Lett. 2019, 123, 100506. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fang, X.-T.; Zeng, P.; Liu, H. Implementation of quantum key distribution surpassing the linear rate-transmittance bound. Nat. Photonics 2020, 14, 422. [Google Scholar] [CrossRef]
- Chen, J.-P.; Zhang, C.; Liu, Y.; Jiang, C.; Zhang, W.; Hu, X.L.; Guan, J.-Y.; Yu, Z.-W.; Xu, H.; Lin, J.; et al. Sending-or-not-sending with independent lasers: Secure twin-field quantum key distribution over 509 km. Phys. Rev. Lett. 2020, 124, 070501. [Google Scholar] [CrossRef] [Green Version]
- Qiao, Y.; Wang, G.; Li, Z.; Xu, B.; Guo, H. Monitoring an untrusted light source with single-photon detectors in measurement-device-independent quantum key distribution. Phys. Rev. A 2019, 99, 052302. [Google Scholar] [CrossRef]
- Qiao, Y.; Wang, G.; Li, Z.; Xu, B.; Guo, H. Sending-or-not-sending twin-field quantum key distribution with light source monitoring. Entropy 2019, 22, 36. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jiang, C.; Yu, Z.-W.; Hu, X.L.; Wang, X.-B. Unconditional security of sending or not sending twin-field quantum key distribution with finite pulses. Phys. Rev. Appl. 2019, 12, 024061. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.H.; Zhang, C.M.; Wang, Q. Twin-field quantum key distribution with modified coherent states. Opt. Lett. 2019, 44, 1468–1471. [Google Scholar] [CrossRef]
- Xu, H.; Yu, Z.-W.; Jiang, C.; Hu, X.L.; Wang, X.-B. Sending-or-not-sending twin-field quantum key distribution: Breaking the directtransmission key rate. Phys. Rev. A 2020, 101, 042330. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, C.-H.; Wang, X.-B. Scheme for realizing passive quantum key distribution with heralded single-photon sources. Phys. Rev. A 2016, 93, 032312. [Google Scholar] [CrossRef]
- Zhang, C.-H.; Wang, D.; Zhou, X.-Y.; Wang, S.; Zhang, L.-B.; Yin, Z.-Q.; Chen, W.; Han, Z.-F.; Guo, G.-C.; Wang, Q. Proof-of-principle demonstration of parametric down-conversion source based quantum key distribution over 40 dB channel loss. Opt. Express 2018, 26, 25921. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.-B.; Peng, C.-Z.; Zhang, J.; Yang, L.; Pan, J.-W. General theory of decoy-state quantum cryptography with source errors. Phys. Rev. A 2008, 77, 042311. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Qi, B.; Lo, H.-K.; Qian, L. Security Analysis of an untrusted source for quantum key distribution: Passive approach. New J. Phys. 2010, 12, 023024. [Google Scholar] [CrossRef]
- Wang, X.-B. Decoy-state quantum key distribution with large random errors of light intensity. Phys. Rev. A 2007, 75, 052301. [Google Scholar] [CrossRef] [Green Version]
- Xu, F.; Zhang, Y.; Zhou, Z.; Chen, W.; Han, Z.; Guo, G. Experimental demonstration of counteracting imperfect sources in a practical one-way quantum-key-distribution system. Phys. Rev. A 2009, 80, 062309. [Google Scholar] [CrossRef]
| M | f | |||||
|---|---|---|---|---|---|---|
| set a | 0.2 dB/km | 16 | ||||
| set b | 0.2 dB/km | 16 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qian, X.; Zhang, C.; Yuan, H.; Zhou, X.; Li, J.; Wang, Q. Passive Light Source Monitoring for Sending or Not Sending Twin-Field Quantum Key Distribution. Entropy 2022, 24, 592. https://doi.org/10.3390/e24050592
Qian X, Zhang C, Yuan H, Zhou X, Li J, Wang Q. Passive Light Source Monitoring for Sending or Not Sending Twin-Field Quantum Key Distribution. Entropy. 2022; 24(5):592. https://doi.org/10.3390/e24050592
Chicago/Turabian StyleQian, Xuerui, Chunhui Zhang, Huawei Yuan, Xingyu Zhou, Jian Li, and Qin Wang. 2022. "Passive Light Source Monitoring for Sending or Not Sending Twin-Field Quantum Key Distribution" Entropy 24, no. 5: 592. https://doi.org/10.3390/e24050592
APA StyleQian, X., Zhang, C., Yuan, H., Zhou, X., Li, J., & Wang, Q. (2022). Passive Light Source Monitoring for Sending or Not Sending Twin-Field Quantum Key Distribution. Entropy, 24(5), 592. https://doi.org/10.3390/e24050592








