Practical Security of High-Dimensional Quantum Key Distribution with Intensity Modulator Extinction
Abstract
:1. Introduction
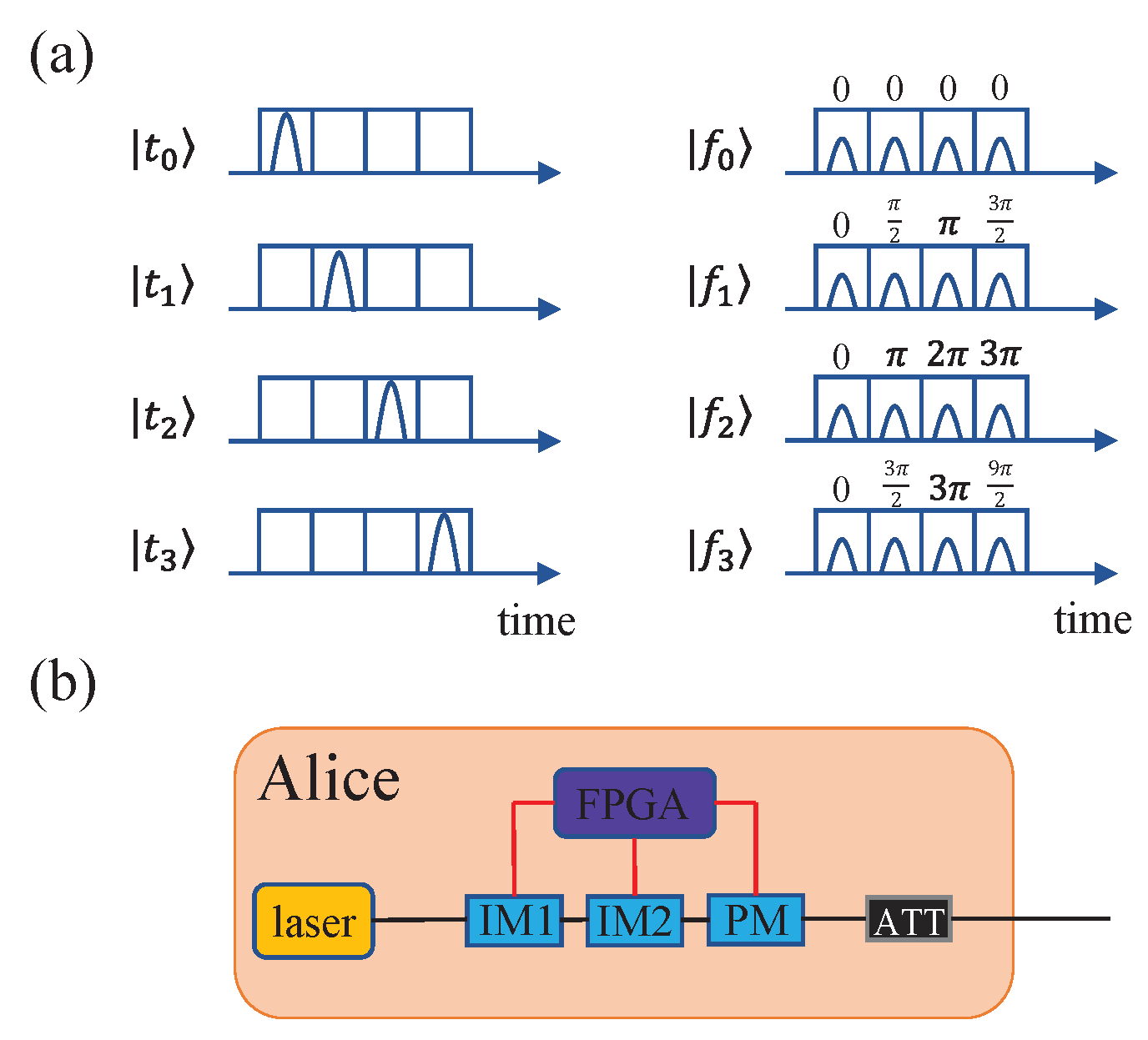
2. Model Characterization of the Extinction Ratio
3. Security Analysis
3.1. HD-QKD with the Single Photon State
3.2. HD-QKD with the Decoy-State Method
3.3. HD-QKD with Both Intensity Fluctuations and the Finite Extinction
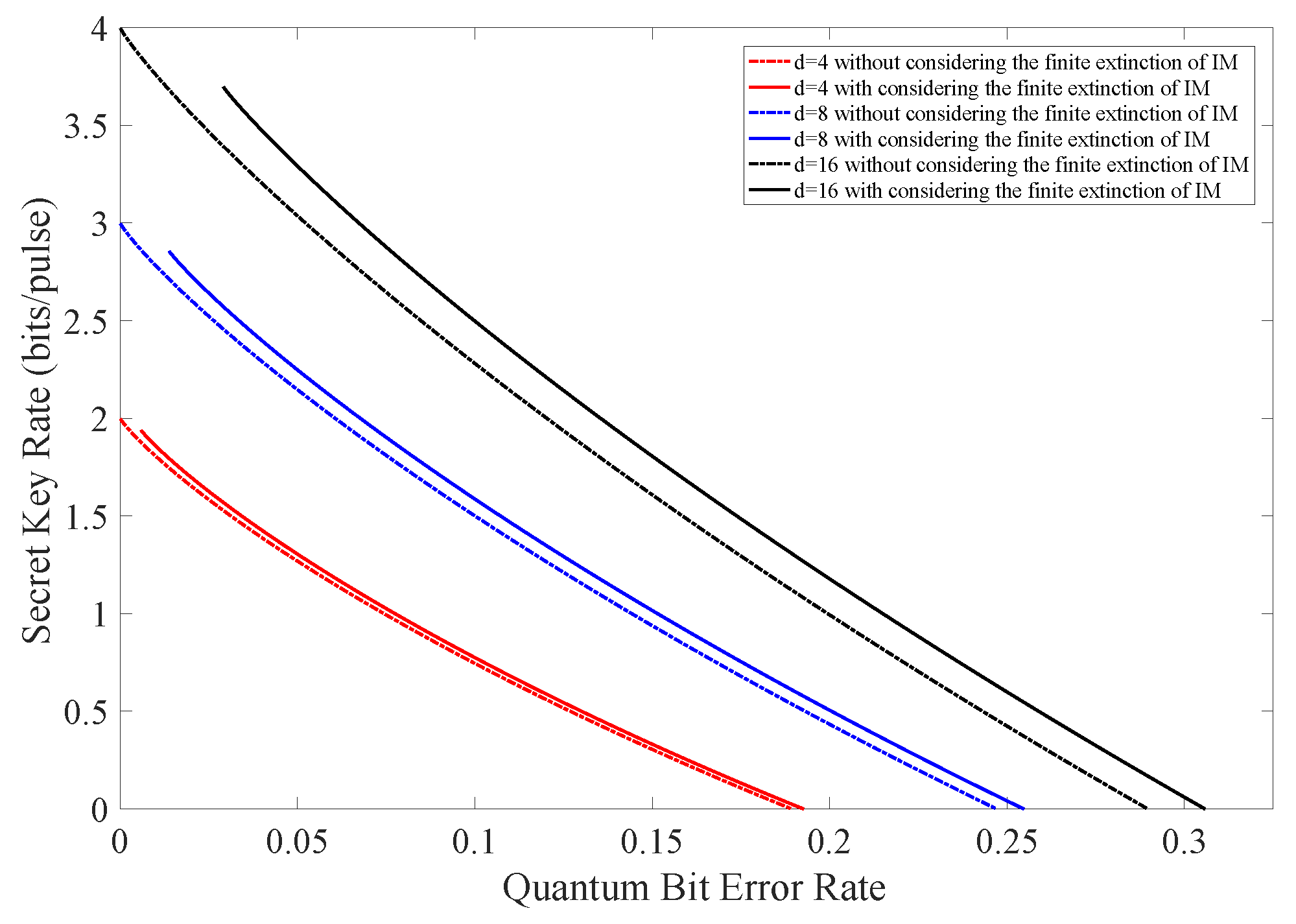
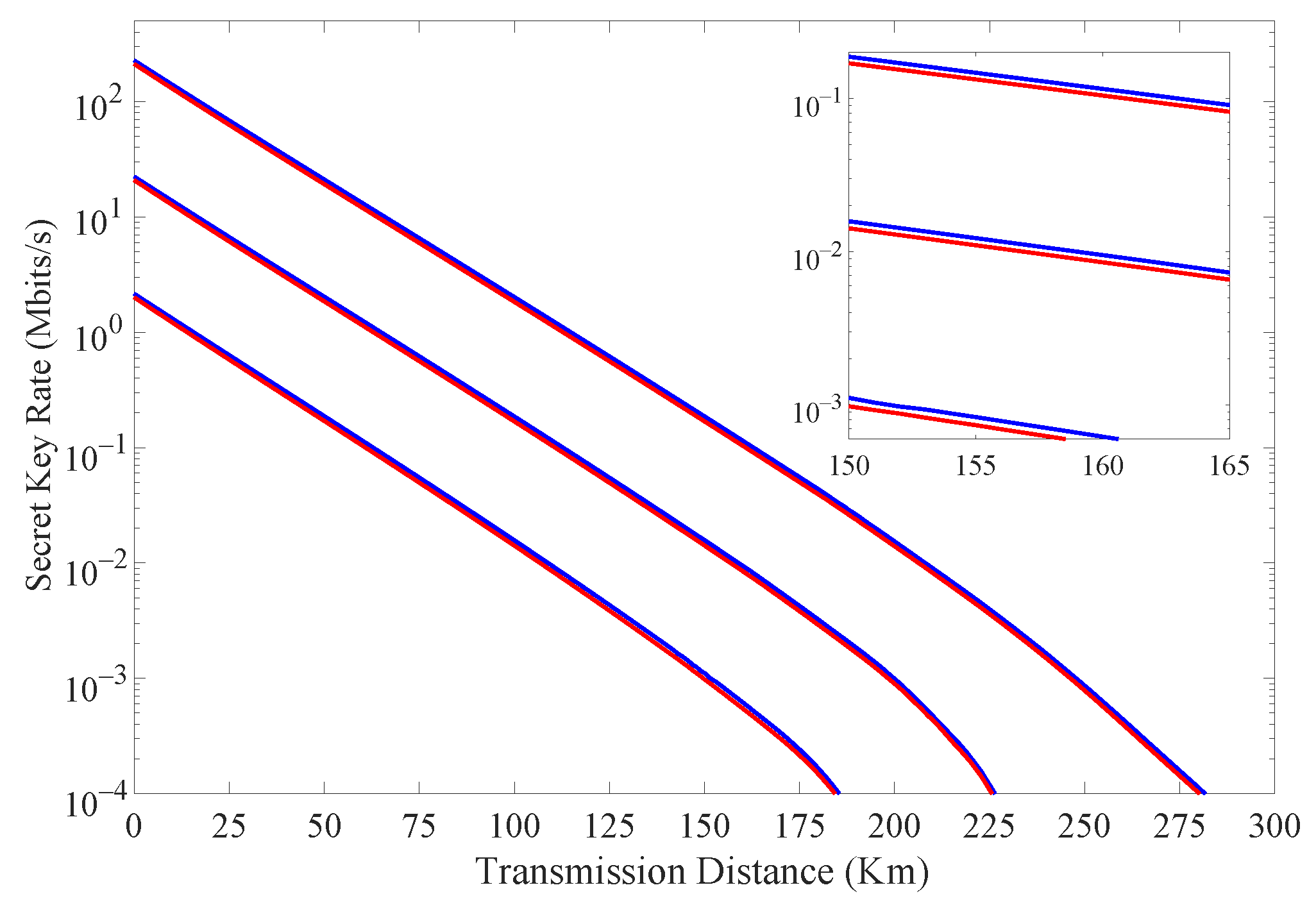
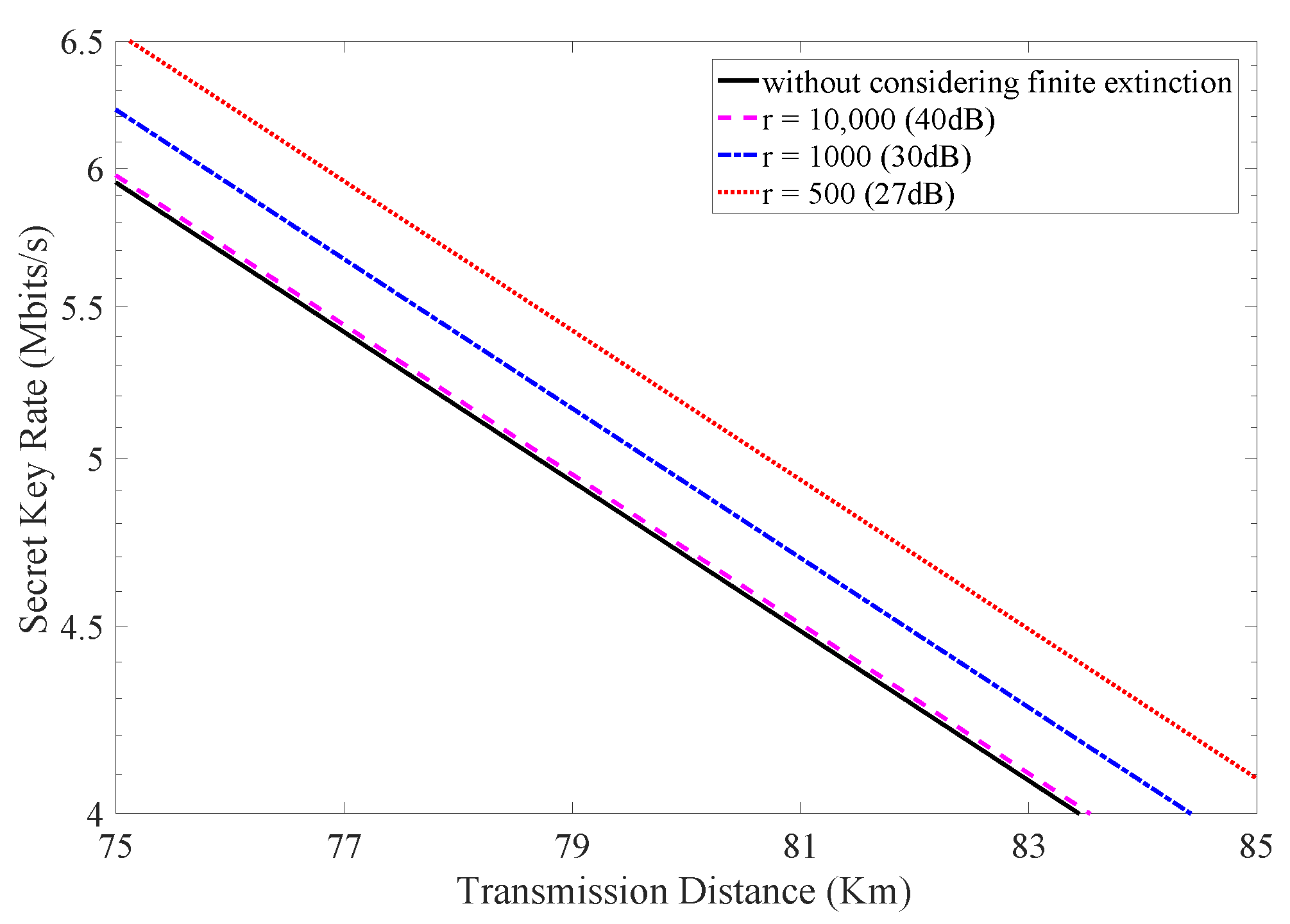
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bennett, C.H.; Brassard, G. Quantum cryptography: Public key distribution and coin tossing. Theor. Comput. Sci. 2014, 560, 7–11. [Google Scholar] [CrossRef]
- Ekert, A.K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 1991, 67, 661–663. [Google Scholar] [CrossRef] [Green Version]
- Xu, F.; Ma, X.; Zhang, Q.; Lo, H.-K.; Pan, J.-W. Secure quantum key distribution with realistic devices. Rev. Mod. Phys. 2020, 92, 025002. [Google Scholar] [CrossRef]
- Pirandola, S.; Andersen, U.L.; Banchi, L.; Berta, M.; Bunandar, D.; Colbeck, R.; Englund, D.; Gehring, T.; Lupo, C.; Ottaviani, C.; et al. Advances in quantum cryptography. Adv. Opt. Photon. 2020, 12, 1012–1236. [Google Scholar] [CrossRef] [Green Version]
- Lo, H.-K.; Chau, H.F. Unconditional security of quantum key distribution over arbitrarily long distances. Science 1999, 283, 2050–2056. [Google Scholar] [CrossRef] [Green Version]
- Shor, P.W.; Preskill, J. Simple proof of security of the BB84 quantum key distribution protocol. Phys. Rev. Lett. 2000, 85, 441–444. [Google Scholar] [CrossRef] [Green Version]
- Renner, R. Security of Quantum Key Distribution. Ph.D. Dissertation, Department of Physics, Swiss Federal Insititute of Technology (ETH), Zürich, Switzerland, 2005. [Google Scholar]
- Ali-Khan, I.; Broadbent, C.J.; Howell, J.C. Large-Alphabet Quantum Key Distribution Using Energy-Time Entangled Bipartite States. Phys. Rev. Lett. 2007, 98, 060503. [Google Scholar] [CrossRef] [Green Version]
- Mower, J.; Zhang, Z.; Desjardins, P.; Lee, C.; Shapiro, J.H.; Englund, D. High-dimensional quantum key distribution using dispersive optics. Phys. Rev. A 2013, 87, 062322. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Bao, W.S.; Bao, H.Z.; Zhou, C.; Jiang, M.S.; Li, H.W. High-dimensional quantum key distribution with the entangled single-photon-added coherent state. Phys. Lett. A 2017, 381, 1393–1397. [Google Scholar] [CrossRef]
- Islam, N.T.; Lim, C.C.W.; Cahall, C.; Kim, J.; Gauthier, D.J. Provably secure and high-rate quantum key distribution with time-bin qudits. Sci. Adv. 2017, 3, e1701491. [Google Scholar] [CrossRef] [Green Version]
- Vagniluca, I.; Lio, B.D.; Rusca, D.; Cozzolino, D.; Ding, Y.; Zbinden, H.; Zavatta, A.; Oxenløwe, L.K.; Bacco, D. Efficient time-bin encoding for practical high-dimensional quantum key distribution. Phys. Rev. Appl. 2020, 14, 014051. [Google Scholar] [CrossRef]
- Lio, B.D.; Cozzolino, D.; Biagi, N.; Ding, Y.; Rottwitt, K.; Zavatta, A.; Bacco, D.; Oxenløwe, L.K. Path-encoded high-dimensional quantum communication over a 2-km multicore fiber. NPJ Quantum Inf. 2021, 7, 63. [Google Scholar] [CrossRef]
- Ding, Y.; Bacco, D.; Dalgaard, K.; Cai, X.; Zhou, X.; Rottwitt, K.; Oxenløwe, L.K. High-dimensional quantum key distribution based on multicore fiber using silicon photonic integrated circuits. NPJ Quantum Inf. 2017, 3, 25. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.K.; Wang, F.X.; Liu, J.; Chen, W.; Han, Z.F.; Forbes, A.; Wang, J. High-dimensional quantum cryptography with hybrid orbital-angular-momentum states through 25 km of ring-core fiber: A proof-of-concept demonstration. Phys. Rev. Appl. 2021, 15, 064034. [Google Scholar] [CrossRef]
- Cozzolino, D.; Bacco, D.; Lio, B.D.; Ingerslev, K.; Ding, Y.; Dalgaard, K.; Kristensen, P.; Galili, M.; Rottwitt, K.; Ramachandran, S.; et al. Orbital angular momentum states enabling fiber-based high-dimensional quantum communication. Phys. Rev. Appl. 2019, 11, 064058. [Google Scholar] [CrossRef] [Green Version]
- Sit, A.; Bouchard, F.; Fickler, R.; Gagnon-Bischoff, J.; Larocque, H.; Heshami, K.; Elser, D.; Peuntinger, C.; Günthner, K.; Heim, B.; et al. High-dimensional intracity quantum cryptography with structured photons. Optica 2017, 4, 1006–1010. [Google Scholar] [CrossRef] [Green Version]
- Cerf, N.J.; Bourennane, M.; Karlsson, A.; Gisin, N. Security of Quantum Key Distribution Using d-Level Systems. Phys. Rev. Lett. 2002, 88, 127902. [Google Scholar] [CrossRef] [Green Version]
- Sheridan, L.; Scarani, V. Security proof for quantum key distribution using qudit systems. Phys. Rev. A 2010, 82, 030301. [Google Scholar] [CrossRef] [Green Version]
- Coles, P.J.; Metodiev, E.M.; Lütkenhaus, N. Numerical approach for unstructured quantum key distribution. Nat. Commun. 2016, 7, 11712. [Google Scholar] [CrossRef]
- Wang, S.; Yin, Z.Q.; Chau, H.F.; Chen, W.; Wang, C.; Guo, G.C.; Han, Z.F. Proof-of-principle experimental realization of a qubit-like qudit-based quantum key distribution scheme. Quantum Sci. Technol. 2018, 3, 025006. [Google Scholar] [CrossRef]
- Lee, C.; Bunandar, D.; Zhang, Z.; Steinbrecher, G.R.; Dixon, P.B.; Wong, F.N.C.; Shapiro, J.H.; Hamilton, S.A.; Englund, D. Large-alphabet encoding for higher-rate quantum key distribution. Opt. Express 2019, 27, 17539–17549. [Google Scholar] [CrossRef] [Green Version]
- Islam, N.T.; Lim, C.C.W.; Cahall, C.; Qi, B.; Kim, J.; Gauthier, D.J. Scalable high-rate, high-dimensional time-bin encoding quantum key distribution. Quantum Sci. Technol. 2019, 4, 035008. [Google Scholar] [CrossRef] [Green Version]
- Lo, H.-K.; Curty, M.; Tamaki, K. Secure quantum key distribution. Nat. Photon. 2014, 8, 595–604. [Google Scholar] [CrossRef] [Green Version]
- Diamanti, E.; Lo, H.-K.; Qi, B.; Yuan, Z. Practical challenges in quantum key distribution. NPJ Quantum Inf. 2016, 2, 16025. [Google Scholar] [CrossRef] [Green Version]
- Fung, C.-H.F.; Qi, B.; Tamaki, K.; Lo, H.K. Phase-remapping attack in practical quantum-key-distribution systems. Phys. Rev. A 2007, 75, 032314. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Wang, S.; Huang, J.; Chen, W.; Yin, Z.; Li, F.; Zhou, Z.; Liu, D.; Zhang, Y.; Guo, G.; et al. Attacking a practical quantum-key-distribution system with wavelength-dependent beam-splitter and multiwavelength sources. Phys. Rev. A 2011, 84, 062308. [Google Scholar] [CrossRef] [Green Version]
- Qi, B.; Fung, C.H.F.; Lo, H.K.; Ma, X.F. Time-shift attack in practical quantum cryptosystems. Quantum Inf. Comput. 2007, 7, 73–82. [Google Scholar] [CrossRef]
- Makarov, V.; Hjelme, D.R. Faked states attack on quantum cryptosystems. J. Mod. Opt. 2005, 52, 691–705. [Google Scholar] [CrossRef]
- Lydersen, L.; Wiechers, C.; Wittmann, C.; Elser, D.; Skaar, J.; Makarov, V. Hacking commercial quantum cryptography systems by tailored bright illumination. Nat. Photon. 2010, 4, 686–689. [Google Scholar] [CrossRef] [Green Version]
- Gerhardt, I.; Liu, Q.; Lamas-Linares, A.; Skaar, J.; Kurtsiefer, C.; Makarov, V. Full-field implementation of a perfect eavesdropper on a quantum cryptography system. Nat. Commun. 2011, 2, 349. [Google Scholar] [CrossRef] [Green Version]
- Zhang, G.; Primaatmaja, I.W.; Haw, J.Y.; Gong, X.; Wang, C.; Lim, C.C.W. Securing Practical Quantum Communication Systems with Optical Power Limiters. PRX Quantum 2021, 2, 030304. [Google Scholar] [CrossRef]
- Qian, Y.J.; He, D.Y.; Wang, S.; Chen, W.; Yin, Z.Q.; Guo, G.C.; Han, Z.F. Robust countermeasure against detector control attack in a practical quantum key distribution system. Optica 2019, 6, 1178–1184. [Google Scholar] [CrossRef] [Green Version]
- Yuan, Z.L.; Dynes, J.F.; Shields, A.J. Avoiding the blinding attack in QKD. Nat. Photon. 2010, 4, 800–801. [Google Scholar] [CrossRef] [Green Version]
- Lo, H.-K.; Curty, M.; Qi, B. Measurement-device-independent quantum key distribution. Phys. Rev. Lett. 2012, 108, 130503. [Google Scholar] [CrossRef] [Green Version]
- Braunstein, S.L.; Pirandola, S. Side-channel-free quantum key distribution. Phys. Rev. Lett. 2012, 108, 130502. [Google Scholar] [CrossRef] [Green Version]
- Lucamarini, M.; Yuan, Z.L.; Dynes, J.F.; Shields, A.J. Overcoming the rate–distance limit of quantum key distribution without quantum repeaters. Nature 2018, 557, 400–403. [Google Scholar] [CrossRef]
- Wang, X.-B.; Yu, Z.-W.; Hu, X.-L. Twin-field quantum key distribution with large misalignment error. Phys. Rev. A 2018, 98, 062323. [Google Scholar] [CrossRef] [Green Version]
- Ma, X.; Zeng, P.; Zhou, H. Phase-matching quantum key distribution. Phys. Rev. X 2018, 8, 031043. [Google Scholar] [CrossRef] [Green Version]
- Cui, C.; Yin, Z.Q.; Wang, R.; Chen, W.; Wang, S.; Guo, G.C.; Han, Z.F. Twin-field quantum key distribution without phase postselection. Phys. Rev. Appl. 2019, 11, 034053. [Google Scholar] [CrossRef] [Green Version]
- Yoshino, K.; Fujiwara, M.; Nakata, K.; Sumiya, T.; Sasaki, T.; Takeoka, M.; Sasaki, M.; Tajima, A.; Koashi, M.; Tomita, A. Quantum key distribution with an efficient countermeasure against correlated intensity fluctuations in optical pulses. NPJ Quantum Inf. 2018, 4, 8. [Google Scholar] [CrossRef]
- Lu, F.; Lin, X.; Wang, S.; Fan-Yuan, G.; Ye, P.; Wang, R.; Yin, Z.; He, D.; Chen, W.; Guo, G.; et al. Intensity modulator for secure, stable, and high-performance decoy-state quantum key distribution. NPJ Quantum Inf. 2021, 7, 75. [Google Scholar] [CrossRef]
- Brassard, G.; Lütkenhaus, N.; Mor, T.; Sanders, B.C. Limitations on practical quantum cryptography. Phys. Rev. Lett. 2000, 85, 1330–1333. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lütkenhaus, N.; Jahma, M. Quantum key distribution with realistic states: Photon-number statistics in the photon-number splitting attack. New J. Phys. 2002, 4, 44. [Google Scholar]
- Zhang, Z.; Mower, J.; Englund, D.; Wong, F.N.C.; Shapiro, J.H. Unconditional security of time-energy entanglement quantum key distribution using dual-basis interferometry. Phys. Rev. Lett. 2014, 112, 120506. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hwang, W.-Y. Quantum key distribution with high loss: Towards global secure communication. Phys. Rev. Lett. 2003, 91, 057901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, X.-B. Beating the photon-number-splitting attack in practical quantum cryptography. Phys. Rev. Lett. 2005, 94, 230503. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lo, H.-K.; Ma, X.; Chen, K. Decoy state quantum key distribution. Phys. Rev. Lett. 2005, 94, 230504. [Google Scholar] [CrossRef] [Green Version]
- Bunandar, D.; Zhang, Z.; Shapiro, J.H.; Englund, D.R. Practical high-dimensional quantum key distribution with decoy states. Phys. Rev. A 2015, 91, 022336. [Google Scholar] [CrossRef] [Green Version]
- Scarani, V.; Renner, R. Quantum cryptography with finite resources: Unconditional security bound for discrete-variable protocols with one-way postprocessing. Phys. Rev. Lett. 2008, 100, 200501. [Google Scholar] [CrossRef] [Green Version]
- Tomamichel, M.; Lim, C.C.W.; Gisin, N.; Renner, R. Tight finite-key analysis for quantum cryptography. Nat. Commun. 2012, 3, 634. [Google Scholar] [CrossRef]
- Bao, H.-Z.; Bao, W.-S.; Wang, Y.; Zhou, C.; Chen, R.-K. Finite-key analysis of a practical decoy-state high-dimensional quantum key distribution. J. Phys. A Math. Theor. 2016, 49, 205301. [Google Scholar] [CrossRef] [Green Version]
- Niu, M.Y.; Xu, F.; Shapiro, J.H.; Furrer, F. Finite-key analysis for time-energy high-dimensional quantum key distribution. Phys. Rev. A 2016, 94, 052323. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.B. Decoy-state quantum key distribution with large random errors of light intensity. Phys. Rev. A 2007, 75, 052301. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.-B.; Peng, C.-Z.; Zhang, J.; Yang, L.; Pan, J.-W. General theory of decoy-state quantum cryptography with source errors. Phys. Rev. A 2008, 77, 042311. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.-B.; Yang, L.; Peng, C.-Z.; Pan, J.-W. Decoy-state quantum key distribution with both source errors and statistical fluctuations. New J. Phys. 2009, 11, 075006. [Google Scholar] [CrossRef]
- Chi, H.-H.; Yu, Z.-W.; Wang, X.-B. Decoy-state method of quantum key distribution with both source errors and statistics fluctuations. Phys. Rev. A 2012, 86, 042307. [Google Scholar] [CrossRef]
- Wang, Y.; Bao, W.-S.; Zhou, C.; Jiang, M.-S.; Li, H.-W. Tight finite-key analysis of a practical decoy-state quantum key distribution with unstable sources. Phys. Rev. A 2016, 94, 032335. [Google Scholar] [CrossRef]
- Gan, Y.H.; Wang, Y.; Bao, W.S.; Zhou, C.; Jiang, M.S.; Li, H.W. Finite-key analysis for high-dimensional quantum key distribution with intensity fluctuations. J. Phys. B At. Mol. Opt. 2018, 51, 245502. [Google Scholar] [CrossRef]
- Wang, Y.; Bao, W.-S.; Zhou, C.; Jiang, M.-S.; Li, H.-W. Finite-key analysis of practical decoy-state measurement-device-independent quantum key distribution with unstable sources. J. Opt. Soc. Am. B 2019, 36, B83–B91. [Google Scholar] [CrossRef]
- Huang, J.Z.; Yin, Z.Q.; Wang, S.; Li, H.W.; Chen, W.; Han, Z.F. Effect of intensity modulator extinction on practical quantum key distribution system. Eur. Phys. J. D 2012, 66, 159. [Google Scholar] [CrossRef]
- Gottesman, D.; Lo, H.-K.; Lütkenhaus, N.; Preskill, J. Security of quantum key distribution with imperfect devices. Quant. Inf. Comput. 2004, 4, 325–360. [Google Scholar]
- Zhang, Z.; Zhao, Q.; Razavi, M.; Ma, X. Improved key-rate bounds for practical decoy-state quantum-key-distribution systems. Phys. Rev. A 2017, 95, 012333. [Google Scholar] [CrossRef] [Green Version]
- Azuma, K. Weighted sums of certain dependent random variables. Tohoku Math. J. 1967, 19, 357–367. [Google Scholar] [CrossRef]

| Dimension | Maximal Tolerable QBER | |
|---|---|---|
| without Considering the Finite Extinction of IM | with Considering the Finite Extinction of IM | |
| d = 4 | 18.93% | 19.27% |
| d = 8 | 24.71% | 25.47% |
| d = 16 | 28.97% | 30.58% |
| Transmission Distance (km) | without Considering the Finite Extinction of IM | with Considering the Finite Extinction of IM |
|---|---|---|
| 30 | 49.54 | 54.09 |
| 80 | 4.703 | 5.171 |
| 130 | 0.4417 | 0.4869 |
| 180 | 0.03927 | 0.04348 |
| 230 | 0.0027 | 0.00297 |
| Intensity Fluctuation | 0.01 | 0.05 | 0.1 |
| Secret key rate without considering the finite extinction of IM | 17.87 | 16.22 | 14.13 |
| Secret key rate with considering the finite extinction of IM | 19.67 | 18.03 | 15.96 |
| Improvement | 10.07% | 11.16% | 12.96% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Du, G.-H.; Xu, Y.-B.; Zhou, C.; Jiang, M.-S.; Li, H.-W.; Bao, W.-S. Practical Security of High-Dimensional Quantum Key Distribution with Intensity Modulator Extinction. Entropy 2022, 24, 460. https://doi.org/10.3390/e24040460
Wang Y, Du G-H, Xu Y-B, Zhou C, Jiang M-S, Li H-W, Bao W-S. Practical Security of High-Dimensional Quantum Key Distribution with Intensity Modulator Extinction. Entropy. 2022; 24(4):460. https://doi.org/10.3390/e24040460
Chicago/Turabian StyleWang, Yang, Ge-Hai Du, Yang-Bin Xu, Chun Zhou, Mu-Sheng Jiang, Hong-Wei Li, and Wan-Su Bao. 2022. "Practical Security of High-Dimensional Quantum Key Distribution with Intensity Modulator Extinction" Entropy 24, no. 4: 460. https://doi.org/10.3390/e24040460
APA StyleWang, Y., Du, G.-H., Xu, Y.-B., Zhou, C., Jiang, M.-S., Li, H.-W., & Bao, W.-S. (2022). Practical Security of High-Dimensional Quantum Key Distribution with Intensity Modulator Extinction. Entropy, 24(4), 460. https://doi.org/10.3390/e24040460






