Multipartite Correlations in Quantum Collision Models
Abstract
1. Introduction
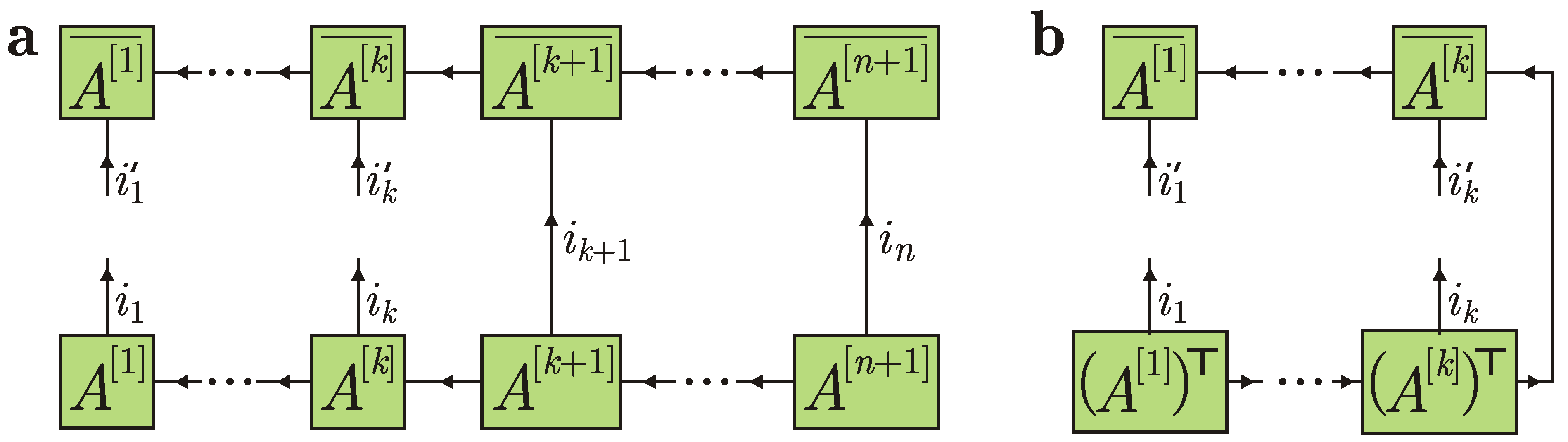
2. Tensor Network Notation
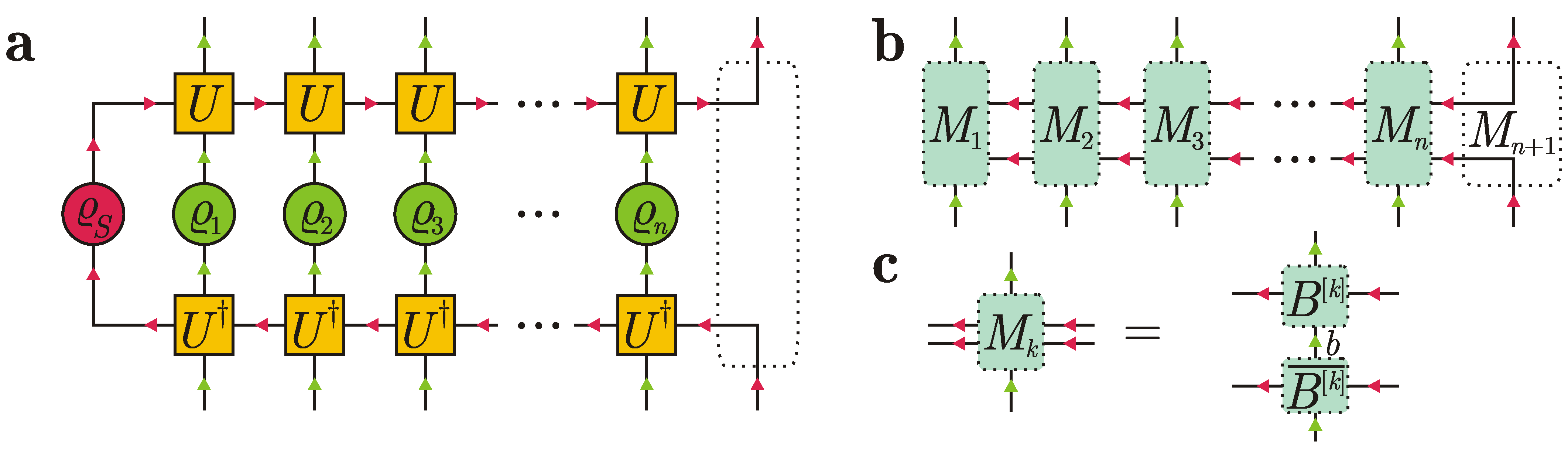
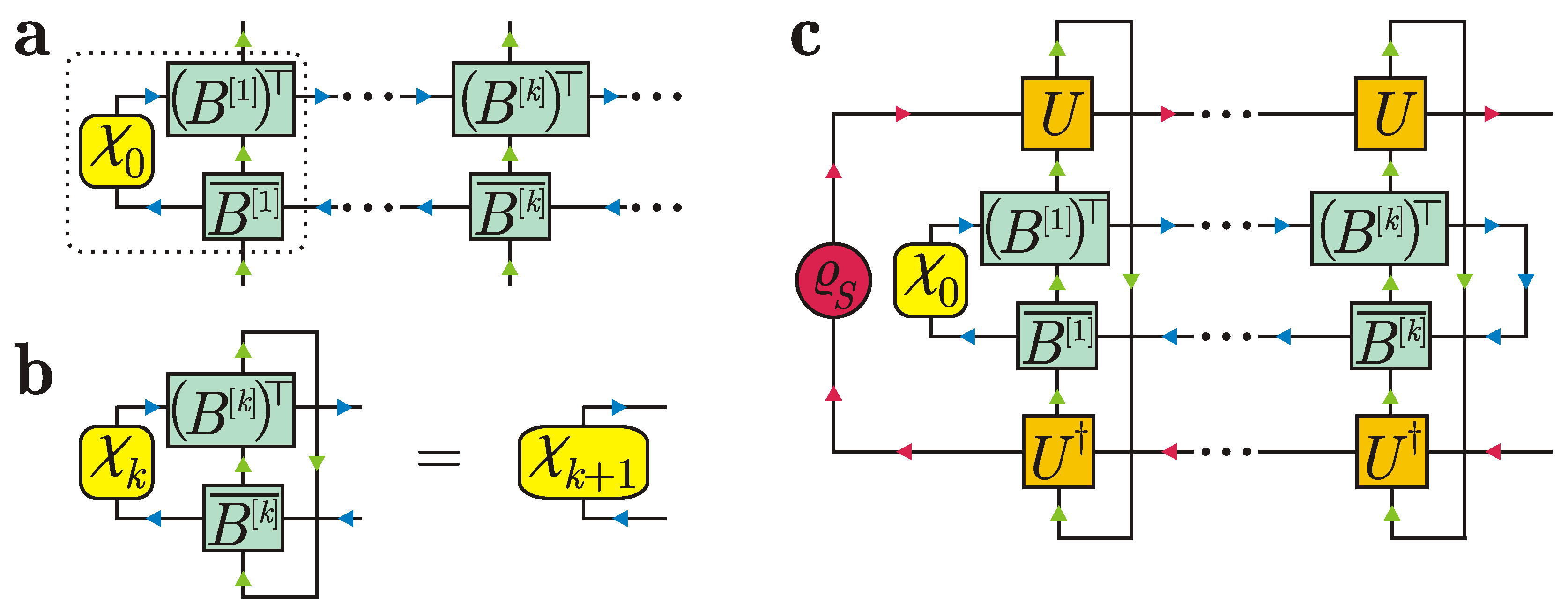
3. Matrix Product State Correlations in the Standard Collision Model
4. Generalization to Mixed States of the System and Ancillas
5. Collision Model with a Generally Correlated State of Ancillas
6. Master Equation
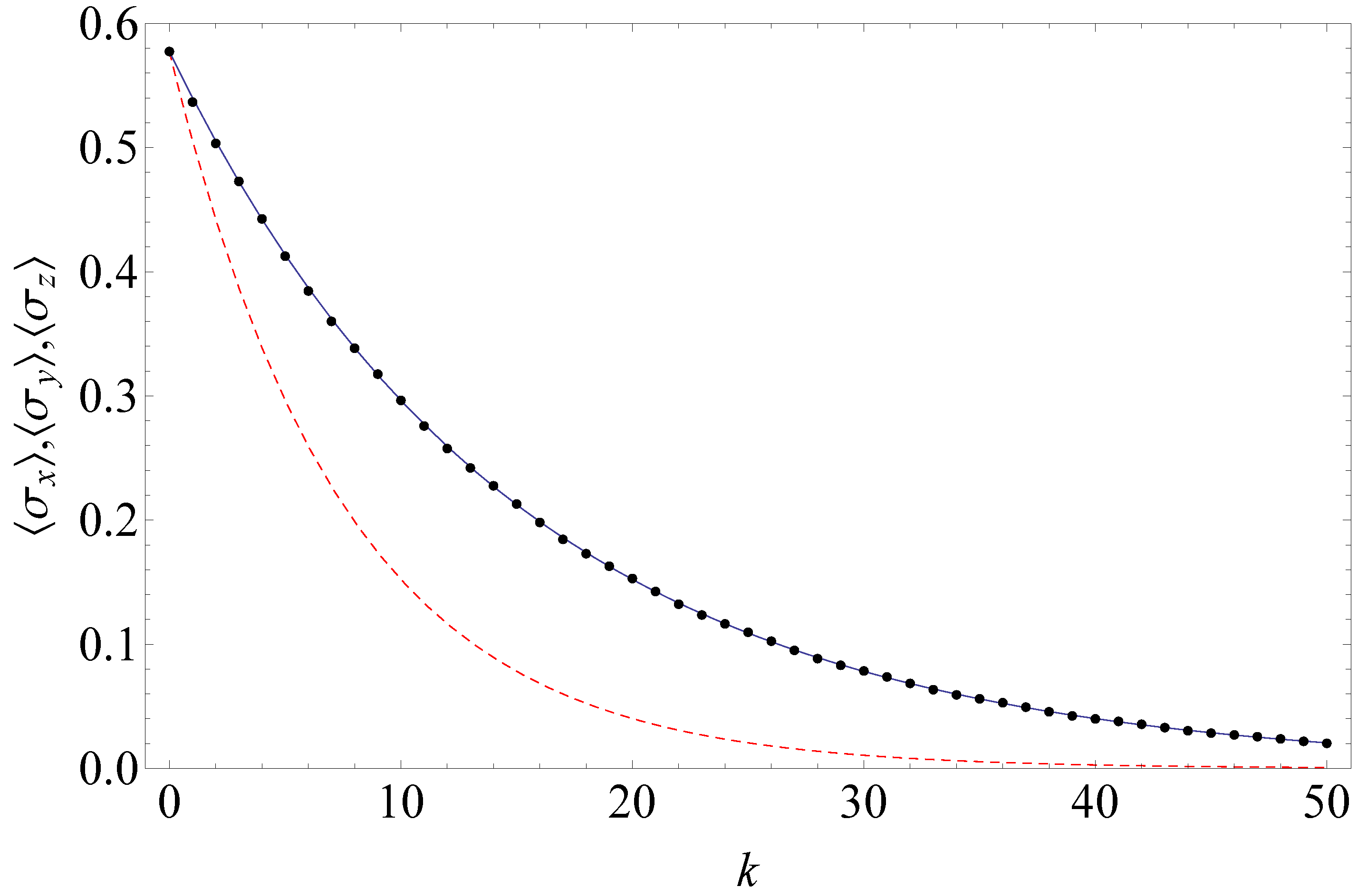
7. Effect of Two-Point Correlations
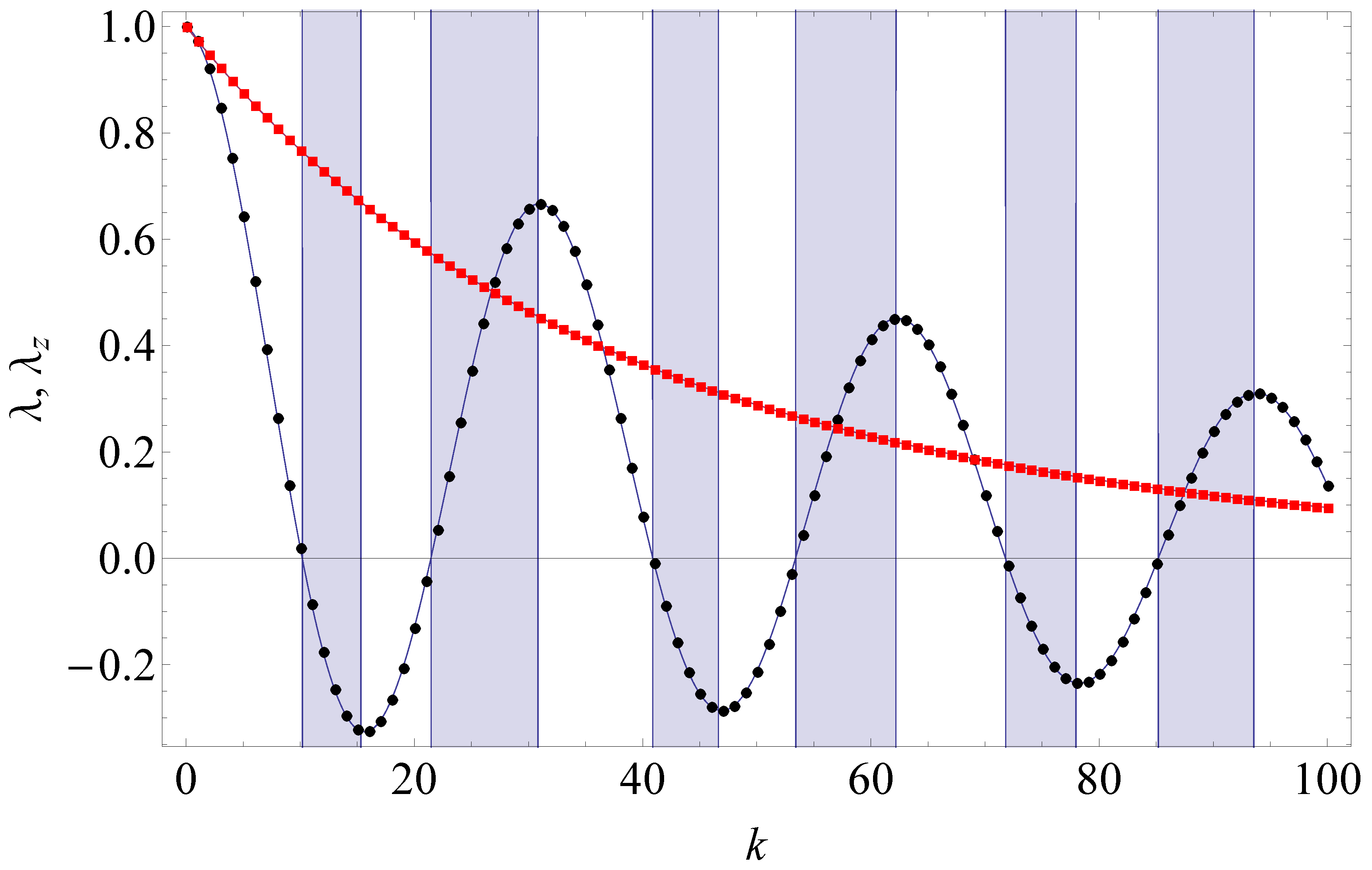
8. Stroboscopic Limit
9. Effect of Multipoint Correlations in the Higher-Order Stroboscopic Limit
10. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rau, J. Relaxation phenomena in spin and harmonic oscillator systems. Phys. Rev. 1963, 129, 1880–1888. [Google Scholar] [CrossRef]
- Nachtergaele, B.; Vershynina, A.; Zagrebnov, V.A. Non-Equilibrium states of a photon cavity pumped by an atomic beam. Ann. Henri Poincaré 2008, 15, 213–262. [Google Scholar] [CrossRef][Green Version]
- Scarani, V.; Ziman, M.; Štelmachovič, P.; Gisin, N.; Bužek, V. Thermalizing quantum machines: Dissipation and entanglement. Phys. Rev. Lett. 2002, 88, 097905. [Google Scholar] [CrossRef]
- Ziman, M.; Štelmachovič, P.; Bužek, V. Description of quantum dynamics of open systems based on collision-like models. Open Syst. Inf. Dyn. 2005, 12, 81–91. [Google Scholar] [CrossRef]
- Ziman, M.; Bužek, V. All (qubit) decoherences: Complete characterization and physical implementation. Phys. Rev. A 2005, 72, 022110. [Google Scholar] [CrossRef]
- Grimmer, D.; Layden, D.; Mann, R.B.; Martın-Martınez, E. Open dynamics under rapid repeated interaction. Phys. Rev. A 2016, 94, 032126. [Google Scholar] [CrossRef]
- Ziman, M.; Štelmachovič, P.; Bužek, V.; Hillery, M.; Scarani, V.; Gisin, N. Diluting quantum information: An analysis of information transfer in system-reservoir interactions. Phys. Rev. A 2002, 65, 042105. [Google Scholar] [CrossRef]
- Ziman, M.; Bužek, V. Open system dynamics of simple collision models. In Quantum Dynamics and Information; Olkiewicz, R., Cegła, W., Frydryszak, A., Garbaczewski, P., Jakóbczyk, L., Eds.; World Scientific: Singapore, 2011; pp. 199–227. [Google Scholar]
- Karevski, D.; Platini, T. Quantum nonequilibrium steady states induced by repeated interactions. Phys. Rev. Lett. 2009, 102, 207207. [Google Scholar] [CrossRef]
- Román-Ancheyta, R.; Kolář, M.; Guarnieri, G.; Filip, R. Enhanced steady-state coherence via repeated system-bath interactions. Phys. Rev. A 2021, 104, 062209. [Google Scholar] [CrossRef]
- Heineken, D.; Beyer, K.; Luoma, K.; Strunz, W.T. Quantum-memory-enhanced dissipative entanglement creation in nonequilibrium steady states. Phys. Rev. A 2021, 104, 052426. [Google Scholar] [CrossRef]
- Daryanoosh, S.; Baragiola, B.Q.; Guff, T.; Gilchrist, A. Quantum master equations for entangled qubit environments. Phys. Rev. A 2018, 98, 062104. [Google Scholar] [CrossRef]
- Çakmak, B.; Campbell, S.; Vacchini, B.; Müstecaplıoğlu, Ö.E.; Paternostro, M. Robust multipartite entanglement generation via a collision model. Phys. Rev. A 2019, 99, 012319. [Google Scholar] [CrossRef]
- Attal, S.; Pautrat, Y. From repeated to continuous quantum interactions. Ann. Henri Poincaré 2006, 7, 59. [Google Scholar] [CrossRef]
- Attal, S.; Joye, A. Weak coupling and continuous limits for repeated quantum interactions. J. Stat. Phys. 2007, 126, 1241–1283. [Google Scholar] [CrossRef]
- Vargas, R. Repeated interaction quantum systems: Van Hove limits and asymptotic states. J. Stat. Phys. 2008, 133, 491–511. [Google Scholar] [CrossRef][Green Version]
- Li, L.; Hall, M.J.W.; Wiseman, H.M. Concepts of quantum non-Markovianity: A hierarchy. Phys. Rep. 2018, 759, 1. [Google Scholar] [CrossRef]
- Attal, S.; Petruccione, F.; Sinayskiy, I. Open quantum walks on graphs. Phys. Lett. A 2012, 376, 1545. [Google Scholar] [CrossRef]
- Attal, S.; Petruccione, F.; Sabot, C.; Sinayskiy, I. Open quantum random walks. J. Stat. Phys. 2012, 147, 832. [Google Scholar] [CrossRef]
- Pellegrini, C. Continuous time open quantum random walks and non-Markovian Lindblad master equations. J. Stat. Phys. 2014, 154, 838–865. [Google Scholar] [CrossRef]
- Sinayskiy, I.; Petruccione, F. Microscopic derivation of open quantum walks. Phys. Rev. A 2015, 92, 032105. [Google Scholar] [CrossRef]
- Liu, C.; Balu, R. Steady states of continuous-time open quantum walks. Quantum Inf. Process. 2017, 16, 173. [Google Scholar] [CrossRef]
- Chia, A.; Paterek, T.; Kwek, L.C. Hitting statistics from quantum jumps. Quantum 2017, 1, 19. [Google Scholar] [CrossRef]
- Bruneau, L.; Joye, A.; Merkli, M. Repeated interactions in open quantum systems. J. Math. Phys. 2014, 55, 075204. [Google Scholar] [CrossRef]
- Bruneau, L.; Joye, A.; Merkli, M. Asymptotics of repeated interaction quantum systems. J. Funct. Anal. 2006, 239, 310–344. [Google Scholar] [CrossRef]
- Tamura, H.; Zagrebnov, V.A. Dynamics of an open system for repeated harmonic perturbation. J. Stat. Phys. 2016, 163, 844–867. [Google Scholar] [CrossRef]
- Bruneau, L.; Joye, A.; Merkli, M. Random repeated interaction quantum systems. Commun. Math. Phys. 2008, 284, 553–581. [Google Scholar] [CrossRef]
- Nechita, I.; Pellegrini, C. Random repeated quantum interactions and random invariant states. Probab. Theory Relat. Fields 2012, 152, 299–320. [Google Scholar] [CrossRef]
- Purkayastha, A.; Guarnieri, G.; Campbell, S.; Prior, J.; Goold, J. Periodically refreshed baths to simulate open quantum many-body dynamics. Phys. Rev. B 2021, 104, 045417. [Google Scholar] [CrossRef]
- Cattaneo, M.; De Chiara, G.; Maniscalco, S.; Zambrini, R.; Giorgi, G.L. Collision models can efficiently simulate any multipartite Markovian quantum dynamics. Phys. Rev. Lett. 2021, 126, 130403. [Google Scholar] [CrossRef]
- García-Pérez, G.; Rossi, M.A.C.; Maniscalco, S. IBM Q Experience as a versatile experimental testbed for simulating open quantum systems. NPJ Quantum Inf. 2020, 6, 1. [Google Scholar] [CrossRef]
- Filippov, S.N.; Semin, G.N.; Pechen, A.N. Quantum master equations for a system interacting with a quantum gas in the low-density limit and for the semiclassical collision model. Phys. Rev. A 2020, 101, 012114. [Google Scholar] [CrossRef]
- Kosloff, R. Quantum thermodynamics and open-systems modeling. J. Chem. Phys. 2019, 150, 204105. [Google Scholar] [CrossRef] [PubMed]
- Seah, S.; Nimmrichter, S.; Grimmer, D.; Santos, J.P.; Scarani, V.; Landi, G.T. Collisional quantum thermometry. Phys. Rev. Lett. 2019, 123, 180602. [Google Scholar] [CrossRef]
- Strasberg, P. Repeated interactions and quantum stochastic thermodynamics at strong coupling. Phys. Rev. Lett. 2019, 123, 180604. [Google Scholar] [CrossRef] [PubMed]
- Pichler, H.; Zoller, P. Photonic circuits with time delays and quantum feedback. Phys. Rev. Lett. 2016, 116, 093601. [Google Scholar] [CrossRef] [PubMed]
- Guimond, P.-O.; Pletyukhov, M.; Pichler, H.; Zoller, P. Delayed coherent quantum feedback from a scattering theory and a matrix product state perspective. Quantum Sci. Technol. 2017, 2, 044012. [Google Scholar] [CrossRef]
- Ciccarello, F. Collision models in quantum optics. Quantum Meas. Quantum Metrol. 2017, 4, 53–63. [Google Scholar] [CrossRef]
- Gross, J.A.; Caves, C.M.; Milburn, G.J.; Combes, J. Qubit models of weak continuous measurements: Markovian conditional and open-system dynamics. Quantum Sci. Technol. 2018, 3, 024005. [Google Scholar] [CrossRef]
- Fischer, K.A.; Trivedi, R.; Ramasesh, V.; Siddiqi, I.; Vučković, J. Scattering into one-dimensional waveguides from a coherently-driven quantum-optical system. Quantum 2018, 2, 69. [Google Scholar] [CrossRef]
- Cilluffo, D.; Carollo, A.; Lorenzo, S.; Gross, J.A.; Palma, G.M.; Ciccarello, F. Collisional picture of quantum optics with giant emitters. Phys. Rev. Res. 2020, 2, 043070. [Google Scholar] [CrossRef]
- Carmele, A.; Nemet, N.; Canela, V.; Parkins, S. Pronounced non-Markovian features in multiply excited, multiple emitter waveguide QED: Retardation induced anomalous population trapping. Phys. Rev. Res. 2020, 2, 013238. [Google Scholar] [CrossRef]
- Ferreira, V.S.; Banker, J.; Sipahigil, A.; Matheny, M.H.; Keller, A.J.; Kim, E.; Mirhosseini, M.; Painter, O. Collapse and revival of an artificial atom coupled to a structured photonic reservoir. Phys. Rev. X 2021, 11, 041043. [Google Scholar] [CrossRef]
- Wein, S.C.; Loredo, J.C.; Maffei, M.; Hilaire, P.; Harouri, A.; Somaschi, N.; Lemaître, A.; Sagnes, I.; Lanco, L.; Krebs, O.; et al. Photon-Number Entanglement Generated by Sequential Excitation of a Two-Level Atom. Available online: https://arxiv.org/abs/2106.02049 (accessed on 21 February 2022).
- Maffei, M.; Camati, P.A.; Auffèves, A. Closed-system solution of the 1D atom from collision model. Entropy 2022, 24, 151. [Google Scholar] [CrossRef] [PubMed]
- Gheri, K.M.; Ellinger, K.; Pellizzari, T.; Zoller, P. Photon-wavepackets as flying quantum bits. Fortschr. Phys. 1998, 46, 401–415. [Google Scholar] [CrossRef]
- Baragiola, B.Q.; Cook, R.L.; Brańczyk, A.M.; Combes, J. N-photon wave packets interacting with an arbitrary quantum system. Phys. Rev. A 2012, 86, 013811. [Google Scholar] [CrossRef]
- Dąbrowska, A.M. From a posteriori to a priori solutions for a two-level system interacting with a single-photon wavepacket. J. Opt. Soc. Am. B 2020, 37, 1240–1248. [Google Scholar] [CrossRef]
- Dąbrowska, A.; Chruściński, D.; Chakraborty, S.; Sarbicki, G. Eternally non-Markovian dynamics of a qubit interacting with a single-photon wavepacket. New J. Phys. 2021, 23, 123019. [Google Scholar] [CrossRef]
- Rybár, T.; Filippov, S.N.; Ziman, M.; Bužek, V. Simulation of indivisible qubit channels in collision models. J. Phys. B At. Mol. Opt. Phys. 2012, 45, 154006. [Google Scholar] [CrossRef]
- Filippov, S.N.; Piilo, J.; Maniscalco, S.; Ziman, M. Divisibility of quantum dynamical maps and collision models. Phys. Rev. A 2017, 96, 032111. [Google Scholar] [CrossRef]
- Ciccarello, F.; Palma, G.M.; Giovannetti, V. Collision-model-based approach to non-Markovian quantum dynamics. Phys. Rev. A 2013, 87, 040103. [Google Scholar] [CrossRef]
- Ciccarello, F.; Giovannetti, V. A quantum non-Markovian collision model: Incoherent swap case. Phys. Scr. 2013, T153, 014010. [Google Scholar] [CrossRef]
- Kretschmer, S.; Luoma, K.; Strunz, W.T. Collision model for non-Markovian quantum dynamics. Phys. Rev. A 2016, 94, 012106. [Google Scholar] [CrossRef]
- Campbell, S.; Ciccarello, F.; Palma, G.M.; Vacchini, B. System-environment correlations and Markovian embedding of quantum non-Markovian dynamics. Phys. Rev. A 2018, 98, 012142. [Google Scholar] [CrossRef]
- Lorenzo, S.; Ciccarello, F.; Palma, G.M. Composite quantum collision models. Phys. Rev. A 2017, 96, 032107. [Google Scholar] [CrossRef]
- Pellegrini, C.; Petruccione, F. Non-Markovian quantum repeated interactions and measurements. J. Phys. A Math. Theor. 2009, 42, 425304. [Google Scholar] [CrossRef]
- Cilluffo, D.; Ciccarello, F. Quantum non-Markovian collision models from colored-noise baths. In Advances in Open Systems and Fundamental Tests of Quantum Mechanics, Springer Proceedings in Physics; Vacchini, B., Breuer, H.-P., Bassi, A., Eds.; Springer: Cham, Switzerland, 2019; Volume 237, pp. 29–40. [Google Scholar]
- Taranto, P.; Milz, S.; Pollock, F.A.; Modi, K. Structure of quantum stochastic processes with finite Markov order. Phys. Rev. A 2019, 99, 042108. [Google Scholar] [CrossRef]
- Kretschmann, D.; Werner, R.F. Quantum channels with memory. Phys. Rev. A 2005, 72, 062323. [Google Scholar] [CrossRef]
- Plenio, M.B.; Virmani, S. Spin chains and channels with memory. Phys. Rev. Lett. 2007, 99, 120504. [Google Scholar] [CrossRef]
- Plenio, M.B.; Virmani, S. Many-body physics and the capacity of quantum channels with memory. New J. Phys. 2008, 10, 043032. [Google Scholar] [CrossRef][Green Version]
- Rybár, T.; Ziman, M. Repeatable quantum memory channels. Phys. Rev. A 2008, 78, 052114. [Google Scholar] [CrossRef]
- Rybár, T.; Ziman, M. Quantum finite-depth memory channels: Case study. Phys. Rev. A 2009, 80, 042306. [Google Scholar] [CrossRef]
- Giovannetti, V.; Palma, G.M. Master equations for correlated quantum channels. Phys. Rev. Lett. 2012, 108, 040401. [Google Scholar] [CrossRef] [PubMed]
- Giovannetti, V.; Palma, G.M. Master equation for cascade quantum channels: A collisional approach. J. Phys. B At. Mol. Opt. Phys. 2012, 45, 154003. [Google Scholar] [CrossRef]
- Rybár, T.; Ziman, M. Process estimation in the presence of time-invariant memory effects. Phys. Rev. A 2015, 92, 042315. [Google Scholar] [CrossRef]
- Ciccarello, F.; Lorenzo, S.; Giovannetti, V.; Palma, G.M. Quantum collision models: Open system dynamics from repeated interactions. Phys. Rep. 2022, 954, 1–70. [Google Scholar] [CrossRef]
- Campbell, S.; Vacchini, B. Collision models in open system dynamics: A versatile tool for deeper insights? EPL 2021, 133, 60001. [Google Scholar] [CrossRef]
- Affleck, I.; Kennedy, T.; Lieb, E.H.; Tasaki, H. Rigorous results on valence-bond ground states in antiferromagnets. Phys. Rev. Lett. 1987, 59, 799. [Google Scholar] [CrossRef]
- Comar, N.E.; Landi, G.T. Correlations breaking homogenization. Phys. Rev. A 2021, 104, 032217. [Google Scholar] [CrossRef]
- Filippov, S.N.; Luchnikov, I.A. Collisional Open Quantum Dynamics with a Generally Correlated Environment: Exact Solvability in Tensor Networks. Available online: https://arxiv.org/abs/2202.04697 (accessed on 21 February 2022).
- Pérez-García, D.; Verstraete, F.; Wolf, M.M.; Cirac, J.I. Matrix product state representations. Quantum Inf. Comput. 2007, 7, 401. [Google Scholar] [CrossRef]
- Verstraete, F.; Murg, V.; Cirac, J.I. Matrix product states, projected entangled pair states, and variational renormalization group methods for quantum spin systems. Adv. Phys. 2008, 57, 143. [Google Scholar] [CrossRef]
- Schollwöck, U. The density-matrix renormalization group in the age of matrix product states. Ann. Phys. 2011, 326, 96. [Google Scholar] [CrossRef]
- Cirac, J.I.; Pérez-García, D.; Schuch, N.; Verstraete, F. Matrix product states and projected entangled pair states: Concepts, symmetries, theorems. Rev. Mod. Phys. 2021, 93, 045003. [Google Scholar] [CrossRef]
- Orús, R. A practical introduction to tensor networks: Matrix product states and projected entangled pair states. Ann. Phys. 2014, 349, 117–158. [Google Scholar] [CrossRef]
- Orús, R. Tensor networks for complex quantum systems. Nat. Rev. Phys. 2019, 1, 538–550. [Google Scholar] [CrossRef]
- Montangero, S. Introduction to Tensor Network Methods; Springer: New York, NY, USA, 2018. [Google Scholar]
- Vidal, G. Efficient classical simulation of slightly entangled quantum computations. Phys. Rev. Lett. 2003, 91, 147902. [Google Scholar] [CrossRef]
- Luchnikov, I.A.; Ryzhov, A.; Filippov, S.N.; Ouerdane, H. QGOpt: Riemannian optimization for quantum technologies. SciPost Phys. 2021, 10, 079. [Google Scholar] [CrossRef]
- Luchnikov, I.A.; Krechetov, M.E.; Filippov, S.N. Riemannian geometry and automatic differentiation for optimization problems of quantum physics and quantum technologies. New J. Phys. 2021, 23, 073006. [Google Scholar] [CrossRef]
- Verstraete, F.; García-Ripoll, J.J.; Cirac, J.I. Matrix product density operators: Simulation of finite-temperature and dissipative systems. Phys. Rev. Lett. 2004, 93, 207204. [Google Scholar] [CrossRef]
- Zwolak, M.; Vidal, G. Mixed-state dynamics in one-dimensional quantum lattice systems: A time-dependent superoperator renormalization algorithm. Phys. Rev. Lett. 2004, 93, 207205. [Google Scholar] [CrossRef]
- Chen, C.-F.; Kato, K.; Brandão, F.G.S.L. Matrix Product Density Operators: When Do They Have a Local Parent Hamiltonian? Available online: https://arxiv.org/abs/2010.14682 (accessed on 21 February 2022).
- Bondarenko, D. Constructing K-Local Parent Lindbladians for Matrix Product Density Operators. Available online: https://arxiv.org/abs/2110.13134 (accessed on 21 February 2022).
- Wood, C.J.; Biamonte, J.D.; Cory, D.G. Tensor networks and graphical calculus for open quantum systems. Quantum Inf. Comput. 2015, 15, 759–811. [Google Scholar] [CrossRef]
- Dhand, I.; Engelkemeier, M.; Sansoni, L.; Barkhofen, S.; Silberhorn, C.; Plenio, M.B. Proposal for quantum simulation via all-optically-generated tensor network states. Phys. Rev. Lett. 2018, 120, 130501. [Google Scholar] [CrossRef] [PubMed]
- Lubasch, M.; Valido, A.A.; Renema, J.J.; Kolthammer, W.S.; Jaksch, D.; Kim, M.S.; Walmsley, I.; Garcıa-Patrón, R. Tensor network states in time-bin quantum optics. Phys. Rev. A 2018, 97, 062304. [Google Scholar] [CrossRef]
- Istrati, D.; Pilnyak, Y.; Loredo, J.C.; Antón, C.; Somaschi, N.; Hilaire, P.; Ollivier, H.; Esmann, M.; Cohen, L.; Vidro, L.; et al. Sequential generation of linear cluster states from a single photon emitter. Nat. Commun. 2020, 11, 5501. [Google Scholar] [CrossRef] [PubMed]
- Besse, J.-C.; Reuer, K.; Collodo, M.C.; Wulff, A.; Wernli, L.; Copetudo, A.; Malz, D.; Magnard, P.; Akin, A.; Gabureac, M.; et al. Realizing a deterministic source of multipartite-entangled photonic qubits. Nat. Commun. 2020, 11, 4877. [Google Scholar] [CrossRef]
- Tiurev, K.; Appel, M.H.; Mirambell, P.L.; Lauritzen, M.B.; Tiranov, A.; Lodahl, P.; Sørensen, A.S. High-Fidelity Multi-Photon-Entangled Cluster State with Solid-State Quantum Emitters in Photonic Nanostructures. Available online: https://arxiv.org/abs/2007.09295 (accessed on 21 February 2022).
- Wei, Z.-Y.; Malz, D.; González-Tudela, A.; Cirac, J.I. Generation of photonic matrix product states with Rydberg atomic arrays. Phys. Rev. Res. 2021, 3, 023021. [Google Scholar] [CrossRef]
- Dalzell, A.M.; Brandão, F.G.S.L. Locally accurate MPS approximations for ground states of one-dimensional gapped local Hamiltonians. Quantum 2019, 3, 187. [Google Scholar] [CrossRef]
- Pollock, F.A.; Rodríguez-Rosario, C.; Frauenheim, T.; Paternostro, M.; Modi, K. Non-Markovian quantum processes: Complete framework and efficient characterization. Phys. Rev. A 2018, 97, 012127. [Google Scholar] [CrossRef]
- Pollock, F.A.; Rodríguez-Rosario, C.; Frauenheim, T.; Paternostro, M.; Modi, K. Operational Markov condition for quantum processes. Phys. Rev. Lett. 2018, 120, 040405. [Google Scholar] [CrossRef]
- White, G.A.L.; Hill, C.D.; Pollock, F.A.; Hollenberg, L.C.L.; Modi, K. Demonstration of non-Markovian process characterisation and control on a quantum processor. Nat. Commun. 2020, 11, 6301. [Google Scholar] [CrossRef]
- Taranto, P. Memory effects in quantum processes. Int. J. Quantum Inf. 2020, 18, 1941002. [Google Scholar] [CrossRef]
- Luchnikov, I.A.; Vintskevich, S.V.; Ouerdane, H.; Filippov, S.N. Simulation complexity of open quantum dynamics: Connection with tensor networks. Phys. Rev. Lett. 2019, 122, 160401. [Google Scholar] [CrossRef] [PubMed]
- Luchnikov, I.A.; Vintskevich, S.V.; Grigoriev, D.A.; Filippov, S.N. Machine learning non-Markovian quantum dynamics. Phys. Rev. Lett. 2020, 124, 140502. [Google Scholar] [CrossRef] [PubMed]
- Chruściński, D.; Maniscalco, S. Degree of non-Markovianity of quantum evolution. Phys. Rev. Lett. 2014, 112, 120404. [Google Scholar] [CrossRef]
- Filippov, S.N.; Glinov, A.N.; Leppäjärvi, L. Phase covariant qubit dynamics and divisibility. Lobachevskii J. Math. 2020, 41, 617–630. [Google Scholar] [CrossRef]
- Breuer, H.-P.; Petruccione, F. The Theory of Open Quantum Systems; Oxford University Press: Oxford, UK, 2002; Chapter 9. [Google Scholar]
- Nakajima, S. On quantum theory of transport phenomena: Steady diffusion. Prog. Theor. Phys. 1958, 20, 948–959. [Google Scholar] [CrossRef]
- Zwanzig, R. Ensemble method in the theory of irreversibility. J. Chem. Phys. 1960, 33, 1338–1341. [Google Scholar] [CrossRef]
- Luchnikov, I.A.; Filippov, S.N. Quantum evolution in the stroboscopic limit of repeated measurements. Phys. Rev. A 2017, 95, 022113. [Google Scholar] [CrossRef]
- Grimaudo, R.; Messina, A.; Sergi, A.; Vitanov, N.V.; Filippov, S.N. Two-qubit entanglement generation through non-Hermitian Hamiltonians induced by repeated measurements on an ancilla. Entropy 2020, 22, 1184. [Google Scholar] [CrossRef]
- Chruściński, D.; Kossakowski, A. Non-Markovian quantum dynamics: Local versus nonlocal. Phys. Rev. Lett. 2010, 104, 070406. [Google Scholar] [CrossRef]
- Smirne, A.; Vacchini, B. Nakajima-Zwanzig versus time-convolutionless master equation for the non-Markovian dynamics of a two-level system. Phys. Rev. A 2010, 82, 022110. [Google Scholar] [CrossRef]
- Filippov, S.N.; Chruściński, D. Time deformations of master equations. Phys. Rev. A 2018, 98, 022123. [Google Scholar] [CrossRef]
- Gorini, V.; Kossakowski, A.; Sudarshan, E.C.G. Completely positive dynamical semigroups of n-level systems. J. Math. Phys. 1976, 17, 821. [Google Scholar] [CrossRef]
- Lindblad, G. On the generators of quantum dynamical semigroups. Comm. Math. Phys. 1976, 48, 119. [Google Scholar] [CrossRef]
- von Waldenfels, W. An approach to the theory of pressure broadening of spectral lines. In Probability and Information Theory II; Behara, M., Krickeberg, K., Wolfowitz, J., Eds.; Springer: Berlin/Heidelberg, Germany, 1973; pp. 19–69. [Google Scholar]
- Hegerfeldt, G.C.; Schulze, H. Noncommutative cumulants for stochastic differential equations and for generalized Dyson series. J. Stat. Phys. 1988, 51, 691–710. [Google Scholar] [CrossRef]
- Pechen, A.N. The multitime correlation functions, free white noise, and the generalized Poisson statistics in the low density limit. J. Math. Phys. 2006, 47, 033507. [Google Scholar] [CrossRef]
- Nosal’, I.A.; Teretenkov, A.E. Exact dynamics of moments and correlation functions for GKSL fermionic equations of Poisson type. Math Notes 2020, 108, 911–915. [Google Scholar] [CrossRef]
- Gherardini, S.; Smirne, A.; Huelga, S.F.; Caruso, F. Transfer-tensor description of memory effects in open-system dynamics and multi-time statistics. Quantum Sci. Technol. 2022, 7, 025005. [Google Scholar] [CrossRef]
- Hübener, R.; Mari, A.; Eisert, J. Wick’s theorem for matrix product states. Phys. Rev. Lett. 2013, 110, 040401. [Google Scholar] [CrossRef]
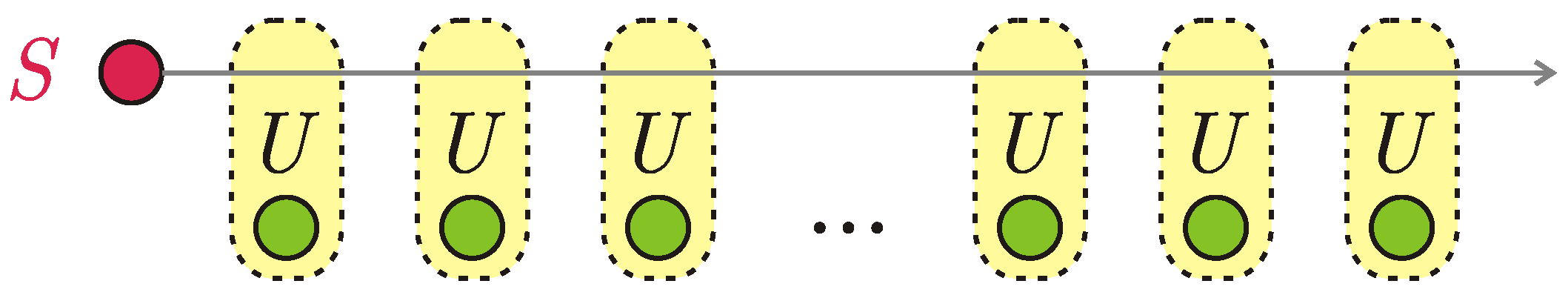

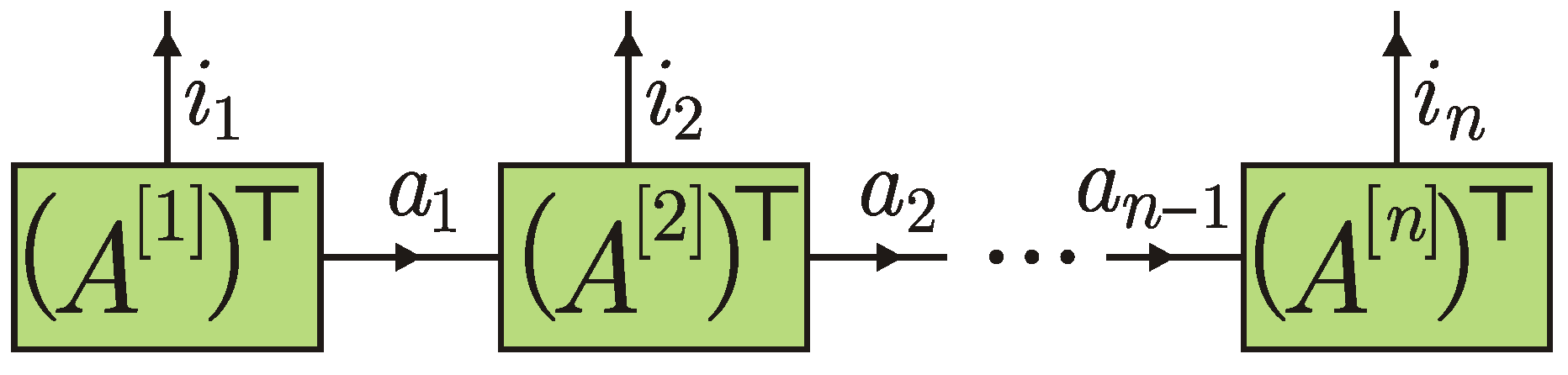


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Filippov, S. Multipartite Correlations in Quantum Collision Models. Entropy 2022, 24, 508. https://doi.org/10.3390/e24040508
Filippov S. Multipartite Correlations in Quantum Collision Models. Entropy. 2022; 24(4):508. https://doi.org/10.3390/e24040508
Chicago/Turabian StyleFilippov, Sergey. 2022. "Multipartite Correlations in Quantum Collision Models" Entropy 24, no. 4: 508. https://doi.org/10.3390/e24040508
APA StyleFilippov, S. (2022). Multipartite Correlations in Quantum Collision Models. Entropy, 24(4), 508. https://doi.org/10.3390/e24040508





