Proof of Equivalence of Carnot Principle to II Law of Thermodynamics and Non-Equivalence to Clausius I and Kelvin Principles
Abstract
1. Introduction
- Carnot principle ()
- The efficiency of the heat conversion process to work W in the device operating in the range between the temperature of the heat source and the temperature of the heat receiver , cannot be greater than the ratio of the difference of these temperatures to the temperature of the heat source:Such a formulation does not explicitly contain the information that the temperature of the heat source must be higher than that of the heat receiver. However, the implicit condition that the engine performs real positive work () entails the aforementioned temperatures relationship . In this case, the condition of the Carnot principle takes the form:
- Clausius I principle ()
- Heat naturally flows from a body at a higher temperature to a body at a lower temperature. Therefore, a direct (not forced by work) process of heat transfer from the body at a lower temperature to the body at a higher temperature is not possible.
- An absolute temperature scale is not needed to determine which reservoir has a higher temperature—even the Celsius scale is sufficient here. The Clausius I principle seems so trivial that one might suppose that it has no far-reaching, less trivial consequences. Nevertheless, it is allegedly proved, that the Clausius I principle is equivalent to the full II law of thermodynamics [12,13,14,15]. Criticism of this popular proof could only be found in a 2008 preprint by a scholar Bhattacharyya [16].
- Kelvin principle ().
- The processes of converting heat to work and work to heat do not run symmetrically. A full conversion of work to heat (internal energy) is possible. However, a full conversion of the heat to the work is not possible in a cyclical process.
- The principle called the Kelvin principle is formulated in various but similar ways. This relates not so much to the original formulation of Kelvin [24,25], but more to a later formulation of Planck (see [26]), called the Kelvin–Planck formulation (see [27]). The above version of the K principle reflects, as intended by the author, the essence of all these formulations—although this form of the principle comes from Planck or Ostwald ([26]) rather than initially from Kelvin. Nevertheless, traditional formulations identically equivalent to the K version of the principle are called the Kelvin principle, not the Kelvin–Planck or Ostwald principle [12,13,14,15,28,29,30,31]. In the publications [24,25,32], Kelvin expressed his principle as follows: “It is impossible, by means of inanimate material agency, to derive mechanical effect from any portion of matter by cooling it below the temperature of the coldest of the surrounding objects”. Such a formulation, however, seems weaker than the formulation of K, as it seems to refer to the performance of work at the expense of the cooler heat, and not more naturally at the expense of the heater heat. Therefore, it is not known which of the following elements Kelvin wanted to emphasize in this formulation: (i) a change in the temperature of the reservoir when taking heat converted into work, (ii) limitations in this conversion of heat to work, (iii) the impossibility of cooling down the coldest body by means of the work performed by this body? Thus, it can be said that Kelvin did not provide his own formulation of the II law of thermodynamics in a very strict and careful manner [2]. Therefore, it is not surprising that we use a version of the rule of the type K slightly different from the original formulation (see also [33]). Nevertheless, Kelvin’s formulation of the II law of thermodynamics is dated to 1851 in connection with his lectures published in the form of articles in two journals [24,25]. In addition, in the second journal, Kelvin separated a short article in which he repeated the formulation of his principle, and also gave a general interpretation of the II law of thermodynamics [32].
- Clausius II principle ()
- There is a function of the state of the thermodynamic system called entropy, which the dependence of the value on time allows to determine the system’s following of the thermodynamic equilibrium. Namely, in thermally insulated systems, the only possible processes are those in which the total entropy of the system (two heat reservoirs) does not decrease:
- For reversible processes, the increase in total entropy is zero, and for irreversible processes it is greater than zero. The change in entropy of a reservoir is here understood as the ratio of the heat introduced into it to its temperature.
- Thus, when using standard notations, Clausius II principle takes the following form for the processes considered here:
- It is assumed that a specific device operating cyclically between heat reservoirs does not change its entropy by definition of cyclicity. Additionally, similarly for the principle, the absolute temperature scale is assumed here.
- Perpetuum mobile ()
- A perpetuum mobile is a hypothetical machine, the movement and efficiency of which would contradict certain recognized laws of physics. The most faithful meaning of the Latin name (“forever moving”) perpetuum mobile type 0 () would not be stopped in spite of the existence of frictional forces and resistance to motion. A perpetuum mobile type I () would do work from nothing (or almost nothing—efficiency greater than 100%) against the principle of conservation of energy and against the I law of thermodynamics. A perpetuum mobile type II () would be 100% efficient and would be against the Kelvin principle. On the other hand, the perpetuum mobile type III () would have efficiency lower than 100%, but higher than the maximum efficiency predicted by the Carnot principle.
- Most often it only stands out perpetuum mobile and . However, perpetuum mobile is crucial for this article. Sometimes the term perpetuum mobile of type III is understood as . However, the proposed terminology seems clear and consistent with the meaning of the Latin words perpetuum mobile for and consistent with the classification of various ways of doing work by —while machine does not do the work. A similar notation to perpetuum motion will also be applied to the process where heat spontaneously flows uphill (towards higher temperature). Such a process, despite its similarities, does not have to be automatically equivalent to .
2. Materials and Methods
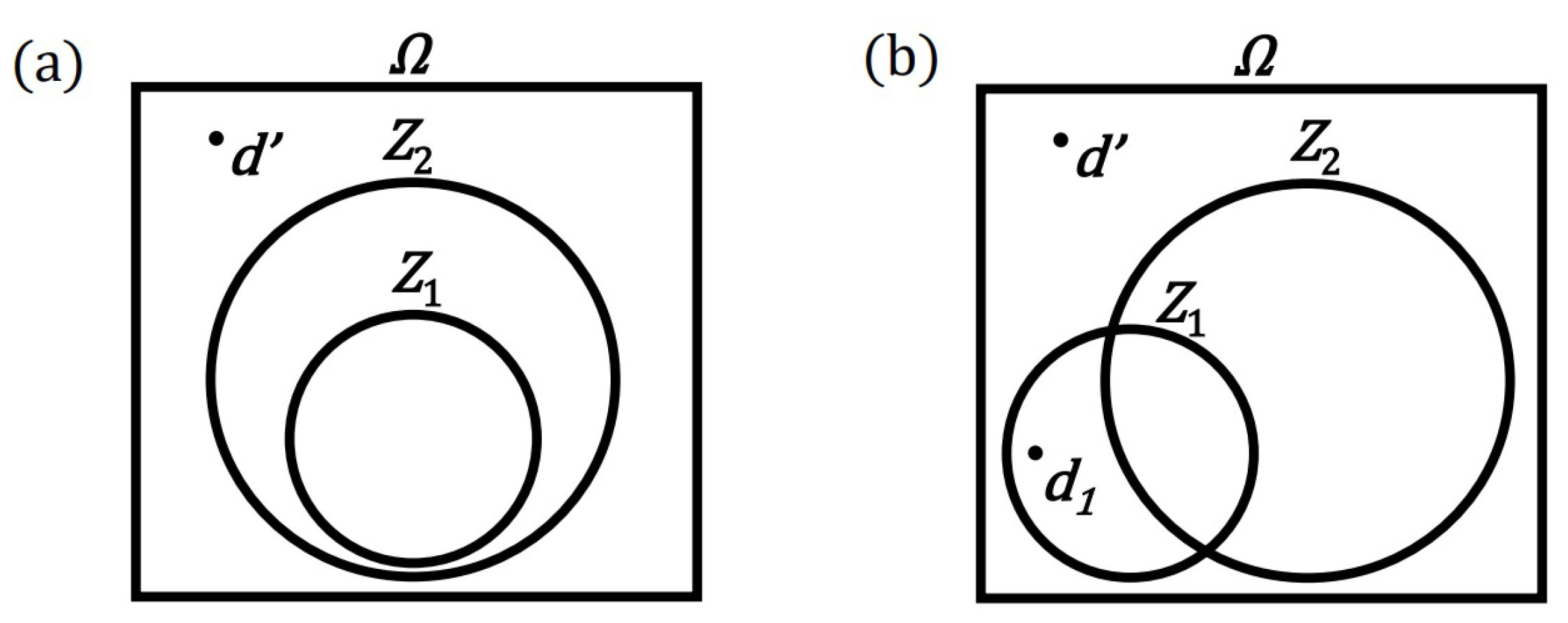
- The definition of a convexity (for a set of diagrams—for a model)
- A set of diagrams will be called convex if the sum of any two diagrams of this set belongs to this set. In other words, the convexity of the set requires that the add diagrams operation be internal to that set.
- Thus, the definition of the convexity of the set is here simplified to the operation of adding elements without having to consider multiplying diagrams by non-negative real numbers. However, the ability to scale diagrams means that the above definition is equivalent to the standard geometric definition of a convex set. The definition of a convex set helps to formulate the following important condition:
- Completeness condition (for model of principle)
- It is assumed that the set of diagrams (processes), consistent with a given principle and called the model of this principle, must be the largest convex set possible. It is allowed to have many alternative sets (models) that meet the above condition, in the sense that a given set (model) cannot be enlarged without breaking compliance with the principle or without breaking the convexity requirement.
- The completeness condition allows for the consideration of richer models (sets of diagrams) for a given principle. Thanks to this condition, diagrams (processes) whose compliance with the principle is not obvious can be attached to the model. An attached diagram (process) can be created as a result of adding two trivial diagrams or diagrams already belonging to the model. In addition, a diagram (process) can be attached to the model, the addition of which to existing diagrams results in a trivial diagram or a diagram belonging to the model. This procedure can fork the model into two models or the entire model family. Regardless of the number of models in the family, each model should be considered an alternative independent model. If there is only one model, it will be called a homogeneous model here, and in the literature it is sometimes called a stable model.
3. Discussion: Principles Structure, Proof and Rebuttals
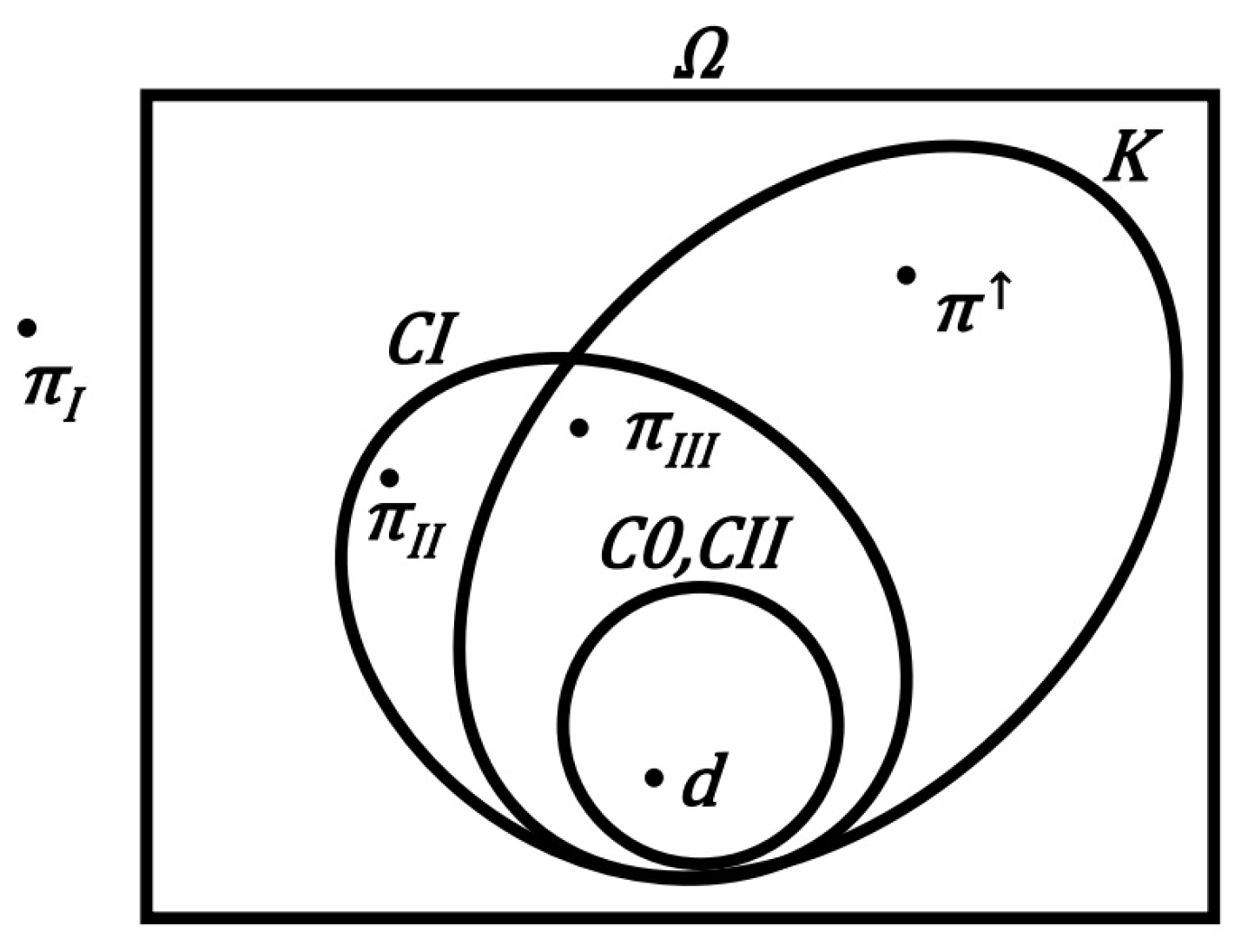
3.1. Structure of the Carnot Principle Model
3.2. Structure of Models for Clausius I Principle
3.3. Structure of Models for Kelvin Principle
3.4. Structure of the Clausius II Principle Model
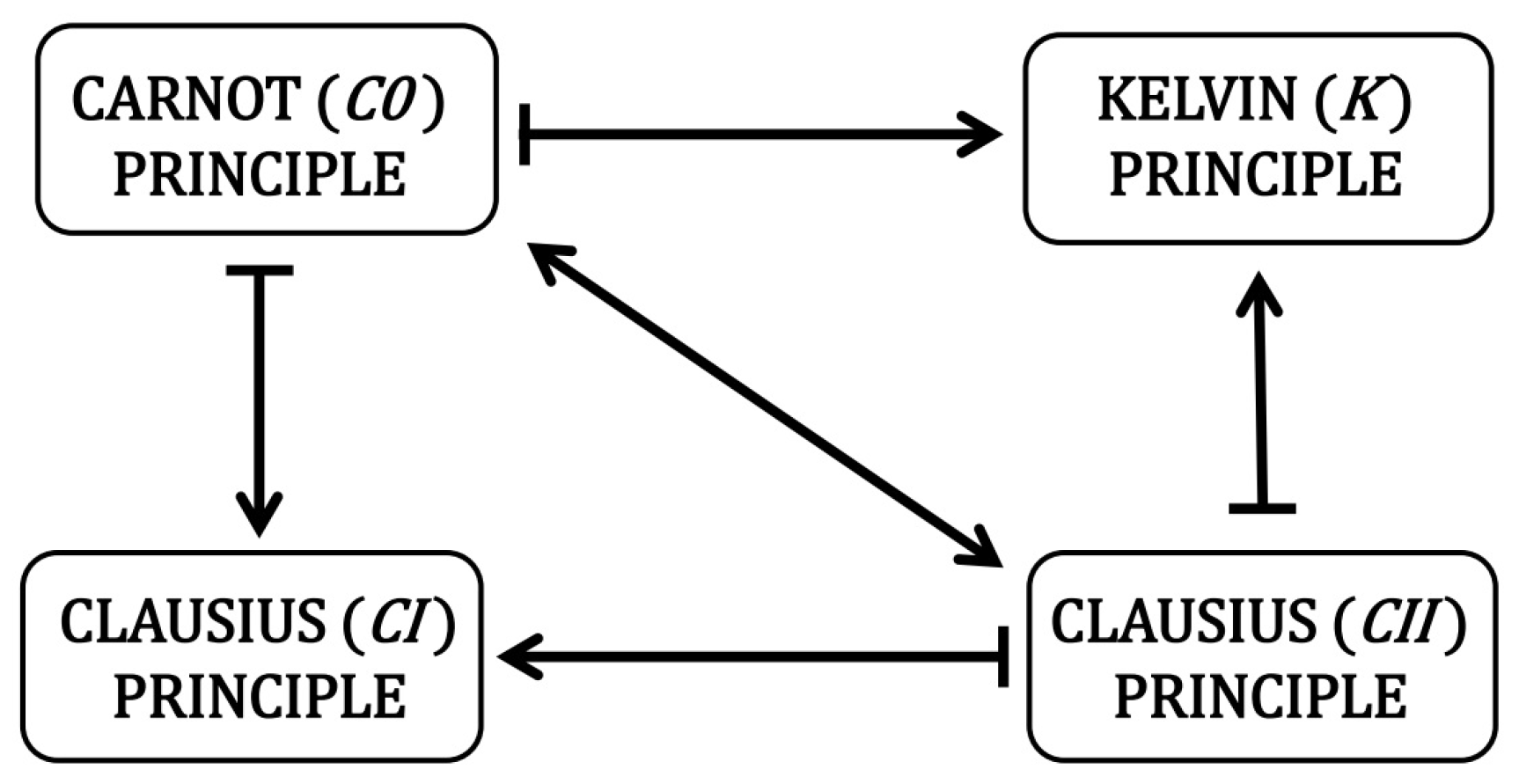
3.5. Theorem
3.6. Theorem
3.7. Theorem
3.8. Theorem
3.9. Theorem
3.10. Theorem )
3.11. Theorem
3.12. Theorem
3.13. Theorem
3.14. Theorem
3.15. Theorem K
3.16. Theorem
4. Results
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Carnot principle | |
| Clausius first principle | |
| K | Kelvin principle |
| Clausius second principle |
References
- Carnot, S. Réflexions sur la Puissance Motrice du Feu et sur les Machines Propres à DéVelopper Cette Puissance (Reflections on the Motive Power of Fire and on the Machines Suitable for Developing This Power), 1st ed.; Bachelier Libraire: Paris, France, 1824; pp. 1–58. [Google Scholar]
- Badur, J. Rozwój PojęCia Energii (The Development of the Concept of Energy), 1st ed.; Wydawnictwo Instytutu Maszyn Przepływowych PAN: Gdańsk, Poland, 2009; pp. 161–264, 726–742. [Google Scholar]
- Thomson, W. On an Absolute Thermometric Scale founded on Carnot’s Theory of the Motive Power of Heat, and calculated from Regnault’s observations. Philos. Mag. J. Sci. 1848, 33, 487–490. [Google Scholar]
- Dias, P.M.C.; Pinto, S.P.; Cassiano, D.H. The Conceptual Import of Carnot’s Theorem to the Discovery of the Entropy. Arch. Hist. Exact Sci. 1995, 49, 135–161. [Google Scholar] [CrossRef]
- Thomson, W. An Account of Carnot’s Theory of the Motive Power of Heat; with Numerical Results deduced from Regnault’s Experiments on Steam. Trans. R. Soc. Edinb. 1849, 16, 541–574. [Google Scholar] [CrossRef]
- Singh, N.; Sharma, U.C. Thermodynamics as Legacy of Sadi Carnot. National Conference on Futuristics in Mechanical Engineering; Excel India Publishers: New Delhi, India, 2015; pp. 36–42. [Google Scholar]
- Srinivasan, J. Sadi Carnot and the Second Law of Thermodynamics. Resonance 2001, 6, 42–48. [Google Scholar] [CrossRef]
- Barnett, M.K. Sadi Carnot and the Second Law of Thermodynamics. Osiris 1958, 13, 327–357. [Google Scholar] [CrossRef]
- Erlichson, H. Sadi Carnot, ‘Founder of the Second Law of Thermodynamics’. Eur. J. Phys. 1999, 20, 183–192. [Google Scholar] [CrossRef]
- Lemons, D.S.; Penner, M.K. Sadi Carnot’s contribution to the second law of thermodynamics. Am. J. Phys. 2008, 76, 21–25. [Google Scholar] [CrossRef]
- Feidt, M. The History and Perspectives of Efficiency at Maximum Power of the Carnot Engine. Entropy 2017, 19, 369. [Google Scholar] [CrossRef]
- Huang, K. Podstawy Fizyki Statystycznej (Inroduction to Statistical Physics), 1st ed.; Wydawnictwo Naukowe PWN: Warsaw, Poland, 2006; pp. 16–20. [Google Scholar]
- Jakubczyk, P. Toporna logika brudnych maszyn (The primitive logic of dirty machines). Delta 2020, 3, 1–3. [Google Scholar]
- Resnick, R.; Halliday, D. Fizyka dla StudentóW nauk Przyrodniczych i Technicznych Tom I (Physics for Students of Science and Engineering), 2nd ed.; Wydawnictwo Naukowe PWN: Warsaw, Poland, 1966; pp. 697–728. [Google Scholar]
- Sawieliew, I.W. Wykłady z Fizyki, tom 1. Mechanika. Fizyka CząSteczkowa (Lectures on Physics, Volume 1. Mechanics. Molecular Physics), 2nd ed.; Wydawnictwo Naukowe PWN: Warsaw, Poland, 1994; pp. 382–394. [Google Scholar]
- Bhattacharyya, K. Critique of some thermodynamic proofs based on the pump-engine couple. arXiv 2008, arXiv:0803.3494. [Google Scholar]
- Clausius, R. Ueber die bewegende Kraft der Wärme und die Gesetze, welche sich daraus für die Wärmelehre selbst ableiten lassen (On the Moving Force of Heat, and the Laws regarding the Nature of Heat itself which are deducible therefrom). Ann. Phys. 1850, 79, 368–397, 500–524. [Google Scholar] [CrossRef]
- Clausius, R. On the Moving Force of Heat, and the Laws regarding the Nature of Heat itself which are deducible therefrom. Philos. Mag. 1851, 2, 1–21, 102–119. [Google Scholar] [CrossRef]
- Clausius, R. Ueber eine veränderte Form des zweiten Hauptsatzes der mechanischen Wärmetheorie (On a Modified Form of the Second Fundamental Theorem in the Mechanical Theory of Heat). Ann. Phys. 1854, 93, 481–506. [Google Scholar] [CrossRef]
- Clausius, R. On a Modified Form of the Second Fundamental Theorem in the Mechanical Theory of Heat. Philos. Mag. 1856, 12, 81–98. [Google Scholar] [CrossRef]
- Xue, T.-W.; Guo, Z.-Y. What Is the Real Clausius Statement of the Second Law of Thermodynamics? Entropy 2019, 21, 926. [Google Scholar] [CrossRef]
- Clausius, R. The Mechanical Theory of Heat, with its Applications to the Steam-Engine and to the Physical Properties of Bodies, 1st ed.; Hirst, T.A., Ed.; John Van Voorst: London, UK, 1867; pp. 1–374. [Google Scholar]
- Clausius, R. The Mechanical Theory of Heat, 1st ed.; Walter, W.R., Translator; Macmillan & Co.: London, UK, 1879; pp. 1–376. [Google Scholar]
- Thomson, W. On the Dynamical Theory of Heat, with numerical results deduced from Mr Joule’s Equivalent of a Thermal Unit, and M. Regnault’s Observations on Steam (Part I–V). Trans. R. Soc. Edinb. 1851, 20, 261–298, 475–482. [Google Scholar] [CrossRef]
- Thomson, W. On the Dynamical Theory of Heat, with numerical results deduced from Mr Joule’s equivalent of a Thermal Unit, and M. Regnault’s Observations on Steam (Part I–III). Philos. Mag. J. Sci. 1852, 4, 8–21, 105–117, 168–256. [Google Scholar] [CrossRef]
- Szargut, J. Termodynamika (Thermodynamics), 5th ed.; Wydawnictwo Naukowe PWN: Warsaw, Poland, 1985; pp. 120–122. [Google Scholar]
- Pudlik, W. Termodynamika (Thermodynamics), 3rd ed.; Wydawnictwo Politechniki Gdańskiej: Gdańsk, Poland, 2020; pp. 130–187. [Google Scholar]
- Kaleta, A.; Górnicki, K. Podstawy Techniki Cieplnej w InżYnierii Rolniczej (Basics of Thermal Technology in Agricultural Engineering), 1st ed.; Wydawnictwo SGGW: Warsaw, Poland, 2009; pp. 105–106. [Google Scholar]
- Pippard, A.B. Elements of Classical Thermodynamics for Advanced Students of Physics, 3nd ed.; Cambridge University Press: Cambridge, UK, 1966; pp. 29–42. [Google Scholar]
- Recknagel, H.; Sprenger, E.; Schramek, E.-R. Kompendium Ogrzewnictwa i Klimatyzacji (Compendium of Heating and Air Conditioning), 1st ed.; OMNI SCALA: Wrocław, Poland, 2008; pp. 103–113. [Google Scholar]
- Wiśniewski, S. Termodynamika techniczna (Technical thermodynamics), 5th ed.; Wydawnictwa Naukowo-Techniczne WNT: Warsaw, Poland, 2009; pp. 81–111. [Google Scholar]
- Thomson, W. On a Universal Tendency in Nature to the Dissipation of Mechanical Energy. Philos. Mag. J. Sci. 1852, 4, 304–306. [Google Scholar] [CrossRef]
- Radhakrishnamurty, P. Are the second law principles of Caratheodory and Kelvin equivalent? arXiv 2011, arXiv:1102.4235. [Google Scholar]
- Hołyst, R.; Poniewierski, A.; Ciach, A. Termodynamika dla ChemikóW, FizykóW i InżYnieróW (Thermodynamics for Chemists, Physicists and Engineers), 1st ed.; Wydawnictwo UKSW: Warsaw, Poland, 2005; pp. 52–62. [Google Scholar]
- Clausius, R. Ueber verschiedene für die Anwendung bequeme Formen der Hauptgleichungen der mechanischen Wärmetheorie (About various convenient Forms of the main Equations of Mechanical Heat Theory). Ann. Phys. 1865, 125, 353–400. [Google Scholar] [CrossRef]
- Weber, P.; Bełdowski, P.; Bier, M.; Gadomski, A. Entropy Production Associated with Aggregation into Granules in a Subdiffusive Environment. Entropy 2018, 20, 651. [Google Scholar] [CrossRef] [PubMed]
- Bier, M.; Lisowski, B.; Gudowska-Nowak, E. Phase transitions and entropies for synchronizing oscillators. Phys. Rev. E 2016, 93, 12143. [Google Scholar] [CrossRef] [PubMed]
- Radhakrishnamurty, P. A Critique on Caratheodory Principle of the Second Law of Thermodynamics. arXiv 2011, arXiv:1103.4359. [Google Scholar]
- Newelski, L. More on locally atomic models. Fundam. Math. 1990, 136, 21–26. [Google Scholar] [CrossRef][Green Version]
- Chang, C.C.; Keisler, J. Model Theory, 3nd ed.; Dover Publications: New York, NY, USA, 2012; pp. 7–60. [Google Scholar]
- Smoluchowski, M. Gültigkeitsgrenzen des zweiten Hauptsatzes des Wärmetheorie (Limits of validity of the second law of thermodynamics). Vorträge über die kinetische Theorie der Materie und der Elektrizität (Lectures on the kinetic theory of matter and electricity). In Mathematische Vorlesungen an der Universität Göttingen; B.G. Teubner: Leipzig, Germany, 1914; pp. 87–121. [Google Scholar]
- Nikulov, A. The Law of Entropy Increase and the Meissner Effect. Entropy 2022, 24, 83. [Google Scholar] [CrossRef]
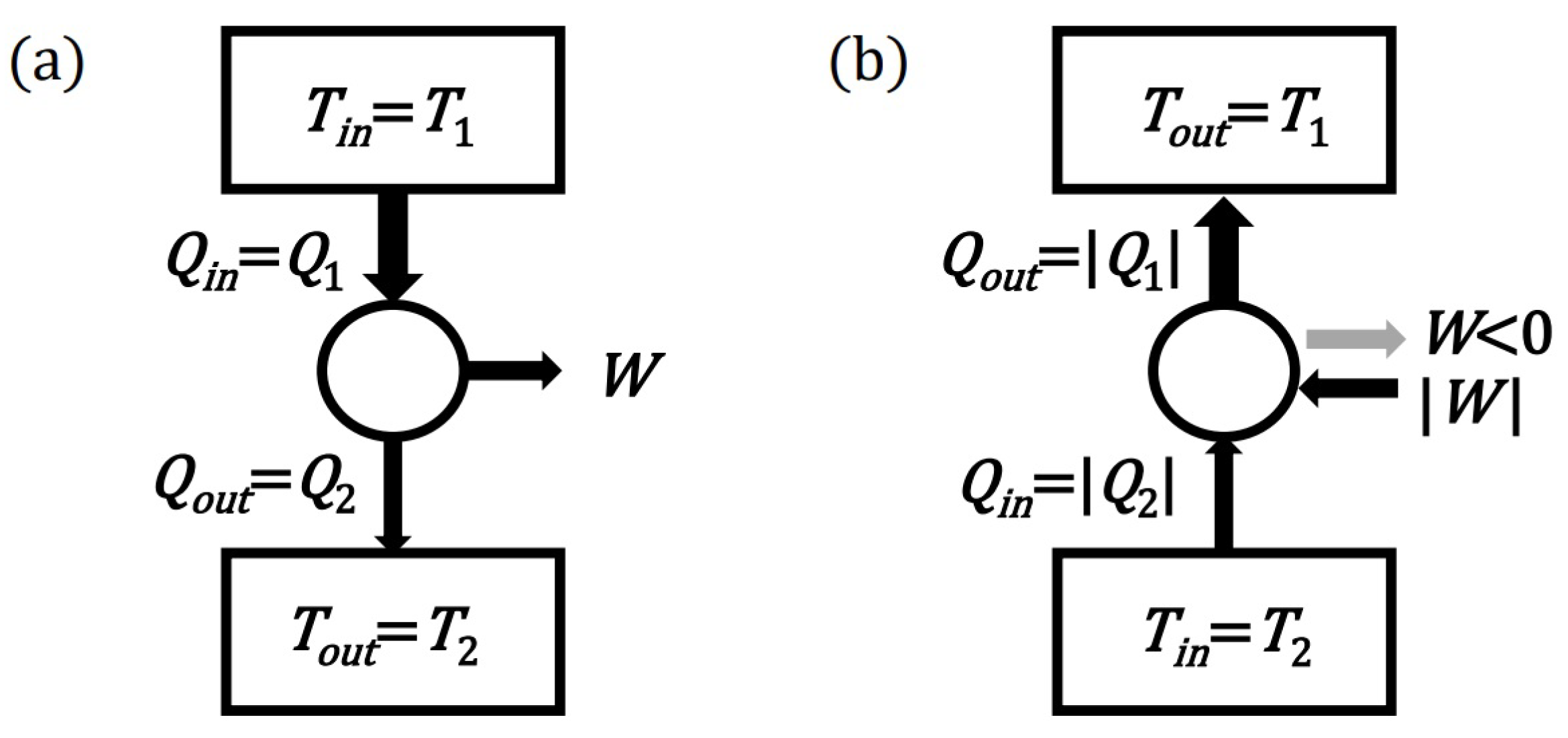
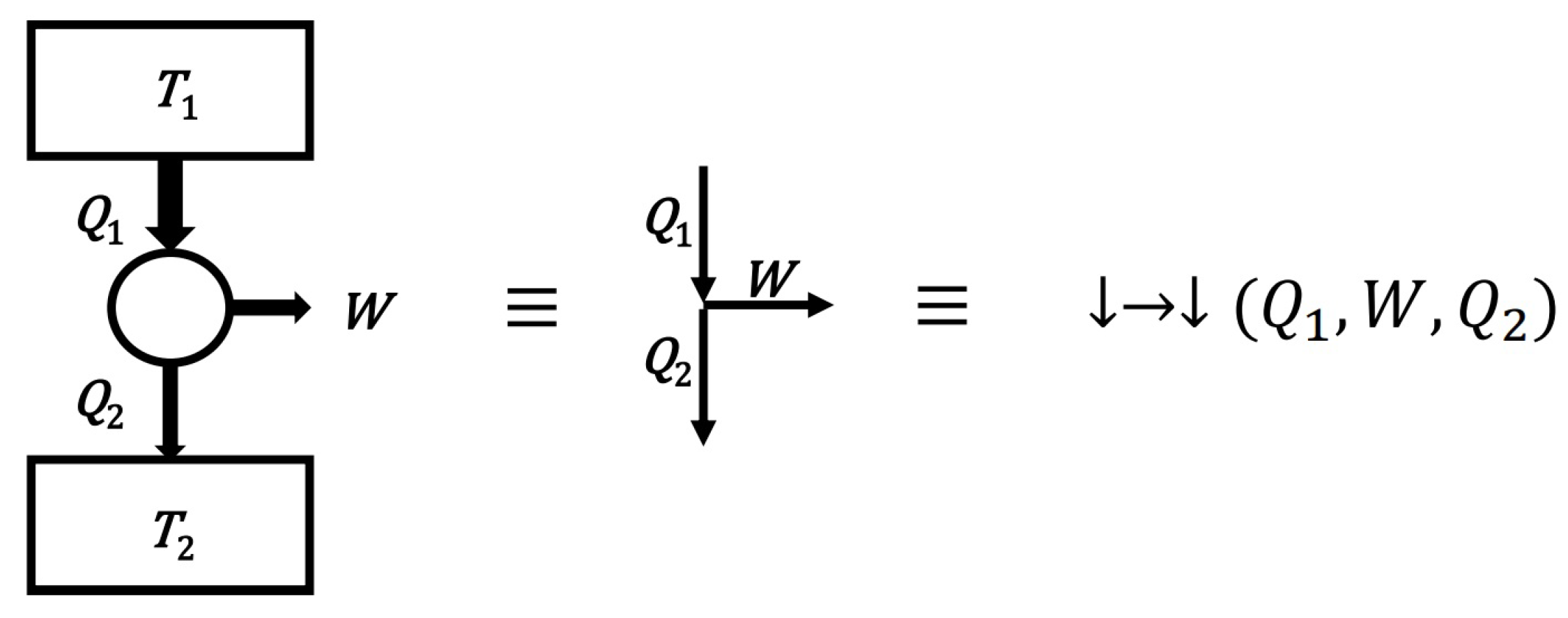
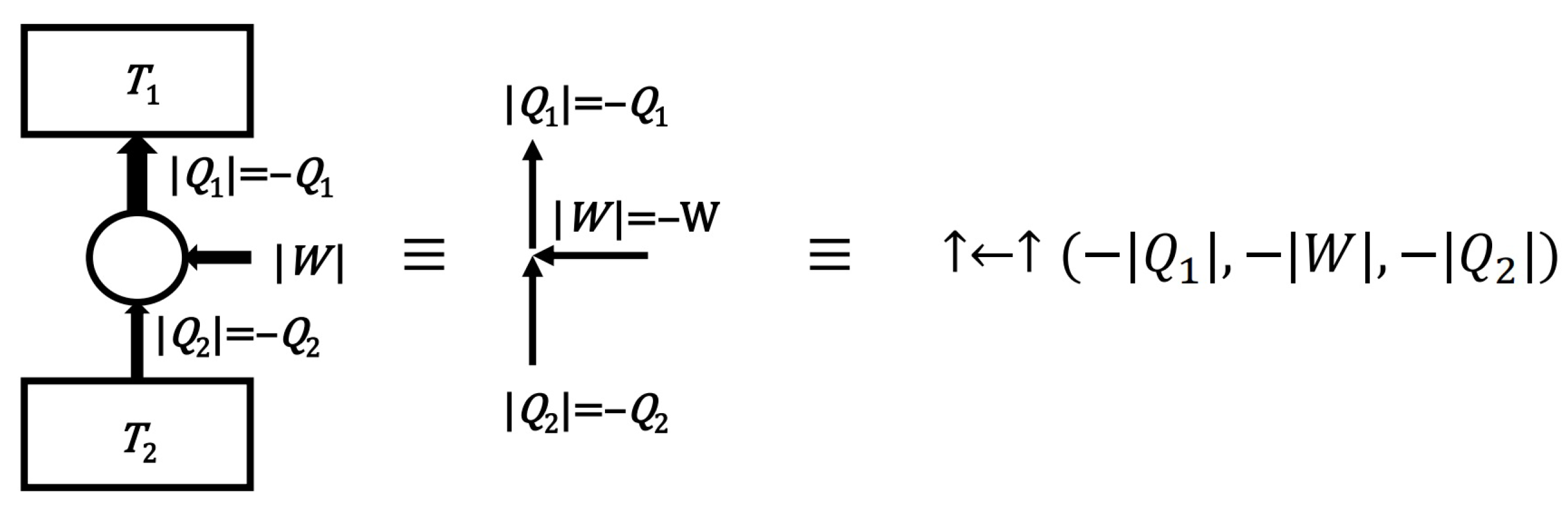
| p | q | ||
|---|---|---|---|
| 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| Principle | Carnot | Clausius I | Kelvin | Clausius II |
|---|---|---|---|---|
| Carnot | ≡ | ? | ? | ? |
| Clausius I | (?) | ≡ | (?) | (?) |
| Kelvin | (?) | (?) | ≡ | (?) |
| Clausius II | ≡ |
| Principle | Carnot | Clausius I | Kelvin | Clausius II |
|---|---|---|---|---|
| Carnot | ≡ | |||
| Clausius I | ≡ | |||
| Kelvin | ≡ | |||
| Clausius II | ≡ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koczan, G.M. Proof of Equivalence of Carnot Principle to II Law of Thermodynamics and Non-Equivalence to Clausius I and Kelvin Principles. Entropy 2022, 24, 392. https://doi.org/10.3390/e24030392
Koczan GM. Proof of Equivalence of Carnot Principle to II Law of Thermodynamics and Non-Equivalence to Clausius I and Kelvin Principles. Entropy. 2022; 24(3):392. https://doi.org/10.3390/e24030392
Chicago/Turabian StyleKoczan, Grzegorz Marcin. 2022. "Proof of Equivalence of Carnot Principle to II Law of Thermodynamics and Non-Equivalence to Clausius I and Kelvin Principles" Entropy 24, no. 3: 392. https://doi.org/10.3390/e24030392
APA StyleKoczan, G. M. (2022). Proof of Equivalence of Carnot Principle to II Law of Thermodynamics and Non-Equivalence to Clausius I and Kelvin Principles. Entropy, 24(3), 392. https://doi.org/10.3390/e24030392






