Generalizations of Talagrand Inequality for Sinkhorn Distance Using Entropy Power Inequality †
Abstract
1. Introduction
1.1. Literature Review
1.2. Contributions
- (1)
- We derive an HWI-type inequality for Sinkhorn distance using a modification of Bolley’s proof in [4] (see Theorem 2).
- (2)
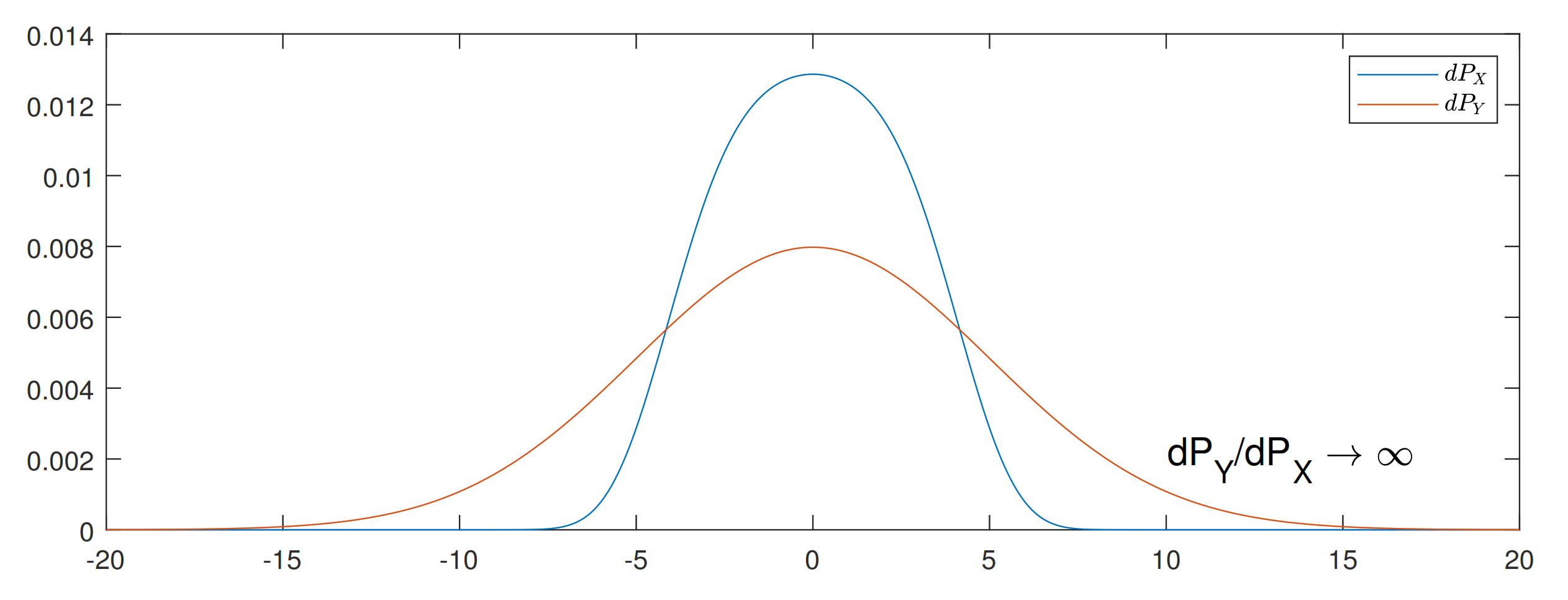
- We prove two new Talagrand-type inequalities (see Theorems 3 and 4). These inequalities are obtained via a numerical term C related to the saturation, or the tightness, of EPI. We claim that this term can be computed with arbitrary deconvolution of one side marginal, while the optimal deconvolution is shown to be unknown beyond the Gaussian case. Nevertheless, we simulate suboptimally this term for a variety of distributions in Figure 1.
- (3)
- We show that the geometry observed by Sinkhorn distance is smoothed in the sense of measure concentration. In other words, Sinkhorn distance implies a dimensional measure concentration inequality following Marton’s method (see Corollary 2). This inequality has a simple form of normal concentration that is related to the term C and is weaker than the one implied by Wasserstein distance.
- (4)
- Our theoretical results are validated via numerical simulations (see Section 4). These simulations reveal several reasons for which our bounds can be either tight or loose.
Connections to Prior Art
1.3. Notation
1.4. Organization of the Paper
2. Preliminaries
2.1. Synopsis of Optimal Transport
2.2. Measure Concentration
- μ satisfies .
- μ has a dimension-free normal concentration with .
2.3. Entropy Power Inequality and Deconvolution
3. Main Theoretical Results

4. Numerical Simulations
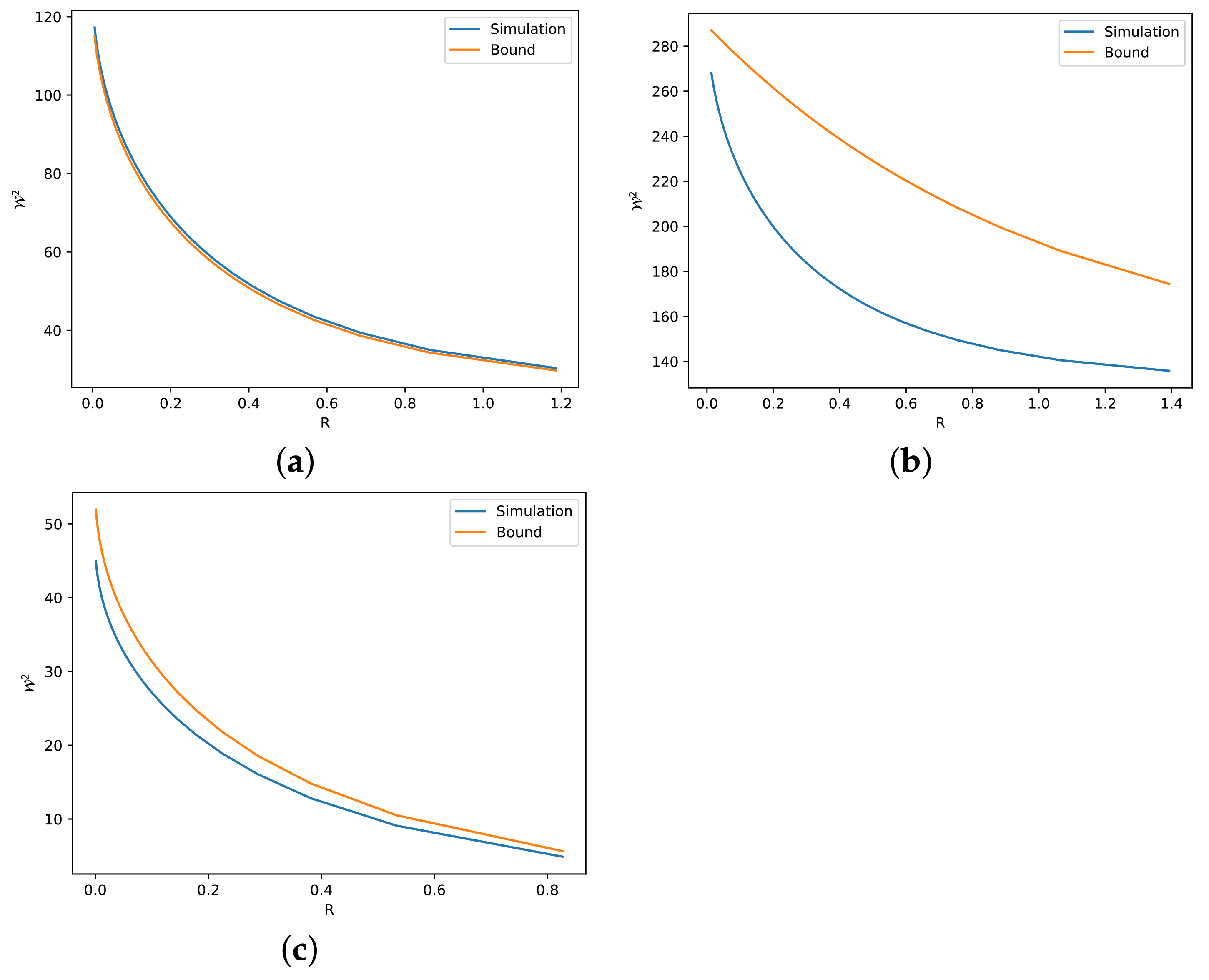
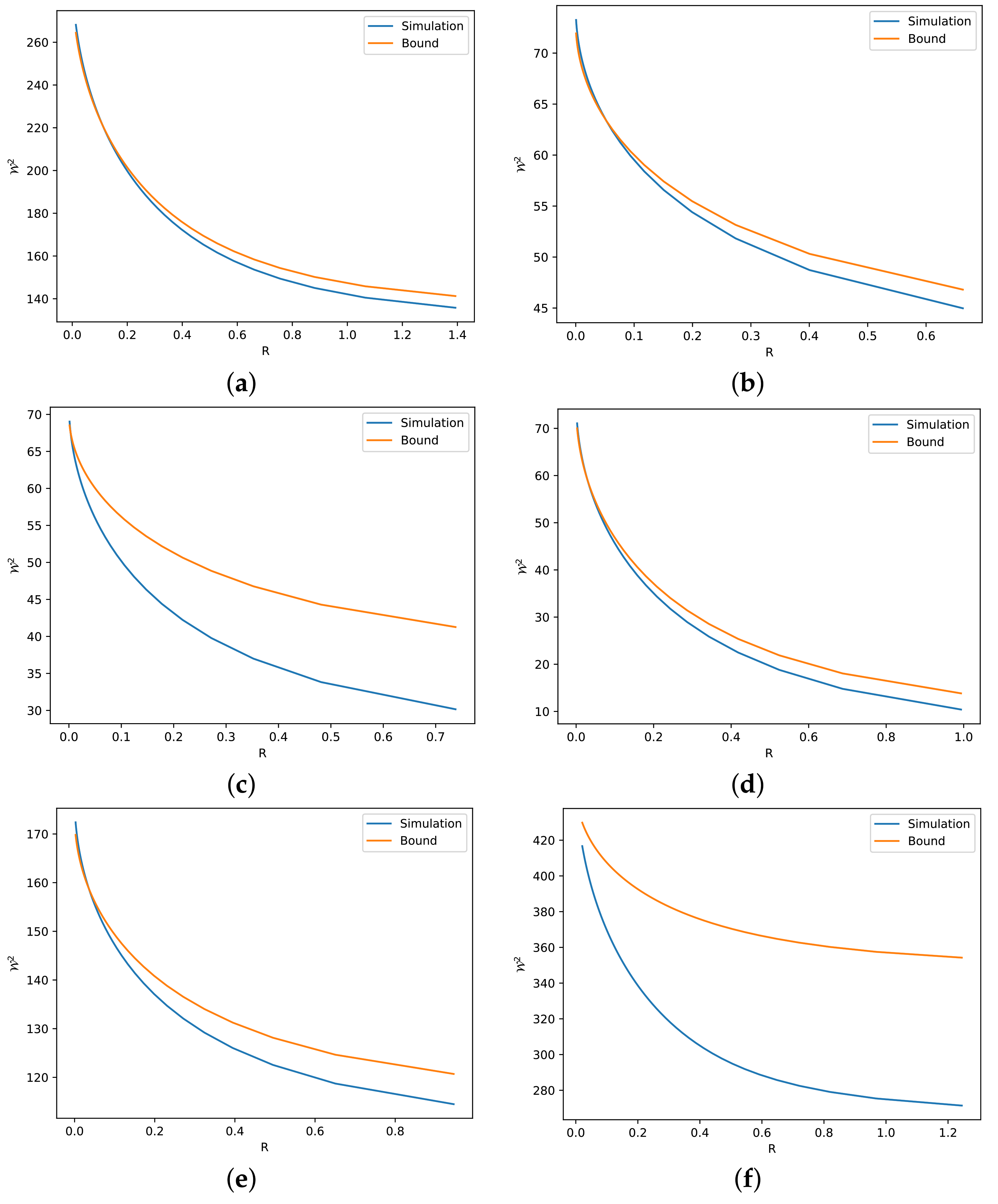
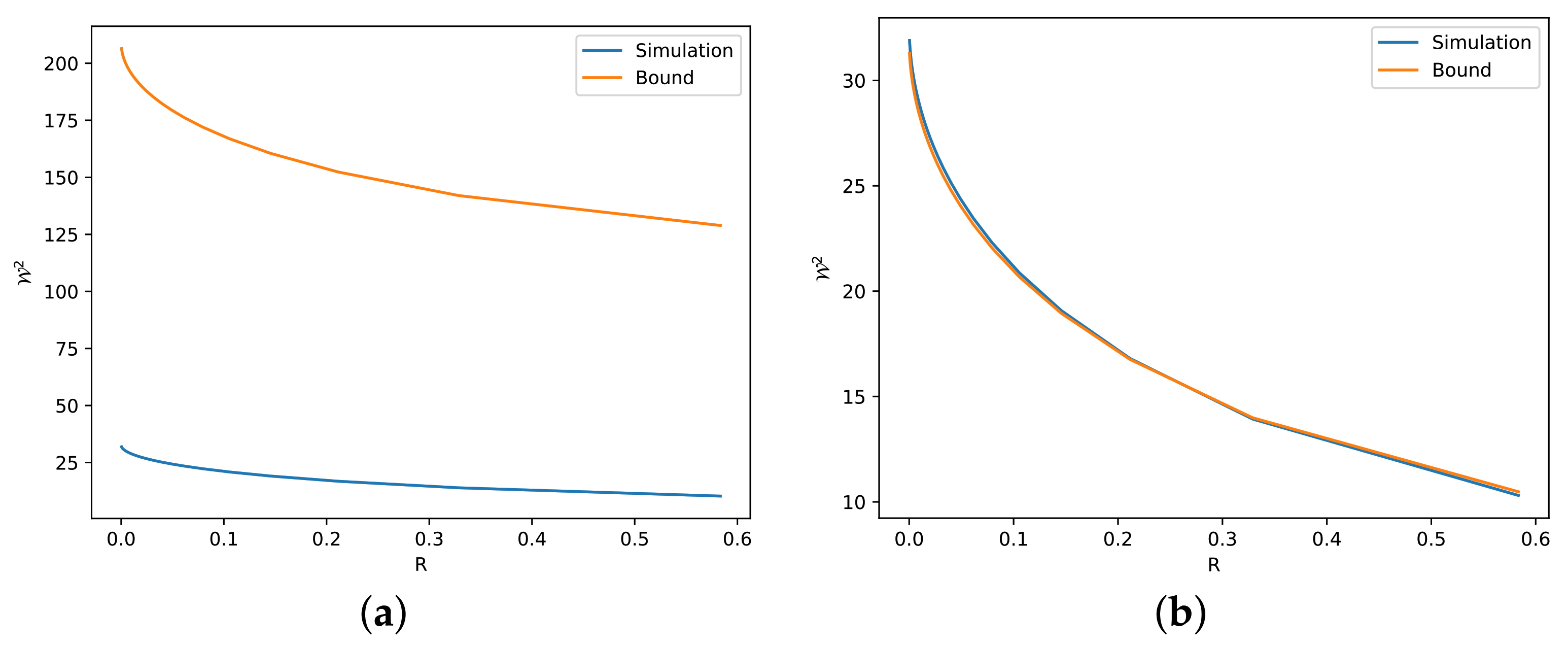
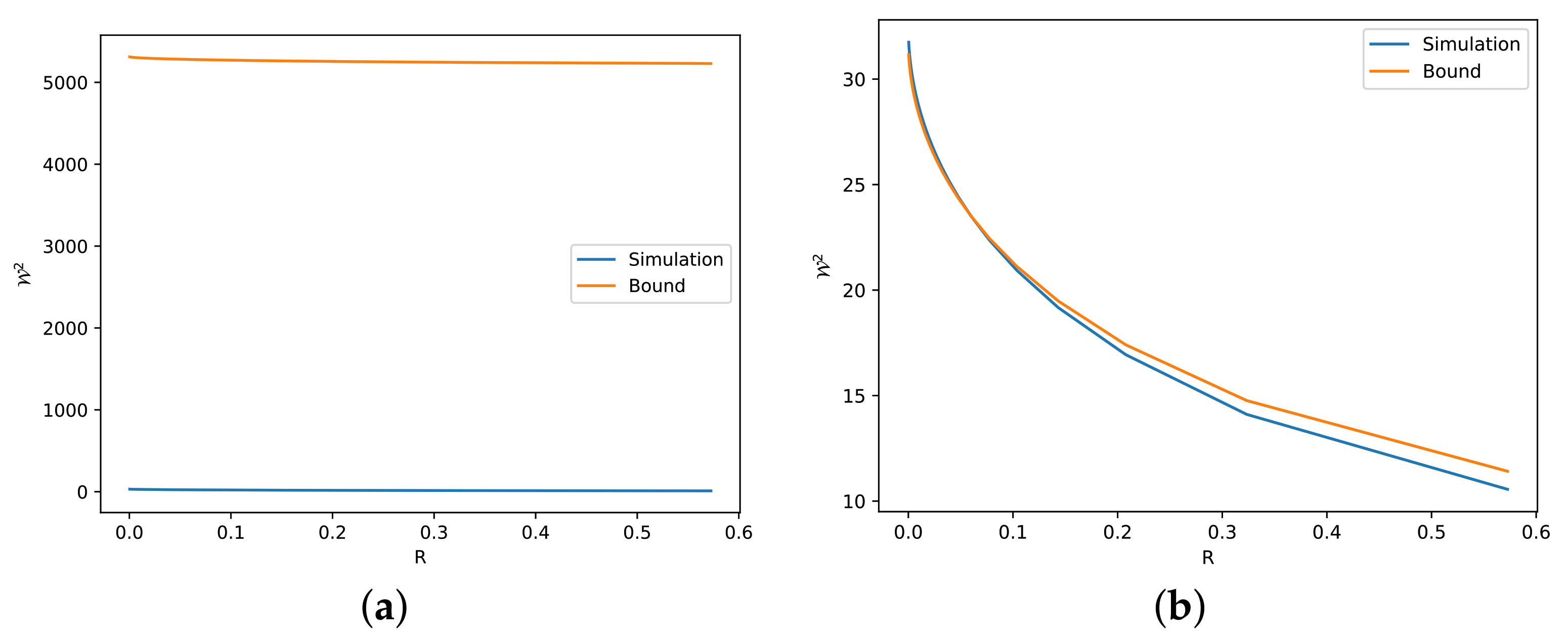
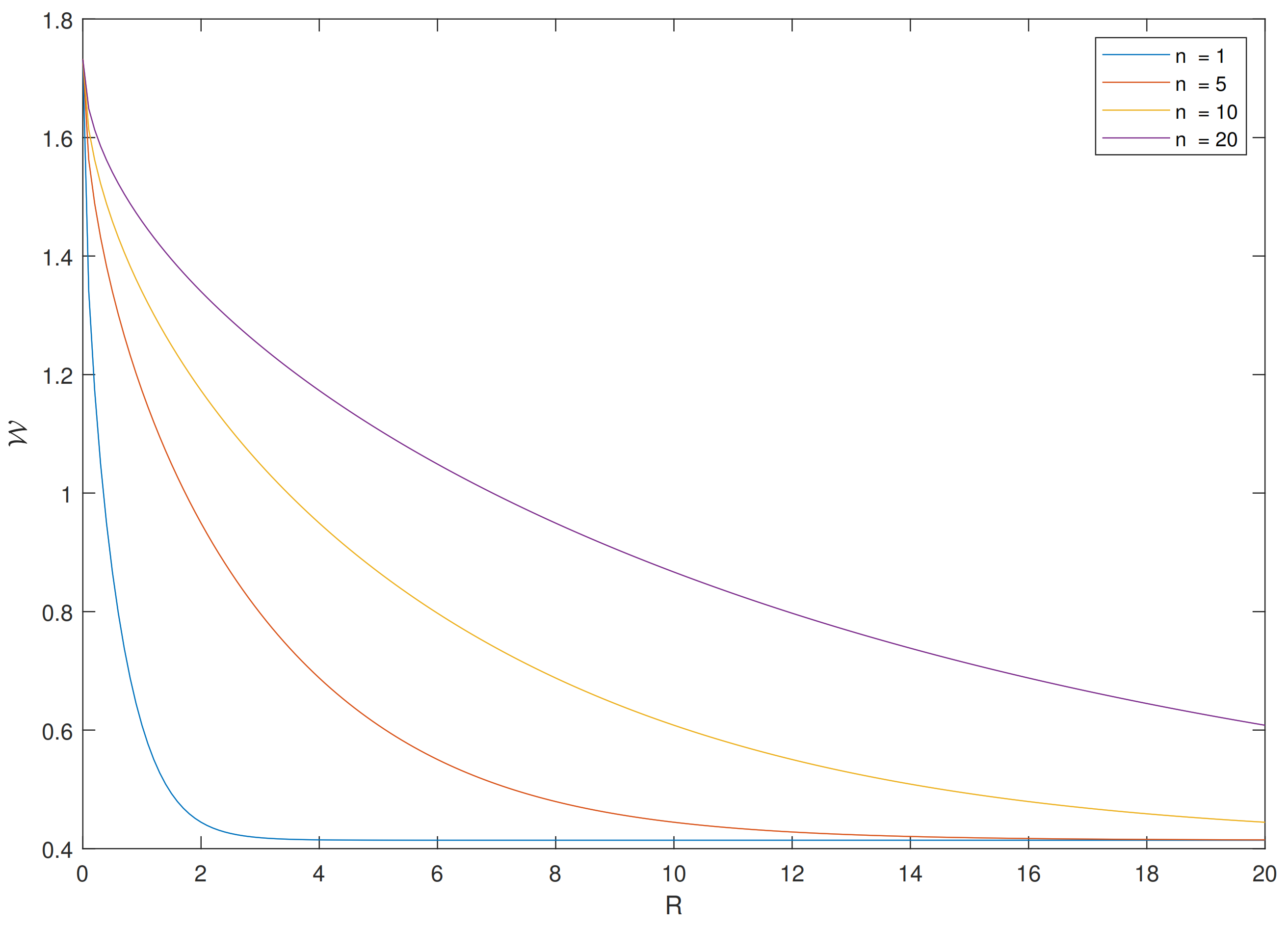
5. Conclusions and Future Directions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| OT | optimal transport |
| EPI | entropy power inequality |
| SP | Schrödinger problem |
| GAN | generative adversarial network |
| RHS | right-hand side |
| a.e. | almost everywhere |
| POT | Python Optimal Transport |
Appendix A. Proof of Theorem 2
Appendix B. Proof of Corollary 2
Appendix C. Proof of the Dimensionality of (20)
Appendix D. Proof of Theorem 4
Appendix E. Proof of Theorem 5
Appendix F. Background Material
References
- Talagrand, M. Transportation cost for Gaussian and other product measures. Geom. Funct. Anal. 1996, 6, 587–600. [Google Scholar] [CrossRef]
- Bakry, D.; Bolley, F.; Gentil, I. Dimension dependent hypercontractivity for Gaussian kernels. Probab. Theory Relat. Fields 2012, 154, 845–874. [Google Scholar] [CrossRef]
- Cordero-Erausquin, D. Transport inequalities for log-concave measures, quantitative forms, and applications. Can. J. Math. 2017, 69, 481–501. [Google Scholar] [CrossRef]
- Bolley, F.; Gentil, I.; Guillin, A. Dimensional improvements of the logarithmic Sobolev, Talagrand and Brascamp–Lieb inequalities. Ann. Probab. 2018, 46, 261–301. [Google Scholar] [CrossRef]
- Raginsky, M.; Sason, I. Concentration of Measure Inequalities in Information Theory, Communications and Coding. In Foundations and Trends in Communications and Information Theory; NOW Publishers: Boston, MA, USA, 2018. [Google Scholar]
- Zhang, R.; Chen, C.; Li, C.; Carin, L. Policy Optimization as Wasserstein Gradient Flows. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 5737–5746. [Google Scholar]
- Montavon, G.; Müller, K.R.; Cuturi, M. Wasserstein Training of Restricted Boltzmann Machines. In Proceedings of the 30th International Conference on Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 3718–3726. [Google Scholar]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein Generative Adversarial Networks. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 214–223. [Google Scholar]
- Rigollet, P.; Weed, J. Uncoupled isotonic regression via minimum Wasserstein deconvolution. Inf. Inference 2019, 8, 691–717. [Google Scholar] [CrossRef]
- Cuturi, M. Sinkhorn Distances: Lightspeed Computation of Optimal Transportation Distances. Adv. Neural Inf. Process. Syst. 2013, 26, 2292–2300. [Google Scholar]
- Wang, S.; Stavrou, P.A.; Skoglund, M. Generalized Talagrand Inequality for Sinkhorn Distance using Entropy Power Inequality. In Proceedings of the 2021 IEEE Information Theory Workshop (ITW), Kanazawa, Japan, 17–21 October 2021; pp. 1–6. [Google Scholar]
- Benamou, J.D.; Brenier, Y. A computational fluid mechanics solution to the Monge-Kantorovich mass transfer problem. Numer. Math. 2000, 84, 375–393. [Google Scholar] [CrossRef]
- Villani, C. Optimal Transport: Old and New; Springer: Norwell, MA, USA, 2008; Volume 338. [Google Scholar]
- Schrödinger, E. Über die Umkehrung der Naturgesetze; Verlag der Akademie der Wissenschaften in Kommission bei Walter De Gruyter: Berlin, Germany, 1931. [Google Scholar]
- Léonard, C. A survey of the Schrödinger problem and some of its connections with optimal transport. Discret. Contin. Dyn. Syst. 2014, 34, 1533–1574. [Google Scholar] [CrossRef]
- Chen, Y.; Georgiou, T.T.; Pavon, M. On the relation between optimal transport and Schrödinger bridges: A stochastic control viewpoint. J. Optim.Theory Appl. 2016, 169, 671–691. [Google Scholar] [CrossRef]
- Chen, Y.; Georgiou, T.T.; Pavon, M. Optimal transport over a linear dynamical system. IEEE Trans. Autom. Control 2016, 62, 2137–2152. [Google Scholar] [CrossRef]
- Conforti, G. A second order equation for Schrödinger bridges with applications to the hot gas experiment and entropic transportation cost. Probab. Theory Relat. Fields 2019, 174, 1–47. [Google Scholar] [CrossRef]
- Conforti, G.; Ripani, L. Around the entropic Talagrand inequality. Bernoulli 2020, 26, 1431–1452. [Google Scholar] [CrossRef]
- Bai, Y.; Wu, X.; Özgür, A. Information Constrained Optimal Transport: From Talagrand, to Marton, to Cover. In Proceedings of the IEEE International Symposium on Information Theory (ISIT), Los Angeles, CA, USA, 21–26 June 2020; pp. 2210–2215. [Google Scholar]
- Rigollet, P.; Weed, J. Entropic optimal transport is maximum-likelihood deconvolution. C. R. Mathem. 2018, 356, 1228–1235. [Google Scholar] [CrossRef]
- Mena, G.; Niles-Weed, J. Statistical bounds for entropic optimal transport: Sample complexity and the central limit theorem. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: New York, NY, USA, 2019; Volume 32. [Google Scholar]
- Genevay, A.; Chizat, L.; Bach, F.; Cuturi, M.; Peyré, G. Sample Complexity of Sinkhorn Divergences. In Proceedings of the Twenty-Second International Conference on Artificial Intelligence and Statistics, Naha, Japan, 16–18 April 2019; pp. 1574–1583. [Google Scholar]
- Reshetova, D.; Bai, Y.; Wu, X.; Özgür, A. Understanding Entropic Regularization in GANs. In Proceedings of the IEEE International Symposium on Information Theory (ISIT), Victoria, Australia, 11–16 July 2021; pp. 825–830. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Stam, A.J. Some inequalities satisfied by the quantities of information of Fisher and Shannon. Inf. Control 1959, 2, 101–112. [Google Scholar] [CrossRef]
- Rioul, O. Information theoretic proofs of entropy power inequalities. IEEE Trans. Inf. Theory 2010, 57, 33–55. [Google Scholar] [CrossRef]
- Courtade, T.A.; Fathi, M.; Pananjady, A. Quantitative stability of the entropy power inequality. IEEE Trans. Inf. Theory 2018, 64, 5691–5703. [Google Scholar] [CrossRef]
- Bobkov, S.; Madiman, M. Reverse Brunn—Minkowski and reverse entropy power inequalities for convex measures. J. Funct. Anal. 2012, 262, 3309–3339. [Google Scholar] [CrossRef][Green Version]
- Bobkov, S.G.; Madiman, M.M. On the problem of reversibility of the entropy power inequality. In Limit Theorems in Probability, Statistics and Number Theory; Springer: Norwell, MA, USA, 2013; pp. 61–74. [Google Scholar]
- Courtade, T.A. A strong entropy power inequality. IEEE Trans. Inf. Theory 2017, 64, 2173–2192. [Google Scholar] [CrossRef]
- Cover, T.M. Elements of Information Theory; John Wiley & Sons: New York, NY, USA, 1999. [Google Scholar]
- Tamanini, L. A generalization of Costa’s Entropy Power Inequality. arXiv 2020, arXiv:2012.12230. [Google Scholar]
- Monge, G. Mémoire sur la théorie des déblais et des remblais. In Histoire de l’Académie Royale des Sciences de Paris; De l’Imprimerie Royale: Paris, France, 1781. [Google Scholar]
- Kantorovich, L.V. On the translocation of masses. J. Math. Sci. 2006, 133, 1381–1382. [Google Scholar] [CrossRef]
- Kantorovich, L.V. On a Problem of Monge. J. Math. Sci. 2006, 133, 1383. [Google Scholar] [CrossRef]
- Dupuis, P.; Ellis, R.S. A Weak Convergence Approach to the Theory of Large Deviations; Wiley Series in Probability and Statistics; Wiley-Interscience: Hoboken, NJ, USA, 2011. [Google Scholar]
- Luenberger, D.G. Optimization by Vector Space Methods; John Wiley & Sons: New York, NY, USA, 1997. [Google Scholar]
- Blower, G. The Gaussian isoperimetric inequality and transportation. Positivity 2003, 7, 203–224. [Google Scholar] [CrossRef]
- Otto, F.; Villani, C. Generalization of an inequality by Talagrand and links with the logarithmic Sobolev inequality. J. Funct. Anal. 2000, 173, 361–400. [Google Scholar] [CrossRef]
- Bakry, D.; Ledoux, M. A logarithmic Sobolev form of the Li-Yau parabolic inequality. Rev. Matemática Iberoam. 2006, 22, 683–702. [Google Scholar] [CrossRef]
- Masry, E. Multivariate probability density deconvolution for stationary random processes. IEEE Trans. Inf. Theory 1991, 37, 1105–1115. [Google Scholar] [CrossRef]
- Stefanski, L.A.; Carroll, R.J. Deconvolving kernel density estimators. Statistics 1990, 21, 169–184. [Google Scholar] [CrossRef]
- Fan, J. On the optimal rates of convergence for nonparametric deconvolution problems. Ann. Stat. 1991, 19, 1257–1272. [Google Scholar] [CrossRef]
- Janati, H.; Muzellec, B.; Peyré, G.; Cuturi, M. Entropic optimal transport between unbalanced Gaussian measures has a closed form. Adv. Neural Inf. Process. Syst. 2020, 33, 10468–10479. [Google Scholar]
- Marton, K. A measure concentration inequality for contracting Markov chains. Geom. Funct. Anal. 1996, 6, 556–571. [Google Scholar] [CrossRef]
- Flamary, R.; Courty, N.; Gramfort, A.; Alaya, M.Z.; Boisbunon, A.; Chambon, S.; Chapel, L.; Corenflos, A.; Fatras, K.; Fournier, N.; et al. POT: Python Optimal Transport. J. Mach. Learn. Res. 2021, 22, 1–8. [Google Scholar]
- Villani, C. Topics in Optimal Transportation; Number 58; American Mathematical Society: Providence, RI, USA, 2003. [Google Scholar]
- Puterman, M.L. Markov Decision Processes: Discrete Stochastic Dynamic Programming; John Wiley & Sons: New York, NY, USA, 2014. [Google Scholar]
- Saumard, A.; Wellner, J.A. Log-concavity and strong log-concavity: A review. Stat. Surv. 2014, 8, 45–114. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Stavrou, P.A.; Skoglund, M. Generalizations of Talagrand Inequality for Sinkhorn Distance Using Entropy Power Inequality. Entropy 2022, 24, 306. https://doi.org/10.3390/e24020306
Wang S, Stavrou PA, Skoglund M. Generalizations of Talagrand Inequality for Sinkhorn Distance Using Entropy Power Inequality. Entropy. 2022; 24(2):306. https://doi.org/10.3390/e24020306
Chicago/Turabian StyleWang, Shuchan, Photios A. Stavrou, and Mikael Skoglund. 2022. "Generalizations of Talagrand Inequality for Sinkhorn Distance Using Entropy Power Inequality" Entropy 24, no. 2: 306. https://doi.org/10.3390/e24020306
APA StyleWang, S., Stavrou, P. A., & Skoglund, M. (2022). Generalizations of Talagrand Inequality for Sinkhorn Distance Using Entropy Power Inequality. Entropy, 24(2), 306. https://doi.org/10.3390/e24020306






