Correlations, Information Backflow, and Objectivity in a Class of Pure Dephasing Models
Abstract
:1. Introduction
2. Dephasing Models
3. Spreading of Correlations
3.1. Quantifiers of Correlations
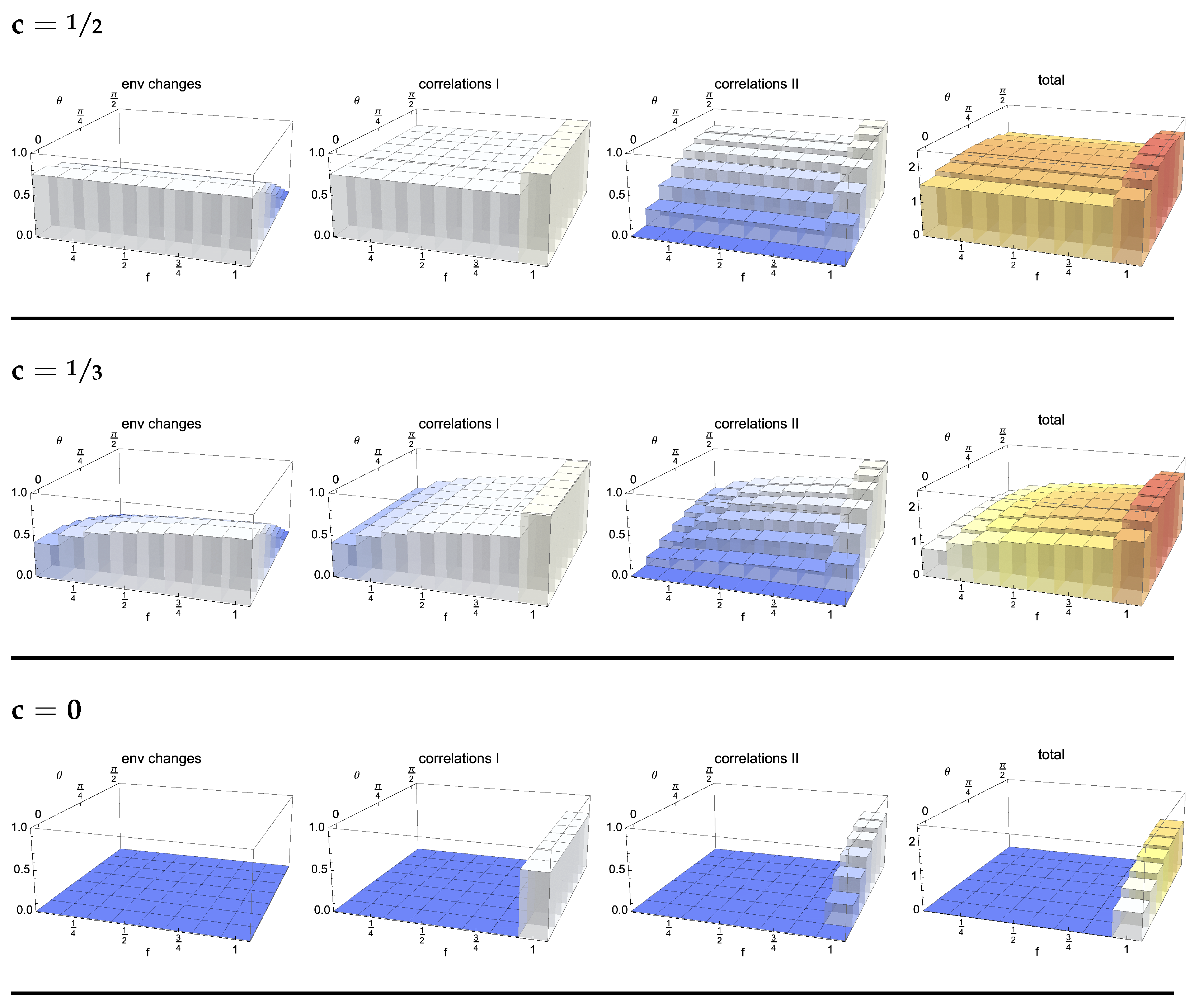
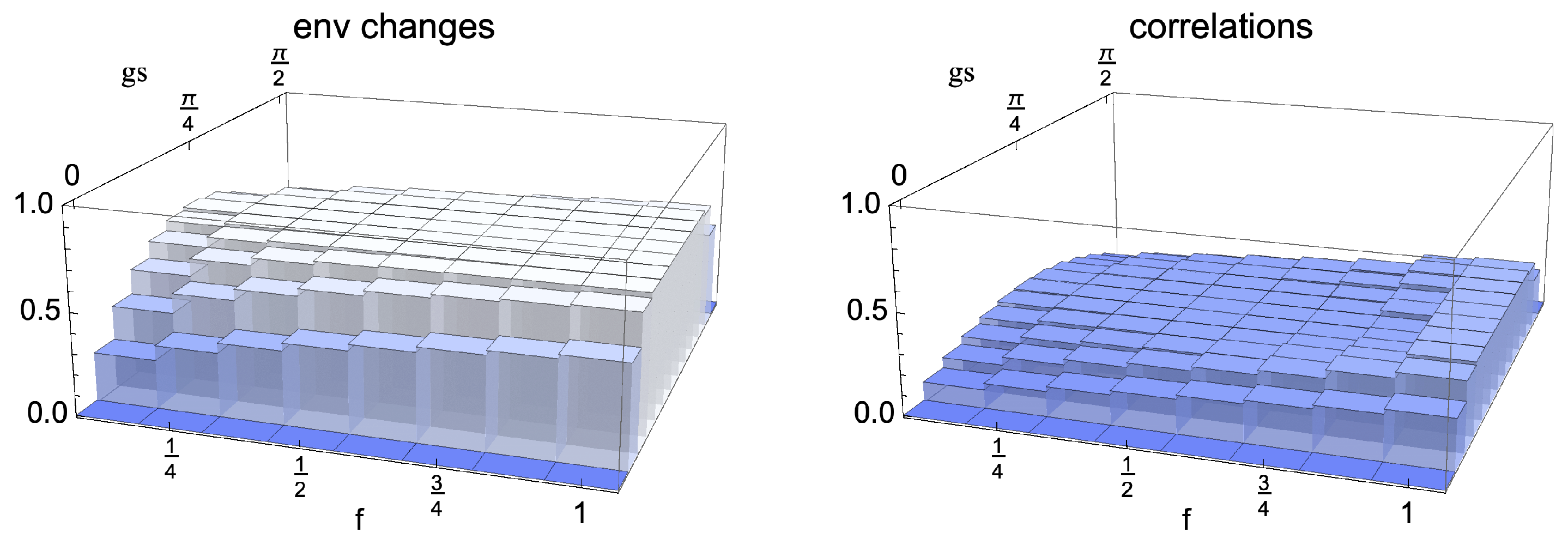
3.2. Model Dependence of Correlation Formation
4. Information Backflow
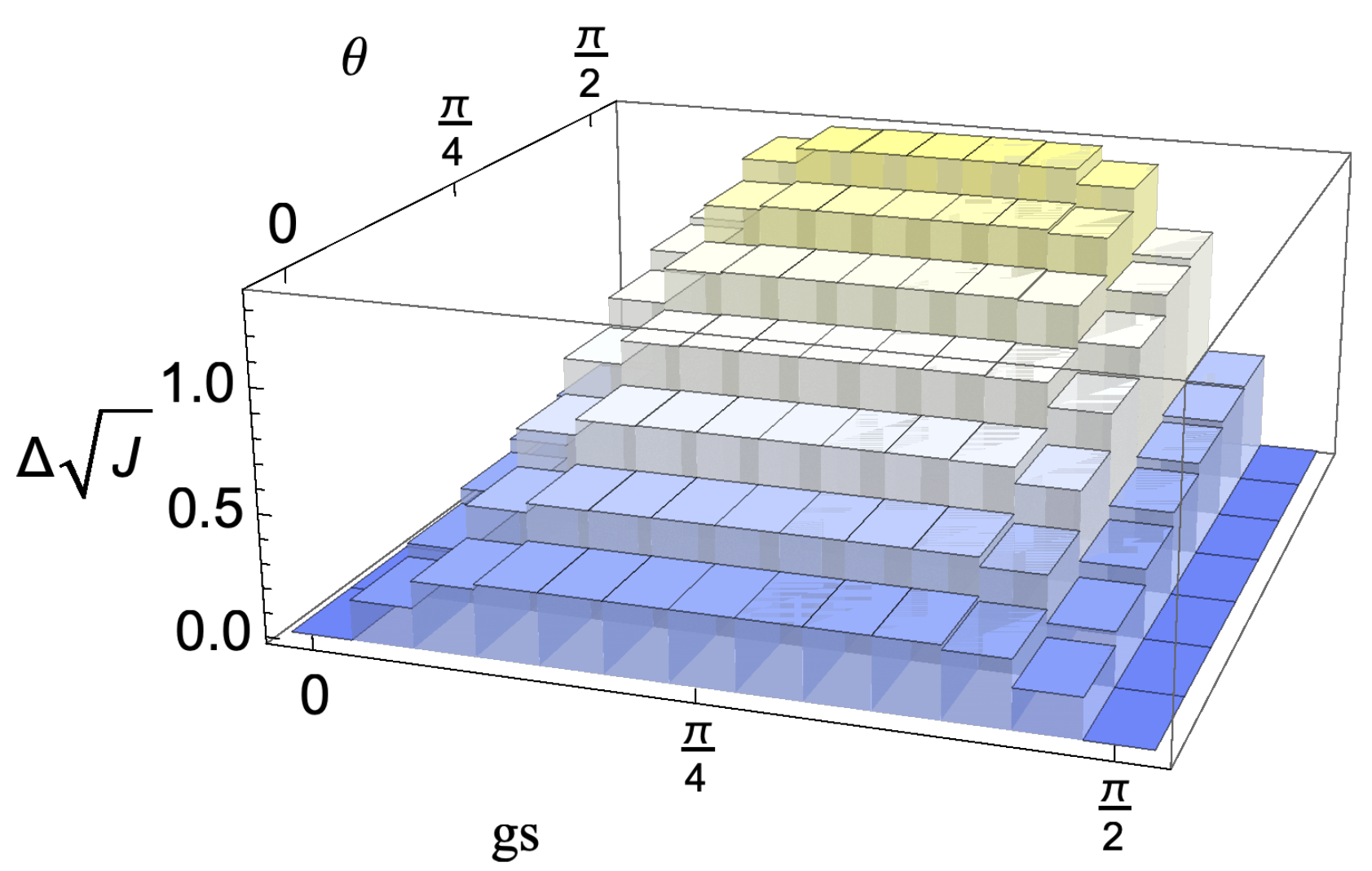
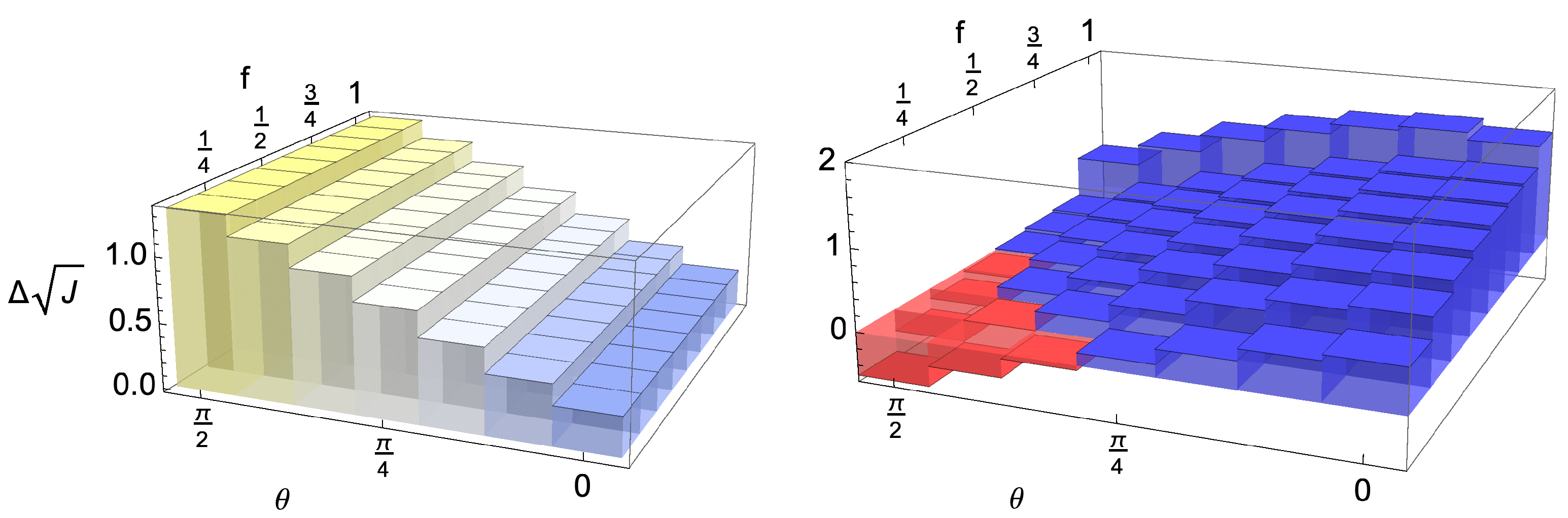
4.1. Model Dependence of Bounds on Distinguishability Revivals
4.2. Fraction Dependence of Bounds on Distinguishability Revivals
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Breuer, H.P.; Petruccione, F. The Theory of Open Quantum Systems; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Rivas, A.; Huelga, S.F. Open Quantum Systems: An Introduction; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Zurek, W.H. Quantum Darwinism. Nat. Phys. 2009, 5, 181–188. [Google Scholar] [CrossRef]
- Horodecki, R.; Korbicz, J.K.; Horodecki, P. Quantum origins of objectivity. Phys. Rev. A 2015, 91, 032122. [Google Scholar] [CrossRef] [Green Version]
- Le, T.P.; Olaya-Castro, A. Objectivity (or lack thereof): Comparison between predictions of quantum Darwinism and spectrum broadcast structure. Phys. Rev. A 2018, 98, 032103. [Google Scholar] [CrossRef] [Green Version]
- Le, T.P.; Olaya-Castro, A. Strong Quantum Darwinism and Strong Independence are Equivalent to Spectrum Broadcast Structure. Phys. Rev. Lett. 2019, 122, 010403. [Google Scholar] [CrossRef] [Green Version]
- Korbicz, J.K. Roads to objectivity: Quantum Darwinism, Spectrum Broadcast Structures, and Strong quantum Darwinism—A review. Quantum 2021, 5, 571. [Google Scholar] [CrossRef]
- Rivas, Á.; Huelga, S.F.; Plenio, M.B. Quantum non-Markovianity: Characterization, quantification and detection. Rep. Prog. Phys. 2014, 77, 094001. [Google Scholar] [CrossRef]
- Breuer, H.P.; Laine, E.M.; Piilo, J.; Vacchini, B. Colloquium: Non-Markovian dynamics in open quantum systems. Rev. Mod. Phys. 2016, 88, 021002. [Google Scholar] [CrossRef] [Green Version]
- Ciampini, M.A.; Pinna, G.; Mataloni, P.; Paternostro, M. Experimental signature of quantum Darwinism in photonic cluster states. Phys. Rev. A 2018, 98, 020101. [Google Scholar] [CrossRef] [Green Version]
- Unden, T.K.; Louzon, D.; Zwolak, M.; Zurek, W.H.; Jelezko, F. Revealing the Emergence of Classicality Using Nitrogen-Vacancy Centers. Phys. Rev. Lett. 2019, 123, 140402. [Google Scholar] [CrossRef]
- Chen, M.C.; Zhong, H.S.; Li, Y.; Wu, D.; Wang, X.L.; Li, L.; Liu, N.L.; Lu, C.Y.; Pan, J.W. Emergence of classical objectivity of quantum Darwinism in a photonic quantum simulator. Sci. Bull. 2019, 64, 580–585. [Google Scholar] [CrossRef] [Green Version]
- Chisholm, D.A.; García-Pérez, G.; Rossi, M.A.C.; Maniscalco, S.; Palma, G.M. Witnessing objectivity on a quantum computer. Quantum Sci. Technol. 2022, 7, 015022. [Google Scholar] [CrossRef]
- Liu, B.H.; Li, L.; Huang, Y.F.; Li, C.F.; Guo, G.C.; Laine, E.M.; Breuer, H.P.; Piilo, J. Experimental control of the transition from Markovian to non-Markovian dynamics of open quantum systems. Nat. Phys. 2011, 7, 931–934. [Google Scholar] [CrossRef]
- Rossi, M.A.C.; Benedetti, C.; Tamascelli, D.; Cialdi, S.; Olivares, S.; Vacchini, B.; Paris, M.G.A. Non-Markovianity by undersampling in quantum optical simulators. Int. J. Quantum Inf. 2017, 15, 1740009. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.D.; Lyyra, H.; Sun, Y.N.; Liu, B.; Li, C.F.; Guo, G.C.; Maniscalco, S.; Piilo, J. Experimental implementation of fully controlled dephasing dynamics and synthetic spectral densities. Nat. Commun. 2018, 9, 1–7. [Google Scholar] [CrossRef]
- Cialdi, S.; Benedetti, C.; Tamascelli, D.; Olivares, S.; Paris, M.G.A.; Vacchini, B. Experimental investigation of the effect of classical noise on quantum non-Markovian dynamics. Phys. Rev. A 2019, 100, 052104. [Google Scholar] [CrossRef] [Green Version]
- White, G.A.L.; Hill, C.D.; Pollock, F.A.; Hollenberg, L.C.L.; Modi, K. Demonstration of non-Markovian process characterisation and control on a quantum processor. Nat. Commun. 2020, 11, 6301. [Google Scholar] [CrossRef]
- Goswami, K.; Giarmatzi, C.; Monterola, C.; Shrapnel, S.; Romero, J.; Costa, F. Experimental characterization of a non-Markovian quantum process. Phys. Rev. A 2021, 104, 022432. [Google Scholar] [CrossRef]
- Lyyra, H.; Siltanen, O.; Piilo, J.; Banerjee, S.; Kuusela, T. Experimental Snapshot Verification of non-Markovianity with Unknown System-Probe Coupling. arXiv 2021, arXiv:2107.07876. [Google Scholar]
- Smirne, A.; Megier, N.; Vacchini, B. On the connection between microscopic description and memory effects in open quantum system dynamics. Quantum 2021, 5, 439. [Google Scholar] [CrossRef]
- Campbell, S.; Popovic, M.; Tamascelli, D.; Vacchini, B. Precursors of non-Markovianity. New J. Phys. 2019, 21, 053036. [Google Scholar] [CrossRef]
- Riedel, C.J.; Zurek, W.H.; Zwolak, M. The rise and fall of redundancy in decoherence and quantum Darwinism. New J. Phys. 2012, 14, 083010. [Google Scholar] [CrossRef]
- Roszak, K.; Korbicz, J.K. Entanglement and objectivity in pure dephasing models. Phys. Rev. A 2019, 100, 062127. [Google Scholar] [CrossRef] [Green Version]
- García-Pérez, G.; Chisholm, D.A.; Rossi, M.A.C.; Palma, G.M.; Maniscalco, S. Decoherence without entanglement and quantum Darwinism. Phys. Rev. Res. 2020, 2, 012061. [Google Scholar] [CrossRef] [Green Version]
- Campbell, S.; Ciccarello, F.; Palma, G.M.; Vacchini, B. System-environment correlations and Markovian embedding of quantum non-Markovian dynamics. Phys. Rev. A 2018, 98, 012142. [Google Scholar] [CrossRef]
- Laine, E.M.; Piilo, J.; Breuer, H.P. Witness for initial system-environment correlations in open system dynamics. EPL 2010, 92, 60010. [Google Scholar] [CrossRef] [Green Version]
- Giorgi, G.L.; Galve, F.; Zambrini, R. Quantum Darwinism and non-Markovian dissipative dynamics from quantum phases of the spin-1/2 XX model. Phys. Rev. A 2015, 92, 022105. [Google Scholar] [CrossRef] [Green Version]
- Galve, F.; Zambrini, R.; Maniscalco, S. Non-Markovianity hinders Quantum Darwinism. Sci. Rep. 2016, 6, 19607. [Google Scholar] [CrossRef]
- Pleasance, G.; Garraway, B.M. Application of quantum Darwinism to a structured environment. Phys. Rev. A 2017, 96, 062105. [Google Scholar] [CrossRef] [Green Version]
- Milazzo, N.; Lorenzo, S.; Paternostro, M.; Palma, G.M. Role of information backflow in the emergence of quantum Darwinism. Phys. Rev. A 2019, 100, 012101. [Google Scholar] [CrossRef] [Green Version]
- Lampo, A.; Tuziemski, J.; Lewenstein, M.; Korbicz, J.K. Objectivity in the non-Markovian spin-boson model. Phys. Rev. A 2017, 96, 012120. [Google Scholar] [CrossRef] [Green Version]
- Ryan, E.; Paternostro, M.; Campbell, S. Quantum Darwinism in a structured spin environment. Phys. Lett. A 2021, 416, 127675. [Google Scholar] [CrossRef]
- Martins, W.S.; Soares-Pinto, D.O. Suppressing information storage in a structured thermal bath: Objectivity and non-Markovianity. arXiv 2021, arXiv:2110.03490. [Google Scholar]
- Chin, A.W.; Rivas, A.; Huelga, S.F.; Plenio, M.B. Exact mapping between system-reservoir quantum models and semi-infinite discrete chains using orthogonal polynomials. J. Math. Phys. 2010, 51, 092109. [Google Scholar] [CrossRef] [Green Version]
- Martinazzo, R.; Vacchini, B.; Hughes, K.H.; Burghardt, I. Universal Markovian reduction of Brownian particle dynamics. J. Chem. Phys. 2011, 134, 011101. [Google Scholar] [CrossRef]
- Tamascelli, D.; Smirne, A.; Huelga, S.F.; Plenio, M.B. Nonperturbative Treatment of non-Markovian Dynamics of Open Quantum Systems. Phys. Rev. Lett. 2018, 120, 030402. [Google Scholar] [CrossRef] [Green Version]
- Tamascelli, D.; Smirne, A.; Lim, J.; Huelga, S.F.; Plenio, M.B. Efficient Simulation of Finite-Temperature Open Quantum Systems. Phys. Rev. Lett. 2019, 123, 090402. [Google Scholar] [CrossRef] [Green Version]
- Zwolak, M.; Quan, H.T.; Zurek, W.H. Redundant imprinting of information in nonideal environments: Objective reality via a noisy channel. Phys. Rev. A 2010, 81, 062110. [Google Scholar] [CrossRef] [Green Version]
- Zwolak, M.; Zurek, W.H. Complementarity of quantum discord and classically accessible information. Sci. Rep. 2013, 3, 1729. [Google Scholar] [CrossRef]
- Çakmak, B.; Müstecaplıoğlu, Ö.E.; Paternostro, M.; Vacchini, B.; Campbell, S. Quantum Darwinism in a Composite System: Objectivity versus Classicality. Entropy 2021, 23, 995. [Google Scholar] [CrossRef]
- Campbell, S.; Çakmak, B.; Müstecaplıoğlu, O.E.; Paternostro, M.; Vacchini, B. Collisional unfolding of quantum Darwinism. Phys. Rev. A 2019, 99, 042103. [Google Scholar] [CrossRef] [Green Version]
- Mirkin, N.; Wisniacki, D.A. Many-Body Localization and the Emergence of Quantum Darwinism. Entropy 2021, 23, 1377. [Google Scholar] [CrossRef] [PubMed]
- Touil, A.; Yan, B.; Girolami, D.; Deffner, S.; Zurek, W.H. Eavesdropping on the Decohering Environment: Quantum Darwinism, Amplification, and the Origin of Objective Classical Reality. Phys. Rev. Lett. 2022, 128, 010401. [Google Scholar] [CrossRef] [PubMed]
- Megier, N.; Smirne, A.; Vacchini, B. Entropic Bounds on Information Backflow. Phys. Rev. Lett. 2021, 127, 030401. [Google Scholar] [CrossRef] [PubMed]
- Smirne, A.; Megier, N.; Vacchini, B. Holevo skew divergence for the characterization of information backflow. arXiv 2022, arXiv:2201.07812. [Google Scholar]
- Bengtsson, I.; Życzkowski, K. Geometry of Quantum States: An Introduction to Quantum Entanglement, 2nd ed.; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Sra, S. Metrics induced by Jensen-Shannon and related divergences on positive definite matrices. Linear Algebra Its Appl. 2021, 616, 125–138. [Google Scholar] [CrossRef]
- Virosztek, D. The metric property of the quantum Jensen-Shannon divergence. Adv. Math. 2021, 380, 107595. [Google Scholar] [CrossRef]
- Zwolak, M.; Quan, H.T.; Zurek, W.H. Quantum Darwinism in a Mixed Environment. Phys. Rev. Lett. 2009, 103, 110402. [Google Scholar] [CrossRef] [Green Version]
- Korbicz, J.K.; Horodecki, P.; Horodecki, R. Objectivity in a Noisy Photonic Environment through Quantum State Information Broadcasting. Phys. Rev. Lett. 2014, 112, 120402. [Google Scholar] [CrossRef] [Green Version]
- Pollock, F.A.; Rodriguez-Rosario, C.; Frauenheim, T.; Paternostro, M.; Modi, K. Operational Markov Condition for Quantum Processes. Phys. Rev. Lett. 2018, 120, 040405. [Google Scholar] [CrossRef] [Green Version]
- Vacchini, B.; Smirne, A.; Laine, E.M.; Piilo, J.; Breuer, H.P. Markovianity and non-Markovianity in quantum and classical systems. New J. Phys. 2011, 13, 093004. [Google Scholar] [CrossRef]
- Breuer, H.P.; Laine, E.M.; Piilo, J. Measure for the Degree of Non-Markovian Behavior of Quantum Processes in Open Systems. Phys. Rev. Lett. 2009, 103, 210401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Laine, E.M.; Piilo, J.; Breuer, H.P. Measure for the non-Markovianity of quantum processes. Phys. Rev. A 2010, 81, 062115. [Google Scholar] [CrossRef] [Green Version]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Megier, N.; Smirne, A.; Campbell, S.; Vacchini, B. Correlations, Information Backflow, and Objectivity in a Class of Pure Dephasing Models. Entropy 2022, 24, 304. https://doi.org/10.3390/e24020304
Megier N, Smirne A, Campbell S, Vacchini B. Correlations, Information Backflow, and Objectivity in a Class of Pure Dephasing Models. Entropy. 2022; 24(2):304. https://doi.org/10.3390/e24020304
Chicago/Turabian StyleMegier, Nina, Andrea Smirne, Steve Campbell, and Bassano Vacchini. 2022. "Correlations, Information Backflow, and Objectivity in a Class of Pure Dephasing Models" Entropy 24, no. 2: 304. https://doi.org/10.3390/e24020304
APA StyleMegier, N., Smirne, A., Campbell, S., & Vacchini, B. (2022). Correlations, Information Backflow, and Objectivity in a Class of Pure Dephasing Models. Entropy, 24(2), 304. https://doi.org/10.3390/e24020304





