Recovery-Based Error Estimator for Natural Convection Equations Based on Defect-Correction Methods
Abstract
:1. Introduction
2. Preliminaries
3. Defect-Correction Method
3.1. The Finite Element Discrete Form of NC Equations
3.2. Application to Natural Convection Equations
3.3. Error Analysis
4. Recovery Error Estimator for NC Equations
4.1. Recovery Error Estimator
4.2. The Reliability Analysis
4.3. Effectiveness Analysis
5. Numerical Experiment
- the number of degrees of freedom of triangulation ;
- denotes the relative value of norm;
- denotes the relative value of global recovery-based estimator;
- denotes the convergence rate of the error;
- denotes the convergence rate of the error;
- denotes effectivity index for the global recovery-based estimator ,
5.1. Smooth True Solution
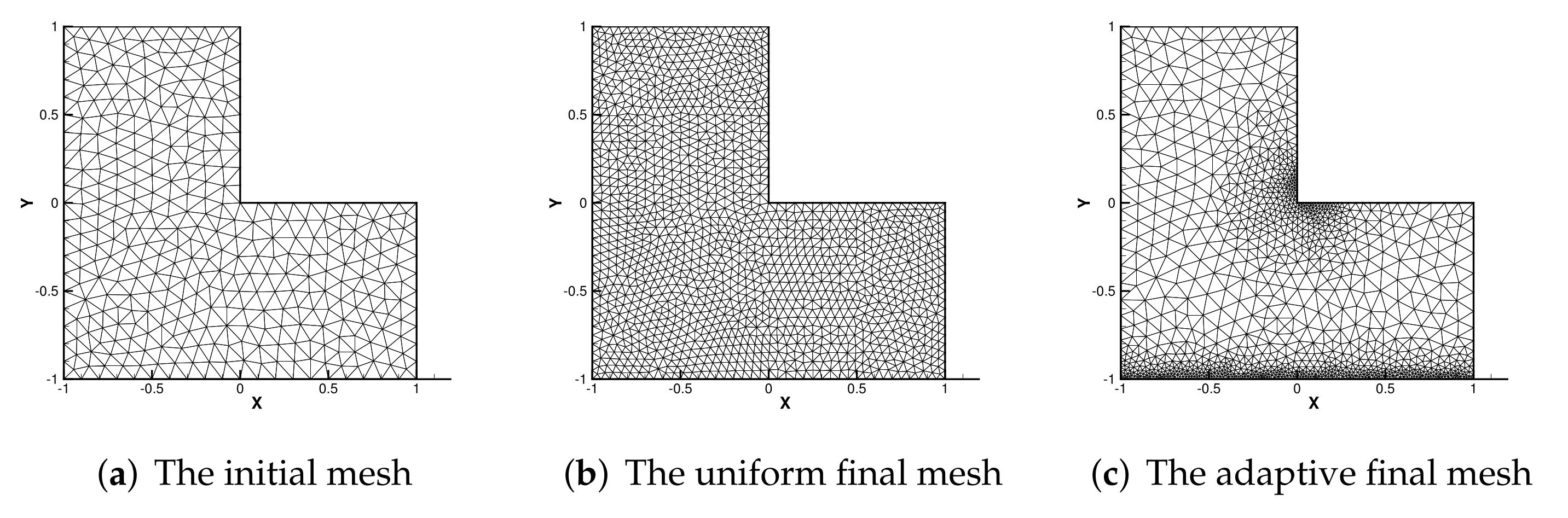
5.2. L-Shape Domain Problem
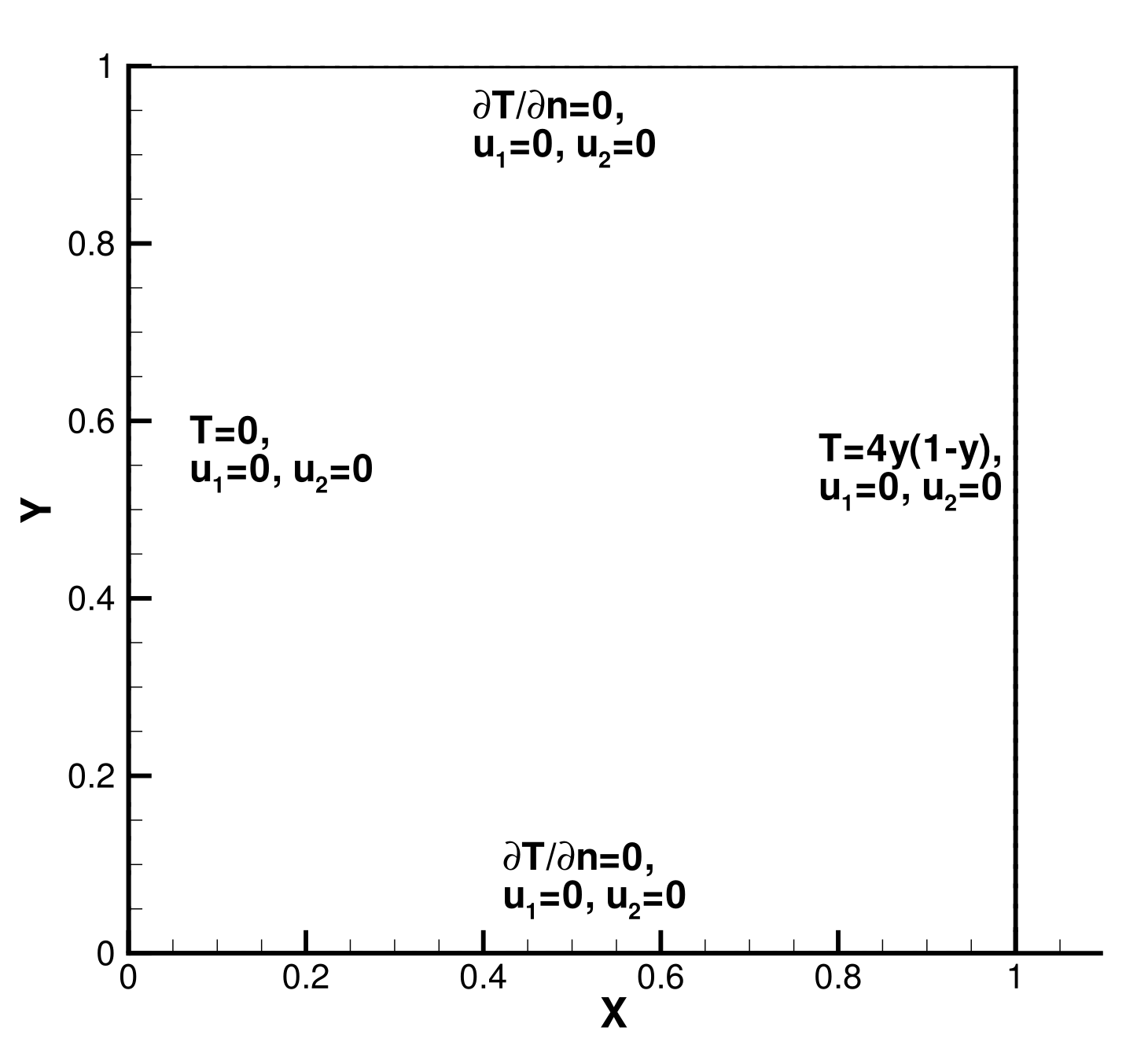
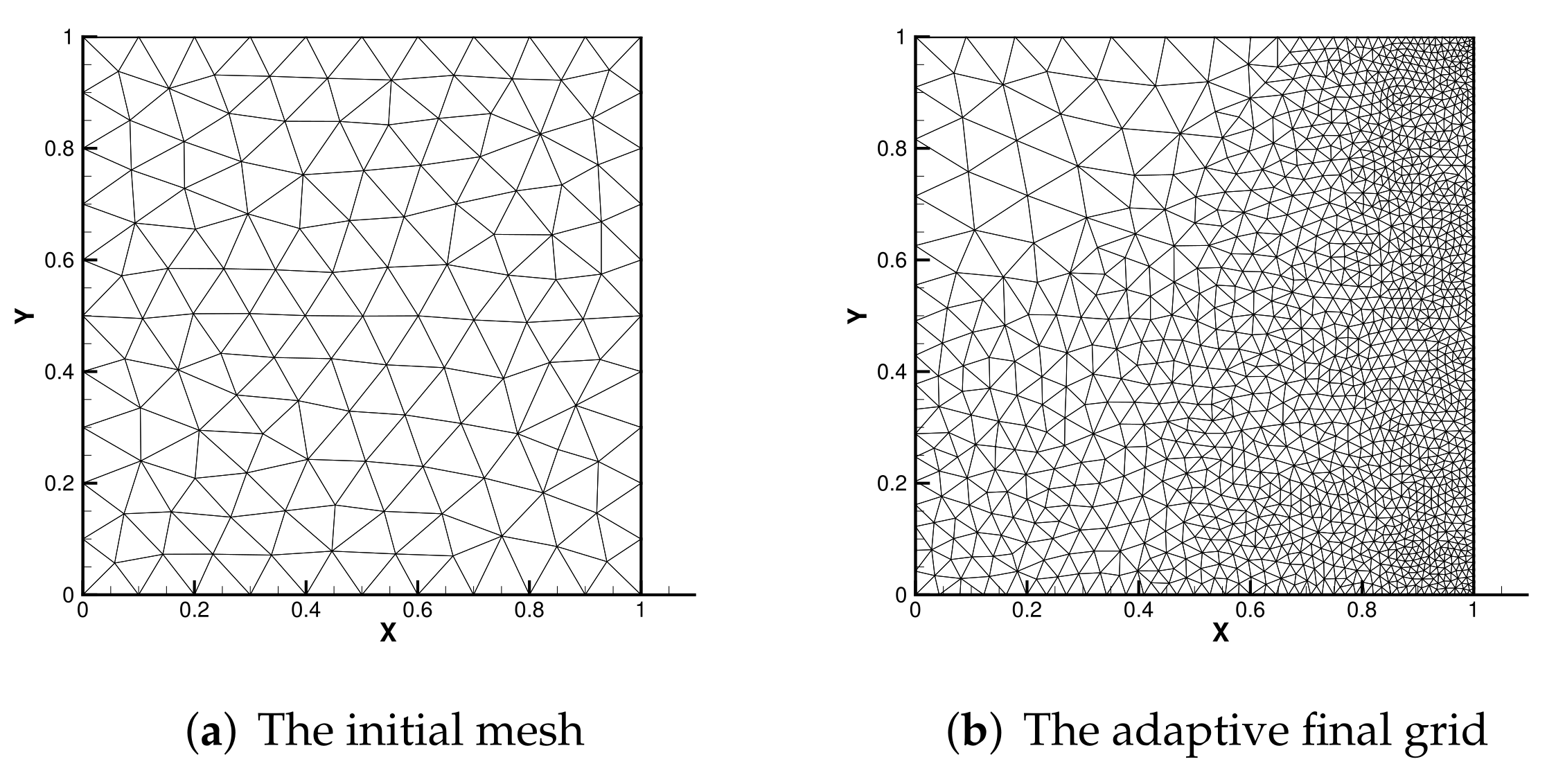
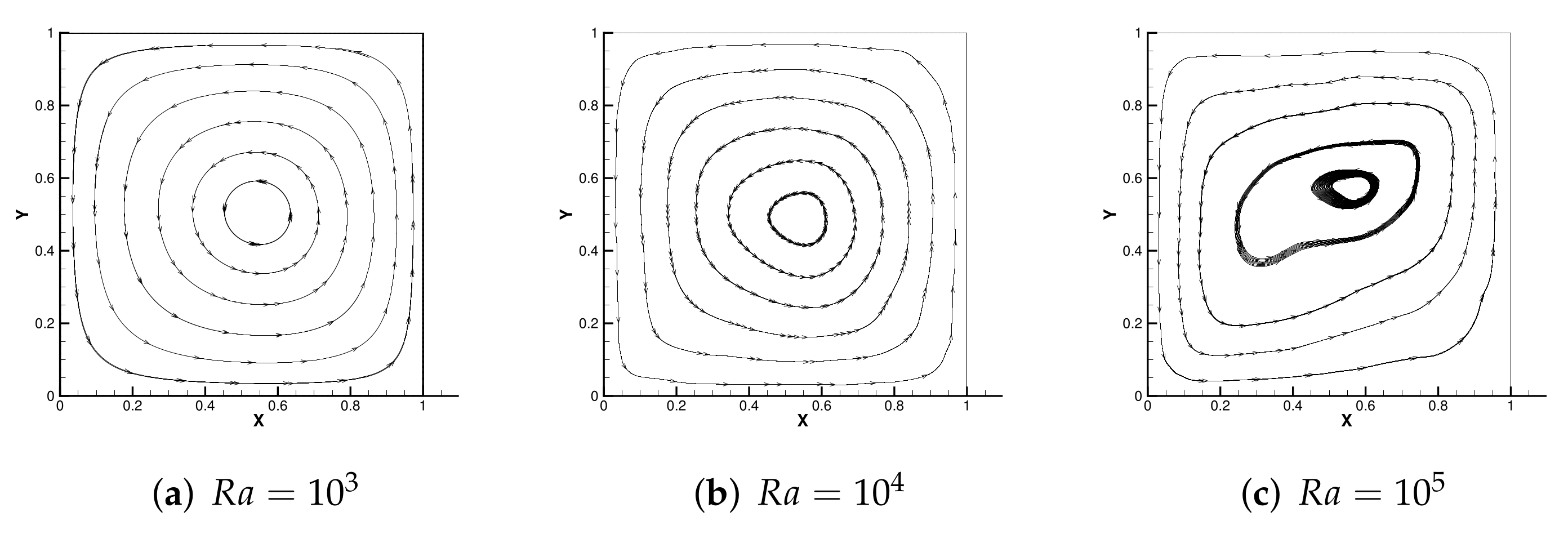
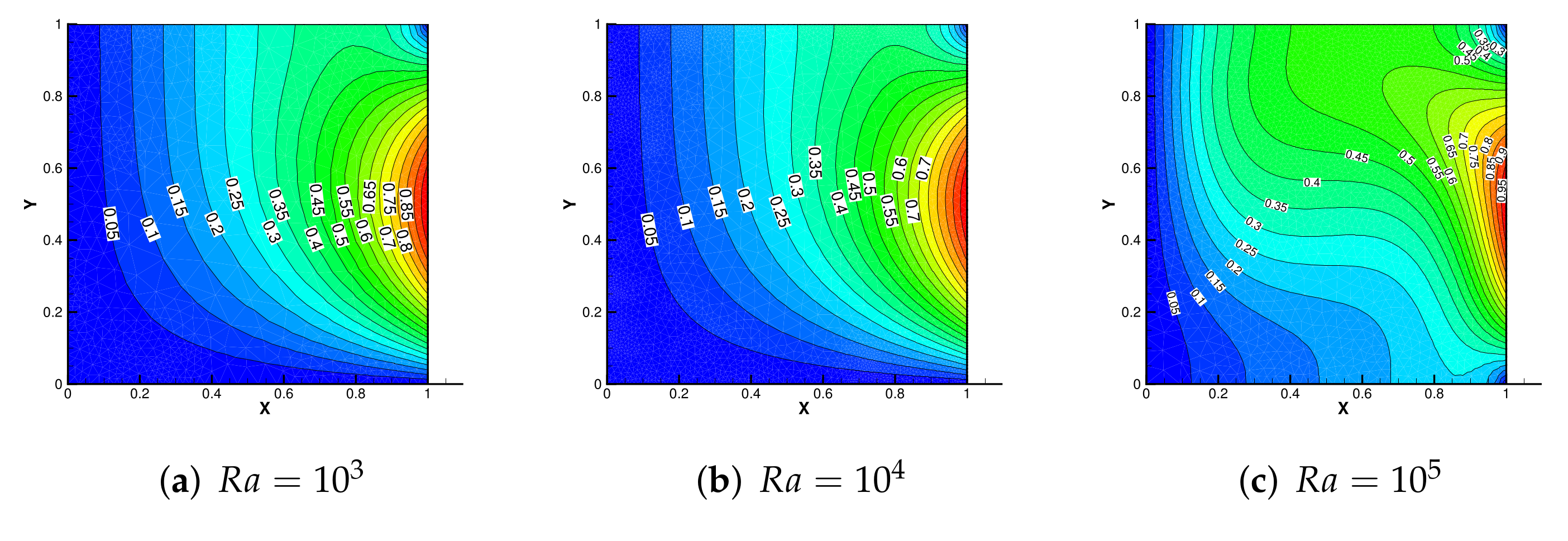
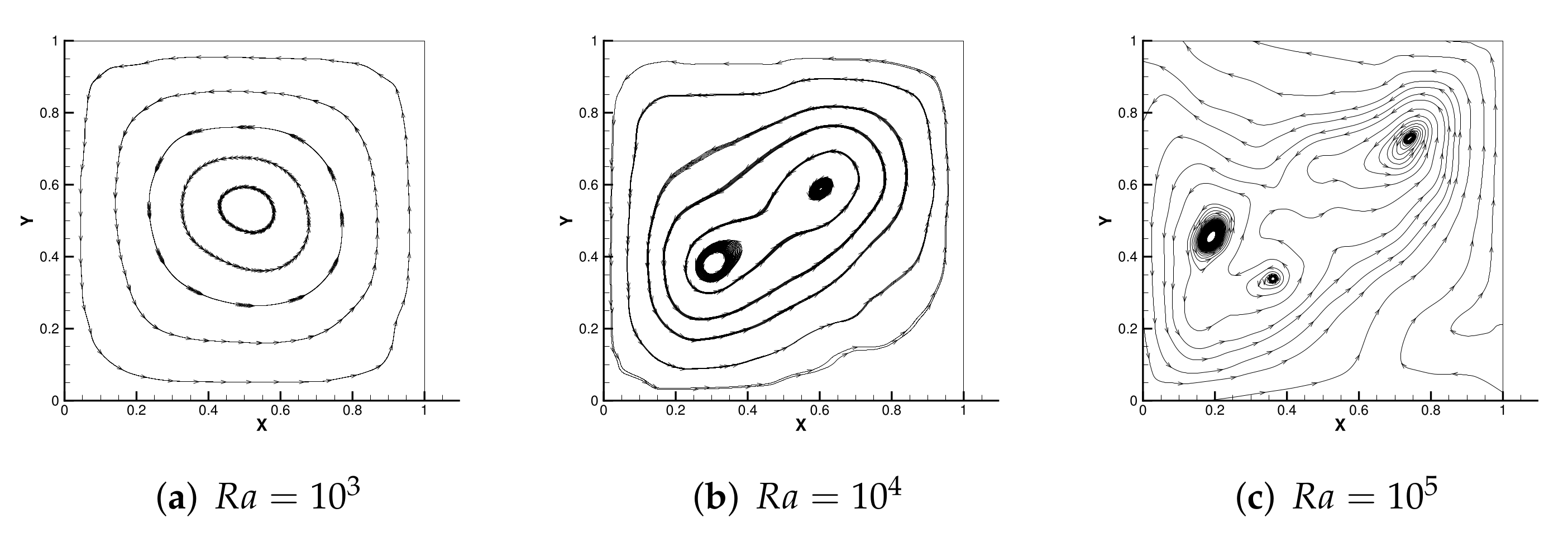
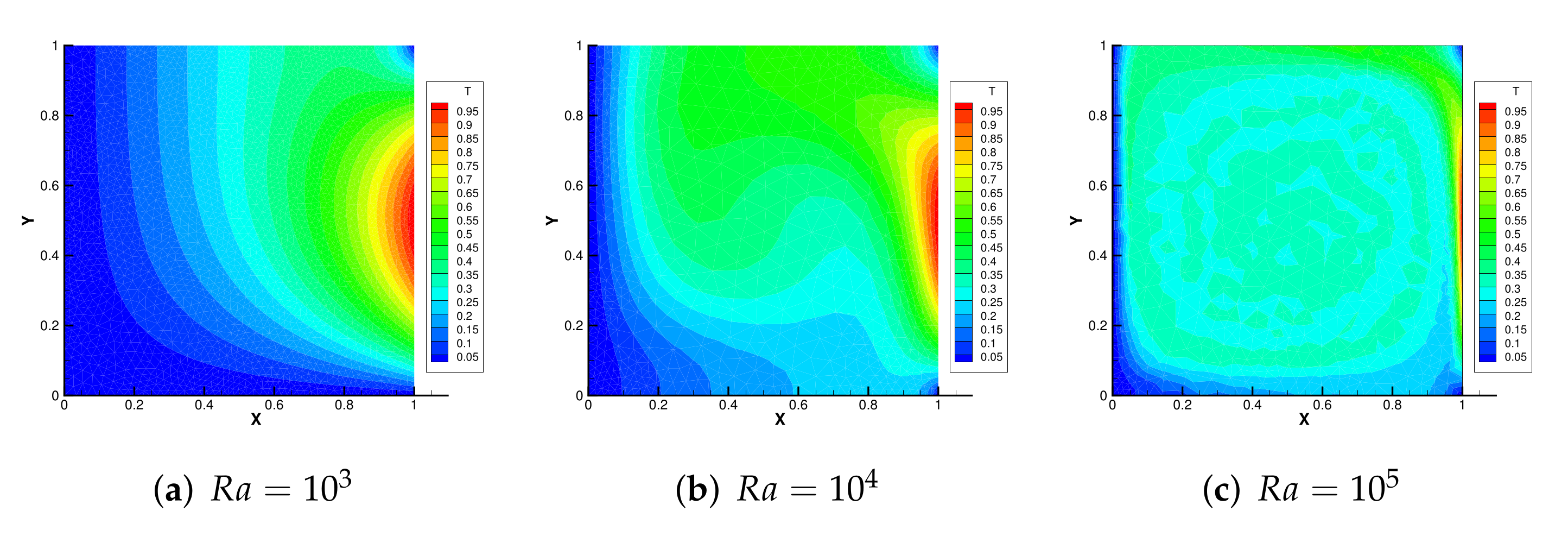
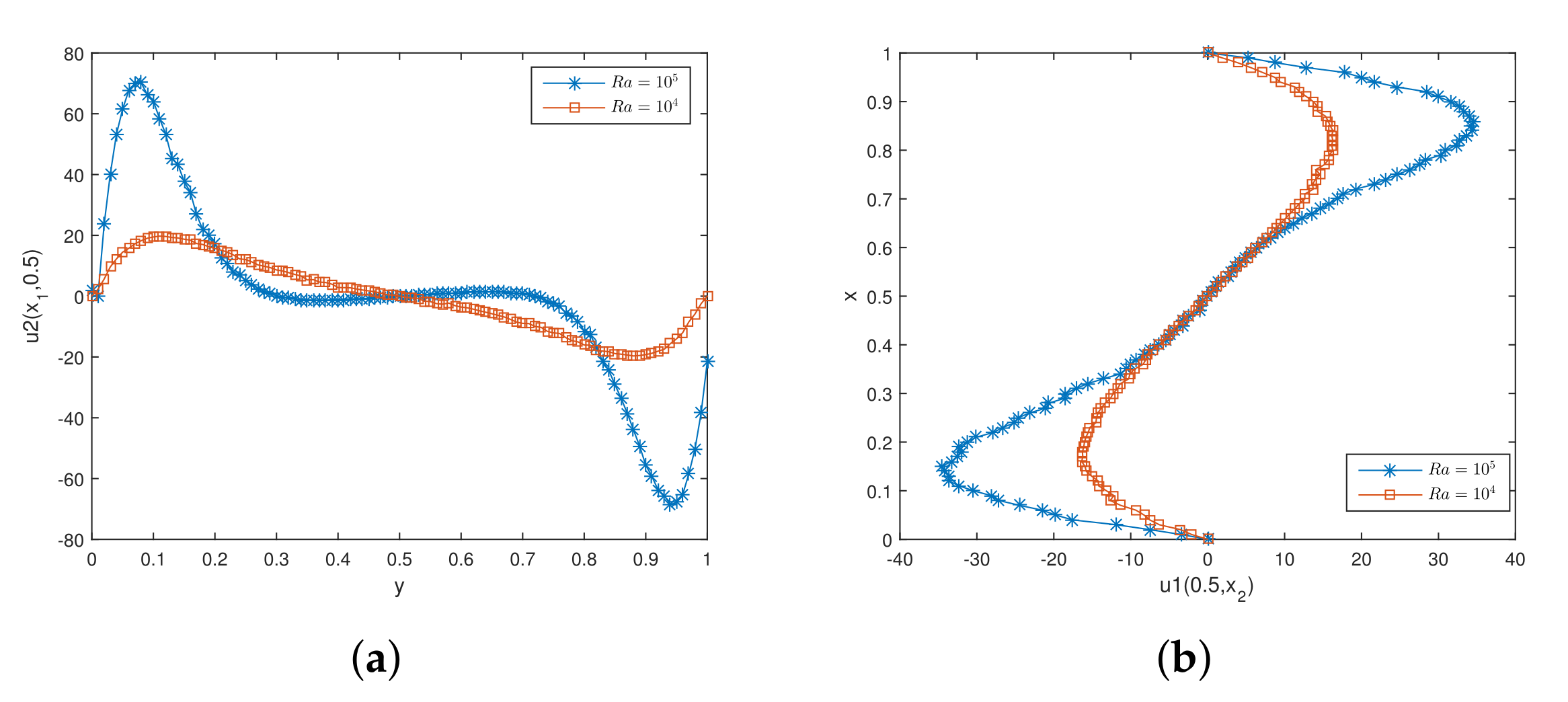
5.3. Thermally Driven Flow
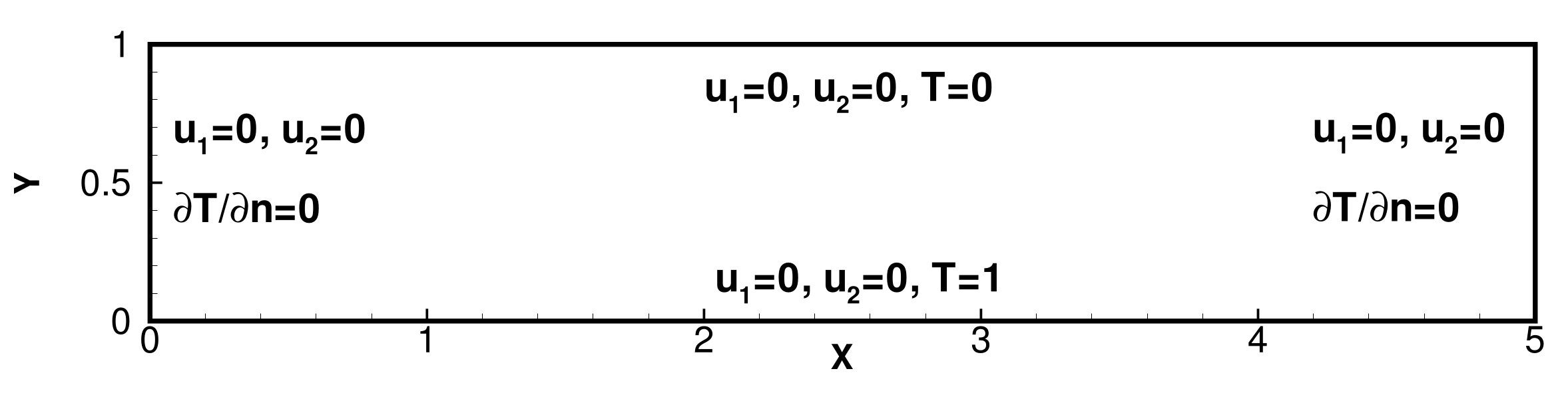
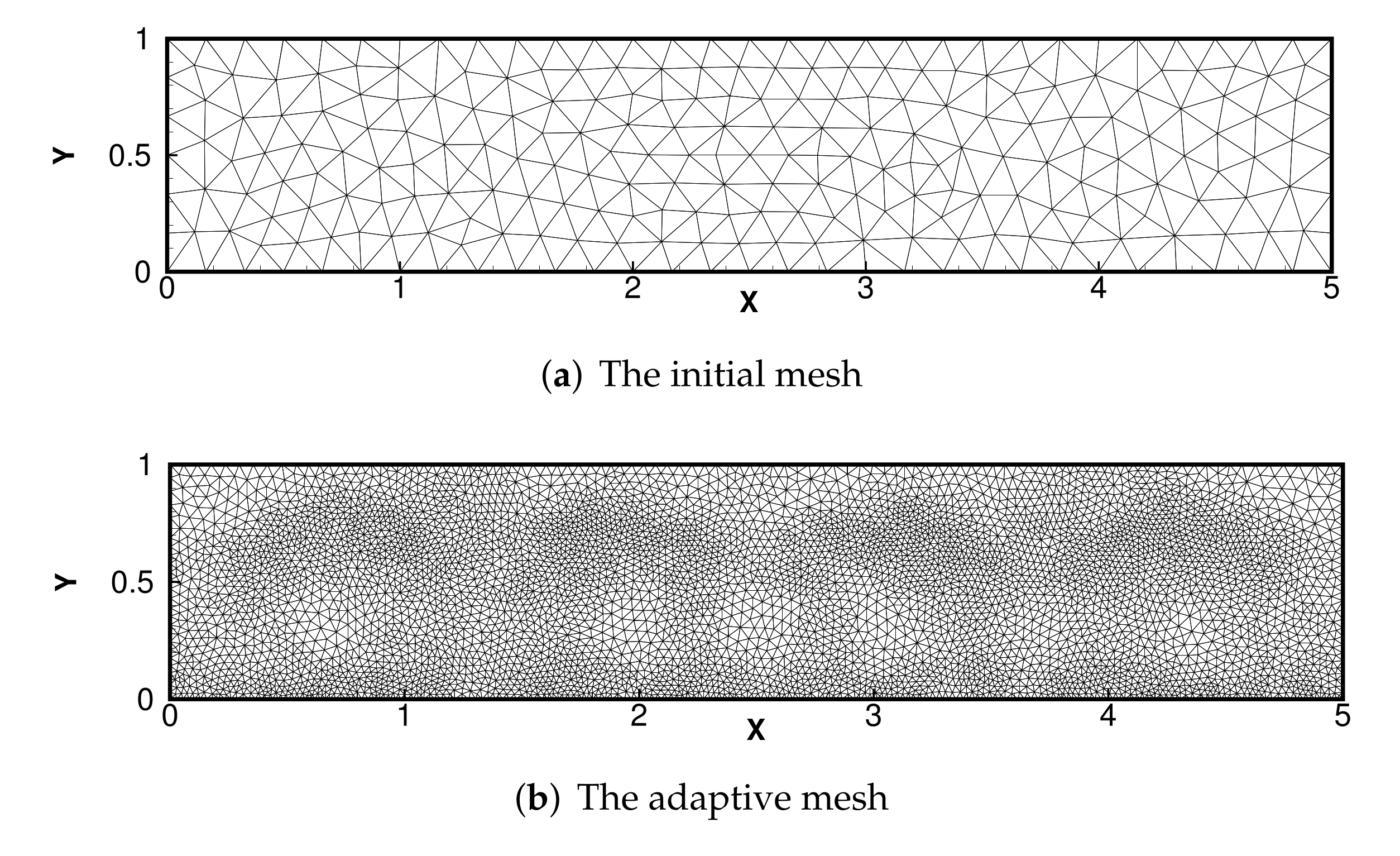
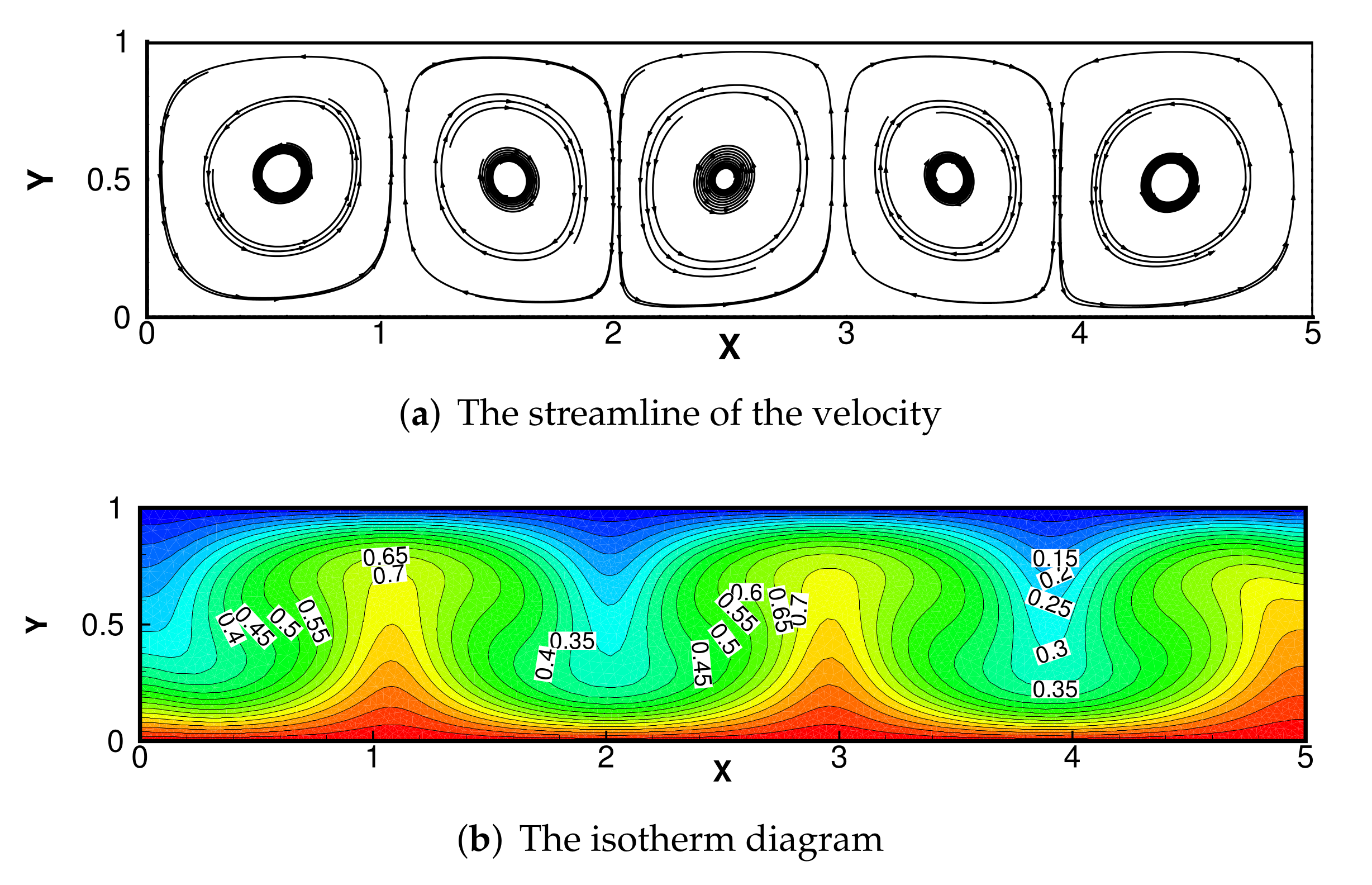
5.4. Bernard Convection Problem
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Christie, I.; Mitchell, A.R. Upwinding of high order Galerkin methods in conduction-convection problems. Int. J. Numer. Methods Eng. 2010, 12, 1764–1771. [Google Scholar] [CrossRef]
- Boland, J.; Layton, W. An analysis of the finite element method for natural convection problems. Numer. Methods Partial. Differ. Equ. 1990, 6, 115–126. [Google Scholar] [CrossRef]
- Boland, J.; Layton, W. Error analysis for finite element methods for steady natural convection problems. Numer. Funct. Anal. Optim. 1990, 11, 449–483. [Google Scholar] [CrossRef]
- Rubino, S. Numerical analysis of a projection-based stabilized POD-ROM for incompressible flows. SIAM J. Numer. Anal. 2020, 58, 2019–2058. [Google Scholar] [CrossRef]
- Davis, G.D.V. Natural convection of air in a square cavity: A benchmark solution. Int. J. Numer. Methods Fluids 1983, 3, 249–264. [Google Scholar] [CrossRef]
- He, Y.; Li, J. A stabilized finite element method based on local polynomial pressure projection for the stationary Navier-Stokes equations. Appl. Numer. Math. 2008, 58, 1503–1514. [Google Scholar] [CrossRef]
- Wu, J.; Huang, P.; Feng, X.; Liu, D. An efficient two-step algorithm for steady-state natural convection problem. Int. J. Heat Mass Transf. 2016, 101, 387–398. [Google Scholar] [CrossRef]
- Oztop, H.; Abu-Nada, E. Numerical study of natural convection in partially heated rectangular enclosures filled with nanofluids. Int. J. Heat Fluid Flow 2008, 29, 1326–1336. [Google Scholar] [CrossRef]
- Wu, J.; Feng, X.; Liu, F. Pressure-Correction Projection FEM for Time-Dependent Natural Convection Problem. Commun. Comput. Phys. 2017, 21, 1090–1117. [Google Scholar] [CrossRef]
- Asmadi, M.S.; Siri, Z.; Kasmani, R.M.; Saleh, H. Nanoparticle shape effect on the natural convection heat transfer of hybrid nanofluid inside a U-shaped enclosure. Therm. Sci. 2021, 26, 139. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Seyednezhad, M. Simulation of nanofluid flow and natural convection in a porous media under the influence of electric field using CVFEM. Int. J. Heat Mass Transf. 2018, 120, 772–781. [Google Scholar] [CrossRef]
- Giwa, S.O.; Sharifpur, M.; Ahmadi, M.H.; Meyer, J.P. A review of magnetic field influence on natural convection heat transfer performance of nanofluids in square cavities. J. Therm. Anal. Calorim. 2021, 145, 2581–2623. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ellahi, R. Three dimensional mesoscopic simulation of magnetic field effect on natural convection of nanofluid. Int. J. Heat Mass Transf. 2015, 89, 799–808. [Google Scholar] [CrossRef]
- Ahmad, U.; Ashraf, M.; Al-Zubaidi, A.; Ali, A.; Saleem, S. Effects of temperature dependent viscosity and thermal conductivity on natural convection flow along a curved surface in the presence of exothermic catalytic chemical reaction. PLoS ONE 2021, 16, e0252485. [Google Scholar] [CrossRef] [PubMed]
- Jarray, K.; Mazgar, A.; Nejma, F. Effect of combined natural convection and non-gray gas radiation on entropy generation through a cylindrical annulus. J. Adv. Mech. Eng. 2019, 11, 1687814019895417. [Google Scholar] [CrossRef]
- Singh, R.; Gohil, T. Numerical Analysis of Unsteady Natural Convection Flow and Heat Transfer in the Existence of Lorentz Force in Suddenly Expanded Cavity Using Open FOAM. J. Therm. Sci. 2020, 29, 1513–1530. [Google Scholar] [CrossRef]
- Ma, Y.; Mohebbi, R.; Rashidi, M.; Yang, Z.; Sheremet, M.A. Numerical study of MHD nanofluid natural convection in a baffled U-shaped enclosure. Int. J. Heat Mass Transf. 2019, 130, 123–134. [Google Scholar] [CrossRef]
- Al-Rashed, A.A.; Kalidasan, K.; Kolsi, L.; Aydi, A.; Malekshah, E.H.; Hussein, A.K.; Kanna, P.R. Three-dimensional investigation of the effects of external magnetic field inclination on laminar natural convection heat transfer in CNT-water nanofluid filled cavity. J. Mol. Liq. 2018, 252, 454–468. [Google Scholar] [CrossRef]
- Zaim, A.; Aissa, A.; Mebarek-Oudina, F.; Mahanthesh, B.; Lorenzini, G.; Sahnoun, M.; El Ganaoui, M. Galerkin finite element analysis of magneto-hydrodynamic natural convection of Cu-water nanoliquid in a baffled U-shaped enclosure. Propuls. Power Res. 2020, 9, 383–393. [Google Scholar] [CrossRef]
- Ezan, M.A.; Kalfa, M. Numerical investigation of transient natural convection heat transfer of freezing water in a square cavity. Int. J. Heat Fluid Flow 2016, 61, 438–448. [Google Scholar] [CrossRef]
- Wei, T.; Koster, J.N. Natural convection of water in a rectangular cavity including density inversion. Int. J. Heat Fluid Flow 1993, 14, 366–375. [Google Scholar]
- Sondak, D.; Smith, L.; Waleffe, F. Optimal Heat Transport in Rayleigh-Bénard Convection. J. Fluid Mech. 2015, 784, 565–595. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.J.; Li, Z.Y.; Xie, W.L.; Wu, X.H. A two-level variational multiscale meshless local Petrov Galerkin (VMS-MLPG) method for convection-diffusion problems with large Peclet number. Comput. Fluids 2018, 164, 73–82. [Google Scholar] [CrossRef]
- Beghetti, M.; Channick, R.N.; Chin, K.M.; Di Scala, L.; Gaine, S.; Ghofrani, H.A.; Hoeper, M.M.; Lang, I.M.; McLaughlin, V.V..; Preiss, R.; et al. Selexipag treatment for pulmonary arterial hypertension associated with congenital heart disease after defect correction: Insights from the randomised controlled GRIPHON study. Eur. J. Heart Fail. 2019, 21, 352–359. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, F.; Chen, L.; Huang, Q. Local defect-correction method based on multilevel discretization for Steklov eigenvalue problem. ESAIM Math. Model. Numer. Anal. 2021, 55, 2899–2920. [Google Scholar] [CrossRef]
- Stetter, J. The defect correction principle and discretization methods. Numer. Math. 1978, 29, 425–443. [Google Scholar] [CrossRef]
- Su, H.; Zhao, J.; Gui, D.; Feng, X. Two-level defect-correction Oseen iterative stabilized finite element method for the stationary conduction-convection equations. Int. Commun. Heat Mass Transf. 2014, 56, 133–145. [Google Scholar] [CrossRef]
- Feng, X.; Tang, T.; Yang, J. Long time numerical simulations for phase-field problems using p-adaptive spectral deferred correction methods. SIAM J. Sci. Comput. 2015, 37, A271–A294. [Google Scholar] [CrossRef]
- Huang, P.; Feng, X.; He, Y. Two-level defect-correction Oseen iterative stabilized finite element methods for the stationary Navier–Stokes equations. Appl. Math. Model. 2013, 37, 728–741. [Google Scholar] [CrossRef]
- Su, H.; Feng, X.; He, Y. Second order fully discrete defect-correction scheme for nonstationary conduction-convection problem at high Reynolds number. Numer. Methods Partial. Differ. Equ. 2017, 33, 681–703. [Google Scholar] [CrossRef]
- Du, B.; Su, H.; Feng, X. Two-level variational multiscale method based on the decoupling approach for the natural convection problem. Int. Commun. Heat Mass Transf. 2015, 61, 128–139. [Google Scholar] [CrossRef]
- Ainsworth, M.; Oden, J.T. A posteriori error estimation in finite element analysis. Comput. Methods Appl. Mech. Eng. 1997, 142, 1–88. [Google Scholar] [CrossRef]
- Chen, H.; Qiu, W.; Shi, K. A priori and computable a posteriori error estimates for an HDG method for the coercive Maxwell equations. Comput. Methods Appl. Mech. Eng. 2018, 333, 287–310. [Google Scholar] [CrossRef]
- Babuška, I.; Rheinboldt, W. Error estimates for adaptive finite element computation. SIAM J. Numer. Anal. 1978, 15, 736–754. [Google Scholar] [CrossRef]
- Babuška, I.; Miller, A. A posteriori error estimates and adaptive techniques for the finite element method. Esaim Math. Model. Numer. Anal. 1981, 20, 995–1016. [Google Scholar]
- Girault, V.; Lu, X.; Wheeler, M. A posteriori error estimates for biot system using enriched galerkin for flow. Comput. Methods Appl. Mech. Eng. 2020, 369, 113185. [Google Scholar] [CrossRef]
- Song, L.; Su, H.; Feng, X. Recovery-based error estimator for stabilized finite element method for the stationary Navier–Stokes problem. SIAM J. Sci. Comput. 2016, 38, A3758–A3772. [Google Scholar] [CrossRef]
- Su, H.; Feng, X.; Zhao, J. Penalty decoupled iterative methods for the stationary natural convection equations with different Rayleigh numbers. Appl. Numer. Math. 2021, 163, 270–291. [Google Scholar] [CrossRef]
- Wan, C.; Patnaik, B.; Wei, D. A new benchmark quality solution for the buoyancy-driven cavity by discrete singular convolution. Numer. Heat Transf. Part Fundam. 2001, 40, 199–228. [Google Scholar]

| Level | DOF | |||||
|---|---|---|---|---|---|---|
| 0 | 370 | 0.1317 | - | 0.1114 | - | 1.1824 |
| 1 | 691 | 0.0920 | 1.1482 | 0.0813 | 1.0056 | 1.1309 |
| 2 | 1395 | 0.0614 | 1.1523 | 0.0576 | 0.9820 | 1.0652 |
| 3 | 2773 | 0.0427 | 1.0528 | 0.0408 | 1.0018 | 1.0467 |
| 4 | 5494 | 0.0305 | 0.9848 | 0.0291 | 0.9898 | 1.0485 |
| Level | DOF | |||||
|---|---|---|---|---|---|---|
| 0 | 450 | 0.1211 | - | 0.1133 | - | 0.9356 |
| 1 | 800 | 0.0928 | 0.9252 | 0.0886 | 0.8548 | 0.9547 |
| 2 | 1250 | 0.0758 | 0.9068 | 0.0732 | 0.8557 | 0.9644 |
| 3 | 5000 | 0.0415 | 0.8691 | 0.0409 | 0.8397 | 0.9855 |
| 4 | 6050 | 0.0383 | 0.8419 | 0.0379 | 0.7993 | 0.9819 |
| DOF | Ra = | DOF | Ra = | Ra = | ||
|---|---|---|---|---|---|---|
| DCM | 2773 | 0.0408 | 2670 | 0.0653 | 2272 | 0.0923 |
| NDCM | 2392 | 0.1114 | 2677 | 13.91 | NAN | NAN |
| Level | Uniform Mesh | Adapt Mesh | ||||
|---|---|---|---|---|---|---|
| DOF | DOF | |||||
| 0 | 676 | 0.3523 | - | 830 | 0.2547 | - |
| 1 | 1516 | 0.2627 | 0.7267 | 1337 | 0.1631 | 1.8698 |
| 2 | 2696 | 0.2043 | 0.8735 | 2344 | 0.1156 | 1.5798 |
| 3 | 4282 | 0.1665 | 0.8844 | 4558 | 0.0833 | 0.9855 |
| 4 | 6170 | 0.1419 | 0.8753 | 6315 | 0.0704 | 1.0135 |
| Level | Uniform Mesh | Adapt Mesh | ||||
|---|---|---|---|---|---|---|
| DOF | DOF | |||||
| 0 | 676 | 0.7098 | - | 676 | 0.7098 | - |
| 1 | 1516 | 0.4955 | 0.8900 | 1423 | 0.4420 | 1.2728 |
| 2 | 2696 | 0.3805 | 0.9174 | 1952 | 0.3770 | 1.0065 |
| 3 | 4282 | 0.3059 | 0.9434 | 3622 | 0.2778 | 0.9879 |
| 4 | 6170 | 0.2602 | 0.9500 | 4970 | 0.2358 | 1.0362 |
| DOF | ||||
|---|---|---|---|---|
| 676 | 0.3610 | - | 0.4953 | - |
| 1516 | 0.2688 | 0.8900 | 0.3637 | 1.2728 |
| 2696 | 0.2086 | 0.9174 | 0.3061 | 1.0065 |
| 4282 | 0.1695 | 0.9434 | 0.2814 | 0.9879 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Su, H.; Feng, X. Recovery-Based Error Estimator for Natural Convection Equations Based on Defect-Correction Methods. Entropy 2022, 24, 255. https://doi.org/10.3390/e24020255
Li L, Su H, Feng X. Recovery-Based Error Estimator for Natural Convection Equations Based on Defect-Correction Methods. Entropy. 2022; 24(2):255. https://doi.org/10.3390/e24020255
Chicago/Turabian StyleLi, Lulu, Haiyan Su, and Xinlong Feng. 2022. "Recovery-Based Error Estimator for Natural Convection Equations Based on Defect-Correction Methods" Entropy 24, no. 2: 255. https://doi.org/10.3390/e24020255
APA StyleLi, L., Su, H., & Feng, X. (2022). Recovery-Based Error Estimator for Natural Convection Equations Based on Defect-Correction Methods. Entropy, 24(2), 255. https://doi.org/10.3390/e24020255





