Stochastic Hydrodynamics of Complex Fluids: Discretisation and Entropy Production
Abstract
1. Introduction
2. Stochastic Thermodynamics of Particles
2.1. Langevin Equation
2.2. Discretised Langevin Equation
2.3. Fokker–Planck Equation
2.4. Path Integral Formalism
2.4.1. Transition Probability
2.4.2. Path Integral
2.5. Entropy Production
2.5.1. Evaluation via Discretised Action
2.5.2. Non-Equilibrium Steady State
2.6. Stochastic Calculus for Degrees of Freedom
2.6.1. Conversion from Stratonovich to Itô Integral
2.6.2. Dynamical Action
3. Scalar Active Field Theories with Additive Noise
3.1. Informatic Entropy Production
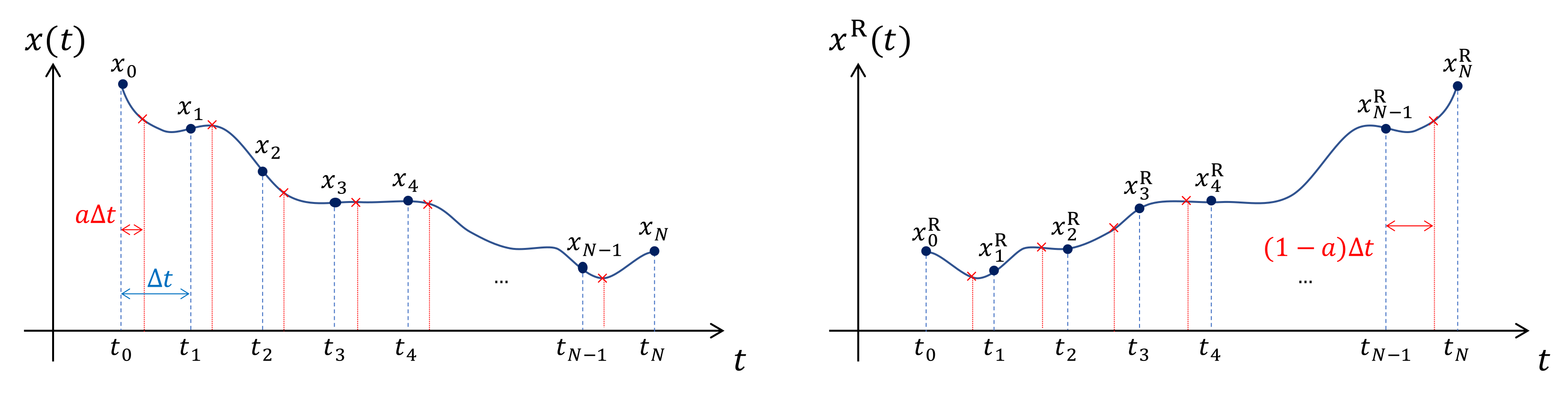
3.2. Spatial Discretisation
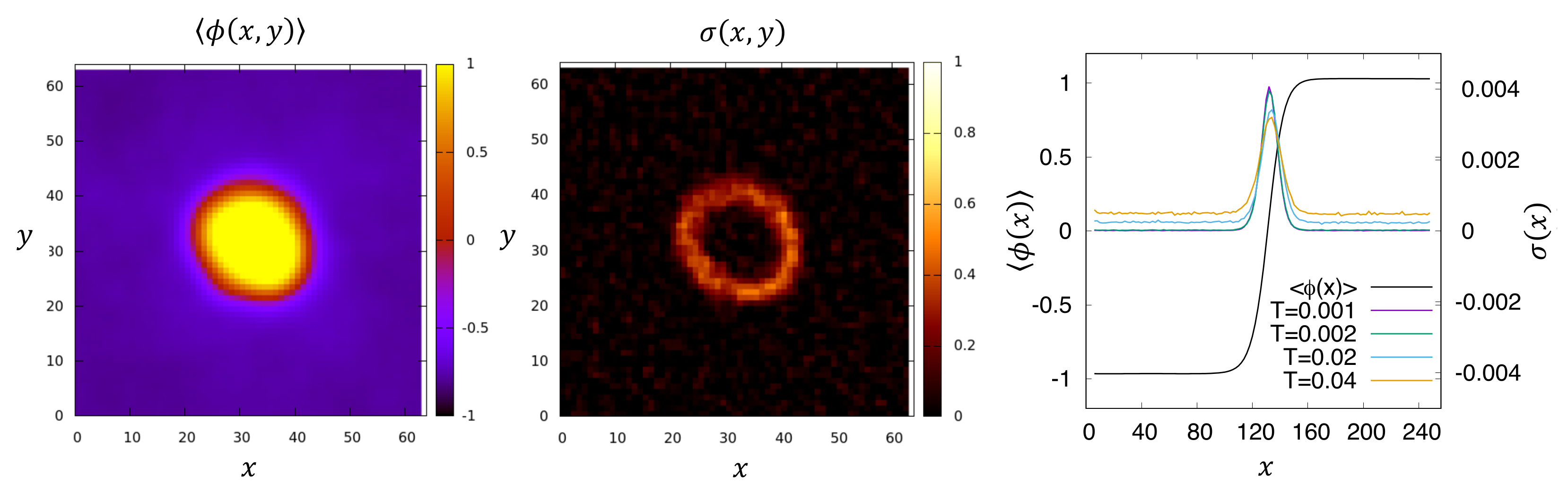
3.3. Computing the IEPR
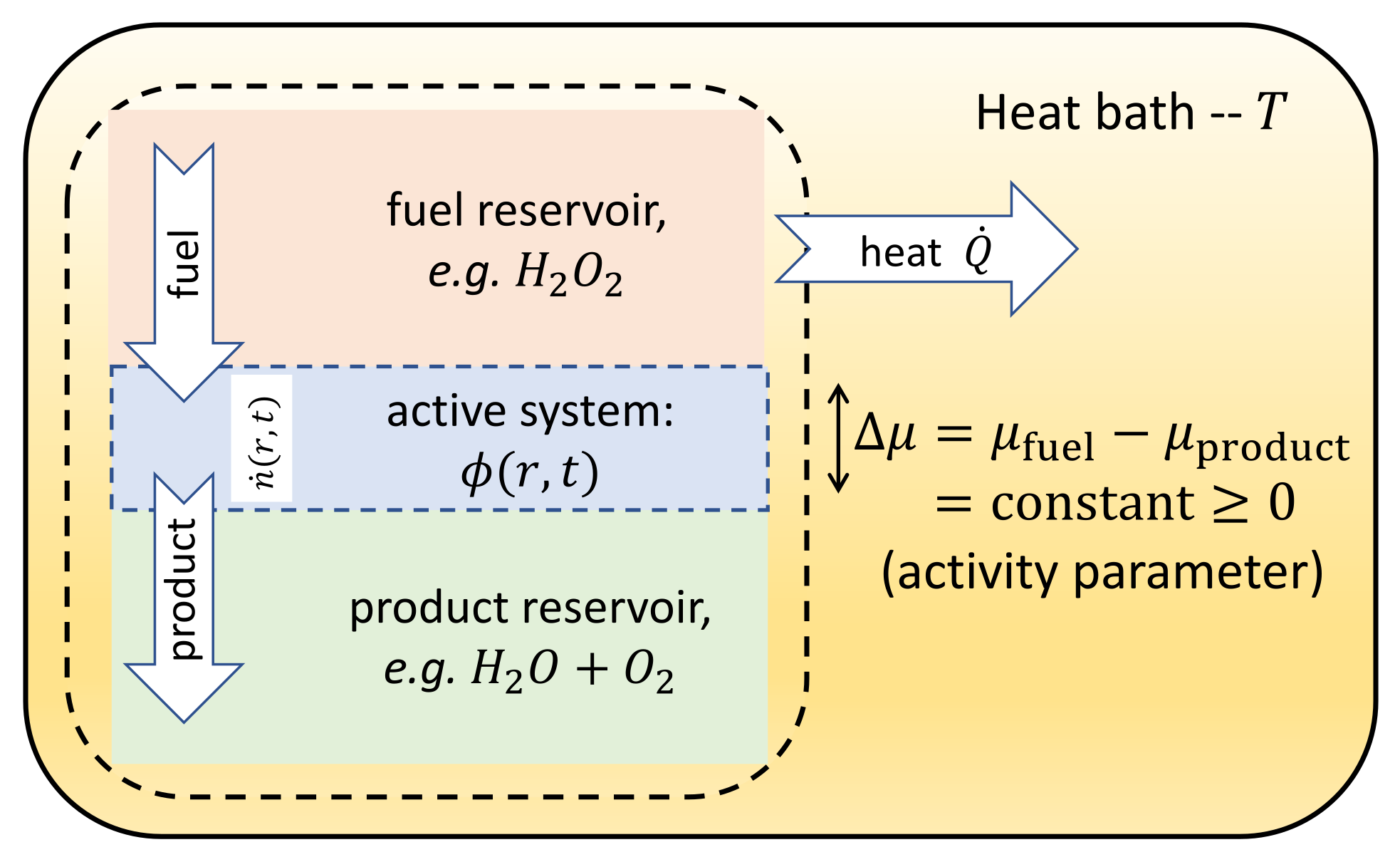
4. Thermodynamics of Active Field Theories
4.1. Onsager Coupling in Two-Dimensional System
4.2. Spatial Discretisation in Stochastic Field-Theories
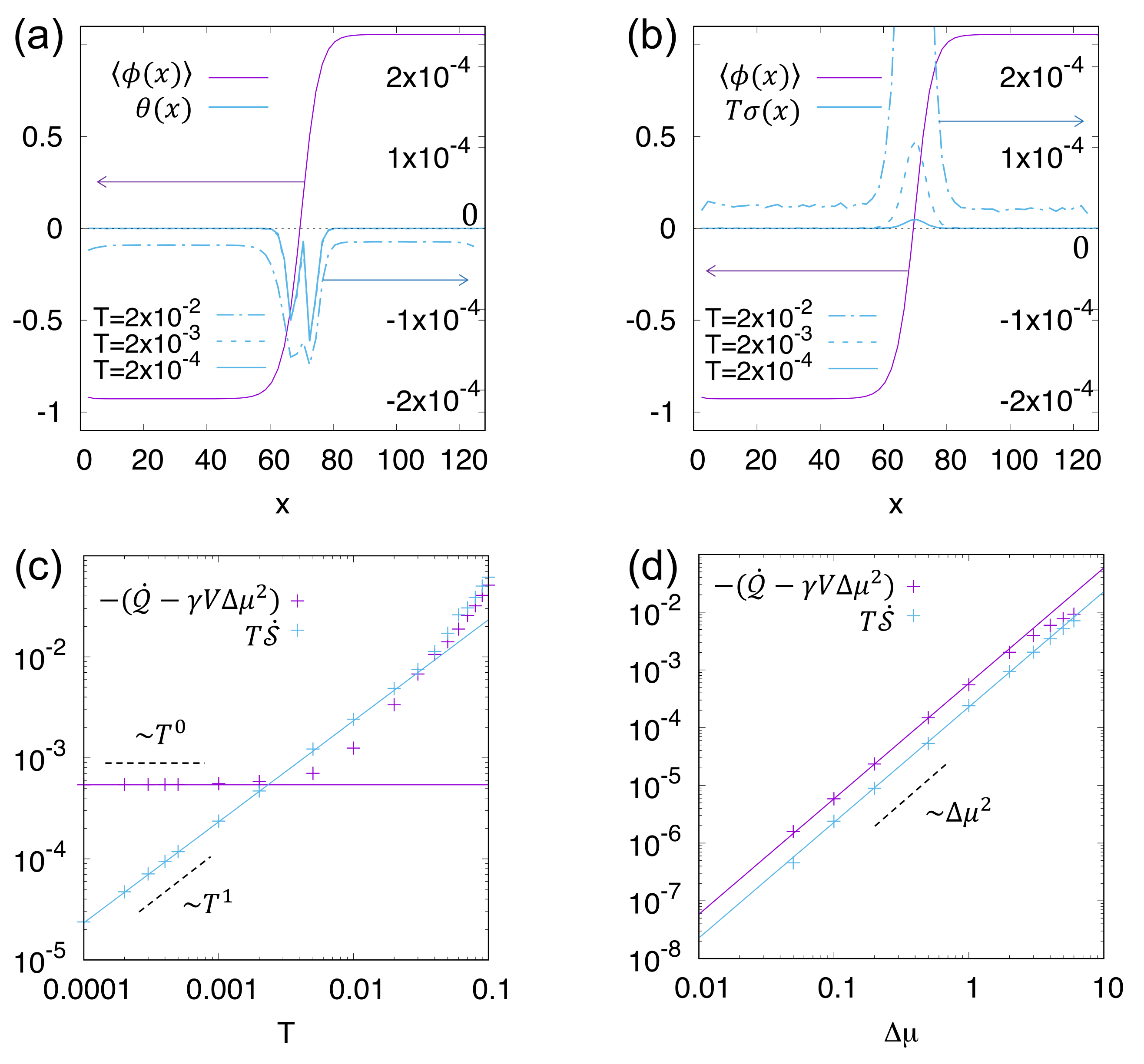
4.3. Thermodynamics of a Conserved Active Scalar Field
Calculation of the Heat Production Rate
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Spurious Drift in Linear Irreversible Thermodynamics
References
- Beris, A.N.; Edwards, B.J. Thermodynamics of Flowing Systems: With Internal Microstructure; Number 36; Oxford University Press: Oxford, UK, 1994. [Google Scholar]
- De Gennes, P.G.; Prost, J. The Physics of Liquid Crystals; Number 83; Oxford University Press: Oxford, UK, 1993. [Google Scholar]
- Cates, M.E.; Tjhung, E. Theories of binary fluid mixtures: From phase-separation kinetics to active emulsions. J. Fluid Mech. 2018, 836. [Google Scholar] [CrossRef]
- Hohenberg, P.C.; Halperin, B.I. Theory of dynamic critical phenomena. Rev. Mod. Phys. 1977, 49, 435. [Google Scholar] [CrossRef]
- Lifshitz, E.M.; Pitaevskii, L.P. Course of Theoretical Physics: Statistical Physics, Part 2; Number v. 9; Butterworth-Heinemann: Oxford, UK, 1980. [Google Scholar]
- Hairer, M. A theory of regularity structures. Invent. Math. 2014, 198, 269–504. [Google Scholar] [CrossRef]
- Cates, M.E. Active Field Theories. arXiv 2019, arXiv:1904.01330. [Google Scholar]
- Marchetti, M.C.; Joanny, J.F.; Ramaswamy, S.; Liverpool, T.B.; Prost, J.; Rao, M.; Simha, R.A. Hydrodynamics of soft active matter. Rev. Mod. Phys. 2013, 85, 1143–1189. [Google Scholar] [CrossRef]
- Nardini, C.; Fodor, É.; Tjhung, E.; Van Wijland, F.; Tailleur, J.; Cates, M.E. Entropy Production in Field Theories without Time-Reversal Symmetry: Quantifying the Non-Equilibrium Character of Active Matter. Phys. Rev. X 2017, 7, 021007. [Google Scholar] [CrossRef]
- Tjhung, E.; Nardini, C.; Cates, M.E. Cluster Phases and Bubbly Phase Separation in Active Fluids: Reversal of the Ostwald Process. Phys. Rev. X 2018, 8, 031080. [Google Scholar] [CrossRef]
- Borthne, ØL.; Fodor, É.; Cates, M.E. Time-reversal symmetry violations and entropy production in field theories of polar active matter. New J. Phys. 2020, 22, 123012. [Google Scholar] [CrossRef]
- Markovich, T.; Fodor, E.; Tjhung, E.; Cates, M.E. Thermodynamics of Active Field Theories: Energetic Cost of Coupling to Reservoirs. Phys. Rev. X 2021, 11, 021057. [Google Scholar] [CrossRef]
- Fodor, É.; Jack, R.L.; Cates, M.E. Irreversibility and Biased Ensembles in Active Matter: Insights from Stochastic Thermodynamics. Annu. Rev. Condens. Matter Phys. 2022, 13, 1. [Google Scholar] [CrossRef]
- Seifert, U. Stochastic thermodynamics, fluctuation theorems and molecular machines. Rep. Prog. Phys. 2012, 75, 126001. [Google Scholar] [CrossRef] [PubMed]
- Tan, T.H.; Watson, G.A.; Chao, Y.C.; Li, J.; Gingrich, T.R.; Horowitz, J.M.; Fakhri, N. Scale-dependent irreversibility in living matter. arXiv 2021, arXiv:2107.05701. [Google Scholar]
- Roldan, E.; Barral, J.; Martin, P.; Parrondo, J.M.R.; Juelicher, F. Quantifying entropy production in active fluctuations of the hair-cell bundle from time irreversibility and uncertainty relations. New J. Phys. 2021, 23, 083013. [Google Scholar] [CrossRef]
- Dabelow, L.; Bo, S.; Eichhorn, R. Irreversibility in Active Matter Systems: Fluctuation Theorem and Mutual Information. Phys. Rev. X 2019, 9, 021009. [Google Scholar] [CrossRef]
- Lau, A.W.C.; Lubensky, T.C. State-dependent diffusion: Thermodynamic consistency and its path integral formulation. Phys. Rev. E 2007, 76, 011123. [Google Scholar] [CrossRef]
- Cugliandolo, L.F.; Lecomte, V. Rules of calculus in the path integral representation of white noise Langevin equations: The Onsager–Machlup approach. J. Phys. A Math. Theor. 2017, 50, 345001. [Google Scholar] [CrossRef]
- Van Kampen, N.G. Stochastic Processes in Physics and Chemistry; Elsevier: Amsterdam, The Netherlands, 1992; Volume 1. [Google Scholar]
- Basu, A.; Joanny, J.F.; Jülicher, F.; Prost, J. Thermal and non-thermal fluctuations in active polar gels. Eur. Phys. J. E 2008, 27, 149. [Google Scholar] [CrossRef][Green Version]
- Peliti, L.; Pigolotti, S. Stochastic Thermodynamics: An Introduction; Princeton University Press: Princeton, NJ, USA, 2021. [Google Scholar]
- Fodor, E.; Nardini, C.; Cates, M.E.; Tailleur, J.; Visco, P.; van Wijland, F. How Far from Equilibrium Is Active Matter? Phys. Rev. Lett. 2016, 117, 038103. [Google Scholar] [CrossRef]
- Jarzynski, C. Equalities and Inequalities: Irreversibility and the Second Law of Thermodynamics at the Nanoscale. Annu. Rev. Condens. Matter Phys. 2011, 2, 329–351. [Google Scholar] [CrossRef]
- Kawai, R.; Parrondo, J.M.; Van den Broeck, C. Dissipation: The Phase-Space Perspective. Phys. Rev. Lett. 2007, 98, 080602. [Google Scholar] [CrossRef]
- Pietzonka, P.; Seifert, U. Entropy production of active particles and for particles in active baths. J. Phys. A Math. Theor. 2018, 51, 01LT01. [Google Scholar] [CrossRef]
- Pietzonka, P.; Fodor, E.; Lohrmann, C.; Cates, M.E.; Seifert, U. Autonomous Engines Driven by Active Matter: Energetics and Design Principles. Phys. Rev. X 2019, 9, 041032. [Google Scholar] [CrossRef]
- Murray, J.D. MathematicalBiology I. An Introduction; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Gardiner, C.W. Stochastic Methods: A Handbook for the Natural and Social Sciences; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Chaikin, P.M.; Lubensky, T.C. Principles of Condensed Matter Physics; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Wittkowski, R.; Tiribocchi, A.; Stenhammar, J.; Allen, R.J.; Marenduzzo, D.; Cates, M.E. Scalar φ4 field theory for active-particle phase separation. Nat. Commun. 2014, 5, 4351. [Google Scholar] [CrossRef] [PubMed]
- Thomsen, F.J.; Rapp, L.; Bergmann, F.; Zimmermann, W. Periodic patterns displace active phase separation. New J. Phys. 2021, 23, 042002. [Google Scholar] [CrossRef]
- Fausti, G.; Tjhung, E.; Cates, M.E.; Nardini, C. Capillary Interfacial Tension in Active Phase Separation. Phys. Rev. Lett. 2021, 127, 068001. [Google Scholar] [CrossRef] [PubMed]
- Tiribocchi, A.; Wittkowski, R.; Marenduzzo, D.; Cates, M.E. Active Model H: Scalar Active Matter in a Momentum-Conserving Fluid. Phys. Rev. Lett. 2015, 115, 188302. [Google Scholar] [CrossRef]
- Singh, R.; Cates, M.E. Hydrodynamically interrupted droplet growth in scalar active matter. Phys. Rev. Lett. 2019, 123, 148005. [Google Scholar] [CrossRef]
- Tjhung, E.; Marenduzzo, D.; Cates, M.E. Spontaneous symmetry breaking in active droplets provides a generic route to motility. Proc. Natl. Acad. Sci. USA 2012, 109, 12381–12386. [Google Scholar] [CrossRef]
- Markovich, T.; Tjhung, E.; Cates, M.E. Shear-Induced First-Order Transition in Polar Liquid Crystals. Phys. Rev. Lett. 2019, 122, 088004. [Google Scholar] [CrossRef]
- Paoluzzi, M.; Maggi, C.; Marini Bettolo Marconi, U.; Gnan, N. Critical phenomena in active matter. Phys. Rev. E 2016, 94, 052602. [Google Scholar] [CrossRef]
- Maggi, C.; Gnan, N.; Paoluzzi, M.; Zaccarelli, E.; Crisanti, A. Critical active dynamics is captured by a colored-noise driven field theory. arXiv 2021, arXiv:2108.13971. [Google Scholar]
- Egolf, D.A. Equilibrium regained: From nonequilibrium chaos to statistical mechanics. Science 2000, 287, 101–104. [Google Scholar] [CrossRef] [PubMed]
- Wensink, H.H.; Dunkel, J.; Heidenreich, S.; Drescher, K.; Goldstein, R.E.; Löwen, H.; Yeomans, J.M. Meso-scale turbulence in living fluids. Proc. Natl. Acad. Sci. USA 2012, 109, 14308–14313. [Google Scholar] [CrossRef]
- Dunkel, J.; Heidenreich, S.; Drescher, K.; Wensink, H.H.; Bär, M.; Goldstein, R.E. Fluid Dynamics of Bacterial Turbulence. Phys. Rev. Lett. 2013, 110, 228102. [Google Scholar] [CrossRef] [PubMed]
- MacKintosh, F.C.; Schmidt, C.F. Active cellular materials. Curr. Opin. Cell Biol. 2010, 22, 29–35. [Google Scholar] [CrossRef] [PubMed]
- Howse, J.R.; Jones, R.A.L.; Ryan, A.J.; Gough, T.; Vafabakhsh, R.; Golestanian, R. Self-Motile Colloidal Particles: From Directed Propulsion to Random Walk. Phys. Rev. Lett. 2007, 99, 048102. [Google Scholar] [CrossRef]
- Buttinoni, I.; Bialké, J.; Kümmel, F.; Löwen, H.; Bechinger, C.; Speck, T. Dynamical Clustering and Phase Separation in Suspensions of Self-Propelled Colloidal Particles. Phys. Rev. Lett. 2013, 110, 238301. [Google Scholar] [CrossRef]
- Palacci, J.; Sacanna, S.; Steinberg, A.P.; Pine, D.J.; Chaikin, P.M. Living Crystals of Light-Activated Colloidal Surfers. Science 2013, 339, 936–940. [Google Scholar] [CrossRef]
- Onsager, L. Reciprocal Relations in Irreversible Processes II. Phys. Rev. 1931, 38, 2265. [Google Scholar] [CrossRef]
- Toner, J.; Tu, Y. Long-Range Order in a Two-Dimensional Dynamical XY Model: How Birds Fly Together. Phys. Rev. Lett. 1995, 75, 4326–4329. [Google Scholar] [CrossRef]
- Solon, A.P.; Cates, M.E.; Tailleur, J. Active brownian particles and run-and-tumble particles: A comparative study. Eur. Phys. J. Spec. Top. 2015, 224, 1231–1262. [Google Scholar] [CrossRef]
- Markovich, T.; Lubensky, T.C. Odd Viscosity in Active Matter: Microscopic Origin and 3D Effects. Phys. Rev. Lett. 2021, 127, 048001. [Google Scholar] [CrossRef]
- Fodor, É.; Marchetti, M.C. The statistical physics of active matter: From self-catalytic colloids to living cells. Phys. A 2018, 504, 106–120. [Google Scholar] [CrossRef]
- De Groot, P.M. Non-Equilibrium Thermodynamics; North-Holland Publishing Company: Amsterdam, The Netherlands, 1962. [Google Scholar]
- Ramaswamy, S. Active matter. J. Stat. Mech. 2017, 2017, 054002. [Google Scholar] [CrossRef]
- Dadhichi, L.P.; Maitra, A.; Ramaswamy, S. Origins and diagnostics of the nonequilibrium character of active systems. J. Stat. Mech. 2018, 2018, 123201. [Google Scholar] [CrossRef]
- Kruse, K.; Joanny, J.F.; Jülicher, F.; Prost, J.; Sekimoto, K. Asters, vortices, and rotating spirals in active gels of polar filaments. Phys. Rev. Lett. 2004, 92, 078101. [Google Scholar] [CrossRef]
- Prost, J.; Jülicher, F.; Joanny, J.F. Active gel physics. Nat. Phys. 2015, 11, 111–117. [Google Scholar] [CrossRef]
- Jülicher, F.; Grill, S.W.; Salbreux, G. Hydrodynamic theory of active matter. Rep. Prog. Phys. 2018, 81, 076601. [Google Scholar] [CrossRef]
- Markovich, T.; Tjhung, E.; Cates, M.E. Chiral active matter: Microscopic ‘torque dipoles’ have more than one hydrodynamic description. New J. Phys. 2019, 21, 112001. [Google Scholar] [CrossRef]
- Bialké, J.; Löwen, H.; Speck, T. Microscopic theory for the phase separation of self-propelled repulsive disks. Eur. Lett. 2013, 103, 30008. [Google Scholar] [CrossRef]
- Cates, M.E.; Tailleur, J. When are active Brownian particles and run-and-tumble particles equivalent? Consequences for motility-induced phase separation. Eur. Lett. 2013, 101, 20010. [Google Scholar] [CrossRef]
- Rapp, L.; Bergmann, F.; Zimmermann, W. Systematic extension of the Cahn-Hilliard model for motility-induced phase separation. Eur. Phys. J. E 2019, 42, 57. [Google Scholar] [CrossRef] [PubMed]
- Tailleur, J.; Cates, M.E. Statistical Mechanics of Interacting Run-and-Tumble Bacteria. Phys. Rev. Lett. 2008, 100, 218103. [Google Scholar] [CrossRef] [PubMed]
- Cates, M.E.; Tailleur, J. Motility-Induced Phase Separation. Annu. Rev. Cond. Matter Phys. 2015, 6, 219–244. [Google Scholar] [CrossRef]
- Seara, D.S.; Machta, B.B.; Murrell, M.P. Irreversibility in dynamical phases and transitions. Nat. Commun. 2021, 12, 392. [Google Scholar] [CrossRef] [PubMed]
- Adhikari, R.; Stratford, K.; Cates, M.; Wagner, A. Fluctuating lattice boltzmann. Europhys. Lett. 2005, 71, 473. [Google Scholar] [CrossRef]
- Fürthauer, S.; Strempel, M.; Grill, S.W.; Jülicher, F. Active chiral fluids. Eur. Phys. J. E 2012, 35, 1–13. [Google Scholar] [CrossRef]
- Joanny, J.F.; Prost, J. Active gels as a description of the actin-myosin cytoskeleton. HFSP J. 2009, 3, 94–104. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cates, M.E.; Fodor, É.; Markovich, T.; Nardini, C.; Tjhung, E. Stochastic Hydrodynamics of Complex Fluids: Discretisation and Entropy Production. Entropy 2022, 24, 254. https://doi.org/10.3390/e24020254
Cates ME, Fodor É, Markovich T, Nardini C, Tjhung E. Stochastic Hydrodynamics of Complex Fluids: Discretisation and Entropy Production. Entropy. 2022; 24(2):254. https://doi.org/10.3390/e24020254
Chicago/Turabian StyleCates, Michael E., Étienne Fodor, Tomer Markovich, Cesare Nardini, and Elsen Tjhung. 2022. "Stochastic Hydrodynamics of Complex Fluids: Discretisation and Entropy Production" Entropy 24, no. 2: 254. https://doi.org/10.3390/e24020254
APA StyleCates, M. E., Fodor, É., Markovich, T., Nardini, C., & Tjhung, E. (2022). Stochastic Hydrodynamics of Complex Fluids: Discretisation and Entropy Production. Entropy, 24(2), 254. https://doi.org/10.3390/e24020254





