A Novel MAGDM Method Based on Hesitant Picture Fuzzy Schweizer–Sklar Maclaurin Symmetric Mean Operators and Their Application
Abstract
1. Introduction
2. Preliminaries
2.1. Picture Fuzzy Set and Hesitant Picture Fuzzy Set
- If , then ;
- If , thenif , then ;if , then
2.2. Schweizer–Sklar t-Norm and t-Conorm
- ;
- ;
- ;
- ;
- ;
- ;
2.3. Maclaurin Symmetric Mean
3. The Hesitant Picture Fuzzy Schweizer–Sklar Maclaurin Symmetric Mean Operators
3.1. The Hesitant Picture Fuzzy Schweizer–Sklar Maclaurin Symmetric Mean (HPFSSMSM) Operator
- Case 1.
- If , the HPFSSMSM is reduced to the hesitant picture fuzzy MSM (HPFMSM) operator.
- Case 2.
- If k = 1, based on the definition of HPFSSMSM, we haveIn this case, the HPFSSMSM reduces to the hesitant picture fuzzy Schweizer–Sklar averaging (HPFSSA) operator. If , the HPFSSMSM operator is reduced to hesitant picture fuzzy averaging operator.
- Case 3.
- If k = 2, based on the definition of HPFSSMSM, we haveIn this case, the HPFSSMSM reduces to the hesitant picture fuzzy Schweizer–Sklar Bonferroni mean (HPFSSBM) operator. If , the HPFSSMSM operator is reduced to the hesitant picture fuzzy Bonferroni mean operator.
- Case 4.
- If k = 3, based on the definition of HPFSSMSM, we haveIn this case, the HFPSSMSM reduces to the hesitant picture fuzzy Schweizer–Sklar generalized Bonferroni mean (HFPSSGBM) operator. If , the HPFSSMSM operator is reduced to hesitant picture fuzzy generalized Bonferroni mean operator.
- Case 5.
- If k = n, based on the definition of HPFSSMSM, we haveIn this case, the HPFSSMSM reduces to the hesitant picture fuzzy Schweizer–Sklar geometric (HPFSSG) operator. If , the HPFSSMSM operator is reduced to the hesitant picture fuzzy geometric operator.From the above analysis, we can further discuss the monotonicity of the HPFSSMSM operator with respect to the parameter k. First, we introduce two lemmas which are used in the following discussion.
3.2. The Hesitant Picture Fuzzy Schweizer–Sklar-Weighted Maclaurin Symmetric Mean (HPFSSWMSM) Operator
3.3. The Hesitant Picture Fuzzy Schweizer–Sklar Weighted Maclaurin Symmetric Mean (HPFSSWMSM) Operator
- Case 1.
- If , the HPFSSDMSM operator is reduced to hesitant picture fuzzy DMSM operator.
- Case 2.
- If k = 1, based on the definition of HPFSSDMSM, we haveIn this case, the HPFSSDMSM reduces to the hesitant picture fuzzy Schweizer–Sklar geometric averaging (HPFSSGA) operator. If , the HPFSSMSM operator is reduced to hesitant picture fuzzy geometric averaging operator.
- Case 3.
- If k = 2, based on the definition of HPFSSDMSM, we haveIn this case, the HPFSSDMSM reduces to the hesitant picture fuzzy Schweizer–Sklar geometric Bonferroni mean (HPFSSGBM) operator. If , the HPFSSMSM operator is reduced to hesitant picture fuzzy geometric Bonferroni mean operator.
- Case 4.
- If k = 3, based on the definition of HPFSSDMSM, we haveIn this case, the HFPSSDMSM reduces to the hesitant picture fuzzy Schweizer–Sklar generalized geometric Bonferroni mean (HFPSSGGBM) operator. If , the HPFSSMSM operator is reduced to hesitant picture fuzzy generalized Bonferroni mean operator.
- Case 5.
- If k = n, based on the definition of HPFSSDMSM, we haveIn this case, the HPFSSDMSM reduces to the hesitant picture fuzzy Schweizer–Sklar averaging (HPFSSA) operator. If , the HPFSSMSM operator is reduced to hesitant picture fuzzy averaging operator.
3.4. The Hesitant Picture Fuzzy Schweizer–Sklar-Weighted Dual Maclaurin Symmetric Mean (HPFSSWDMSM) Operator
4. A Novel Approach to MAGDM Based on the Proposed Operators
5. The Application of the Proposed Method to Enterprise Informatization Level Evaluation
5.1. Enterprise Informatization Level Evaluation Process with HPFSSWMSM Operator
- Step 1.
- According to the case description, all attributes are classified as positive and therefore no need to be normalized.
- Step 2.
- We know that the parameter variable (PV) k plays an important role in considering the interrelationship among the input arguments. As for the DMs in this example are independent among each other, it is appropriate to take k = 1 as the value of PV. Then, the HPFSSWMSM operator reduces to the weighted form of Equation (47), that is, hesitant picture fuzzy Schweizer–Sklar-weighted averaging (HPFSSWA) operator:Compute the overall comprehensive assessments of alternatives with respect to . According to Equation (47) (suppose that ), we can obtain the comprehensive evaluations, which is shown in Appendix A (Comprehensive matrix of subsection 5.1).
- Step 3.
- Compute the global evaluation values with the proposed HPFSSWMSM operator (suppose that ) and the scores of alternatives with Definition 3, we can deriveAccording to the scores of alternatives, the ranking order is . Therefore, is the best alternative.
5.2. Enterprise Informatization Level Evaluation Process with HPFSSWDMSM Operator
- Step 1.
- The step 1 of decision-making process with HPFSSWDMSM operator is same as the above.
- Step 2.
- For the same reason as the above, we assign k = 1 to the HPFSSWDMSM operator, which can make it reduce to the weighted form of Equation (48), that is, hesitant picture fuzzy Schweizer–Sklar-weighed geometric (HPFSSWG) operator:Compute the overall comprehensive assessments of alternatives with respect to . According to Equation (48) (suppose that ), then we can obtain the comprehensive evaluations, which is shown in Appendix A (Comprehensive matrix of subsection 5.2).
- Step 3.
- Compute the global evaluation values with the proposed HPFSSWDMSM operator (suppose that ) and the scores of alternatives with Definition 3, we can deriveAccording to the scores of alternatives, the ranking order is . Therefore, is the best alternative.
5.3. Parameter Analysis
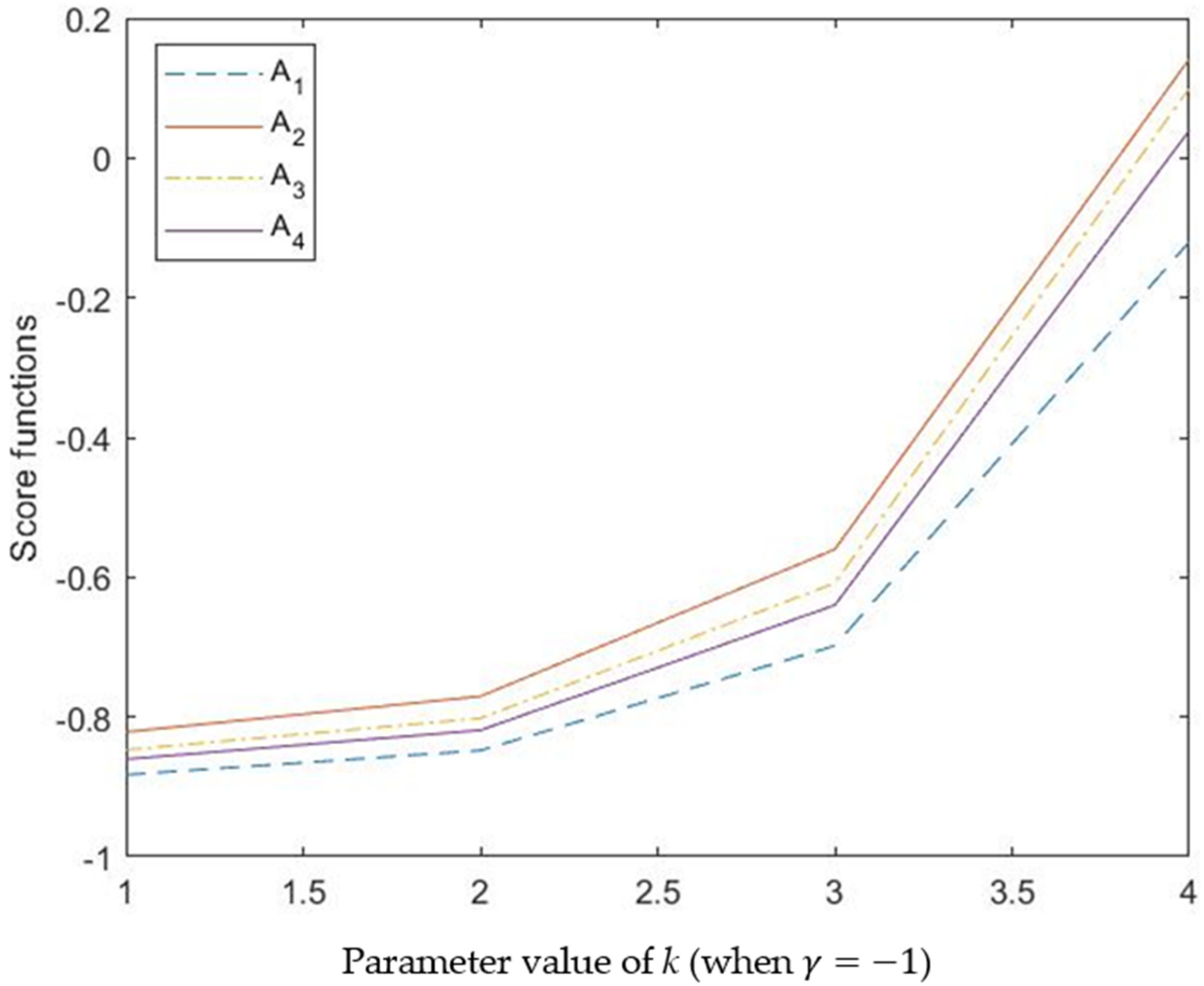
5.3.1. The Influence of k
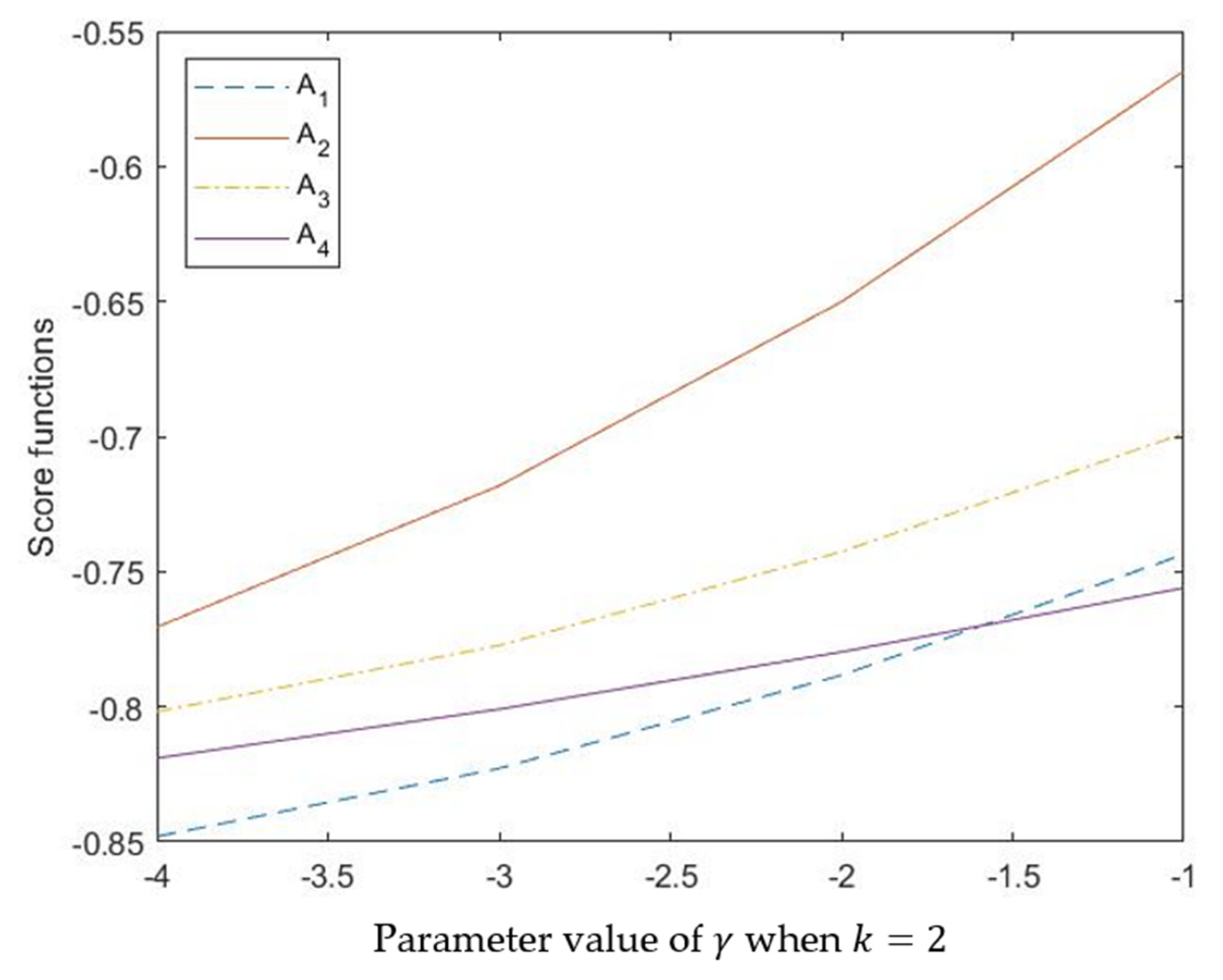
5.3.2. The Influence of γ
5.4. Validity Analysis
5.5. Comparative Analysis
- Compared with Wei’s [38] method, our proposed method is more generic and flexible. Wei’s method is based on the PFWA operator, which consists of the Pythagorean fuzzy sets and basically the most traditional weighted average operator. Both the information expression method and the information aggregation method of Wei’s [38] basic operator is only suitable for simple and independent general fuzzy decision-making problems. The information aggregation method is based on the premise that the input variables are independent of each other. This harsh assumption severely limits the scope of application of this method. In real-life decision-making problems, it is common that the evaluation criteria are interdependent and are related to each other. Therefore, our method with the MSM operator as the information fusion operator has much stronger practical application value. Because of that, by assigning different values to the PV k, our method can handle several kinds of situations with complex relationships.
- Compared with Wang et al.’s [39] method, our proposed method can be employed in a wider range. Wang et al.’s [39] method is based on the PFS just as Wei’s [38] method, and it allows the square sum of the PMD and the NEMD to be no larger than one, which is a strict condition for DMs to spend time and energy to confirm their evaluations. The proposed method gives DMs the greatest tolerance, allowing them to provide several possible values of their uncertain information with nothing to worry about. On the other hand, Wang et al.’s [39] method is based on the traditional operational rules of ATT, while our method is based on the new operational rules of SSTT, which is more flexible and can take the risk preference of DMs into consideration by the parameter γ.
- Compared with Wang and Liu’s [33] method, our proposed method provides DMs more freedom when they feel hesitant or uncertain among several evaluation values and thus more adaptive at coping with the MAGDM problems with a high degree of complexity and more friendly to the qualitative problems that rely on the subjective decision making of DMs. These advantages are due to the fact that the information expression module of our method is based on the hesitant picture fuzzy set, whose elements are constructed with a PMD, an NLMD, and an NEMD, with which the HPFEs are able to tolerate the ambiguity of DMs’ assessments to the greatest extent.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Schinckus, C. The Santa fe institute and econophysics: A possible genealogy? Found. Sci. 2021, 26, 925–945. [Google Scholar] [CrossRef]
- Schinckus, C. 1996–2016: Two decades of econophysics: Between methodological diversification and conceptual coherence. Eur. Phys. J.-Spec. Top. 2016, 225, 3299–3311. [Google Scholar] [CrossRef][Green Version]
- Jovanovic, F.; Mantegna, R.N.; Schinckus, C. When financial economics influences physics: The role of Econophysics. Int. Rev. Financ. Anal. 2019, 65, 101378. [Google Scholar] [CrossRef]
- Gandotra, N.; Kizielewicz, B.; Anand, A.; Bączkiewicz, A.; Shekhovtsov, A.; Wątróbski, J.; Rezaei, A.; Sałabun, W. New Pythagorean entropy measure with application in multi-criteria decision analysis. Entropy 2021, 23, 1600. [Google Scholar] [CrossRef]
- Kou, Y.; Feng, X.; Wang, J. A novel q-rung dual hesitant fuzzy multi-attribute decision-making method based on entropy weights. Entropy 2021, 23, 1322. [Google Scholar] [CrossRef]
- Alizadeh, R.; Soltanisehat, L.; Lund, P.D.; Zamanisabzi, H. Improving renewable energy policy planning and decision-making through a hybrid MCDM method. Energy Policy 2020, 137, 111174. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–356. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Set Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Yager, R.R. Pythagorean membership grades in multicriteria decision making. IEEE Trans. Fuzzy Syst. 2014, 22, 958–965. [Google Scholar] [CrossRef]
- Li, D.F.; Wang, Y.C.; Liu, S.; Shan, F. Fractional programming methodology for multi-attribute group decision-making using IFS. Appl. Soft Comput. 2009, 9, 219–225. [Google Scholar] [CrossRef]
- Lang, G.; Miao, D.; Fujita, H. Three-way group conflict analysis based on Pythagorean fuzzy set theory. IEEE Trans. Fuzzy Syst. 2019, 28, 447–461. [Google Scholar] [CrossRef]
- Cuong, B. Picture fuzzy sets-first results. Part 1. In Neuro-Fuzzy Systems with Applications; Institute of Mathematics: Hanoi, Vietnam, 2013. [Google Scholar]
- Singh, P. Correlation coefficients for picture fuzzy sets. J. Intell. Fuzzy Syst. 2014, 27, 2857–2868. [Google Scholar] [CrossRef]
- Son, L. DPFCM: A novel distributed picture fuzzy clustering method on picture fuzzy sets. Expert Syst. Appl. 2015, 2, 51–66. [Google Scholar] [CrossRef]
- Son, L.H. Generalized picture distance measure and applications to picture fuzzy clustering. Appl. Soft Comput. 2016, 46, 284–295. [Google Scholar] [CrossRef]
- Luo, M.; Zhang, Y. A new similarity measure between picture fuzzy sets and its application. Eng. Appl. Artif. Intel. 2020, 96, 103956. [Google Scholar] [CrossRef]
- Ullah, K. Picture fuzzy Maclaurin symmetric mean operators and their applications in solving multi-attribute decision-making problems. Math. Probl. Eng. 2021, 2021, 1098631. [Google Scholar] [CrossRef]
- Liu, P.; Zhang, X. A novel picture fuzzy linguistic aggregation operator and its application to group decision-making. Cogn. Comput. 2018, 10, 242–259. [Google Scholar] [CrossRef]
- Torra, V. Hesitant fuzzy sets. Int. J. Intell. Syst. 2010, 25, 529–539. [Google Scholar] [CrossRef]
- Peng, J.J.; Wang, J.Q.; Wu, X.H.; Tian, C. Hesitant intuitionistic fuzzy aggregation operators based on the Archimedean t-norms and t-conorms. Int. J. Fuzzy Syst. 2017, 19, 702–714. [Google Scholar] [CrossRef]
- Yang, W.; Wang, C.; Liu, Y.; Sun, Y. Hesitant Pythagorean fuzzy interaction aggregation operators and their application in multiple attribute decision-making. Complex Intell. Syst. 2019, 5, 199–216. [Google Scholar] [CrossRef]
- Merigo, J.M. A unified model between the weighted average and the induced OWA operator. Expert Syst. Appl. 2011, 38, 11560–11572. [Google Scholar] [CrossRef]
- Liu, F.; Zhang, W.G.; Zhang, L.H. A group decision making model based on a generalized ordered weighted geometric average operator with interval preference matrices. Fuzzy Set. Syst. 2014, 246, 1–18. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, R.; Huang, H.; Wang, J. Some picture fuzzy Dombi Heronian mean operators with their application to multi-attribute decision-making. Symmetry 2018, 10, 593. [Google Scholar] [CrossRef]
- Liu, P.; Li, H. Multiple attribute decision-making method based on some normal neutrosophic Bonferroni mean operators. Neural Comput. Appl. 2017, 28, 179–194. [Google Scholar] [CrossRef]
- Maclaurin, C. A second letter to Martin Folkes, Esq.; concerning the roots of equations, with demonstration of other rules of algebra. Philos Trans. Roy. Soc. Lond. Ser. A 1729, 36, 59–96. [Google Scholar]
- Wei, G.; Lu, M. Pythagorean fuzzy Maclaurin symmetric mean operators in multiple attribute decision making. Int. J. Intell. Syst. 2018, 33, 1043–1070. [Google Scholar] [CrossRef]
- Xia, M.M.; Xu, Z.S.; Zhu, B. Some issues on intuitionistic fuzzy aggregation operators based on Archimedean t-conorm and t-norm. Knowl.-Based Syst. 2012, 31, 78–88. [Google Scholar] [CrossRef]
- Liu, P.D.; Li, Y.H.; Chen, Y.B. Some generalized einstein aggregation operators based on the interval-valued intuitionistic fuzzy numbers and their application to group decision making. Sci. Iran 2015, 22, 2684–2701. [Google Scholar]
- Liu, P.D.; Liu, J.L.; Chen, S.M. Some intuitionistic fuzzy Dombi Bonferroni mean operators and their application to multi-attribute group decision making. J. Oper. Res. Soc. 2018, 69, 1–24. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, P.D.; Wang, Y.M. Multiple attribute group decision making methods based on intuitionistic fuzzy frank power aggregation operators. J. Intell. Fuzzy Syst. 2015, 29, 2235–2246. [Google Scholar] [CrossRef]
- Liu, P.D. Some Hamacher aggregation operators based on the interval-valued intuitionistic fuzzy numbers and their application to group decision making. IEEE Trans. Fuzzy Syst. 2014, 22, 83–97. [Google Scholar] [CrossRef]
- Wand, P.; Liu, P. Some Maclaurin symmetric mean aggregation operators based on Schweizer-Sklar operations for intuitionistic fuzzy numbers and their application to decision making. J. Intell Fuzzy Syst. 2019, 36, 3801–3824. [Google Scholar]
- Khan, Q.; Gwak, J.; Shahzad, M.; Alam, M.K. A novel approached based on T-spherical fuzzy Schweizer-Sklar power Heronian mean operator for evaluating water reuse applications under uncertainty. Sustainability 2021, 13, 7108. [Google Scholar] [CrossRef]
- Qin, J.D.; Liu, X.W. Approaches to uncertain linguistic multiple attribute decision making based on dual Maclaurin symmetric mean. J. Intell Fuzzy Syst. 2015, 29, 171–186. [Google Scholar] [CrossRef]
- Xu, Z.S. On consistency of the weighted geometric mean complex judgement matrix in AHP. Eur. J. Oper. Res. 2000, 126, 683–687. [Google Scholar] [CrossRef]
- Biswas, A.; Deb, N. Pythagorean fuzzy Schweizer and Sklar power aggregation operators for solving multi-attribute decision-making problems. Granul. Comput. 2021, 6, 991–1007. [Google Scholar] [CrossRef]
- Wei, G. Picture fuzzy aggregation operators and their application to multiple attribute decision making. J. Intell Fuzzy Syst. 2017, 33, 713–724. [Google Scholar] [CrossRef]
- Wang, R.; Wang, J.; Gao, H.; Wei, G. Methods for MADM with picture fuzzy muirhead mean operators and their application for evaluating the financial investment risk. Symmetry 2019, 11, 6. [Google Scholar] [CrossRef]
| G1 | G2 | G3 | G4 | |
|---|---|---|---|---|
| A1 | ||||
| A2 | ||||
| A3 | ||||
| A4 |
| Tab | G1 | G2 | G3 | G4 |
|---|---|---|---|---|
| A1 | ||||
| A2 | ||||
| A3 | ||||
| A4 |
| G1 | G2 | G3 | G4 | |
|---|---|---|---|---|
| A1 | ||||
| A2 | ||||
| A3 | ||||
| A4 |
| k | Ranking Orders | |
|---|---|---|
| k = 1 | , , , | |
| k = 2 | , , , | |
| k = 3 | , , , | |
| k = 4 | , , , |
| 𝛾 | Ranking Orders | |
|---|---|---|
| 𝛾 = −1 | , , , | |
| 𝛾 = −2 | , , , | |
| 𝛾 = −3 | , , , | |
| 𝛾 = −4 | , , , |
| Methods | Ranking Orders | |
|---|---|---|
| Wang and Liu’s [33] method based on IFSSWMSM operator | , , , , | |
| Biswas and Deb’s [37] method based on PFSSPWA operator | ||
| G1 | G2 | G3 | G4 | |
|---|---|---|---|---|
| A1 | ||||
| A2 | ||||
| A3 | ||||
| A4 | ||||
| A5 |
| G1 | G2 | G3 | G4 | |
|---|---|---|---|---|
| A1 | ||||
| A2 | ||||
| A3 | ||||
| A4 | ||||
| A5 |
| Methods | Ranking Orders | |
|---|---|---|
| Wei’s [38] method based on PFWA operator | ||
| Wang et al.’s [39] method based on PFWMM operator | ||
| Wang and Liu’ [33] method based on IFSSWMSM operator | ||
| G1 | G2 | G3 | G4 | |
|---|---|---|---|---|
| A1 | ||||
| A2 | ||||
| A3 | ||||
| A4 | ||||
| A5 |
| Capture Relationship among Attributes | Deal with Evaluation Information with Several Elements in MD and NMD | Based on a Flexible Operational Rule | Capture Neutral Membership Degree | |
|---|---|---|---|---|
| Wang and Liu’s [33] method | Yes | No | No | No |
| Wei’s [38] method | No | No | No | Yes |
| Wang et al.’s [39] method | Yes | No | No | Yes |
| The proposed method | Yes | Yes | Yes | Yes |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, T.; Ye, L. A Novel MAGDM Method Based on Hesitant Picture Fuzzy Schweizer–Sklar Maclaurin Symmetric Mean Operators and Their Application. Entropy 2022, 24, 238. https://doi.org/10.3390/e24020238
Chen T, Ye L. A Novel MAGDM Method Based on Hesitant Picture Fuzzy Schweizer–Sklar Maclaurin Symmetric Mean Operators and Their Application. Entropy. 2022; 24(2):238. https://doi.org/10.3390/e24020238
Chicago/Turabian StyleChen, Tiedong, and Long Ye. 2022. "A Novel MAGDM Method Based on Hesitant Picture Fuzzy Schweizer–Sklar Maclaurin Symmetric Mean Operators and Their Application" Entropy 24, no. 2: 238. https://doi.org/10.3390/e24020238
APA StyleChen, T., & Ye, L. (2022). A Novel MAGDM Method Based on Hesitant Picture Fuzzy Schweizer–Sklar Maclaurin Symmetric Mean Operators and Their Application. Entropy, 24(2), 238. https://doi.org/10.3390/e24020238





