Recurrence-Based Synchronization Analysis of Weakly Coupled Bursting Neurons under External ELF Fields
Abstract
1. Introduction
2. Model
2.1. Morris–Lecar Neuron Model under an Extremely Low Frequency Electric Field
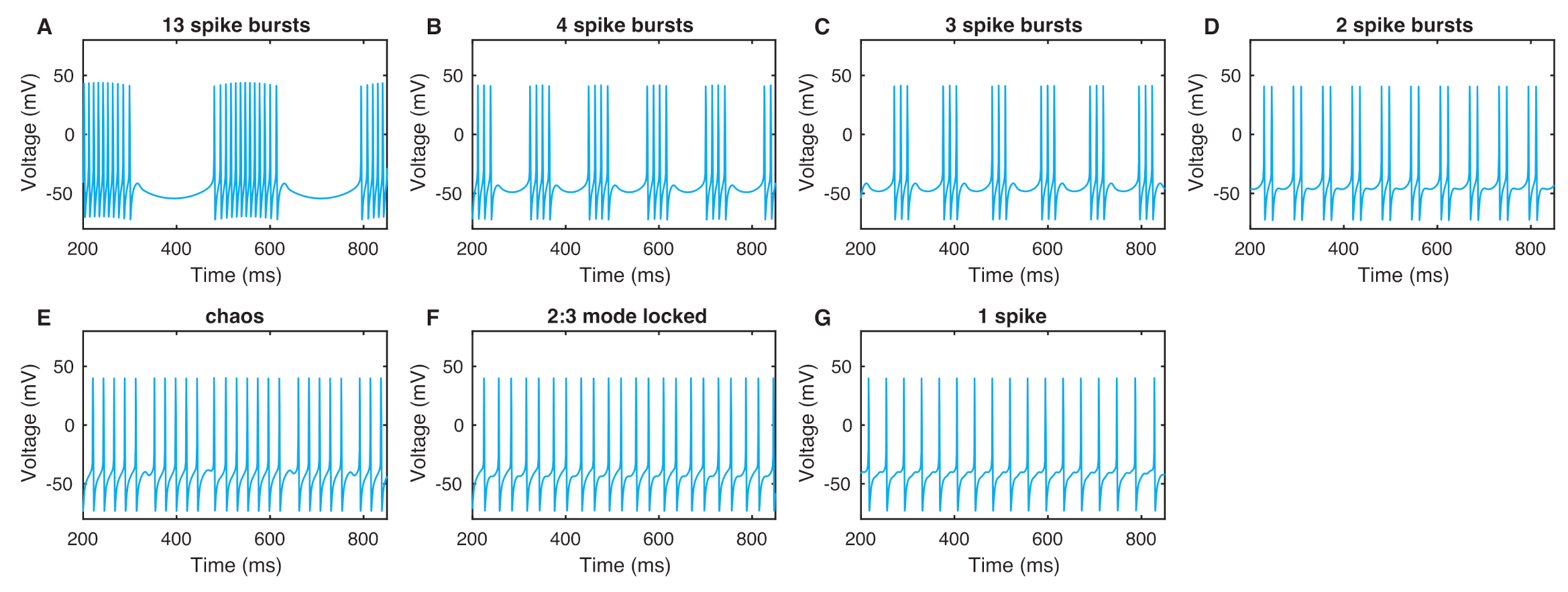
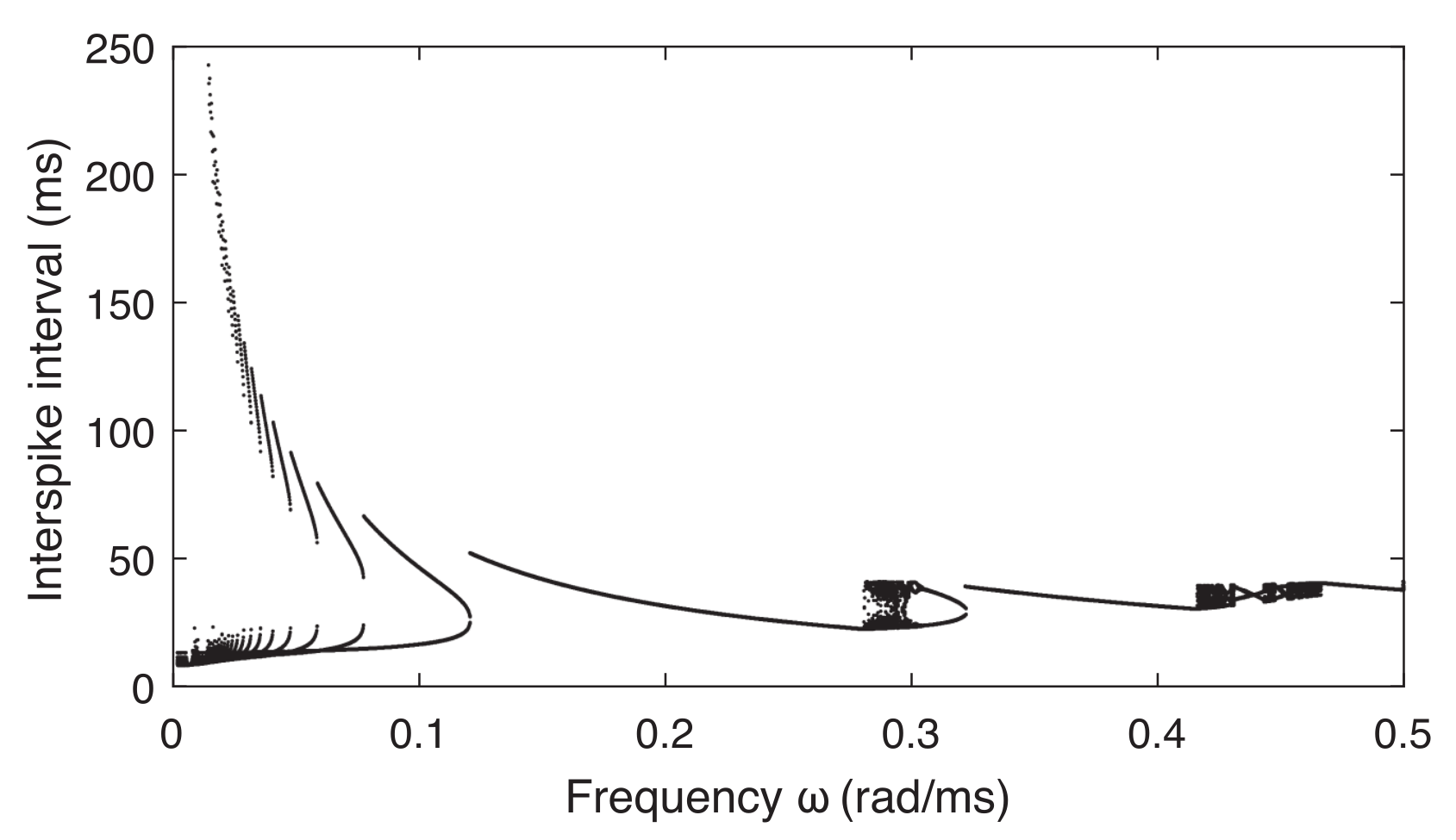
2.2. Bursting Patterns of a Neuron
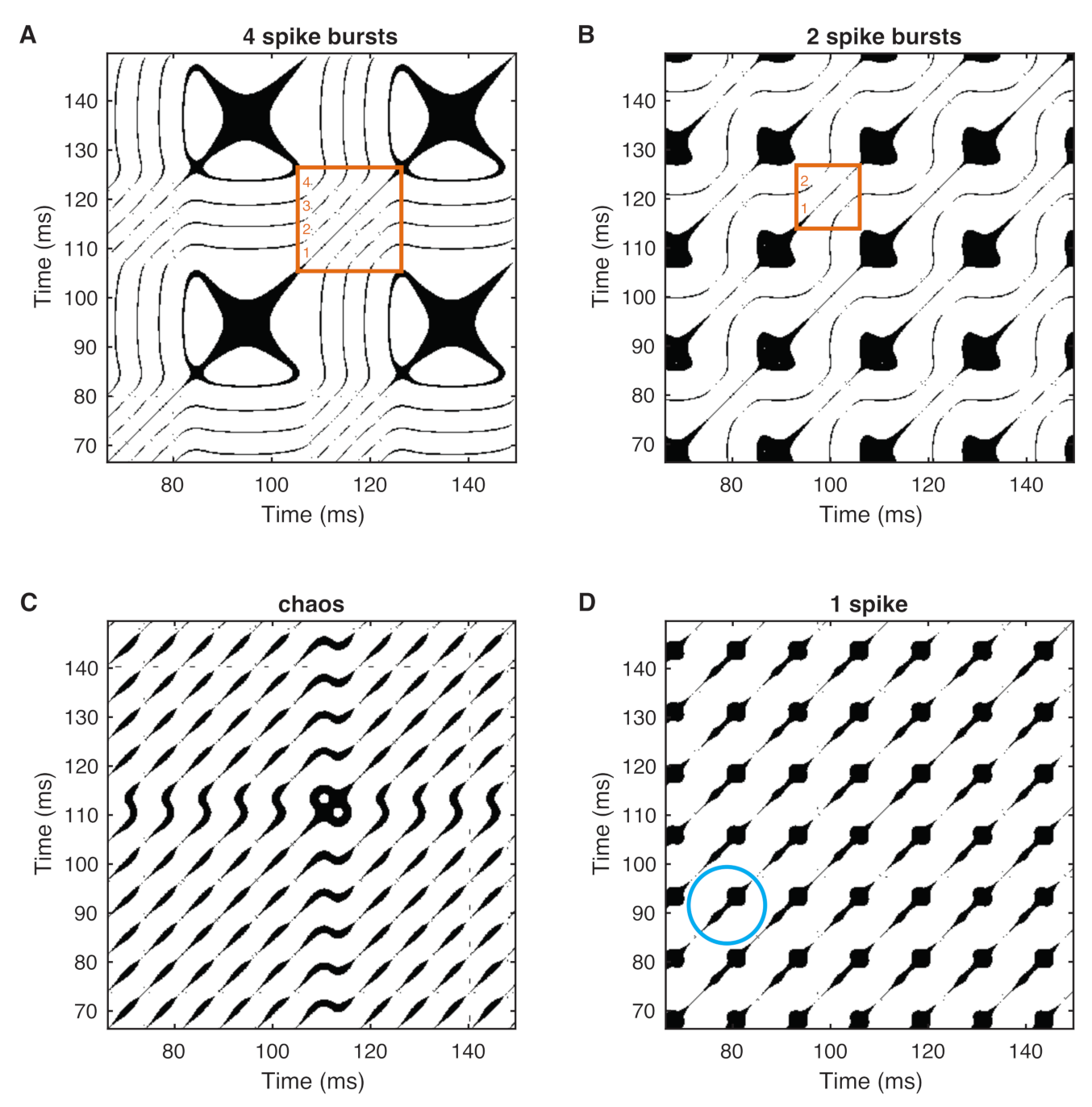
3. Recurrence Quantification Analysis (RQA)
4. Coupling of Two Bursting Neurons
4.1. Model and Numerical Simulation
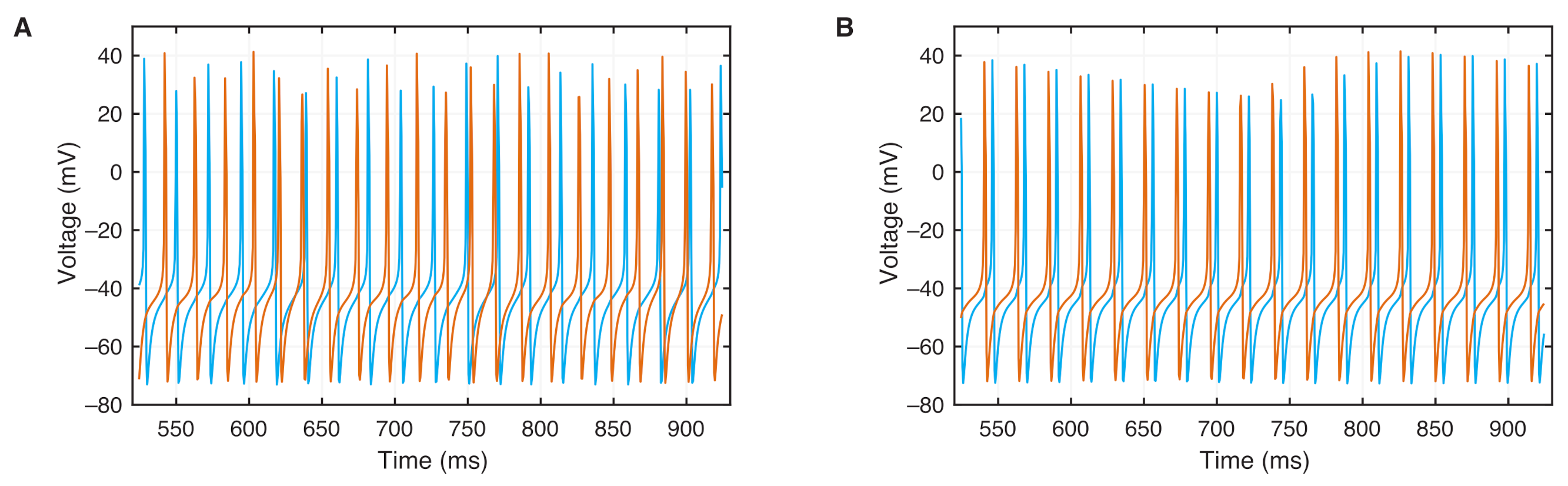
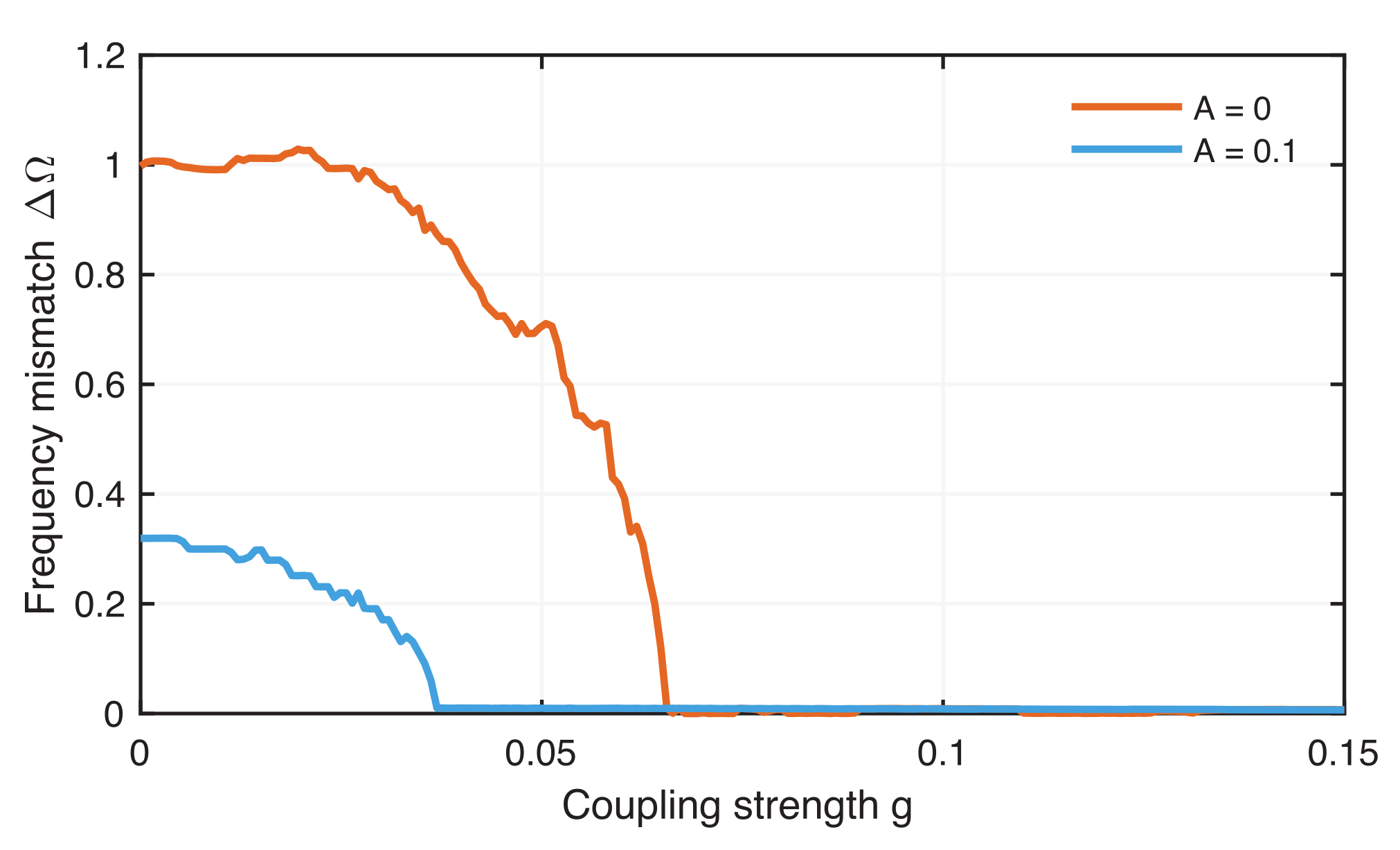
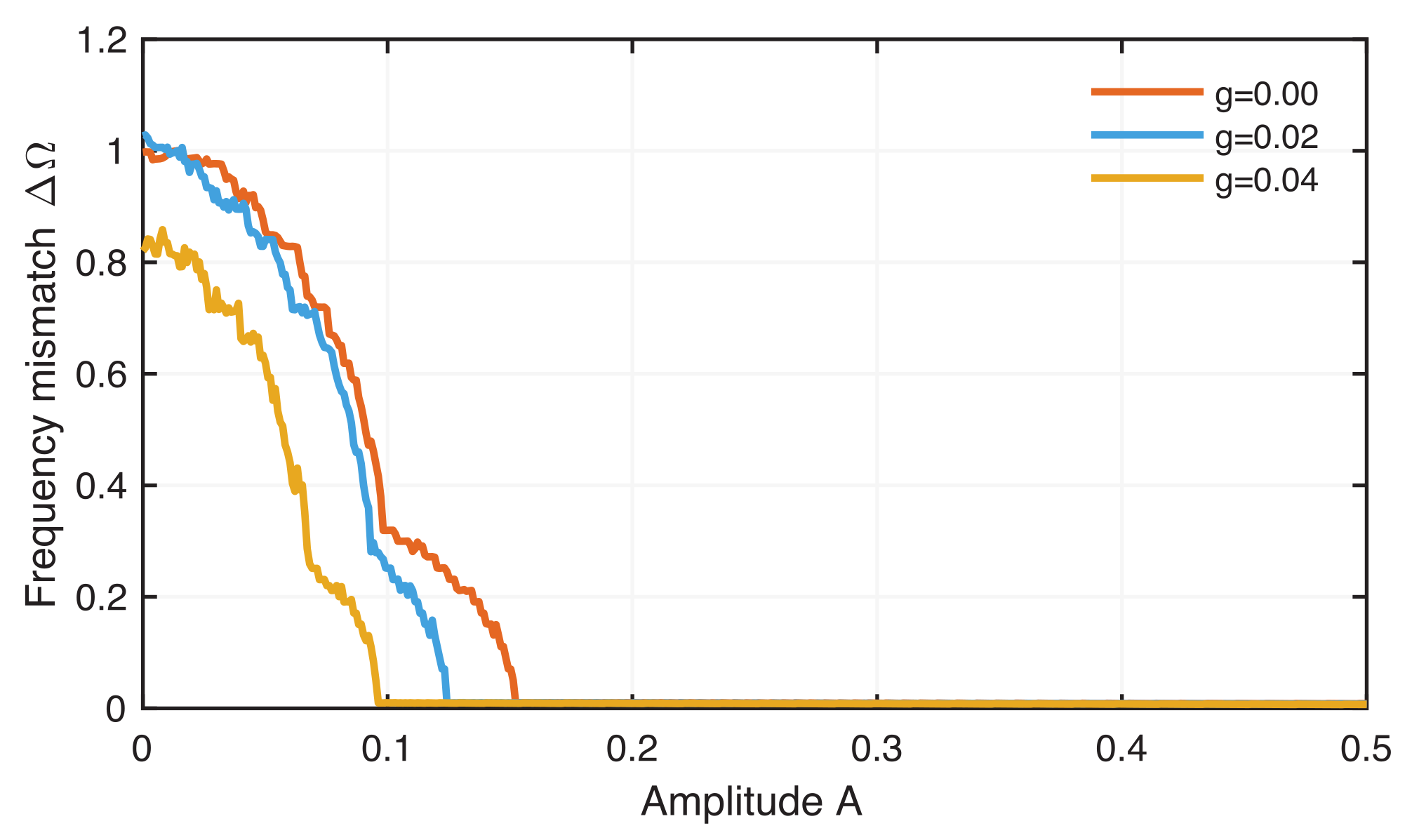
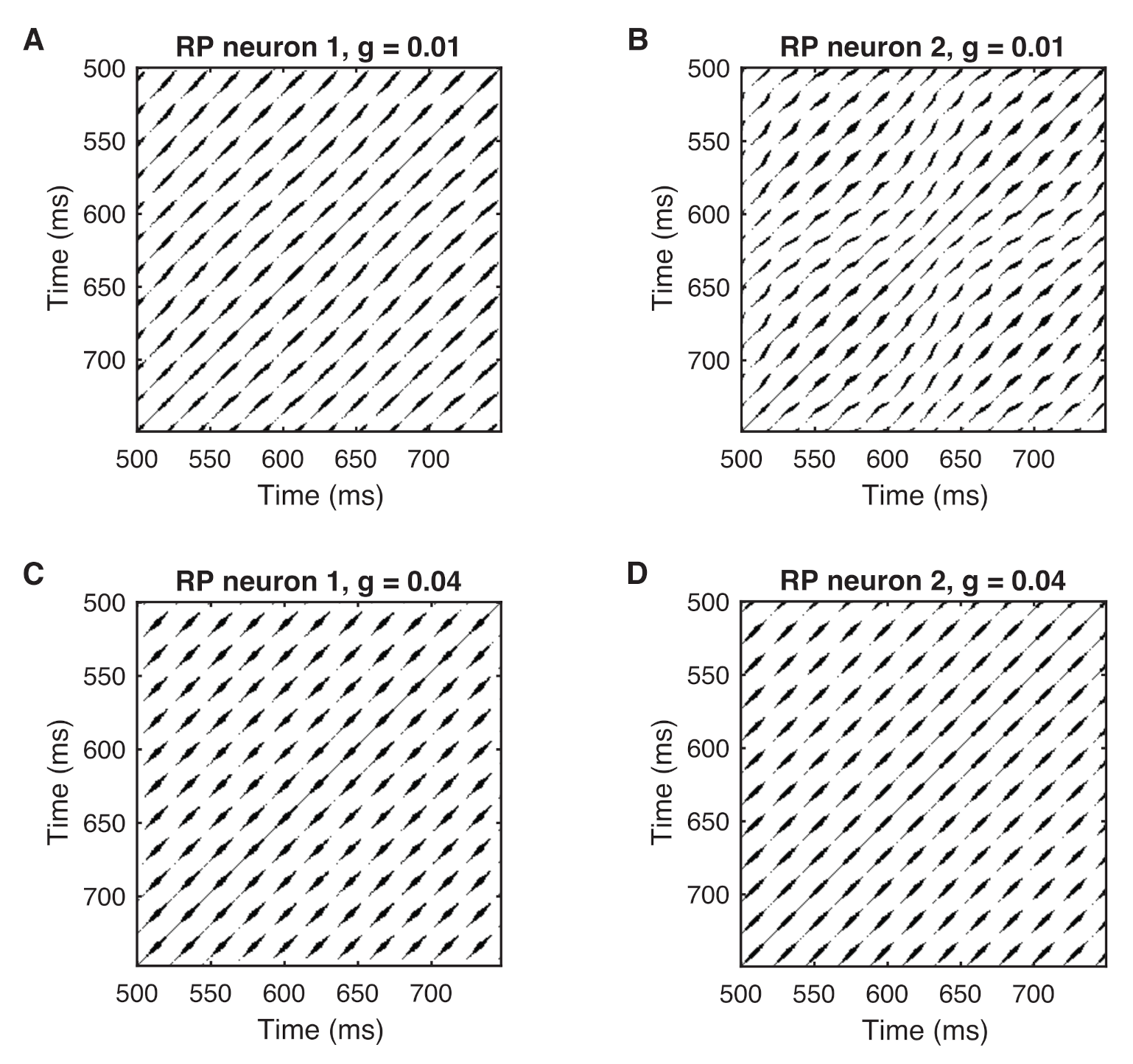
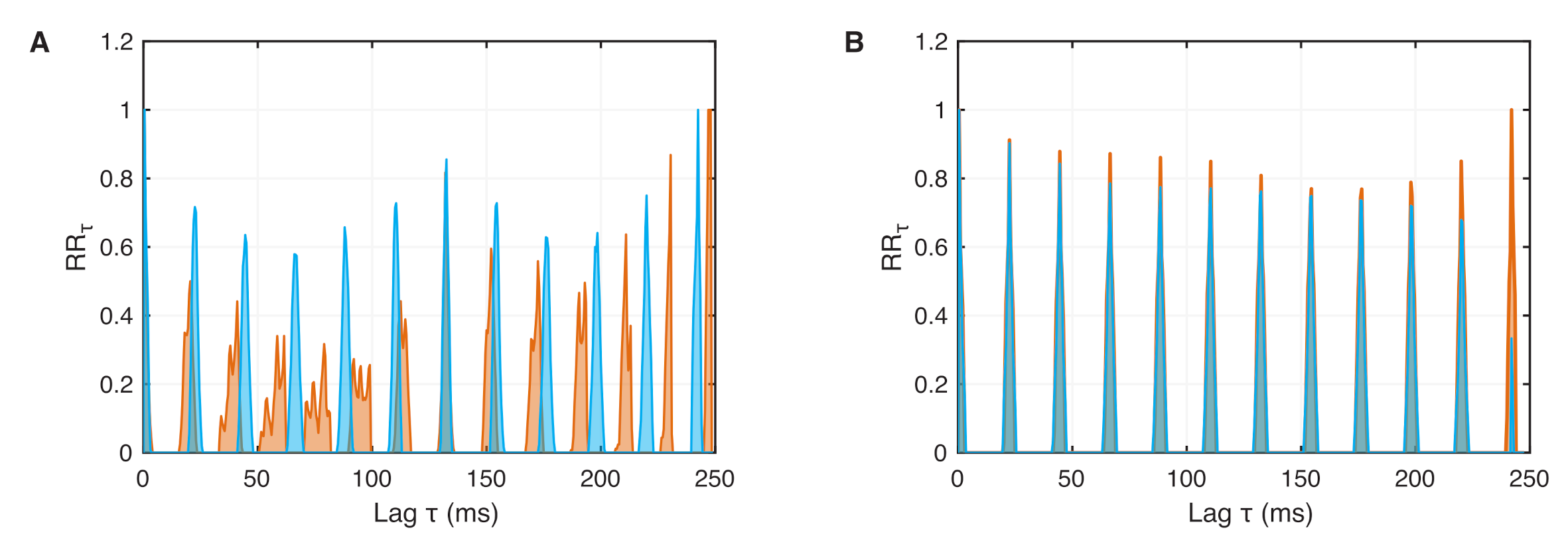
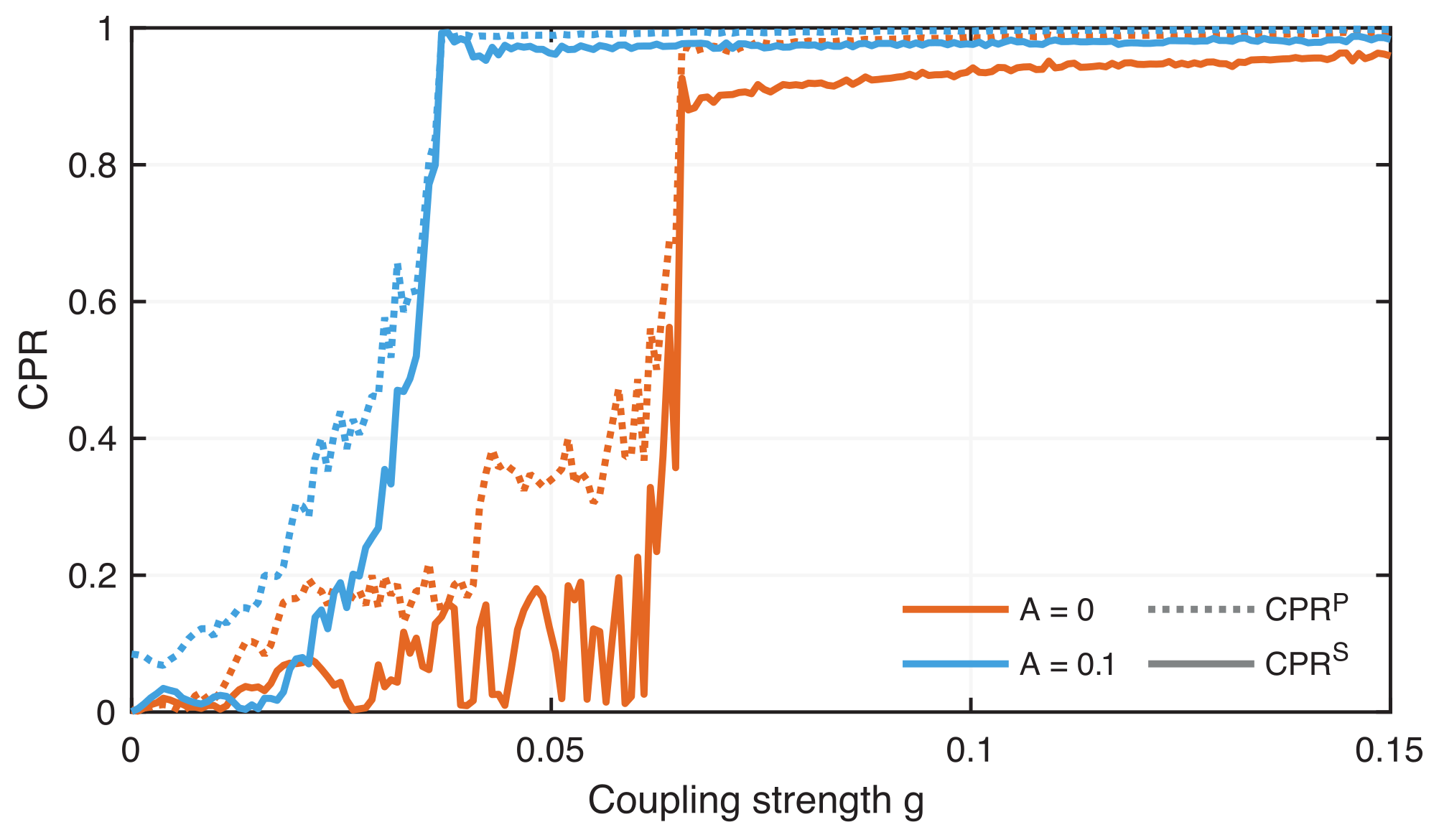
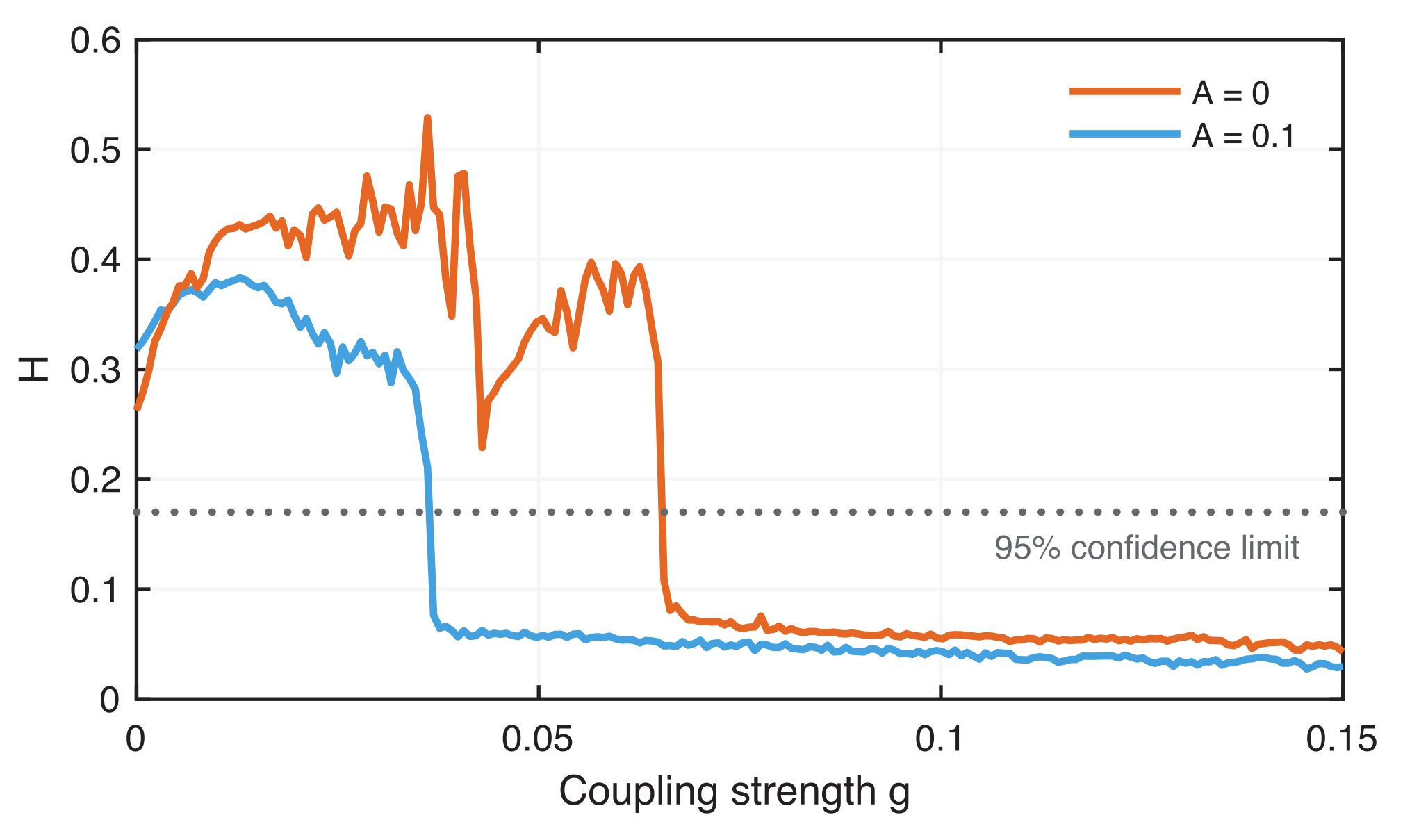
4.2. Phase Synchronization Analysis Using Recurrence Features
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CPR | correlation of probability of recurrence |
| EF | electric field |
| ELF | extremely low frequency |
| HH | Hodgkin–Huxley model |
| ML | Morris–Lecar model |
| RP | recurrence plot |
| RQA | recurrence quantification analysis |
| RR | recurrence rate |
References
- Adrian, E.D. The Mechanism of Nervous Action, Electrical Studies of the Neurone; University of Pennsylvania Press: Philadelphia, PA, USA, 1932. [Google Scholar]
- Huang, K.; Li, Y.; Yang, C.; Gu, M. The dynamic principle of interaction between weak electromagnetic fields and living system–Interference of electromagnetic waves in dynamic metabolism. Chin. J. Med. Phys. 1996, 14, 205–207. [Google Scholar]
- Reato, D.; Rahman, A.; Bikson, M.; Parra, L.C. Low-Intensity Electrical Stimulation Affects Network Dynamics by Modulating Population Rate and Spike Timing. J. Neurosci. 2010, 30, 15067–15079. [Google Scholar] [CrossRef]
- Opitz, A.; Falchier, A.; Yan, C.G.; Yeagle, E.M.; Linn, G.S.; Megevand, P.; Thielscher, A.; Deborah, A.R.; Milham, M.P.; Mehta, A.D.; et al. Spatiotemporal structure of intracranial electric fields induced by transcranial electric stimulation in humans and nonhuman primates. Sci. Rep. 2016, 6, 31236. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, A.A.; Lafon, B.; Friedman, D.; Dayan, M.; Wang, X.; Bikson, M.; Doyle, W.K.; Devinsky, O.; Parra, L.C. Measurements and models of electric fields in the in vivo human brain during transcranial electric stimulation. eLife 2017, 6, e18834. [Google Scholar] [CrossRef]
- Savitz, D.A.; Loomis, D.P.; Tse, C.K.J. Electrical occupations and neurodegenerative disease: Analysis of US mortality data. Arch. Environ. Health Int. J. 1998, 53, 71–74. [Google Scholar] [CrossRef]
- Johansen, C. Exposure to electromagnetic fields and risk of central nervous system disease in utility workers. Epidemiology 2000, 11, 539–543. [Google Scholar] [CrossRef]
- Radman, T.; Su, Y.; An, J.H.; Parra, L.C.; Bikson, M. Spike timing amplifies the effect of electric fields on neurons: Implications for endogenous field effects. J. Neurosci. 2007, 27, 3030–3036. [Google Scholar] [CrossRef]
- Nkomidio, A.M.; Woafo, P. Effects of imperfection of ionic channels and exposure to electromagnetic fields on the generation and propagation of front waves in nervous fibre. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 2350–2360. [Google Scholar] [CrossRef]
- Eichwald, C.; Kaiser, F. Model for external influences on cellular signal transduction pathways including cytosolic calcium oscillations. Bioelectromagnetics 1995, 16, 75–85. [Google Scholar] [CrossRef]
- Huang, C.; Xu, B.; Lin, J. Effects of extremely low frequency magnetic fields on hormone-induced cytosolic calcium oscillations. Shengwu Wuli Xuebao 1998, 15, 543–546. [Google Scholar]
- Wertheimer, N.; Leeper, E. Electrical wiring configurations and childhood cancer. Am. J. Epidemiol. 1979, 109, 273–284. [Google Scholar] [CrossRef] [PubMed]
- Moulder, J.E. Power-frequency fields and cancer. Crit. Rev. Biomed. Eng. 1998, 26, 1–116. [Google Scholar] [CrossRef] [PubMed]
- Stuchly, M.A.; Dawson, T.W. Interaction of low-frequency electric and magnetic fields with the human body. Proc. IEEE 2000, 88, 643–664. [Google Scholar] [CrossRef]
- Pikovsky, A.; Rosenblum, M.; Kurths, J. Synchronization—A Universal Concept in Nonlinear Sciences; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Golomb, D.; Rinzel, J. Clustering in globally coupled inhibitory neurons. Phys. D Nonlinear Phenom. 1994, 72, 259–282. [Google Scholar] [CrossRef]
- Dayan, P.; Abbott, L. Theoretical Neuroscience: Computational and Mathematical Modeling of Neural Systems; MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Gray, C.M.; König, P.; Engel, A.K.; Singer, W. Oscillatory responses in cat visual cortex exhibit inter-columnar synchronization which reflects global stimulus properties. Nature 1989, 338, 334–337. [Google Scholar] [CrossRef]
- Morris, C.; Lecar, H. Voltage oscillations in the barnacle giant muscle fiber. Biophys. J. 1981, 35, 193. [Google Scholar] [CrossRef]
- Rinzel, J.; Ermentrout, G.B. Analysis of Neural Excitability and Oscillations. In Methods in Neuronal Modeling; Koch, C., Segev, I., Eds.; MIT Press: Cambridge, MA, USA, 1989; pp. 251–291. [Google Scholar]
- Kitajima, H.; Kurths, J. Forced synchronization in Morris–Lecar neurons. Int. J. Bifurc. Chaos 2007, 17, 3523–3528. [Google Scholar] [CrossRef]
- Hoppensteadt, F.C.; Izhikevich, E.M. Weakly Connected Neural Networks; Springer: New York, NY, USA, 1997. [Google Scholar]
- Hoppensteadt, F.C.; Izhikevich, E.M. Synaptic organizations and dynamical properties of weakly connected neural oscillators II. Learning phase information. Biol. Cybern. 1996, 75, 129–135. [Google Scholar] [CrossRef]
- Izhikevich, E.M. Synchronization of elliptic bursters. Siam Rev. 2001, 43, 315–344. [Google Scholar] [CrossRef]
- Gutfreund, Y.; Yarom, Y.; Segev, I. Subthreshold oscillations and resonant frequency in guinea-pig cortical neurons: Physiology and modelling. J. Physiol. 1995, 483, 621–640. [Google Scholar] [CrossRef]
- Hutcheon, B.; Miura, R.M.; Puil, E. Subthreshold membrane resonance in neocortical neurons. J. Neurophysiol. 1996, 76, 683–697. [Google Scholar] [CrossRef] [PubMed]
- Hu, H.; Vervaeke, K.; Storm, J.F. Two forms of electrical resonance at theta frequencies, generated by M-current, h-current and persistent Na + current in rat hippocampal pyramidal cells. J. Physiol. 2002, 545, 783–805. [Google Scholar] [CrossRef] [PubMed]
- Giocomo, L.M.; Zilli, E.A.; Fransén, E.; Hasselmo, M.E. Temporal Frequency of Subthreshold Oscillations Scales with Entorhinal Grid Cell Field Spacing. Science 2007, 315, 1719–1722. [Google Scholar] [CrossRef] [PubMed]
- Vera, J.; Pezzoli, M.; Pereira, U.; Bacigalupo, J.; Sanhueza, M. Electrical Resonance in the θ Frequency Range in Olfactory Amygdala Neurons. PLoS ONE 2014, 9, e85826. [Google Scholar] [CrossRef]
- Fischer, L.; Leibold, C.; Felmy, F. Resonance Properties in Auditory Brainstem Neurons. Front. Cell. Neurosci. 2018, 12, 8. [Google Scholar] [CrossRef]
- Bennett, M.V.; Zukin, R. Electrical Coupling and Neuronal Synchronization in the Mammalian Brain. Neuron 2004, 41, 495–511. [Google Scholar] [CrossRef]
- Dong, A.; Liu, S.; Li, Y. Gap Junctions in the Nervous System: Probing Functional Connections Using New Imaging Approaches. Front. Cell. Neurosci. 2018, 12, 320. [Google Scholar] [CrossRef]
- Sabatini, B.L.; Regehr, W.G. Timing of neurotransmission at fast synapses in the mammalian brain. Nature 1996, 384, 170–172. [Google Scholar] [CrossRef]
- Romano, M.C.; Thiel, M.; Kurths, J.; Kiss, I.Z.; Hudson, J.L. Detection of synchronization for non-phase-coherent and non-stationary data. Europhys. Lett. 2005, 71, 466–472. [Google Scholar] [CrossRef]
- Marwan, N.; Romano, M.C.; Thiel, M.; Kurths, J. Recurrence Plots for the Analysis of Complex Systems. Phys. Rep. 2007, 438, 237–329. [Google Scholar] [CrossRef]
- Marwan, N. A Historical Review of Recurrence Plots. Eur. Phys. J. Spec. Top. 2008, 164, 3–12. [Google Scholar] [CrossRef]
- Babloyantz, A. Evidence for slow brain waves: A dynamical approach. Electroencephalogr. Clin. Neurophysiol. 1991, 78, 402–405. [Google Scholar] [CrossRef]
- Song, I.H.; Lee, D.S.; Kim, S.I. Recurrence quantification analysis of sleep electoencephalogram in sleep apnea syndrome in humans. Neurosci. Lett. 2004, 366, 148–153. [Google Scholar] [CrossRef]
- Bergner, A.; Romano, M.C.; Kurths, J.; Thiel, M. Synchronization analysis of neuronal networks by means of recurrence plots. In Lectures in Supercomputational Neurosciences; Beim Graben, P., Zhou, C., Thiel, M., Kurths, J., Eds.; Understanding Complex Systems; Springer: Berlin/ Heidelberg, Germany, 2008; pp. 177–191. [Google Scholar] [CrossRef]
- Ouyang, G.; Li, X.; Dang, C.; Richards, D.A. Using recurrence plot for determinism analysis of EEG recordings in genetic absence epilepsy rats. Clin. Neurophysiol. 2008, 119, 1747–1755. [Google Scholar] [CrossRef] [PubMed]
- Budzinski, R.C.; Boaretto, B.R.R.; Prado, T.L.; Lopes, S.R. Phase synchronization and intermittent behavior in healthy and Alzheimer-affected human-brain-based neural network. Phys. Rev. 2019, 99, 022402. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez-Sabate, C.; Rodriguez, M.; Morales, I. Studying the functional connectivity of the primary motor cortex with the binarized cross recurrence plot: The influence of Parkinson’s disease. PLoS ONE 2021, 16, e0252565. [Google Scholar] [CrossRef] [PubMed]
- Mendonça, P.R.F.; Vargas-Caballero, M.; Erdélyi, F.; Szabó, G.; Paulsen, O.; Robinson, H.P.C. Stochastic and deterministic dynamics of intrinsically irregular firing in cortical inhibitory interneurons. eLife 2016, 5, e16475. [Google Scholar] [CrossRef] [PubMed]
- Boaretto, B.R.R.; Budzinski, R.C.; Prado, T.L.; Kurths, J.; Lopes, S.R. Neuron dynamics variability and anomalous phase synchronization of neural networks. Chaos 2018, 28, 106304. [Google Scholar] [CrossRef]
- Tibau, E.; Soriano, J. Analysis of spontaneous activity in neuronal cultures through recurrence plots: Impact of varying connectivity. Eur. Phys. J. Spec. Top. 2018, 227, 999–1014. [Google Scholar] [CrossRef]
- Marwan, N.; Thiel, M.; Nowaczyk, N.R. Cross Recurrence Plot Based Synchronization of Time Series. Nonlinear Process. Geophys. 2002, 9, 325–331. [Google Scholar] [CrossRef]
- Hirata, Y.; Aihara, K. Identifying hidden common causes from bivariate time series: A method using recurrence plots. Phys. Rev. E 2010, 81, 016203. [Google Scholar] [CrossRef] [PubMed]
- Astakhov, S.V.; Dvorak, A.; Anishchenko, V.S. Influence of chaotic synchronization on mixing in the phase space of interacting systems. Chaos 2013, 23, 013103. [Google Scholar] [CrossRef] [PubMed]
- Konvalinka, I.; Xygalatas, D.; Bulbulia, J.; Schjodt, U.; Jegindø, E.M.; Wallot, S.; Van Orden, G.C.; Roepstorff, A. Synchronized arousal between performers and related spectators in a fire-walking ritual. Proc. Natl. Acad. Sci. USA 2011, 108, 8514–8519. [Google Scholar] [CrossRef] [PubMed]
- Goswami, B.; Ambika, G.; Marwan, N.; Kurths, J. On interrelations of recurrences and connectivity trends between stock indices. Physica A 2012, 391, 4364–4376. [Google Scholar] [CrossRef]
- Ramos, A.M.T.; Builes-Jaramillo, A.; Poveda, G.; Goswami, B.; Macau, E.E.N.; Kurths, J.; Marwan, N. Recurrence measure of conditional dependence and applications. Phys. Rev. E 2017, 95, 052206. [Google Scholar] [CrossRef]
- Hobbs, B.; Ord, A. Nonlinear dynamical analysis of GNSS data: Quantification, precursors and synchronisation. Prog. Earth Planet. Sci. 2018, 5, 36. [Google Scholar] [CrossRef]
- Godavarthi, V.; Pawar, S.A.; Unni, V.R.; Sujith, R.I.; Marwan, N.; Kurths, J. Coupled interaction between unsteady flame dynamics and acoustic field in a turbulent combustor. Chaos 2018, 28, 113111. [Google Scholar] [CrossRef]
- Schinkel, S.; Zamora-López, G.; Dimigen, O.; Sommer, W.; Kurths, J. Functional network analysis reveals differences in the semantic priming task. J. Neurosci. Methods 2011, 197, 333–339. [Google Scholar] [CrossRef]
- Rangaprakash, D. Connectivity analysis of multichannel EEG signals using recurrence based phase synchronization technique. Comput. Biol. Med. 2014, 46, 11–21. [Google Scholar] [CrossRef]
- Izhikevich, E.M. Neural exciability, spiking and bursting. Int. J. Bifurc. Chaos 2000, 10, 1171–1266. [Google Scholar] [CrossRef]
- Prescott, S.A.; De Koninck, Y.; Sejnowski, T.J. Biophysical basis for three distinct dynamical mechanisms of action potential initiation. PLoS Comput. Biol. 2008, 4, e1000198. [Google Scholar] [CrossRef] [PubMed]
- Orr, D.; Ermentrout, B. Synchronization of oscillators via active media. Phys. Rev. E 2019, 99, 052218. [Google Scholar] [CrossRef] [PubMed]
- Attwell, D. Interaction of low frequency electric fields with the nervous system: The retina as a model system. Radiat. Prot. Dosim. 2003, 106, 341–348. [Google Scholar] [CrossRef] [PubMed]
- Bédard, C.; Kröger, H.; Destexhe, A. Model of low-pass filtering of local field potentials in brain tissue. Phys. Rev. E 2006, 73, 051911. [Google Scholar] [CrossRef] [PubMed]
- Modolo, J.; Thomas, A.; Stodilka, R.; Prato, F.; Legros, A. Modulation of neuronal activity with extremely low-frequency magnetic fields: Insights from biophysical modeling. In Proceedings of the IEEE Fifth International Conference on Bio-Inspired Computing: Theories and Applications (BIC-TA 2010), Changsha, China, 23–26 September 2010. [Google Scholar]
- Yi, G.S.; Wang, J.; Han, C.X.; Deng, B.; Wei, X.L. Spiking patterns of a minimal neuron to ELF sinusoidal electric field. Appl. Math. Model. 2012, 36, 3673–3684. [Google Scholar] [CrossRef]
- Eckmann, J.P.; Oliffson Kamphorst, S.; Ruelle, D. Recurrence Plots of Dynamical Systems. Europhys. Lett. 1987, 4, 973–977. [Google Scholar] [CrossRef]
- Matassini, L.; Kantz, H.; Hołyst, J.A.; Hegger, R. Optimizing of recurrence plots for noise reduction. Phys. Rev. E 2002, 65, 021102. [Google Scholar] [CrossRef]
- Marwan, N. How to avoid potential pitfalls in recurrence plot based data analysis. Int. J. Bifurc. Chaos 2011, 21, 1003–1017. [Google Scholar] [CrossRef]
- beim Graben, P.; Hutt, A. Detecting Recurrence Domains of Dynamical Systems by Symbolic Dynamics. Phys. Rev. Lett. 2013, 110, 154101. [Google Scholar] [CrossRef]
- Vega, I.; Schütte, C.; Conrad, T.O.F. Finding metastable states in real-world time series with recurrence networks. Phys. A 2016, 445, 1–17. [Google Scholar] [CrossRef][Green Version]
- Kraemer, K.H.; Donner, R.V.; Heitzig, J.; Marwan, N. Recurrence threshold selection for obtaining robust recurrence characteristics in different embedding dimensions. Chaos 2018, 28, 085720. [Google Scholar] [CrossRef] [PubMed]
- Andreadis, I.; Fragkou, A.; Karakasidis, T. On a topological criterion to select a recurrence threshold. Chaos 2020, 30, 013124. [Google Scholar] [CrossRef] [PubMed]
- Kraemer, K.H.; Datseris, G.; Kurths, J.; Kiss, I.Z.; Ocampo-Espindola, J.L.; Marwan, N. A unified and automated approach to attractor reconstruction. New J. Phys. 2021, 23, 033017. [Google Scholar] [CrossRef]
- Kasthuri, P.; Pavithran, I.; Krishnan, A.; Pawar, S.A.; Sujith, R.I.; Gejji, R.; Anderson, W.; Marwan, N.; Kurths, J. Recurrence analysis of slow–fast systems. Chaos 2020, 30, 063152. [Google Scholar] [CrossRef]
- Zbilut, J.P.; Webber, C.L., Jr. Embeddings and delays as derived from quantification of recurrence plots. Phys. Lett. A 1992, 171, 199–203. [Google Scholar] [CrossRef]
- Ivanchenko, M.V.; Osipov, G.V.; Shalfeev, V.D.; Kurths, J. Phase synchronization in ensembles of bursting oscillators. Phys. Rev. Lett. 2004, 93, 134101. [Google Scholar] [CrossRef]
- Rosenblum, M.G.; Pikovsky, A.S.; Kurths, J. Phase synchronization of chaotic oscillators. Phys. Rev. Lett. 1996, 76, 1804. [Google Scholar] [CrossRef]
- Theiler, J. Spurious dimension from correlation algorithms applied to limited time-series data. Phys. Rev. A 1986, 34, 2427–2432. [Google Scholar] [CrossRef]
- Amari, S. Information Geometry and Its Applications; Springer: Tokyo, Japan, 2016; Volume 194. [Google Scholar] [CrossRef]
- Pollard, D. Densities and derivatives. In A User’s Guide to Measure Theoretic Probability; Cambridge University Press: Cambridge, UK, 2001; pp. 53–76. [Google Scholar] [CrossRef]

| mV | 20 mS/cm | 50 mV | 0.15 | ||||
|---|---|---|---|---|---|---|---|
| 18 mV | 20 mS/cm | mV | c | 2 | |||
| mV | 2 mS/cm | mV | mV | ||||
| 10 mV |
| Time Series | Dimension | Delay |
|---|---|---|
| 4 spike burst ( rad/ms) | 3 | 17, 22 |
| 2 spike burst ( rad/ms) | 2 | 16, 20 |
| chaos ( rad/ms) | 2 | 20 |
| 1 spike ( rad/ms | 2 | 19 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nkomidio, A.M.; Ngamga, E.K.; Nbendjo, B.R.N.; Kurths, J.; Marwan, N. Recurrence-Based Synchronization Analysis of Weakly Coupled Bursting Neurons under External ELF Fields. Entropy 2022, 24, 235. https://doi.org/10.3390/e24020235
Nkomidio AM, Ngamga EK, Nbendjo BRN, Kurths J, Marwan N. Recurrence-Based Synchronization Analysis of Weakly Coupled Bursting Neurons under External ELF Fields. Entropy. 2022; 24(2):235. https://doi.org/10.3390/e24020235
Chicago/Turabian StyleNkomidio, Aissatou Mboussi, Eulalie Ketchamen Ngamga, Blaise Romeo Nana Nbendjo, Jürgen Kurths, and Norbert Marwan. 2022. "Recurrence-Based Synchronization Analysis of Weakly Coupled Bursting Neurons under External ELF Fields" Entropy 24, no. 2: 235. https://doi.org/10.3390/e24020235
APA StyleNkomidio, A. M., Ngamga, E. K., Nbendjo, B. R. N., Kurths, J., & Marwan, N. (2022). Recurrence-Based Synchronization Analysis of Weakly Coupled Bursting Neurons under External ELF Fields. Entropy, 24(2), 235. https://doi.org/10.3390/e24020235







