Speeding up Training of Linear Predictors for Multi-Antenna Frequency-Selective Channels via Meta-Learning
Abstract
1. Introduction
1.1. Context and Prior Art
1.2. Contributions
- We develop efficient predictors for single-antenna frequency-flat channels based on transfer/meta-learned quadratic regularization. Transfer and meta-learning are used to leverage data from multiple frames in order to extract shared useful knowledge that can be used for prediction on the current frame (see Figure 2).
- Targeting multi-antenna frequency-selective channels, we introduce the LSTD-based model class of linear predictors that builds on the well-known disaggregation of standard channel models into long-term space-time signatures and fading amplitudes [5,41,42,43,44]. Accordingly, the channel is described by multipath features, such as angle of arrivals, delays, and path loss, that change slowly across the frame, as well as by fast-varying fading amplitudes. Transfer learning and meta-learning algorithms for LSTD-based prediction models are proposed that build on equilibrium propagation (EP) and alternating least squares (ALS).
- Numerical results under the 3GPP 5G standard channel model demonstrate the impact of transfer and meta-learning on reducing the number of pilots for channel prediction, as well as the merits of the proposed LSTD parametrization.
1.3. Organization
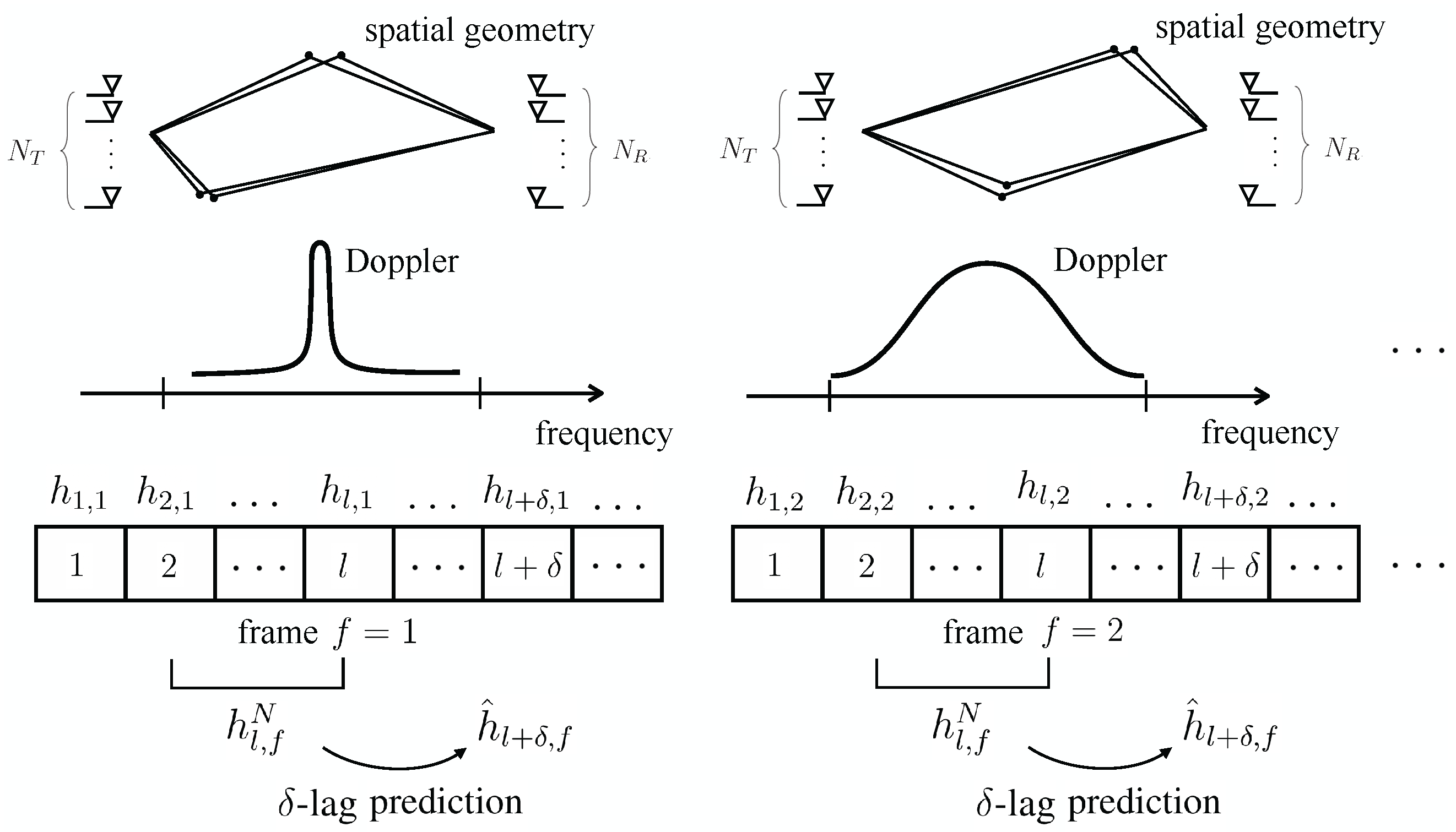
2. System Model
2.1. System Model
2.2. Channel Model
2.3. Conventional Learning
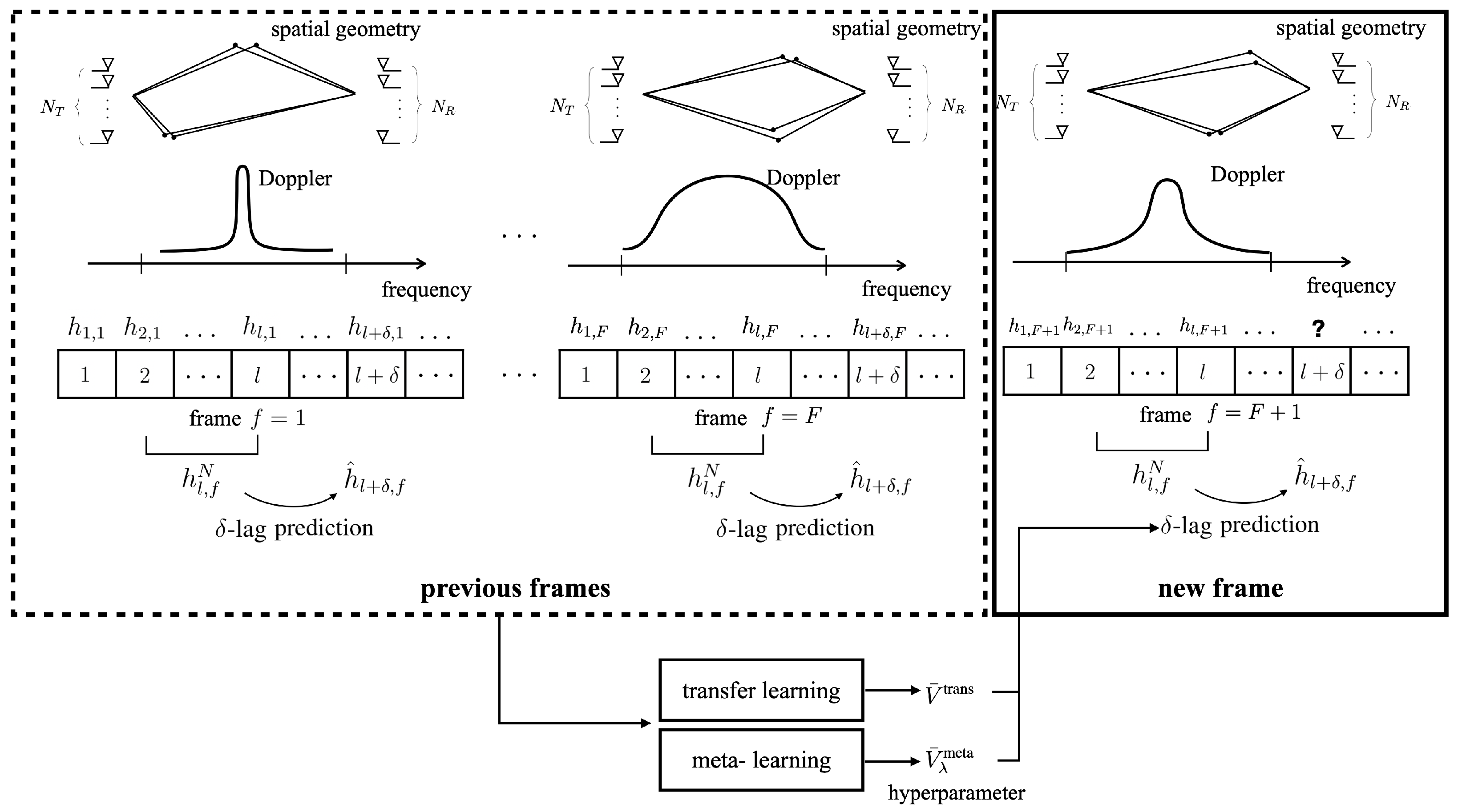
2.4. Transfer Learning and Meta-Learning
2.5. Incorporating Estimation Noise
3. Single-Antenna Frequency-Flat Channels
3.1. Conventional Learning
3.2. Transfer Learning
3.3. Meta-Learning
4. Multi-Antenna Frequency-Selective Channels
4.1. Naïve Extension
4.2. LSTD Channel Model
4.3. LSTD-Based Prediction Model
4.4. Conventional Learning for LSTD-Based Prediction
| Algorithm 1: LSTD-based conventional learning for channel prediction for |
 |
4.5. Transfer Learning for LSTD-Based Prediction
| Algorithm 2: LSTD-based transfer-learning for channel prediction for |
 |
4.6. Meta-Learning for LSTD-Based Prediction
| Algorithm 3: LSTD-based meta-learning for channel prediction for |
 |
4.7. Rank-Estimation for LSTD-Based Prediction
5. Experiments
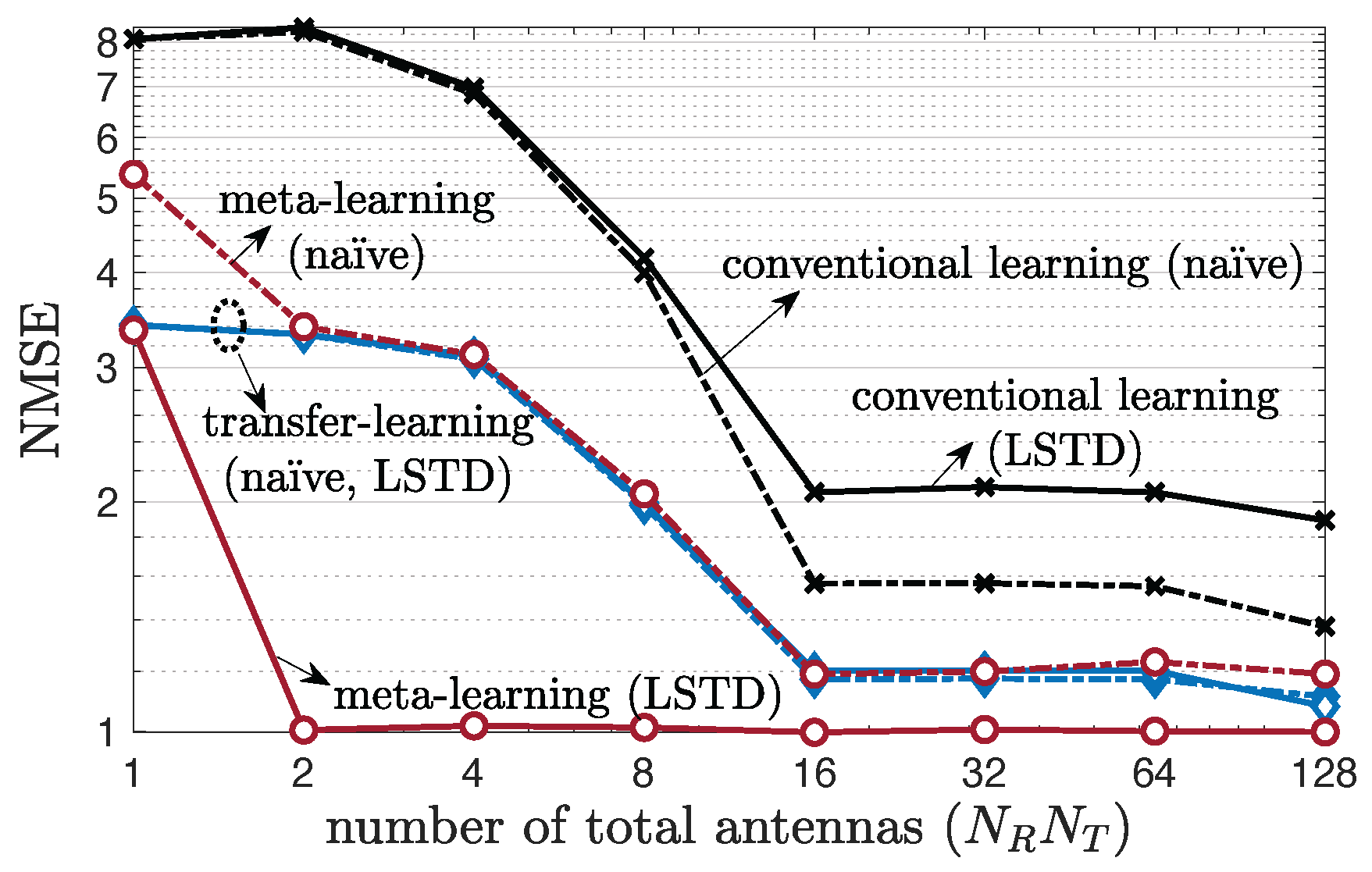
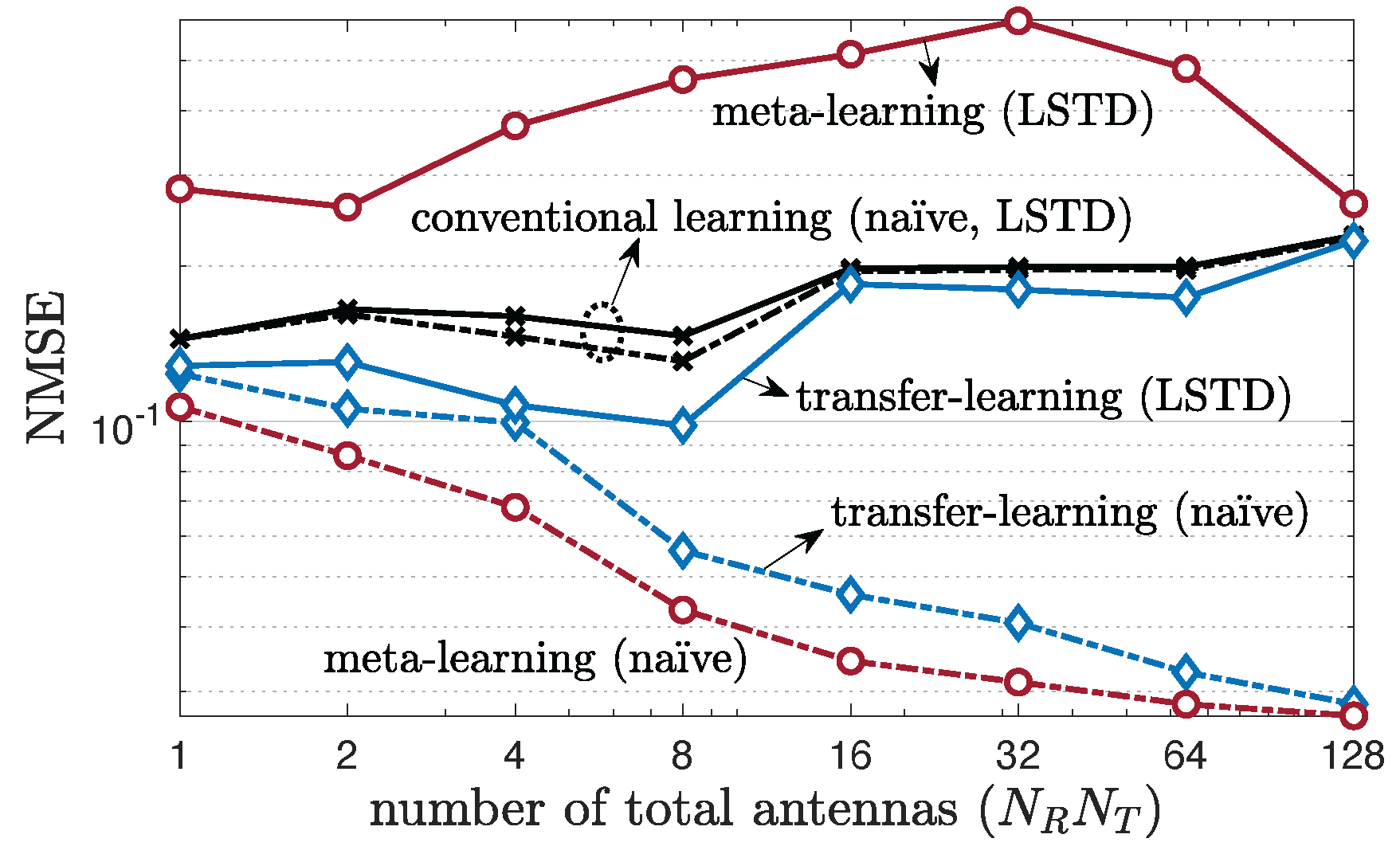
5.1. Multi-Antenna Frequency-Flat Channels
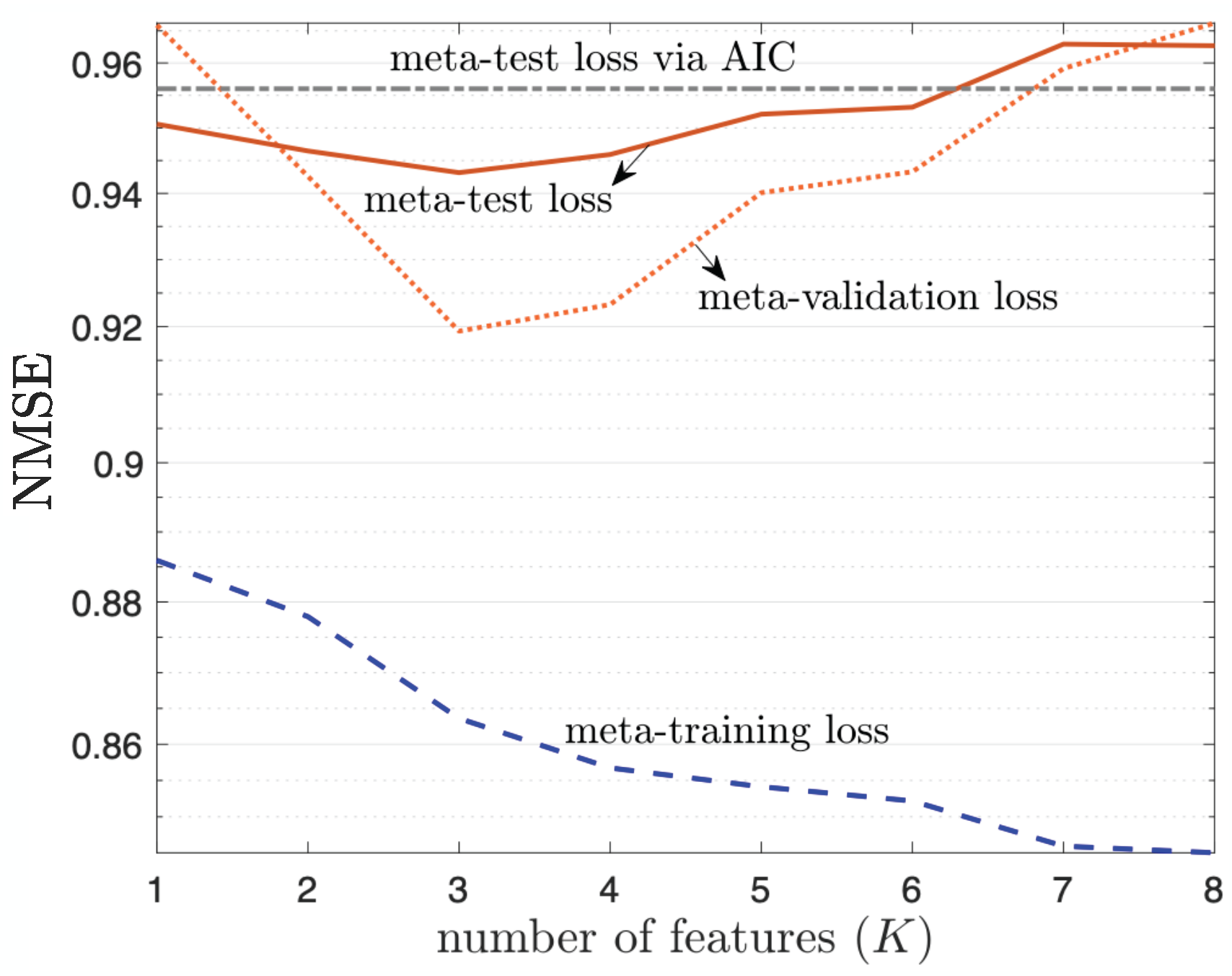
5.2. Rank Estimation
5.3. Single-Antenna Frequency-Selective Channels
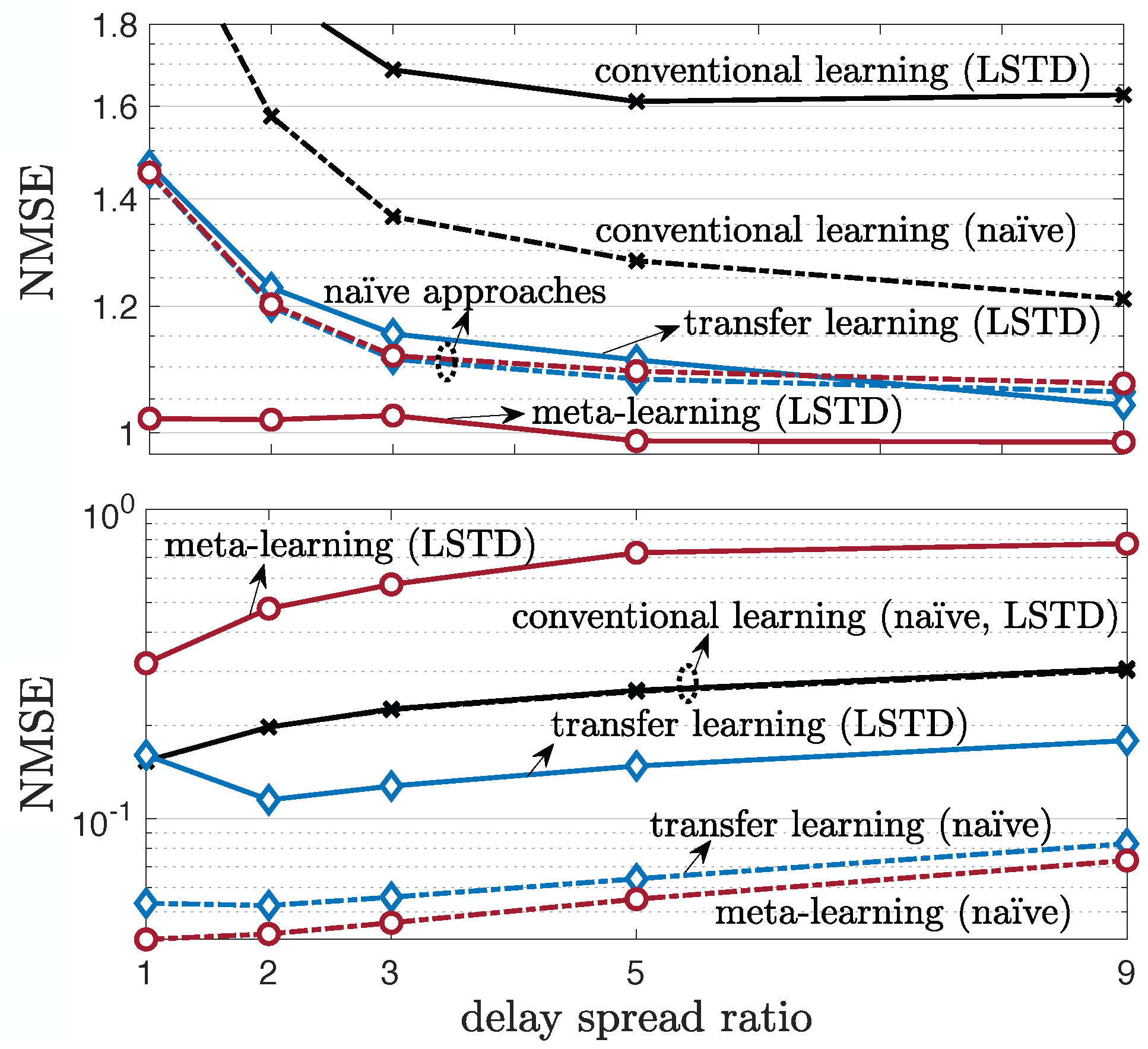
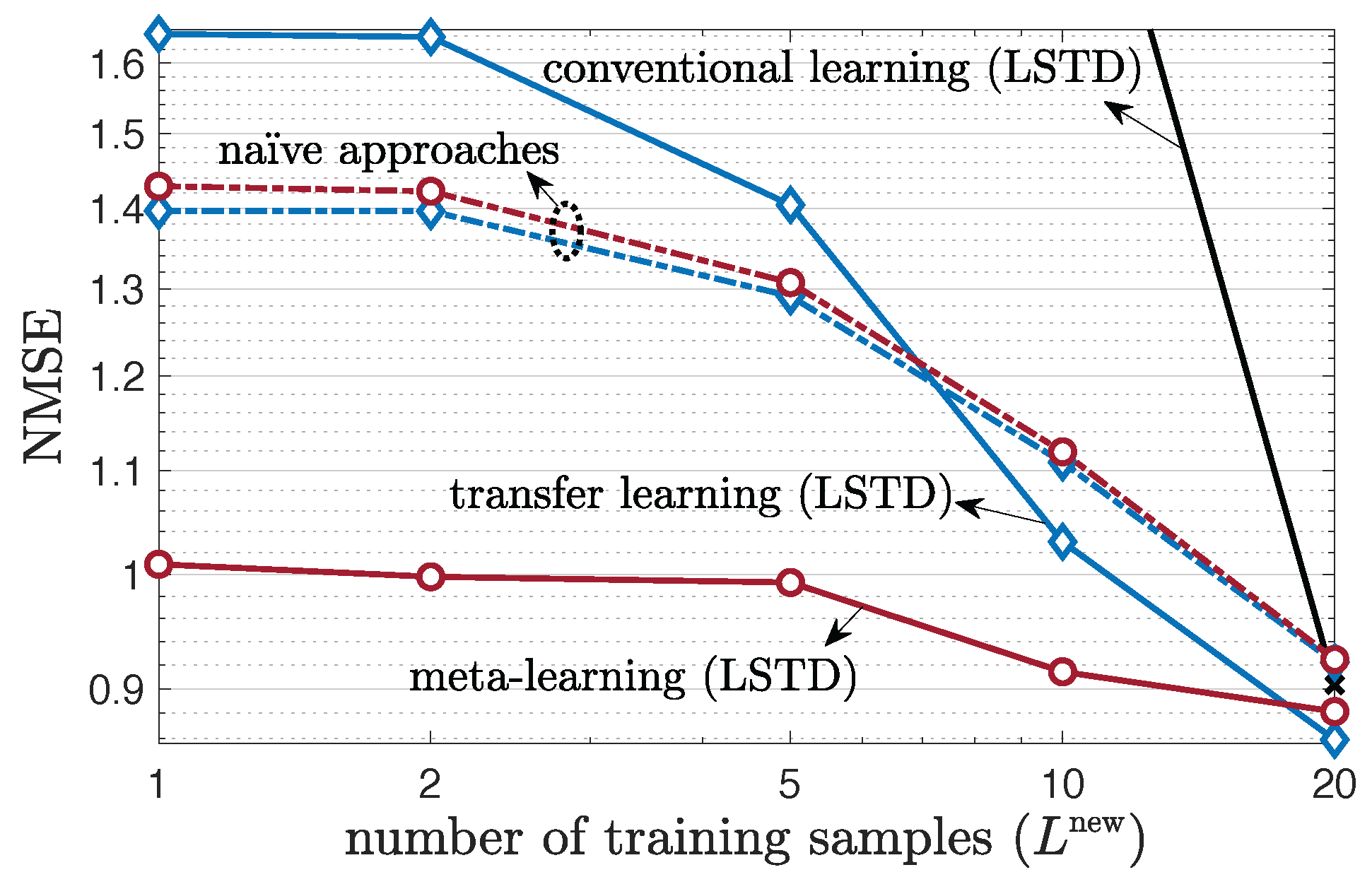
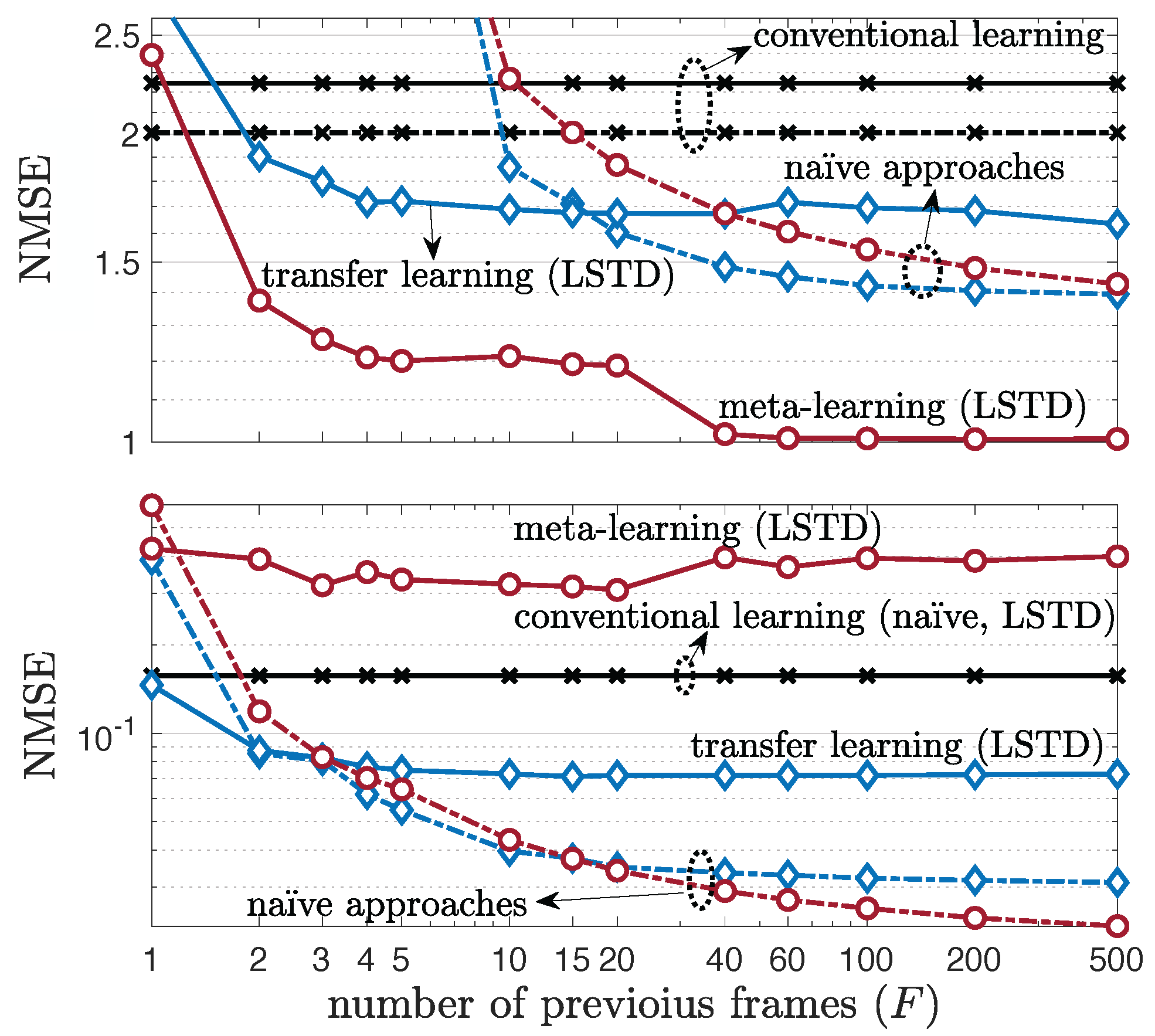
5.4. Multi-Antenna Frequency-Selective Channel Case
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Derivation for Long-Short-Term-Decomposition (LSTD)-Based Predictor
Appendix B. Details on Conventional Learning for LSTD-Based Prediction
Appendix C. Details on Transfer Learning for LSTD-Based Prediction
Appendix D. Details on Meta-Learning for LSTD-Based Prediction
Appendix E. Details on the Antenna Configuration in Section 5.1
| Number of | Antenna Configuration |
|---|---|
| Total Antennas () | () |
| 1 | |
| 2 | |
| 4 | |
| 8 | |
| 16 | |
| 32 | |
| 64 | |
| 128 |
References
- Tang, F.; Kawamoto, Y.; Kato, N.; Liu, J. Future intelligent and secure vehicular network toward 6G: Machine-learning approaches. Proc. IEEE 2019, 108, 292–307. [Google Scholar] [CrossRef]
- Hoeher, P.; Kaiser, S.; Robertson, P. Two-dimensional pilot-symbol-aided channel estimation by Wiener filtering. In Proceedings of the 1997 IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Munich, Germany, 21–24 April 1997. [Google Scholar]
- Baddour, K.E.; Beaulieu, N.C. Autoregressive modeling for fading channel simulation. IEEE Trans. Wirel. Commun. 2005, 4, 1650–1662. [Google Scholar] [CrossRef]
- Duel-Hallen, A.; Hu, S.; Hallen, H. Long-range prediction of fading signals. IEEE Signal Process. Mag. 2000, 17, 62–75. [Google Scholar] [CrossRef]
- Liu, L.; Feng, H.; Yang, T.; Hu, B. MIMO-OFDM wireless channel prediction by exploiting spatial-temporal correlation. IEEE Trans. Wirel. Commun. 2013, 13, 310–319. [Google Scholar] [CrossRef]
- Min, C.; Chang, N.; Cha, J.; Kang, J. MIMO-OFDM downlink channel prediction for IEEE802.16e systems using Kalman filter. In Proceedings of the 2007 IEEE Wireless Communications and Networking Conference (WCNC), Hong Kong, China, 11–15 March 2007; pp. 942–946. [Google Scholar]
- Komninakis, C.; Fragouli, C.; Sayed, A.H.; Wesel, R.D. Multi-input multi-output fading channel tracking and equalization using Kalman estimation. IEEE Trans. Signal Process. 2002, 50, 1065–1076. [Google Scholar] [CrossRef]
- Kashyap, S.; Mollén, C.; Björnson, E.; Larsson, E.G. Performance analysis of (TDD) massive MIMO with Kalman channel prediction. In Proceedings of the 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; pp. 3554–3558. [Google Scholar]
- Simmons, N.; Gomes, S.B.F.; Yacoub, M.D.; Simeone, O.; Cotton, S.L.; Simmons, D.E. AI-Based Channel Prediction in D2D Links: An Empirical Validation. IEEE Access 2022, 10, 65459–65472. [Google Scholar] [CrossRef]
- Simon, D.; Shmaliy, Y.S. Unified forms for Kalman and finite impulse response filtering and smoothing. Automatica 2013, 49, 1892–1899. [Google Scholar] [CrossRef]
- Shmaliy, Y.S. Linear optimal FIR estimation of discrete time-invariant state-space models. IEEE Trans. Signal Process. 2010, 58, 3086–3096. [Google Scholar] [CrossRef]
- Pratik, K.; Amjad, R.A.; Behboodi, A.; Soriaga, J.B.; Welling, M. Neural Augmentation of Kalman Filter with Hypernetwork for Channel Tracking. arXiv 2021, arXiv:2109.12561. [Google Scholar]
- Liu, W.; Yang, L.L.; Hanzo, L. Recurrent neural network based narrowband channel prediction. In Proceedings of the 2006 IEEE 63rd Vehicular Technology Conference, Melbourne, VIC, Australia, 7–10 May 2006; Volume 5, pp. 2173–2177. [Google Scholar]
- Jiang, W.; Schotten, H.D. A comparison of wireless channel predictors: Artificial Intelligence versus Kalman filter. In Proceedings of the ICC 2019—2019 IEEE International Conference on Communications (ICC), Shanghai, China, 20–24 May 2019; pp. 1–6. [Google Scholar]
- Jiang, W.; Strufe, M.; Schotten, H.D. Long-range MIMO channel prediction using recurrent neural networks. In Proceedings of the 2020 IEEE 17th Annual Consumer Communications & Networking Conference (CCNC), Las Vegas, NV, USA, 10–13 January 2020. [Google Scholar]
- Kibugi, J.; Ribeiro, L.N.; Haardt, M. Machine Learning Prediction of Time-Varying Rayleigh Channels. arXiv 2021, arXiv:2103.06131. [Google Scholar]
- Yuan, J.; Ngo, H.Q.; Matthaiou, M. Machine learning-based channel prediction in massive MIMO with channel aging. IEEE Trans. Wirel. Commun. 2020, 19, 2960–2973. [Google Scholar] [CrossRef]
- Zhang, Y.; Alkhateeb, A.; Madadi, P.; Jeon, J.; Cho, J.; Zhang, C. Predicting Future CSI Feedback For Highly-Mobile Massive MIMO Systems. arXiv 2022, arXiv:2202.02492. [Google Scholar]
- Kim, H.; Kim, S.; Lee, H.; Jang, C.; Choi, Y.; Choi, J. Massive MIMO channel prediction: Kalman filtering vs. machine learning. IEEE Trans. Commun. 2020, 69, 518–528. [Google Scholar] [CrossRef]
- Bogale, T.E.; Wang, X.; Le, L.B. Adaptive channel prediction, beamforming and scheduling design for 5G V2I network: Analytical and machine learning approaches. IEEE Trans. Veh. Technol. 2020, 69, 5055–5067. [Google Scholar] [CrossRef]
- Torrey, L.; Shavlik, J. Transfer learning. In Handbook of Research on Machine Learning Applications and Trends: Algorithms, Methods, and Techniques; IGI Global: Hershey, PA, USA, 2010. [Google Scholar]
- Thrun, S.; Pratt, L. Learning to Learn; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Raghu, A.; Raghu, M.; Bengio, S.; Vinyals, O. Rapid learning or feature reuse? towards understanding the effectiveness of maml. arXiv 2019, arXiv:1909.09157. [Google Scholar]
- Jose, S.T.; Park, S.; Simeone, O. Information-Theoretic Analysis of Epistemic Uncertainty in Bayesian Meta-learning. In Proceedings of the AISTATS, Virtual Event, 28–30 March 2022. [Google Scholar]
- Yuan, Y.; Zheng, G.; Wong, K.K.; Ottersten, B.; Luo, Z.Q. Transfer learning and meta learning-based fast downlink beamforming adaptation. IEEE Trans. Wirel. Commun. 2020, 20, 1742–1755. [Google Scholar] [CrossRef]
- Ge, Y.; Fan, J. Beamforming optimization for intelligent reflecting surface assisted MISO: A deep transfer learning approach. IEEE Trans. Veh. Technol. 2021, 70, 3902–3907. [Google Scholar] [CrossRef]
- Yang, Y.; Gao, F.; Zhong, Z.; Ai, B.; Alkhateeb, A. Deep transfer learning-based downlink channel prediction for FDD massive MIMO systems. IEEE Trans. Commun. 2020, 68, 7485–7497. [Google Scholar] [CrossRef]
- Parera, C.; Redondi, A.E.; Cesana, M.; Liao, Q.; Malanchini, I. Transfer learning for channel quality prediction. In Proceedings of the 2019 IEEE International Symposium on Measurements & Networking (M&N), Catania, Italy, 8–10 July 2019; pp. 1–6. [Google Scholar]
- Park, S.; Jang, H.; Simeone, O.; Kang, J. Learning to demodulate from few pilots via offline and online meta-learning. IEEE Trans. Signal Process. 2020, 69, 226–239. [Google Scholar] [CrossRef]
- Cohen, K.M.; Park, S.; Simeone, O.; Shamai, S. Learning to Learn to Demodulate with Uncertainty Quantification via Bayesian Meta-Learning. arXiv 2021, arXiv:2108.00785. [Google Scholar]
- Mao, H.; Lu, H.; Lu, Y.; Zhu, D. RoemNet: Robust Meta Learning Based Channel Estimation in OFDM Systems. In Proceedings of the ICC 2019—2019 IEEE International Conference on Communications (ICC), Shanghai, China, 20–24 May 2019. [Google Scholar]
- Raviv, T.; Park, S.; Simeone, O.; Eldar, Y.C.; Shlezinger, N. Online Meta-Learning For Hybrid Model-Based Deep Receivers. arXiv 2022, arXiv:2203.14359. [Google Scholar]
- Jiang, Y.; Kim, H.; Asnani, H.; Kannan, S. MIND: Model Independent Neural Decoder. In Proceedings of the 2019 IEEE 20th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Cannes, France, 2–5 July 2019. [Google Scholar]
- Park, S.; Simeone, O.; Kang, J. Meta-learning to communicate: Fast end-to-end training for fading channels. In Proceedings of the ICASSP 2020—2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020. [Google Scholar]
- Park, S.; Simeone, O.; Kang, J. End-to-end fast training of communication links without a channel model via online meta-learning. In Proceedings of the 2020 IEEE 21st International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Atlanta, GA, USA, 26–29 May 2020. [Google Scholar]
- Goutay, M.; Aoudia, F.A.; Hoydis, J. Deep hypernetwork-based MIMO detection. In Proceedings of the 2020 IEEE 21st International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Atlanta, GA, USA, 26–29 May 2020. [Google Scholar]
- Zhang, J.; Yuan, Y.; Zheng, G.; Krikidis, I.; Wong, K.K. Embedding Model Based Fast Meta Learning for Downlink Beamforming Adaptation. IEEE Trans. Wirel. Commun. 2021, 21, 149–162. [Google Scholar] [CrossRef]
- Karasik, R.; Simeone, O.; Jang, H.; Shamai, S. Learning to Broadcast for Ultra-Reliable Communication with Differential Quality of Service via the Conditional Value at Risk. arXiv 2021, arXiv:2112.02007. [Google Scholar]
- Hu, Y.; Chen, M.; Saad, W.; Poor, H.V.; Cui, S. Distributed multi-agent meta learning for trajectory design in wireless drone networks. IEEE J. Sel. Areas Commun. 2021, 39, 3177–3192. [Google Scholar] [CrossRef]
- Nikoloska, I.; Simeone, O. Black-Box and Modular Meta-Learning for Power Control via Random Edge Graph Neural Networks. arXiv 2021, arXiv:2108.13178. [Google Scholar]
- Simeone, O.; Spagnolini, U. Lower bound on training-based channel estimation error for frequency-selective block-fading Rayleigh MIMO channels. IEEE Trans. Signal Process. 2004, 52, 3265–3277. [Google Scholar] [CrossRef]
- Cicerone, M.; Simeone, O.; Spagnolini, U. Channel estimation for MIMO-OFDM systems by modal analysis/filtering. IEEE Trans. Commun. 2006, 54, 2062–2074. [Google Scholar] [CrossRef]
- Pedersen, K.I.; Andersen, J.B.; Kermoal, J.P.; Mogensen, P. A stochastic multiple-input-multiple-output radio channel model for evaluation of space-time coding algorithms. In Proceedings of the Vehicular Technology Conference Fall 2000. IEEE VTS Fall VTC2000. 52nd Vehicular Technology Conference (Cat. No. 00CH37152), Boston, MA, USA, 24–28 September 2000; Volume 2, pp. 893–897. [Google Scholar]
- Abdi, A.; Kaveh, M. A space-time correlation model for multielement antenna systems in mobile fading channels. IEEE J. Sel. Areas Commun. 2002, 20, 550–560. [Google Scholar] [CrossRef]
- Park, S.; Simeone, O. Predicting Flat-Fading Channels via Meta-Learned Closed-Form Linear Filters and Equilibrium Propagation. arXiv 2021, arXiv:2110.00414. [Google Scholar]
- 3GPP. Study on Channel Model for Frequencies From 0.5 to 100 GHz (3GPP TR 38.901 Version 16.1.0 Release 16). TR 38.901. 2020. Available online: https://www.etsi.org/deliver/etsi_tr/138900_138999/138901/16.01.00_60/tr_138901v160100p.pdf (accessed on 16 September 2022).
- Gallager, R.G. Principles of Digital Communication; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Simeone, O. A brief introduction to machine learning for engineers. Found. Trends® Signal Process. 2018, 12, 200–431. [Google Scholar] [CrossRef]
- Simeone, O. Machine Learning for Engineers; Cambridge University Press: Cambridge, UK, 2022. [Google Scholar]
- Prasad, R.; Murthy, C.R.; Rao, B.D. Joint approximately sparse channel estimation and data detection in OFDM systems using sparse Bayesian learning. IEEE Trans. Signal Process. 2014, 62, 3591–3603. [Google Scholar] [CrossRef]
- Huang, C.; Liu, L.; Yuen, C.; Sun, S. Iterative channel estimation using LSE and sparse message passing for mmWave MIMO systems. IEEE Trans. Signal Process. 2018, 67, 245–259. [Google Scholar] [CrossRef]
- Denevi, G.; Ciliberto, C.; Stamos, D.; Pontil, M. Learning to learn around a common mean. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Montreal, QC, Canada, 3–8 December 2018. [Google Scholar]
- Yin, M.; Tucker, G.; Zhou, M.; Levine, S.; Finn, C. Meta-learning without memorization. arXiv 2019, arXiv:1912.03820. [Google Scholar]
- Swindlehurst, A.L. Time delay and spatial signature estimation using known asynchronous signals. IEEE Trans. Signal Process. 1998, 46, 449–462. [Google Scholar] [CrossRef]
- Nicoli, M.; Simeone, O.; Spagnolini, U. Multislot estimation of fast-varying space-time communication channels. IEEE Trans. Signal Process. 2003, 51, 1184–1195. [Google Scholar] [CrossRef]
- Cortes, C.; Mohri, M.; Rostamizadeh, A. Algorithms for learning kernels based on centered alignment. J. Mach. Learn. Res. 2012, 13, 795–828. [Google Scholar]
- Wold, S.; Esbensen, K.; Geladi, P. Principal component analysis. Chemom. Intell. Lab. Syst. 1987, 2, 37–52. [Google Scholar] [CrossRef]
- Wong, A.S.Y.; Wong, K.W.; Leung, C.S. A unified sequential method for PCA. In Proceedings of the ICECS’99 6th IEEE International Conference on Electronics, Circuits and Systems (Cat. No. 99EX357), Paphos, Cyprus, 5–8 September 1999; Volume 1, pp. 583–586. [Google Scholar]
- Sidiropoulos, N.D.; De Lathauwer, L.; Fu, X.; Huang, K.; Papalexakis, E.E.; Faloutsos, C. Tensor decomposition for signal processing and machine learning. IEEE Trans. Signal Process. 2017, 65, 3551–3582. [Google Scholar] [CrossRef]
- Scellier, B.; Bengio, Y. Equilibrium propagation: Bridging the gap between energy-based models and backpropagation. Front. Comput. Neurosci. 2017, 11, 24. [Google Scholar] [CrossRef]
- Zucchet, N.; Schug, S.; von Oswald, J.; Zhao, D.; Sacramento, J. A contrastive rule for meta-learning. arXiv 2021, arXiv:2104.01677. [Google Scholar]
- Wax, M.; Kailath, T. Detection of signals by information theoretic criteria. IEEE Trans. Acoust. Speech Signal Process. 1985, 33, 387–392. [Google Scholar] [CrossRef]
- Liavas, A.P.; Regalia, P.A.; Delmas, J.P. Blind channel approximation: Effective channel order determination. IEEE Trans. Signal Process. 1999, 47, 3336–3344. [Google Scholar] [CrossRef]
- Agrawal, A.; Andrews, J.G.; Cioffi, J.M.; Meng, T. Iterative power control for imperfect successive interference cancellation. IEEE Trans. Wirel. Commun. 2005, 4, 878–884. [Google Scholar] [CrossRef]
- Recommendations ITU-R. Multipath Propagation and Parameterization of its Characteristics. Available online: https://www.itu.int/dms_pubrec/itu-r/rec/p/R-REC-P.1407-0-199907-S!!PDF-E.pdf (accessed on 22 September 2022).
- Xiao, C.; Yang, C.; Li, M. Efficient alternating least squares algorithms for low multilinear rank approximation of tensors. J. Sci. Comput. 2021, 87, 1–25. [Google Scholar] [CrossRef]
- Lorraine, J.; Vicol, P.; Duvenaud, D. Optimizing millions of hyperparameters by implicit differentiation. In Proceedings of the AISTATS, Virtual Event, 26–28 August 2020. [Google Scholar]


| Learning Type | for Naïve Approach | for LSTD-Based Approach |
|---|---|---|
| Conventional learning | ||
| Transfer learning | ||
| Meta-learning |
| Learning Type | for Naïve Approach | for LSTD-Based Approach |
|---|---|---|
| Conventional learning | − | − |
| Transfer learning | ||
| Meta-learning | ||
| Window size | 5 |
| Lag size | 3 |
| Number of previous frames | 500 |
| Number of slots | 107 |
| Frequency of the pilot signals () | 200 |
| Normalized Doppler frequency | |
| for slow-varying environment | |
| Normalized Doppler frequency | |
| for fast-varying environment | |
| SNR for channel estimation | 20 dB |
| Number of pilots for channel estimation | 100 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, S.; Simeone, O. Speeding up Training of Linear Predictors for Multi-Antenna Frequency-Selective Channels via Meta-Learning. Entropy 2022, 24, 1363. https://doi.org/10.3390/e24101363
Park S, Simeone O. Speeding up Training of Linear Predictors for Multi-Antenna Frequency-Selective Channels via Meta-Learning. Entropy. 2022; 24(10):1363. https://doi.org/10.3390/e24101363
Chicago/Turabian StylePark, Sangwoo, and Osvaldo Simeone. 2022. "Speeding up Training of Linear Predictors for Multi-Antenna Frequency-Selective Channels via Meta-Learning" Entropy 24, no. 10: 1363. https://doi.org/10.3390/e24101363
APA StylePark, S., & Simeone, O. (2022). Speeding up Training of Linear Predictors for Multi-Antenna Frequency-Selective Channels via Meta-Learning. Entropy, 24(10), 1363. https://doi.org/10.3390/e24101363





