The Listsize Capacity of the Gaussian Channel with Decoder Assistance
Abstract
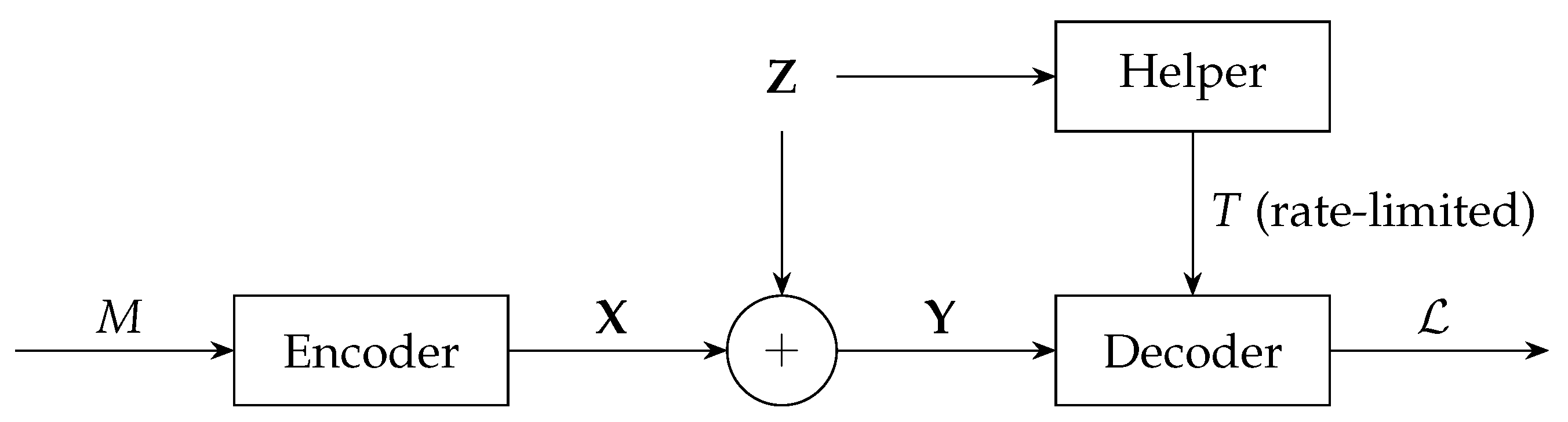
1. Introduction
2. The Main Result
3. Preliminaries
4. The Cutoff Rate of the Gaussian Channel
4.1. Computing
4.1.1. Upper-Bounding
4.1.2. Lower-Bounding
4.2. The Mapping Is Monotonically Decreasing
4.3. Achievability of
- (i)
- (ii)
4.4. No Rate Exceeding Is Achievable
5. The Direct Part of Theorem 2
5.1. Case 1:
5.2. Case 2:
Author Contributions
Funding
Conflicts of Interest
Appendix A. Proof of Lemma 2
Appendix B. Proof of Lemma 3
References
- Gallager, R.G. Information Theory and Reliable Communication; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1968. [Google Scholar]
- Verdú, S. Error exponents and α-mutual information. Entropy 2021, 23, 199. [Google Scholar] [CrossRef] [PubMed]
- Lapidoth, A.; Marti, G.; Yan, Y. Other helper capacities. In Proceedings of the 2021 IEEE International Symposium on Information Theory (ISIT), Victoria, Australia, 12–20 July 2021; pp. 1272–1277. [Google Scholar] [CrossRef]
- Cover, T.M. Elements of Information Theory, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006. [Google Scholar]
- Kim, Y. Capacity of a class of deterministic relay channels. IEEE Trans. Inf. Theory 2008, 54, 1328–1329. [Google Scholar] [CrossRef]
- Bross, S.I.; Lapidoth, A.; Marti, G. Decoder-assisted communications over additive noise channels. IEEE Trans. Commun. 2020, 68, 4150–4161. [Google Scholar] [CrossRef]
- Lapidoth, A.; Marti, G. Encoder-assisted communications over additive noise channels. IEEE Trans. Inf. Theory 2020, 66, 6607–6616. [Google Scholar] [CrossRef]
- Merhav, N. On error exponents of encoder-assisted communication systems. IEEE Trans. Inf. Theory 2021, 67, 7019–7029. [Google Scholar] [CrossRef]
- Bunte, C.; Lapidoth, A. Encoding tasks and Rényi entropy. IEEE Trans. Inf. Theory 2014, 60, 5065–5076. [Google Scholar] [CrossRef]
- Pinsker, M.S.; Sheverdjaev, A.Y. Transmission capacity with zero error and erasure. Probl. Peredachi Informatsii 1970, 6, 20–24. [Google Scholar]
- Csiszar, I.; Narayan, P. Channel capacity for a given decoding metric. IEEE Trans. Inf. Theory 1995, 41, 35–43. [Google Scholar] [CrossRef]
- Telatar, I.E. Zero-error list capacities of discrete memoryless channels. IEEE Trans. Inf. Theory 1997, 43, 1977–1982. [Google Scholar] [CrossRef]
- Ahlswede, R.; Cai, N.; Zhang, Z. Erasure, list, and detection zero-error capacities for low noise and a relation to identification. IEEE Trans. Inf. Theory 1996, 42, 55–62. [Google Scholar] [CrossRef]
- Bunte, C.; Lapidoth, A.; Samorodnitsky, A. The zero-undetected-error capacity approaches the Sperner capacity. IEEE Trans. Inf. Theory 2014, 60, 3825–3833. [Google Scholar] [CrossRef]
- Nakiboğlu, B.; Zheng, L. Errors-and-erasures decoding for block codes with feedback. IEEE Trans. Inf. Theory 2012, 58, 24–49. [Google Scholar] [CrossRef][Green Version]
- Bunte, C.; Lapidoth, A. The zero-undetected-error capacity of discrete memoryless channels with feedback. In Proceedings of the 2012 50th Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 1–5 October 2012; pp. 1838–1842. [Google Scholar] [CrossRef]
- Bunte, C.; Lapidoth, A. On the listsize capacity with feedback. IEEE Trans. Inf. Theory 2014, 60, 6733–6748. [Google Scholar] [CrossRef]
- Lapidoth, A.; Miliou, N. Duality bounds on the cutoff rate with applications to Ricean fading. IEEE Trans. Inf. Theory 2006, 52, 3003–3018. [Google Scholar] [CrossRef][Green Version]
- Pfister, C. On Rényi Information Measures and Their Applications. Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 2019. [Google Scholar]
- Rosenthal, H.P. On the subspaces of Lp (p > 2) spanned by sequences of independent random variables. Isr. J. Math. 1970, 8, 273–303. [Google Scholar] [CrossRef]
- Arıkan, E. An inequality on guessing and its application to sequential decoding. IEEE Trans. Inf. Theory 1996, 42, 99–105. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lapidoth, A.; Yan, Y. The Listsize Capacity of the Gaussian Channel with Decoder Assistance. Entropy 2022, 24, 29. https://doi.org/10.3390/e24010029
Lapidoth A, Yan Y. The Listsize Capacity of the Gaussian Channel with Decoder Assistance. Entropy. 2022; 24(1):29. https://doi.org/10.3390/e24010029
Chicago/Turabian StyleLapidoth, Amos, and Yiming Yan. 2022. "The Listsize Capacity of the Gaussian Channel with Decoder Assistance" Entropy 24, no. 1: 29. https://doi.org/10.3390/e24010029
APA StyleLapidoth, A., & Yan, Y. (2022). The Listsize Capacity of the Gaussian Channel with Decoder Assistance. Entropy, 24(1), 29. https://doi.org/10.3390/e24010029






