Learning from Scarce Information: Using Synthetic Data to Classify Roman Fine Ware Pottery
Abstract
:1. Introduction
2. Materials and Methods
- The four neural network architectures used in this experiment were modified from their standard and initialised with the ImageNet weights (see Section 2.2).
- Three different sets of simulated pottery vessels were generated so that the impact of (the quality of) simulation on the classifier’s performance could be assessed by comparison. The production of the synthetic datasets is discussed in Section 2.3.
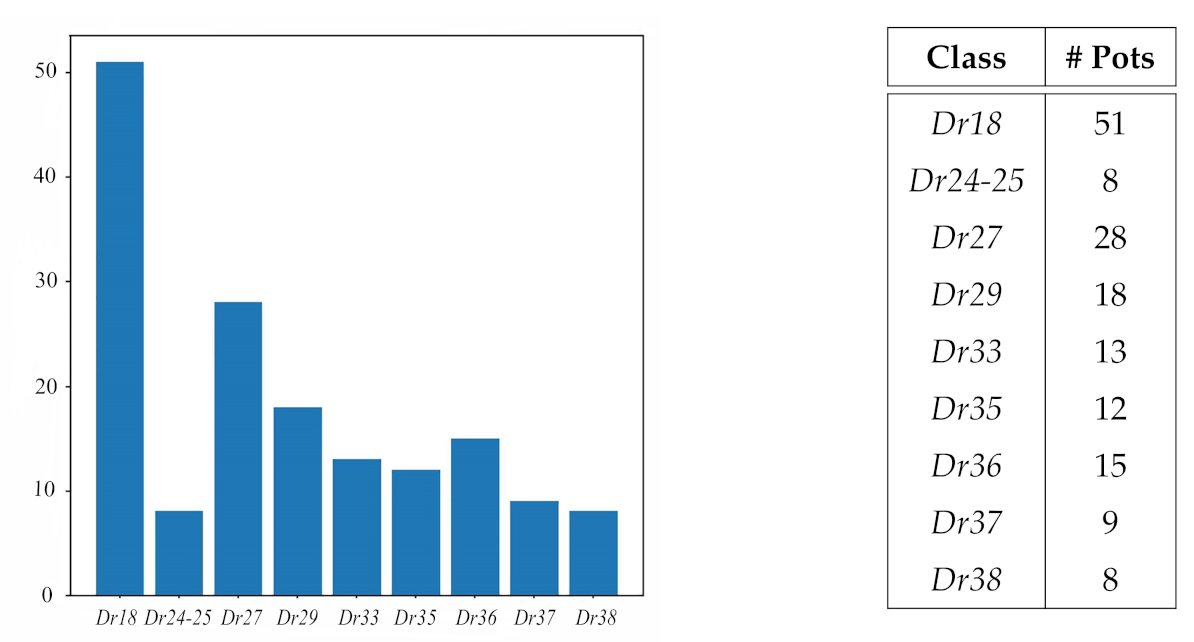
- Training, validating, and testing the different neural networks was done using the smartphone photographs of real terra sigillata vessels from the Museum of London. To make sure these photographs were usable, we created an algorithm which automatically detects the pot, centers it in the photograph and crops out unnecessary surroundings. This process is detailed in Section 2.4.
- To mitigate the impact of small sample size on our performance metrics, we created 20 different training-validation-test partitions, the creation process of which is detailed in Section 2.5.
- We then trained each of the combinations of four networks and four sets of initial weights with these partitions.
- The results of each of 16 combinations of network architectures and pre-training regimes were assessed across the 20 training-validation-test partitions. The definition of the metrics used for this evaluation is discussed in Section 2.6, the results themselves are detailed in Section 3.
2.1. Data Collection
- With the vessel placed upright on its base and assuming the origin of coordinates is located at the center of the pot, photographs were taken from azimuth angles of 0, 45 and 90 degrees and declination angles 0, 45 and 90 degrees. A last photograph with a declination higher than 90 degrees was taken by resting the mobile on the table.
- The vessel was rotated by an azimuth angle of 90 degrees and the process of point 1 repeated.
- The vessel was then turned upside down, thus using the rim to support it, and 4 photographs at azimuth 45 degrees from the declination detailed in point 1 were taken.
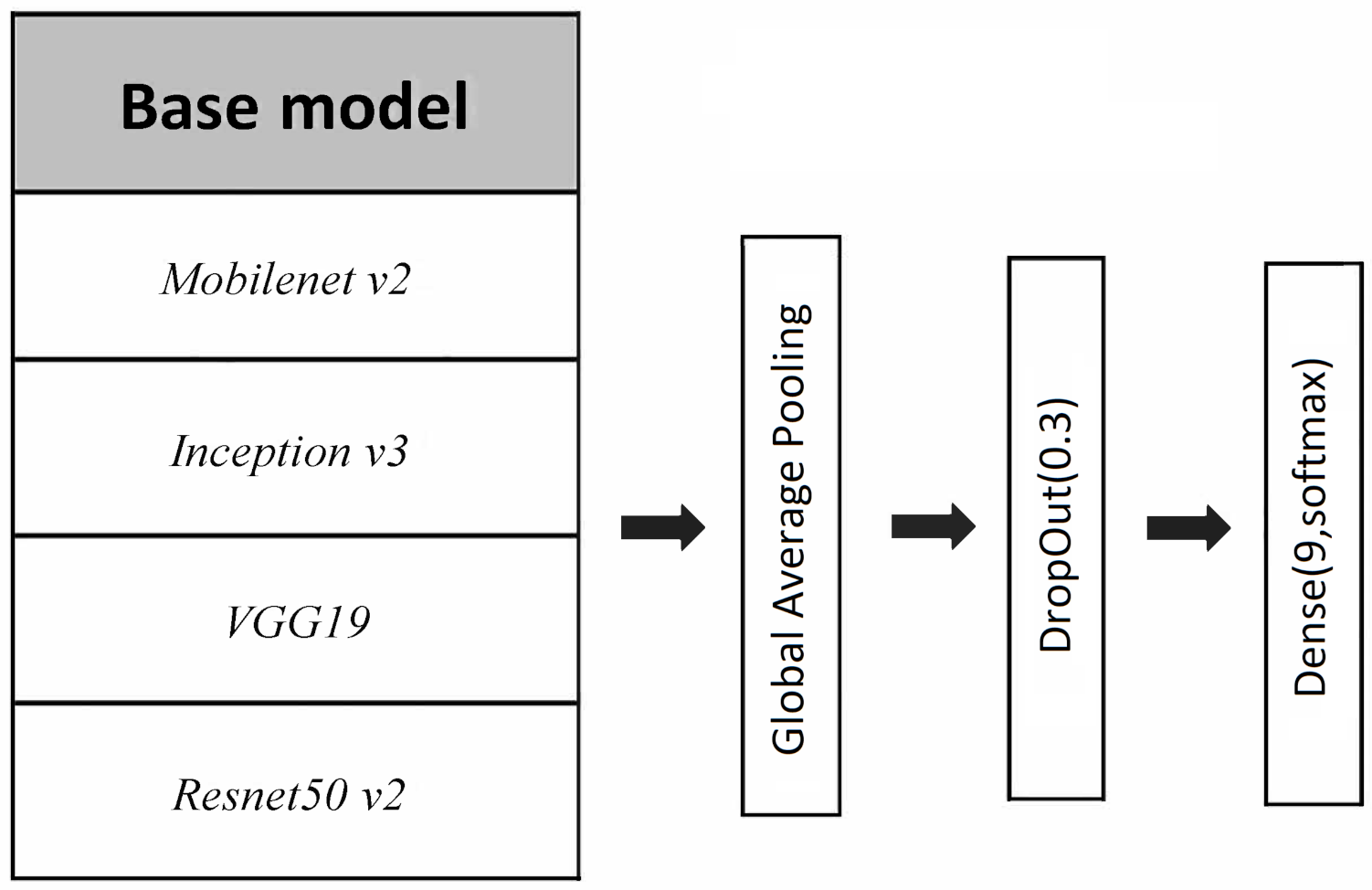
2.2. Neural Nets Configurations
- Backbone convolutional neural net base architecture (i.e., the last layers of these architectures were removed until the convolutional structure);
- A global average pooling layer after the convolutional structure;
- A drop out layer with 0.3 exclusion probability;
- A final bottleneck dense layer with softmax activation, that is, a linear dense layer followed by a softmax transformation of the outputs.
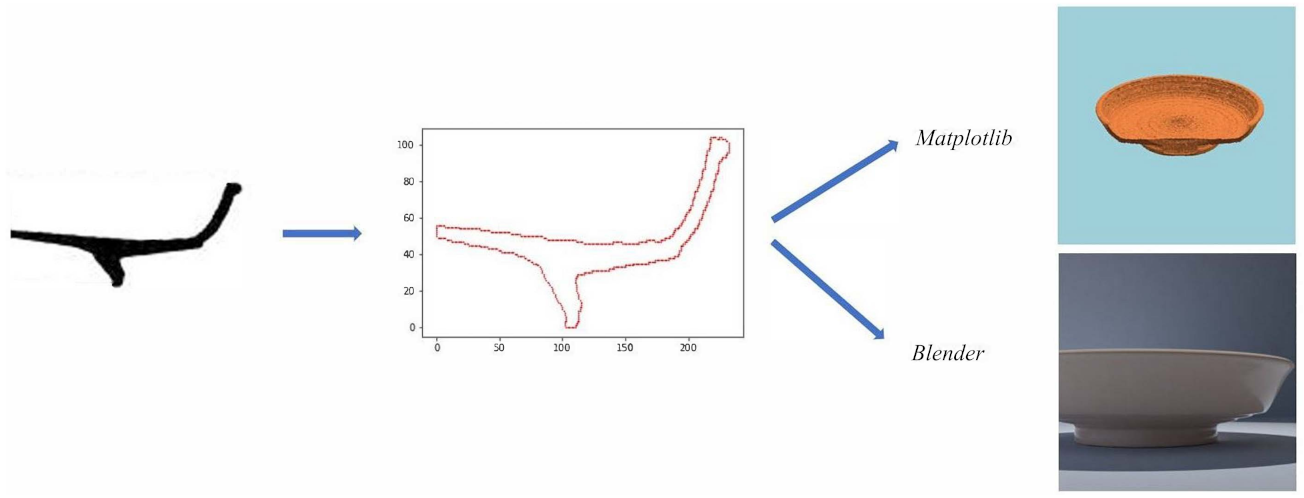
2.3. Pot Simulations
- Matplotlib (1000 images per class):To generate this dataset, the Python package Matplotlib [52] was used. The simulated pot was floated in a homogeneous background, no shadow is projected but the pot color is affected by the light. The light source is a point far away so only the angle has been changed. The profiles were softened to avoid their small defects creating circular patterns that could be identified by the neural net. For the same reason, a small amount of random noise was added to the surface mesh points position.
- Blender1 (1400 images per class):This dataset was generated using Blender [53]. We built a background set close to the original photography setting with a uniform color. The lighting conditions were randomly chosen using the different lighting classes available, namely: sun, spot, point. Thanks to the rendering feature Cycles, we could simulate shadow projections as well as changes of illumination in both pot and setting. The profile was softened by distance using the software and no noise was added. The material properties where not changed from the default ones except for the color.
- Blender2 (1300 images per class):The process followed to create this dataset is similar to the one used to create Blender1, however, the material properties were changed to make them more similar to the terra sigillata pots. Thus, some images exhibit simulated pots with a reflective material which creates light-saturated regions in the image of the pot. We also added decoration and motifs to some classes, namely:
- -
- Dr24–25: half of the images show a striped pattern near the top.
- -
- Dr35 & Dr36: half of the images show a pattern of four or six leaves on their rim.
- -
- Dr29 & Dr37: The decoration has a lot of variability in reality. We have simulated it in half of the images through two noise pattern displacements (Blender Musgrave and Magic textures).
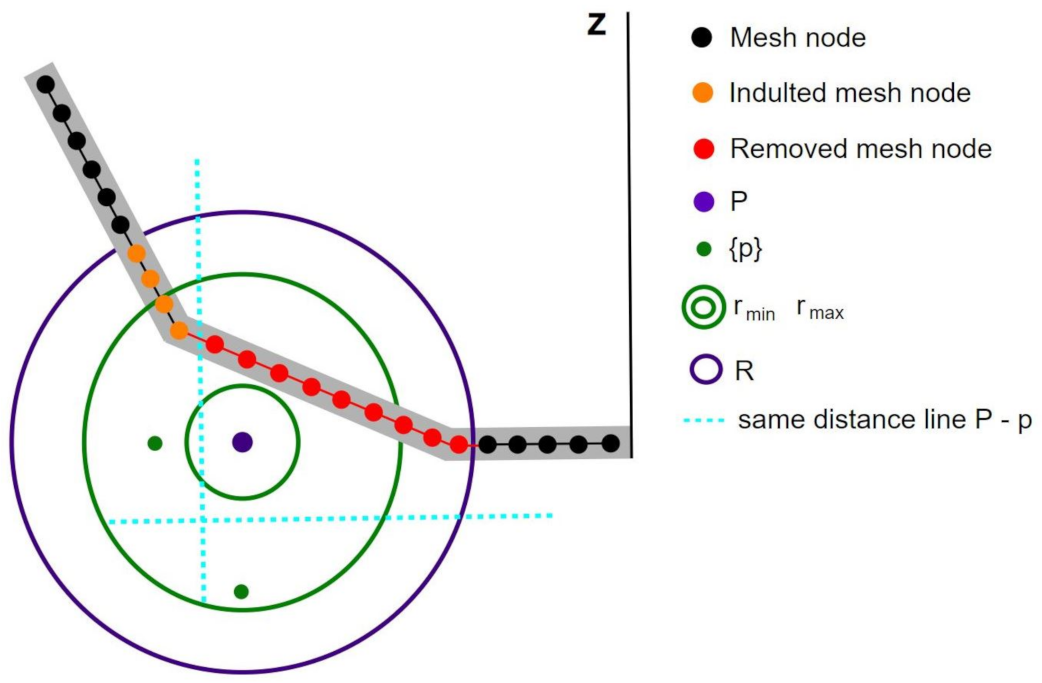
No other decoration or characteristic details were reproduced in our simulated data. Finally, we sieved each synthetic dataset, removing images that were taken from too close or show some defects resulting from the simulated breaking procedure.
2.4. Pot Detector: Cropping and Centering the Images
| Algorithm 1: Locate and crop pot images |
| Input: Image Output: Image_output. Cropped and centered pot image. scaled_image = scale input Image to ; scaled_image = change color basis from RGB to HSV; dataset_pixels = create dataset where each pixel in scaled_image have features: [Saturation, Value, , ]; dataset_pixels = linearly normalize dataset_pixels features into [0,1] interval; pixel_group = assign cluster to each pixel using DBSCAN (Eps = 0.1, MinPts = 5) algorithm; dataset_pixels = dataset_pixels remove pixels of groups with less than 25 pixels; group_distance = for all groups compute mean(+ ); pot_group = argmin(group_distance); dataset_pixels = dataset_pixels remove pixels not in pot_group; = max()) − min()); = max()) − min()); scale and to the original size; L = max(, ); L_half = integer_part(L/2); = mean(); = mean(); Image_output = Image[from − L_half to + L_half, from − L_half to + L_half]; |
2.5. Training-Validation-Test Partitions
2.6. Performance Metrics
- Uniform prior: all classes have the same probability and, thus, are equally weighted in the final metrics.
- MoL prior: We assume that the MoL pot classes distribution is a good estimator of . Let be the full dataset of our collection, the probability will be given by the number of pots of class i over the total number of pots:Each prior provides us with an interesting perspective. On the one hand, the uniform prior assesses how well the algorithm has learnt the classes without prioritising any one class. On the other hand, were the MoL prior close to the field frequency of the classes, it would give us scores closer to the user performance perception who would find more frequent classes more often.
3. Results
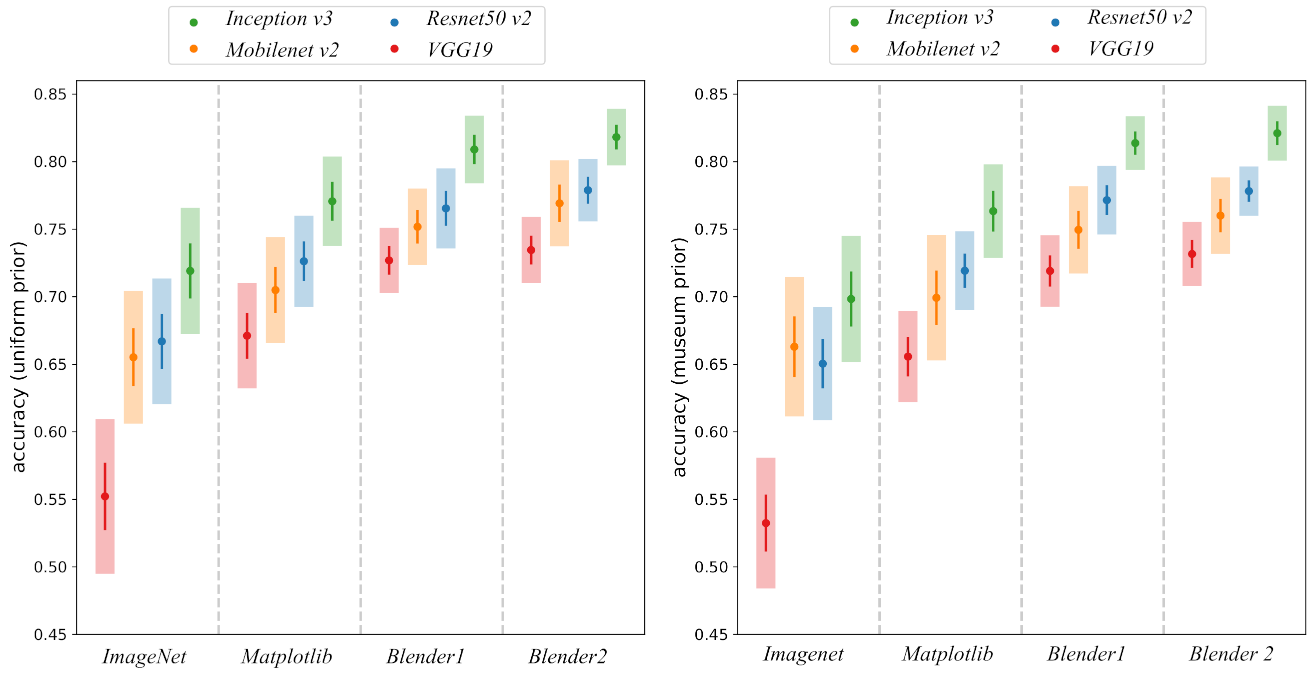
3.1. Accuracy
3.2. Confusion Matrix
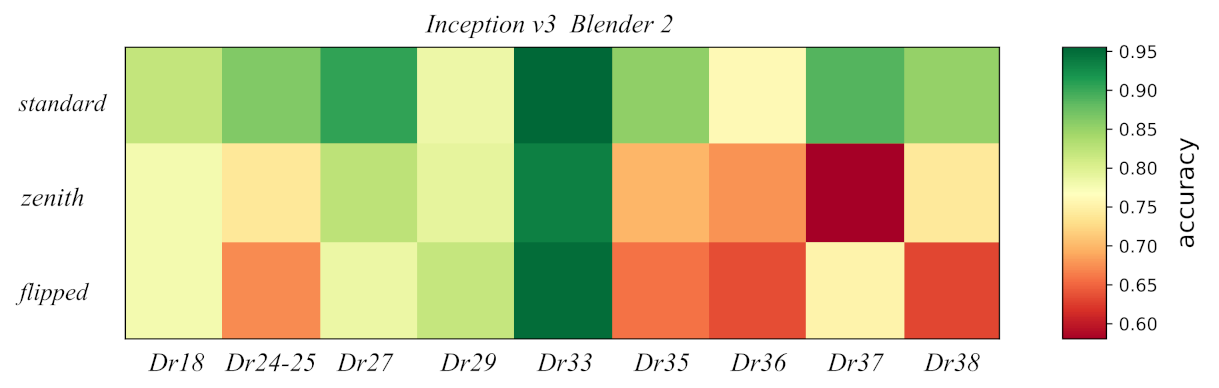
3.3. Effects of Damage
3.4. Effects of Viewpoint
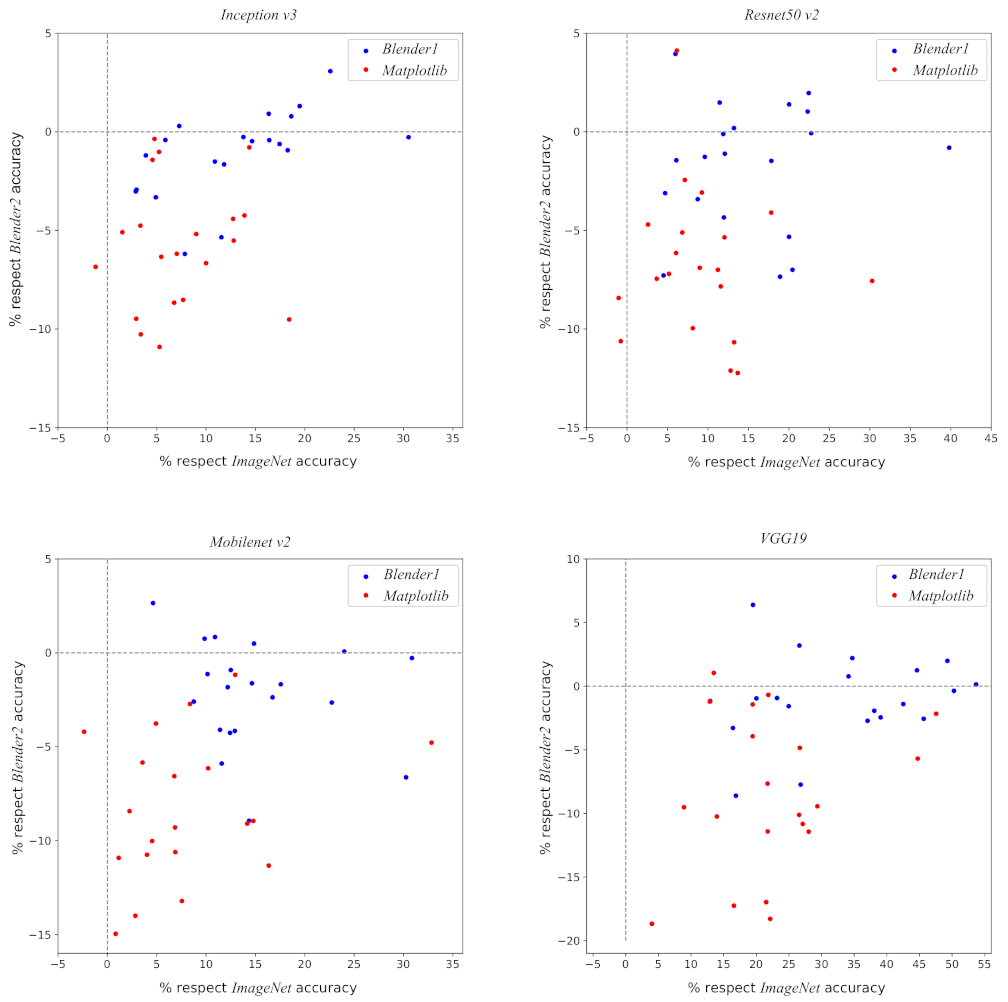
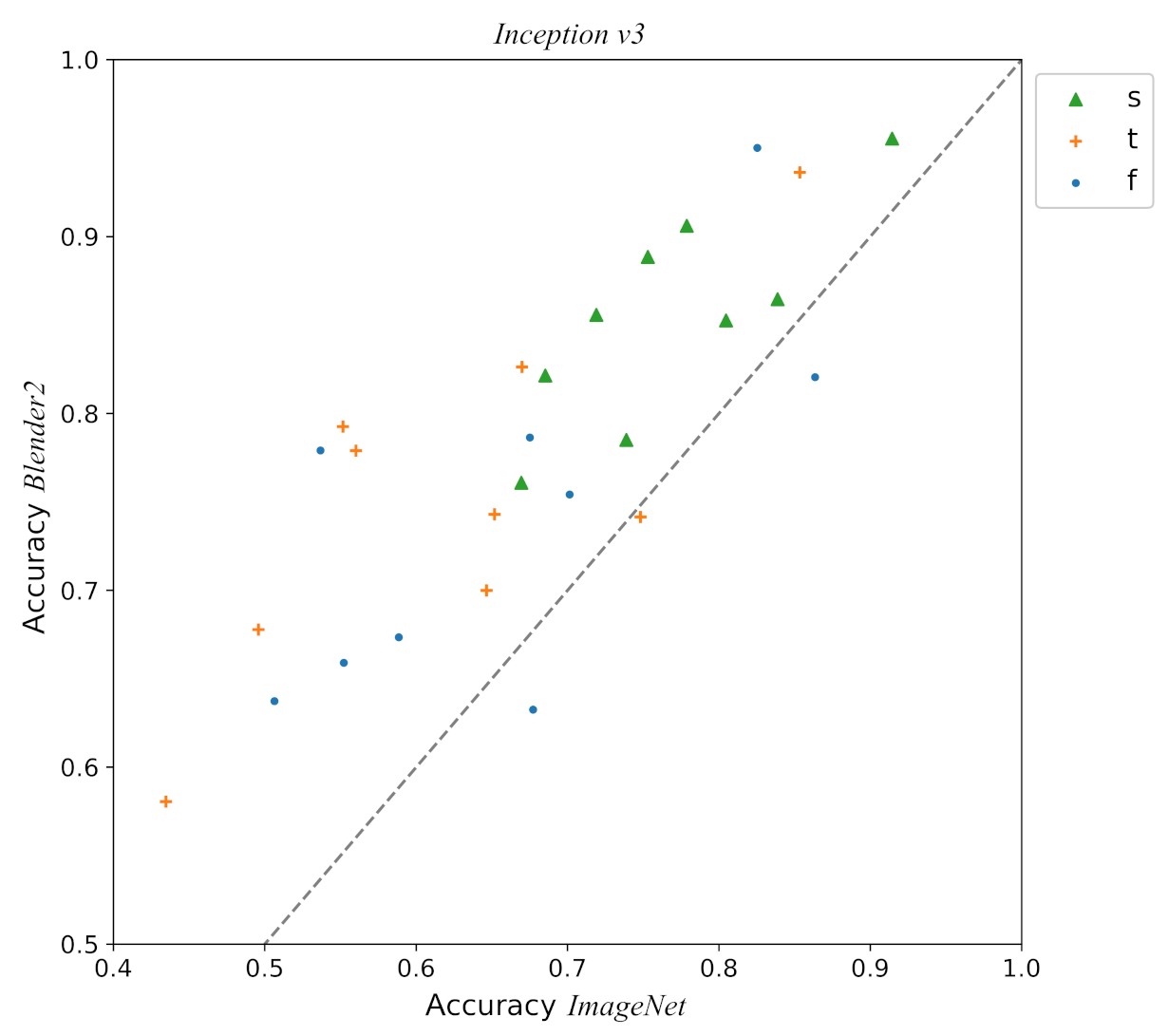
3.5. Reality Gap
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. In Advances in Neural Information Processing Systems; Curran Associates Inc.: Red Hook, NY, USA, 2012; pp. 1097–1105. [Google Scholar]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; et al. ImageNet large scale visual recognition challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef] [Green Version]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Li, F.-F. ImageNet: A large-scale hierarchical image database. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Lin, T.Y.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; Zitnick, C.L. Microsoft coco: Common objects in context. In European Conference on Computer Vision, Proceedings of the Computer Vision—ECCV 2014, 13th European Conference, Zurich, Switzerland, 6–12 September 2014; Springer: Cham, Switzerland, 2014; pp. 740–755. [Google Scholar]
- Vapnik, V. Statistical Learning Theory; Wiley-Interscience: New York, NY, USA, 1998. [Google Scholar]
- Bousquet, O.; Boucheron, S.; Lugosi, G. Introduction to statistical learning theory. In Summer School on Machine Learning, Proceedings of the ML 2003: Advanced Lectures on Machine Learning, ML Summer Schools 2003, Canberra, Australia, 2–14 February 2003; Springer: Berlin/Heidelberg, Germany, 2003; pp. 169–207. [Google Scholar]
- Mohri, M.; Rostamizadeh, A.; Talwalkar, A. Foundations of Machine Learning; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Bartlett, P.L.; Maiorov, V.; Meir, R. Almost linear VC-dimension bounds for piecewise polynomial networks. Neural Comput. 1998, 10, 2159–2173. [Google Scholar] [CrossRef] [PubMed]
- Bartlett, P.L.; Harvey, N.; Liaw, C.; Mehrabian, A. Nearly-tight VC-dimension and pseudodimension bounds for piecewise linear neural networks. J. Mach. Learn. Res. 2019, 20, 1–17. [Google Scholar]
- Vinyals, O.; Blundell, C.; Lillicrap, T.; Kavukcuoglu, K.; Wierstra, D. Matching networks for one shot learning. arXiv 2016, arXiv:1606.04080. [Google Scholar]
- Snell, J.; Swersky, K.; Zemel, R.S. Prototypical networks for few-shot learning. arXiv 2017, arXiv:1703.05175. [Google Scholar]
- Tyukin, I.Y.; Gorban, A.N.; Alkhudaydi, M.H.; Zhou, Q. Demystification of few-shot and one-shot learning. arXiv 2021, arXiv:2104.12174. [Google Scholar]
- Tyukin, I.Y.; Gorban, A.N.; McEwan, A.A.; Meshkinfamfard, S.; Tang, L. Blessing of dimensionality at the edge and geometry of few-shot learning. Inf. Sci. 2021, 564, 124–143. [Google Scholar] [CrossRef]
- Pawlowicz, L.M.; Downum, C.E. Applications of deep learning to decorated ceramic typology and classification: A case study using Tusayan White Ware from Northeast Arizona. J. Archaeol. Sci. 2021, 130, 105375. [Google Scholar] [CrossRef]
- Anichini, F.; Dershowitz, N.; Dubbini, N.; Gattiglia, G.; Itkin, B.; Wolf, L. The automatic recognition of ceramics from only one photo: The ArchAIDE app. J. Archaeol. Sci. Rep. 2021, 36, 102788. [Google Scholar]
- Allison, P.M. Understanding Pompeian household practices through their material culture. FACTA J. Rom. Mater. Cult. Stud. 2009, 3, 11–32. [Google Scholar]
- Allison, P.M. The ceramics from the Insula del Menandro and the significance of their distribution. In ‘Fecisti Cretaria’: Dal Frammento al Contesto: Studi sul Vasellame del Territorio Vesuviano. Studi e Richerche del Parco Archeologico di Pompei; Ossana, M., Toniolo, L., Eds.; L’erma di BretBretschneider: Rome, Italy, 2020; Volume 40, pp. 199–209. [Google Scholar]
- Webster, P. Roman Samian Pottery in Britain; Number 13; Council for British Archaeology: London, UK, 1996. [Google Scholar]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the Inception architecture for computer vision. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2818–2826. [Google Scholar]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.C. Mobilenetv2: Inverted residuals and linear bottlenecks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4510–4520. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Sadeghi, F.; Levine, S. Cad2rl: Real single-image flight without a single real image. arXiv 2016, arXiv:1611.04201. [Google Scholar]
- Deist, T.M.; Patti, A.; Wang, Z.; Krane, D.; Sorenson, T.; Craft, D. Simulation-assisted machine learning. Bioinformatics 2019, 35, 4072–4080. [Google Scholar] [CrossRef]
- Piprek, J. Simulation-based machine learning for optoelectronic device design: Perspectives, problems, and prospects. Opt. Quantum Electron. 2021, 53, 175. [Google Scholar] [CrossRef]
- Ros, G.; Sellart, L.; Materzynska, J.; Vazquez, D.; Lopez, A.M. The SYNTHIA dataset: A large collection of synthetic images for semantic segmentation of urban scenes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 3234–3243. [Google Scholar]
- Hwang, H.; Jang, C.; Park, G.; Cho, J.; Kim, I.J. ElderSim: A synthetic data generation platform for human action recognition in Eldercare applications. arXiv 2020, arXiv:2010.14742. [Google Scholar]
- Varol, G.; Romero, J.; Martin, X.; Mahmood, N.; Black, M.J.; Laptev, I.; Schmid, C. Learning from synthetic humans. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4627–4635. [Google Scholar]
- Gupta, A.; Vedaldi, A.; Zisserman, A. Synthetic data for text localisation in natural images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2315–2324. [Google Scholar]
- Deneke, W.; Plunkett, G.; Dixon, S.; Harley, R. Towards a simulation platform for generation of synthetic videos for human activity recognition. In Proceedings of the International Conference on Computational Science and Computational Intelligence (CSCI), Las Vegas, NV, USA, 12–14 December 2018; pp. 1234–1237. [Google Scholar]
- Collins, J.; Brown, R.; Leitner, J.; Howard, D. Traversing the reality gap via simulator tuning. arXiv 2020, arXiv:2003.01369. [Google Scholar]
- Xiang, Y.; Kim, W.; Chen, W.; Ji, J.; Choy, C.; Su, H.; Mottaghi, R.; Guibas, L.; Savarese, S. Objectnet3d: A large scale database for 3D object recognition. In European Conference on Computer Vision, ECCV 2016: Computer Vision—ECCV 2016, 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Springer: Cham, Switzerland, 2016; pp. 160–176. [Google Scholar]
- Mo, K.; Zhu, S.; Chang, A.X.; Yi, L.; Tripathi, S.; Guibas, L.J.; Su, H. PartNet: A large-scale benchmark for fine-grained and hierarchical part-level 3D object understanding. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 909–918. [Google Scholar]
- Yao, Z.; Nagel, C.; Kunde, F.; Hudra, G.; Willkomm, P.; Donaubauer, A.; Adolphi, T.; Kolbe, T.H. 3DCityDB-a 3D geodatabase solution for the management, analysis, and visualization of semantic 3D city models based on CityGML. Open Geospat. Data Softw. Stand. 2018, 3, 1–26. [Google Scholar] [CrossRef] [Green Version]
- Movshovitz-Attias, Y.; Kanade, T.; Sheikh, Y. How useful is photo-realistic rendering for visual learning? In European Conference on Computer Vision; Springer: Cham, Switzerland, 2016; pp. 202–217. [Google Scholar]
- Bousmalis, K.; Silberman, N.; Dohan, D.; Erhan, D.; Krishnan, D. Unsupervised pixel-level domain adaptation with generative adversarial networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 95–104. [Google Scholar]
- Shrivastava, A.; Pfister, T.; Tuzel, O.; Susskind, J.; Wang, W.; Webb, R. Learning from simulated and unsupervised images through adversarial training. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2242–2251. [Google Scholar]
- Tobin, J.; Fong, R.; Ray, A.; Schneider, J.; Zaremba, W.; Abbeel, P. Domain randomization for transferring deep neural networks from simulation to the real world. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 23–30. [Google Scholar]
- Peng, X.B.; Andrychowicz, M.; Zaremba, W.; Abbeel, P. Sim-to-real transfer of robotic control with dynamics randomization. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 3803–3810. [Google Scholar]
- Zakharov, S.; Kehl, W.; Ilic, S. Deceptionnet: Network-driven domain randomization. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Korea, 27–28 October 2019; pp. 532–541. [Google Scholar]
- Mehta, B.; Diaz, M.; Golemo, F.; Pal, C.J.; Paull, L. Active domain randomization. In Proceedings of the Conference on Robot Learning, Online, 16–18 November 2020; pp. 1162–1176. [Google Scholar]
- Hinterstoisser, S.; Lepetit, V.; Wohlhart, P.; Konolige, K. On pre-trained image features and synthetic images for deep learning. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 682–697. [Google Scholar]
- Donoho, D. High-dimensional data analysis: The curses and blessings of dimensionality. In Proceedings of the Invited lecture at Mathematical Challenges of the 21st Century (AMS National Meeting), Los Angeles, CA, USA, 6–12 August 2000; Available online: http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.329.3392 (accessed on 29 August 2021).
- Gorban, A.N.; Grechuk, B.; Mirkes, E.M.; Stasenko, S.V.; Tyukin, I.Y. High-dimensional separability for one-and few-shot learning. arXiv 2021, arXiv:2106.15416. [Google Scholar]
- Moczko, E.; Mirkes, E.M.; Cáceres, C.; Gorban, A.N.; Piletsky, S. Fluorescence-based assay as a new screening tool for toxic chemicals. Sci. Rep. 2016, 6, 33922. [Google Scholar] [CrossRef] [Green Version]
- Liu, B.; Wei, Y.; Zhang, Y.; Yang, Q. Deep neural networks for high dimension, low sample size data. In Proceedings of the Twenty-Sixth International Joint Conference on Artificial Intelligence (IJCAI-17), Melbourne, Australia, 19–25 August 2017; pp. 2287–2293. [Google Scholar]
- Peshkin, L.; Shelton, C.R. Learning from scarce experience. In Proceedings of the Nineteenth International Conference on Machine Learning, Sydney, Australia, 8–12 July 2002; pp. 498–505. [Google Scholar]
- Devroye, L.; Györfi, L.; Lugosi, G. A probabilistic theory of pattern recognition; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1996; Volume 31. [Google Scholar]
- Dragendorff, H. Terra sigillata: Ein Beitrag zur Geschichte des griechischen und römischen Keramik. Bonn. Jahrbücher 1895, 96, 18–55. [Google Scholar]
- Brown, L.G. A survey of image registration techniques. ACM Comput. Surv. (CSUR) 1992, 24, 325–376. [Google Scholar] [CrossRef]
- Núñez Jareño, S.J.; van Helden, D.P.; Mirkes, E.M.; Tyukin, I.Y.; Allison, P.M. Arch-I-Scan Data Repository. 2021. Available online: https://github.com/ArchiScn/Access (accessed on 29 August 2021).
- Hunter, J.D. Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Blender Online Community. Blender—A 3D modelling and rendering package; Blender Foundation, Stichting Blender Foundation: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Tsirikoglou, A.; Eilertsen, G.; Unger, J. A survey of image synthesis methods for visual machine learning. In Computer Graphics Forum; Wiley Online Library: Hoboken, NJ, USA, 2020; Volume 39, pp. 426–451. [Google Scholar]
- Itkin, B.; Wolf, L.; Dershowitz, N. Computational Ceramicology. arXiv 2019, arXiv:1911.09960. [Google Scholar]
- Anichini, F.; Banterle, F.; Garrigós, J. Developing the ArchAIDE application: A digital workflow for identifying, organising and sharing archaeological pottery using automated image recognition. Internet Archaeol. 2020, 52, 1–48. [Google Scholar] [CrossRef]
- Zhao, Z.Q.; Zheng, P.; Xu, S.T.; Wu, X. Object detection with deep learning: A review. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 3212–3232. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. Kdd 1996, 96, 226–231. [Google Scholar]
- Schubert, E.; Sander, J.; Ester, M.; Kriegel, H.P.; Xu, X. DBSCAN revisited, revisited: Why and how you should (still) use DBSCAN. ACM Trans. Database Syst. (TODS) 2017, 42, 1–21. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]




| Phone Model | Camera Resolution | Aperture | Focal Length | Pixel Size |
|---|---|---|---|---|
| Samsung Galaxy A20e | 13 MP | f/1.9 | 28 mm | 1.4 m |
| Apple iPhone 6 | 8 MP | f/2.2 | 29 mm | 1.5 m |
| Motorola Moto E Play 5th gen. | 8 MP | f/2.0 | 28.3 mm | 1.12 m |
| Samsung Galaxy A70 | 32 MP | f/1.7 | 26 mm | 0.8 m |
| Model | Pretrain | ||||
|---|---|---|---|---|---|
| Inception v3 | Blender2 | 0.818 ± 0.008 | 0.021 | 0.78 | 0.87 |
| Inception v3 | Blender1 | 0.809 ± 0.011 | 0.025 | 0.76 | 0.84 |
| Inception v3 | Matplotlib | 0.771 ± 0.014 | 0.033 | 0.72 | 0.85 |
| Inception v3 | ImageNet | 0.719 ± 0.020 | 0.047 | 0.61 | 0.82 |
| Resnet50 v2 | Blender2 | 0.779 ± 0.010 | 0.023 | 0.74 | 0.82 |
| Resnet50 v2 | Blender1 | 0.765 ± 0.013 | 0.030 | 0.72 | 0.82 |
| Resnet50 v2 | Matplotlib | 0.726 ± 0.014 | 0.034 | 0.67 | 0.82 |
| Resnet50 v2 | ImageNet | 0.667 ± 0.020 | 0.047 | 0.55 | 0.77 |
| Mobilenet v2 | Blender2 | 0.769 ± 0.014 | 0.032 | 0.72 | 0.84 |
| Mobilenet v2 | Blender1 | 0.752 ± 0.012 | 0.028 | 0.70 | 0.82 |
| Mobilenet v2 | Matplotlib | 0.705 ± 0.017 | 0.039 | 0.65 | 0.78 |
| Mobilenet v2 | ImageNet | 0.655 ± 0.021 | 0.049 | 0.56 | 0.76 |
| VGG19 | Blender2 | 0.735 ± 0.010 | 0.025 | 0.69 | 0.77 |
| VGG19 | Blender1 | 0.727 ± 0.010 | 0.024 | 0.69 | 0.78 |
| VGG19 | Matplotlib | 0.671 ± 0.017 | 0.039 | 0.60 | 0.74 |
| VGG19 | ImageNet | 0.552± 0.024 | 0.057 | 0.47 | 0.65 |
| Model | Pretrain | ||||
|---|---|---|---|---|---|
| Inception v3 | Blender2 | 0.821 ± 0.009 | 0.020 | 0.78 | 0.86 |
| Inception v3 | Blender1 | 0.814 ± 0.008 | 0.020 | 0.78 | 0.85 |
| Inception v3 | Matplotlib | 0.763 ± 0.015 | 0.035 | 0.71 | 0.82 |
| Inception v3 | ImageNet | 0.698 ± 0.020 | 0.047 | 0.62 | 0.80 |
| Resnet50 v2 | Blender2 | 0.778 ± 0.008 | 0.018 | 0.74 | 0.81 |
| Resnet50 v2 | Blender1 | 0.772 ± 0.011 | 0.025 | 0.73 | 0.81 |
| Resnet50 v2 | Matplotlib | 0.719 ± 0.012 | 0.029 | 0.66 | 0.79 |
| Resnet50 v2 | ImageNet | 0.651 ± 0.018 | 0.042 | 0.54 | 0.74 |
| Mobilenet v2 | Blender2 | 0.760 ± 0.012 | 0.028 | 0.71 | 0.81 |
| Mobilenet v2 | Blender1 | 0.750 ± 0.014 | 0.032 | 0.69 | 0.81 |
| Mobilenet v2 | Matplotlib | 0.699 ± 0.020 | 0.046 | 0.59 | 0.77 |
| Mobilenet v2 | ImageNet | 0.663 ± 0.022 | 0.052 | 0.55 | 0.74 |
| VGG19 | Blender2 | 0.732 ± 0.010 | 0.024 | 0.68 | 0.77 |
| VGG19 | Blender1 | 0.719 ± 0.011 | 0.026 | 0.67 | 0.77 |
| VGG19 | Matplotlib | 0.656 ± 0.014 | 0.034 | 0.58 | 0.72 |
| VGG19 | ImageNet | 0.532 ± 0.021 | 0.048 | 0.46 | 0.61 |
| Predicted Class | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Real Class | Dr18 | Dr24–25 | Dr27 | Dr29 | Dr33 | Dr35 | Dr36 | Dr37 | Dr38 |
| Dr18 | 63 | 4 | 2 | 2 | 6 | 2 | 14 | 3 | 3 |
| Dr24-25 | 5 | 76 | 5 | 1 | 3 | 3 | 2 | 1 | 4 |
| Dr27 | 2 | 4 | 74 | 2 | 2 | 9 | 2 | 2 | 4 |
| Dr29 | 2 | 2 | 3 | 74 | 2 | 1 | 4 | 7 | 5 |
| Dr33 | 3 | 2 | 2 | 1 | 89 | 2 | 0 | 1 | 1 |
| Dr35 | 1 | 4 | 11 | 1 | 1 | 67 | 11 | 1 | 3 |
| Dr36 | 8 | 4 | 2 | 4 | 1 | 12 | 60 | 2 | 8 |
| Dr37 | 2 | 9 | 1 | 11 | 3 | 1 | 1 | 68 | 4 |
| Dr38 | 1 | 6 | 2 | 3 | 2 | 2 | 7 | 1 | 76 |
| Predicted Class | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Real Class | Dr18 | Dr24–25 | Dr27 | Dr29 | Dr33 | Dr35 | Dr36 | Dr37 | Dr38 |
| Dr18 | 81 | 2 | 1 | 3 | 2 | 1 | 7 | 2 | 1 |
| Dr24-25 | 3 | 80 | 1 | 2 | 2 | 3 | 2 | 2 | 6 |
| Dr27 | 1 | 2 | 87 | 1 | 3 | 3 | 1 | 1 | 1 |
| Dr29 | 2 | 2 | 1 | 81 | 2 | 1 | 2 | 7 | 3 |
| Dr33 | 0 | 1 | 0 | 1 | 95 | 1 | 0 | 0 | 0 |
| Dr35 | 1 | 0 | 4 | 1 | 1 | 80 | 10 | 0 | 2 |
| Dr36 | 6 | 2 | 0 | 1 | 1 | 11 | 72 | 1 | 6 |
| Dr37 | 1 | 6 | 1 | 7 | 1 | 0 | 0 | 82 | 3 |
| Dr38 | 2 | 3 | 2 | 1 | 1 | 3 | 8 | 1 | 79 |
| Damaged | |||||
|---|---|---|---|---|---|
| Class | ImageNet | Matplotlib | Blender1 | Blender2 | |
| Dr18 | 0.48 | 0.52 | 0.55 | 0.60 | 13.60 |
| Dr24–25 | 0.31 | 0.56 | 0.41 | 0.36 | 0.20 |
| Dr27 | 0.53 | 0.60 | 0.69 | 0.69 | 4.75 |
| Dr29 | 0.69 | 0.73 | 0.77 | 0.72 | 5.55 |
| Dr33 | 0.81 | 0.85 | 0.91 | 0.93 | 1.95 |
| Dr35 | - | - | - | - | 0.00 |
| Dr36 | 0.53 | 0.62 | 0.60 | 0.63 | 3.05 |
| Dr37 | 0.56 | 0.33 | 0.69 | 0.76 | 0.40 |
| Dr38 | 0.79 | 0.74 | 0.78 | 0.78 | 1.05 |
| Non-Damaged | |||||
|---|---|---|---|---|---|
| Class | ImageNet | Matplotlib | Blender1 | Blender2 | |
| Dr18 | 0.70 | 0.81 | 0.90 | 0.90 | 31.40 |
| Dr24–25 | 0.86 | 0.89 | 0.85 | 0.89 | 1.80 |
| Dr27 | 0.8 | 0.90 | 0.92 | 0.92 | 17.25 |
| Dr29 | 0.79 | 0.82 | 0.89 | 0.88 | 6.45 |
| Dr33 | 0.92 | 0.91 | 0.95 | 0.96 | 5.05 |
| Dr35 | 0.67 | 0.69 | 0.78 | 0.80 | 6.00 |
| Dr36 | 0.64 | 0.72 | 0.79 | 0.77 | 5.95 |
| Dr37 | 0.64 | 0.86 | 0.79 | 0.82 | 2.60 |
| Dr38 | 0.75 | 0.81 | 0.77 | 0.82 | 0.95 |
| Matplotlib | Blender1 | Blender2 | ||||
|---|---|---|---|---|---|---|
| Model | Mean | Std | Mean | Std | Mean | Std |
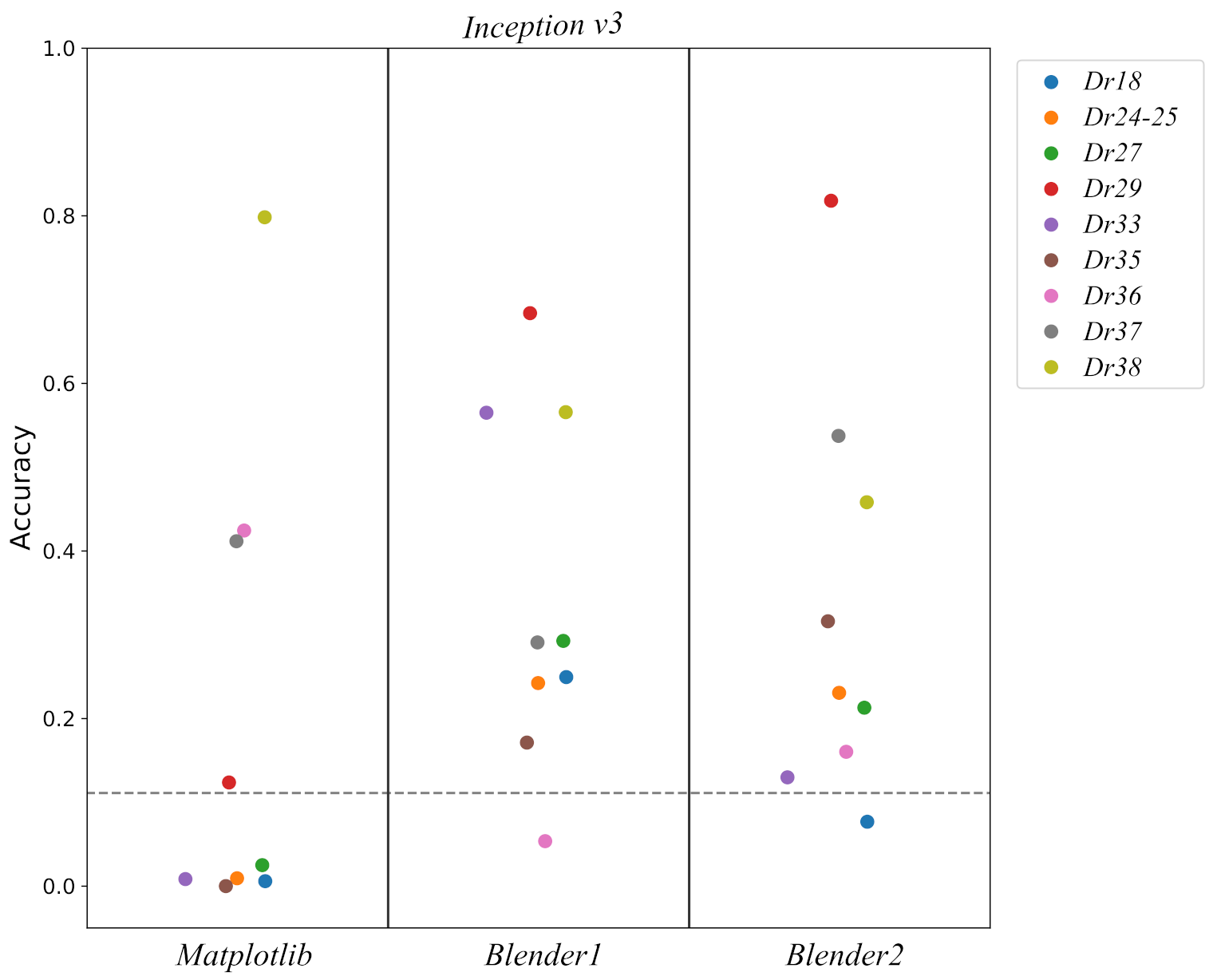
| Inception v3 | 0.20 | 0.28 | 0.35 | 0.21 | 0.33 | 0.24 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Núñez Jareño, S.J.; van Helden, D.P.; Mirkes, E.M.; Tyukin, I.Y.; Allison, P.M. Learning from Scarce Information: Using Synthetic Data to Classify Roman Fine Ware Pottery. Entropy 2021, 23, 1140. https://doi.org/10.3390/e23091140
Núñez Jareño SJ, van Helden DP, Mirkes EM, Tyukin IY, Allison PM. Learning from Scarce Information: Using Synthetic Data to Classify Roman Fine Ware Pottery. Entropy. 2021; 23(9):1140. https://doi.org/10.3390/e23091140
Chicago/Turabian StyleNúñez Jareño, Santos J., Daniël P. van Helden, Evgeny M. Mirkes, Ivan Y. Tyukin, and Penelope M. Allison. 2021. "Learning from Scarce Information: Using Synthetic Data to Classify Roman Fine Ware Pottery" Entropy 23, no. 9: 1140. https://doi.org/10.3390/e23091140
APA StyleNúñez Jareño, S. J., van Helden, D. P., Mirkes, E. M., Tyukin, I. Y., & Allison, P. M. (2021). Learning from Scarce Information: Using Synthetic Data to Classify Roman Fine Ware Pottery. Entropy, 23(9), 1140. https://doi.org/10.3390/e23091140








