Common Coherence Witnesses and Common Coherent States
Abstract
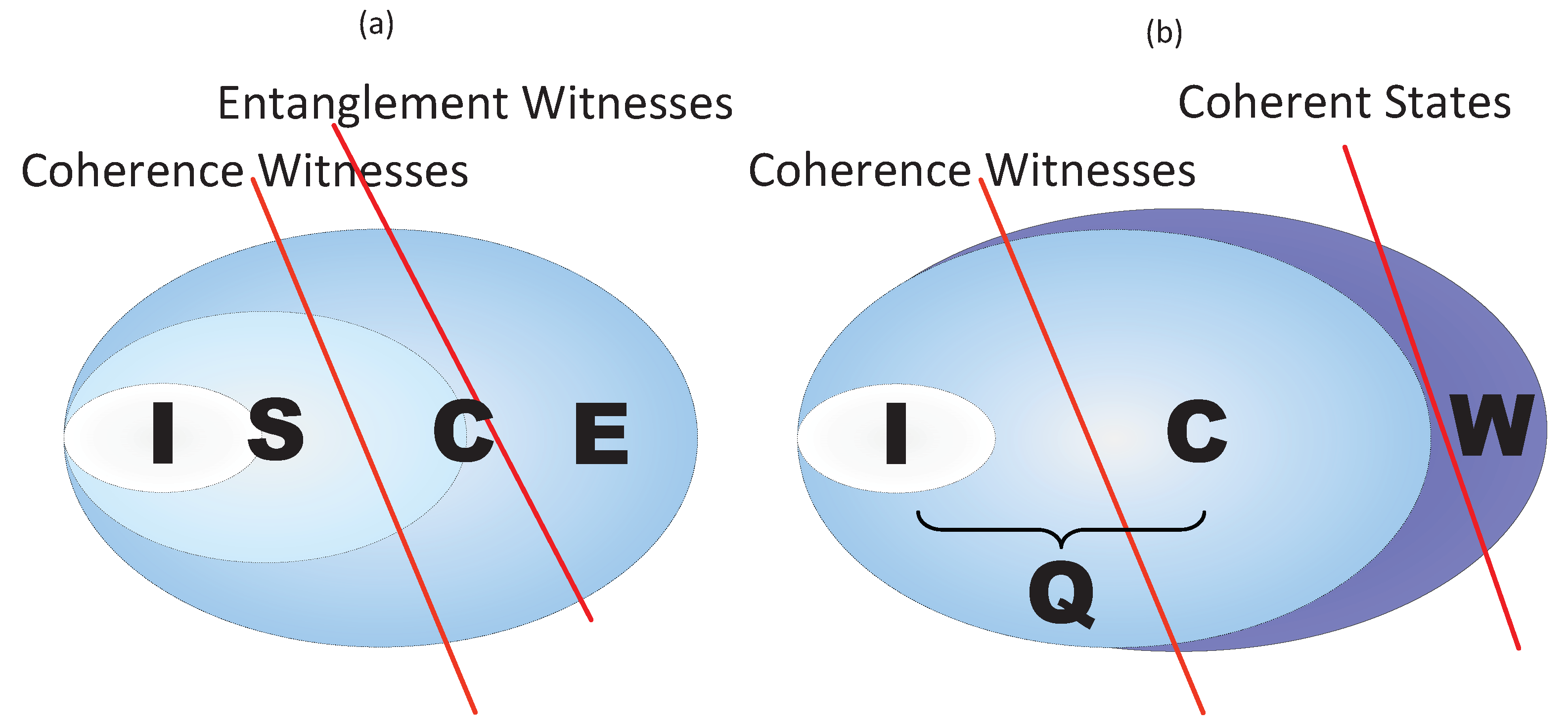
:1. Introduction
2. Common Coherence Witnesses
3. Common Coherent States
4. Summary and Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Streltsov, A.; Adesso, G.; Plenio, M.B. Colloquium: Quantum coherence as a resource. Rev. Mod. Phys. 2017, arXiv:quant-ph/1609.0243989, 041003. [Google Scholar] [CrossRef] [Green Version]
- Hu, M.-L.; Hu, X.; Wang, J.-C.; Peng, Y.; Zhang, Y.-R.; Fan, H. Quantum coherence and geometric quantum discord. Phys. Rep. 2018, 1, 762–764. [Google Scholar] [CrossRef] [Green Version]
- Giovannetti, V.; Lloyd, S.; Maccone, L. Quantum-Enhanced Measurements: Beating the Standard Quantum Limit. Science 2004, 306, 1330. [Google Scholar] [CrossRef] [Green Version]
- Giovannetti, V.; Lloyd, S.; Maccone, L. Advances in quantum metrology. Nat. Photonics 2011, 5, 222. [Google Scholar] [CrossRef]
- Hillery, M. Coherence as a resource in decision problems: The Deutsch-Jozsa algorithm and a variation. Phys. Rev. A 2016, 93, 012111. [Google Scholar] [CrossRef] [Green Version]
- Åberg, J. Catalytic coherence. Phys. Rev. Lett. 2014, 113, 150402. [Google Scholar] [CrossRef] [Green Version]
- Gour, G.; Müller, M.P.; Narasimhachar, V.; Spekkens, R.W.; Halpern, N.Y. The Resource Theory of Informational Nonequilibrium in Thermodynamics. Phys. Rep. 2015, 583, 1–58. [Google Scholar] [CrossRef] [Green Version]
- Lostaglio, M.; Jennings, D.; Rudolph, T. Description of quantum coherence in thermodynamic processes requires constraints beyond free energy. Nat. Commun. 2015, 6, 6383. [Google Scholar] [CrossRef] [Green Version]
- Narasimhachar, V.; Gour, G. Low-temperature thermodynamics with quantum coherence. Nat. Commun. 2015, 6, 7689. [Google Scholar] [CrossRef]
- Francica, G.; Goold, J.; Plastina, F. Role of coherence in the nonequilibrium thermodynamics of quantum systems. Phys. Rev. E 2019, 99, 042105. [Google Scholar] [CrossRef] [Green Version]
- Lloyd, S. Quantum coherence in biological systems. J. Phys. Conf. Ser. 2011, 302, 012037. [Google Scholar] [CrossRef]
- Huelga, S.F.; Plenio, M.B. Vibrations, quanta and biology. Contemp. Phys. 2013, 54, 181. [Google Scholar] [CrossRef]
- Lambert, N.; Chen, Y.-N.; Cheng, Y.-C.; Li, C.-M.; Chen, G.-Y.; Nori, F. Quantum biology. Nat. Phys. 2013, 9, 10. [Google Scholar] [CrossRef]
- Romero, E.; Augulis, R.; Novoderezhkin, V.I.; Ferretti, M.; Thieme, J.; Zigmantas, D.; van Grondelle, R. Quantum coherence in photosynthesis for efficient solar-energy conversion. Nat. Phys. 2014, 10, 676. [Google Scholar] [CrossRef] [PubMed]
- Baumgratz, T.; Cramer, M.; Plenio, M.B. Quantifying Coherence. Phys. Rev. Lett. 2014, 113, 140401. [Google Scholar] [CrossRef] [Green Version]
- Yuan, X.; Zhou, H.; Cao, Z.; Ma, X. Intrinsic randomness as a measure of quantum coherence. Phys. Rev. A 2015, 92, 022124. [Google Scholar] [CrossRef] [Green Version]
- Fang, K.; Wang, X.; Lami, L.; Regula, B.; Adesso, G. Probabilistic Distillation of Quantum Coherence. Phys. Rev. Lett. 2018, 121, 070404. [Google Scholar] [CrossRef] [Green Version]
- Winter, A.; Yang, D. Operational Resource Theory of Coherence. Phys. Rev. Lett. 2016, 116, 120404. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Streltsov, A.; Singh, U.; Dhar, H.S.; Bera, M.N.; Adesso, G. Measuring Quantum Coherence with Entanglement. Phys. Rev. Lett. 2015, 115, 020403. [Google Scholar] [CrossRef] [Green Version]
- Du, S.; Bai, S.; Qi, X. Coherence measures and optimal conversion for coherent states. Quantum Inf. Comput. 2015, 15, 1307. [Google Scholar]
- Qi, X.; Gao, T.; Yan, F. Measuring coherence with entanglement concurrence. J. Phys. A Math. Theor. 2017, 50, 285301. [Google Scholar] [CrossRef]
- Bu, K.F.; Singh, U.; Fei, S.M.; Pati, A.K.; Wu, J.D. Maximum Relative Entropy of Coherence: An Operational Coherence Measure. Phys. Rev. Lett. 2017, 119, 150405. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, Z.; Situ, H. Dynamics of quantum correlation and coherence for two atoms coupled with a bath of fluctuating massless scalar field. Ann. Phys. 2017, 377, 484. [Google Scholar] [CrossRef]
- Jin, Z.-X.; Fei, S.-M. Quantifying quantum coherence and nonclassical correlation based on Hellinger distance. Phys. Rev. A 2018, 97, 062342. [Google Scholar] [CrossRef] [Green Version]
- Xi, Z.; Yuwen, S. Coherence measure: Logarithmic coherence number. Phys. Rev. A 2019, 99, 022340. [Google Scholar] [CrossRef] [Green Version]
- Napoli, C.; Bromley, T.R.; Cianciaruso, M.; Piani, M.; Johnston, N.; Adesso, G. Robustness of Coherence: An Operational and Observable Measure of Quantum Coherence. Phys. Rev. Lett. 2016, 116, 150502. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Piani, M.; Cianciaruso, M.; Bromley, T.R.; Napoli, C.; Johnston, N.; Adesso, G. Robustness of asymmetry and coherence of quantum states. Phys. Rev. A 2016, 93, 042107. [Google Scholar] [CrossRef] [Green Version]
- Nie, Y.; Zhou, H.; Guan, J.-Y.; Zhang, Q.; Ma, X.; Zhang, J.; Pan, J.-W. Quantum Coherence Witness with Untrusted Measurement Devices. Phys. Rev. Lett. 2019, 123, 090502. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.-T.; Tang, J.-S.; Wei, Z.-Y.; Yu, S.; Ke, Z.-J.; Xu, X.; Li, C.-F.; Guo, G.-C. Directly Measuring the Degree of Quantum Coherence using Interference Fringes. Phys. Rev. Lett. 2017, 118, 020403. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zheng, W.; Ma, Z.; Wang, H.; Fei, S.-M.; Peng, X. Experimental Demonstration of Observability and Operability of Robustness of Coherence. Phys. Rev. Lett. 2018, 120, 230504. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ringbauer, M.; Bromley, T.R.; Cianciaruso, M.; Lami, L.; Lau, W.Y.S.; Adesso, G.; White, A.G.; Fedrizzi, A.; Piani, M. Certification and Quantification of Multilevel Quantum Coherence. Phys. Rev. X 2018, 8, 041007. [Google Scholar] [CrossRef] [Green Version]
- Ma, J.; Hakande, A.; Yuan, X.; Ma, X. Coherence as a resource for source-independent quantum random-number generation. Phys. Rev. A 2019, 99, 022328. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.-H.; Zhou, S.-Q.; Ma, Z.; Fei, S.-M. Tomographic Witnessing and Holographic Quantifying of Coherence. Quant. Inform. Proc. 2021, 20. [Google Scholar]
- Ma, Z.; Zhang, Z.; Dai, Y.; Dong, Y.; Zhang, C. Detecting and estimating coherence based on coherence witnesses. Phys. Rev. A 2021, 103, 012409. [Google Scholar] [CrossRef]
- Wu, Y.; Han, Y.; Guo, G. Tetrahedral-octahedral network structure transition in simulated vitreous SiO2. Phys. Lett. A 2006, 356, 402. [Google Scholar] [CrossRef]
- Wu, Y.-C.; Guo, G.-C. The hierarchies of “witnesses” and the properties and characterization of entangled states as super entanglement witnesses. Phys. Rev. A 2007, 75, 052333. [Google Scholar] [CrossRef]
- Hou, J.; Guo, Y. When different entanglement witnesses detect the same entangled states. Phys. Rev. A 2010, 82, 052301. [Google Scholar] [CrossRef] [Green Version]
- Edwards, R.E. Functional Analysis, Theory and Application; Holt, Rinehart and Winston: New York, NY, USA, 1965. [Google Scholar]
- Ren, H.; Lin, A.; He, S.; Hu, X. Quantitative coherence witness for finite dimensional states. Ann. Phys. 2017, 387, 281–289. [Google Scholar] [CrossRef] [Green Version]
- Gühne, O.; Tóth, G. Entanglement detection. Phys. Rep. 2009, 474, 1–75. [Google Scholar] [CrossRef] [Green Version]
- Horodecki, R.; Horodecki, P.; Horodecki, M.; Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 2009, 81, 865. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.-H. Entangled states in the role of witnesses. Phys. Rev. A 2018, 97, 050302(R). [Google Scholar] [CrossRef] [Green Version]
- Bruß, D.; Cirac, J.I.; Horodecki, P.; Hulpke, F.; Kraus, B.; Lewenstein, M.; Sanpera, A. Reflections upon separability and distillability. J. Mod. Opt. 2002, 49, 1399. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.-H.; Ding, Z.-H.; Ma, Z.; Fei, S.-M. Common Coherence Witnesses and Common Coherent States. Entropy 2021, 23, 1136. https://doi.org/10.3390/e23091136
Wang B-H, Ding Z-H, Ma Z, Fei S-M. Common Coherence Witnesses and Common Coherent States. Entropy. 2021; 23(9):1136. https://doi.org/10.3390/e23091136
Chicago/Turabian StyleWang, Bang-Hai, Zi-Heng Ding, Zhihao Ma, and Shao-Ming Fei. 2021. "Common Coherence Witnesses and Common Coherent States" Entropy 23, no. 9: 1136. https://doi.org/10.3390/e23091136
APA StyleWang, B.-H., Ding, Z.-H., Ma, Z., & Fei, S.-M. (2021). Common Coherence Witnesses and Common Coherent States. Entropy, 23(9), 1136. https://doi.org/10.3390/e23091136






