Research on the Longitudinal Section of River Restoration Using Probabilistic Theory
Abstract
:1. Introduction
2. Methodology
3. Theoretical Background
3.1. Nonlinear Regression
3.2. Entropy Theory
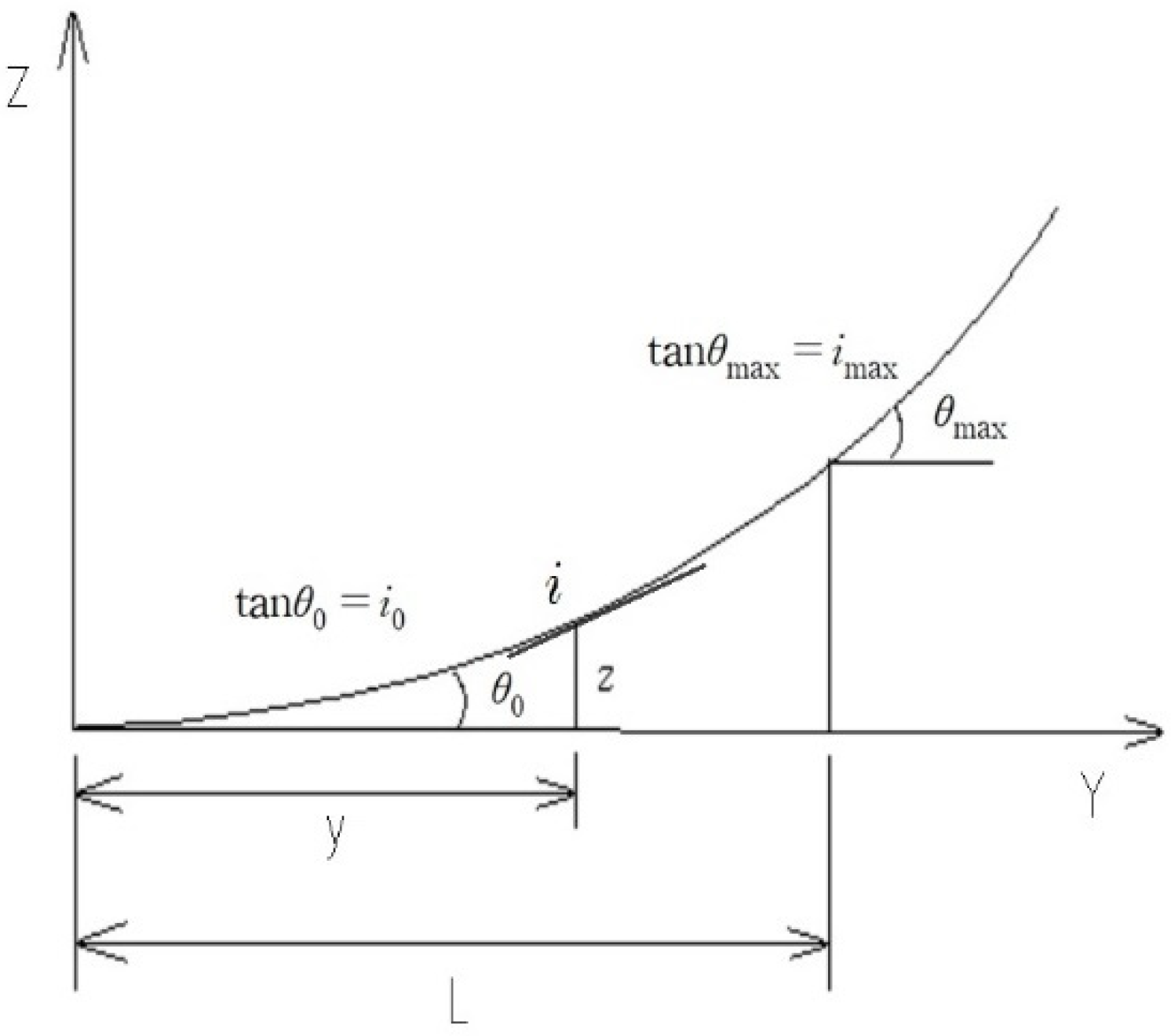
3.3. River Mean Slope Formula Development
3.4. RMSE
4. Application to Real River
4.1. Determination of Parameter by Measured Values
4.2. River Longitudinal Elevation
5. Conclusions
- (1)
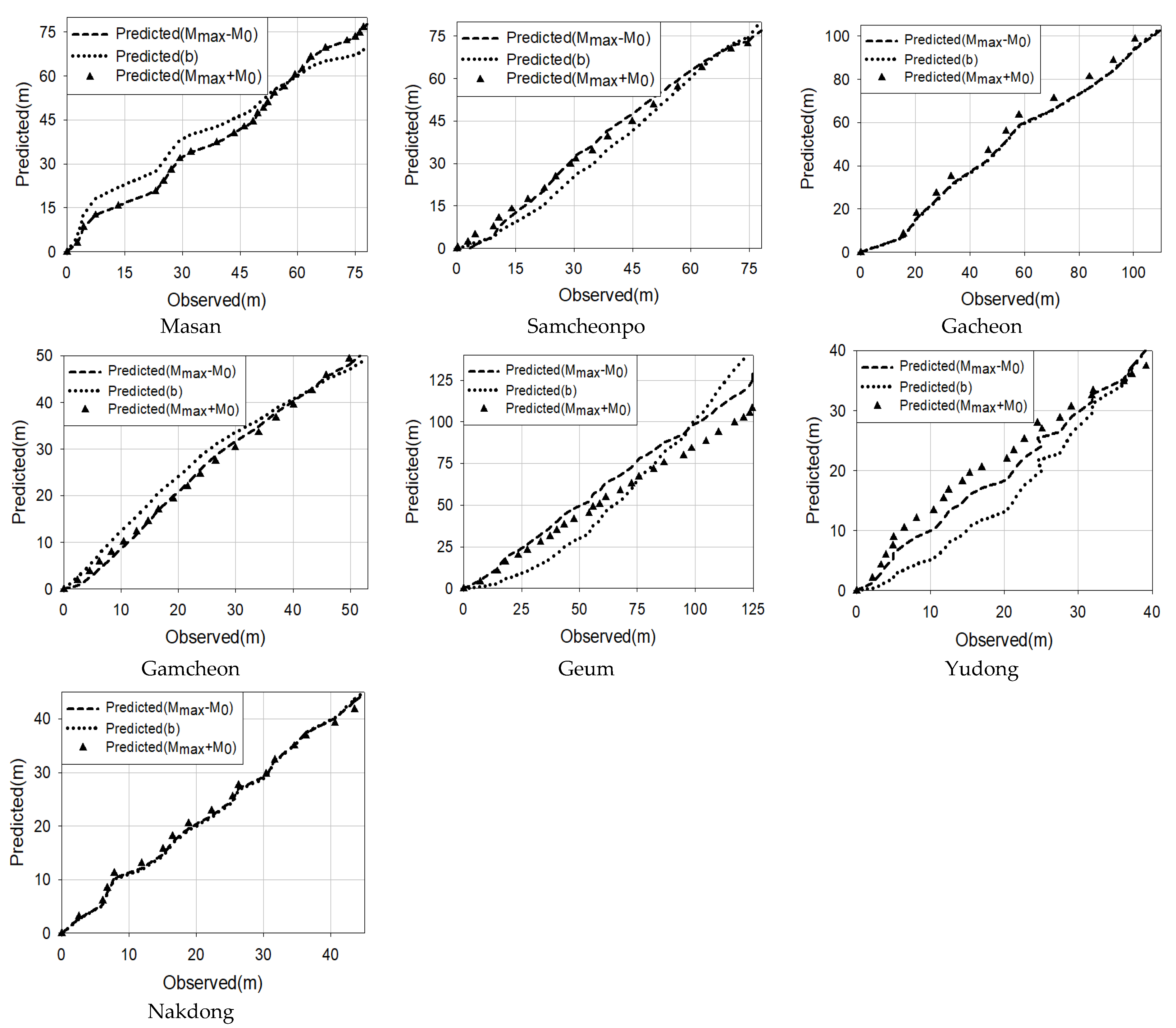
- The verification of the accuracy of the equation in this paper is based on the nonlinear regression analysis with SPSS 26 and SYSTAT 6.0. The value is 0.8150 to 0.9950. The values show that the equation is valid, and the application to actual rivers is considered significant.
- (2)
- Gacheon river shows the highest accuracy of prediction (close to 0.99) out of all methods. Yoodong river has parts that do not increase monotonically, and all three methods predict that singularity similarly. The suggested formulae are able to predict the section where the slope changes are large.
- (3)
- Since Mmax and M0 are parameters of the river, once the parameter is calculated the longitudinal section of the river can be obtained before it is destroyed. The reliability of this method can be further enhanced by using the data measured over 40 years or over 100 years.
- (4)
- When making calculations using the equation presented in this study, it is easy to calculate the slope and elevation at a random point in the river basin.
- (5)
- It is expected that one use the river longitudinal section obtained through the equation to restore damaged rivers to their longitudinal elevations and ramps before development.
- (6)
- Using the method proposed in this paper, the river elevation can be obtained more accurately, which can help more precisely in the production of a digital elevation model or modify the data in places where it is hard to measure.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Han, S.M.; Park, T.S. The comparative analysis of LiDAR data and actual measurement data. J. Korea Soc. Geospat. Inf. Syst. 2009, 72–77. [Google Scholar] [CrossRef]
- Lienhard, J.H. A Statistical Mechanical Prediction of the Dimensionless Unit Hydrograph. J. Geophys. Res. 1964, 24, 5231–5238. [Google Scholar] [CrossRef]
- Wilson, G. The use of the concept of entropy in system modeling. J. Oper. Res. Soc. 1970, 21, 247–265. [Google Scholar] [CrossRef]
- Leopold, L.B.; Langbein, W.B. The Concept of Entropy in Landscape Evolution; U.S Government Printing Office: Washington, DC, USA, 1962. [CrossRef]
- Yang, T. Potential Energy and Stream Morphology. Water Resour. Res. 1971, 7, 311–322. [Google Scholar] [CrossRef]
- Singh, V.P.; Fiorentino, M. A historical perspective of entropy application in water resources. Entropy Energy Dissipation Water Resour. 1992, 21–61. [Google Scholar] [CrossRef]
- Chapman, T.G. Entropy as measure of hydrologic data uncertainty and model performance. J. Hydrol. 1986, 85, 111–126. [Google Scholar] [CrossRef]
- Chiu, L. Entropy and probability concepts in hydraulics. J. Hydraul. Eng. 1987, 113, 583–600. [Google Scholar] [CrossRef]
- Chiu, L. Entropy and 2-D velocity distribution in open channels. J. Hydraul. Eng. 1988, 114, 738–756. [Google Scholar] [CrossRef]
- Chiu, C.L. Velocity distribution in open channel flow. J. Hydraul. Eng. 1989, 115, 576–594. [Google Scholar] [CrossRef]
- Fiorentino, M.; Claps, P.; Singh, V.P. An Entropy-based Morphological Analysis of River Basin Networks. Water Resour. Res. 1993, 29, 1215–1224. [Google Scholar] [CrossRef] [Green Version]
- Claps, P.; Fiorentino, M.; Oilveto, G. Informational entropy of fractal river networks. J. Hydrol. 1996, 187, 145–156. [Google Scholar] [CrossRef] [Green Version]
- Mirauda, D.; Pannone, M.; de Vincenzo, A. An entropic model for the assessment of stream-wise velocity dip in wide open channels. Entropy 2018, 20, 69. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kundu, S. Prediction of velocity-dip-position at the central section of open channels using entropy theory. J. Appl. Fluid Mech. 2017, 10, 221–229. [Google Scholar] [CrossRef]
| River | Length (km) | ||
|---|---|---|---|
| Masan | 18.57 (entire) | ||
| Samcheonpo | 7 (entire) | ||
| Gacheon | 21.19 (entire) | ||
| Gamcheon | 13.13 (entire) | ||
| Geum | 3.25 (entire) | ||
| Yudong | 11.31 (entire) | ||
| Nakdong | 21.42 (selected) |
| River | b | ||||
|---|---|---|---|---|---|
| Masan | −44.778 | −8.481 | −53.336 | −8.481 | −104.898 |
| Samcheonpo | −1311.532 | −708.388 | −2.056 | 3.428 | −5.911 |
| Gacheon | −48.3386 | −21.8701 | −21.2442 | −47.2009 | −602.821 |
| Gamcheon | 1 | 0.9944 | −24.804 | 5.113 | −88,000 |
| Geum | −2.6198 | −101.655 | −2.6195 | −13.8264 | −456.546 |
| Yudong | −15.179 | −9.616 | −2.517 | −8.917 | 39.952 |
| Nakdong | −155.335 | −20.034 | −11.929 | −91.464 | −2458.048 |
| River | Measured | Predicted | ||
|---|---|---|---|---|
| b | ||||
| Masan | 0.01818 | 0.022464 | 0.022648 | 0.019296 |
| Samcheonpo | 0.054015 | 0.05124 | 0.194054 | 0.054411 |
| Gacheon | 0.015634 | 0.015098 | 0.01483 | 0.014972 |
| Gamcheon | 0.001508 | 0.001588 | 0.001247 | 0.001284 |
| Geum | 0.001591 | 0.001052 | 0.000876 | 0.001145 |
| Yudong | 0.003771 | 0.002601 | 0.002624 | 0.002942 |
| Nakdong | 0.028358 | 0.003568 | 0.00355 | 0.003488 |
| River | b | |||||
|---|---|---|---|---|---|---|
| R2 | RMSE | R2 | RMSE | R2 | RMSE | |
| Masan | 0.987 | 2.153 | 0.987 | 2.153 | 0.938 | 5.883 |
| Samcheonpo | 0.94 | 0.828 | 0.991 | 2.72 | 0.979 | 4.175 |
| Gacheon | 0.995 | 2.794 | 0.987 | 4.908 | 0.987 | 5.142 |
| Gamcheon | 0.998 | 0.549 | 0.992 | 1.321 | 0.966 | 2.862 |
| Geum | 0.998 | 10.821 | 0.955 | 1.605 | 0.815 | 15.775 |
| Yoodong | 0.995 | 2.687 | 0.949 | 0.822 | 0.94 | 3.831 |
| Nakdong | 0.993 | 1.369 | 0.995 | 0.834 | 0.994 | 0.801 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choo, Y.-M.; Kim, J.-M.; An, I.-T. Research on the Longitudinal Section of River Restoration Using Probabilistic Theory. Entropy 2021, 23, 965. https://doi.org/10.3390/e23080965
Choo Y-M, Kim J-M, An I-T. Research on the Longitudinal Section of River Restoration Using Probabilistic Theory. Entropy. 2021; 23(8):965. https://doi.org/10.3390/e23080965
Chicago/Turabian StyleChoo, Yeon-Moon, Ji-Min Kim, and Ik-Tae An. 2021. "Research on the Longitudinal Section of River Restoration Using Probabilistic Theory" Entropy 23, no. 8: 965. https://doi.org/10.3390/e23080965
APA StyleChoo, Y.-M., Kim, J.-M., & An, I.-T. (2021). Research on the Longitudinal Section of River Restoration Using Probabilistic Theory. Entropy, 23(8), 965. https://doi.org/10.3390/e23080965






