Learning Ordinal Embedding from Sets
Abstract
:1. Introduction
- A Set-valued Ordinal Embedding (SetOE) is proposed to embed data points in a low-dimensional space. We reformulate the classical ordinal embedding problem based on single data points into a generalization based on sets while assuring the permutation invariance necessary when dealing with the set. We develop an architecture to allow for conditioning with possibly different sizes of sets and adapt the margin-based loss for set-valued input;
- We propose a distributional approach that does not rely on the features of the individual data points for the ordinal embedding problem with sets. We motivate the advantages of such a setting and explain the properties we use to enable this;
- Experiments on both artificial and reals datasets demonstrate the validity of our approach for embedding datasets of considerable size in a significantly low-dimensional space (e.g., two). We evaluate our approach on several datasets. First, we present a proof-of-concept with different synthetic datasets. Then, we escalate the complexity of the tasks to the MNIST dataset, poker, and more real-word datasets such as Reuters.
2. Ordinal Embedding
2.1. Classical Ordinal Embedding
2.2. Distributional Ordinal Embedding
2.2.1. The Two-Wasserstein Distance
2.2.2. Learning Gaussian Embeddings
3. Ordinal Embedding for Sets
3.1. Problem Statement
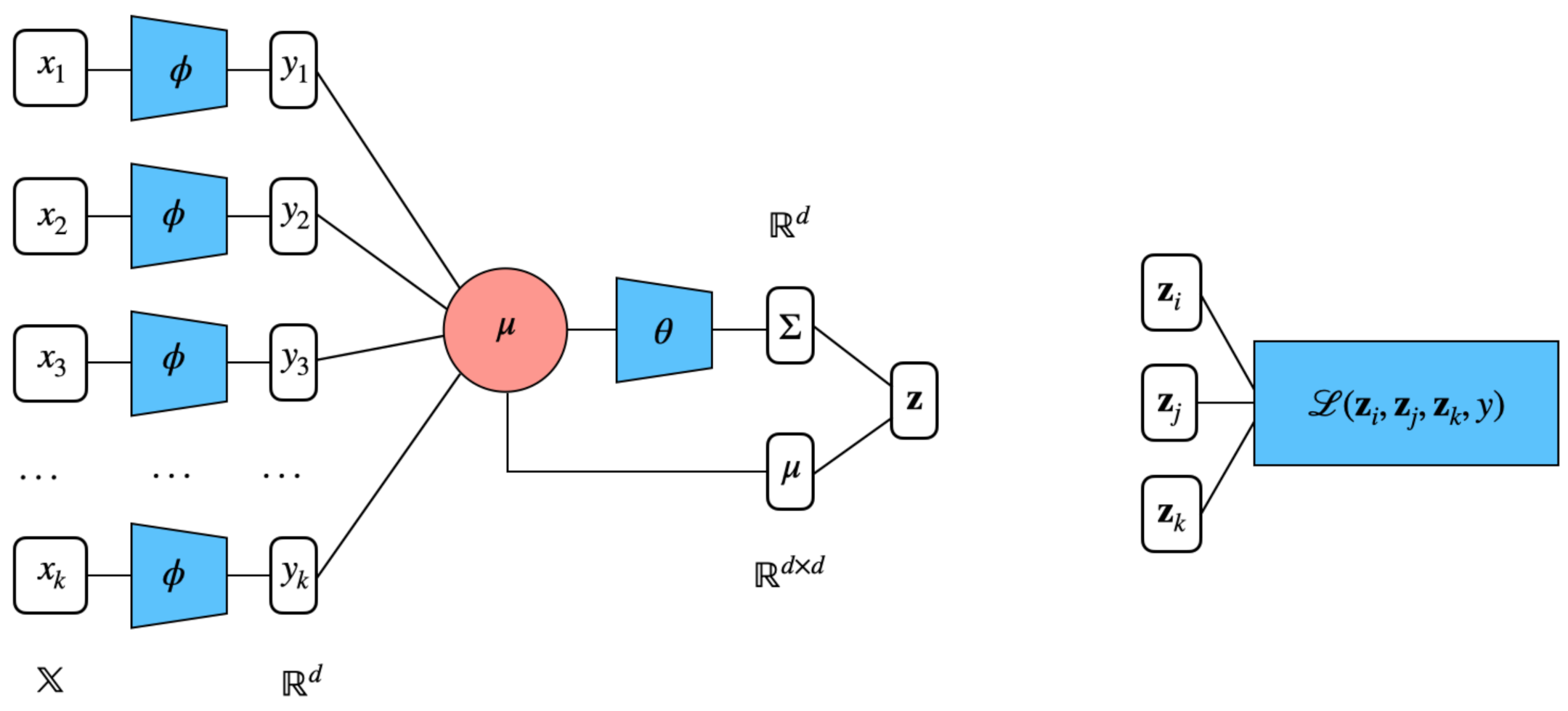
3.2. Set Encoding
3.3. Distributional Embeddings for Sets
| Algorithm 1 Distributional ordinal embeddings from set constraints. |
|
3.4. Deep Set Encoder
3.5. Complexity
3.6. Practical Tricks
4. Experiments
4.1. Synthetic Datasets
- (i)
- Gaussian isotropic blobs;
- (ii)
- A large circle containing a smaller circle in 2D;
- (iii)
- Two interwoven spirals;
- (iv)
- Two interleaving half circles;
- Fix n and with , respectively the number of sets of items, and the size of each set;
- Generate n points that follow the pattern of the chosen dataset. These points are the centroids of the n sets;
- Given , draw random points from a normal distribution parameterized as . We chose , the spread of the set, between 0 and 0.5;
- We divided the obtained n cloud of points in overlapping sets.
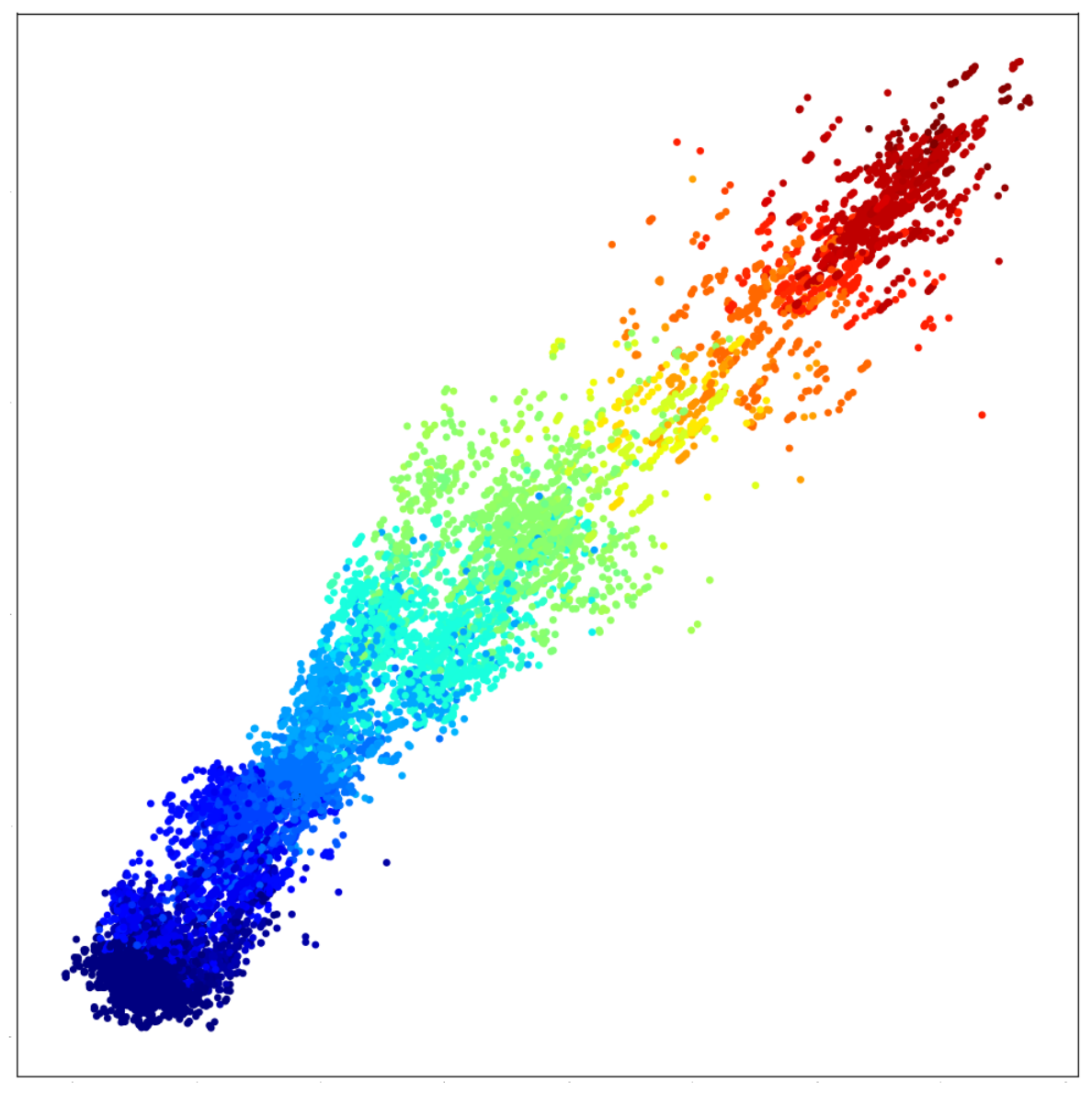
4.2. Sum of MNIST Digits
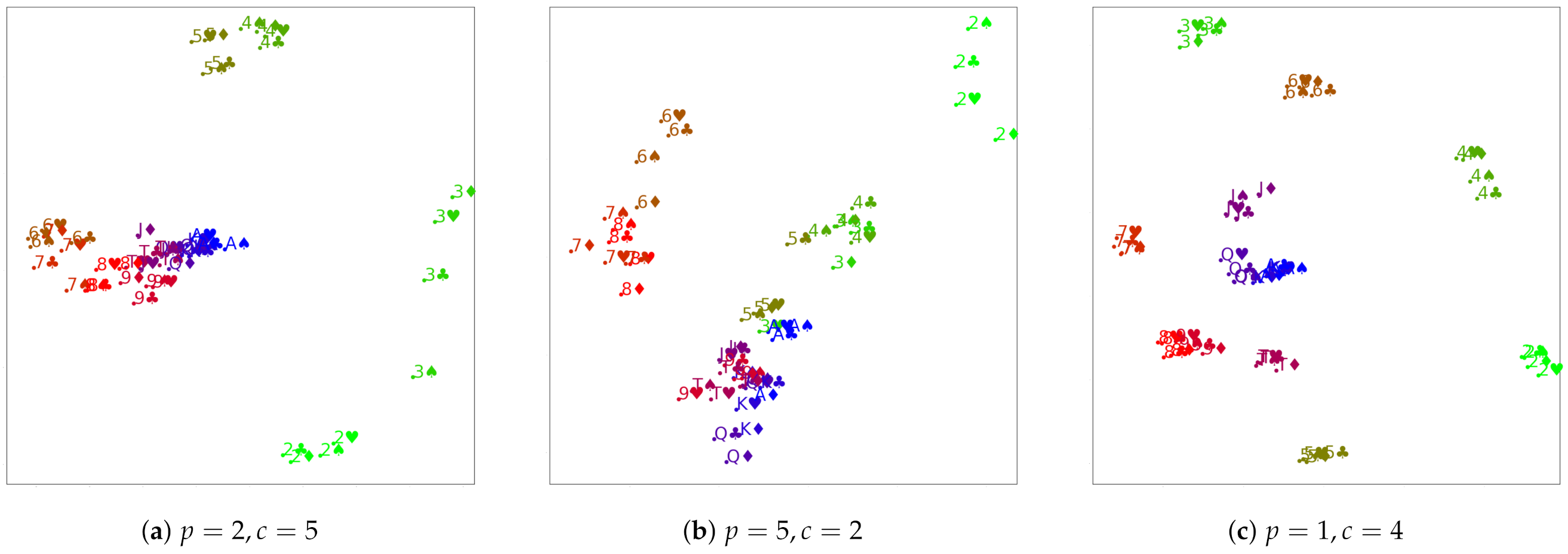
4.3. Poker Hands
4.4. Reuters
5. Related Work
5.1. Ordinal Embeddings
5.2. Sets’ Representation
5.3. Sets Encoder Models
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shepard, R.N. The analysis of proximities: Multidimensional scaling with an unknown distance function. I. Psychometrika 1962, 27, 125–140. [Google Scholar] [CrossRef]
- Shepard, R.N. Metric structures in ordinal data. J. Math. Psychol. 1966, 3, 287–315. [Google Scholar] [CrossRef]
- Agarwal, S.; Wills, J.; Cayton, L.; Lanckriet, G.; Kriegman, D.; Belongie, S. Generalized non-metric multidimensional scaling. In Proceedings of the 11th International Conference on Artificial Intelligence and Statistics (AISTATS), San Juan, PR, USA, 21–24 March 2007; pp. 11–18. [Google Scholar]
- McFee, B. More Like This: Machine Learning Approaches to Music Similarity. Ph.D. Thesis, University of California, San Diego, CA, USA, 2012. [Google Scholar]
- Tamuz, O.; Liu, C.; Belongie, S.; Shamir, O.; Kalai, A. Adaptively Learning the Crowd Kernel. In Proceedings of the 28th International Conference on Machine Learning (ICML), Bellevue, WA, USA, 28 June–2 July 2011; pp. 673–680. [Google Scholar]
- Van Der Maaten, L.; Weinberger, K. Stochastic triplet embedding. In Proceedings of the IEEE International Workshop on Machine Learning for Signal Processing, Santander, Spain, 23–26 September 2012; pp. 1–6. [Google Scholar]
- Terada, Y.; von Luxburg, U. Local ordinal embedding. In Proceedings of the 31st International Conference on Machine Learning (ICML), Beijing, China, 21–26 June 2014; pp. 847–855. [Google Scholar]
- Kleindessner, M.; von Luxburg, U. Kernel functions based on triplet comparisons. In Proceedings of the Advances in Neural Information Processing Systems 30, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Jamieson, K.G.; Nowak, R.D. Low-dimensional embedding using adaptively selected ordinal data. In Proceedings of the 49th Annual Allerton Conference on Communication, Control, and Computing, Monticello, IL, USA, 28–30 September 2011. [Google Scholar]
- Diallo, A.; Fürnkranz, J. Elliptical Ordinal Embedding. arXiv 2021, arXiv:2105.10457. [Google Scholar]
- Joachims, T.; Granka, L.; Pan, B.; Hembrooke, H.; Gay, G. Accurately interpreting clickthrough data as implicit feedback. ACM SIGIR Forum 2017, 51, 4–11. [Google Scholar] [CrossRef]
- Muzellec, B.; Cuturi, M. Generalizing point embeddings using the Wasserstein space of elliptical distributions. In Proceedings of the Advances in Neural Information Processing System 31, Montréal, QC, Canada, 3–8 December 2018; pp. 10258–10269. [Google Scholar]
- Olkin, I.; Pukelsheim, F. The distance between two random vectors with given dispersion matrices. Linear Algebra Appl. 1982, 48, 257–263. [Google Scholar] [CrossRef] [Green Version]
- Frogner, C.; Zhang, C.; Mobahi, H.; Araya, M.; Poggio, T.A. Learning with a Wasserstein loss. In Proceedings of the Advances in Neural Information Processing Systems 28, Montréal, QB, Canada, 2–5 December 2015. [Google Scholar]
- Dittmann, J. Explicit formulae for the Bures metric. J. Phys. Math. Gen. 1999, 32, 2663–2670. [Google Scholar] [CrossRef]
- Beran, R. Minimum Hellinger distance estimates for parametric models. Ann. Stat. 1977, 5, 445–463. [Google Scholar] [CrossRef]
- LeCun, Y.; Chopra, S.; Hadsell, R.; Ranzato, M.; Huang, F.J. A Tutorial on Energy-Based Learning. In “Predicting Structured Data; MIT Press: Cambridge, MA, USA, 2006; Volume 1. [Google Scholar]
- Hoffer, E.; Ailon, N. Deep metric learning using triplet network. In Proceedings of the 3rd International Conference on Similarity-Based Pattern Recognition (ICLR Workshop Track), San Diego, CA, USA, 7–9 May 2015; pp. 84–92. [Google Scholar]
- Haghiri, S.; Vankadara, L.C.; von Luxburg, U. Large scale representation learning from triplet comparisons. arXiv 2019, arXiv:1912.01666. [Google Scholar]
- Chen, B.; Ankenman, J. The Mathematics of Poker; ConJelCo LLC., Jerrod: Pittsburgh, PA, USA, 2006. [Google Scholar]
- Xue, N.; Bird, E. Natural language processing with python. Nat. Lang. Eng. 2011, 17, 419. [Google Scholar] [CrossRef]
- Jain, L.; Jamieson, K.G.; Nowak, R. Finite Sample Prediction and Recovery Bounds for Ordinal Embedding. In Proceedings of the Advances in Neural Information Processing Systems 29, Barcelona, Spain, 5–10 December 2016; pp. 2711–2719. [Google Scholar]
- Heikinheimo, H.; Ukkonen, A. The crowd-median algorithm. In Proceedings of the 1st AAAI Conference on Human Computation and Crowdsourcing (HCOMP), Palm Springs, CA, USA, 7–9 November 2013. [Google Scholar]
- Ukkonen, A.; Derakhshan, B.; Heikinheimo, H. Crowdsourced nonparametric density estimation using relative distances. In Proceedings of the 3rd AAAI Conference on Human Computation and (HCOMP), San Diego, CA, USA, 8–11 November 2015. [Google Scholar]
- Ukkonen, A. Crowdsourced correlation clustering with relative distance comparisons. In Proceedings of the IEEE International Conference on Data Mining (ICDM), New Orleans, LA, USA, 18–21 November 2017; pp. 1117–1122. [Google Scholar]
- Zaheer, M.; Kottur, S.; Ravanbakhsh, S.; Poczos, B.; Salakhutdinov, R.R.; Smola, A.J. Deep Sets. In Advances in Neural Information Processing Systems 30; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2017. [Google Scholar]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. Pointnet: Deep learning on point sets for 3d classification and segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 652–660. [Google Scholar]
- Vinyals, O.; Fortunato, M.; Jaitly, N. Pointer Networks. In Advances in Neural Information Processing Systems 28; Cortes, C., Lawrence, N., Lee, D., Sugiyama, M., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2015. [Google Scholar]
- Vinyals, O.; Bengio, S.; Kudlur, M. Order Matters: Sequence to sequence for sets. In Proceedings of the 4th International Conference on Learning Representations (ICLR), San Juan, PR, USA, 2–4 May 2016. [Google Scholar]
- Zhang, Y.; Hare, J.; Prügel-Bennett, A. FSPool: Learning Set Representations with Featurewise Sort Pooling. In Proceedings of the International Conference on Learning Representations (ICLR), Addis Ababa, Ethiopia, 26 April–1 May 2020. [Google Scholar]
- Zhang, Y.; Hare, J.; Prügel-Bennett, A. Deep Set Prediction Networks. In Proceedings of the Advances in Neural Information Processing Systems 32, Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Zhang, Y.; Hare, J.; Prügel-Bennett, A. Learning Representations of Sets through Optimized Permutations. In Proceedings of the International Conference on Learning Representations (ICLR), New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Diallo, A.; Zopf, M.; Fürnkranz, J. Permutation Learning via Lehmer Codes. In Proceedings of the 24th European Conference on Artificial Intelligence (ECAI), Santiago de Compostela, Spain, 31 August–2 September 2020. [Google Scholar]
- Mena, G.; Belanger, D.; Linderman, S.; Snoek, J. Learning Latent Permutations with Gumbel-Sinkhorn Networks. In Proceedings of the International Conference on Learning Representations (ICLR), Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Weston, J.; Chopra, S.; Bordes, A. Memory networks. arXiv 2014, arXiv:1410.3916. [Google Scholar]
- Lee, J.; Lee, Y.; Kim, J.; Kosiorek, A.; Choi, S.; Teh, Y.W. Set transformer: A framework for attention-based permutation-invariant neural networks. In Proceedings of the International Conference on Machine Learning, PMLR, Long Beach, CA, USA, 10–15 June 2019; pp. 3744–3753. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 5998–6008. [Google Scholar]
- Murphy, R.L.; Srinivasan, B.; Rao, V.; Ribeiro, B. Janossy Pooling: Learning Deep Permutation-Invariant Functions for Variable-Size Inputs. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Yang, B.; Wang, S.; Markham, A.; Trigoni, N. Robust attentional aggregation of deep feature sets for multi-view 3D reconstruction. Int. J. Comput. Vis. 2020, 128, 53–73. [Google Scholar] [CrossRef] [Green Version]
- Skianis, K.; Nikolentzos, G.; Limnios, S.; Vazirgiannis, M. Rep the set: Neural networks for learning set representations. In Proceedings of the International Conference on Artificial Intelligence and Statistics. PMLR, Palermo, Italy, 26–28 August 2020; pp. 1410–1420. [Google Scholar]


| Ours | Baseline | |
|---|---|---|
| Circles | 0.12 | 0.18 |
| Moons | 0.09 | 0.33 |
| Spirals | 0.25 | 0.91 |
| Blobs | 0.03 | 0.04 |
| Baseline | Ours | |
|---|---|---|
| 0.76 | 0.78 | |
| 0.76 | 0.82 | |
| 0.77 | 0.79 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Diallo, A.; Fürnkranz, J. Learning Ordinal Embedding from Sets. Entropy 2021, 23, 964. https://doi.org/10.3390/e23080964
Diallo A, Fürnkranz J. Learning Ordinal Embedding from Sets. Entropy. 2021; 23(8):964. https://doi.org/10.3390/e23080964
Chicago/Turabian StyleDiallo, Aïssatou, and Johannes Fürnkranz. 2021. "Learning Ordinal Embedding from Sets" Entropy 23, no. 8: 964. https://doi.org/10.3390/e23080964
APA StyleDiallo, A., & Fürnkranz, J. (2021). Learning Ordinal Embedding from Sets. Entropy, 23(8), 964. https://doi.org/10.3390/e23080964






