The Problem of Engines in Statistical Physics
Abstract
1. Introduction
2. Feedback in Classical Engines
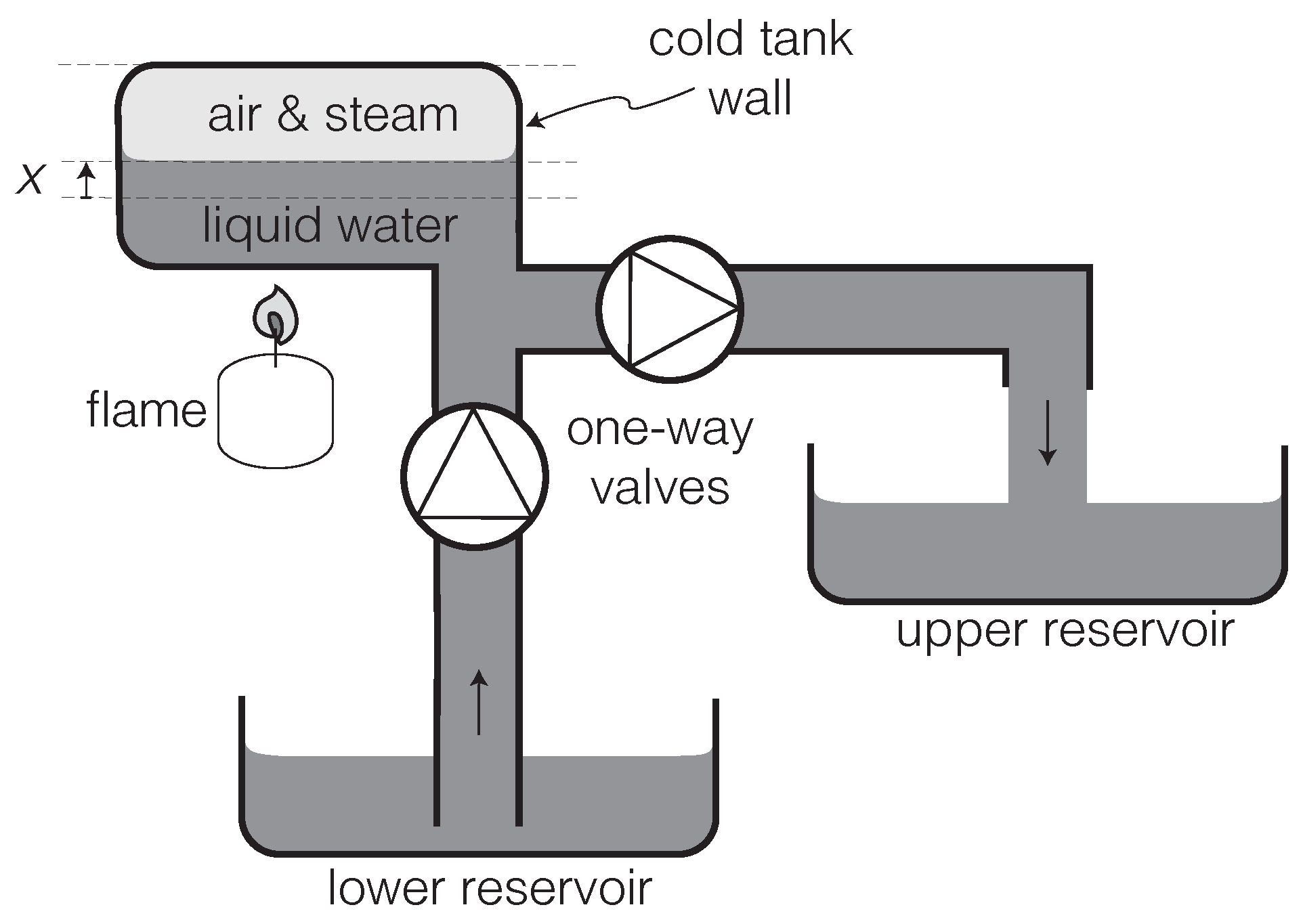
2.1. Rayleigh-Eddington Criterion
2.2. Active Force
2.3. Electrostatic Engines
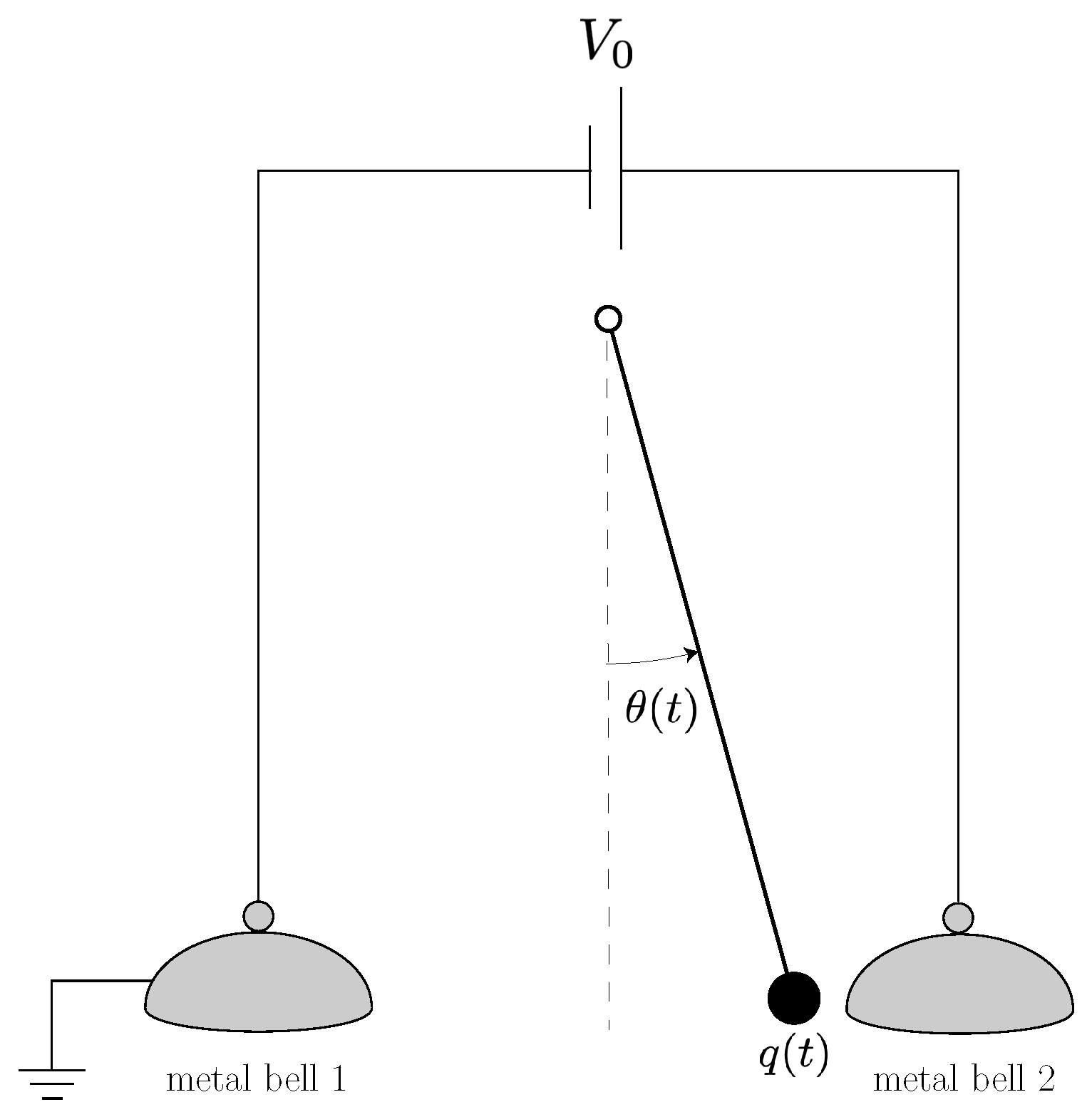
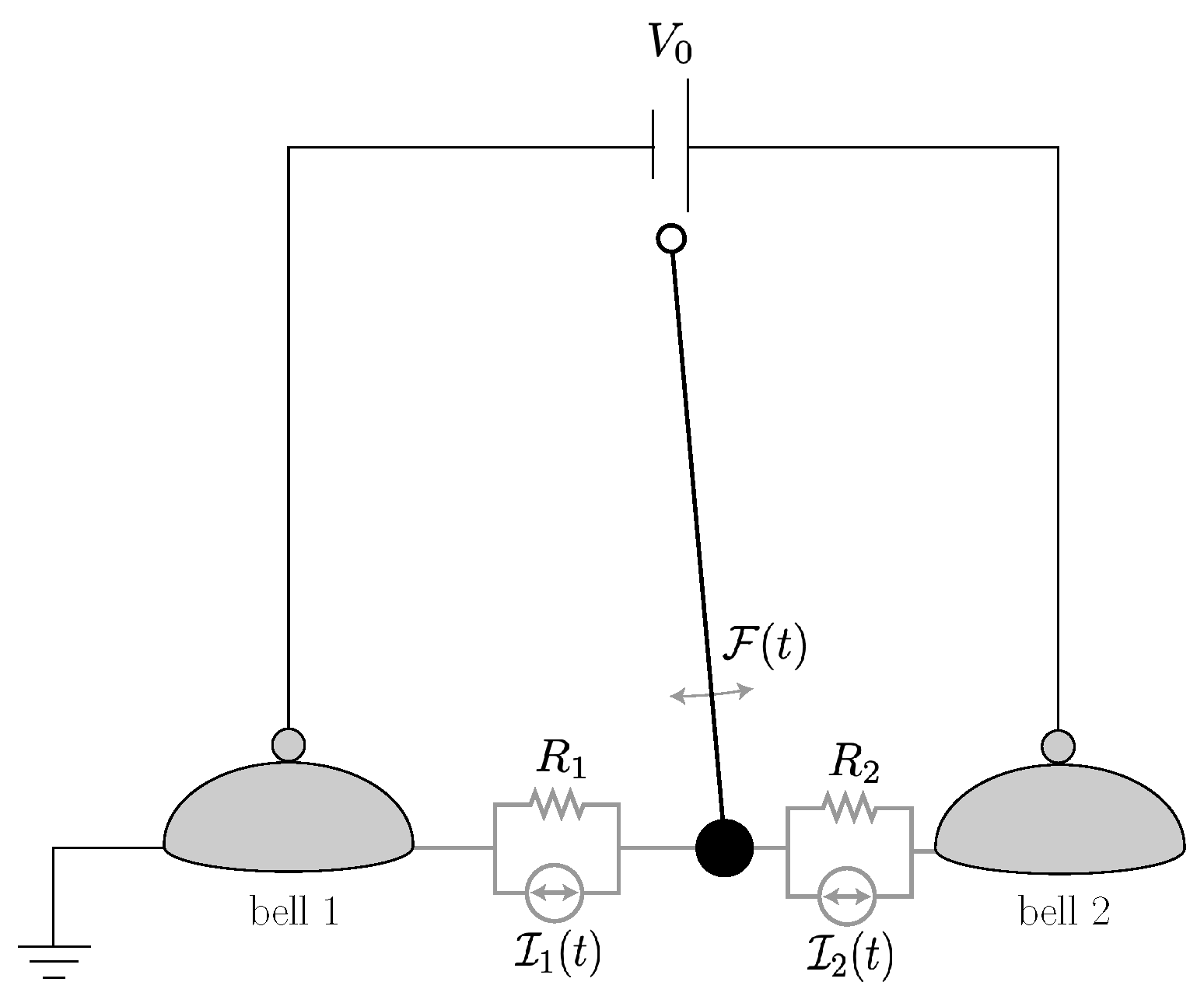
2.3.1. Franklin Bells
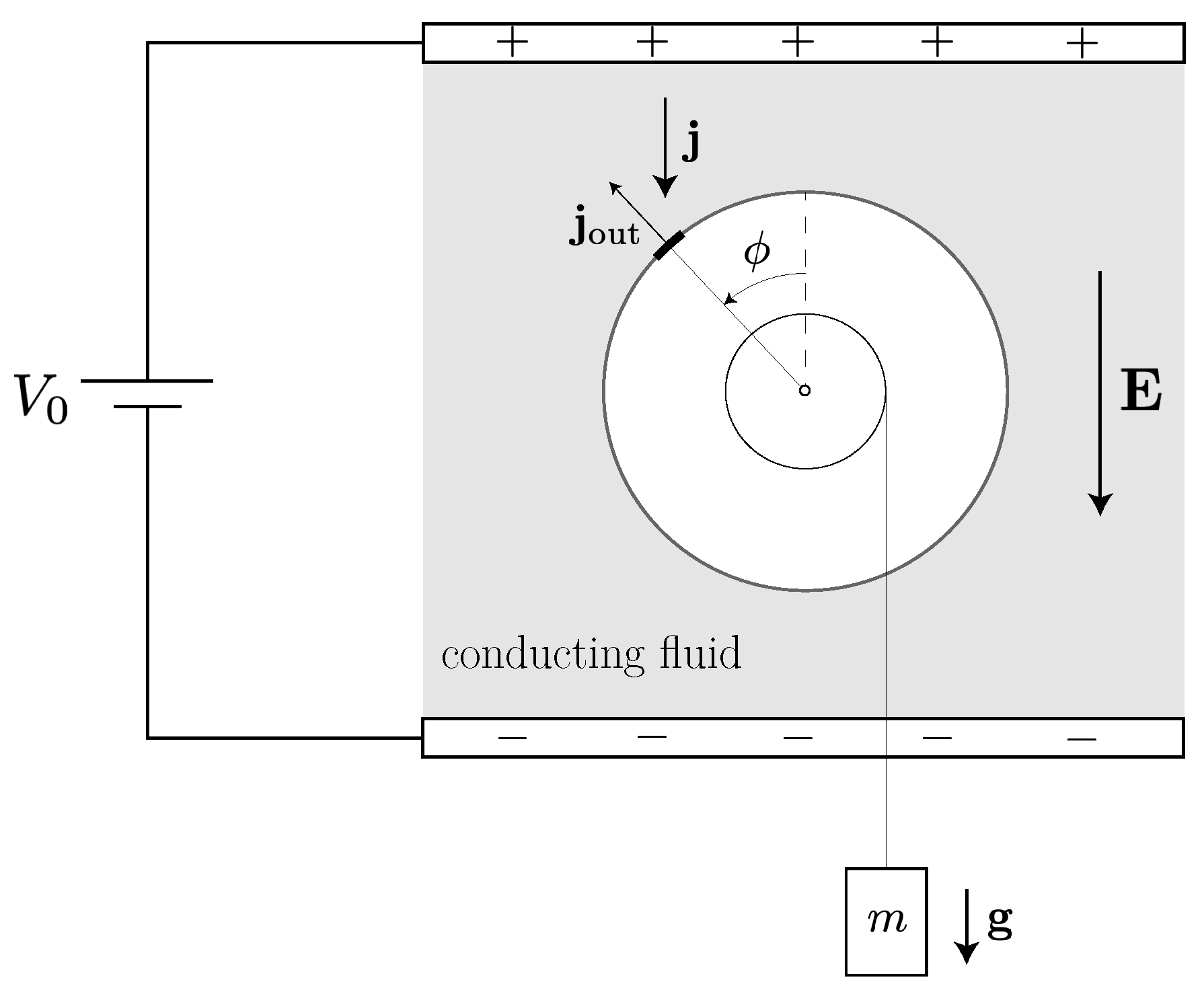
2.3.2. Quincke Rotor
3. Fluctuations
3.1. Quantum Thermodynamics
3.2. Stochastic Thermodynamics
4. Deterministic and Stochastic Engine Dynamics
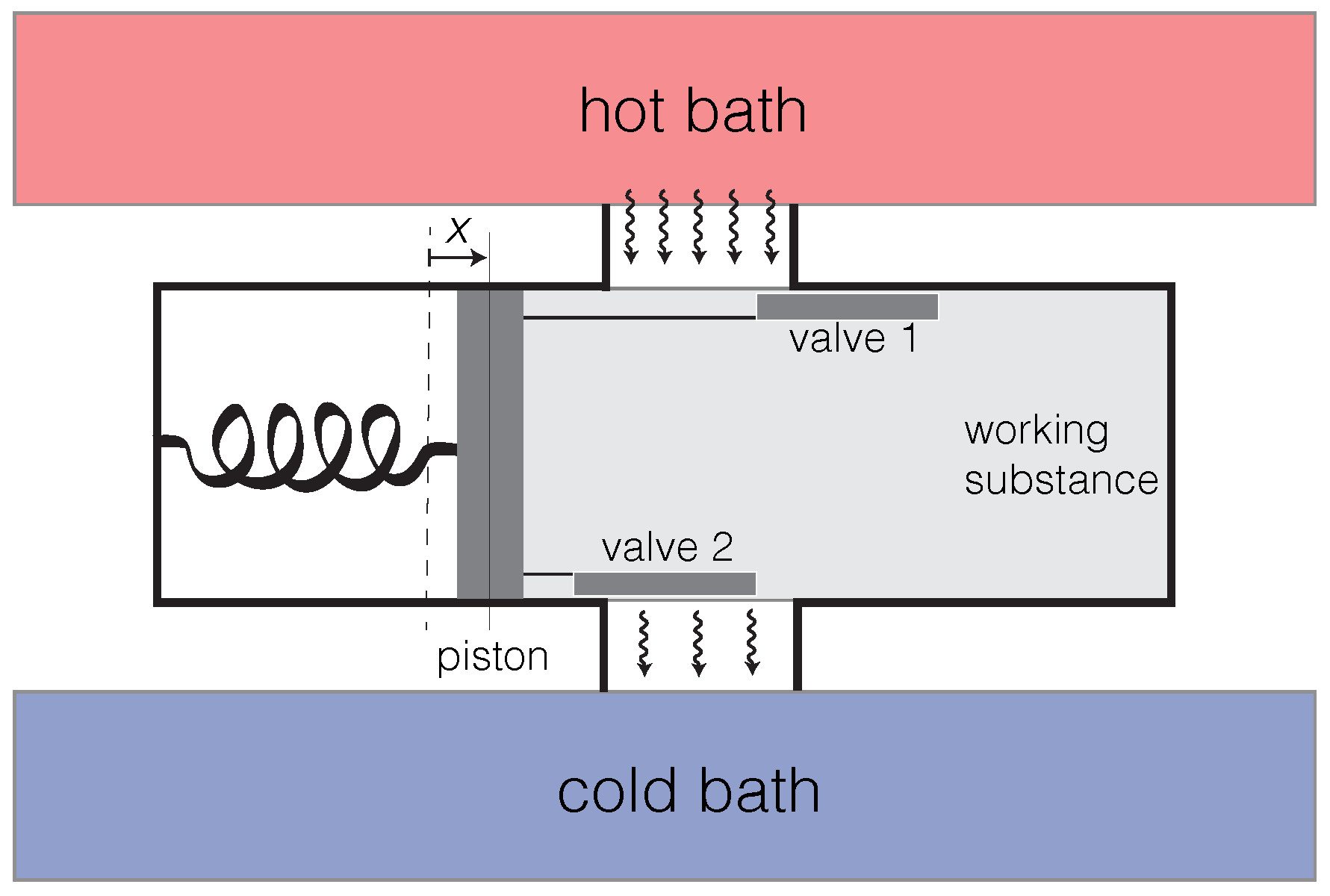
4.1. Deterministic Model of Oscillating Engine
4.2. Stochastic Model of Oscillating Engine
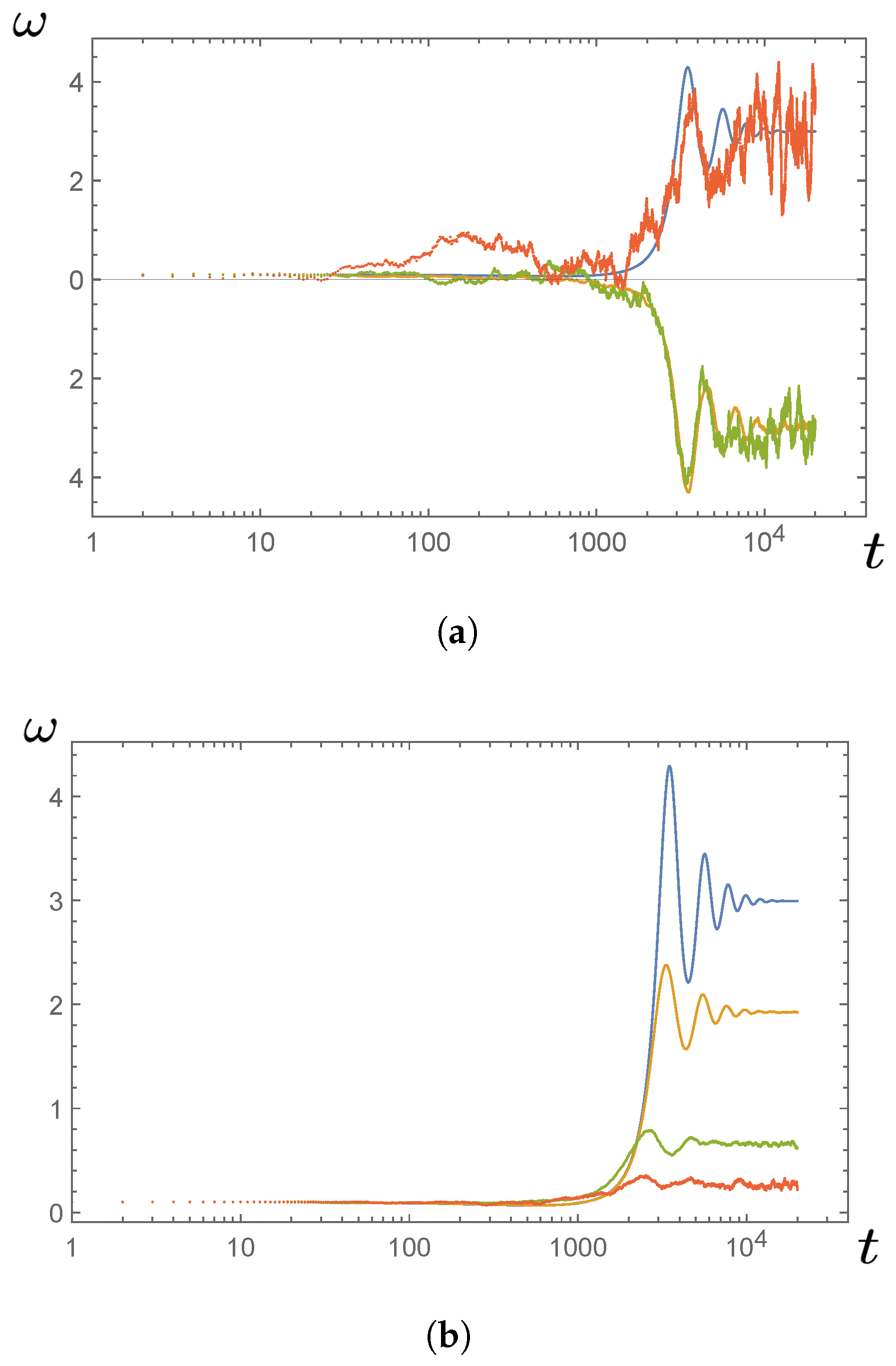
4.3. Stochastic Model of Rotating Engine
4.4. The Puzzle of Stationary States
5. Discussion and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DC | direct current |
| EDL | electrical double layer |
| emf | electromotive force |
| MME | Markovian master Equation |
| NESS | non-equilibrium steady state |
References
- Schroeder, D.V. An Introduction to Thermal Physics; Section 4.1; Addison Wesley Longman: San Francisco, CA, USA, 2000. [Google Scholar]
- Alicki, R.; Kosloff, R. Introduction to quantum thermodynamics: History and prospects. In Thermodynamics in the Quantum Regime; Binder, F., Correa, L.A., Gogolin, C., Anders, J., Adesso, G., Eds.; Springer: Cham, Switzerland, 2019; pp. 1–33. [Google Scholar] [CrossRef]
- Todorov, T.N.; Dundas, D.; Lü, J.-T.; Brandbyge, M.; Hedegård, P. Current-induced forces: A simple derivation. Eur. J. Phys. 2014, 35, 065004. [Google Scholar] [CrossRef]
- Bustos-Marún, R.; Refael, G.; von Oppen, F. Adiabatic quantum motors. Phys. Rev. Lett. 2013, 111, 060802. [Google Scholar] [CrossRef]
- Bruch, A.; Kusminskiy, S.V.; Refael, G.; von Oppen, F. Interacting adiabatic quantum motor. Phys. Rev. B 2018, 97, 195411. [Google Scholar] [CrossRef]
- Kubo, R. The fluctuation-dissipation theorem. Rep. Prog. Phys. 1966, 29, 255. [Google Scholar] [CrossRef]
- Onsager, L. Reciprocal Relations in Irreversible Processes I. Phys. Rev. 1931, 37, 405. [Google Scholar] [CrossRef]
- Onsager, L. Reciprocal Relations in Irreversible Processes II. Phys. Rev. 1931, 38, 2265. [Google Scholar] [CrossRef]
- Martyushev, L.M.; Seleznev, V.D. Maximum entropy production principle in physics, chemistry and biology. Phys. Rep. 2006, 426, 1–45. [Google Scholar] [CrossRef]
- Landauer, R. Stability and entropy production in electrical circuits. J. Stat. Phys. 1975, 13, 1–16. [Google Scholar] [CrossRef]
- Landauer, R. Inadequacy of entropy and entropy derivatives in characterizing the steady state. Phys. Rev. A 1975, 12, 636. [Google Scholar] [CrossRef]
- Nicolis, G.; Prigogine, I. Self-Organization in Nonequilibrium Systems; Wiley: New York, NY, USA, 1977. [Google Scholar]
- Haken, H. Synergetics: An Introduction; Springer: Berlin, Germany, 1977. [Google Scholar]
- Anderson, P.W.; Stein, D.L. Broken Symmetry, Emergent Properties, Dissipative Structures, Life: Are They Related. In Self-Organizing Systems: The Emergence of Order; Yates, F.E., Ed.; Plenum Press: New York, NY, USA, 1987; pp. 445–457. [Google Scholar] [CrossRef]
- Alicki, R.; Gelbwaser-Klimovsky, D.; Jenkins, A. Leaking elastic capacitor as model for active matter. Phys. Rev. E 2021, 103, 052131. [Google Scholar] [CrossRef]
- Andronov, A.A.; Vitt, A.A.; Khaĭkin, S. Theory of Oscillators; Fishwick, W., Ed.; Dover: Mineola, NY, USA, 1987; p. 200. [Google Scholar]
- Airy, G.B. On certain Conditions under which a Perpetual Motion is possible. Trans. Camb. Philos. Soc. 1830, 3, 369. [Google Scholar]
- Strutt, J.W. The Theory of Sound, 2nd ed.; Dover: Mineola, NY, USA, 1945; Volumes I and II, Sections 66a, 68a–68b, 103a–103b, 322a–322k, 397, appendix to Chapter V. [Google Scholar]
- Strogatz, S.H. Nonlinear Dynamics and Chaos, 2nd ed.; Westview Press: Boulder, CO, USA, 2014. [Google Scholar]
- Kirillov, O.N. Nonconservative Stability Problems of Modern Physics, 2nd ed.; De Gruyter: Berlin, Germany, 2021. [Google Scholar]
- Le Corbeiller, P. The non-linear theory of the maintenance of oscillations. J. Inst. Electr. Eng. 1936, 79, 361–378, reprinted in Inst. Electr. Eng. 1936, 11, 292–309. [Google Scholar] [CrossRef]
- Le Corbeiller, P. Theory of prime movers. In Non-Linear Mechanics; Friedrichs, K.O., Corbeiller, P.L., Levinson, N., Stoker, J.J., Eds.; Brown U.: Providence, RI, USA, 1943; pp. 2.1–2.18. [Google Scholar]
- Jenkins, A. Self-oscillation. Phys. Rep. 2013, 525, 167. [Google Scholar] [CrossRef]
- Lugt, H.J. Autorotation. Ann. Rev. Fluid Mech. 1983, 15, 123. [Google Scholar] [CrossRef]
- Seah, S.; Nimmrichter, S.; Scarani, V. Work production of quantum rotor engines. New J. Phys. 2018, 20, 043045. [Google Scholar] [CrossRef]
- Jaffe, R.L.; Taylor, W. The Physics of Energy; Cambridge University Press: Cambridge, UK, 2018; Chapters 29–30. [Google Scholar]
- Regis, E. The Enigma of Aerodynamic Lift. Sci. Am. 2020, 322, 44. [Google Scholar] [CrossRef]
- Nakanishi, H.; Fujiwara, S.; Takayama, K.; Kawayama, I.; Murakami, H.; Tonouchi, M. Imaging of a Polycrystalline Silicon Solar Cell Using a Laser Terahertz Emission Microscope. Appl. Phys. Express 2012, 5, 112301. [Google Scholar] [CrossRef]
- Guzelturk, B.; Belisle, R.A.; Smith, M.D.; Bruening, K.; Prasanna, R.; Yuan, Y.; Gopalan, V.; Tassone, C.J.; Karunadasa, H.I.; McGehee, M.D.; et al. Terahertz Emission from Hybrid Perovskites Driven by Ultrafast Charge Separation and Strong Electron–Phonon Coupling. Adv. Mater. 2018, 30, 1704737. [Google Scholar] [CrossRef]
- Alicki, R.; Gelbwaser-Klimovsky, D.; Szczygielski, K. Solar cell as a self-oscillating heat engine. J. Phys. A Math. Theor. 2016, 49, 015002. [Google Scholar] [CrossRef]
- Alicki, R. Thermoelectric generators as self-oscillating heat engines. J. Phys. A Math. Theor. 2016, 49, 085001. [Google Scholar] [CrossRef]
- Alicki, R. Unified Quantum Model of Work Generation in Thermoelectric Generators, Solar and Fuel Cells. Entropy 2016, 18, 210. [Google Scholar] [CrossRef]
- Alicki, R.; Gelbwaser-Klimovsky, D.; Jenkins, A. A thermodynamic cycle for the solar cell. Ann. Phys. (NY) 2017, 378, 71. [Google Scholar] [CrossRef]
- Alicki, R. From the GKLS equation to the theory of solar and fuel cells. Open Syst. Inf. Dyn. 2017, 24, 1740007. [Google Scholar] [CrossRef]
- Alicki, R.; Gelbwaser-Klimovsky, D.; Jenkins, A.; von Hauff, E. A dynamic picture of energy conversion in photovoltaic devices. arXiv 2019, arXiv:1901.10873. [Google Scholar]
- Alicki, R.; Gelbwaser-Klimovsky, D.; Jenkins, A.; von Hauff, E. A dynamical theory of the battery’s electromotive force. Phys. Chem. Chem. Phys. 2021, 23, 9428. [Google Scholar] [CrossRef]
- Goupil, C.; Ouerdane, H.; Herbert, E.; Benenti, G.; D’Angelo, Y.; Lecoeur, P. Closed-loop approach to thermodynamics. Phys. Rev. E 2016, 94, 032136. [Google Scholar] [CrossRef]
- Wächtler, C.W.; Strasberg, P.; Klapp, S.H.L.; Schaller, G.; Jarzynski, C. Stochastic thermodynamics of self-oscillations: The electron shuttle. New J. Phys. 2019, 21, 073009. [Google Scholar] [CrossRef]
- Wächtler, C.W.; Strasberg, P.; Schaller, G. Proposal of a Realistic Stochastic Rotor Engine Based on Electron Shuttling. Phys. Rev. Appl. 2019, 12, 024001. [Google Scholar] [CrossRef]
- Strasberg, P.; Wächtler, C.W.; Schaller, G. Autonomous implementation of thermodynamic cycles at the nanoscale. Phys. Rev. Lett. 2021, 126, 180605. [Google Scholar] [CrossRef] [PubMed]
- Ouerdane, H.; Apertet, Y.; Goupil, C.; Lecoeur, P. Continuity and boundary conditions in thermodynamics: From Carnot’s efficiency to efficiencies at maximum power. Eur. Phys. J. Spec. Top. 2015, 224, 839. [Google Scholar] [CrossRef]
- Díaz-Marín, C.D.; Jenkins, A. A physical approach to dissipation-induced instabilities. arXiv 2018, arXiv:1806.01527. [Google Scholar]
- Jaynes, E.T. The Muscle as an Engine. Unpublished Manuscript. 1983. Available online: https://bayes.wustl.edu/etj/articles/muscle.pdf (accessed on 26 July 2021).
- Eddington, A.S. The Pulsations of a Gaseous Star and the Problem of the Cepheid Variables II. Mon. Not. R. Astron. Soc. 1919, 79, 177–189. [Google Scholar] [CrossRef]
- Eddington, A.S. The Internal Constitution of the Stars; Cambridge University Press: Cambridge, UK, 1988. [Google Scholar]
- Strutt, J.W. The Explanation of Certain Acoustical Phenomena. Nature 1878, 18, 319–321. [Google Scholar] [CrossRef]
- Strutt, J.W. The Theory of Sound, 2nd ed.; Dover: New York, NY, USA, 1945; Volume II, Section 322g. [Google Scholar]
- De Rochas, A.B. Nouvelles Recherches sur les Conditions Pratiques de Plus Grande Utilisation de la Chaleur et, en Général, de la Force Motrice; E. Lacroix: Paris, France, 1862. [Google Scholar]
- Çengel, Y.A.; Boles, M.A. Thermodynamics: An Engineering Approach, 8th ed.; McGraw-Hill: New York, NY, USA, 2011. [Google Scholar]
- Walker, G. Stirling Engines; Oxford University Press: Oxford, UK, 1980. [Google Scholar]
- Strutt, J.W.; Rayleigh, B. XXXIII. On maintained vibrations. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1883, 15, 229–235. [Google Scholar] [CrossRef]
- Van der Pol, B. LXXXVIII. On “relaxation-oscillations”. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1926, 2, 978. [Google Scholar] [CrossRef]
- Van der Pol, B. Forced Oscillations in a Circuit with non-linear Resistance. (Reception with reactive Triode.). In Selected Papers on Mathematical Trends in Control Theory; Bellmann, R., Kalaba, R., Eds.; Dover: New York, NY, USA, 1964; pp. 124–140, reprinted in Lond. Edinb. Dublin Philos. Mag. J. Sci. 1927, 3, 65–80. [Google Scholar] [CrossRef]
- Kuramoto, Y. Chemical Oscillations, Waves, and Turbulence; Springer: Berlin, Germany, 1984; Volume Chapter 2. [Google Scholar]
- Ebeling, W.; Schweitzer, F.; Tilch, B. Active Brownian particles with energy depots modeling animal mobility. BioSystems 1999, 49, 17. [Google Scholar] [CrossRef]
- Bechinger, C.; Leonardo, R.D.; Löwen, H.; Reichhardt, C.; Volpe, G.; Volpe, G. Active particles in complex and crowded environments. Rev. Mod. Phys. 2016, 88, 045006. [Google Scholar] [CrossRef]
- Seifert, U. Stochastic thermodynamics, fluctuation theorems and molecular machines. Rep. Prog. Phys. 2012, 75, 126001. [Google Scholar] [CrossRef]
- Minorsky, N. Self-excited Oscillations in Dynamical Systems Possessing Retarded Action. In Selected Papers on Mathematical Trends in Control Theory; Bellmann, R., Kalaba, R., Eds.; Dover: New York, NY, USA, 1964; pp. 141–149, reprinted in J. Appl. Mech. 1942, 9, 65. [Google Scholar] [CrossRef]
- Novák, B.; Tyson, J.J. Design principles of biochemical oscillators. Nat. Rev. Mol. Cell Biol. 2008, 9, 981. [Google Scholar] [CrossRef] [PubMed]
- Hänggi, P.; Marchesoni, F. Artificial Brownian motors: Controlling transport on the nanoscale. Rev. Mod. Phys. 2009, 81, 387. [Google Scholar] [CrossRef]
- Finnie, I.; Curl, R.L. On the functioning of a familiar nonlinear thermodynamic oscillator. In Proceedings of the IUTAM Symposium on Nonlinear Vibration, Kiev, Russia, 12–18 September 1961; Volume III, pp. 486–497. [Google Scholar]
- Finnie, I.; Curl, R.L. Physics in a Toy Boat. Am. J. Phys. 1963, 31, 289–293. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Mechanics, 3rd ed.; Elsevier: Oxford, UK, 1976; Volume Section 25. [Google Scholar]
- Jefimenko, O.D. Electrostatic Motors; Electret Scientific Co.: Star City, WV, USA, 1973. [Google Scholar]
- Pathria, R.K.; Beale, P.D. Statistical Mechanics, 4th ed.; Academic Press: London, UK, 2022; Volume Chapter 15. [Google Scholar]
- Gorelik, L.Y.; Isacsson, A.; Voinova, M.V.; Kasemo, B.; Shekhter, R.I.; Jonson, M. Shuttle Mechanism for Charge Transfer in Coulomb Blockade. Phys. Rev. Lett. 1998, 80, 4526. [Google Scholar] [CrossRef]
- Weiler, W. Zur Darstellung elektrischer Kraftlinien. Z. Phys. Chem. Unterr. 1893, 194. [Google Scholar]
- Quincke, G. Ueber Rotationen im constanten electrischen Felde. Ann. Phys. Chem. 1896, 295, 417. [Google Scholar] [CrossRef]
- Jones, T.B. Electromechanics of Particles; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar] [CrossRef]
- Alicki, R. The quantum open system as a model of the heat engine. J. Phys. A Math. Gen. 1979, 12, L103. [Google Scholar] [CrossRef]
- Kosloff, R. A quantum mechanical open system as a model of a heat engine. J. Chem. Phys. 1984, 80, 1625. [Google Scholar] [CrossRef]
- Dundas, D.; McEniry, E.J.; Todorov, T.N. Current-driven atomic waterwheels. Nat. Nanotechnol. 2009, 4, 99. [Google Scholar] [CrossRef]
- Bode, N.; Kusminskiy, S.V.; Egger, R.; von Oppen, F. Scattering theory of current-induced forces in mesoscopic systems. Phys. Rev. Lett. 2011, 107, 036804. [Google Scholar] [CrossRef]
- Alicki, R.; Lendi, K. Quantum Dynamical Semigroups and Applications, 2nd ed.; Springer: Berlin, Germany, 2007; Volume 717, p. 1. [Google Scholar] [CrossRef]
- McAdory, R.T., Jr.; Schieve, W.C. On entropy production in a stochastic model of open systems. J. Chem. Phys. 1977, 67, 1899. [Google Scholar] [CrossRef]
- Spohn, H. Entropy production for quantum dynamical semigroups. J. Math. Phys. 1978, 19, 1227. [Google Scholar] [CrossRef]
- Gelbwaser-Klimovsky, D.; Alicki, R.; Kurizki, G. Work and energy gain of heat-pumped quantized amplifiers. EPL 2013, 103, 60005. [Google Scholar] [CrossRef]
- Levy, A.; Diósi, L.; Kosloff, R. Quantum Flywheel. Phys. Rev. A 2016, 93, 052119. [Google Scholar] [CrossRef]
- Roulet, A.; Nimmrichter, S.; Arrazola, J.M.; Seah, S.; Scarani, V. Autonomous Rotor Heat Engine. Phys. Rev. E 2017, 95, 062131. [Google Scholar] [CrossRef]
- Platt, N.; Spiegel, E.; Tresser, C. On-off intermittency: A mechanism for bursting. Phys. Rev. Lett. 1993, 70, 279. [Google Scholar] [CrossRef]
- Mallick, K.; Marcq, P. Stability analysis of a noise-induced Hopf bifurcation. Eur. Phys. J. B 2003, 36, 119. [Google Scholar] [CrossRef][Green Version]
- Frisch, U. Turbulence: The Legacy of A. N. Kolmogorov; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Jenkins, A. Chandler wobble: Stochastic and deterministic dynamics. In Dynamical Systems: Theoretical and Experimental Analysis; Awrejcewicz, J., Ed.; Springer: Berlin/Heidelberg, Germany, 2016; Volume 182, pp. 177–186. [Google Scholar] [CrossRef]
- Jenkins, A. Towards a microeconomic theory of the finance-driven business cycle. arXiv 2013, arXiv:1312.0323. [Google Scholar]
- Groszkowski, J. Frequency of Self-Oscillations; Pergamon Press: Oxford, UK, 1964; Volume Section 9.4. [Google Scholar]
- Harrison, D. Analysis of the Mechanisms for Compensation in Clock B. In Harrison Decoded: Towards a Perfect Pendulum Clock; McEvoy, R., Betts, J., Eds.; Oxford University Press: Oxford, UK, 2020; pp. 149–174. [Google Scholar] [CrossRef]
- Barato, A.C.; Seifert, U. Thermodynamic Uncertainty Relation for Biomolecular Processes. Phys. Rev. Lett. 2015, 114, 158101. [Google Scholar] [CrossRef]
- Cao, Y.; Wang, H.; Ouyang, Q.; Tu, Y. The free-energy cost of accurate biochemical oscillations. Nat. Phys. 2015, 11, 772. [Google Scholar] [CrossRef]
- Alicki, R.; Jenkins, A. Quantum theory of triboelectricity. Phys. Rev. Lett. 2020, 125, 186101. [Google Scholar] [CrossRef]
- Ramaswamy, S. The Mechanics and Statistics of Active Matter. Annu. Rev. Condens. Matter Phys. 2010, 1, 323. [Google Scholar] [CrossRef]
- Markovich, T.; Fodor, É.; Tjhung, E.; Cates, M.E. Thermodynamics of Active Field Theories: Energetic Cost of Coupling to Reservoirs. Phys. Rev. X 2021, 11, 021057. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alicki, R.; Gelbwaser-Klimovsky, D.; Jenkins, A. The Problem of Engines in Statistical Physics. Entropy 2021, 23, 1095. https://doi.org/10.3390/e23081095
Alicki R, Gelbwaser-Klimovsky D, Jenkins A. The Problem of Engines in Statistical Physics. Entropy. 2021; 23(8):1095. https://doi.org/10.3390/e23081095
Chicago/Turabian StyleAlicki, Robert, David Gelbwaser-Klimovsky, and Alejandro Jenkins. 2021. "The Problem of Engines in Statistical Physics" Entropy 23, no. 8: 1095. https://doi.org/10.3390/e23081095
APA StyleAlicki, R., Gelbwaser-Klimovsky, D., & Jenkins, A. (2021). The Problem of Engines in Statistical Physics. Entropy, 23(8), 1095. https://doi.org/10.3390/e23081095





