Improving Seismic Inversion Robustness via Deformed Jackson Gaussian
Abstract
:1. Introduction
2. Post-Stack Seismic Inversion
3. Likelihood Based on Jackson Statistics
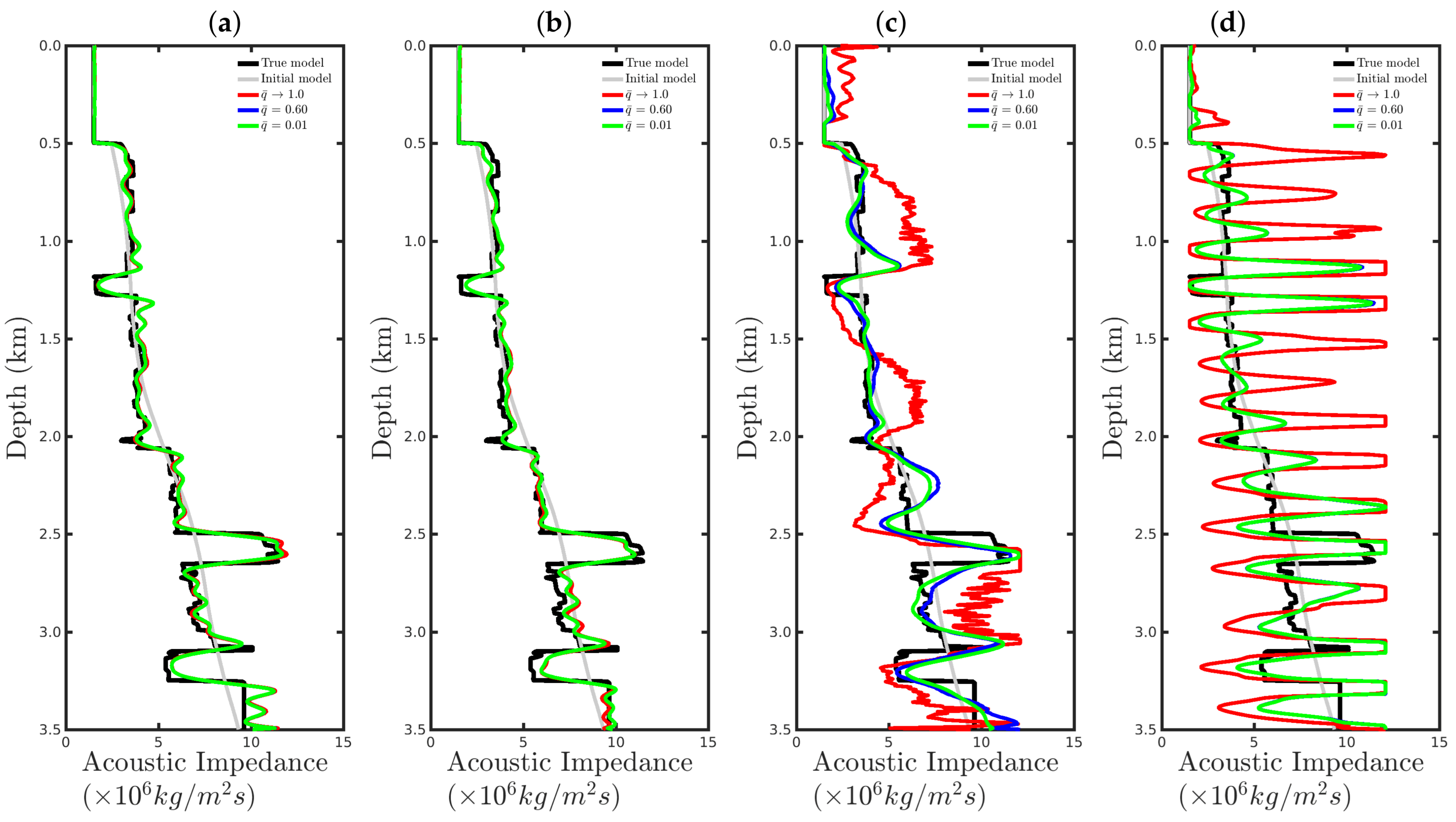
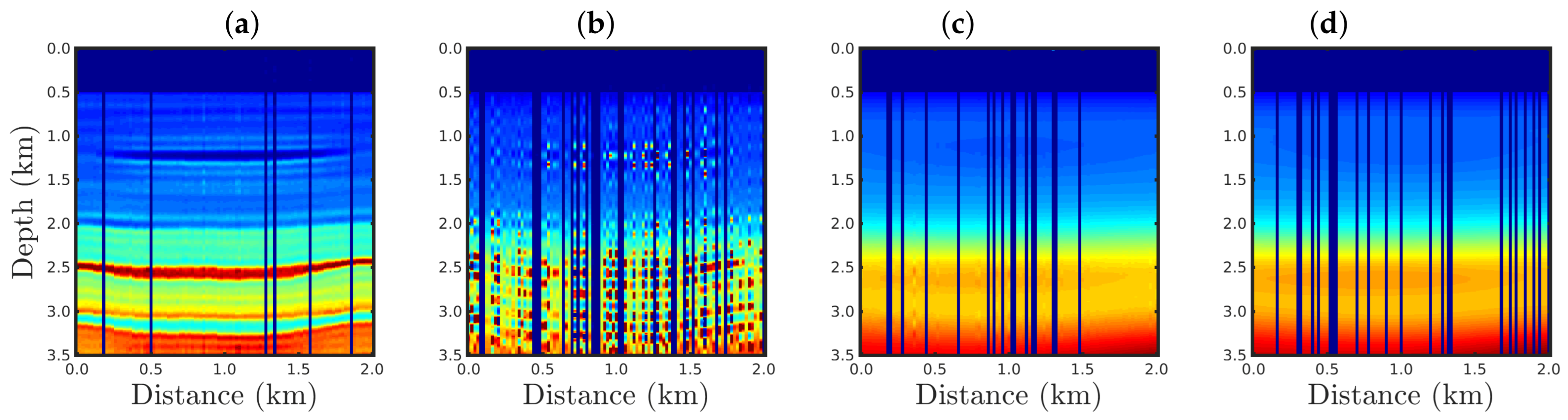
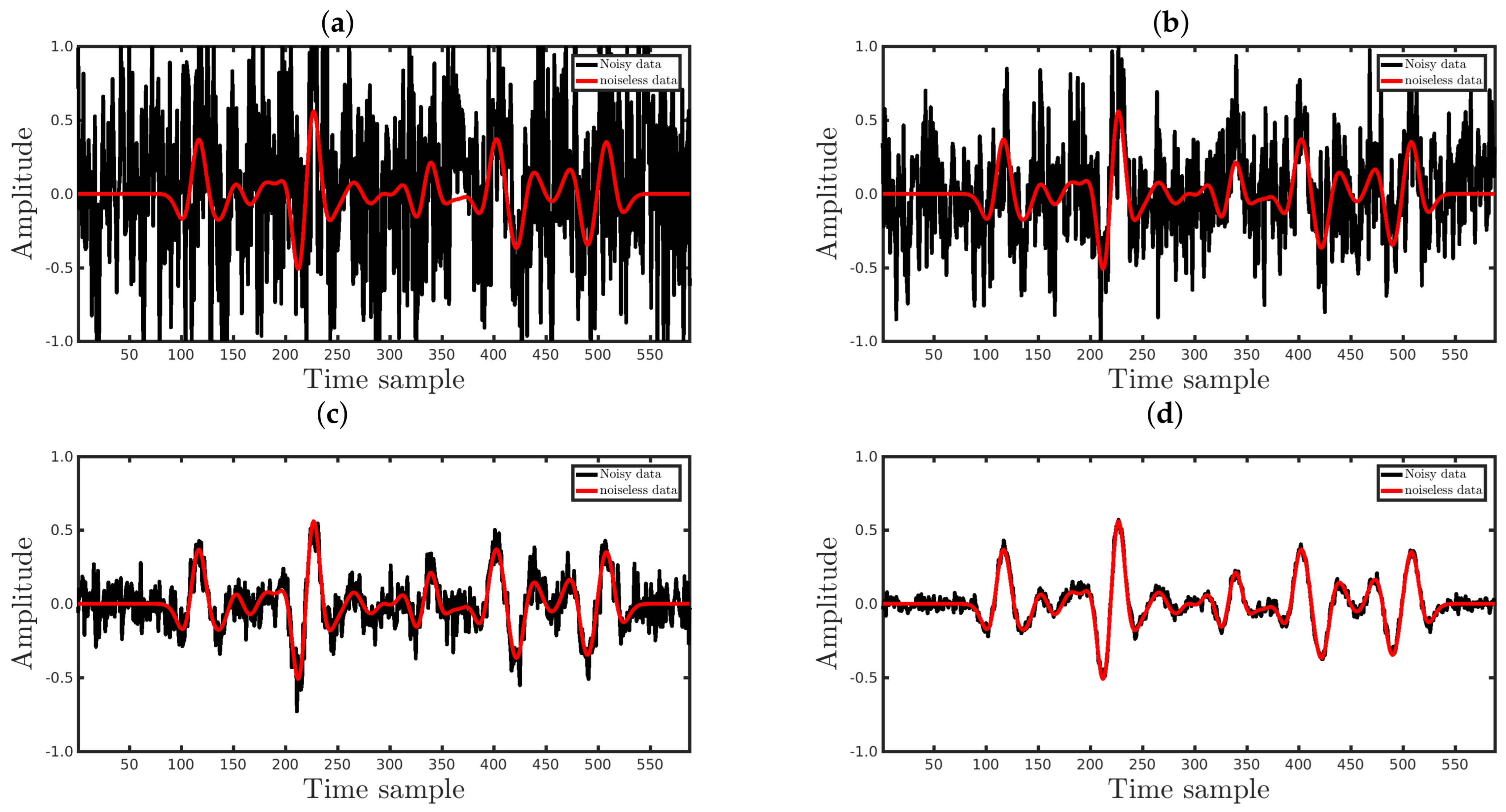
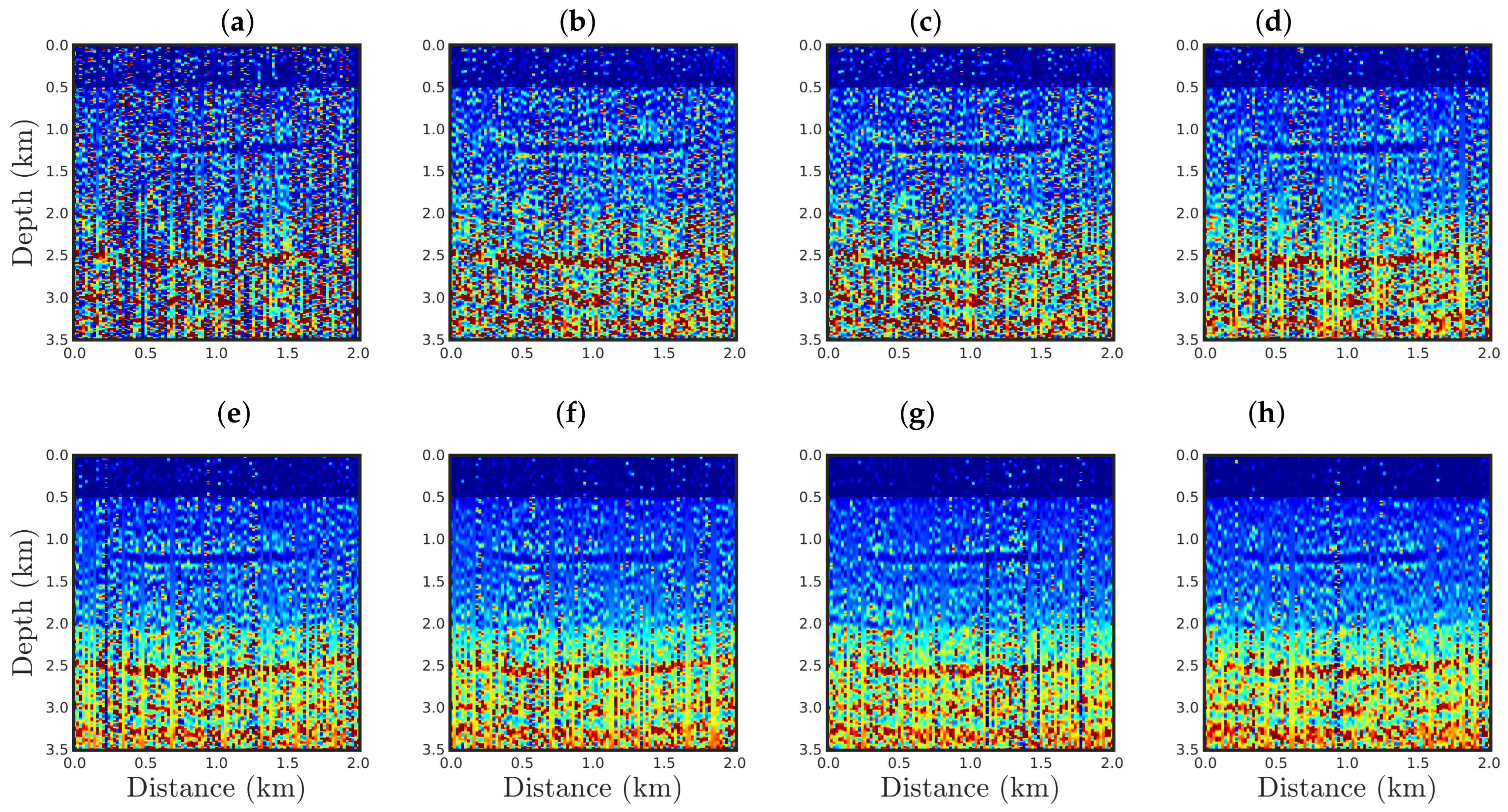
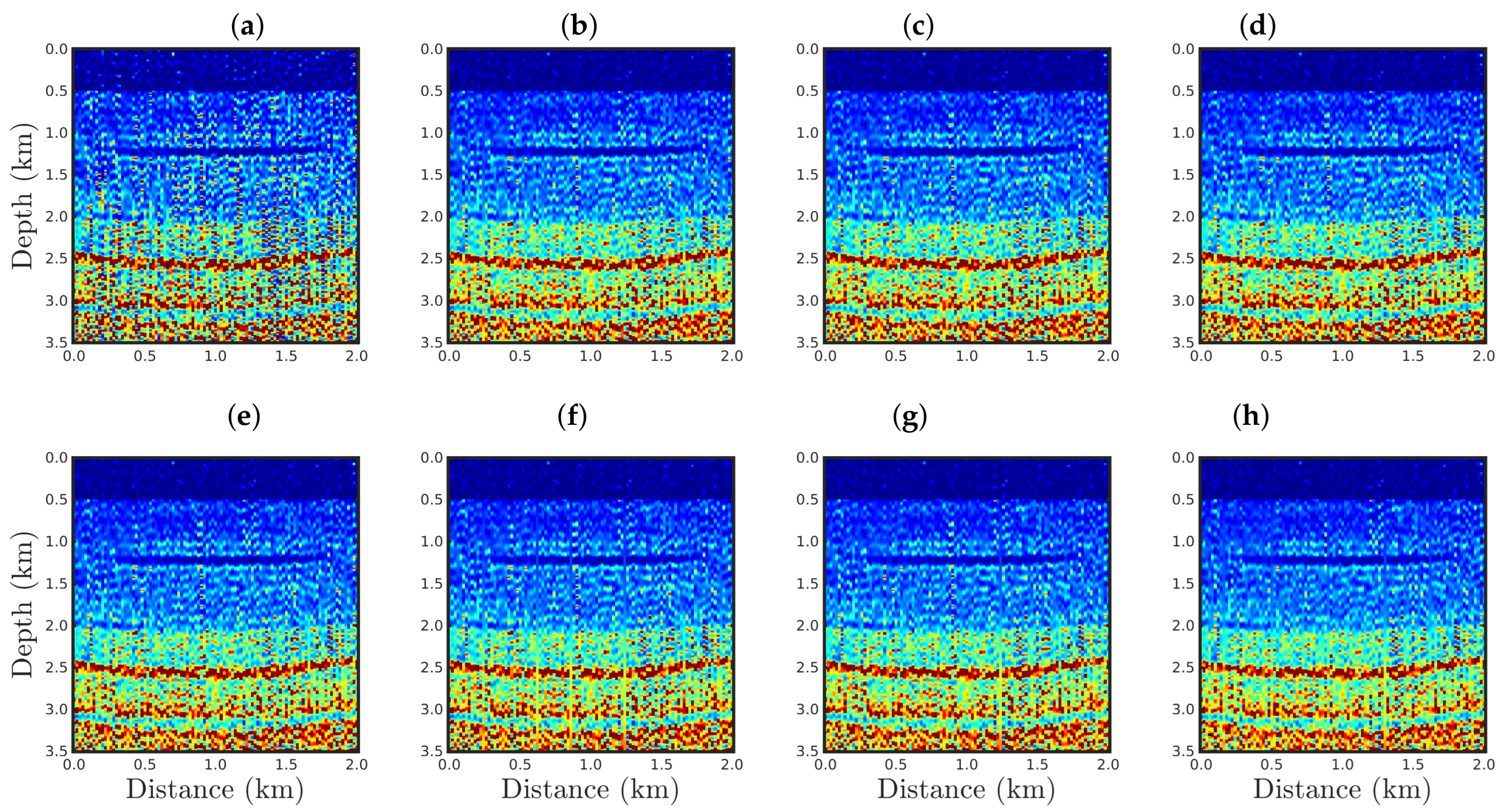
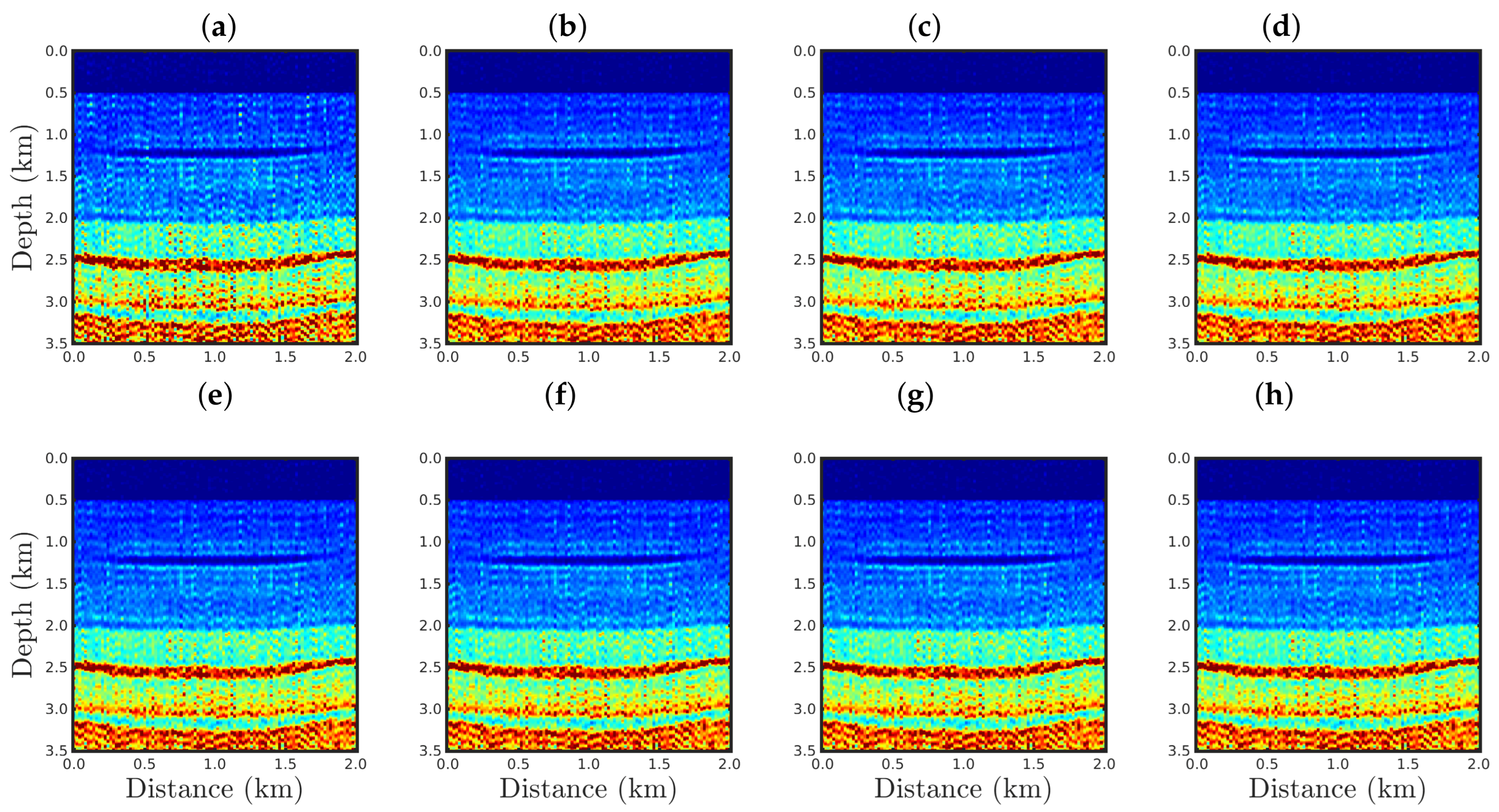
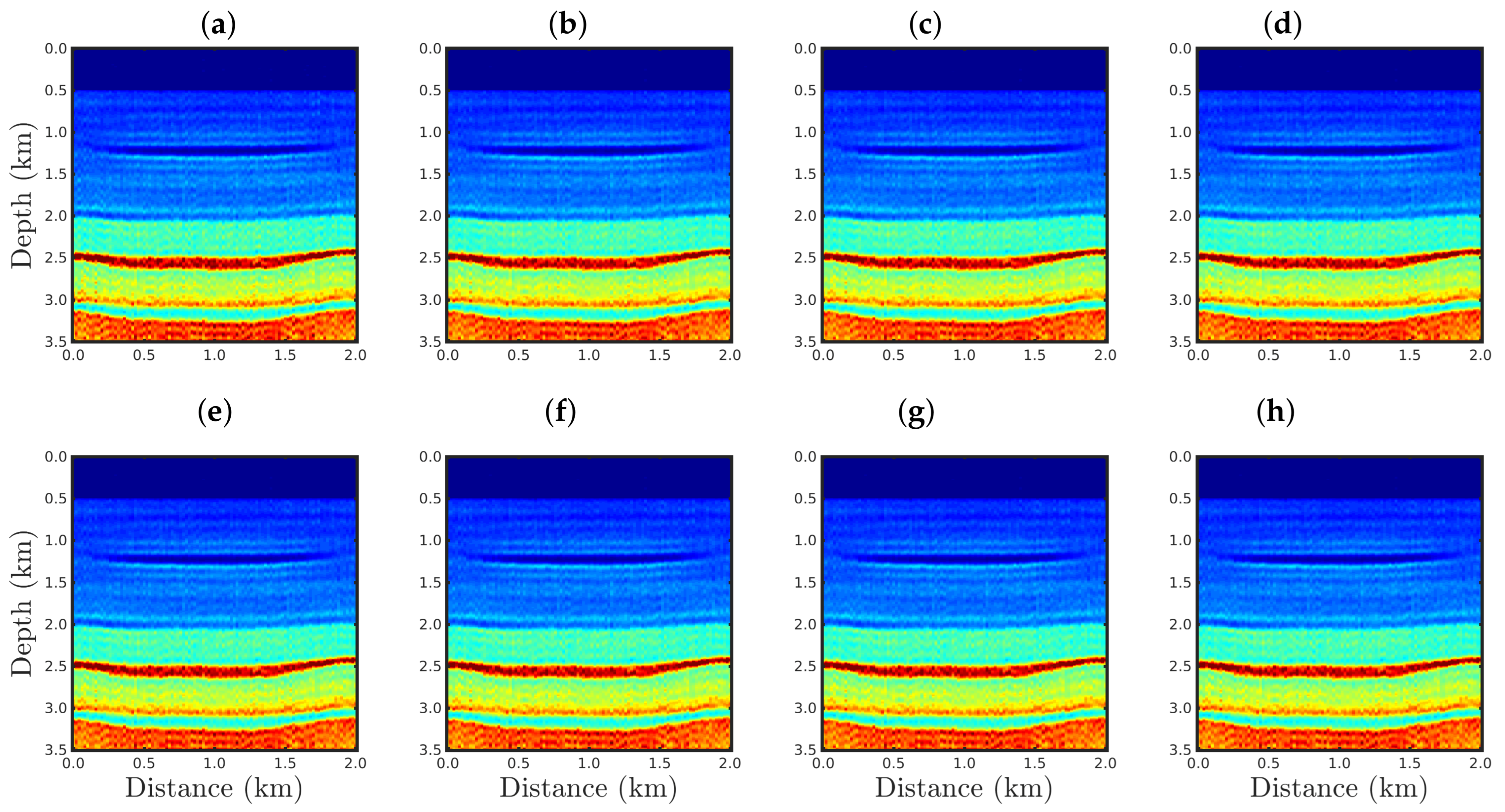
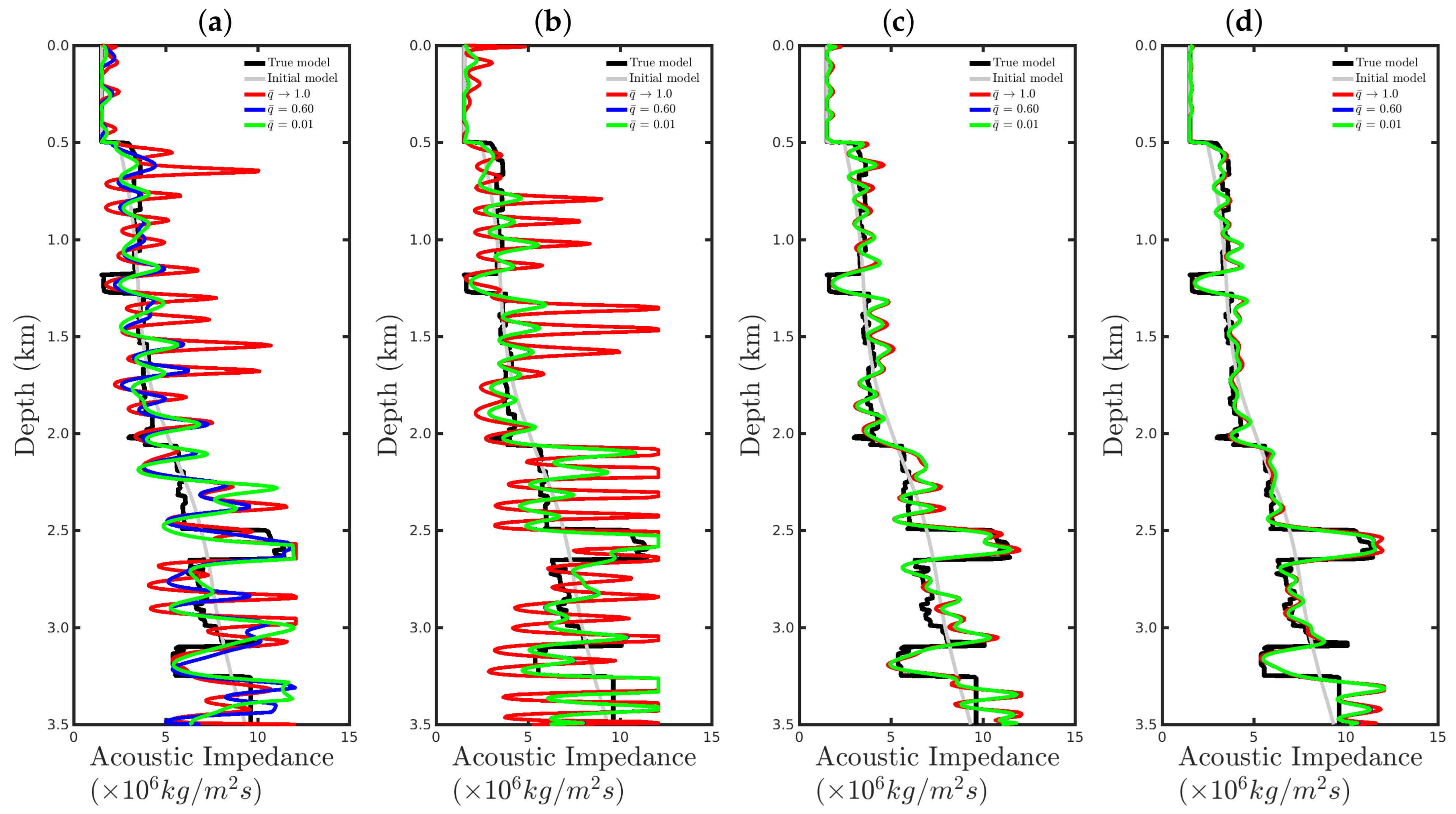
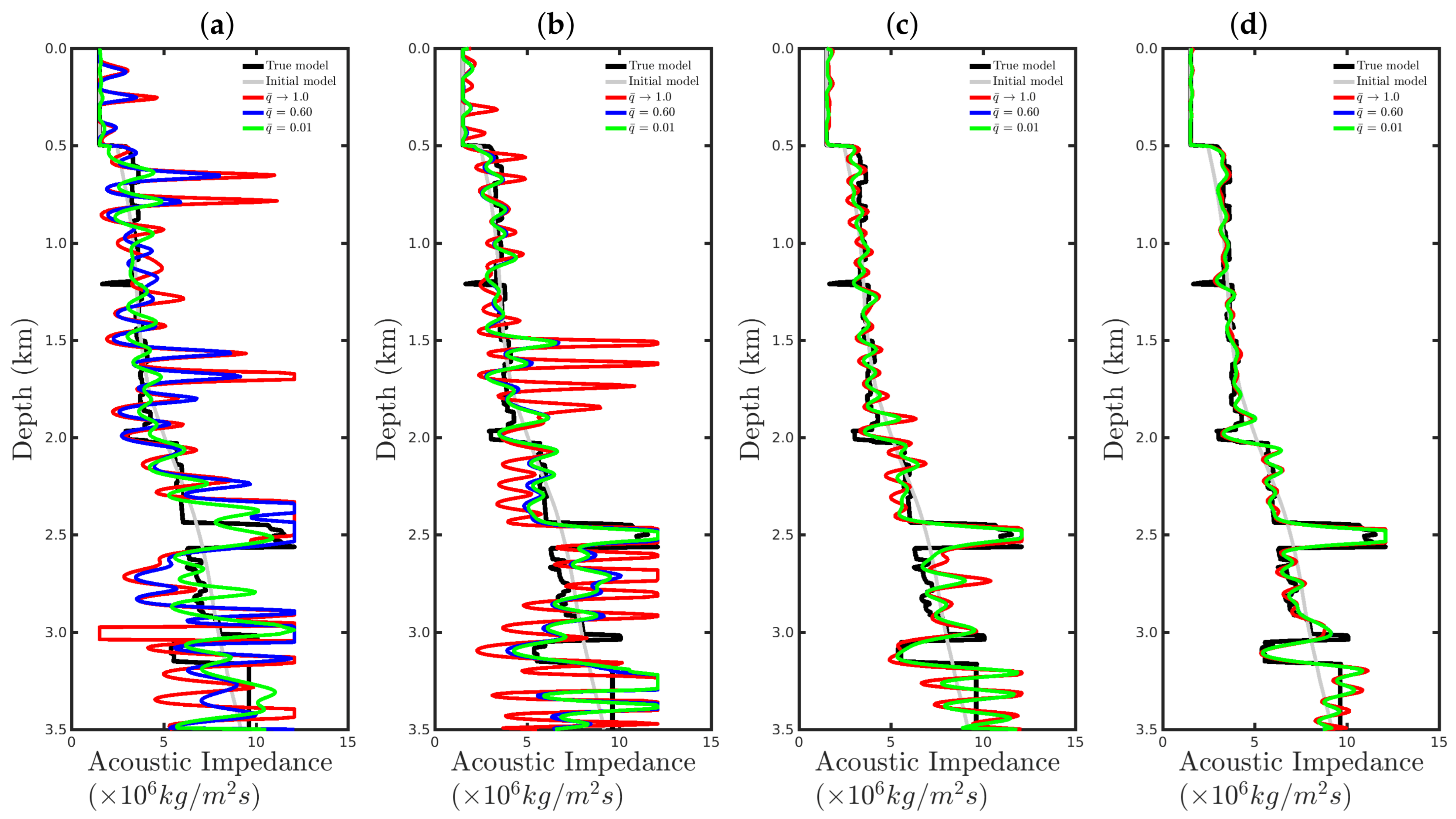
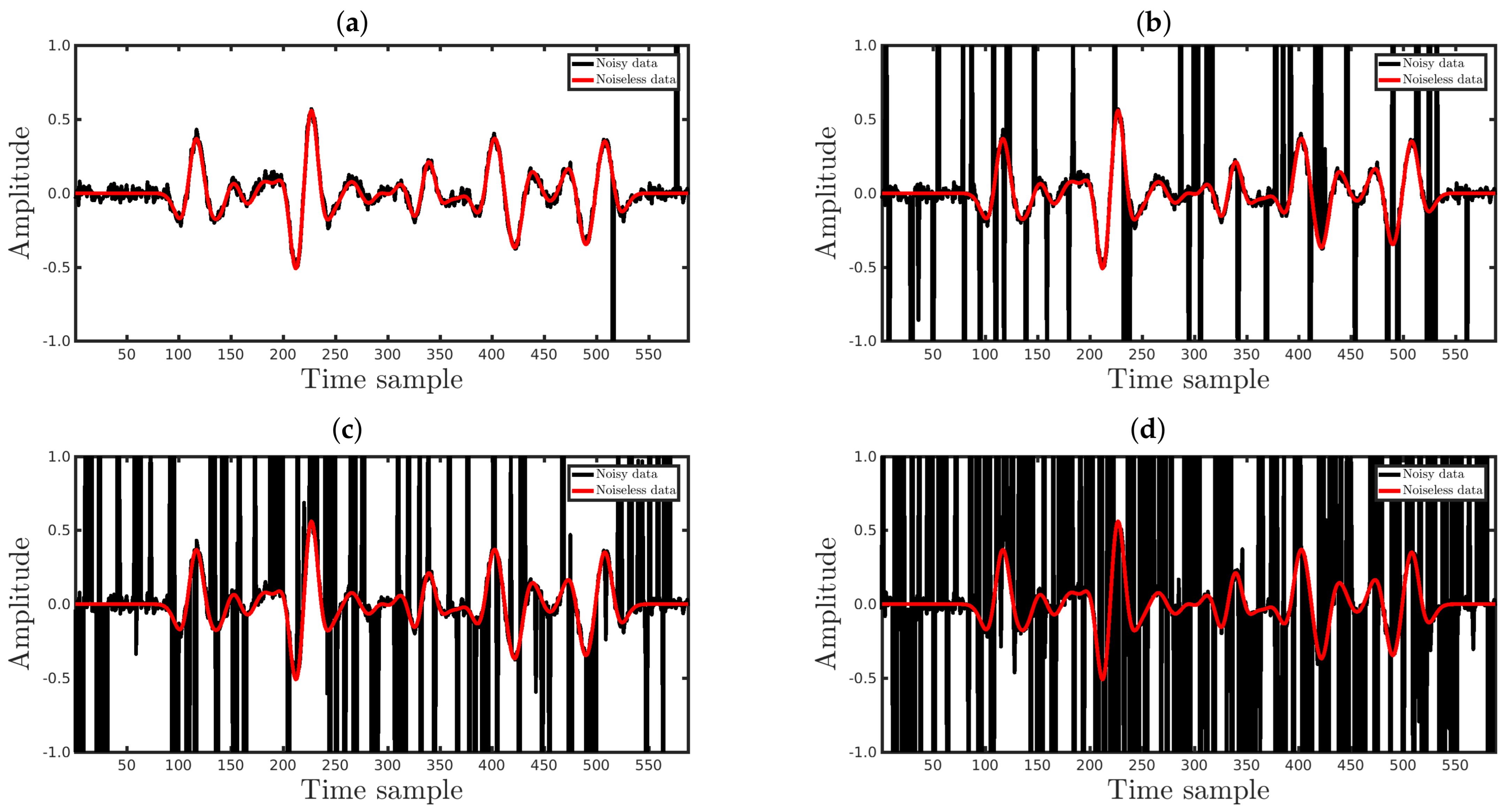
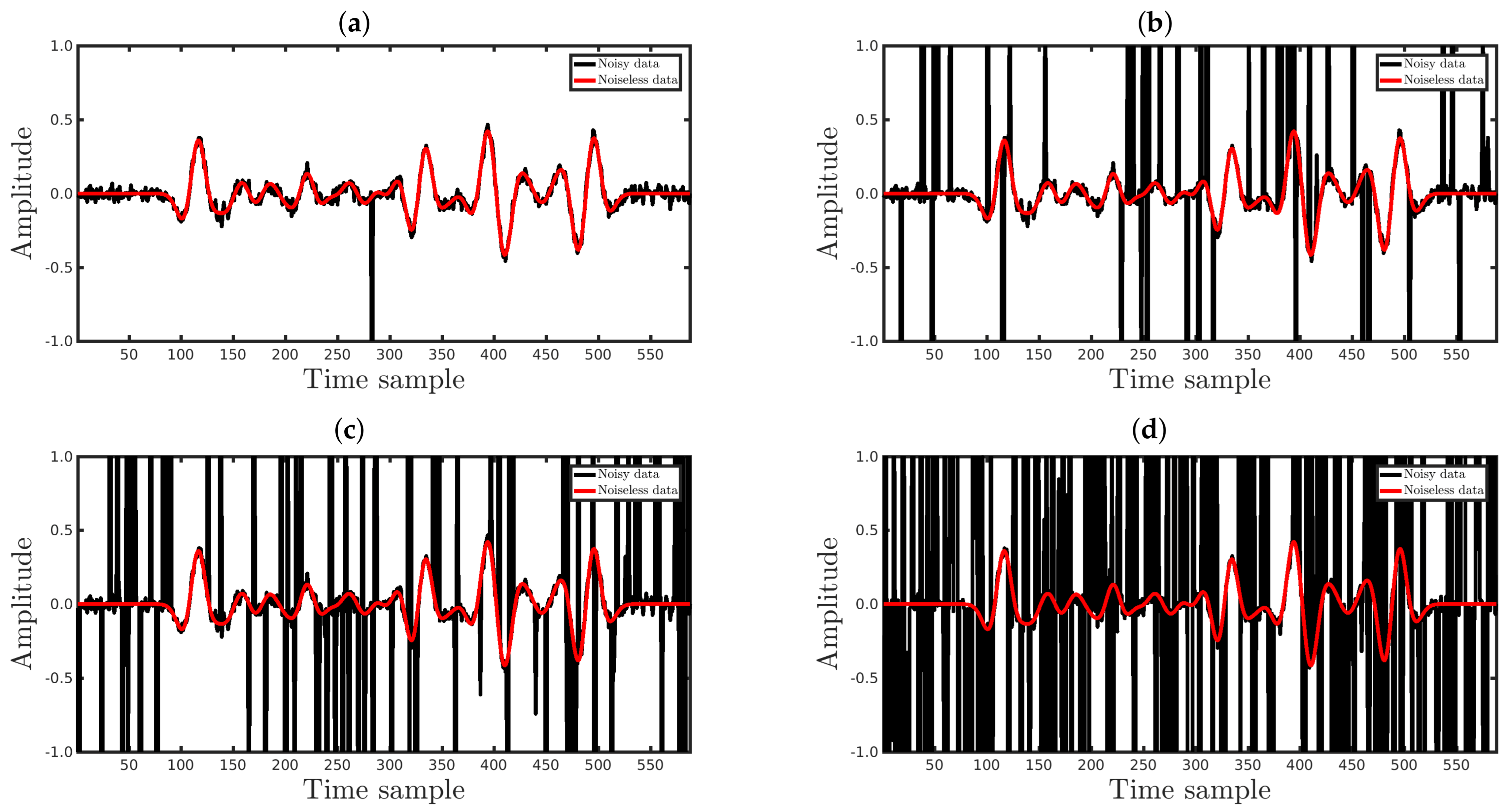
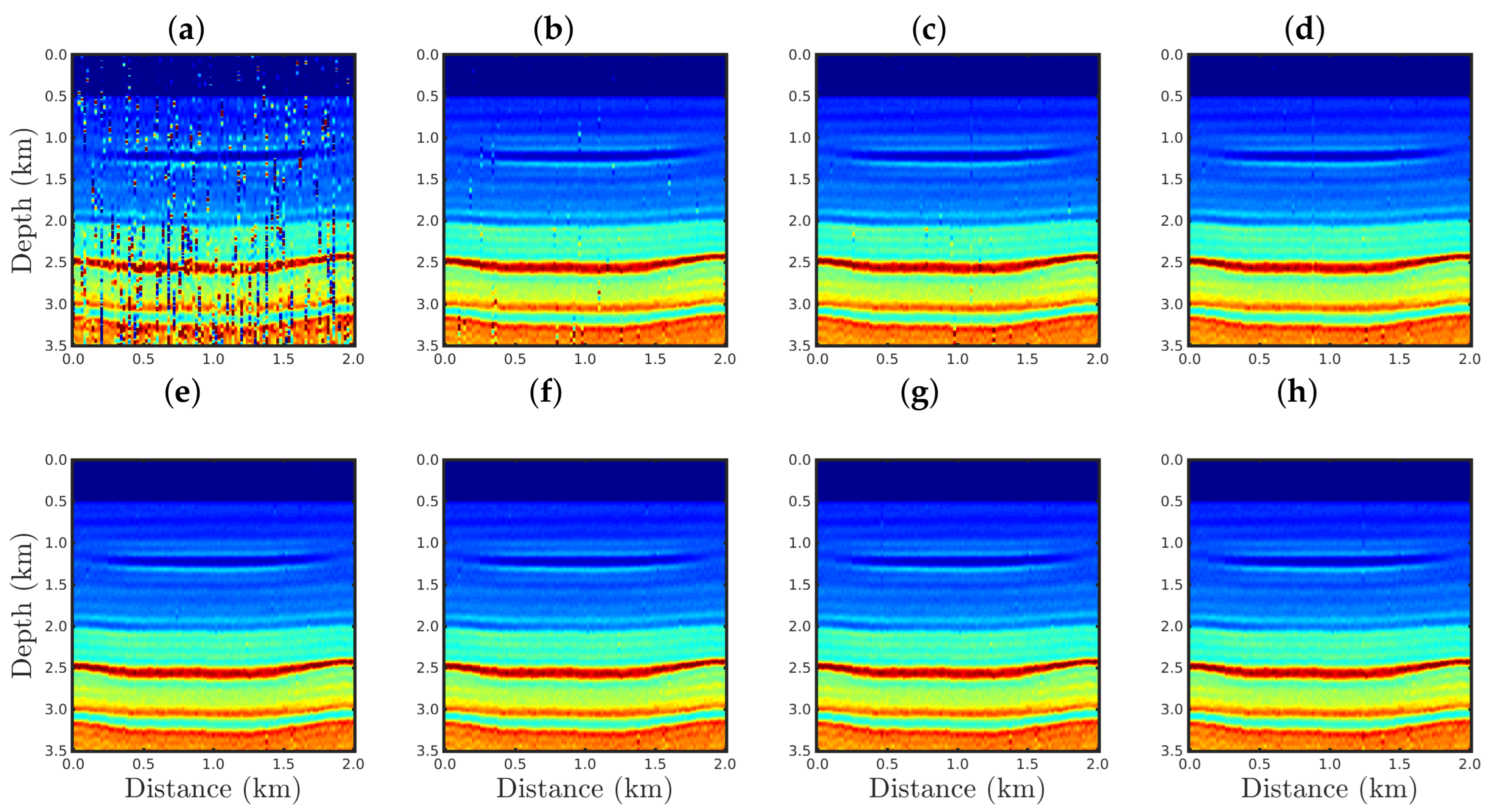
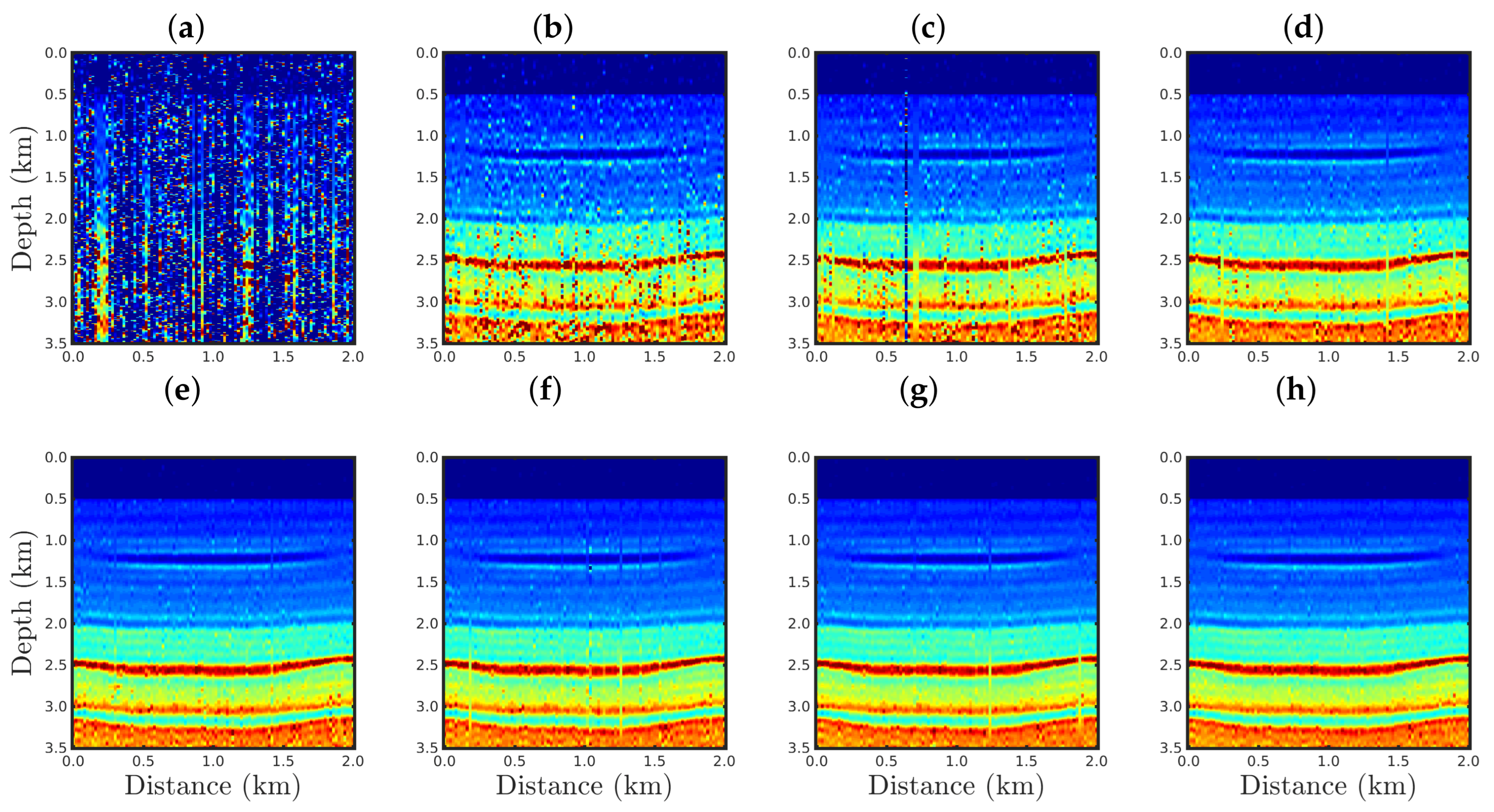
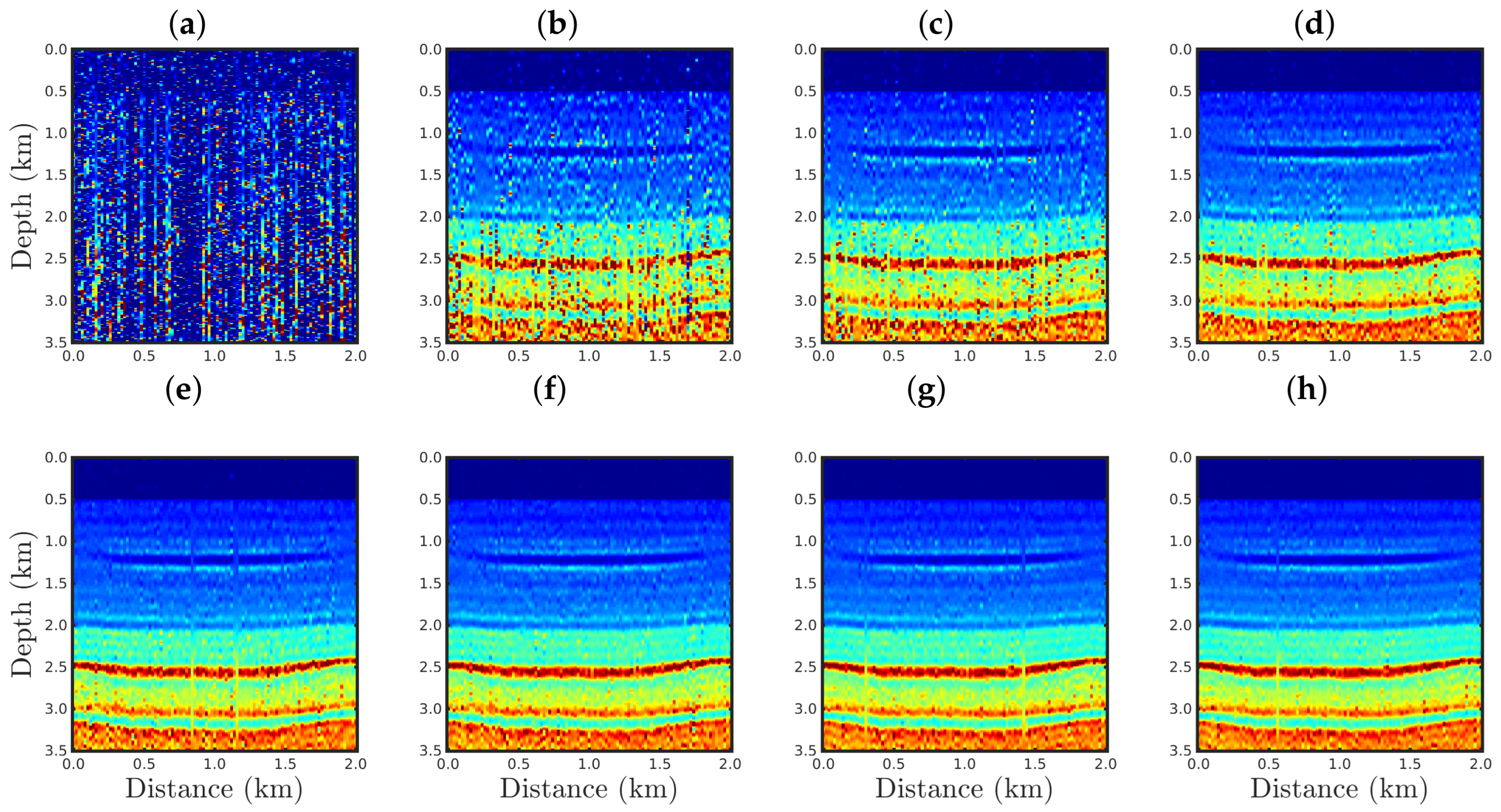
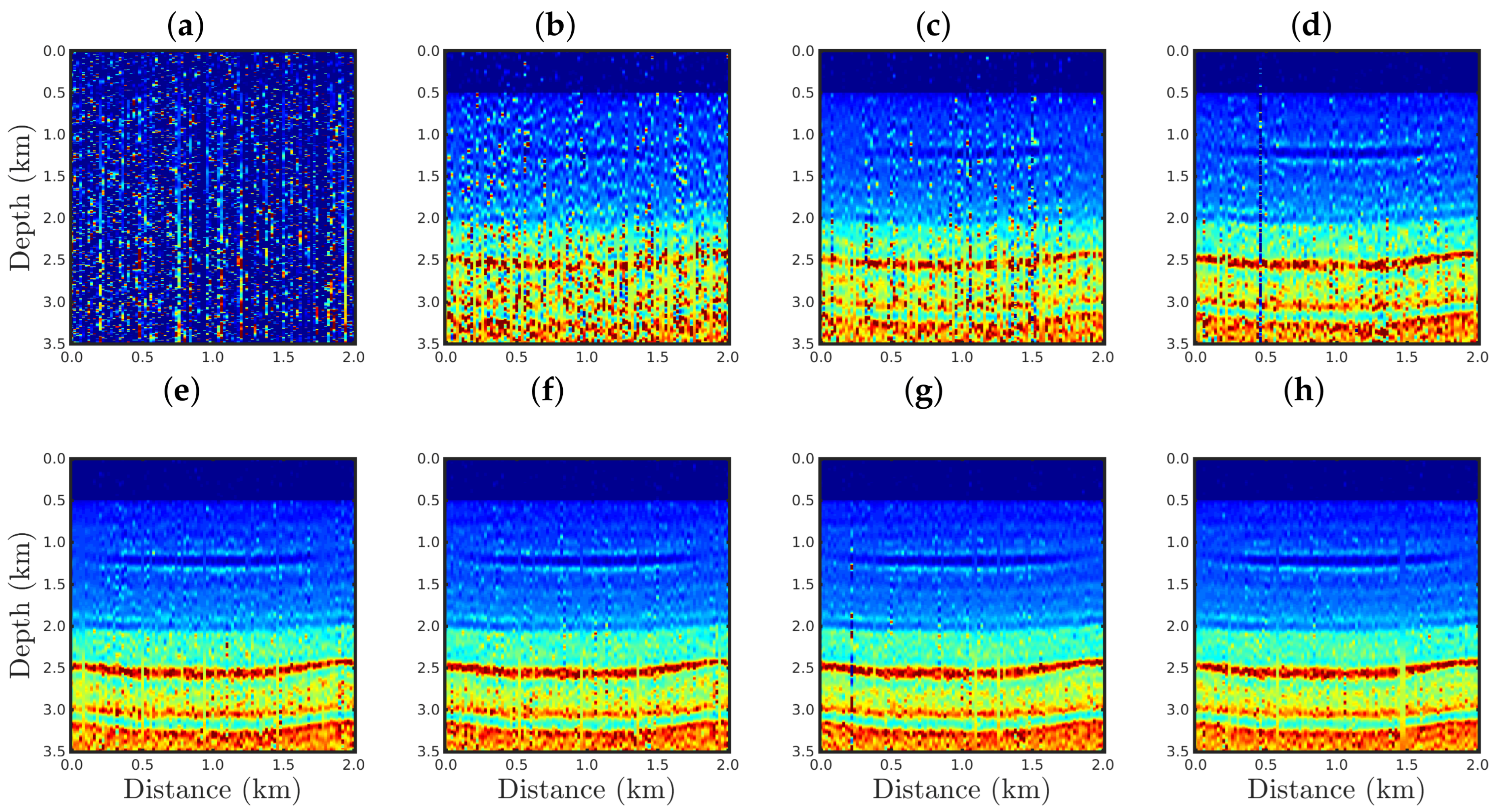
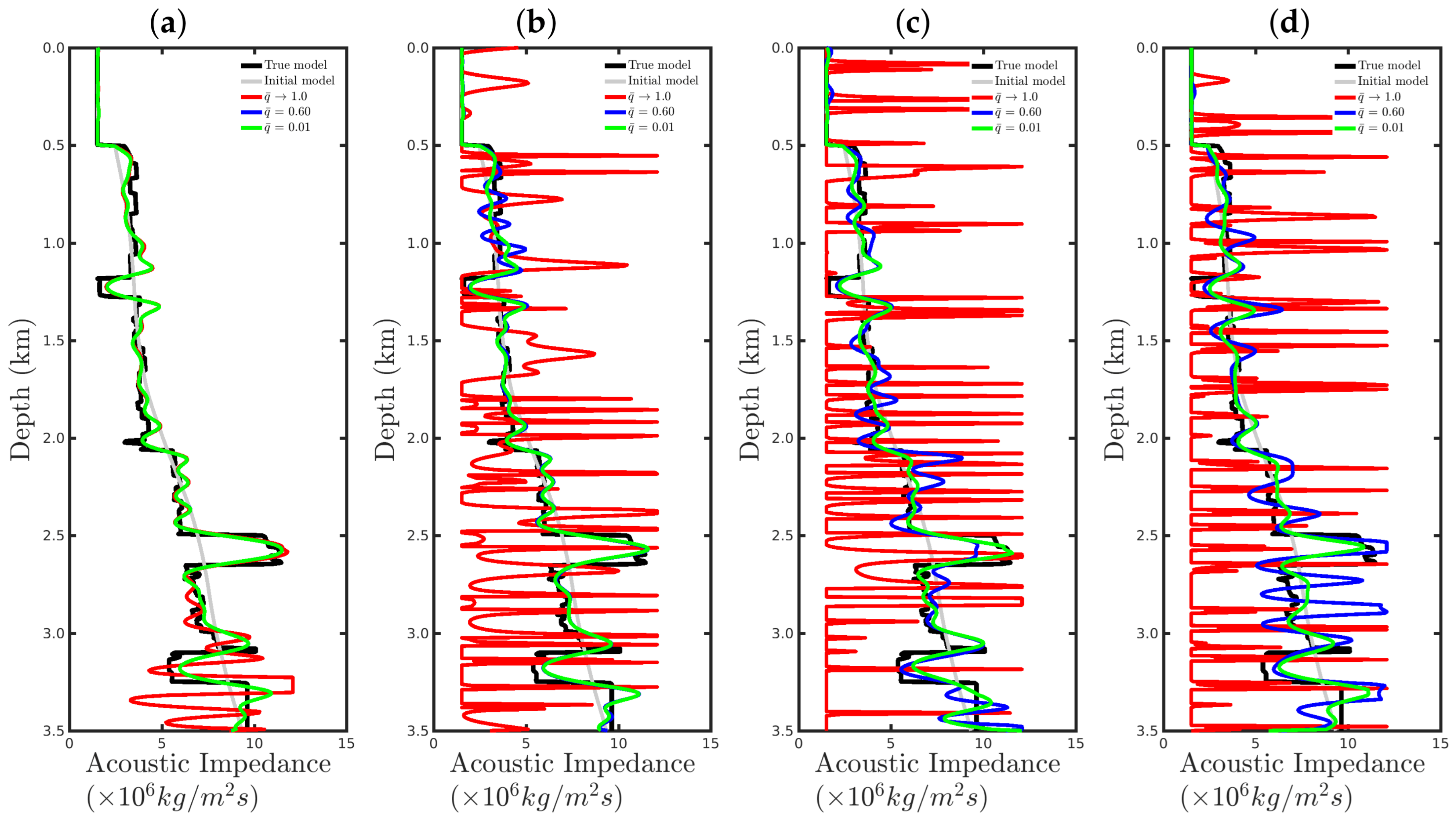
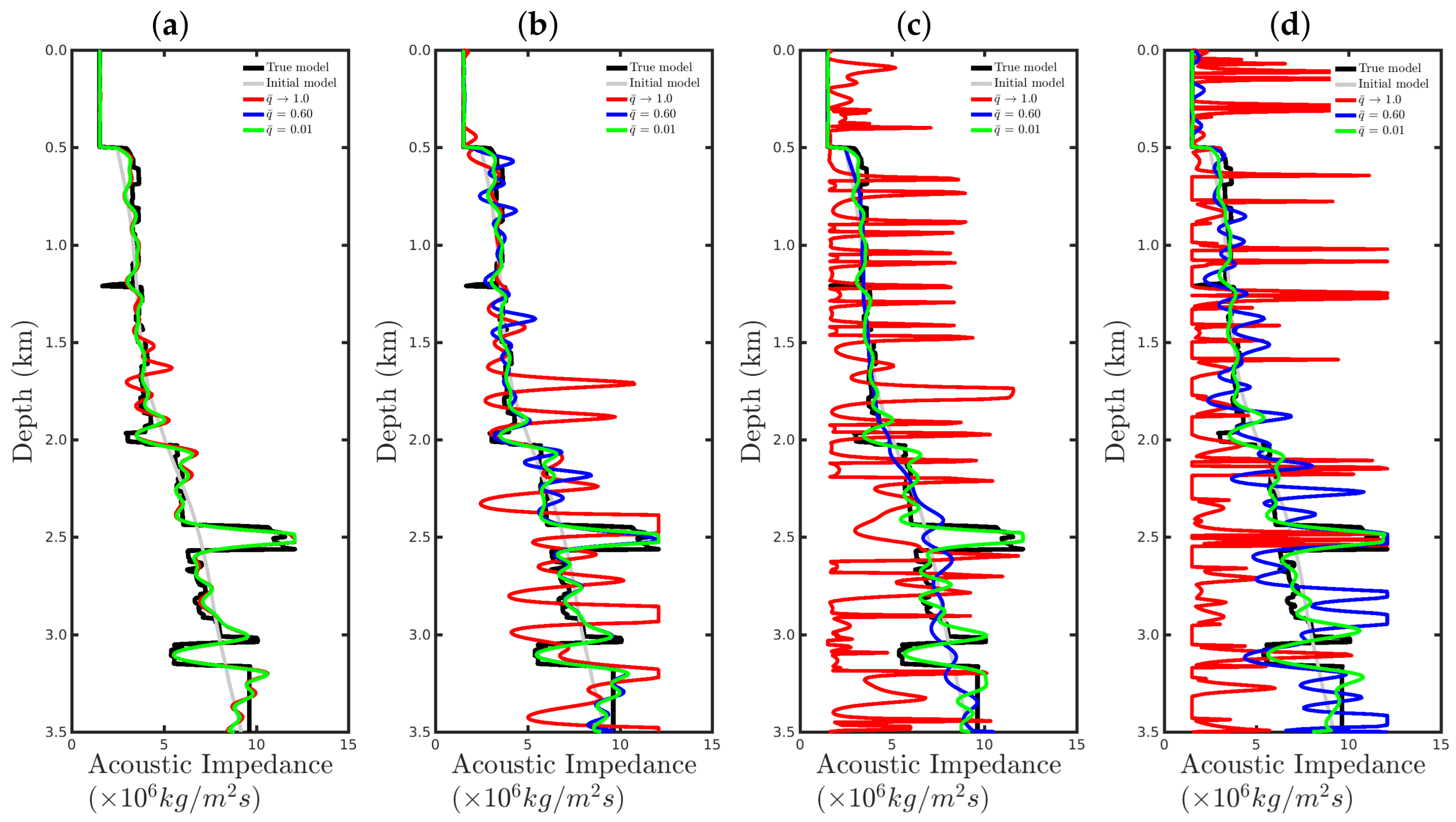
4. Numerical Results
4.1. Sensitivity to the Source Signature
4.2. Sensitivity to Gaussian Noise
4.3. Sensitivity to Erratic Data (Outliers)
5. Final Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PSI | post-stack inversion |
| CG | conjugate gradient |
| NRMS | normalized root mean square |
References
- King, P. Physics boosts oil production. Phys. World 1997, 10, 33. [Google Scholar] [CrossRef]
- Yilmaz, Ö. Seismic Data Analysis: Processing, Inversion and Interpretation of Seismic Data; Society of Exploration Geophysicists (SEG): Tulsa, OK, USA, 2001. [Google Scholar]
- Tarantola, A. Inverse Problem Theory and Methods for Model Parameter Estimation; Society for Industrial and Applied Mathematics (SIAM): University City, PA, USA, 2005. [Google Scholar]
- Menke, W. Geophysical Data Analysis: Discrete Inverse Theory; Academic Press: New York, NY, USA, 2012. [Google Scholar]
- Hadamard, J. Sur les problèmes aux dérivés partielles et leur signification physique. Princet. Univ. Bull. 1902, 13, 49. [Google Scholar]
- Claerbout, J.F.; Muir, F. Robust modeling with erratic data. Geophysics 1973, 38, 826. [Google Scholar] [CrossRef]
- Constable, C.G. Parameter estimation in non-Gaussian noise. Geophys. J. Int. 1988, 94, 131. [Google Scholar] [CrossRef] [Green Version]
- Aravkin, A.Y.; Friedlander, M.P.; Herrmann, F.J.; van Leeuwen, T. Robust inversion, dimensionality reduction and randomized sampling. Math. Program. 2012, 134, 101. [Google Scholar] [CrossRef] [Green Version]
- Ubaidillah, A.; Notodiputro, K.A.; Kurnia, A.; Fitrianto, A.; Mangku, I.W. A robustness study of student-t distributions in regression models with application to infant birth weight data in Indonesia. IOP Conf. Ser. Earth Environ. Sci. 2017, 58, 012013. [Google Scholar] [CrossRef] [Green Version]
- Guitton, A.; Symes, W.W. Robust inversion of seismic data using the Huber norm. Geophysics 2003, 68, 1310. [Google Scholar] [CrossRef]
- Bube, K.P.; Langan, R.T. Hybrid l1/l2 minimization with applications to tomography. Geophysics 1997, 62, 1183. [Google Scholar] [CrossRef]
- Da Silva, S.L.E.F.; Carvalho, P.T.C.; da Costa, C.A.N.; de Araújo, J.M.; Corso, G. Misfit Function for Full Waveform Inversion Based on Shannon Entropy for Deeper Velocity Model Updates. In Proceedings of the SEG International Exposition and Annual Meeting, San Antonio, TX, USA, 15–20 September 2019; p. 1556. Available online: https://library.seg.org/doi/abs/10.1190/segam2019-3214969.1 (accessed on 1 July 2021).
- Johnson, O.; Vignat, C. Some results concerning maximum Rényi entropy distributions. Ann. Inst. Henri Poincaré (B) Probab. Stat. 2007, 43, 339. [Google Scholar] [CrossRef] [Green Version]
- Tanaka, H.-A.; Nakagawa, M.; Oohama, Y. A direct link between Rényi–Tsallis entropy and Holder’s inequality—Yet another proof of Rényi–Tsallis entropy maximization. Entropy 2019, 21, 549. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Da Silva, S.L.E.F.; dos Santos Lima, G.Z.; de Araújo, J.M.; Corso, G. Extensive and non-extensive statistics in seismic inversion. Phys. A 2021, 563, 125496. [Google Scholar] [CrossRef]
- Da Silva, S.L.; Da Costa, C.A.; Carvalho, P.; Araújo, J.; Lucena, L.; Corso, G. An Objective Function Based on q-Gaussian Distribution for Full-Waveform Inversion. In Proceedings of the EAGE 2020 Annual Conference & Exhibition, Online, 8–11 December 2020; pp. 1–5. [Google Scholar]
- De Lima, I.P.; da Silva, S.L.E.F.; Corso, G.; de Araújo, J.M. Tsallis entropy, likelihood, and the robust seismic inversion. Entropy 2020, 22, 464. [Google Scholar] [CrossRef] [Green Version]
- Da Silva, S.L.E.F.; da Costa, C.A.N.; Carvalho, P.T.C.; de Araújo, J.M.; Lucena, L.S.; Corso, G. Robust full-waveform inversion using q-statistics. Phys. A 2020, 548, 124473. [Google Scholar] [CrossRef]
- De Lima, J.V.T.; da Silva, S.L.E.F.; de Araújo, J.M.; Corso, G.; dos Santos Lima, G.Z. Nonextensive statistical mechanics for robust physical parameter estimation: The role of entropic index. Eur. Phys. J. Plus 2021, 136, 269. [Google Scholar] [CrossRef]
- Wada, T.; Suyari, H. κ-generalization of Gauss’ law of error. Phys. Lett. A 2006, 348, 89. [Google Scholar] [CrossRef] [Green Version]
- Da Silva, S.L.E.F.; Carvalho, P.T.C.; de Araújo, J.M.; Corso, G. Full-waveform inversion based on Kaniadakis statistics. Phys. Rev. E 2020, 101, 053311. [Google Scholar] [CrossRef] [PubMed]
- Da Silva, S.L.E.F.; dos Santos Lima, G.Z.; Volpe, E.V.; de Araújo, J.M.; Corso, G. Robust approaches for inverse problems based on Tsallis and Kaniadakis generalised statistics. Eur. Phys. J. Plus 2021, 136, 518. [Google Scholar] [CrossRef]
- Marinho, A.A.; Viswanathan, G.M.; Brito, F.A.; Bezerra, C.G. The connection between Jackson and Hausdorff derivatives in the context of generalized statistical mechanics. arXiv 2020, arXiv:2006.00378. [Google Scholar]
- Russell, B.; Hampson, D. Comparison of poststack seismic inversion methods. In SEG Technical Program Expanded Abstracts; Society of Exploration Geophysicists: Tulsa, OK, USA, 1991; pp. 876–878. [Google Scholar]
- Sen, M.K. Seismic Inversion; Society of Petroleum Engineers (SPE): Richardson, TX, USA, 2006. [Google Scholar]
- Díaz, R.; Pariguan, E. On the gaussian q-distribution. J. Math. Anal. Appl. 2009, 358, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Jackson, F.H. q-difference equations. Am. J. Math. 1910, 32, 305. [Google Scholar] [CrossRef]
- Jackson, F.H. On q-functions and a certain difference operator. Trans. R. Soc. Edinb. 1909, 46, 253. [Google Scholar] [CrossRef]
- Bonatsos, D.; Daskaloyannis, C. Quantum groups and their applications in nuclear physics. Prog. Part. Nucl. Phys. 1999, 43, 537. [Google Scholar] [CrossRef] [Green Version]
- Brito, F.; Marinho, A.A. q-deformed landau diamagnetism problem embedded in d-dimensions. Phys. A 2011, 390, 2497. [Google Scholar] [CrossRef] [Green Version]
- Marinho, A.A.; Costa, N.P.; Pereira, L.F.C.; Brito, F.A.; Chesman, C. Thermoelectric properties of BiSbTe alloy nanofilms produced by dc sputtering: Experiments and modeling. J. Mater Sci. 2020, 55, 2429. [Google Scholar] [CrossRef] [Green Version]
- Martin, G.; Wiley, R.; Marfurt, K. Marmousi2: An elastic upgrade for Marmousi. Lead. Edge 2006, 25, 156. [Google Scholar] [CrossRef]
- Versteeg, R. The Marmousi experience: Velocity model determination on a synthetic complex data set. Lead. Edge 1994, 13, 927. [Google Scholar] [CrossRef]
- Cramez, C.; Jackson, M. Superposed deformation straddling the continental-oceanic transition in deep-water Angola. Mar. Pet. Geol. 2000, 17, 1095. [Google Scholar] [CrossRef] [Green Version]
- Yao, G.; da Silva, N.V.; Wu, D. An effective absorbing layer for the boundary condition in acoustic seismic wave simulation. J. Geophys. Eng. 2018, 15, 495. [Google Scholar] [CrossRef] [Green Version]
- Freitas Silva, F.W.; da Silva, S.L.E.F.; Henriques, M.V.C.; Corso, G. Using fish lateral line sensing to improve seismic acquisition and processing. PLoS ONE 2019, 14, e0213847. [Google Scholar] [CrossRef]
- da Silva, S.L.E.F.; Carvalho, P.T.C.; da Costa, C.A.N.; de Araújo, J.M.; Corso, G. An objective function for full-waveform inversion based on frequency-dependent offset-preconditioning. PLoS ONE 2020, 15, e0240999. [Google Scholar] [CrossRef]
- Ricker, N. Further developments in the wavelet theory of seismogram structure. Bull. Seismol. Am. 1943, 33, 197. [Google Scholar] [CrossRef]
- Ricker, N. Wavelet functions and their polynomials. Geophysics 1944, 9, 314. [Google Scholar] [CrossRef]
- Press, W.H. Numerical Recipes in FORTRAN 90; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Nocedal, J.; Wright, S.J. Numerical Optimization; Springer: New York, NY, USA, 2006. [Google Scholar]
- Köhn, D. Time Domain 2D Elastic Full Waveform Tomography. Ph.D. Thesis, Christian-Albrechts Universität Kiel, Kiel, Germany, 2011. [Google Scholar]
- Vigh, D.; Starr, E. 3D prestack plane-wave, full-waveform inversion. Geophysics 2008, 73, VE135–VE144. [Google Scholar] [CrossRef]
- Gómez, L.; Pestana, R.C. Full-waveform inversion using alternative objective functions in the presence of noise and uncertainties of source signature. In Proceedings of the 15th International Congress of the Brazilian Geophysical Society & EXPOGEF, Rio de Janeiro, Brazil, 31 July–3 August 2017; pp. 296–301. [Google Scholar]
- Pearson, K. Mathematical contributions to the theory of evolution. III. Regression, heredity, and panmixia, Philosophical Transactions of the Royal Society of London. Series A. Contain. Pap. Math. Phys. Character 1896, 187, 253. [Google Scholar]


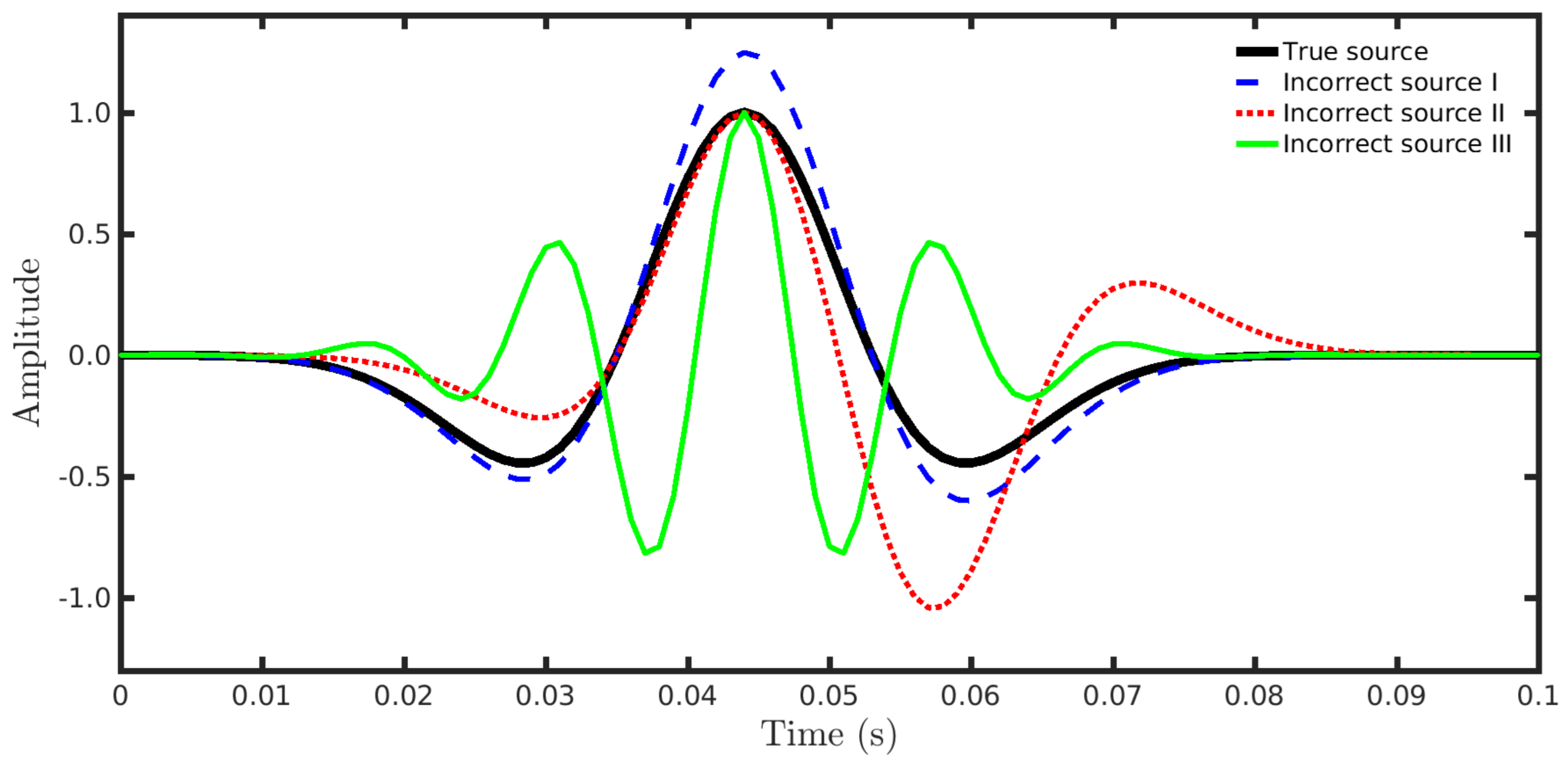
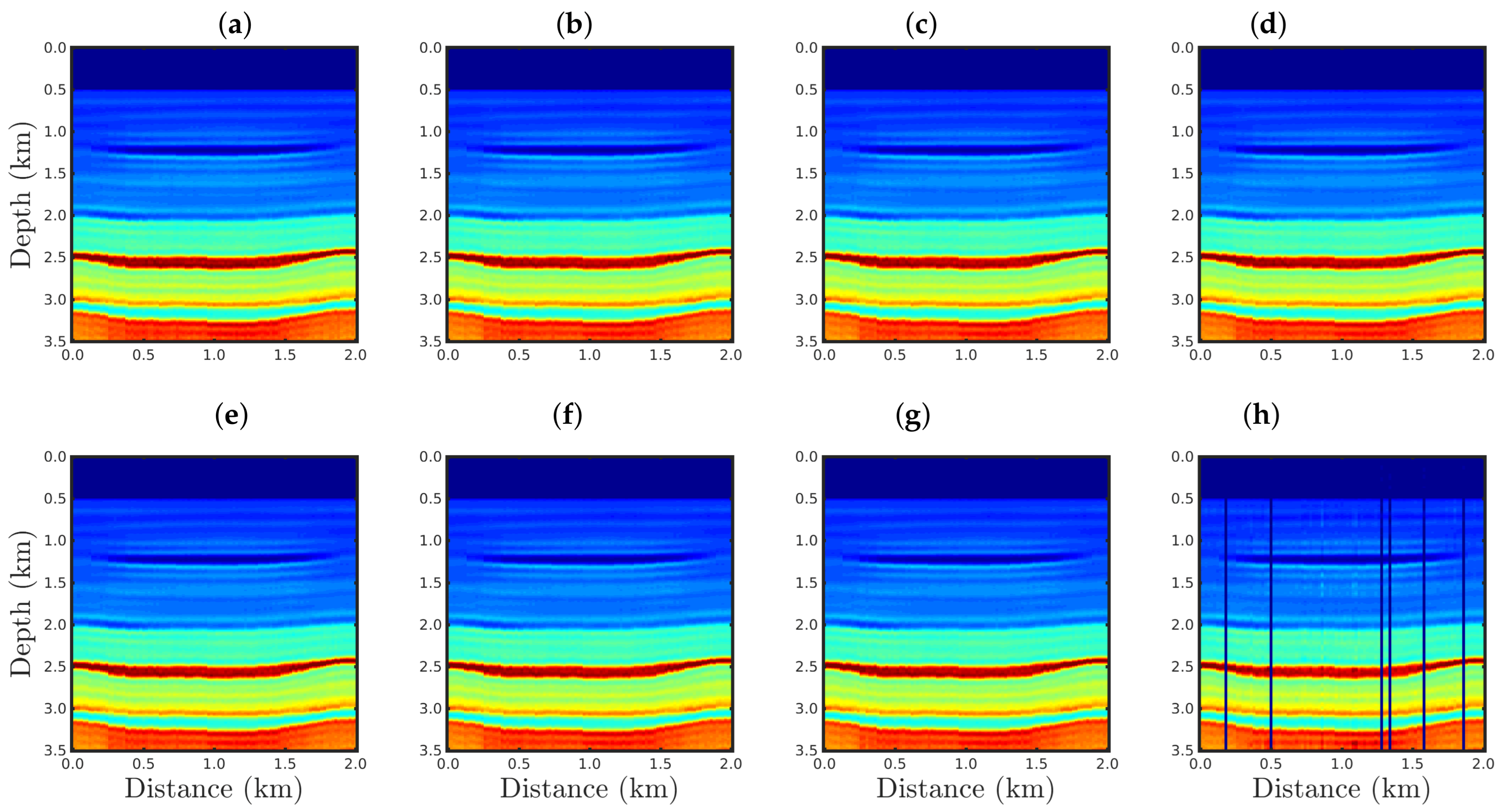
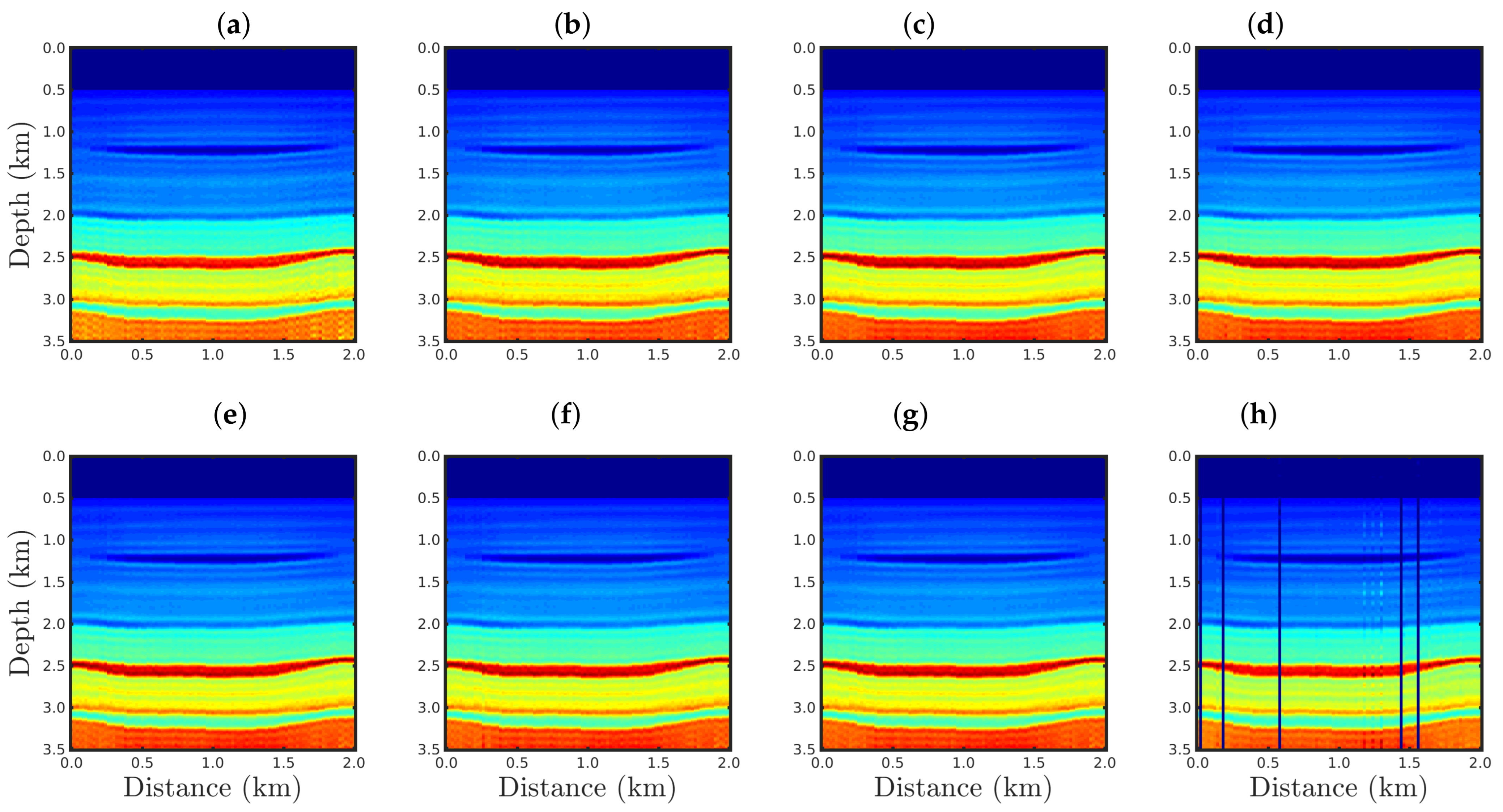
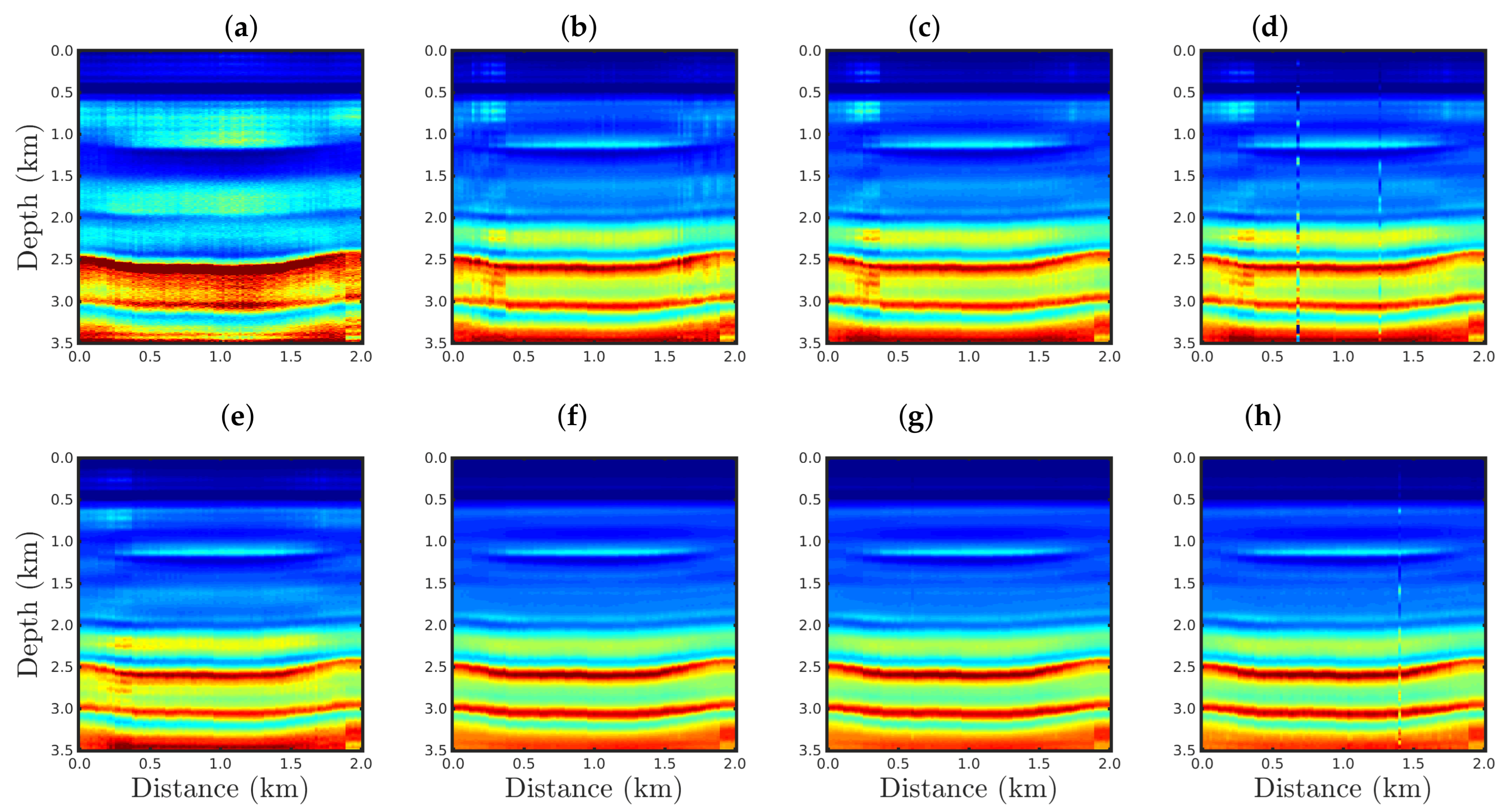


| Strategy | SNR = 5 dB | SNR = 10 dB | SNR = 20 dB | SNR = 30 dB | ||||
|---|---|---|---|---|---|---|---|---|
| NRMS | R | NRMS | R | NRMS | R | NRMS | R | |
| Conventional PSI () | 0.6144 | 0.4342 | 0.3678 | 0.7587 | 0.1889 | 0.9290 | 0.1019 | 0.9789 |
| Our proposal () | 0.4784 | 0.6287 | 0.2779 | 0.8528 | 0.1589 | 0.9486 | 0.1004 | 0.9791 |
| Our proposal () | 0.4662 | 0.6435 | 0.2788 | 0.8520 | 0.1588 | 0.9487 | 0.1003 | 0.9791 |
| Our proposal () | 0.4068 | 0.7077 | 0.2787 | 0.8520 | 0.1586 | 0.9488 | 0.1003 | 0.9792 |
| Our proposal () | 0.3594 | 0.7542 | 0.2770 | 0.8536 | 0.1588 | 0.9487 | 0.1004 | 0.9791 |
| Our proposal () | 0.3162 | 0.8013 | 0.2746 | 0.8549 | 0.1591 | 0.9485 | 0.1004 | 0.9791 |
| Our proposal () | 0.3176 | 0.7957 | 0.2666 | 0.8623 | 0.1589 | 0.9486 | 0.1003 | 0.9791 |
| Our proposal () | 0.2947 | 0.8234 | 0.2566 | 0.8698 | 0.1590 | 0.9486 | 0.1004 | 0.9791 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Silva, S.A.; da Silva, S.L.E.F.; de Souza, R.F.; Marinho, A.A.; de Araújo, J.M.; Bezerra, C.G. Improving Seismic Inversion Robustness via Deformed Jackson Gaussian. Entropy 2021, 23, 1081. https://doi.org/10.3390/e23081081
Silva SA, da Silva SLEF, de Souza RF, Marinho AA, de Araújo JM, Bezerra CG. Improving Seismic Inversion Robustness via Deformed Jackson Gaussian. Entropy. 2021; 23(8):1081. https://doi.org/10.3390/e23081081
Chicago/Turabian StyleSilva, Suzane A., Sérgio Luiz E. F. da Silva, Renato F. de Souza, Andre A. Marinho, João M. de Araújo, and Claudionor G. Bezerra. 2021. "Improving Seismic Inversion Robustness via Deformed Jackson Gaussian" Entropy 23, no. 8: 1081. https://doi.org/10.3390/e23081081
APA StyleSilva, S. A., da Silva, S. L. E. F., de Souza, R. F., Marinho, A. A., de Araújo, J. M., & Bezerra, C. G. (2021). Improving Seismic Inversion Robustness via Deformed Jackson Gaussian. Entropy, 23(8), 1081. https://doi.org/10.3390/e23081081









