Isospectral Twirling and Quantum Chaos
Abstract
:1. Introduction
2. Isospectral Twirling
3. The Integrability-Chaos Transition
4. OTOCs
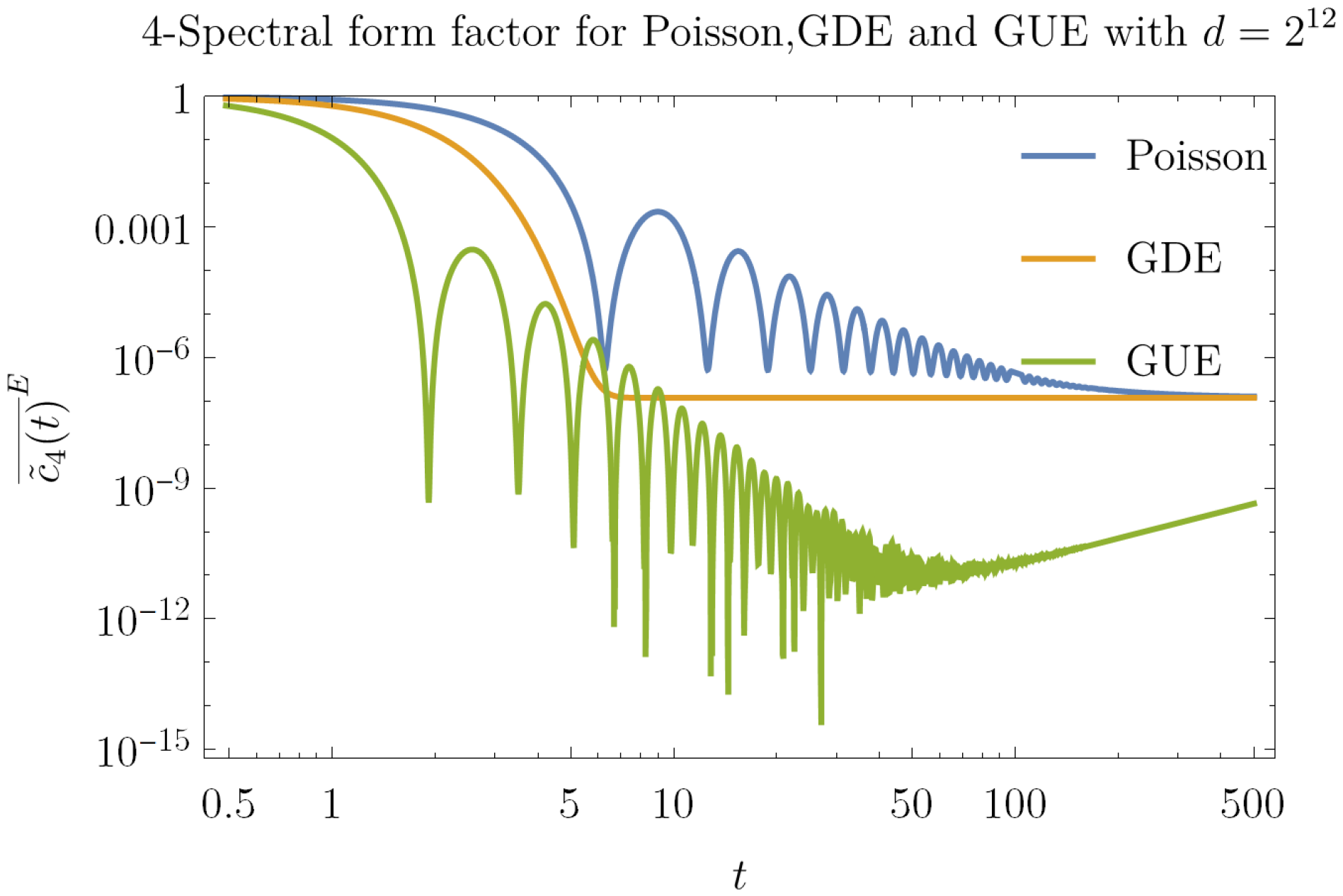
5. Finite Time Behavior
6. Randomness of the Ensemble
7. Loschmidt Echo and OTOC
8. Entanglement
9. Tripartite Mutual Information
10. Conclusions and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. 4k—Point OTOC
Appendix A.1. Proof of Proposition 1
Appendix A.2. Proof of Equation (10)
Appendix B. Calculations for the Clifford Averages
Appendix B.1. Calculation of tr(QTσ)
Appendix B.2. Calculation of
Appendix C. Frame Potential
Appendix C.1. Proof of Proposition 3
Appendix C.2. Proof of Proposition 4
Appendix C.3. Definition of Generic Spectrum
Appendix C.4. Proof of Proposition 5
Appendix C.5. Proof of Proposition 6
Appendix D. Loschmidt Echo
Appendix D.1. Proof of Proposition 7
Appendix E. Entanglement
Appendix E.1. Proof of Proposition 8
Appendix F. Tripartite Mutual Information
Appendix F.1. Choi State: Definition and Properties
Appendix F.2. 2—Rényi TMI
Appendix F.3. Proof of Equation (26) and Proposition 9
References
- Lloyd, S. Black Holes, Demons and the Loss of Coherence: How Complex Systems Get Information, and What They Do with It. Ph.D. Thesis, Rockefeller University, New York, NY, USA, 1988. [Google Scholar]
- Rigol, M.; Dunjko, V.; Olshanii, M. Thermalization and its mechanism for generic isolated quantum systems. Nature 2008, 452, 854–858. [Google Scholar] [CrossRef] [Green Version]
- Santos, L.F.; Rigol, M. Onset of quantum chaos in one-dimensional bosonic and fermionic systems and its relation to thermalization. Phys. Rev. E 2010, 81, 036206. [Google Scholar] [CrossRef] [Green Version]
- Popescu, S.; Short, A.J.; Winter, A. Entanglement and the foundations of statistical mechanics. Nat. Phys. 2006, 2, 754–758. [Google Scholar] [CrossRef] [Green Version]
- Srednicki, M. Chaos and quantum thermalization. Phys. Rev. E 1994, 50, 888–901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Reimann, P. Typicality for Generalized Microcanonical Ensembles. Phys. Rev. Lett. 2007, 99, 160404. [Google Scholar] [CrossRef] [Green Version]
- Eisert, J.; Friesdorf, M.; Gogolin, C. Quantum many-body systems out of equilibrium. Nat. Phys. 2015, 11, 124–130. [Google Scholar] [CrossRef] [Green Version]
- Polkovnikov, A.; Sengupta, K.; Silva, A.; Vengalattore, M. Colloquium: Nonequilibrium dynamics of closed interacting quantum systems. Rev. Mod. Phys. 2011, 83, 863–883. [Google Scholar] [CrossRef] [Green Version]
- Garcia-March, M.A.; van Frank, S.; Bonneau, M.; Schmiedmayer, J.; Lewenstein, M.; Santos, L.F. Relaxation, chaos, and thermalization in a three-mode model of a Bose–Einstein condensate. New J. Phys. 2018, 20, 113039. [Google Scholar] [CrossRef]
- Tasaki, H. Typicality of Thermal Equilibrium and Thermalization in Isolated Macroscopic Quantum Systems. J. Stat. Phys. 2016, 163, 937–997. [Google Scholar] [CrossRef] [Green Version]
- Reimann, P. Generalization of von Neumann’s Approach to Thermalization. Phys. Rev. Lett. 2015, 115, 010403. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hosur, P.; Qi, X.L.; Roberts, D.A.; Yoshida, B. Chaos in quantum channels. J. High Energy Phys. 2016, 2016, 4. [Google Scholar] [CrossRef] [Green Version]
- Ding, D.; Hayden, P.; Walter, M. Conditional mutual information of bipartite unitaries and scrambling. J. High Energy Phys. 2016, 2016, 145. [Google Scholar] [CrossRef] [Green Version]
- Brown, W.G.; Fawzi, O. Scrambling speed of random quantum circuits. arXiv 2013, arXiv:quant-ph/1210.6644. [Google Scholar]
- Liu, Z.W.; Lloyd, S.; Zhu, E.; Zhu, H. Entanglement, quantum randomness, and complexity beyond scrambling. J. High Energy Phys. 2018, 2018, 41. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.W.; Lloyd, S.; Zhu, E.Y.; Zhu, H. Generalized Entanglement Entropies of Quantum Designs. Phys. Rev. Lett. 2018, 120, 130502. [Google Scholar] [CrossRef] [Green Version]
- Styliaris, G.; Anand, N.; Zanardi, P. Information Scrambling over Bipartitions: Equilibration, Entropy Production, and Typicality. arXiv 2020, arXiv:quant-ph/2007.08570. [Google Scholar]
- Hayden, P.; Preskill, J. Black holes as mirrors: Quantum information in random subsystems. J. High Energy Phys. 2007, 2007, 120. [Google Scholar] [CrossRef] [Green Version]
- Shenker, S.H.; Stanford, D. Stringy effects in scrambling. J. High Energy Phys. 2015, 2015, 132. [Google Scholar] [CrossRef] [Green Version]
- Kitaev, A. Hidden Correlations in the Hawking Radiation and Thermal Noise. Talk Given at the Fundamental Physics Prize Symposium, 2014. Available online: https://online.kitp.ucsb.edu/online/joint98/kitaev/ (accessed on 15 August 2021).
- Cotler, J.S.; Gur-Ari, G.; Hanada, M.; Polchinski, J.; Saad, P.; Shenker, S.H.; Stanford, D.; Streicher, A.; Tezuka, M. Black holes and random matrices. J. High Energy Phys. 2017, 2017, 118. [Google Scholar] [CrossRef]
- Yang, Z.C.; Hamma, A.; Giampaolo, S.M.; Mucciolo, E.R.; Chamon, C. Entanglement complexity in quantum many-body dynamics, thermalization, and localization. Phys. Rev. B 2017, 96, 020408. [Google Scholar] [CrossRef] [Green Version]
- Chamon, C.; Hamma, A.; Mucciolo, E.R. Emergent Irreversibility and Entanglement Spectrum Statistics. Phys. Rev. Lett. 2014, 112, 240501. [Google Scholar] [CrossRef] [Green Version]
- Harrow, A.W.; Low, R.A. Random Quantum Circuits are Approximate 2-designs. Commun. Math. Phys. 2009, 291, 257–302. [Google Scholar] [CrossRef] [Green Version]
- Gharibyan, H.; Hanada, M.; Shenker, S.H.; Tezuka, M. Onset of random matrix behavior in scrambling systems. J. High Energy Phys. 2018, 2018, 124. [Google Scholar] [CrossRef] [Green Version]
- Brown, W.G. Random Quantum Dynamics: From Random Quantum Circuits to Quantum Chaos. Ph.D. Thesis, Dartmouth College, Hanover, NH, USA, 2010. [Google Scholar]
- Brown, W.G.; Viola, L. Convergence Rates for Arbitrary Statistical Moments of Random Quantum Circuits. Phys. Rev. Lett. 2010, 104, 250501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nahum, A.; Vijay, S.; Haah, J. Operator Spreading in Random Unitary Circuits. Phys. Rev. X 2018, 8, 021014. [Google Scholar] [CrossRef] [Green Version]
- Brown, A.R.; Susskind, L. Second law of quantum complexity. Phys. Rev. D 2018, 97, 086015. [Google Scholar] [CrossRef] [Green Version]
- Dowling, M.R.; Nielsen, M.A. The geometry of quantum computation. Quantum Inf. Comput. 2008, 8, 861–899. [Google Scholar]
- Zhou, T.; Luitz, D.J. Operator entanglement entropy of the time evolution operator in chaotic systems. Phys. Rev. B 2017, 95, 094206. [Google Scholar] [CrossRef] [Green Version]
- Benenti, G.; Casati, G. How complex is quantum motion? Phys. Rev. E 2009, 79, 025201. [Google Scholar] [CrossRef] [Green Version]
- Maldacena, J.; Shenker, S.H.; Stanford, D. A bound on chaos. J. High Energy Phys. 2016, 2016, 106. [Google Scholar] [CrossRef] [Green Version]
- Lashkari, N.; Stanford, D.; Hastings, M.; Osborne, T.; Hayden, P. Towards the fast scrambling conjecture. J. High Energy Phys. 2013, 2013, 22. [Google Scholar] [CrossRef] [Green Version]
- Xu, S.; Swingle, B. Locality, Quantum Fluctuations, and Scrambling. Phys. Rev. X 2019, 9, 031048. [Google Scholar] [CrossRef] [Green Version]
- Anand, N.; Styliaris, G.; Kumari, M.; Zanardi, P. Quantum coherence as a signature of chaos. arXiv 2020, arXiv:quant-ph/2009.02760. [Google Scholar]
- Larkin, A.I.; Ovchinnikov, Y.N. Quasiclassical method in the theory of superconductivity. J. Exp. Theor. Phys. 1969, 28, 1200–1205. [Google Scholar]
- Lin, C.J.; Motrunich, O.I. Out-of-time-ordered correlators in a quantum Ising chain. Phys. Rev. B 2018, 97, 144304. [Google Scholar] [CrossRef] [Green Version]
- Chenu, A.; Molina-Vilaplana, J.; del Campo, A. Work Statistics, Loschmidt Echo and Information Scrambling in Chaotic Quantum Systems. Quantum 2019, 3, 127. [Google Scholar] [CrossRef]
- Touil, A.; Deffner, S. Quantum scrambling and the growth of mutual information. Quantum Sci. Technol. 2020, 5, 035005. [Google Scholar] [CrossRef]
- Häppölä, J.; Halász, G.B.; Hamma, A. Universality and robustness of revivals in the transverse field XY model. Phys. Rev. A 2012, 85, 032114. [Google Scholar] [CrossRef] [Green Version]
- Swingle, B.; Bentsen, G.; Schleier-Smith, M.; Hayden, P. Measuring the scrambling of quantum information. Phys. Rev. A 2016, 94, 040302. [Google Scholar] [CrossRef] [Green Version]
- von Keyserlingk, C.W.; Rakovszky, T.; Pollmann, F.; Sondhi, S.L. Operator Hydrodynamics, OTOCs, and Entanglement Growth in Systems without Conservation Laws. Phys. Rev. X 2018, 8, 021013. [Google Scholar] [CrossRef] [Green Version]
- Swingle, B. Unscrambling the physics of out-of-time-order correlators. Nat. Phys. 2018, 14, 988–990. [Google Scholar] [CrossRef]
- Huang, Y.; Brandão, F.G.S.L.; Zhang, Y.L. Finite-Size Scaling of Out-of-Time-Ordered Correlators at Late Times. Phys. Rev. Lett. 2019, 123, 010601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Scott, A.J. Optimizing quantum process tomography with unitary 2-designs. J. Phys. A Math. Theor. 2008, 41, 055308. [Google Scholar] [CrossRef] [Green Version]
- Roberts, D.A.; Yoshida, B. Chaos and complexity by design. J. High Energy Phys. 2017, 2017, 121. [Google Scholar] [CrossRef] [Green Version]
- Wigner, E.P. On the statistical distribution of the widths and spacings of nuclear resonance levels. Math. Proc. Camb. Philos. Soc. 1951, 47, 790–798. [Google Scholar] [CrossRef]
- Haake, F.; Gnutzmann, S.; Kuś, M. Quantum Signatures of Chaos; Springer International Publishing: Berlin/Heidelberg, Germany, 2018. [Google Scholar] [CrossRef]
- Mehta, M.L. Random Matrices; Elsevier: Amsterdam, The Netherlands, 1991. [Google Scholar] [CrossRef]
- Tao, T. Topics in Random Matrix Theory; American Mathematical Society: Providence, RI, USA, 2012. [Google Scholar] [CrossRef]
- Rao, W.J. Higher-order level spacings in random matrix theory based on Wigner’s conjecture. Phys. Rev. B 2020, 102, 054202. [Google Scholar] [CrossRef]
- Chen, X.; Zhou, T. Operator scrambling and quantum chaos. arXiv 2018, arXiv:cond-mat.str-el/1804.08655. [Google Scholar]
- Cotler, J.; Hunter-Jones, N.; Liu, J.; Yoshida, B. Chaos, complexity, and random matrices. J. High Energy Phys. 2017, 2017, 48. [Google Scholar] [CrossRef] [Green Version]
- Hunter-Jones, N.R. Chaos and Randomness in Strongly-Interacting Quantum Systems. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 2018. [Google Scholar]
- Balasubramanian, V.; Berkooz, M.; Ross, S.F.; Simón, J. Black holes, entanglement and random matrices. Class. Quantum Gravity 2014, 31, 185009. [Google Scholar] [CrossRef]
- Bao, J.H.; Zhang, C.Y. Out-of-time-order correlators in the one-dimensional XY model. Commun. Theor. Phys. 2020, 72, 085103. [Google Scholar] [CrossRef]
- Scaramazza, J.A.; Shastry, B.S.; Yuzbashyan, E.A. Integrable matrix theory: Level statistics. Phys. Rev. E 2016, 94, 032106. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Riser, R.; Kanzieper, E. Power spectrum and form factor in random diagonal matrices and integrable billiards. arXiv 2020, arXiv:nlin.CD/2011.02210. [Google Scholar]
- Prakash, A.; Pixley, J.H.; Kulkarni, M. The universal spectral form factor for many-body localization. arXiv 2020, arXiv:cond-mat.dis-nn/2008.07547. [Google Scholar]
- Riser, R.; Osipov, V.A.; Kanzieper, E. Nonperturbative theory of power spectrum in complex systems. Ann. Phys. 2020, 413, 168065. [Google Scholar] [CrossRef]
- Brandão, F.G.S.L.; Ćwikliński, P.; Horodecki, M.; Horodecki, P.; Korbicz, J.K.; Mozrzymas, M. Convergence to equilibrium under a random Hamiltonian. Phys. Rev. E 2012, 86, 031101. [Google Scholar] [CrossRef] [Green Version]
- Caravelli, F.; Coulter-De Wit, G.; García-Pintos, L.P.; Hamma, A. Random quantum batteries. Phys. Rev. Res. 2020, 2, 023095. [Google Scholar] [CrossRef]
- Collins, B. Moments and cumulants of polynomial random variables on unitary groups, the Itzykson-Zuber integral, and free probability. Int. Math. Res. Not. 2003, 2003, 953–982. [Google Scholar] [CrossRef]
- Roth, I.; Kueng, R.; Kimmel, S.; Liu, Y.K.; Gross, D.; Eisert, J.; Kliesch, M. Recovering Quantum Gates from Few Average Gate Fidelities. Phys. Rev. Lett. 2018, 121, 170502. [Google Scholar] [CrossRef] [Green Version]
- Leone, L.; Oliviero, S.F.E.; Zhou, Y.; Hamma, A. Quantum Chaos is Quantum. Quantum 2021, 5, 453. [Google Scholar] [CrossRef]
- Oliviero, S.F.E.; Leone, L.; Caravelli, F.; Hamma, A. Random Matrix Theory of the Isospectral twirling. SciPost Phys. 2021, 10, 76. [Google Scholar] [CrossRef]
- Gemmer, J.; Michel, M.; Mahler, G. Quantum Thermodynamics; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef] [Green Version]
- Canali, C.M.; Kravtsov, V.E. Normalization sum rule and spontaneous breaking of U(N) invariance in random matrix ensembles. Phys. Rev. E 1995, 51, R5185–R5188. [Google Scholar] [CrossRef] [Green Version]
- Pato, M.P. Spontaneous symmetry breaking in U(N) invariant ensembles with a soft confinement potential. Phys. Rev. E 2000, 61, R3291–R3294. [Google Scholar] [CrossRef]
- Liu, J. Spectral form factors and late time quantum chaos. Phys. Rev. D 2018, 98, 086026. [Google Scholar] [CrossRef] [Green Version]
- Yan, B.; Cincio, L.; Zurek, W.H. Information Scrambling and Loschmidt Echo. Phys. Rev. Lett. 2020, 124, 160603. [Google Scholar] [CrossRef] [Green Version]
- Bhattacharyya, A.; Chemissany, W.; Haque, S.S.; Yan, B. Towards the Web of Quantum Chaos Diagnostics. arXiv 2019, arXiv:hep-th/1909.01894. [Google Scholar]
- Peres, A. Stability of quantum motion in chaotic and regular systems. Phys. Rev. A 1984, 30, 1610–1615. [Google Scholar] [CrossRef]
- Weinstein, Y.S.; Lloyd, S.; Tsallis, C. Border between Regular and Chaotic Quantum Dynamics. Phys. Rev. Lett. 2002, 89, 214101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kowalewska-Kudłaszyk, A.; Kalaga, J.; Leoński, W. Long-time fidelity and chaos for a kicked nonlinear oscillator system. Phys. Lett. A 2009, 373, 1334–1340. [Google Scholar] [CrossRef] [Green Version]
- Choi, M. Completely positive linear maps on complex matrices. Linear Algebra Its Appl. 1975, 10, 285–290. [Google Scholar] [CrossRef] [Green Version]
- Zanardi, P. Entanglement of quantum evolutions. Phys. Rev. A 2001, 63, 040304. [Google Scholar] [CrossRef] [Green Version]
- Zhou, S.; Yang, Z.C.; Hamma, A.; Chamon, C. Single T gate in a Clifford circuit drives transition to universal entanglement spectrum statistics. SciPost Phys. 2020, 9, 87. [Google Scholar] [CrossRef]
- Watrous, J. The Theory of Quantum Information; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar] [CrossRef] [Green Version]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leone, L.; Oliviero, S.F.E.; Hamma, A. Isospectral Twirling and Quantum Chaos. Entropy 2021, 23, 1073. https://doi.org/10.3390/e23081073
Leone L, Oliviero SFE, Hamma A. Isospectral Twirling and Quantum Chaos. Entropy. 2021; 23(8):1073. https://doi.org/10.3390/e23081073
Chicago/Turabian StyleLeone, Lorenzo, Salvatore F. E. Oliviero, and Alioscia Hamma. 2021. "Isospectral Twirling and Quantum Chaos" Entropy 23, no. 8: 1073. https://doi.org/10.3390/e23081073
APA StyleLeone, L., Oliviero, S. F. E., & Hamma, A. (2021). Isospectral Twirling and Quantum Chaos. Entropy, 23(8), 1073. https://doi.org/10.3390/e23081073






