Heat Transfer and Entropy in a Vertical Porous Plate Subjected to Suction Velocity and MHD
Abstract
:1. Introduction
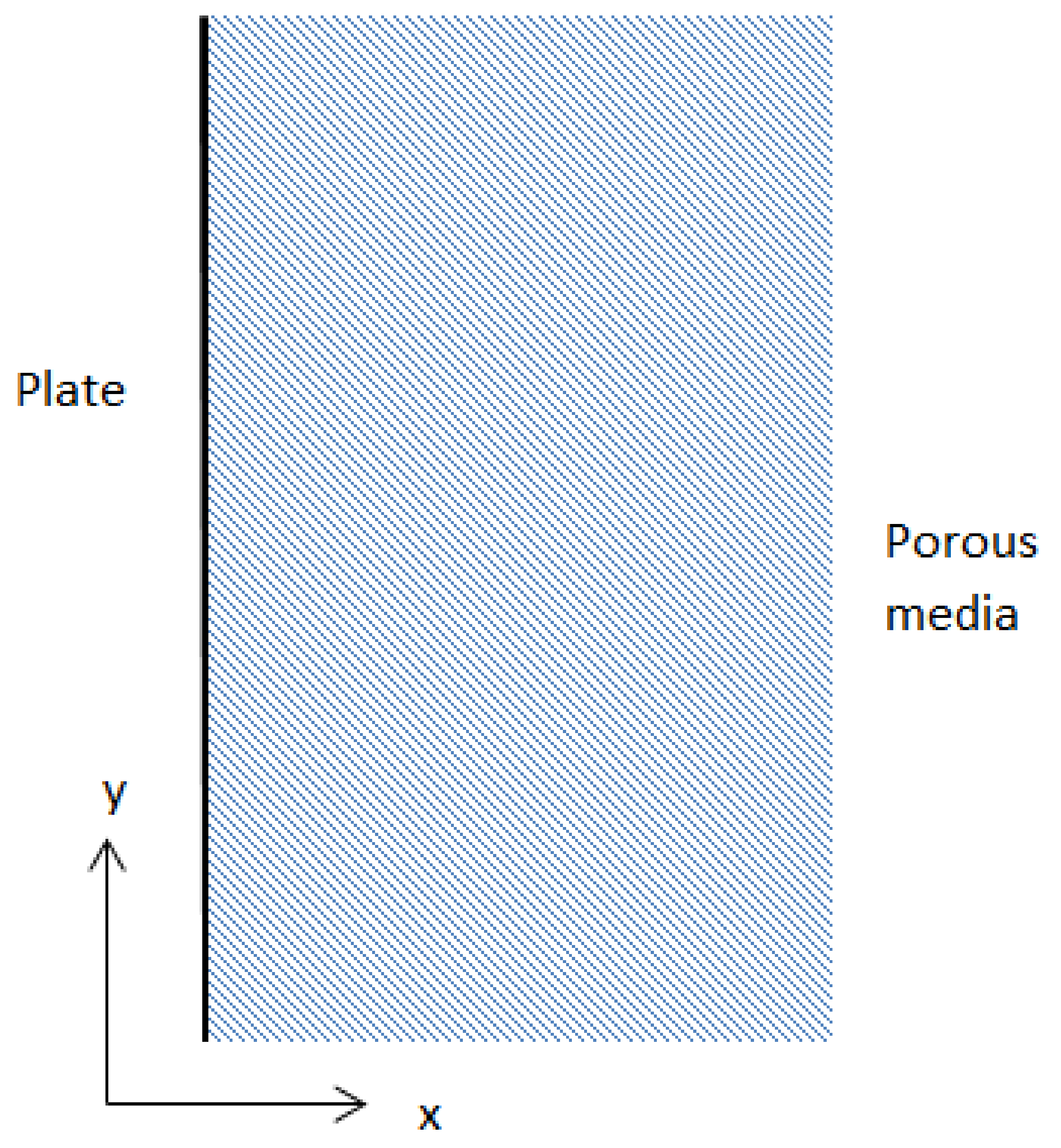
2. Methodology
2.1. Entropy Generation
2.2. Numerical Scheme
3. Results and Discussion
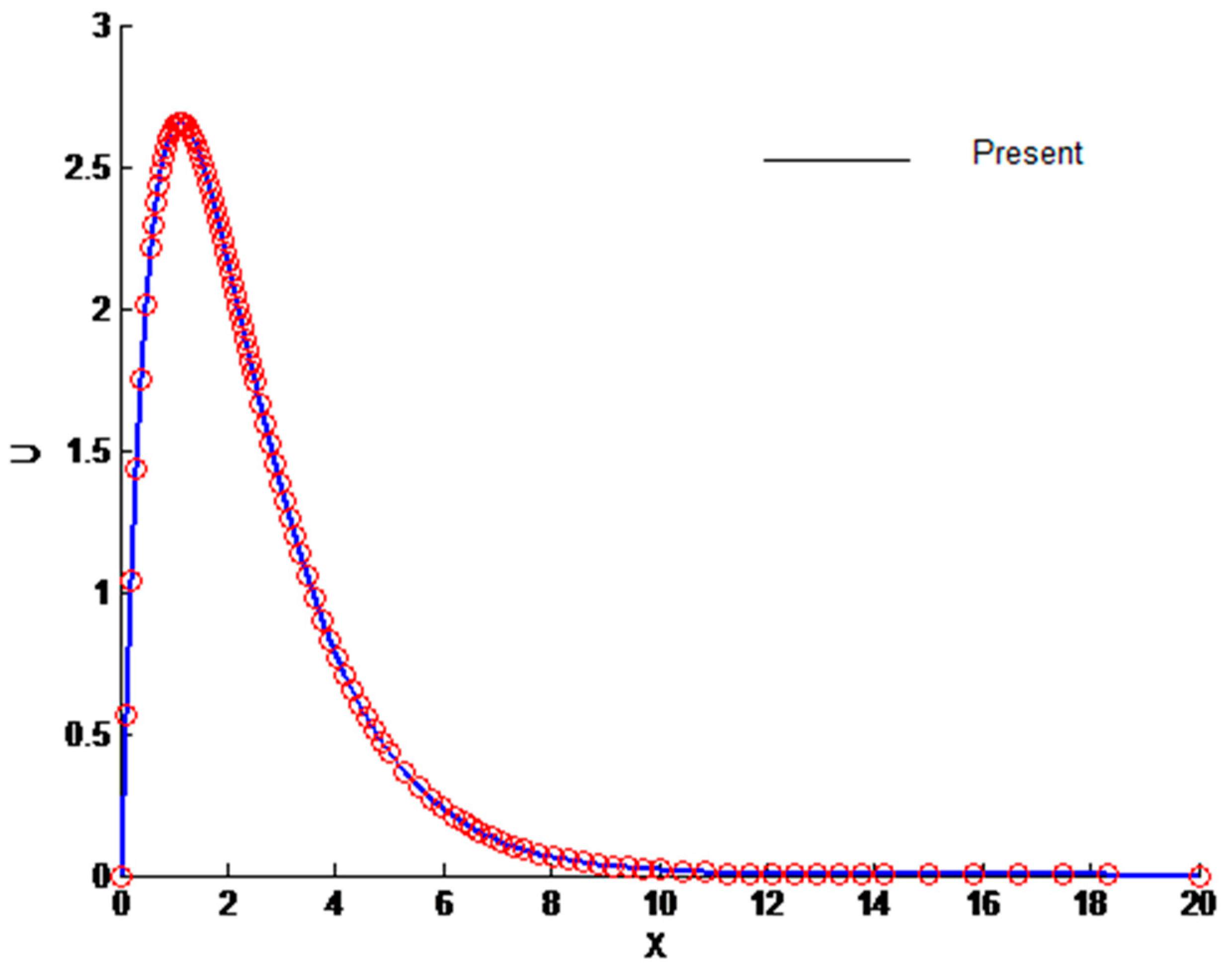
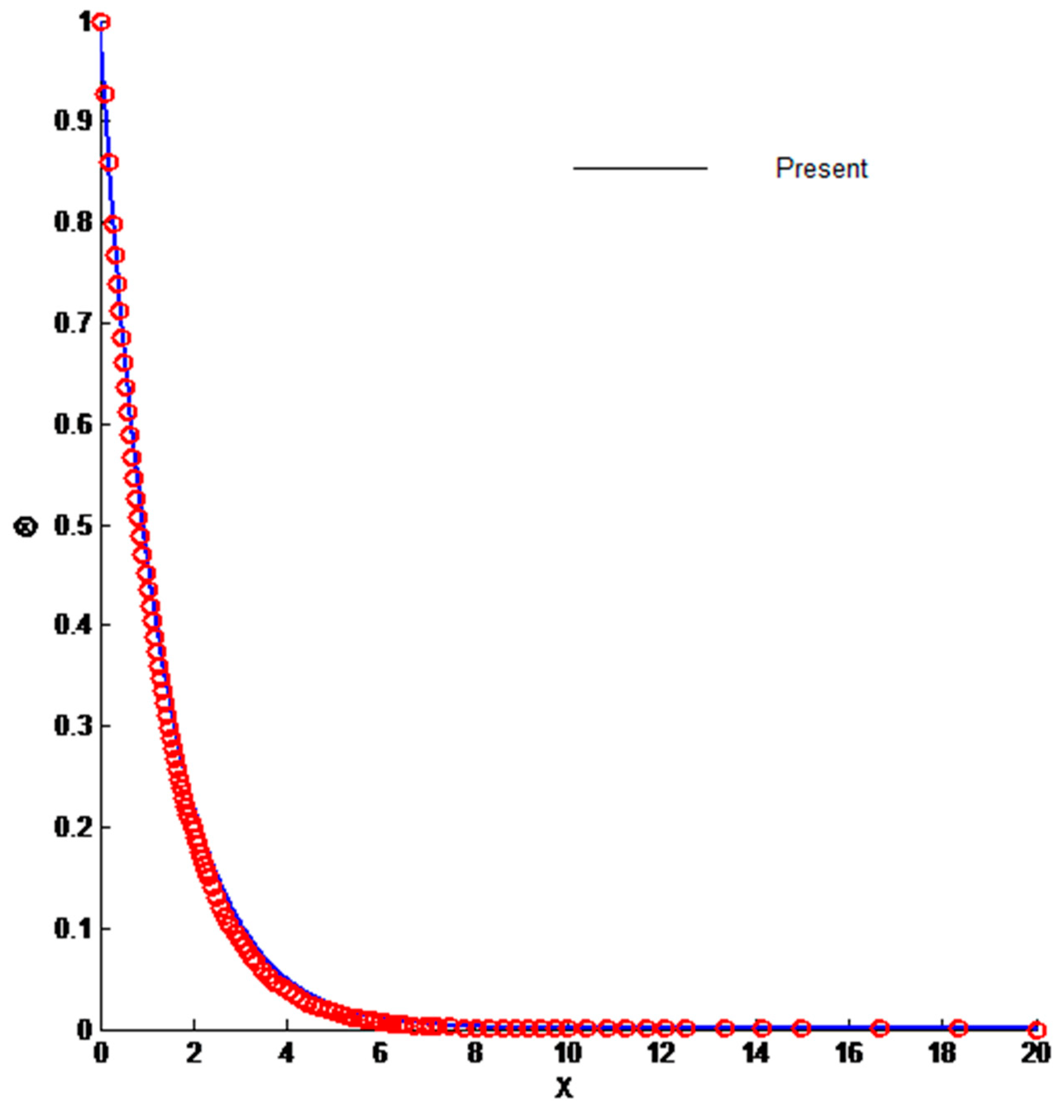
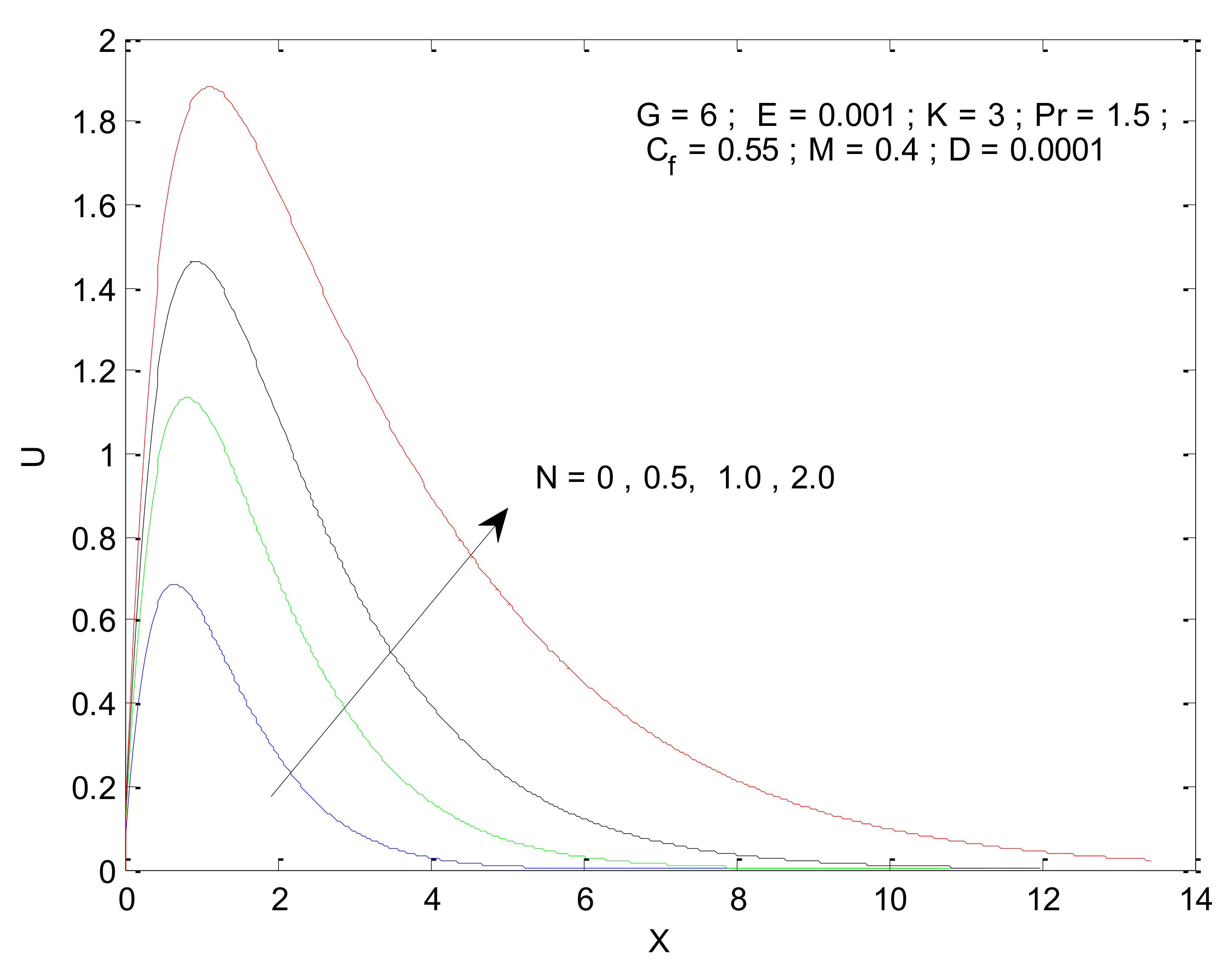
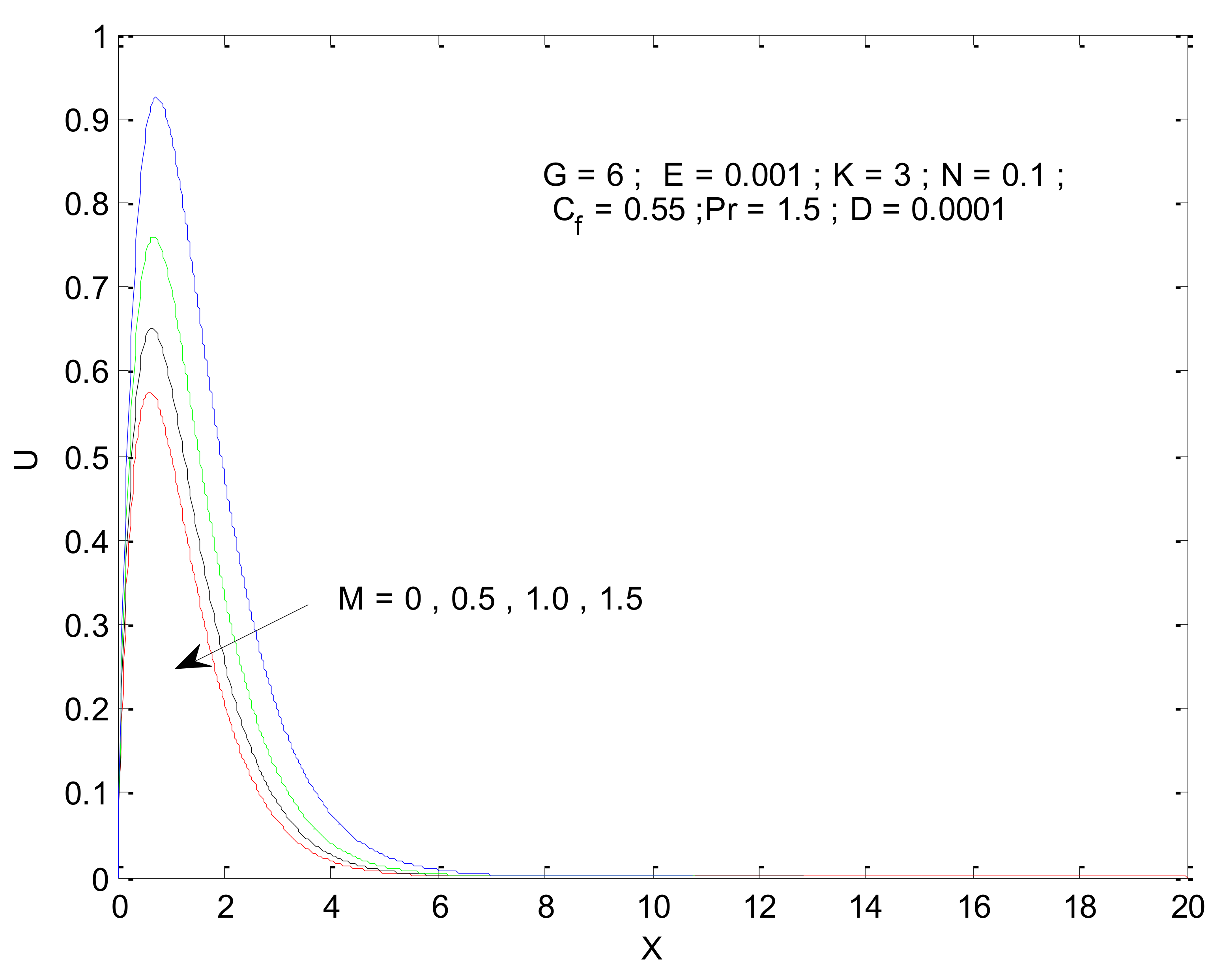
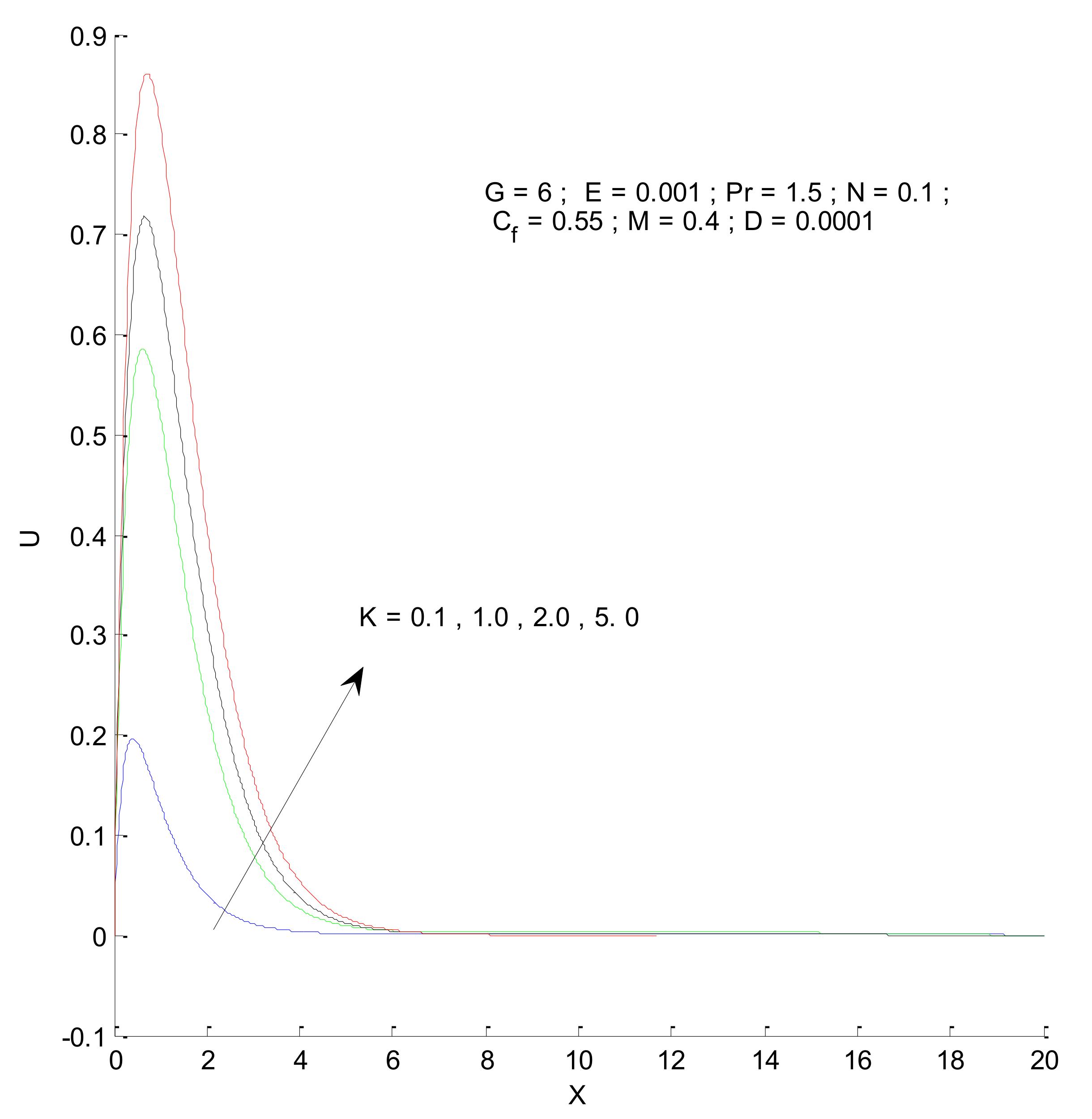
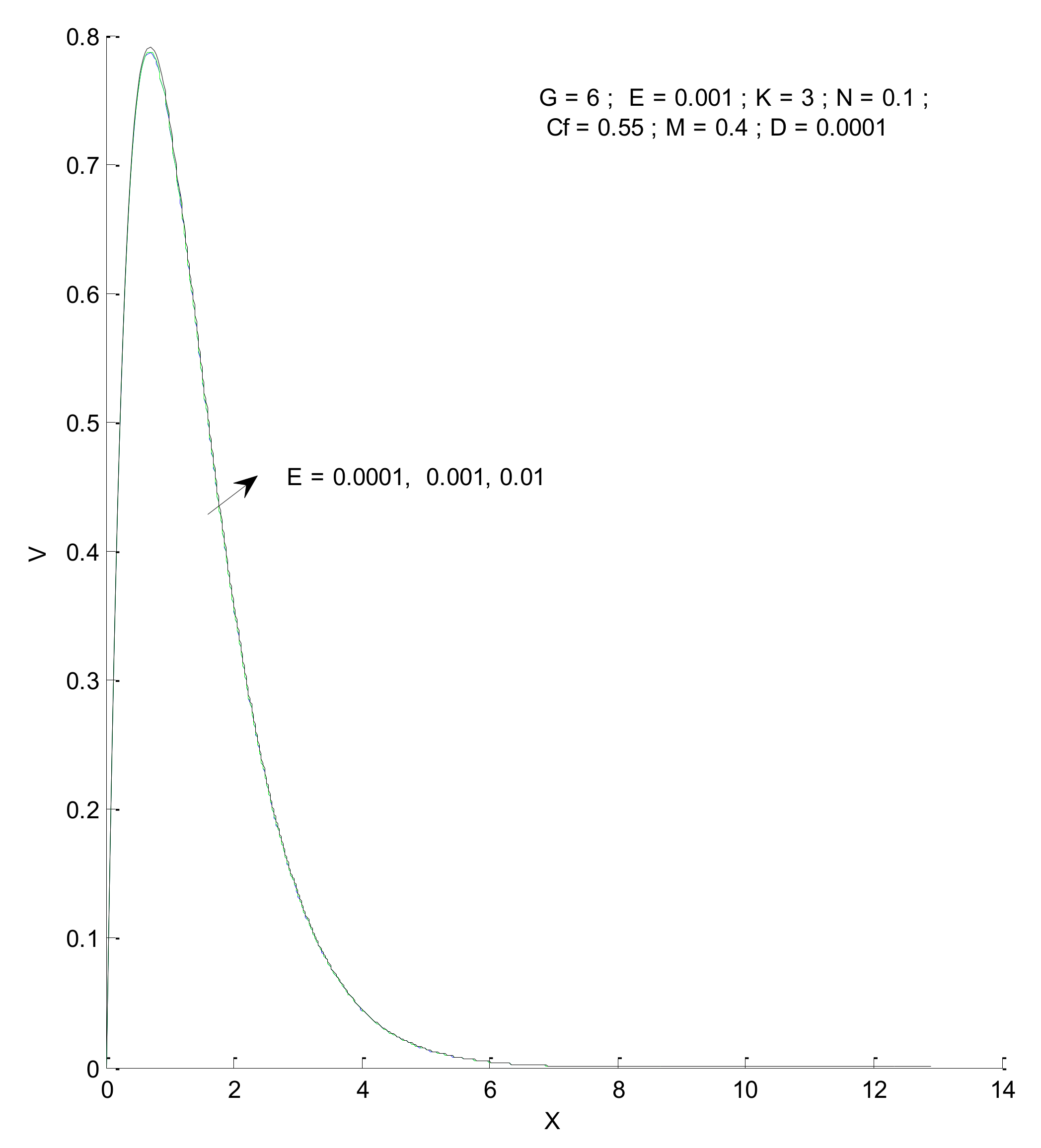
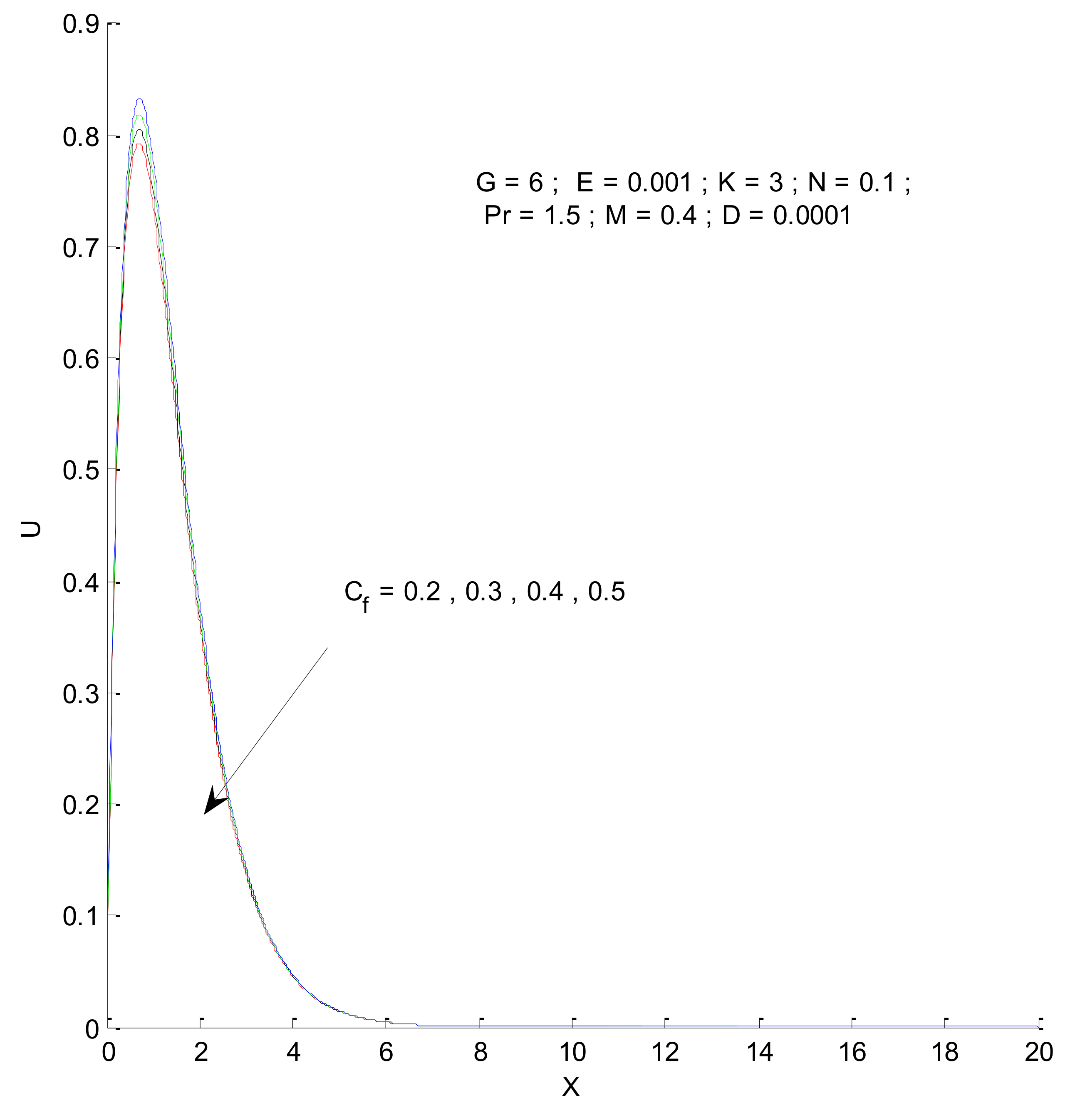
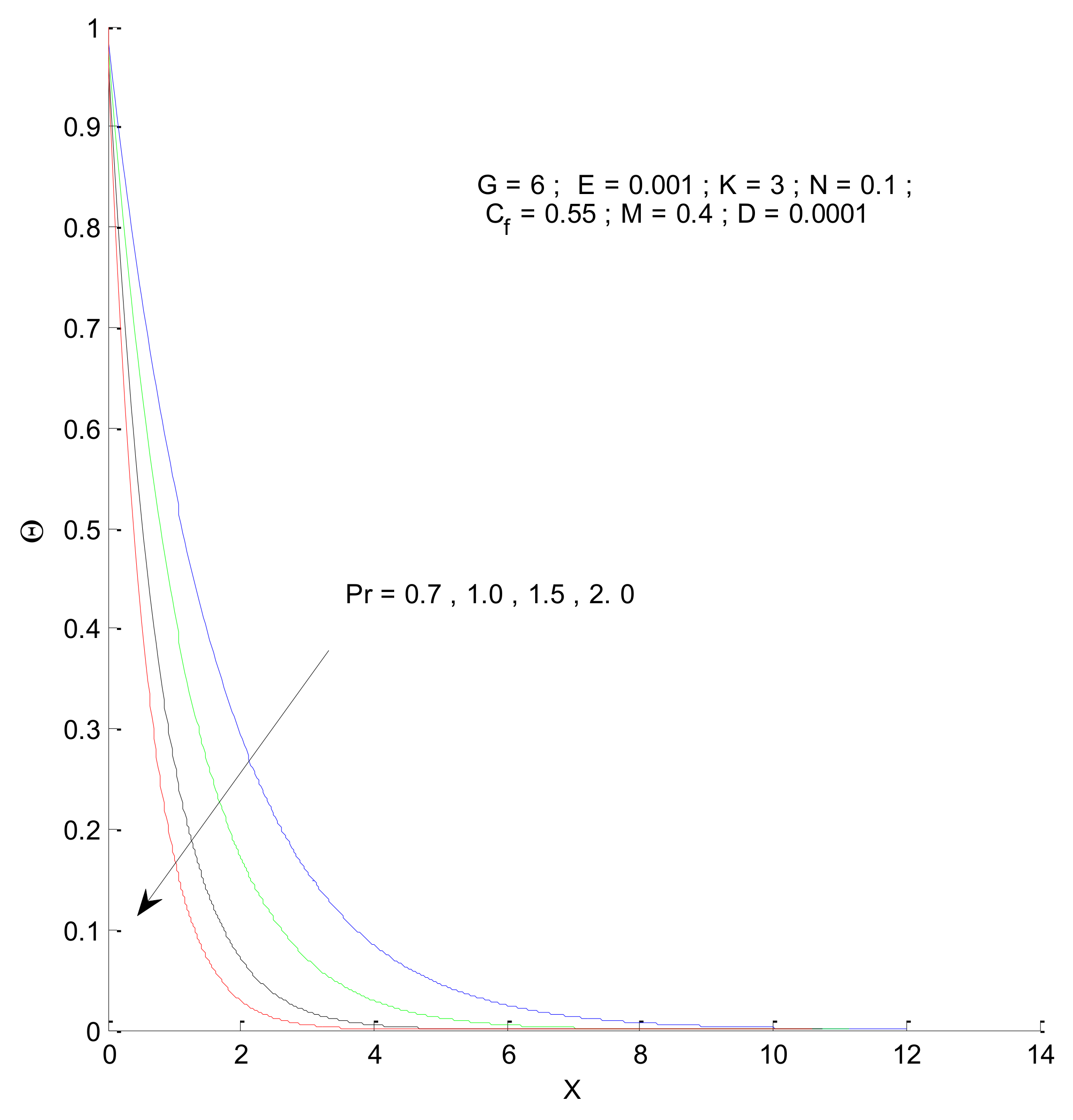
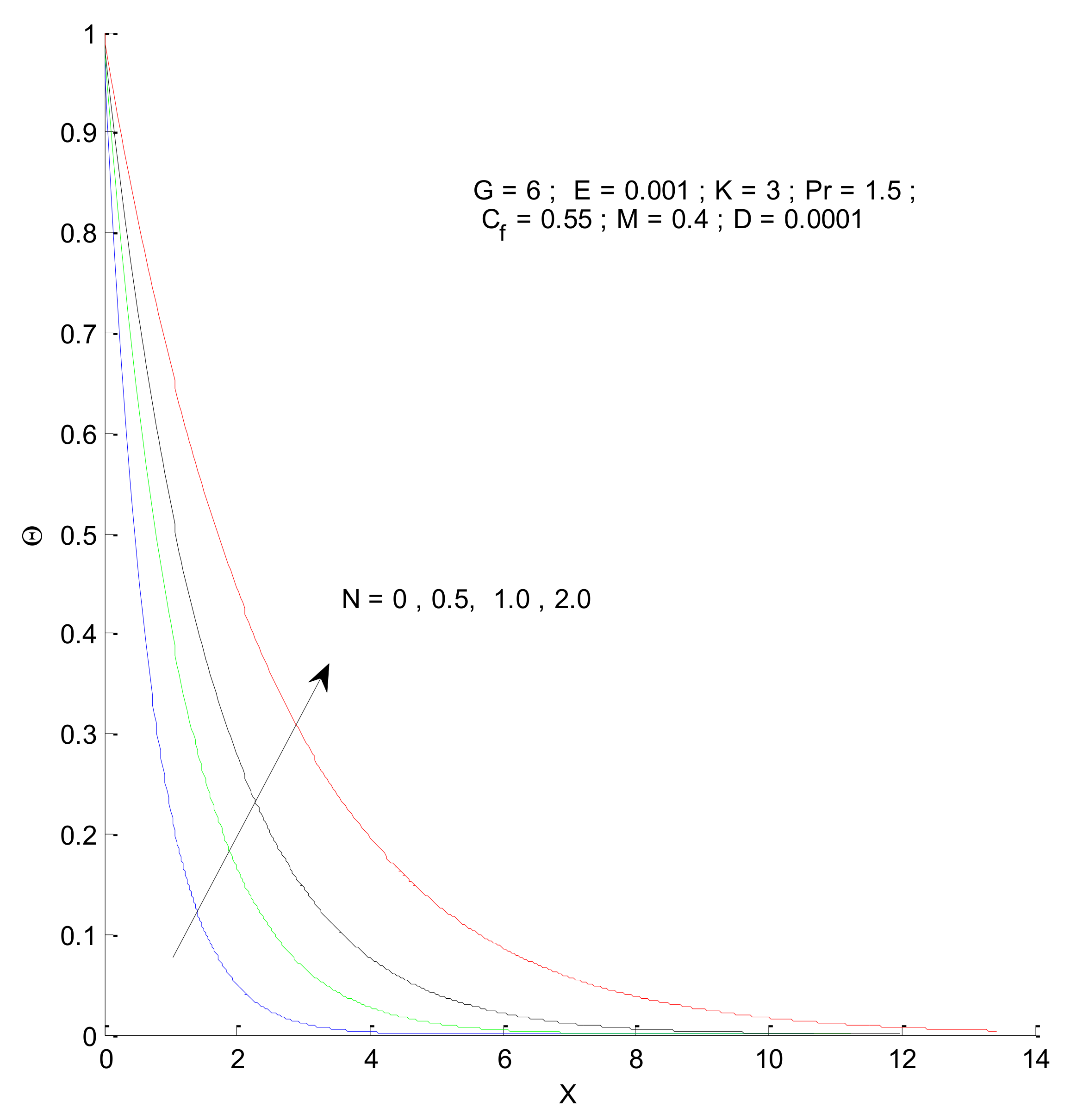
3.1. Velocity and Temperature Profile
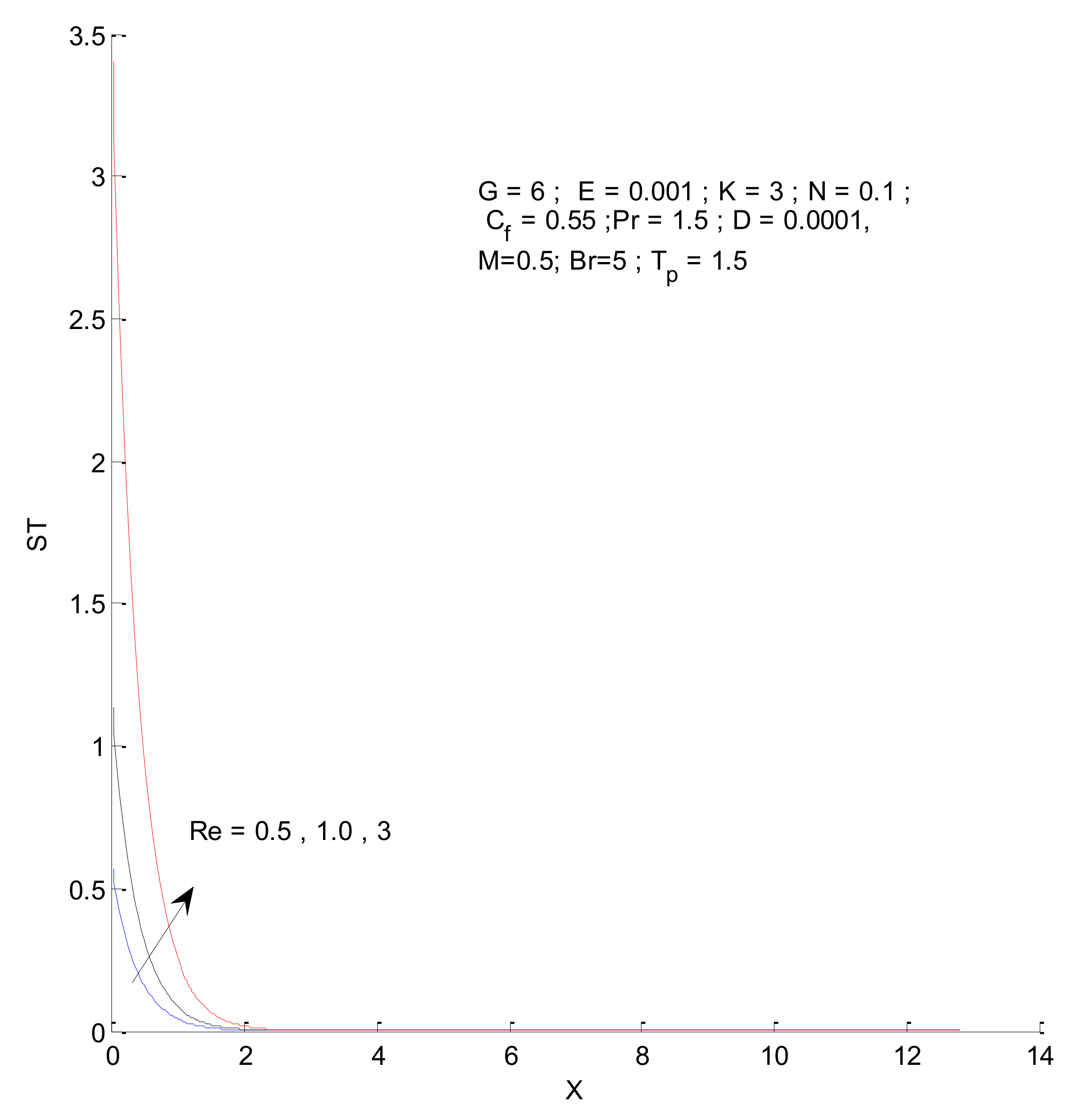
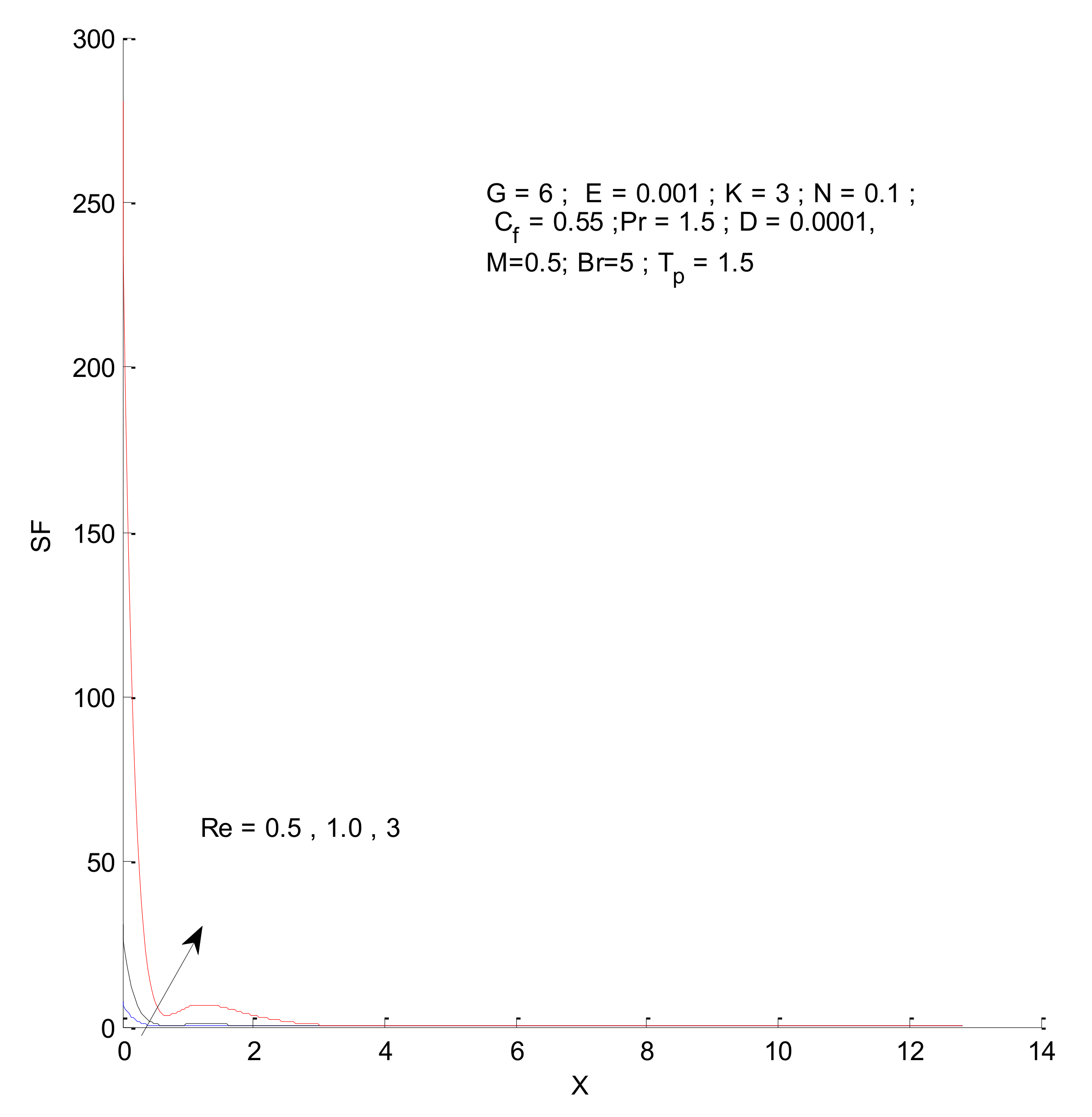
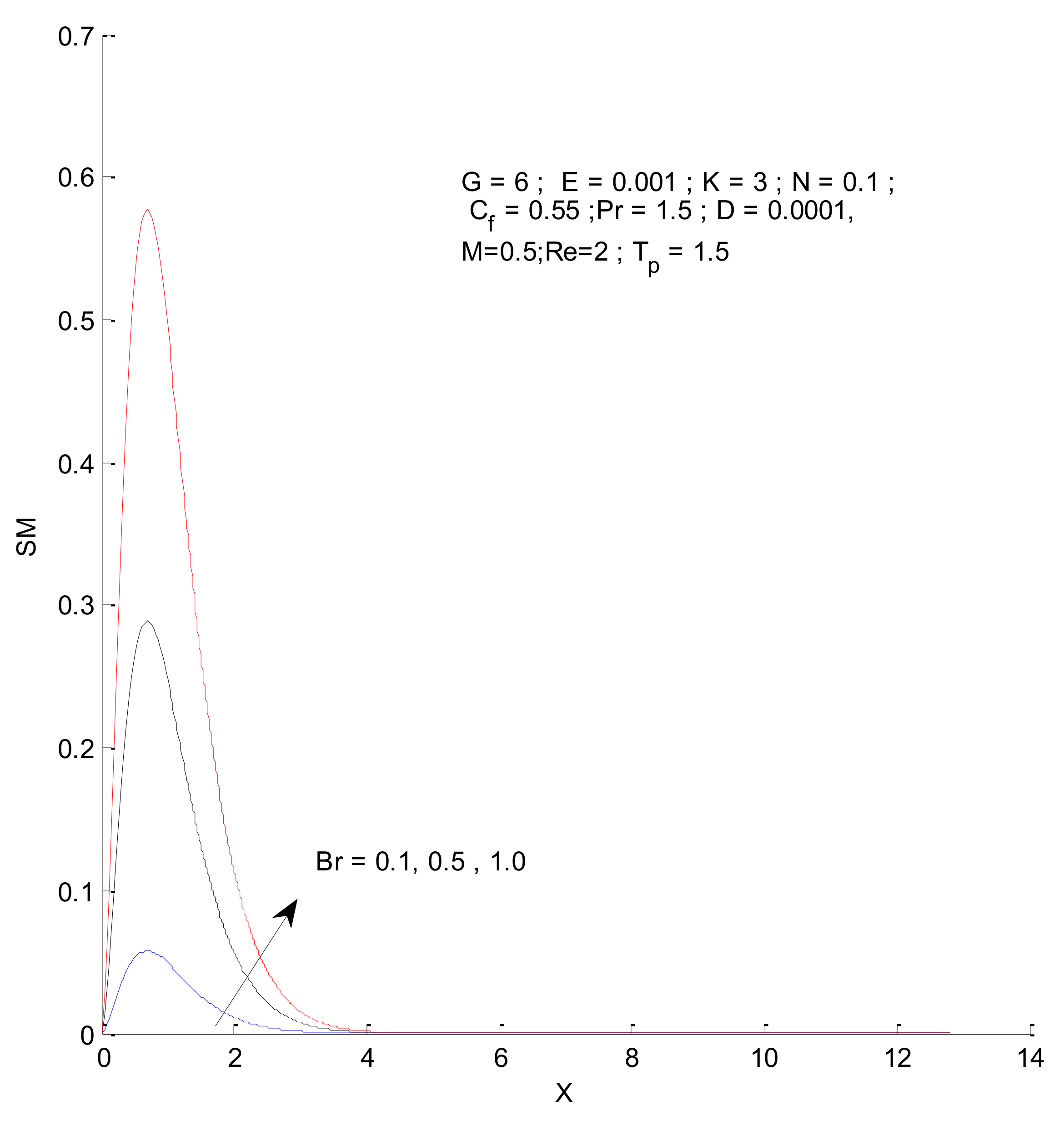
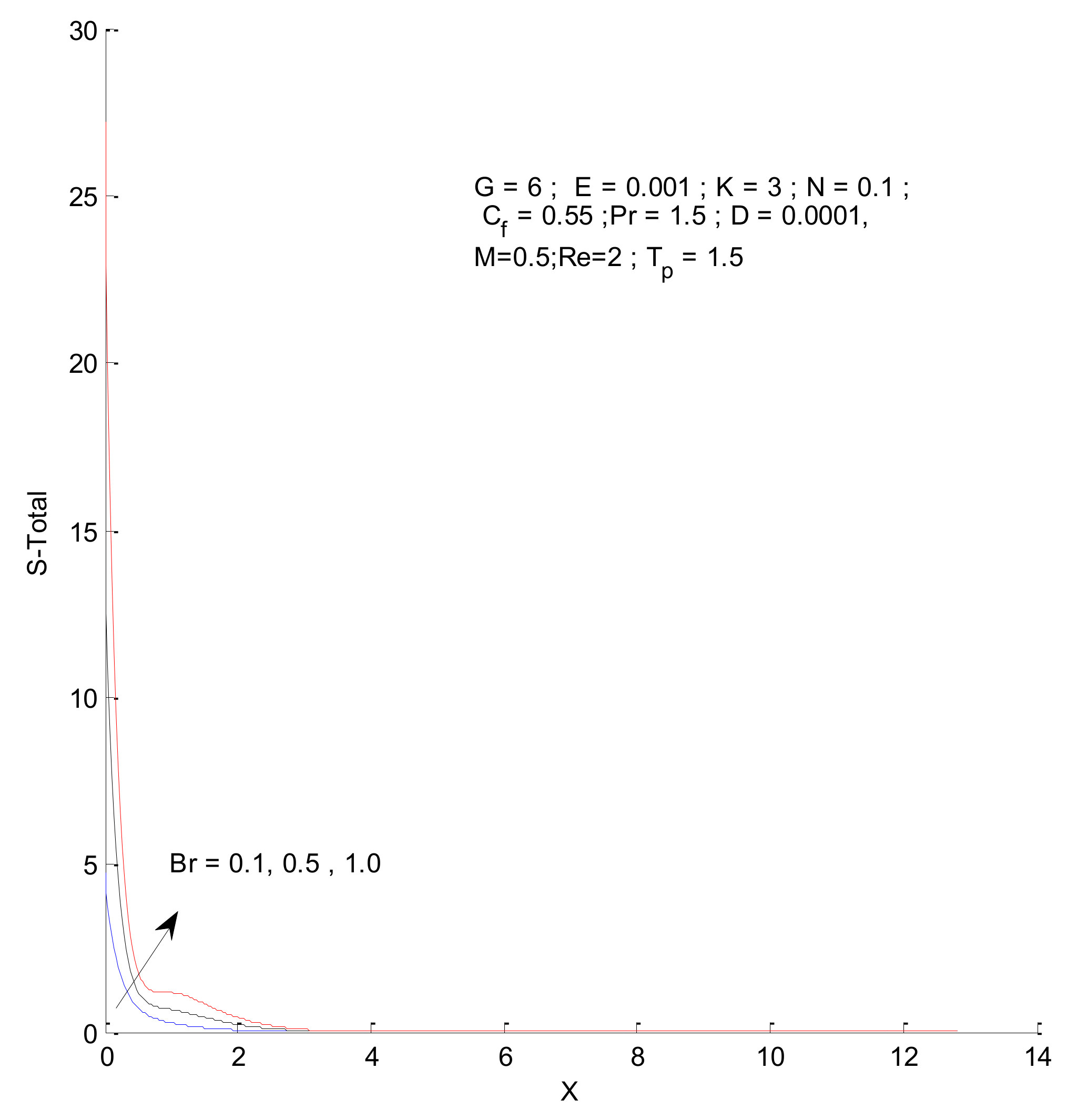
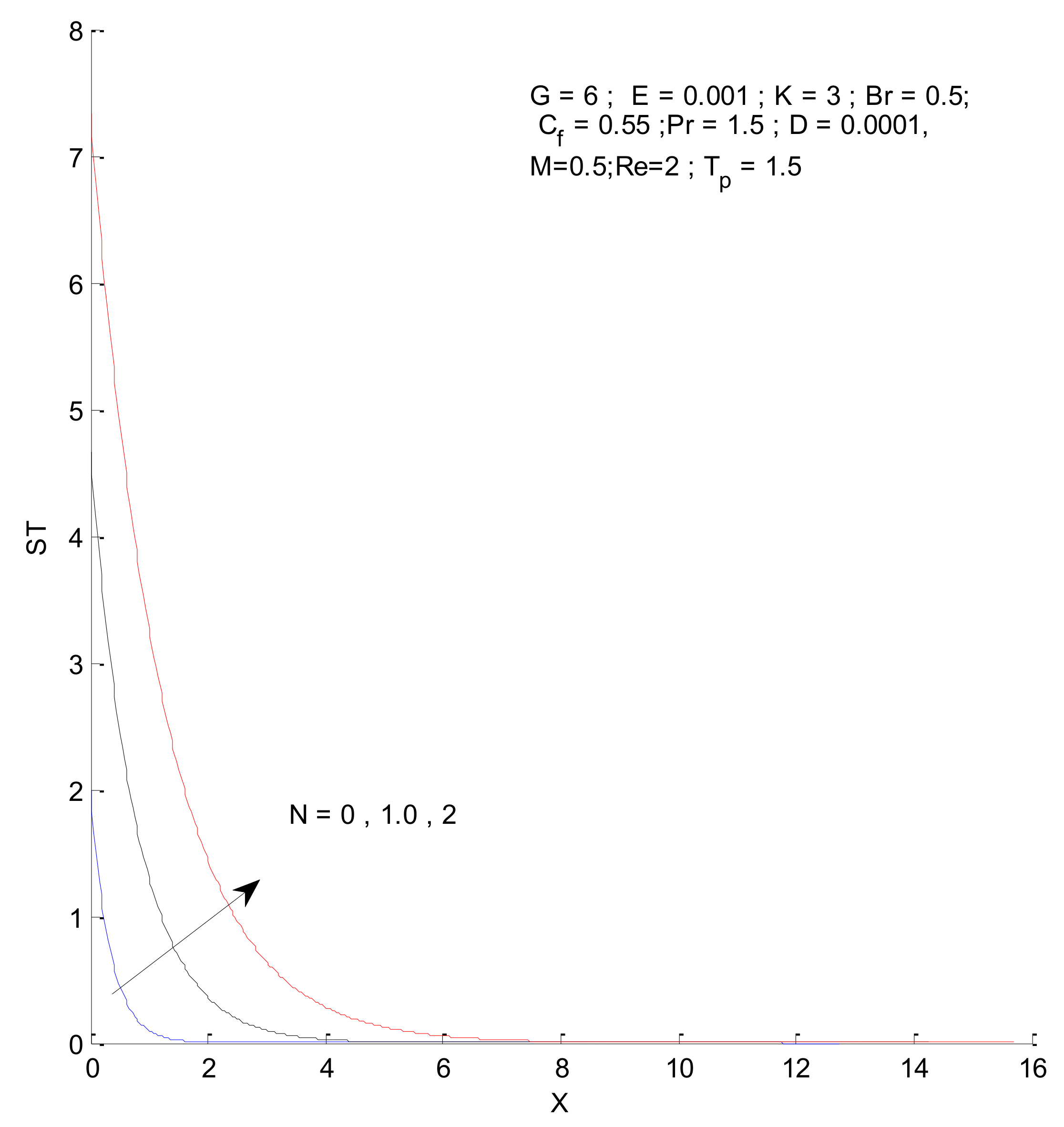
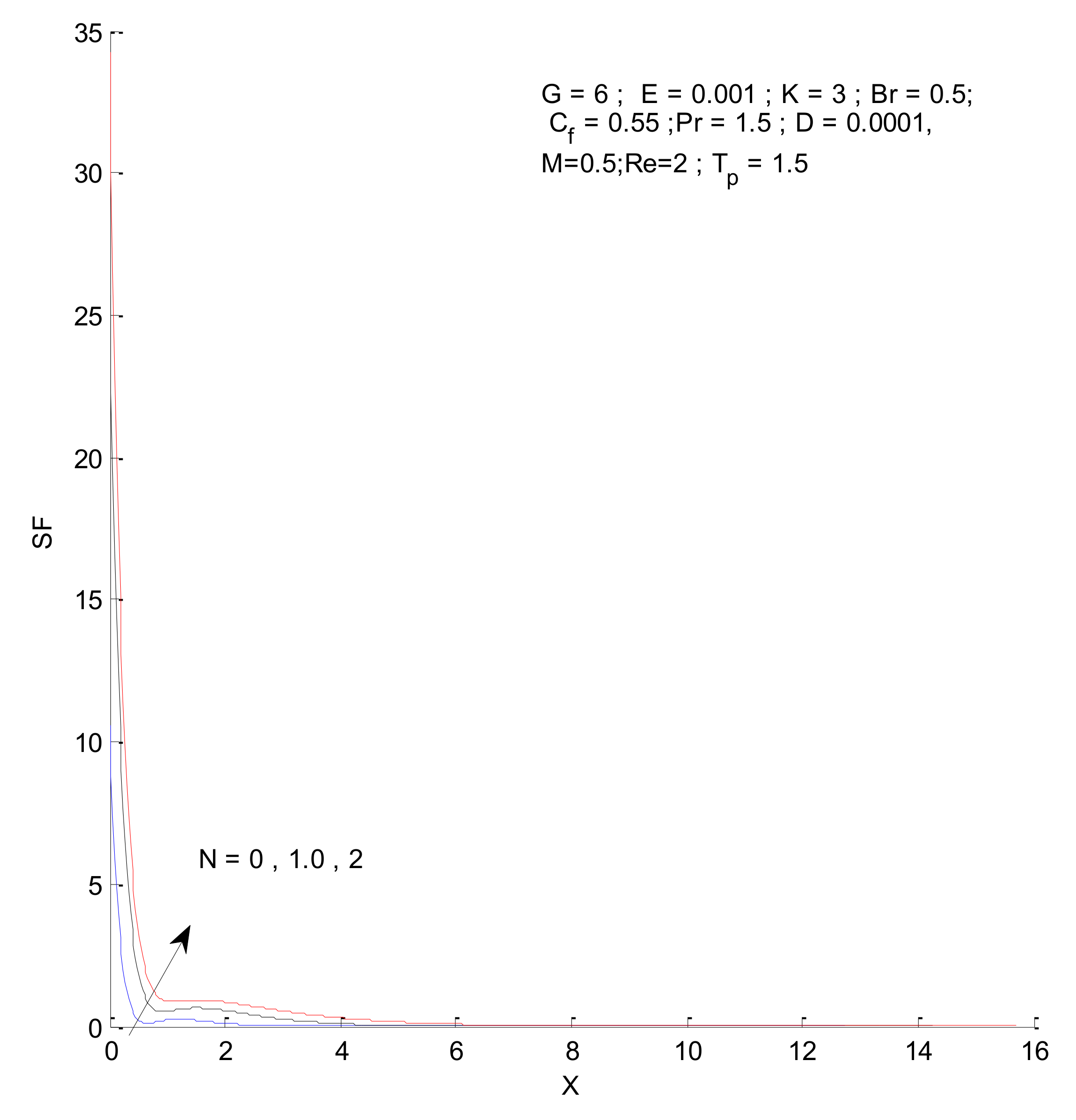
3.2. Entropy Generation
4. Conclusions
- The velocity profile is affected, to a greater extent, by the Prandtl number, Grashof number, radiation parameter, magnetic parameter, and permeability parameter, whereas the impact of the Eckert number, form-drag coefficient, and viscous dissipation parameter is significantly less.
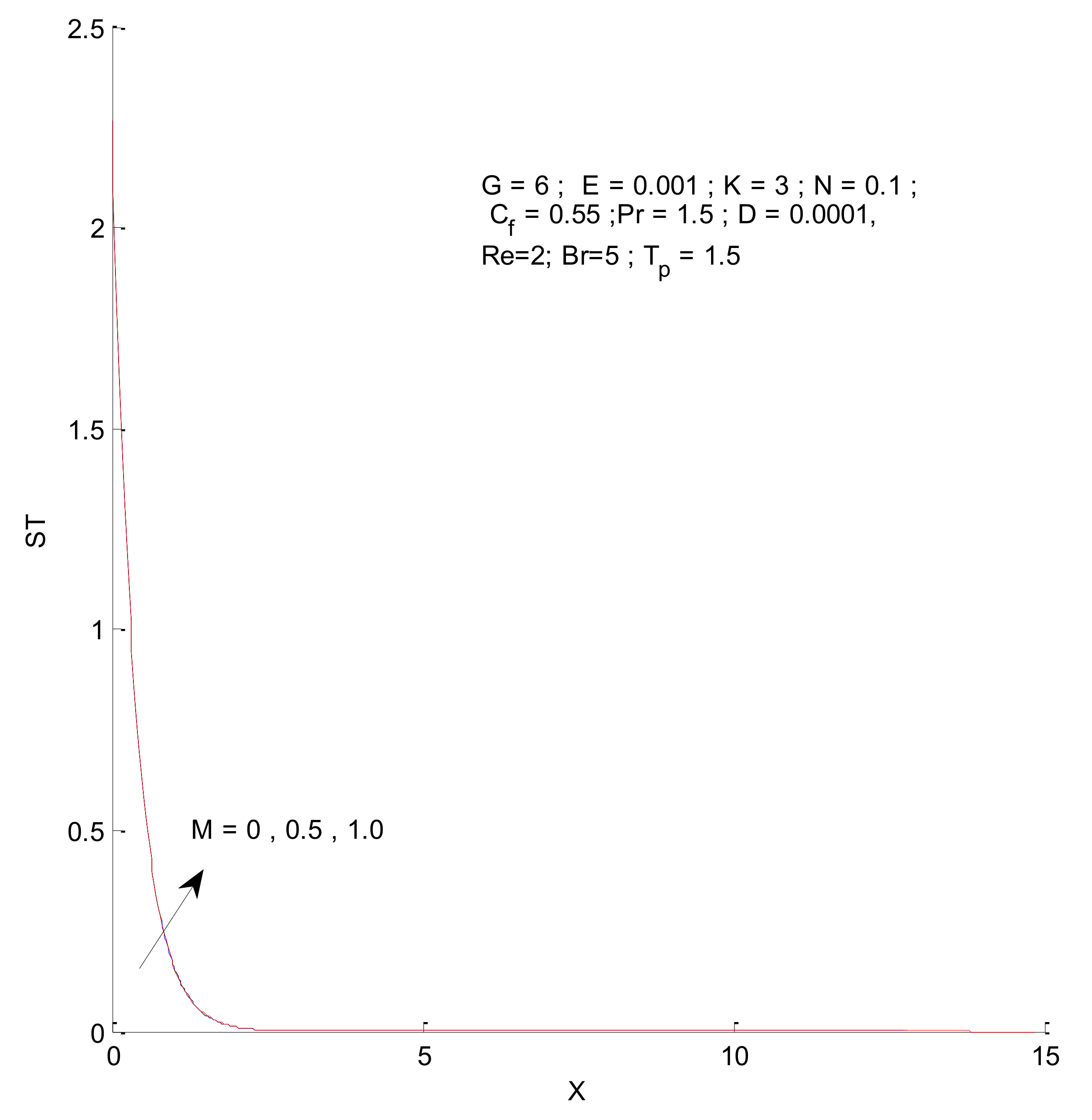
- The velocity profile decreases owing to the Prandtl number and magnetic parameter. However, a reverse trend is observed with respect to the radiation parameter, permeability parameter, and Grashof number.
- The temperature profile decreases with increasing Prandtl number, whereas it increases with increase in the radiation parameter.
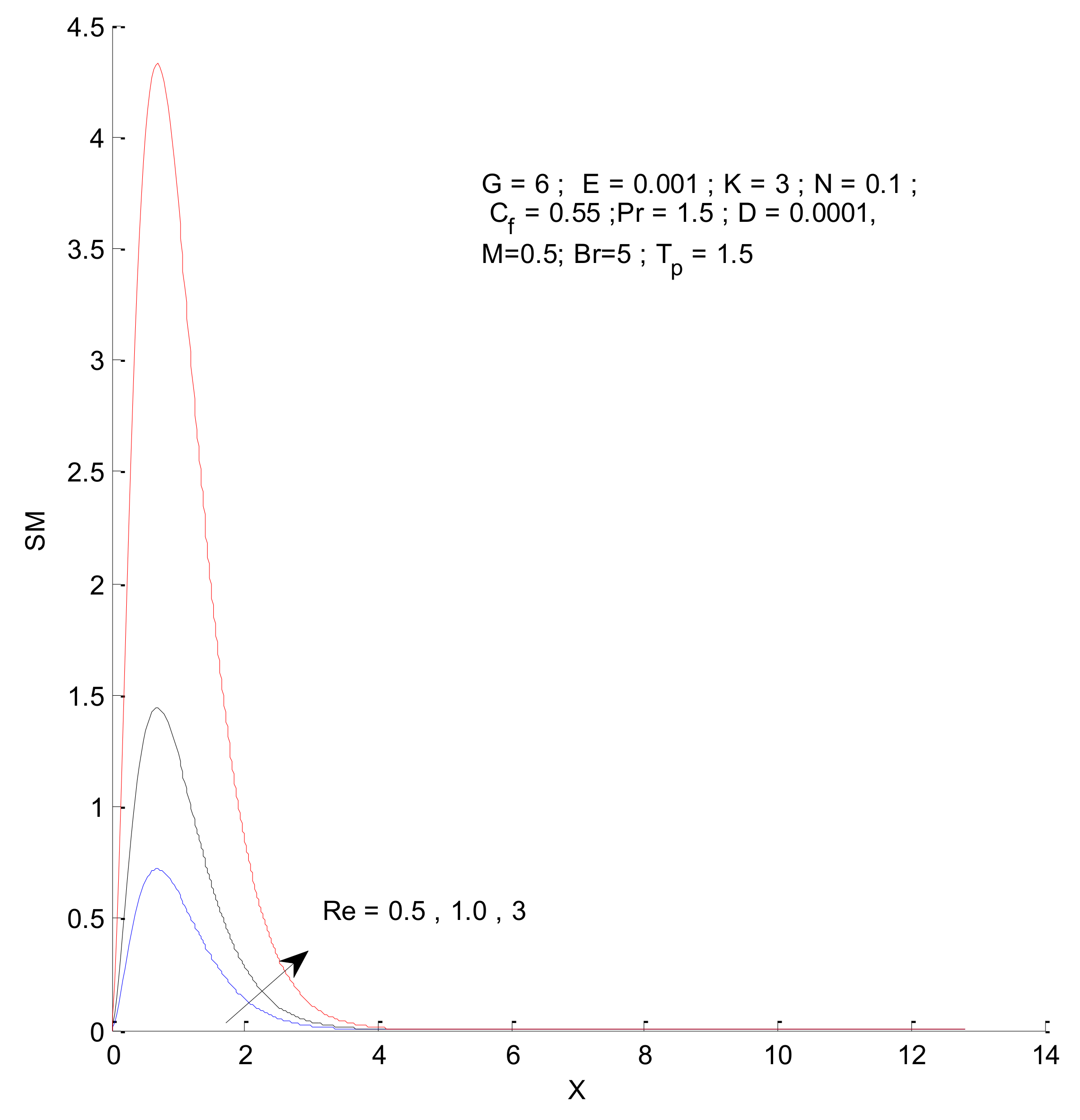
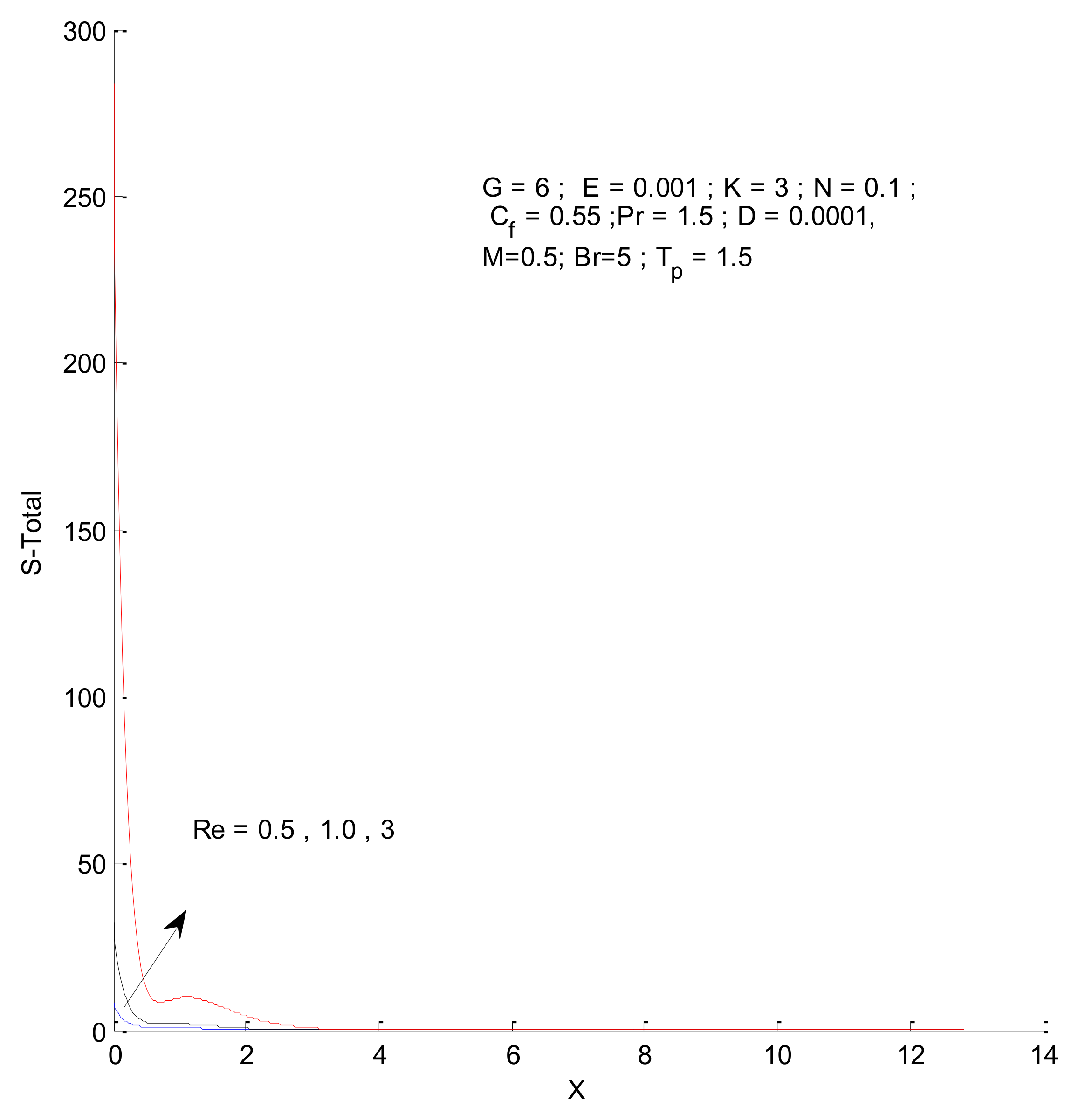
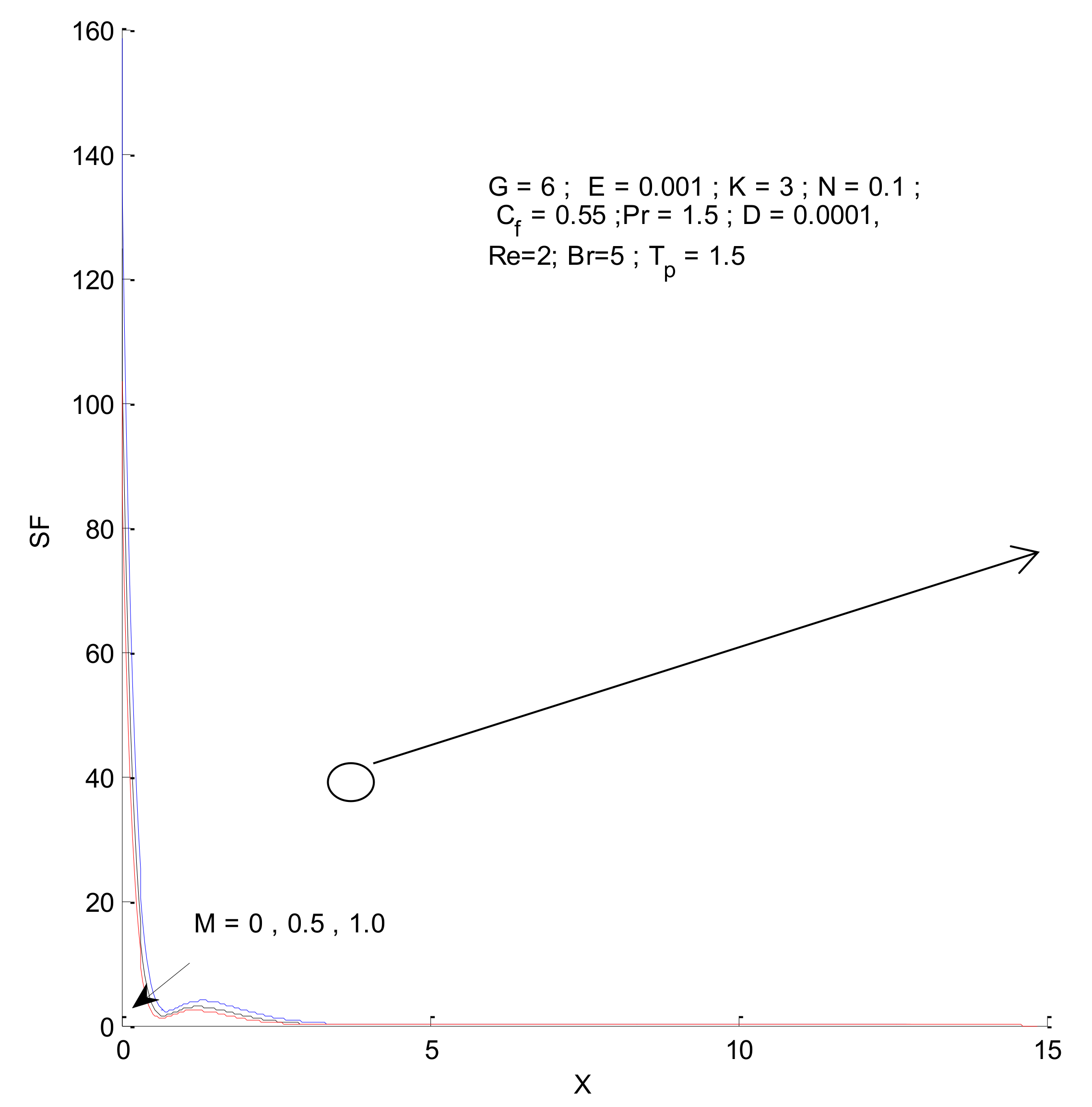
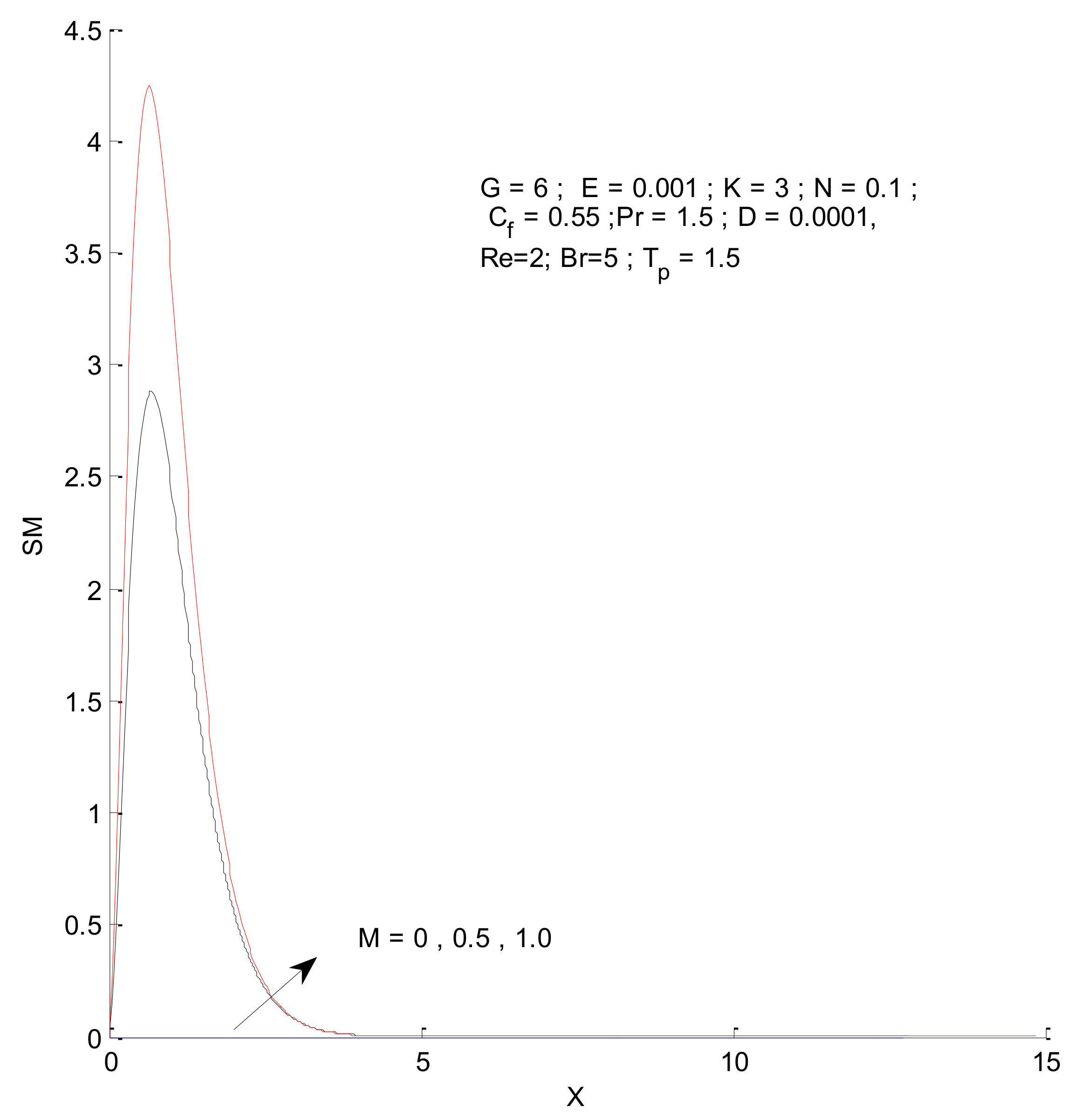
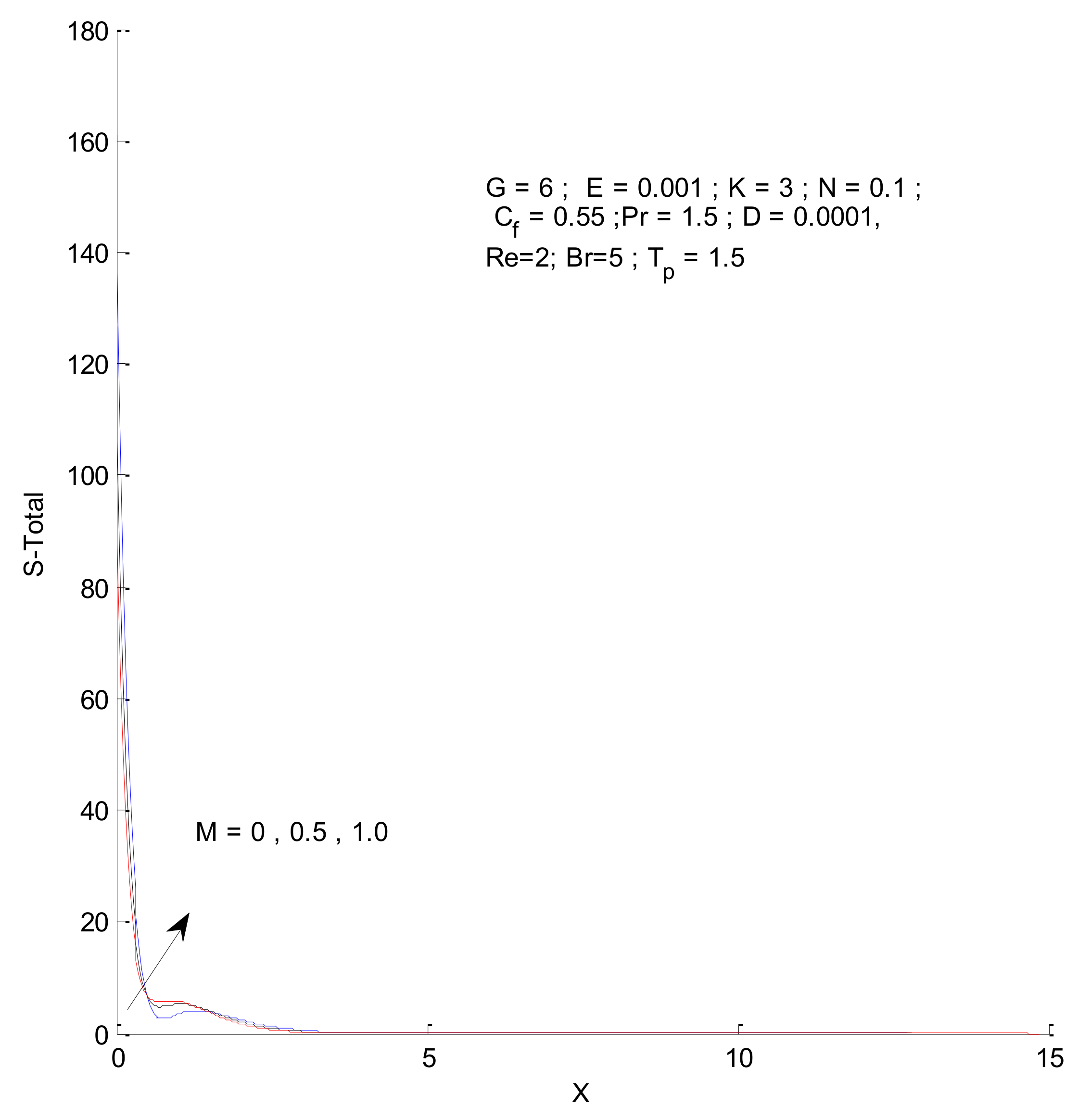
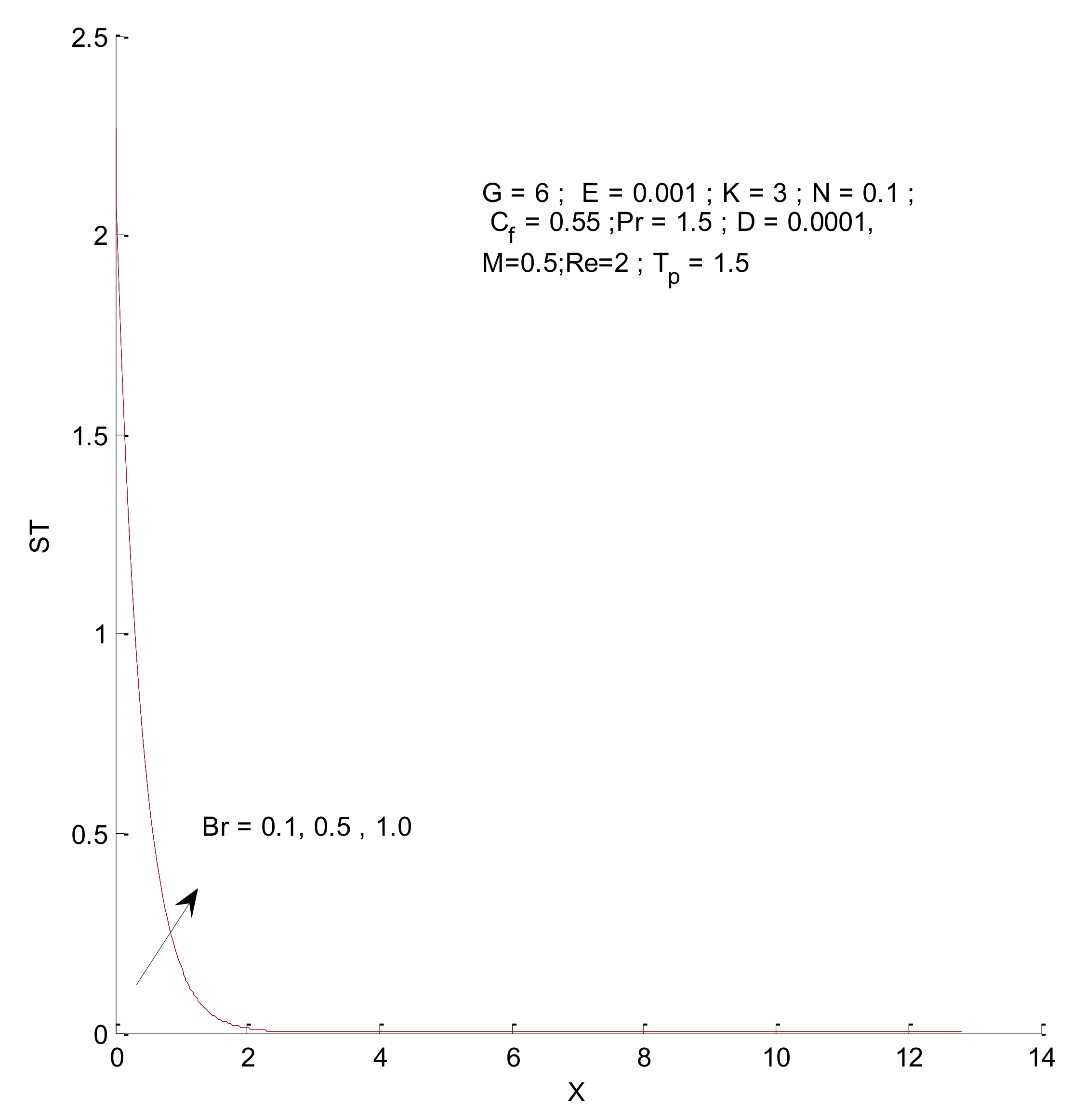
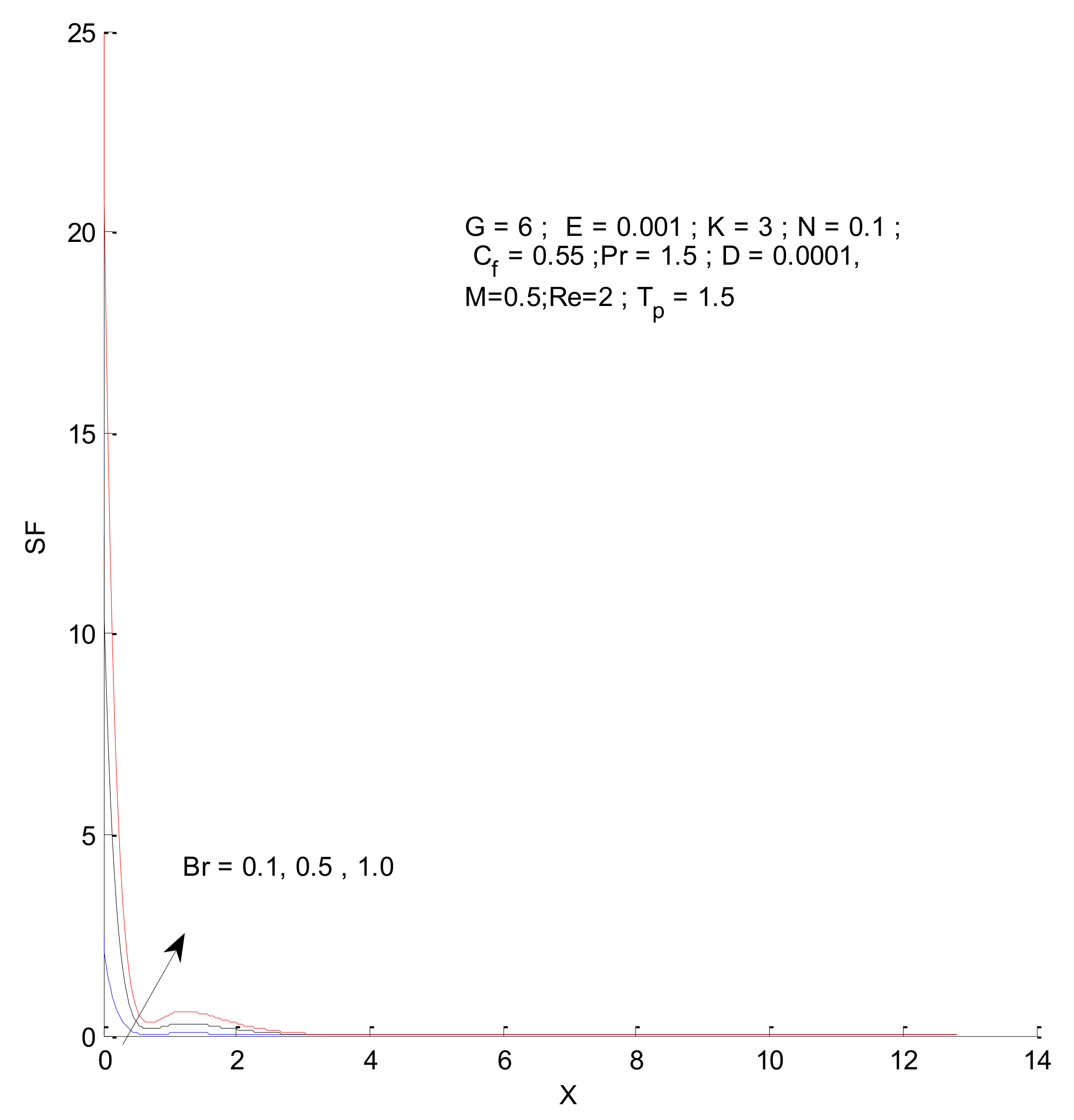
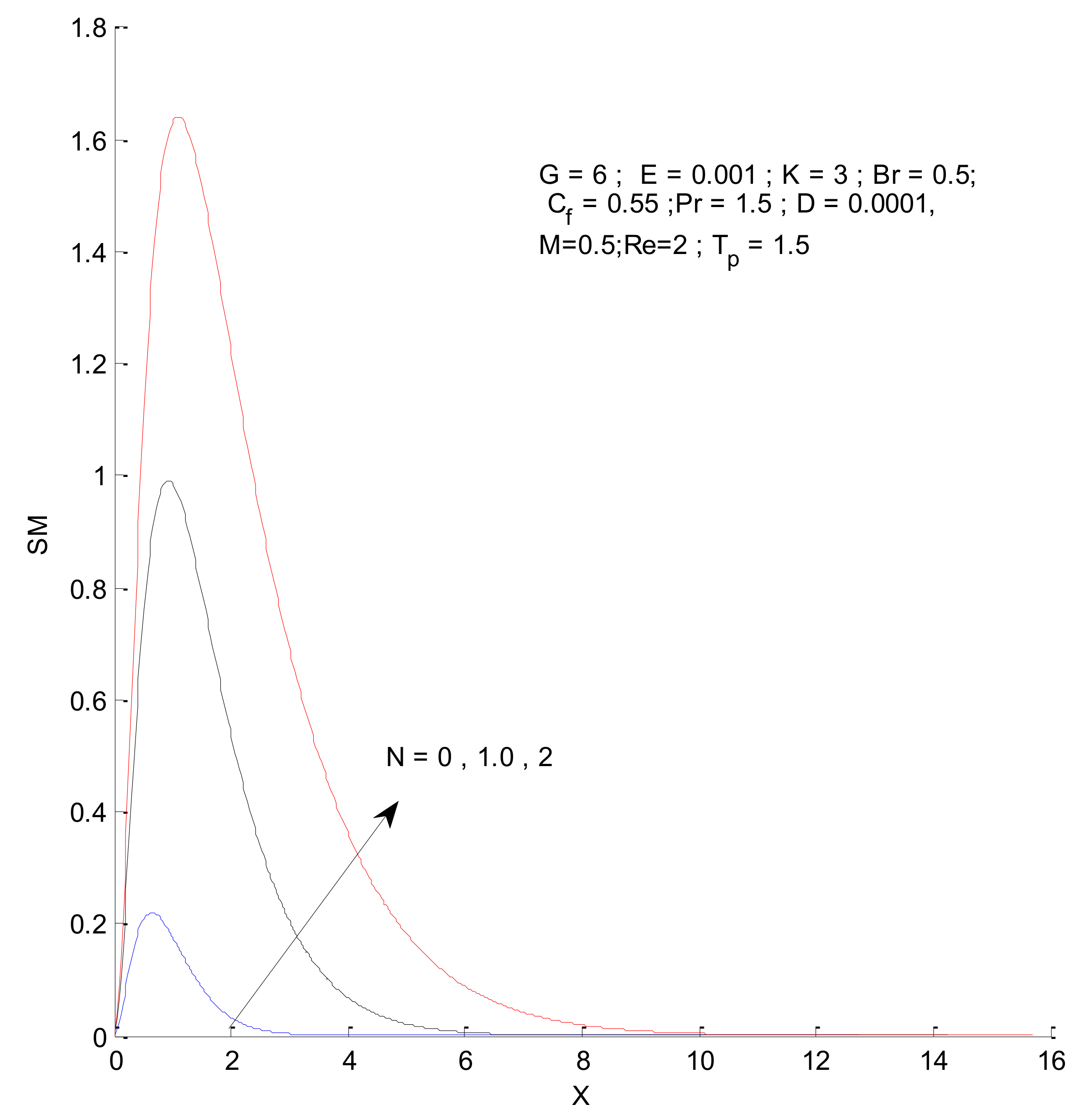
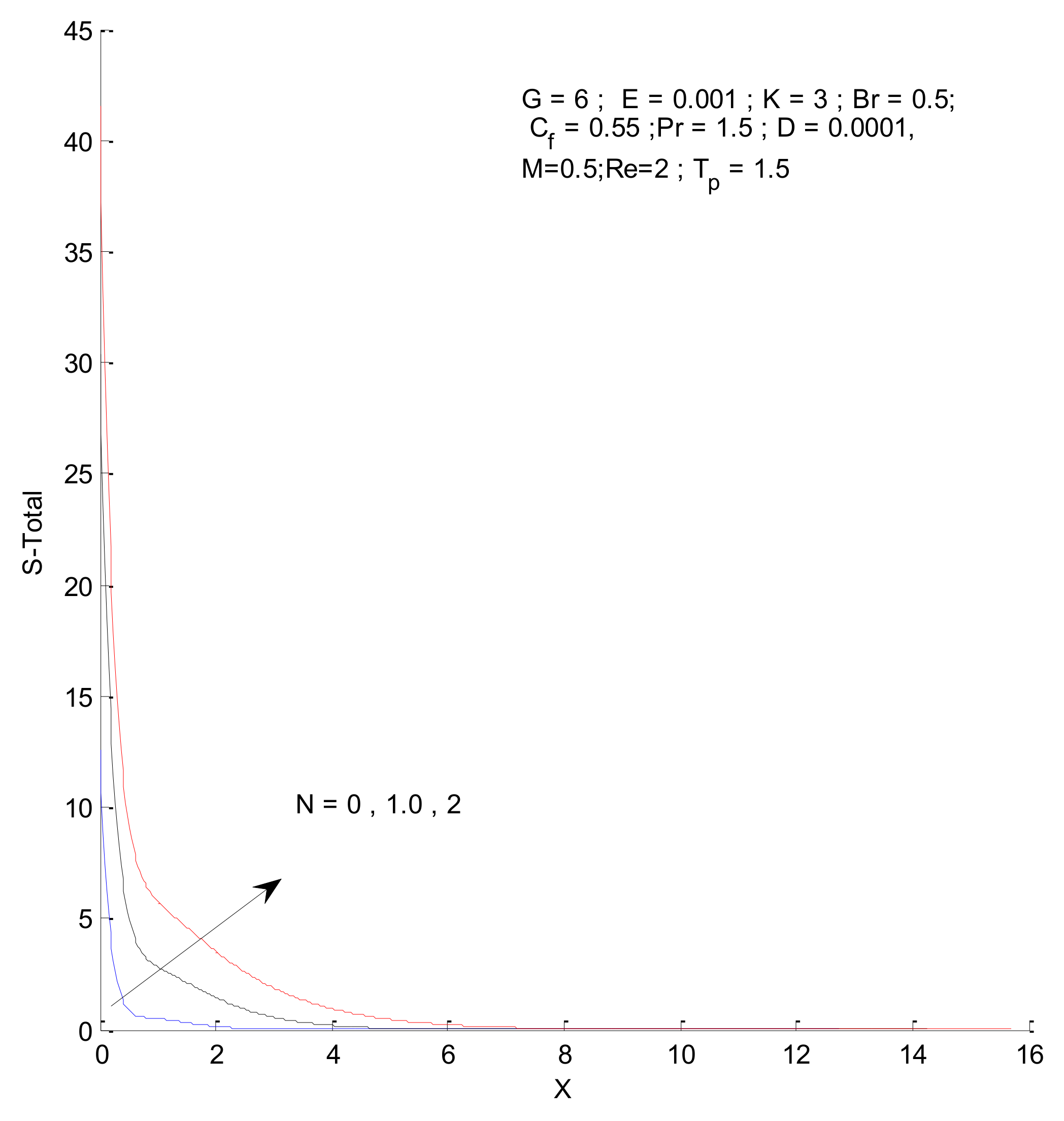
- The entropy generation increases with an increase in the Reynold’s number, Brinkman number, and radiation parameter
- The fluid entropy dominates compared to thermal and magnetic entropy.
- The fluid and thermal entropy sharply decrease near the vertical plate, whereas magnetic entropy produces a different profile than the fluid and thermal entropy.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Bo | magnetic intensity |
| form-drag constant | |
| g | gravitational acceleration |
| G | modified Grashof number |
| k | thermal conductivity |
| k* | mean absorption coefficient |
| K | permeability parameter |
| Permeability of porous medium | |
| L | length |
| N | radiation parameter |
| Pr | Prandtl number |
| qr | radiation flux |
| temperature | |
| v | vertical velocity along the plate |
| uo | suction velocity perpendicular to plate |
| dimensionless vertical velocity | |
| x | x-coordinate in horizontal direction |
| dimensionless coordinate in horizontal direction | |
| Prandtl number | |
| viscous dissipation parameter | |
| magnetic parameter | |
| Ecker number | |
| Renolds number | |
| Brinkman number | |
| Temperature difference parameter | |
| Greek Symbols | |
| α | thermal diffusivity |
| β | coefficient of thermal expansion |
| ρ | density |
| dimensionless temperature | |
| μ, v | coefficients of dynamic and kinematic viscosity, respectively |
| Stephan Boltzmann constant | |
| absorption coefficient | |
| Subscripts | |
| w | wall |
| far away condition | |
References
- Iasiello, M.; Bianco, N.; Chiu, W.K.S.; Naso, V. Anisotropic convective heat transfer in open-cell metal foams: Assessment and correlations. Int. J. Heat Mass Transf. 2020, 154, 119682. [Google Scholar] [CrossRef]
- Iasiello, M.; Bianco, N.; Chiu, W.K.; Naso, V. The effects of variable porosity and cell size on the thermal performance of functionally-graded foams. Int. J. Therm. Sci. 2021, 160, 106696. [Google Scholar] [CrossRef]
- Yang, X.; Yu, J.; Guo, Z.; Jin, L.; He, Y.-L. Role of porous metal foam on the heat transfer enhancement for a thermal energy storage tube. Appl. Energy 2019, 239, 142–156. [Google Scholar] [CrossRef]
- Yang, X.; Wei, P.; Cui, X.; Jin, L.; He, Y.L. Thermal response of annuli filled with metal foam for thermal energy storage: An experimental study. Appl. Energy 2019, 250, 1457–1467. [Google Scholar] [CrossRef]
- Mellouli, S.; Dhaou, H.; Askri, F.; Jemni, A.; Ben Nasrallah, S. Hydrogen storage in metal hydride tanks equipped with metal foam heat exchanger. Int. J. Hydrogen Energy 2009, 34, 9393–9401. [Google Scholar] [CrossRef]
- Huisseune, H.; De Schampheleire, S.; Ameel, B.; De Paepe, M. Comparison of metal foam heat ex-changers to a finned heat exchanger for low Reynolds number applications. Int. J. Heat Mass Transf. 2015, 89, 1–9. [Google Scholar] [CrossRef]
- Andreozzi, A.; Bianco, N.; Iasiello, M.; Naso, V. Thermo-fluid-dynamics of a ceramic foam solar receiver: A parametric analysis. Heat Transf. Eng. 2020, 41, 1085–1099. [Google Scholar] [CrossRef]
- Raptis, A. Radiation and free convection flow through a porous medium. Int. Commun. Heat Mass Transf. 1998, 25, 289–295. [Google Scholar] [CrossRef]
- Huang, C.-J. Influence of Internal Heat Generation on the Natural Convection of Non-Newtonian Fluids over a Vertical Plate in Porous Media with Thermal Radiation and Soret/Dufour Effects: Variable Wall Temperature/Concentration. Proc. Natl. Acad. Sci. India Sect. A Phys. Sci. 2018, 89, 737–745. [Google Scholar] [CrossRef]
- Akter, R.; Ferdows, M.; Miyara, A. Effect of Internal Heat Generation and Concentration Change on Free Convection Boundary Layer from Vertical Flat Plate Embedded in Porous Medium. J. Eng. Thermophys. 2019, 28, 410–430. [Google Scholar] [CrossRef]
- Shanta, S.S.; Islam, A.I.; Mondol, K.; Ahmmed, S. Numerical Study on Unsteady Flow and Mass Transfer Past a Vertical Porous Plate with Variable Viscosity. Math. Model. Eng. Probl. 2020, 7, 273–282. [Google Scholar] [CrossRef]
- Khan, D.; Khan, A.; Khan, I.; Ali, F.; Karim, F.U.; Tlili, I. Effects of Relative Magnetic Field, Chemical Reaction, Heat Generation and Newtonian Heating on Convection Flow of Casson Fluid over a Moving Vertical Plate Embedded in a Porous Medium. Sci. Rep. 2019, 9, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Rajakumar, K.V.; Rayaprolu, V.S.P.K.; Balamurugan, K.S.; Kumar, V.B. Unsteady MHD Casson Dissipative Fluid Flow past a Semi-infinite Vertical Porous Plate with Radiation Absorption and Chemical Reaction in Presence of Heat Generation. Math. Model. Eng. Probl. 2020, 7, 160–172. [Google Scholar] [CrossRef] [Green Version]
- Kumari, S.S.; Raju, G.S.S. Unsteady MHD Free Convective Flow Past a Vertical Porous Plate with Span-Wise Fluctuating Heat and Mass Transfer Effects. Fluid Dyn. Mater. Process. 2019, 15, 471–489. [Google Scholar] [CrossRef]
- El-Dabe, N.T.M.; Gabr, M.E.; Elshekhipy, A.A.; Zaher, S. The Motion of a Non-Newtonian Nanofluid over a Semi-Infinite Moving Vertical Plate Through Porous Medium with Heat and Mass Transfer. Therm. Sci. 2020, 24, 1311–1321. [Google Scholar] [CrossRef] [Green Version]
- Badruddin, I.A. Investigation of heat transfer in irregular porous cavity subjected to various boundary conditions. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 418–447. [Google Scholar] [CrossRef]
- Badruddin, I.A. Thermal Non-equilibrium in Porous Annulus: A New Finite Element Solution Technique. Arab. J. Sci. Eng. 2020, 45, 1279–1292. [Google Scholar] [CrossRef]
- Badruddin, I.A. Numerical Analysis of Thermal Non-Equilibrium in Porous Medium Subjected to Internal Heating. Mathematics 2019, 7, 1085. [Google Scholar] [CrossRef] [Green Version]
- Mansour, M.A.; El-Shaer, N.A. Radiative effects on magnetohydrodynamic natural convection flows saturated in porous media. J. Magn. Magn. Mater. 2001, 237, 327–341. [Google Scholar] [CrossRef]
- Azeem, I.A.B.; Nik-Ghazali, N.; Mohd, Y.I.I.; Ali, E.A.; Salman, A.N.J.; Sarfaraz, K.; Al-Rashed, A.A.A.A. Effect of size and location of solid on conjugate heat transfer in porous cavity. Indian J. Pure Appl. Phys. 2018, 56, 792–801. [Google Scholar]
- Azeema, I.A.; Badruddin, M.Y.I.I.; Nik-Ghazali, N.; Salman Ahmed, N.J.; Abdullah, A.A.A.A. Conjugate heat and mass transfer in square porous cavity. Indian J. Pure Appl. Phys. 2016, 54, 777–786. [Google Scholar]
- Ali, M.; Chen, T.; Armaly, B. Natural convection—Radiation interaction in boundary layer flow over horizontal surfaces. AIAA J. 1984, 22, 1797–1803. [Google Scholar] [CrossRef]
- Bakier, A. Thermal radiation effect on mixed convection from vertical surfaces in saturated porous media. Int. Commun. Heat Mass Transf. 2001, 28, 119–126. [Google Scholar] [CrossRef]
- Mohammadien, A.A.; El-Amin, M.F. Thermal radiation effects on power law fluid over a horizontal plate embedded in a porous medium. Int. Comm. Heat Mass Transf. 2000, 27, 1025–1035. [Google Scholar] [CrossRef]
- Sayed, A.Y.; Abdel-Wahed, M.S. Entropy analysis for an MHD nanofluid with a microrotation boundary layer over a moving permeable plate. Eur. Phys. J. Plus 2020, 135, 1–17. [Google Scholar] [CrossRef]
- Ramzan, M.; Mohammad, M.; Howari, F.; Chung, J.D. Entropy Analysis of Carbon Nanotubes Based Nanofluid Flow Past a Vertical Cone with Thermal Radiation. Entropy 2019, 21, 642. [Google Scholar] [CrossRef] [Green Version]
- Shit, G.C.; Mandal, S. Entropy Analysis on Unsteady MHD Flow of Casson Nanofluid over a Stretching Vertical Plate with Thermal Radiation Effect. Int. J. Appl. Comput. Math. 2020, 6, 2. [Google Scholar] [CrossRef]
- Tayebi, T.; Chamkha, A.J. Entropy generation analysis due to MHD natural convection flow in a cavity occupied with hybrid nanofluid and equipped with a conducting hollow cylinder. J. Therm. Anal. Calorim. 2020, 139, 2165–2179. [Google Scholar] [CrossRef]
- Khan, M.; Ahmed, J.; Rasheed, Z. Entropy generation analysis for axisymmetric flow of Carreau nanofluid over a radially stretching disk. Appl. Nanosci. 2020. [Google Scholar] [CrossRef]
- Shit, G.C.; Haldar, R.; Mandal, S. Entropy generation on MHD flow and convective heat transfer in a porous medium of exponentially stretching surface saturated by nanofluids. Adv. Powder Technol. 2017, 28, 1519–1530. [Google Scholar] [CrossRef]
- Sheremet, M.A.; Grosan, T.; Pop, I. Natural convection and entropy generation in a square cavity with variable temperature side walls filled with a nanofluid. Buongiornos Math. Model Entropy 2017, 19, 337. [Google Scholar]
- San, J.Y.; Worek, W.M.; LaVan, Z. Entropy Generation in Convective Heat Transfer and Isothermal Convective Mass Transfer. J. Heat Transf. 1987, 109, 647–652. [Google Scholar] [CrossRef]
- Khan, M.I.; Khan, S.A.; Hayat, T.; Qayyum, S.; Alsaedi, A. Entropy generation analysis in MHD flow of viscous fluid by a curved stretching surface with cubic autocatalysis chemical reaction. Eur. Phys. J. Plus 2020, 135, 249. [Google Scholar] [CrossRef]
- Ellahi, R.; Sait, S.M.; Shehzad, N.; Mobin, N. Numerical Simulation and Mathematical Modeling of Electro-Osmotic Couette–Poiseuille Flow of MHD Power-Law Nanofluid with Entropy Generation. Symmetry 2019, 11, 1038. [Google Scholar] [CrossRef] [Green Version]
- Ellahi, R.; Hassan, M.; Zeeshan, A.; Khan, A.A. The shape effects of nanoparticles suspended in HFE-7100 over wedge with entropy generation and mixed convection. Appl. Nanosci. 2016, 6, 641–651. [Google Scholar] [CrossRef] [Green Version]
- Modest, M.F. Radiative Heat Transfer; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Badruddin, I.A.; Zainal, Z.A.; Narayana, P.A.A.; Seetharamu, K.N.; Siew, L.W. Free convection and radiation characteristics for a vertical plate embedded in a porous medium. Int. J. Numer. Methods Eng. 2006, 65, 2265–2278. [Google Scholar] [CrossRef]
- Rasool, G.; Shafiq, A.; Khan, I.; Baleanu, D.; Nisar, K.S.; Shahzadi, G. Entropy Generation and Consequences of MHD in Darcy–Forchheimer Nanofluid Flow Bounded by Non-Linearly Stretching Surface. Symmetry 2020, 12, 652. [Google Scholar] [CrossRef] [Green Version]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahammad, N.A.; Badruddin, I.A.; Kamangar, S.; Khaleed, H.M.T.; Saleel, C.A.; Mahlia, T.M.I. Heat Transfer and Entropy in a Vertical Porous Plate Subjected to Suction Velocity and MHD. Entropy 2021, 23, 1069. https://doi.org/10.3390/e23081069
Ahammad NA, Badruddin IA, Kamangar S, Khaleed HMT, Saleel CA, Mahlia TMI. Heat Transfer and Entropy in a Vertical Porous Plate Subjected to Suction Velocity and MHD. Entropy. 2021; 23(8):1069. https://doi.org/10.3390/e23081069
Chicago/Turabian StyleAhammad, N. Ameer, Irfan Anjum Badruddin, Sarfaraz Kamangar, H.M.T. Khaleed, C. Ahamed Saleel, and Teuku Meurah Indra Mahlia. 2021. "Heat Transfer and Entropy in a Vertical Porous Plate Subjected to Suction Velocity and MHD" Entropy 23, no. 8: 1069. https://doi.org/10.3390/e23081069
APA StyleAhammad, N. A., Badruddin, I. A., Kamangar, S., Khaleed, H. M. T., Saleel, C. A., & Mahlia, T. M. I. (2021). Heat Transfer and Entropy in a Vertical Porous Plate Subjected to Suction Velocity and MHD. Entropy, 23(8), 1069. https://doi.org/10.3390/e23081069







