Finite-Time Thermodynamic Model for Evaluating Heat Engines in Ocean Thermal Energy Conversion
Abstract
1. Introduction
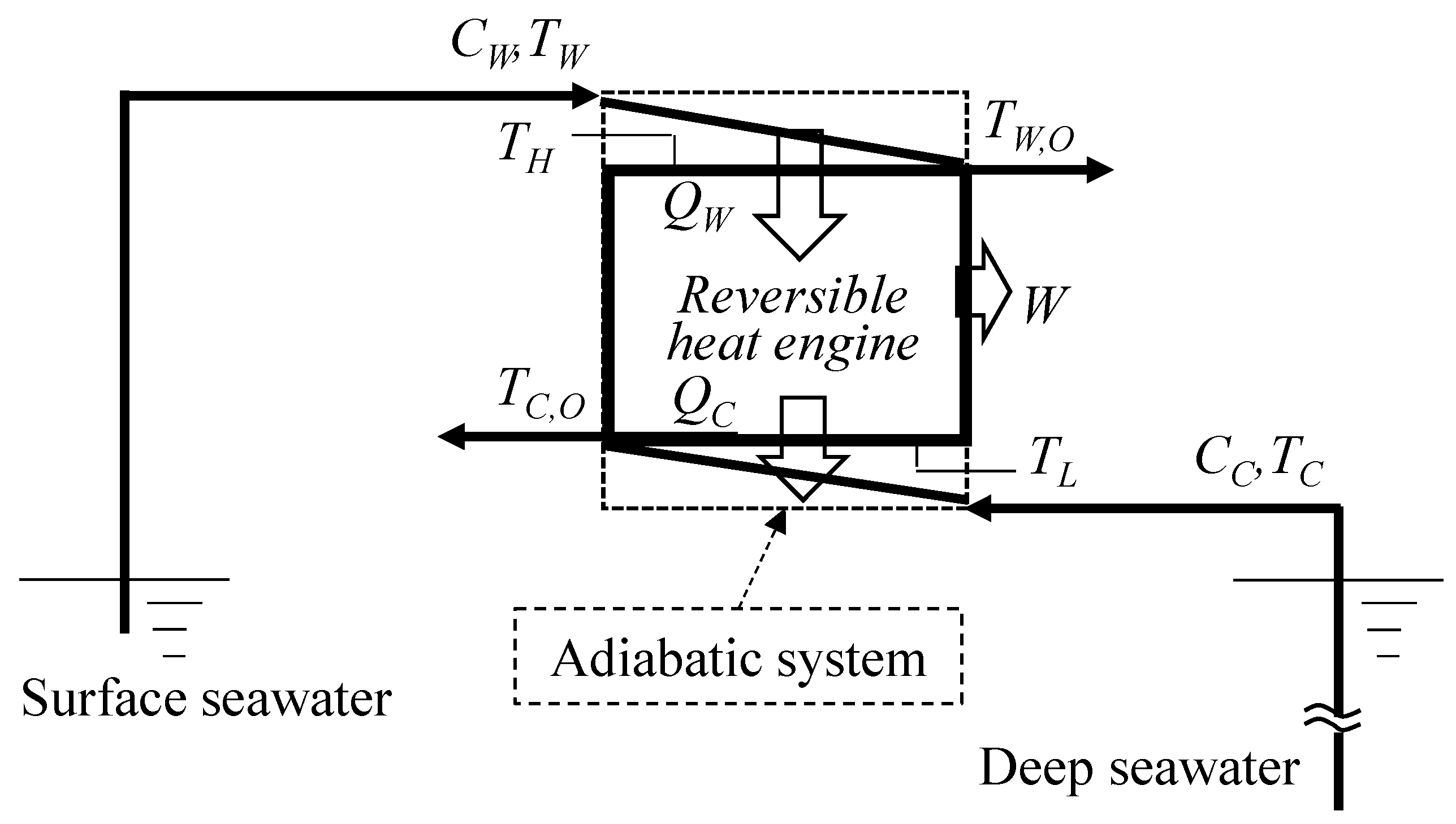
2. First Law of Thermodynamics
2.1. Available Work with Ideal Conditions
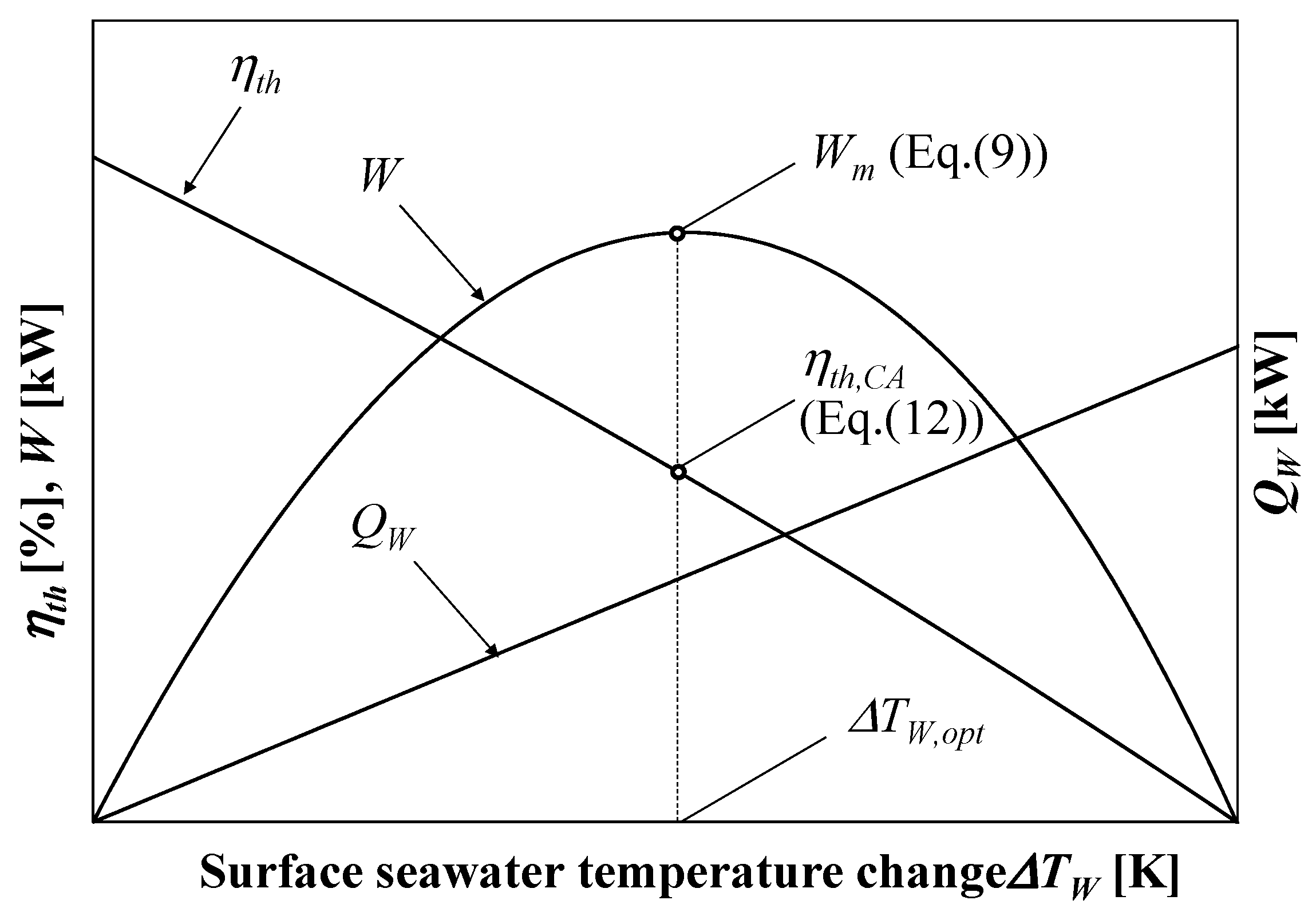
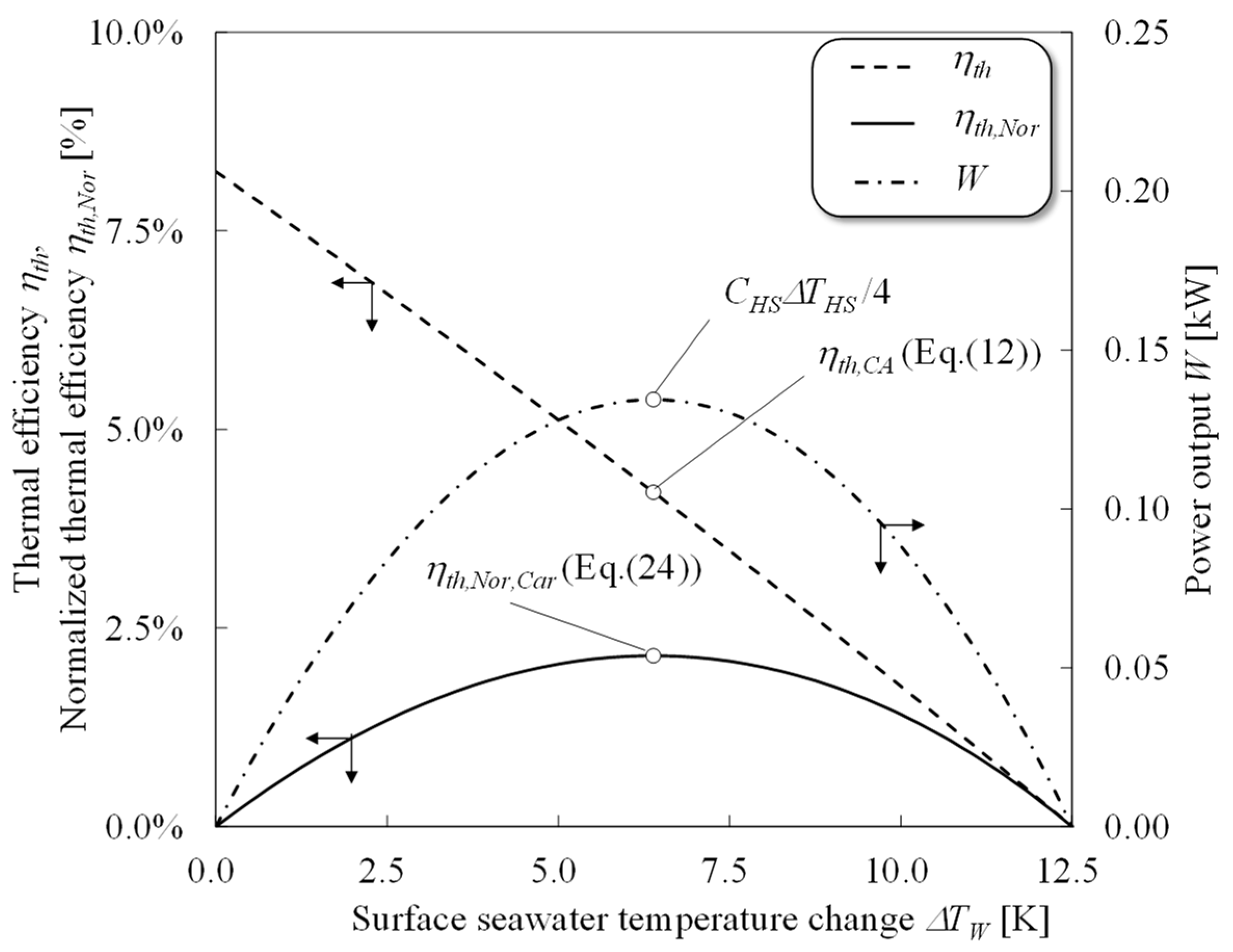
2.2. Normalization of the Thermal Efficiency
3. Second Law of Thermodynamics
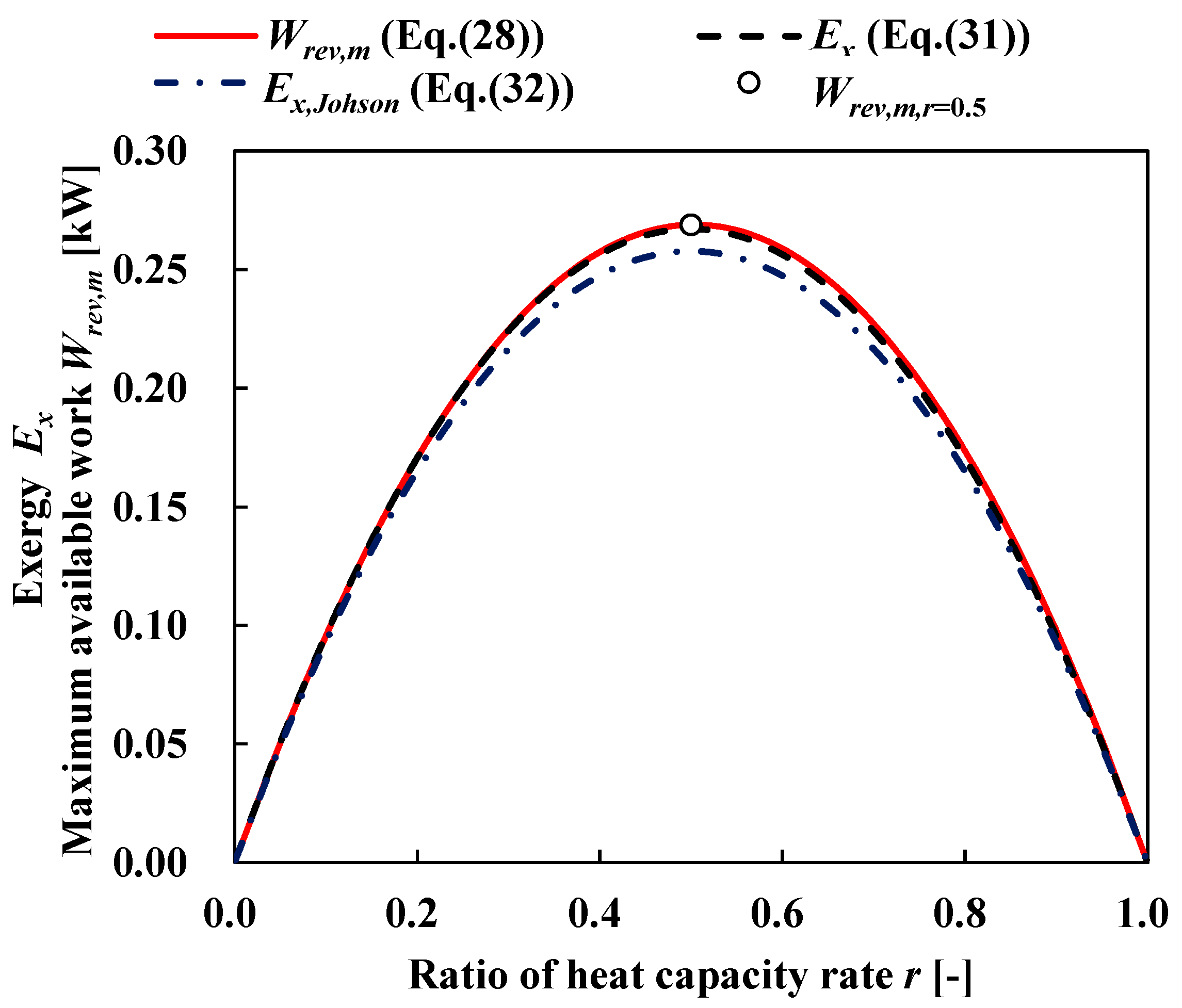
3.1. Available Work Maximization
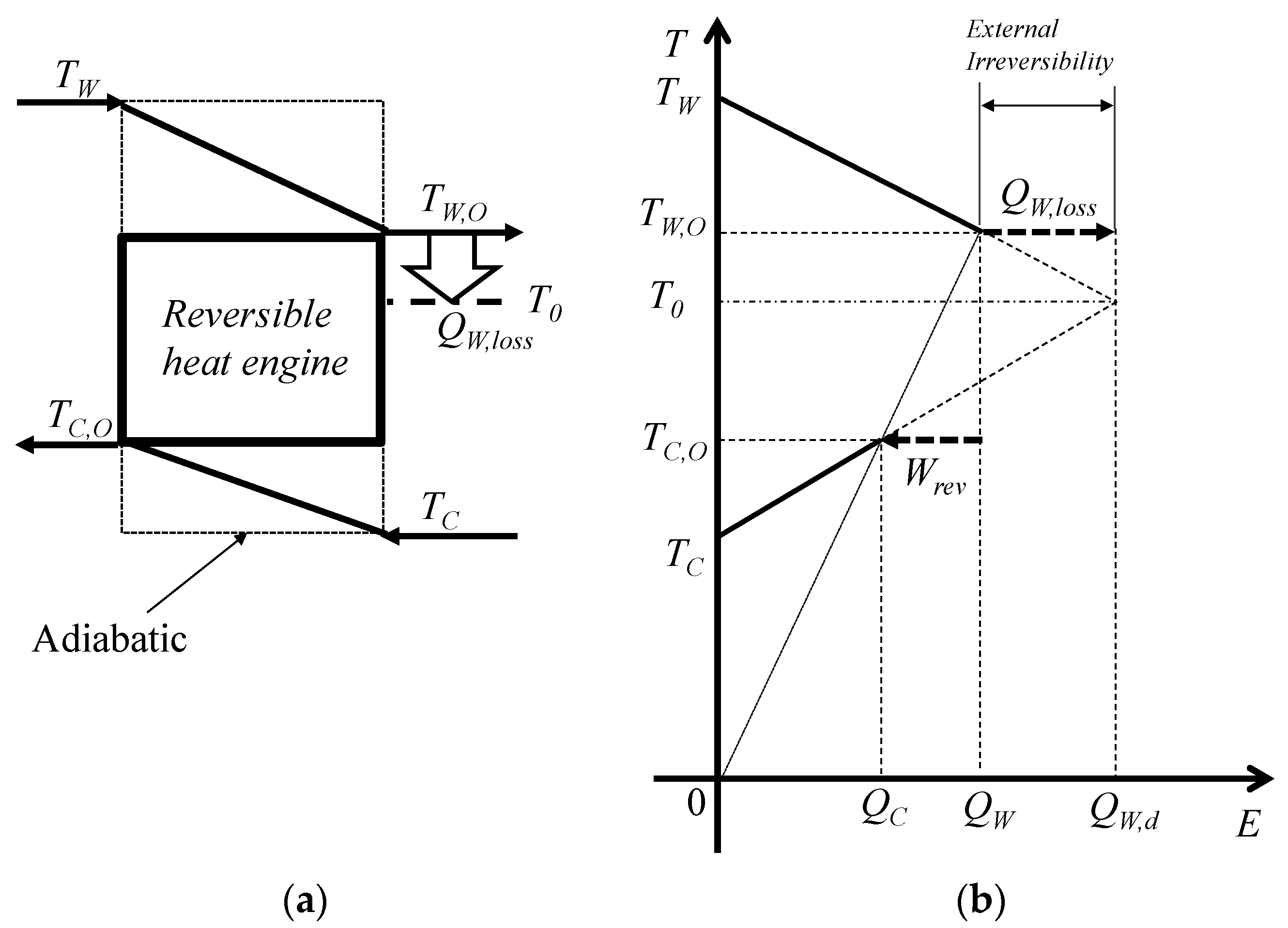
3.2. Exergy and Entropy Generation
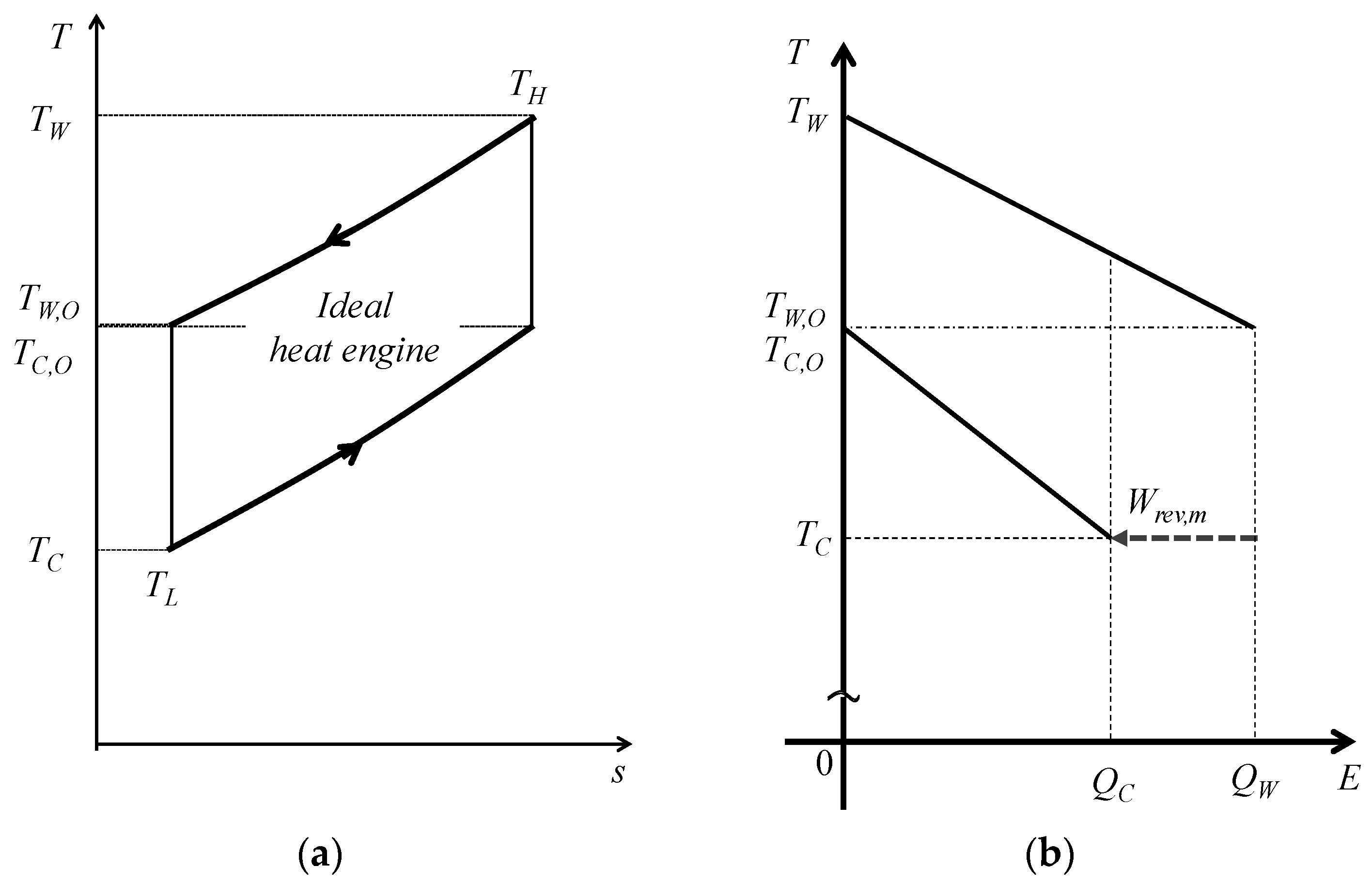
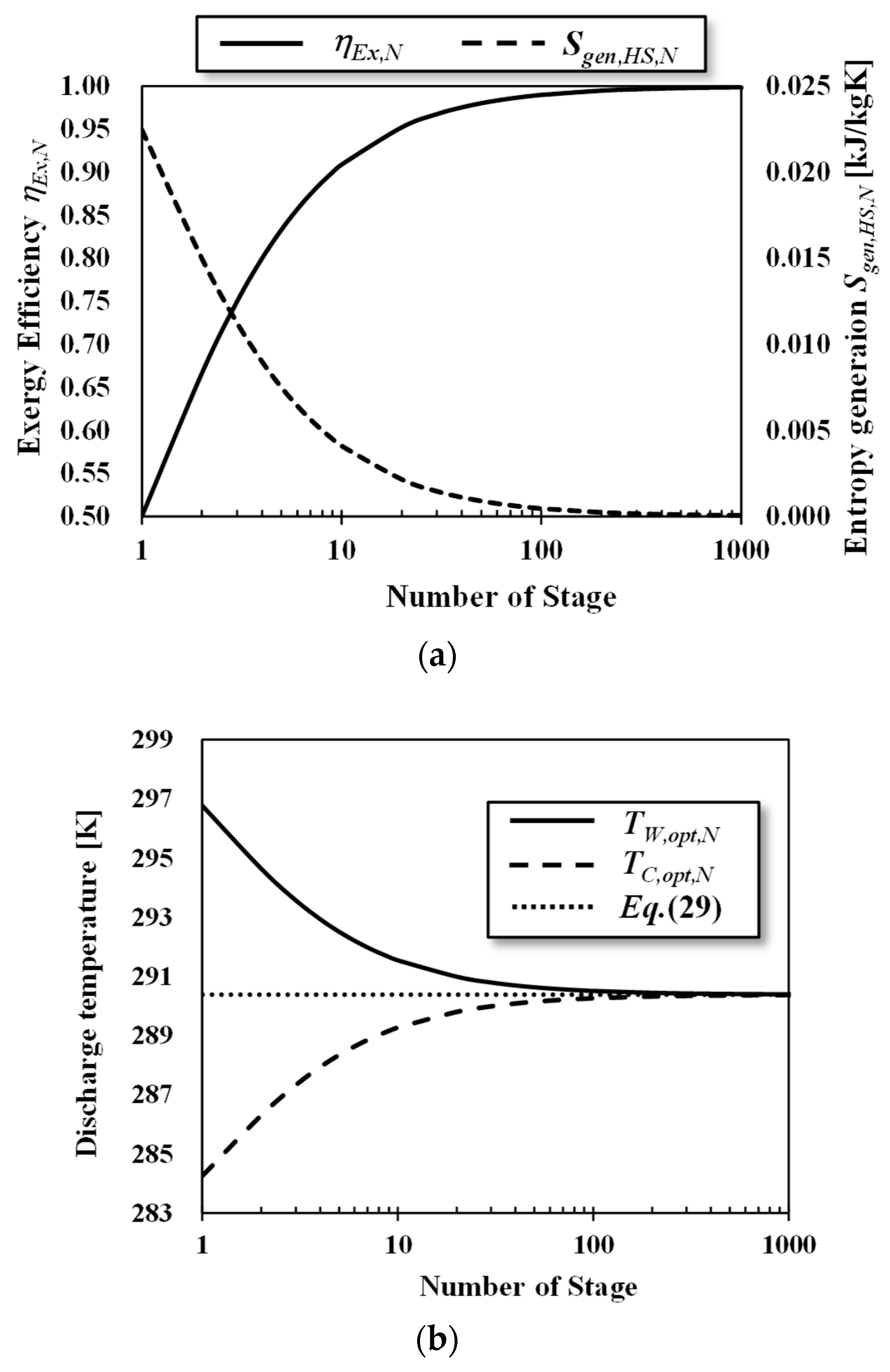
3.3. Ideal and Staging Carnot Heat Engines
4. Performance Evaluation of OTEC Heat Engines
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| C | (kW/K) | Heat capacity |
| cp | (kJ/(kg K)) | Specific heat |
| Ex | (kW) | Exergy |
| H | (kJ) | Enthalpy |
| m | (kg/s) | Mass flow rate |
| Q | (kW) | Heat flow rate |
| R | (-) | Ratio of warm seawater heat-source Heat capacity |
| S | (kJ/(kg K)) | Entropy |
| T | (K) | Temperature |
| ΔT | (K) | Temperature difference |
| ΔTHS | (K) | |
| Greek Symbols | ||
| η | (%) | Efficiency |
| Subscripts | ||
| C | Cold deep seawater | |
| CA | Curzon-Ahlborn | |
| Car | Carnot cycle | |
| d | Transferable | |
| H | High-temperature working fluid temperature on heat engine | |
| HS | Heat source | |
| L | Low-temperature working fluid temperature on heat engine | |
| loss | Lost thermal energy (defines as the difference from the equilibrium state) | |
| N | Number of stage | |
| Nor | Normalized | |
| m | Maximized | |
| O | Outlet | |
| opt | Optimum | |
| rev | Reversible | |
| th | Thermal | |
| W | Warm surface seawater | |
References
- Martin, B.; Okamura, S.; Nakamura, Y.; Yasunaga, T.; Ikegami, Y. Status of the “Kumejima Model” for advanced deep seawater utilization. In Proceedings of the IEE Conference Publications, Kobe, Japan, 6–8 October 2016; pp. 211–216. [Google Scholar]
- Uehara, H.; Ikegami, Y. Parametric performance analysis of OTEC using Kalina cycle. In Proceedings of the ASME/ASES Joint Solar Engineering Conference, Washington, DC, USA, 4–8 April 1993; pp. 203–207. [Google Scholar]
- Kalina, A.L. Combined cycle system with novel bottoming cycle. Trans. ASME J. Eng. Gas Turbines Power 1984, 106, 737–742. [Google Scholar] [CrossRef]
- Uehara, H.; Ikegami, Y.; Nishida, T. OTEC system using a new cycle with Absorption and Extraction Process. Phys. Chem. Aqueous Sys. 1995, 862–869. [Google Scholar] [CrossRef]
- Anderson, J.H.; Anderson, J.H. Thermal power form seawater. Mech. Eng. 1966, 88, 41–46. [Google Scholar]
- Morisaki, T.; Ikegami, Y. Maximum power of a multistage Rankine cycle in low-grade thermal energy conversion. Appl. Therm. Eng. 2014, 69, 78–85. [Google Scholar] [CrossRef]
- Ikegami, Y.; Yasunaga, T.; Morisaki, T. Ocean Thermal Energy Conversion Using Double-Stage Rankine Cycle. J. Sci. Mar. Eng. 2018, 6, 32. [Google Scholar]
- Bombarda, P.; Invernizzi, C.; Gaia, M. Performance Analysis of OTEC Plants with Multilevel Organic Rankine Cycle and Solar Hybridization. Trams. ASME J. Eng. Gas Turbine Power 2013, 135, 042302–1–042302–8. [Google Scholar] [CrossRef]
- Wu, C. Performance Bound for Real OTEC Heat Engines. Ocean Eng. 1987, 14, 349–354. [Google Scholar] [CrossRef]
- Ikegami, Y.; Bejan, A. On the thermodynamic optimization of power plants with heat transfer and fluid flow irreversibilities. Trans. ASME J. Sol. Energy Eng. 1998, 120, 139–144. [Google Scholar] [CrossRef]
- Sinama, F.; Martins, M.; Journoud, A.; Marc, O.; Lucas, F. Thermodynamic analysis and optimization of a 10 MW OTEC Rankine cycle in Reunion Island with the equivalent Gibbs system method and generic optimization program GenOpt. Appl. Ocean Res. 2015, 53, 54–66. [Google Scholar] [CrossRef]
- Bejan, A. Advanced Engineering Thermodynamics, 3rd ed.; Wiley: New York, NY, USA, 1998; pp. 352–417. [Google Scholar]
- Novikov, I.I. The efficiency of atomic power stations. Nucl. Energy II-7 1958, 7, 125–128. [Google Scholar]
- Curzon, F.L.; Ahlborn, B. Efficiency of a Carnot engine at maximum power output. Am. J. Phys. 1957, 43, 22–24. [Google Scholar] [CrossRef]
- Bejam, A. Models of power plants that generate minimum entropy while operating at maximum power. Am. J. Phys. 1996, 64, 1054–1059. [Google Scholar] [CrossRef]
- Gordon, J.M.; Huleihil, M. General Performance characteristics of real heat engines. J. Appl. Phys. 1992, 72, 829–835. [Google Scholar] [CrossRef]
- Gordon, J.M.; Orlov, V.N. Performance characteristics of endoreversible chemical engines. J. Appl. Phys. 1993, 74, 5303–5309. [Google Scholar] [CrossRef]
- Brongioli, D.; Mantina, F.L.; Yip, N.Y. Energy efficiency analysis of distillation for thermally regenerative salinity gradient power technologies. Renew. Energy 2019, 133, 1034–1045. [Google Scholar] [CrossRef]
- Chen, J.; Yan, Z.; Lin, G.; Andersen, B. On the Curzon-Ahlborn efficiency and its connection with the efficiencies of the real heat engines. Energy Convers. Manag. 2001, 42, 173–181. [Google Scholar] [CrossRef]
- Bejan, A. Entropy Generation Minimization, 1st ed.; CRC: Boca Raton, FL, USA, 1996; pp. 205–248. [Google Scholar]
- Bejan, A. Maximum power from fluid flow. Int. J. Heat Mass Transfer 1996, 39, 1175–1181. [Google Scholar] [CrossRef]
- Sekulic, D.P. A fallacious argument in the finite time thermodynamics concept of endoreversibility. J. Appl. Phys. 1998, 83, 4561–4565. [Google Scholar] [CrossRef]
- Leff, H.S. Thermal efficiency at maximum work output: New results for old heat engines. Am. J. Phys. 1987, 55, 602–610. [Google Scholar] [CrossRef]
- Marcella, T.V. Entropy production and the second law of thermodynamics: An introduction to second law analysis. Am. J. Phys. 1992, 60, 888–895. [Google Scholar] [CrossRef]
- Khaliq, A. Finite-time heat-transfer analysis and generalized power-optimization of an endoreversible Rankine heat-negine. Appl. Energy 2004, 29, 27–40. [Google Scholar] [CrossRef]
- Gyftopoulos, E.P. On the Curzon-Ahlborn efficiency and its lack of connection to power producing process. Energy Convers. Manag. 2002, 43, 609–615. [Google Scholar] [CrossRef]
- Chen, L.; Sun, F.; Wu, C. Optimal configuration of a two-heat-reservoir heat-engine with heat-leak and finite thermal-capacity. Appl. Energy 2006, 83, 71–81. [Google Scholar] [CrossRef]
- Bejan, A.; Errera, M.R. Maximum power from a hot stream. Int. J. Heat Mass Transfer 1998, 14, 2025–2035. [Google Scholar] [CrossRef]
- Ohman, H.; Lundqvist, P. Theory and method for analysis of low temperature driven power cycles. Appl. Therm. Eng. 2012, 37, 44–50. [Google Scholar] [CrossRef]
- Ohman, H.; Lundqvist, P. Comparison and analysis of performance using Low Temperature Power Cycles. Appl. Therm. Eng. 2013, 52, 160–169. [Google Scholar] [CrossRef]
- Morisaki, T.; Ikegami, Y. Evaluation of performance characteristics of multi-stage Rankine cycle based on maximum power. In Proceedings of the International Conference on Power Engineering-15 (ICOPE-15), Yokohama, Japan, 30 November–4 December 2015. Paper-ID. ICOPE-15-1154. [Google Scholar]
- Acikkalp, E. Method used for evaluation of actual power generating thermal cycles and comparing them. Int. J. Electr. Power Energy Syst. 2015, 69, 85–89. [Google Scholar] [CrossRef]
- Radcentco, V.; Vasilescu, E.E.; Popescu, G.; Apostol, V. New approach to thermal power plants operation regimes maximum power versus maximum power versus maximum efficiency. Int. J. Therm. Sci. 2007, 46, 1259–1266. [Google Scholar] [CrossRef]
- Yasunaga, T.; Morisaki, T.; Ikegami, Y. Basic Heat Exchanger Performance Evaluation Method on OTEC. J. Sci. Mar. Eng. 2018, 6, 32. [Google Scholar] [CrossRef]
- Fontaine, K.; Yasunaga, T.; Ikegami, Y. OTEC maximum net power output using Carnot cycle and application to simplify heat exchanger selection. Entropy 2019, 21, 1143. [Google Scholar] [CrossRef]
- Yasunaga, T.; Ikegami, Y. Application of Finite-time Thermodynamics for Evaluation Method of Heat Engines. Energy Procedia 2017, 129, 995–1001. [Google Scholar] [CrossRef]
- Bucher, M. New diagram for heat flows and work in a Carnot cycle. Am. J. Phys. 1986, 54, 850–851. [Google Scholar] [CrossRef]
- Wallingford, J. Inefficiency and irreversibility in the Bucher diagram. Am. J. Phys. 1989, 57, 379–381. [Google Scholar] [CrossRef]
- Bejan, A. Graphic Techniques for Teaching Engineering Thermodynamics. Mech. Eng. News 1997, 14, 26–28. [Google Scholar]
- Johnson, D.H. The exergy of the ocean thermal resource and analysis of second-law efficiencies of idealized ocean thermal energy conversion power cycles. Energy 1983, 8, 927–946. [Google Scholar] [CrossRef]
- Salamon, P.; Hoffmann, K.H.; Schubert, S.; Berry, R.S.; Anderson, B. What conditions make minimum entropy production equivalent to maximum power production. J. NonEquilib. Thermodyn. 2001, 26, 73–83. [Google Scholar] [CrossRef]
- Nihous, G.C. An estimation of Atlantic Ocean thermal energy conversion (OTEC) resources. Ocean Eng. 2007, 34, 2210–2221. [Google Scholar] [CrossRef]
- Rajagopalan, K.; Nihous, G.C. Estimates of global Ocean Thermal Energy Conversion (OTEC) resources using an ocean general circulation model. Renew. Energy 2013, 50, 532–540. [Google Scholar] [CrossRef]
- Bernardoni, C.; Binotti, M.; Giostri, A. Techno-economic analysis of closed OTEC cycles for power generation. Renew. Energy 2019, 132, 1018–1033. [Google Scholar] [CrossRef]
- Yoon, J.; Son, C.; Baek, S.; Ye, B.H.; Kim, H. Performance characteristics of a high-efficiency R717 OTEC power cycle. Appl. Therm. Eng. 2014, 72, 304–308. [Google Scholar] [CrossRef]


| Ideal Heat Engines | Carnot Cycle | Ideal Cycle |
|---|---|---|
| Practical heat engines | Rankine and Claud | Uehara and Kalina |
| Maximum work | ||
| Potential (r = 0.5) | ||
| Normalized thermal efficiency | ||
| Exergy efficiency | 1 |
| Case | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Heat engine (Stages) | Rankine | Rankine | Rankine | Rankine | Rankine | Rankine (Two) | Rankine (Two) | Rankine (Three) | Kalina | Kalina |
| W (kW) | 3877 | 5750 | 15,733 | 20 | 5000 | 6350 | 6079 | 6425 | 20 | 6420 |
| TW (°C) | 28 | 29 | 28 | 26 | 28 | 29 | 28 | 28 | 26 | 29 |
| TC (°C) | 4 | 6 | 5 | 5 | 4 | 6 | 4 | 4 | 5 | 6 |
| CHS (kW/K) | 69192 | 69856 | 347476 | 505 | 66891 | 69856 | 66891 | 66891 | 505 | 69856 |
| r | 0.51 | 0.50 | 0.59 | 0.51 | 0.51 | 0.50 | 0.51 | 0.51 | 0.51 | 0.50 |
| Wm/ExHS | 50% | 50% | 50% | 50% | 50% | 67% | 67% | 75% | 91% | 90% |
| ηth | 2.2% | 3.2% | 3.2% | 2.4% | 3.1% | 3.2% | 3.7% | 3.9% | 2.4% | 3.2% |
| ηth,Nor | 0.93% | 1.43% | 0.81% | 0.76% | 1.25% | 1.58% | 1.52% | 1.60% | 0.76% | 1.60% |
| ηEX | 22.5% | 36.2% | 20.4% | 20.7% | 30.0% | 39.9% | 36.5% | 38.6% | 20.7% | 40.4% |
| Reference | [44] | [7] | [11] | [45] | [8] | [7] | [8] | [8] | [45] | [7] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yasunaga, T.; Ikegami, Y. Finite-Time Thermodynamic Model for Evaluating Heat Engines in Ocean Thermal Energy Conversion. Entropy 2020, 22, 211. https://doi.org/10.3390/e22020211
Yasunaga T, Ikegami Y. Finite-Time Thermodynamic Model for Evaluating Heat Engines in Ocean Thermal Energy Conversion. Entropy. 2020; 22(2):211. https://doi.org/10.3390/e22020211
Chicago/Turabian StyleYasunaga, Takeshi, and Yasuyuki Ikegami. 2020. "Finite-Time Thermodynamic Model for Evaluating Heat Engines in Ocean Thermal Energy Conversion" Entropy 22, no. 2: 211. https://doi.org/10.3390/e22020211
APA StyleYasunaga, T., & Ikegami, Y. (2020). Finite-Time Thermodynamic Model for Evaluating Heat Engines in Ocean Thermal Energy Conversion. Entropy, 22(2), 211. https://doi.org/10.3390/e22020211





