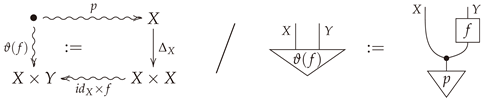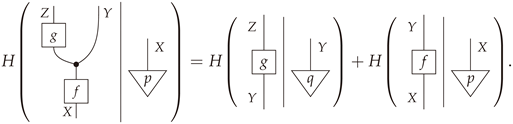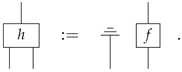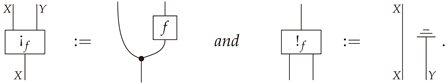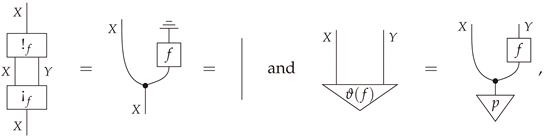1. Introduction
The information loss
associated with a measure-preserving function
between finite probability spaces is given by the Shannon entropy difference
where
is the Shannon entropy of
p (and similarly for
q). In [
1], Baez, Fritz, and Leinster proved that the information loss satisfies, and is uniquely characterized up to a non-negative multiplicative factor by, the following conditions:
- 0.
Positivity: for all . This says that the information loss associated with a deterministic process is always non-negative.
- 1.
Functoriality: for every composable pair of measure-preserving maps. This says that the information loss of two successive processes is the sum of the information losses associated with each process.
- 2.
Convex Linearity: for all . This says that the information loss associated with tossing a (possibly unfair) coin in deciding amongst two processes is the associated weighted sum of their information losses.
- 3.
Continuity: is a continuous function of f. This says that the information loss does not change much under small perturbations (i.e., is robust with respect to errors).
As measure-preserving functions may be viewed as deterministic stochastic maps, it is natural to ask whether there exist extensions of the Baez–Fritz–Leinster (BFL) characterization of information loss to maps that are inherently random (i.e., stochastic) in nature. In particular, what information-theoretic quantity captures such an information loss in this larger category?
This question is answered in the present work. Namely, we extend the BFL characterization theorem, which is valid on
deterministic maps, to the larger category of
stochastic maps. In doing so, we also find a characterization of the conditional entropy. Although the resulting extension is not functorial on the larger category of stochastic maps, we formalize a weakening of functoriality that restricts to functoriality on deterministic maps. This weaker notion of functoriality is definable in any Markov category [
2,
3], and it provides a key axiom in our characterization.
To explain how we arrive at our characterization, let us first recall the definition of stochastic maps between finite probability spaces, for which the measure-preserving functions are a special case. A stochastic map associates with every a probability distribution on Y such that , where is the distribution evaluated at . In terms of information flow, the space may be thought of as a probability distribution on the set of inputs for a communication channel described by the stochastic matrix , while is then thought of as the induced distribution on the set of outputs of the channel.
Extending the information loss functor by assigning
to any
stochastic map
would indeed result in an assignment that satisfies conditions 1–3 listed above. However, it would no longer be positive and the interpretation as an information loss would be gone. Furthermore, no additional information about the stochasticity of the map
f would be used in determining this assignment. In order to guarantee positivity, an additional term, depending on the stochasticity of
f, is needed. This term is provided by the
conditional entropy of
and is given by the the non-negative real number
where
is the Shannon entropy of the distribution
on
Y (in the case that
and
are probability spaces associated with the alphabets of random variables
and
, then
coincides with conditional entropy
[
4]). If
is in fact deterministic, i.e., if
is a point-mass distribution for all
, then
for all
. As such,
is a measure of the uncertainty (or randomness) of the outputs of
f averaged over the prior distribution
p on the set
X of its inputs. Indeed,
is maximized precisely when
is the uniform distribution on
Y for all
.
Therefore, given a stochastic map
, we call
the
conditional information loss of
(the same letter
K is used here because it agrees with the Shannon entropy difference when
f is deterministic). As
whenever
f is deterministic, the conditional information loss restricts to the category of measure preserving functions as the information loss functor of Baez, Fritz, and Leinster, while also satisfying conditions 0, 2, and 3 (i.e., positivity, convex linearity, and continuity) on the larger category of stochastic maps. However, conditional information loss is
not functorial in general, and while this may seem like a defect at first glance, we prove that there is no extension of the information loss functor that remains functorial on the larger category of stochastic maps if the positivity axiom is to be preserved, thus retaining an interpretation as information loss. In spite of this, conditional information loss does satisfy a weakened form of functoriality, which we briefly describe now.
A pair of composable stochastic maps is a.e. coalescable if and only if for every pair of elements and for which and , there exists a unique such that and . Intuitively, this says that the information about the intermediate step can be recovered given knowledge about the input and output. In particular, if f is deterministic, then the pair is a.e. colescable (for obvious reasons, since knowing x alone is enough to determine the intermediate value). However, there are other many situations where a pair could be a.e. coalescable and the maps need not be deterministic. With this definition in place (which we also generalize to the setting of arbitrary Markov categories), we replace functoriality with the following weaker condition.
- 1🟉.
Semi-functoriality: for every a.e. coalescable pair of stochastic maps. This says that the conditional information loss of two successive processes is the sum of the conditional information losses associated with each process provided that the information in the intermediate step can always be recovered.
Replacing functoriality with semi-functoriality is not enough to characterize the conditional information loss. However, it comes quite close, as only one more axiom is needed. Assuming positivity, semi-functoriality, convex linearity, and continuity, there are several equivalent axioms that may be stipulated to characterize the conditional information loss. To explain the first option, we introduce a convenient factorization of every stochastic map
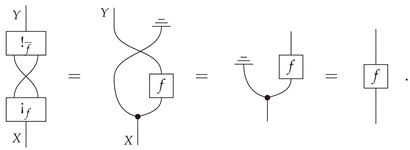
. The
bloom-shriek factorization of
f is given by the decomposition
, where
is the
bloom of
f whose value at
is the probability measure on
given by sending
to
, where
is the Kronecker delta. In other words,
records each of the probability measures
on a copy of
Y indexed by
. A visualization of the bloom of
f is given in
Figure 1a. When one is given the additional data of probability measures
p and
q on
X and
Y, respectively, then
Figure 1b illustrates the bloom-shriek factorization of
f. From this point of view,
keeps track of the information encoded in
both p and
f, while the projection map
forgets, or loses,
some of this information.
With this in mind, our final axiom to characterize the conditional information loss is
- 4(a).
Reduction: , where is the bloom-shriek factorization of f. This says that the conditional information loss of f equals the information loss of the projection using the associated joint distribution on .
Note that this axiom describes how K is determined by its action on an associated class of deterministic morphisms. These slightly modified axioms, namely, semi-functoriality, convex linearity, continuity, and reduction, characterize the conditional information loss and therefore extend Baez, Fritz, and Leinster’s characterization of information loss. A much simpler axiom that may be invoked in place of the reduction axiom which also characterizes conditional information loss is the following.
- 4(b).
Blooming: , where is the unique map from a one point probability space to . This says that if a process begins with no prior information, then there is no information to be lost in the process.
The conditional entropy itself can be extracted from the conditional information loss by a process known as Bayesian inversion, which we now briefly recall. Given a stochastic map , there exists a stochastic map such that for all and (the stochastic map is the almost everywhere unique conditional probability so that Bayes’ rule holds). Such a map is called a Bayesian inverse of f. The Bayesian inverse can be visualized using the bloom-shriek factorization because it itself has a bloom-shriek factorization . This is obtained by finding the stochastic maps in the opposite direction of the arrows so that they reproduce the appropriate volumes of the water droplets.
Given this perspective on Bayesian inversion, we prove that the
conditional entropy of
equals the
conditional information loss of its Bayesian inverse
. Moreover, since the conditional information loss of
is just the information loss of
, this indicates how the conditional entropy and conditional information losses are the ordinary information losses associated with the two projections
and
in
Figure 1b. This duality also provides an interesting perspective on conditional entropy and its characterization. Indeed, using Bayesian inversion, we also characterize the
conditional entropy as the unique assignment
F sending measure-preserving stochastic maps between finite probability spaces to real numbers satisfying conditions 0,
, 2, and 3 above, but with a new axiom that reads as follows.
- 4(c).
Entropic Bayes’ Rule: for all . This is an information theoretic analogue of Bayes’ rule, which reads for all and , or in more traditional probabilistic notation
In other words, we obtain a
Bayesian characterization of the conditional entropy. This provides an entropic and information-theoretic description of Bayes’ rule from the Markov category perspective, in a way that we interpret as answering an open question of Fritz [
6].
2. Categories of Stochastic Maps
In the first few sections, we define all the concepts involved in proving that the conditional information loss satisfies the properties that we will later prove characterize it. This section introduces the domain category and its convex structure.
Definition 1. Let X and Y be finite sets. Astochastic map associates a probability measure to every . If is such that is a point-mass distribution for every , then f is said to bedeterministic.
Notation 1. Given a stochastic map (also written as ), the value will be denoted by . As there exists a canonical bijection between deterministic maps of the form and functions , deterministic maps from X to Y will be denoted by the functional notation .
Definition 2. A stochastic map of the form from a single element set to a finite set X is a single probability measure on X. Its unique value at x will be denoted by for all . The set will be referred to as thenullspaceof p.
Definition 3. LetFinStochbe the category of stochastic maps between finite sets. Given a finite set X, the identity map of X inFinStochcorresponds to the identity function . Second, given stochastic maps and , the composite is given by the Chapmann–Kolmogorov equation
Definition 4. Let X be a finite set. Thecopyof X is the diagonal embedding , and thediscardof X is the unique map from X to the terminal object • inFinStoch, which will be denoted by . If Y is another finite set, theswap mapis the map given by . Given morphisms and inFinStoch, theproductof f and g is the stochastic map given by
The product of stochastic maps endows
FinStoch with the structure of a monoidal category. Together with the copy, discard, and swap maps,
FinStoch is a Markov category [
2,
3].
Definition 5. Let (this stands for “finiteprobabilities andstochastic maps”) be the co-slice category , i.e., the category whose objects are pairs consisting of a finite set X equipped with a probability measure p, and a morphism from to is a stochastic map such that for all . The subcategory of deterministic maps in will then be denoted by (which stands for “finiteprobabilities anddeterministic maps”). A pair of morphisms in is said to be acomposable pairiff exists.
Note that the category
was called
in [
1].
Remark 1. Though it is often the case that we will denote a morphism in simply by f, such notation is potentially ambiguous, as the morphism is distinct from the morphsim whenever . As such, we will only employ the shorthand of denoting a morphism in by its underlying stochastic map whenever the source and target of the morphism are clear from the context.
Lemma 1. The object given by a single element set equipped with the unique probability measure is a zero object (i.e., terminal and initial) in .
Definition 6. Given an object in , theshriekandbloomof p are the unique maps to and from respectively, which will be denoted and (the former is deterministic, while the latter is stochastic). The underlying stochastic maps associated with and are and , respectively.
Example 1. Since is a zero object, given any two objects and , there exists at least one morphism , namely the composite .
Definition 7. Let be a morphism in . Thejoint distributionassociated with f is the probability measure given by .
It is possible to take convex combinations of both objects and morphisms in , and such assignments will play a role in our characterization of conditional entropy.
Definition 8. Let be a probability measure and let be a collection of objects in indexed by X. The p-weighted convex sum is defined to be the set equipped with the probability measure given byIn addition, if is a collection of morphisms in indexed by X, the p-weighted convex sum is given by 3. The Baez–Fritz–Leinster Characterization of Information Loss
In [
1], Baez, Fritz, and Leinster (BFL) characterized the Shannon entropy difference associated with measure-preserving functions between finite probability spaces as the only non-vanishing, continuous, convex linear functor from
to the non-negative reals (up to a multiplicative constant). It is then natural to ask whether there exist either extensions or analogues of their result by including non-deterministic morphisms from the larger category
. Before delving deeper into such inquiry, we first recall in detail the characterization theorem of BFL.
Definition 9. Let be the convex category consisting of a single object and whose set of morphisms is . The composition in is given by addition. Convex combinations of morphisms are given by ordinary convex combinations of numbers. The subcategory of non-negative reals will be denoted .
In the rest of the paper, we will not necessarily assume that assignments from one category to another are functors. Nevertheless, we do assume they form (class) functions (see ([
7], Section I.7) for more details). Furthermore, we assume that they respect or reflect source and targets in the following sense. If
and
are two categories, all functions
are either
covariant or
contravariant in the sense that for any morphism
in
,
is a morphism from
to
or from
to
, respectively. These are the only types of functions between categories we will consider in this work. As such, we therefore abuse terminology and use the term
functions for such assignments throughout. If
M is a
commutative monoid and
denotes its one object category, then every covariant function
is also contravariant and vice-versa.
We now define a notion of continuity for functions of the form .
Definition 10. A sequence of morphisms in convergesto a morphism if and only if the following two conditions hold.
- (a)
There exists an for which and for all .
- (b)
The following limits hold: and (note that these limits necessarily imply ).
A function iscontinuousif and only if whenever is a sequence in converging to f.
Remark 2. In the subcategory , since the topology of the collection of functions from a finite set X to another finite set Y is discrete, one can equivalently assume that a sequence as in Definition 10, but this time with all deterministic, converges to if and only if the following two conditions hold.
- (a)
There exists an for which for all .
- (b)
For , one has .
In this way, our definition of convergence agrees with the definition of convergence of BFL on the subcategory [1]. Definition 11. A function is said to beconvex linearif and only if for all objects in ,for all collections in . Definition 12. A function is said to befunctorialif and only if it is in fact a functor, i.e., if and only if for every composable pair in .
Definition 13. Let be a probability measure. TheShannon entropyof p is given by When considering any entropic quantity, we will always adhere to the convention that .
Definition 14. Given a map in , the Shannon entropy difference will be referred to as theinformation lossof f. Information loss defines a functor , henceforth referred to as theinformation loss functoron .
Theorem 1 (Baez–Fritz–Leinster [
1])
. Suppose is a function which satisfies the following conditions.- 1.
F is functorial.
- 2.
F is convex linear.
- 3.
F is continuous.
Then F is a non-negative multiple of information loss. Conversely, the information loss functor is non-negative and satisfies conditions 1–3.
In light of Theorem 1, it is natural to question whether or not there exists a functor that restricts to as the information loss functor. It turns out that no such non-vanishing functor exists, as we prove in the following proposition.
Proposition 1. If is a functor, then for all morphisms f in .
Proof. Let
be a morphism in
. Since
F is a functor,
Let
be
any morphism in
(which necessarily exists by Example 1, for instance). Then a similar calculation yields
Hence,
. □
4. Extending the Information Loss Functor
Proposition 1 shows it is not possible to extend the information loss functor to a functor on
. Nevertheless, in this section, we define a non-vanishing
function that restricts to the information loss
functor on
, which we refer to as
conditional information loss. While
K is not functorial, we show that it satisfies many important properties such as continuity, convex linearity, and invariance with respect to compositions with isomorphisms. Furthermore, in
Section 5 we show
K is functorial on a restricted class of composable pairs of morphisms (cf. Definition 18), which are definable in any Markov category. At the end of this section we characterize conditional information loss as the unique extension of the information loss functor satisfying the reduction axiom 4(a) as stated in the introduction. In
Section 8, we prove an intrinsic characterization theorem for
K without reference to the deterministic subcategory
inside
.
Appendix A provides an interpretation of the vanishing of conditional information loss in terms of correctable codes.
Definition 15. Theconditional information lossof a morphism in is the real number given bywhereis theconditional entropyof . Proposition 2. The function , uniquely determined on morphisms by sending to , satisfies the following conditions.
- (i)
.
- (ii)
K restricted to agrees with the information loss functor (cf. Definition 14).
- (iii)
K is convex linear.
- (iv)
K is continuous.
- (v)
Given , then , where is the projection and is the joint distribution (cf. Definition 7).
Lemma 2. Let be a morphism in . Then Proof of Proposition 2. - (i)
The non-negativity of K follows from Lemma 2 and the equality .
- (ii)
This follows from the fact that for all deterministic f.
- (iii)
Let
be a probability measure, and let
be a collection of morphisms in
indexed by
X. Then the
p-weighted convex sum
is a morphism in
of the form
, where
,
,
,
, and
. Then
which shows that
K is convex linear.
- (iv)
Let
be a sequence (indexed by
) of probability-preserving stochastic maps such that
and
for large enough
n, and where
and
. Then
where the last equality follows from the fact that the limit and sum (which is finite) can be interchanged and all expressions are continuous on
.
- (v)
This follows from
and the fact that
. □
Remark 3. Since conditional entropy vanishes for deterministic morphisms, conditional information loss restricts to as the information loss functor. It is important to note that if the term was not included in the expression for , then the inequality would fail in general. When f is deterministic, Baez, Fritz, and Leinster proved . However, when f is stochastic, the inequality does not hold in general. This has to do with the fact that stochastic maps may increase entropy, whereas deterministic maps always decrease it(while this claim holds in the classical setting as stated, it no longer holds for quantum systems [8]). As such, the term is needed to retain non-negativity as one attempts to extend BFL’s functor K on to a function on . Item (v) of Proposition 2 says that the conditional information loss of a map in is the information loss of the deterministic map in , so that conditional information loss of a morphism in may always be reduced to the information loss of a deterministic map in naturally associated with it having the same target. This motivates the following definition.
Definition 16. A function isreductiveif and only if for every morphism in (cf. Proposition 2 item (v) for notation).
Proposition 3 (Reductive characterization of conditional information loss). Let be a function satisfying the following conditions.
- (i)
F restricted to is functorial, convex linear, and continuous.
- (ii)
F is reductive.
Then F is a non-negative multiple of conditional information loss. Conversely, conditional information loss satisfies conditions (i) and (ii).
Proof. This follows immediately from Theorem 1 and item (v) of Proposition 2. □
In what follows, we will characterize conditional information loss without any explicit reference to the subcatgeory or the information loss functor of Baez, Fritz, and Leinster. To do this, we first need to develop some machinery.
5. Coalescable Morphisms and Semi-Functoriality
While conditional information loss is not functorial on
, we know it acts functorially on deterministic maps. As such, it is natural to ask for which pairs of composable stochastic maps does the conditional information loss act functorially. In this section, we answer this question, and then we use our result to define a property of functions
that is a weakening of functoriality, and which we refer to as
semi-functoriality. Our definitions are valid in any Markov category (cf.
Appendix B).
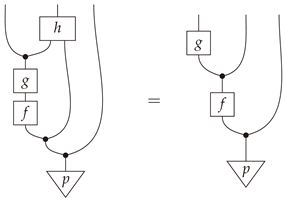
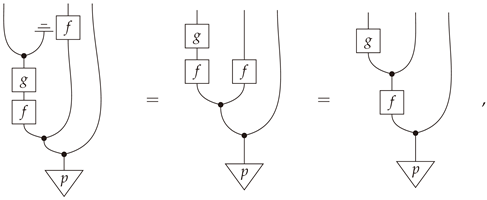
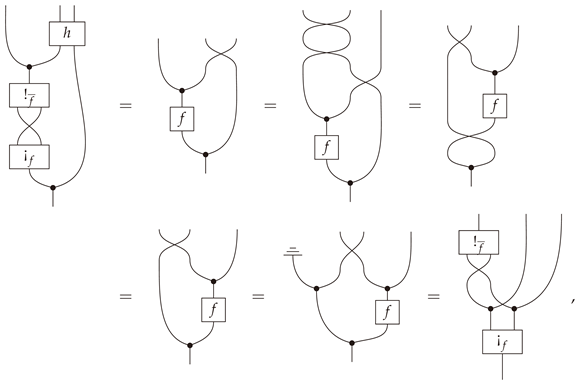
Definition 17. A deterministic map is said to be amediatorfor the composable pair in if and only ifIf in fact Equation (1) holds for all , then h is said to be astrong mediatorfor the composable pair inFinStoch.
Remark 4. Mediators do not exist for general composable pairs, as one can see by considering any composable pair such that (cf. Definitions 7 and 13).
Proposition 4. Let be a composable pair of morphisms in . Then the following statements are equivalent.
- (a)
For every and , there exists at most one such that .
- (b)
The pair admits a mediator .
- (c)
There exists a function such that
Proof. ((a)⇒(b)) For every for which such a y exists, set . If no such y exists or if , set to be anything. Then h is a mediator for .
((b)⇒(c)) Let
h be a mediator for
. Since (
2) holds automatically for
, suppose
, in which case (
2) is equivalent to
for all
. This follows from Equation (
1) and the fact that
h is a function.
((c)⇒(a)) Let and suppose . If h is the mediator, then . But since for all , there is only one non-vanishing term in this sum, and it is precisely . □
Theorem 2 (Functoriality of Conditional Entropy)
. Let be a composable pair of morphisms in . Thenholds if and only if there exists a mediator for . We first prove two lemmas.
Lemma 3. Let be a pair of composable morphisms. ThenIn particular, if and only if . Proof of Lemma 3. On components,
. Hence,
Note that this equality still holds if
or
as each step in this calculation accounted for such possibilities. □
Lemma 4. Let be a pair of composable morphisms in . ThenNote that the order of the sums matters in this expression and also note that it is always well-defined since implies . Proof of Lemma 4. For convenience, temporarily set
. Then
which proves the claim due to the definition of the composition of stochastic maps. □
Proof of Theorem 2. Temporarily set
. In addition, note that the set of all
and
can be given a more explicit description in terms of the joint distribution
associated with the composite
and prior
p, namely
. Then,
(⇒) Suppose
, which is equivalent to Equation (
3) by Lemma 3. Then since each term in the sum from Lemma 4 is non-negative,
Hence, fix such an
. The expression here vanishes if and only if
Hence, for every
and
, there exists a unique
such that
. But by (
5), this means that for every
, there exists a unique
such that
. This defines a function
which can be extended in an
s-a.e. unique manner to a function
We now show the function
h is in fact a mediator for the composable pair
. The equality clearly holds if
since both sides vanish. Hence, suppose that
. Given
, the left-hand-side of (2) is given by
by Equation (
6). Similarly, if
and
, then
for all
because otherwise
would be nonzero. If instead
, then
and
for all
by (
6). Therefore, (
2) holds.
(⇐) Conversely, suppose a mediator
h exists and let
be the stochastic map given on components by
Then
as desired. □
Corollary 1 (Functoriality of Conditional Information Loss). Let be a composable pair of morphisms in . Then if and only if there exists a mediator for the pair .
Proof. Since the Shannon entropy difference is always functorial, the conditional information loss is functorial on a pair of morphisms if and only if the conditional entropy is functorial on that pair. Theorem 2 then completes the proof. □
Example 2. In the notation of Theorem 2, suppose that f isa.e. deterministic, which means for all for some function f (abusive notation is used). In this case, the deviation from functoriality, (4), simplifies toTherefore, if f is p-a.e. deterministic, . In this case, the mediator is given by . Definition 18. A pair of composable morphisms in is calleda.e. coalescableif and only if admits a mediator . Similarly, a pair of composable morphisms inFinStochis calledcoalescableiff admits a strong mediator .
Remark 5. Example 2 showed that if is p-a.e. deterministic, then the pair is a.e. coalescable for any g. In particular, every pair of composable morphisms in is coalescable.
In light of Theorem 2 and Corollary 1, we make the following definition, which will serve as one of the axioms in our later characterizions of both conditional information loss and conditional entropy.
Definition 19. A function is said to besemi-functorialiff for every a.e. coalescable pair in .
Example 3. By Theorem 2 and Corollary 1, conditional information loss and conditional entropy are both semi-functorial.
Proposition 5. Suppose is semi-functorial. Then the restriction of F to is functorial. In particular, if F is, in addition, convex linear, continuous, and reductive, then F is a non-negative multiple of conditional information loss.
Proof. By Example 2, every pair of composable morphisms in is a.e. coalescable. Therefore, F is functorial on . The second claim then follows from Proposition 3. □
The following lemma will be used in later sections and serves to illustrate some examples of a.e. coalescable pairs.
Lemma 5. Let be a triple of composable morphisms with e deterministic and g invertible. Then each of the following pairs are a.e. coalescable:
- (i)
- (ii)
- (iii)
- (iv)
Proof. The proof that is coalescable was provided (in a stronger form) in Example 2. To see that is coalescable, note that since g is an isomorphism we have . Thus, is a mediator function for , thus is coalescable. The last two claims follow from the proofs of the first two claims. □
6. Bayesian Inversion
In this section, we recall the concepts of a.e. equivalence and Bayesian inversion phrased in a categorical manner [
2,
3,
9], as they will play a significant role moving forward.
Definition 20. Let and be two morphisms in with the same source and target. Then f and g are said toalmost everywhere equivalent(or p-a.e.equivalent) if and only if for every with . In such a case, the p-a.e. equivalence of f and g will be denoted .
Theorem 3 (Bayesian Inversion [
2,
9,
10])
. Let be a morphism in . Then there exists a morphism such that for all and . Furthermore, for any other morphism satisfying this condition, . Definition 21. The morphism appearing in Theorem 3 will be referred to as aBayesian inverseof . It follows that for all with .
Proposition 6. Bayesian inversion satisfies the following properties.
- (i)
Suppose and are p-a.e. equivalent, and let and be Bayesian inverses of f and g, respectively. Then .
- (ii)
Given two morphisms and in , then f is a Bayesian inverse of g if and only if g is a Bayesian inverse of f.
- (iii)
Let be a Bayesian inverse of , and let be the swap map (as in Definition 4). Then
- (iv)
Let be a composable pair of morphisms in , and suppose and are Bayesian inverses of f and g respectively. Then is a composable pair, and is a Bayesian inverse of .
Proof. These are immediate consequences of the categorical definition of a Bayesian inverse (see [
3,
10,
11] for proofs). □
Definition 22. A contravariant function is said to be aBayesian inversion functorif and only if acts as the identity on objects and is a Bayesian inverse of f for all morphisms f in .
This is mildly abusive terminology since functoriality only holds in the a.e. sense, as explained in the following remark.
Remark 6. A Bayesian inversion functor exists. Given any , set to be given by for all with and for all with . Note that this does not define a functor. Indeed, if is a probability space with for some , then is the uniform measure on X instead of the Dirac delta measure concentrated on . In other words, . Similar issues of measure zero occur, indicating that for a composable pair of morphisms . Nevertheless, Bayesian inversion is a.e. functorial in the sense that and .
Corollary 2. for any Bayesian inversion functor and every in .
Proposition 7. Let be a Bayesian inversion functor on (as in Definition 22). Then isa.e. convex linearin the sense thatwhere and the other notation is as in Definition 8. Proof. First note that it is immediate that
is convex linear on objects since Bayesian inversion acts as the identity on objects. Let
be a probability measure,
be a collection of morphisms in
indexed by
X, and suppose
is a Bayesian inversion functor. Then for
with
, we have
Thus, is a.e. convex linear. □
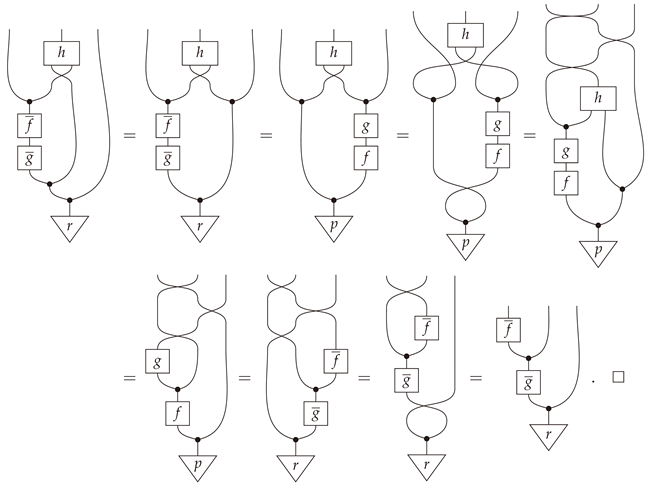
Proposition 8. Given in , and let and be Bayesian inverses of f and g respectively. Then is a.e. coalescable if and only if is a.e. coalescable.
Proof. Since Bayesian inversion is a dagger functor on a.e. equivalence classes ([
3], (Remark 13.10)), it suffices to prove one direction in this claim. Hence, suppose
is a.e. coalescable and let
h be a mediator function realizing this. Then
is a mediator for
because
A completely string-diagrammatic proof is provided in
Appendix B. □
The following proposition is a reformulation of the conditional entropy identity in terms of Bayesian inversion.
Proposition 9. Let be a morphism in , and suppose is a Bayesian inverse of f. Then Proof. This follows from the fact that both sides of (
7) are equal to
. □
Proposition 9 implies Bayesian inversion takes conditional entropy to conditional information loss and vice versa, which is formally stated as follows.
Corollary 3. Let and be given by conditional information loss and conditional entropy, respectively, and let be a Bayesian inversion functor. Then, and .
Remark 7. If is a deterministic morphism in , Baez, Fritz, and Leinster point out that the information loss of f is in fact the conditional entropy of x given y [1]. Here, we see this duality as a special case of Corollary 3 applied to deterministic morphisms. 7. Bloom-Shriek Factorization
We now introduce a simple, but surprisingly useful, factorization for every morphism in , and we use it to prove some essential lemmas for our characterization theorems for conditional information loss and conditional entropy, which appear in the following sections.
Definition 23. Given a stochastic map , thebloom of fis the stochastic map given by the composite , and theshriek of fis the deterministic map given by the projection .
Proposition 10. Let be a morphism in . Then the following statement hold.
- (i)
The composite is equal to the identity .
- (ii)
The morphism f equals the composite , where denotes any Bayesian inverse of f and is the swap map.
- (iii)
The pair is coalescable.
Definition 24. The decomposition in item (ii) Proposition 10 will be referred to as thebloom-shriek factorizationof f.
Proof of Propostion 10. Element-wise proofs are left as exercises.
Appendix B contains an abstract proof using string diagrams in Markov categories. □
The bloom of f can be expressed as a convex combination of simpler morphisms up to isomorphism. To describe this and its behavior under convex linear semi-functors, we introduce the notion of an invariant and examine some of its properties.
Definition 25. A function is said to be aninvariantif and only if for every triple of composable morphisms such that e and g are isomorphisms, then .
Lemma 6. If a function is semi-functorial, then F is an invariant.
Proof. Consider a composable triple
such that
e and
g are isomorphisms. Then
by Lemma 5. Secondly, since
g and
e are isomorphisms, and since the pairs
and
are coalescable,
. But since
(by semi-functoriality), this requires that
for an isomorphism
g since
and
. The same is true for
. Hence,
. □
Lemma 7. Let be a morphism in , and suppose is semi-functorial and convex linear. Then the following statements hold.
- (i)
- (ii)
- (iii)
Proof. For items (ii) and (iii), note that
and
can be expressed as composites of isomorphisms and certain convex combinations, namely
Hence,
Proposition 11. Suppose is semi-functorial and convex linear. If are two morphisms in such that , then .
Proof. Suppose
and
are such that
, and let
and
be Bayesian inverses for
f and
g. Then
as desired. □
8. An Intrinsic Characterization of Conditional Information Loss
Theorem 4. Suppose is a function satisfying the following conditions.
- 1.
F is semi-functorial.
- 2.
F is convex linear.
- 3.
F is continuous.
- 4.
for every probability distribution .
Then F is a non-negative multiple of conditional information loss. Conversely, conditional information loss satisfies conditions 1–4.
Proof. Suppose
F satisfies conditions 1–4, let
be an arbitrary morphism in
, and let
be the swap map, so that
. Then
Thus, F is reductive (see Definition 16) and Proposition 5 applies. □
Remark 8. Under the assumption that is semi-functorial and convex linear, one may show F satisfies condition 4 in Theorem 4 if and only if F is reductive (see Definition 16 and Proposition 5). While the reductive axiom specifies how the semi-functor acts on all morphisms in , condition 4 in Theorem 4 only specifies how it acts on morphisms from the initial object. This gives not just a simple mathematical criterion, but one with a simple intuitive interpretation as well. Namely, condition 4 says that if a process begins with no prior information, then there is no information to be lost in the process.
We now use Theorem 4 and Bayesian inversion to prove a statement dual to Theorem 4.
Theorem 5. Suppose is a function satisfying the following conditions.
- 1.
F is semi-functorial.
- 2.
F is convex linear.
- 3.
F is continuous.
- 4.
for every probability distribution .
Then F is a non-negative multiple of conditional entropy. Conversely, conditional entropy satisfies conditions 1–4.
Before giving a proof, we introduce some terminology and prove a few lemmas. We also would like to point out that condition 4 may be given an operational interpretation as follows: if a communication channel has a constant output, then it has no conditional entropy.
Definition 26. Let be a function and let be a Bayesian inversion functor. Then will be referred to as aBayesian reflectionof F.
Remark 9. By Proposition 11, if is a convex linear semi-functor, then a Bayesian reflection is independent of the choice of a Bayesian inversion functor, and as such, is necessarily unique.
Lemma 8. Let be a morphism in , suppose is a convex linear semi-functor, and let be a Bayesian inverse of f. Then .
Proof of Lemma 8. Let be a Bayesian inversion functor, so that . Then where the last equality follows from Proposition 11. □
Lemma 9. Let be a Bayesian inversion functor and let be a sequence of morphisms in converging to . Then .
Proof of Lemma 9. Set
. For all
with
, we have
Lemma 10. Suppose is a function satisfying conditions 1–4 of Theorem 5. Then the Bayesian reflection is a non-negative multiple of conditional information loss.
Proof of Lemma 10. We show satisfies conditions 1–4 of Theorem 4. Throughout the proof, let denote a Bayesian inversion functor, so that .
Semi-functoriality: Suppose
is an a.e. coalescable pair of composable morphisms in
. Then
Thus, is semi-functorial.
Convex Linearity: Given any probability space
and a family of morphisms
in
indexed by
X,
Thus, is convex linear.
Continuity: This follows from Lemma 9 and Proposition 11.
for every probability distribution : This follows from Lemma 8, since is the unique Bayesian inverse of . □
Proof of Theorem 5. Suppose is a function satisfying conditions 1–4 of Theorem 5, and let be a Bayesian inversion functor. Since F is semi-functorial and convex linear it follows from Proposition 11 that , and by Lemma 10 it follows that for some non-negative constant . We then have . Thus, F is a non-negative multiple of conditional entropy. □
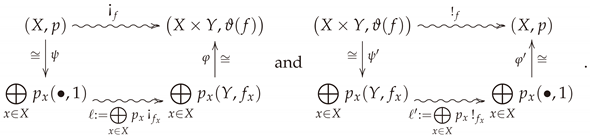
 : X → I and ΔX ≡
: X → I and ΔX ≡  : X → X X, all satisfying the following conditions
: X → X X, all satisfying the following conditions
 in the sense that
in the sense that  . Astateon X is a morphism , which is drawn as
. Astateon X is a morphism , which is drawn as  .
.