Dynamic Time Warping Algorithm in Modeling Systemic Risk in the European Insurance Sector
Abstract
:1. Introduction
2. Data and Methodology
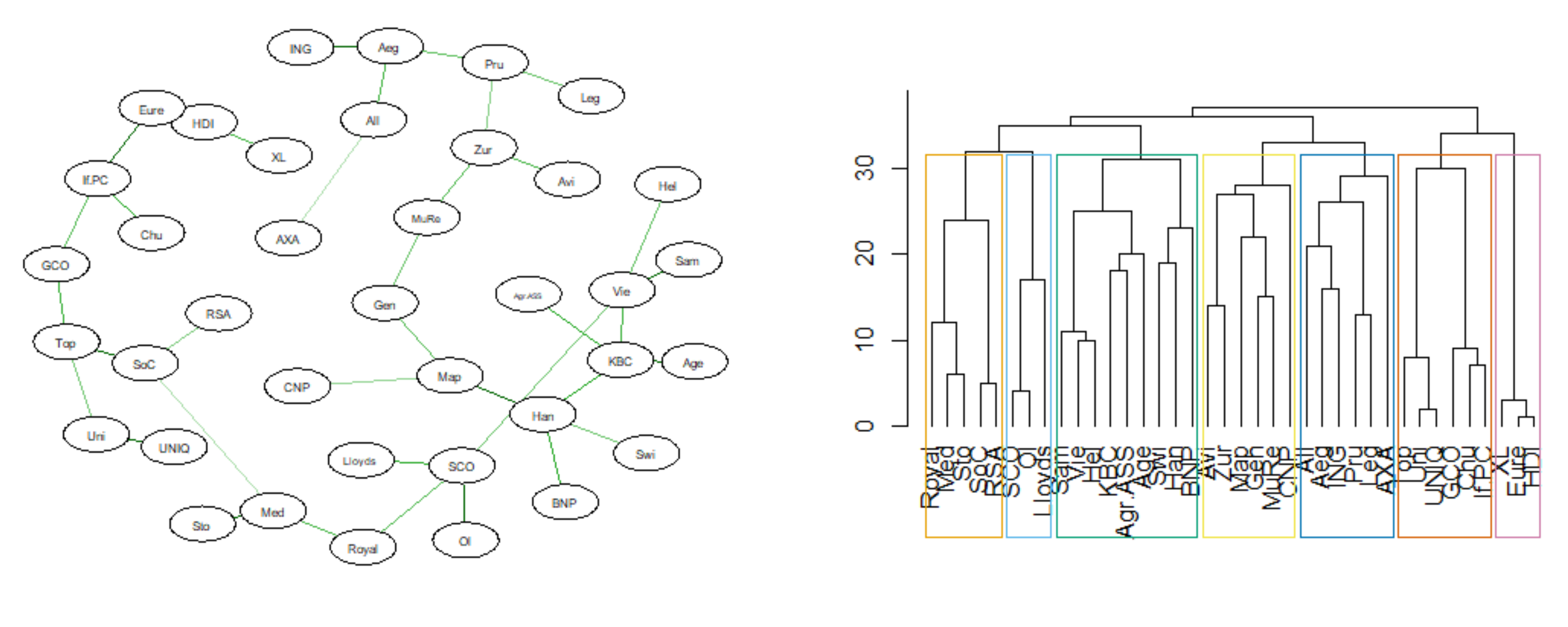
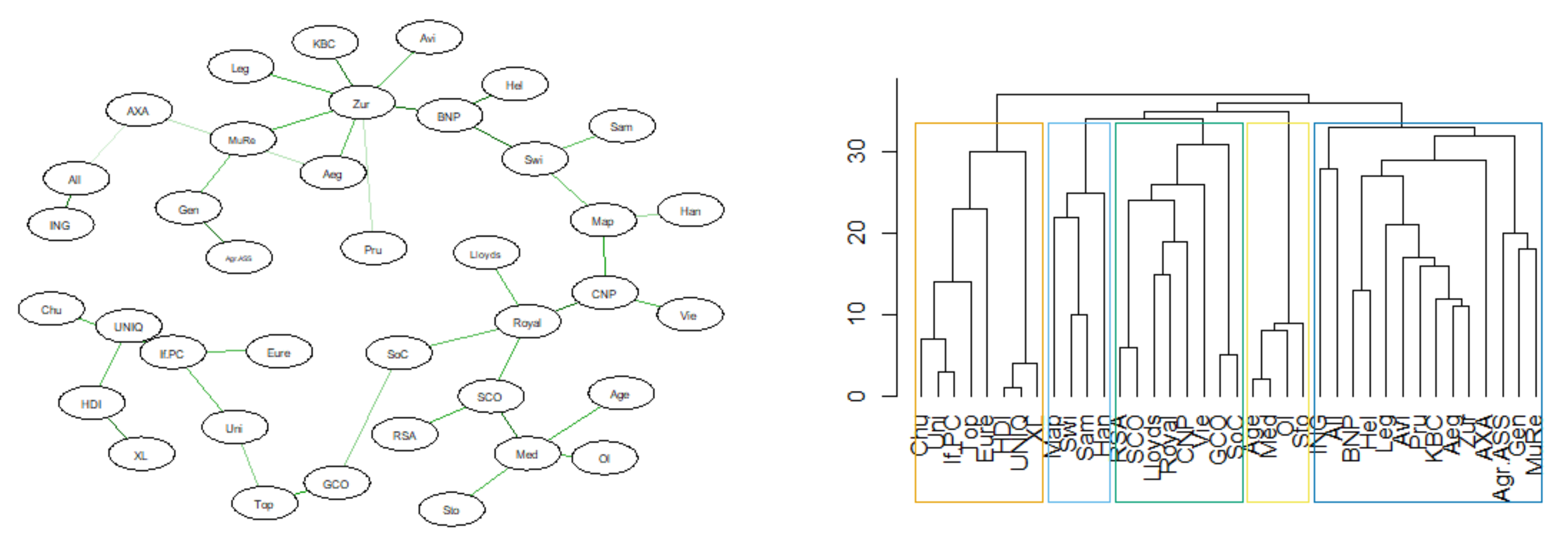
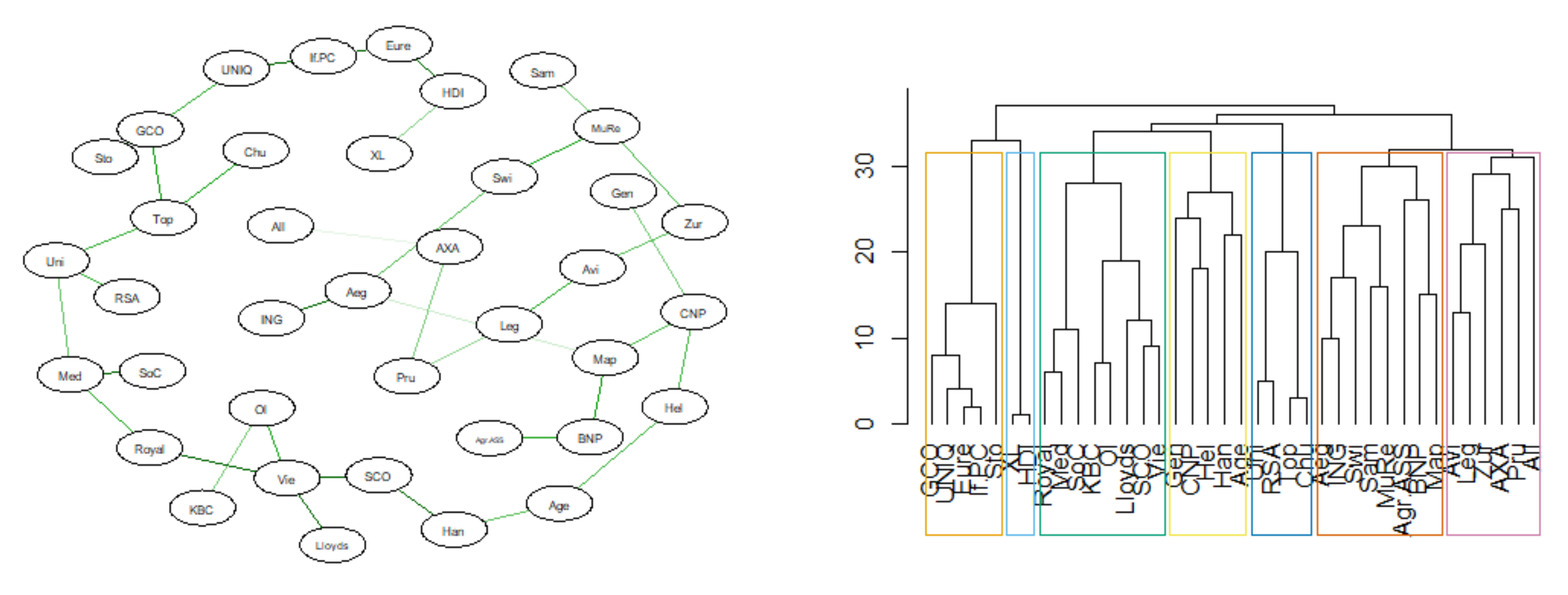
2.1. MST Construction Based on the Tail Dependencies of the Log-Returns
2.2. MST Topological Indicators
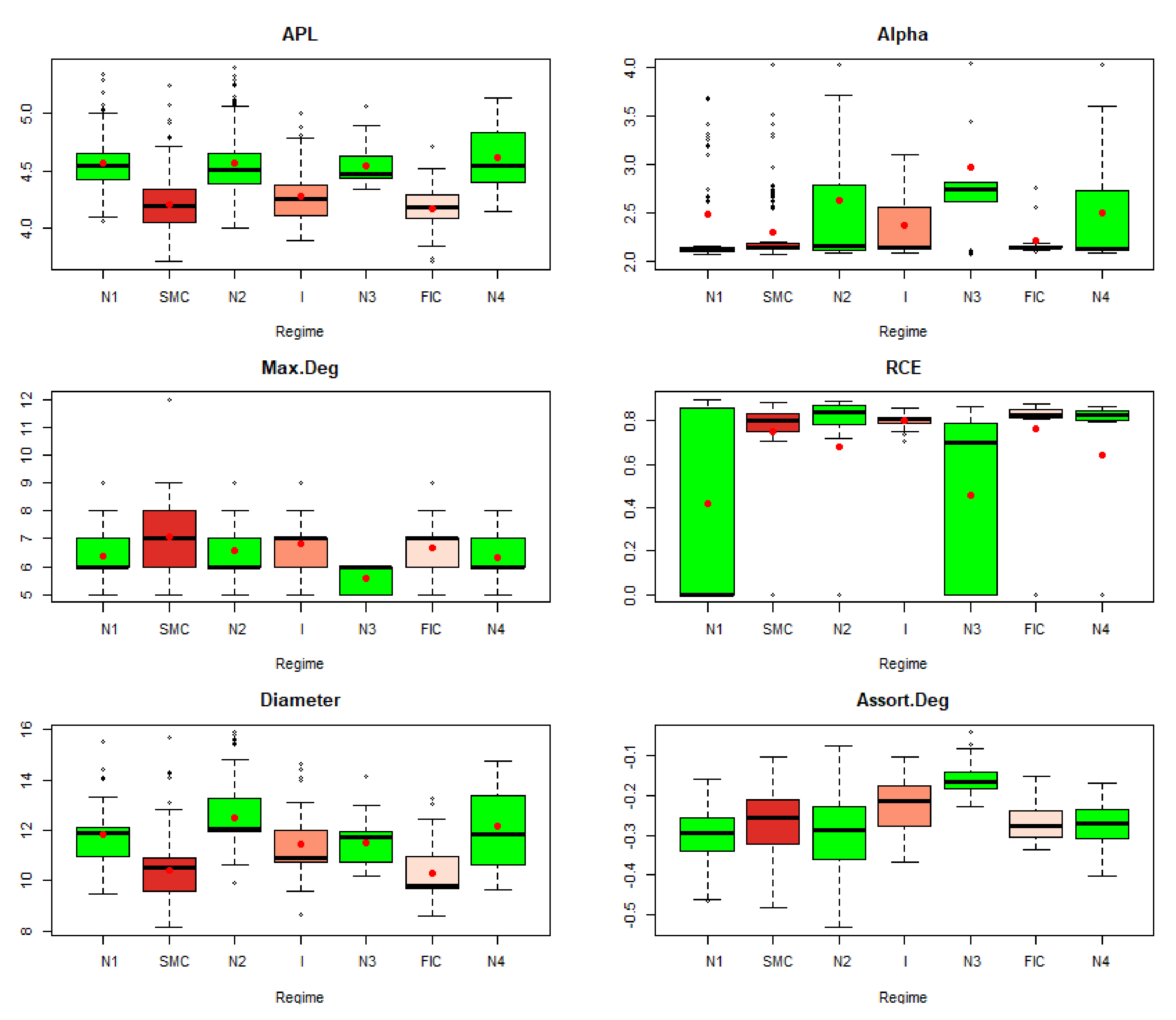
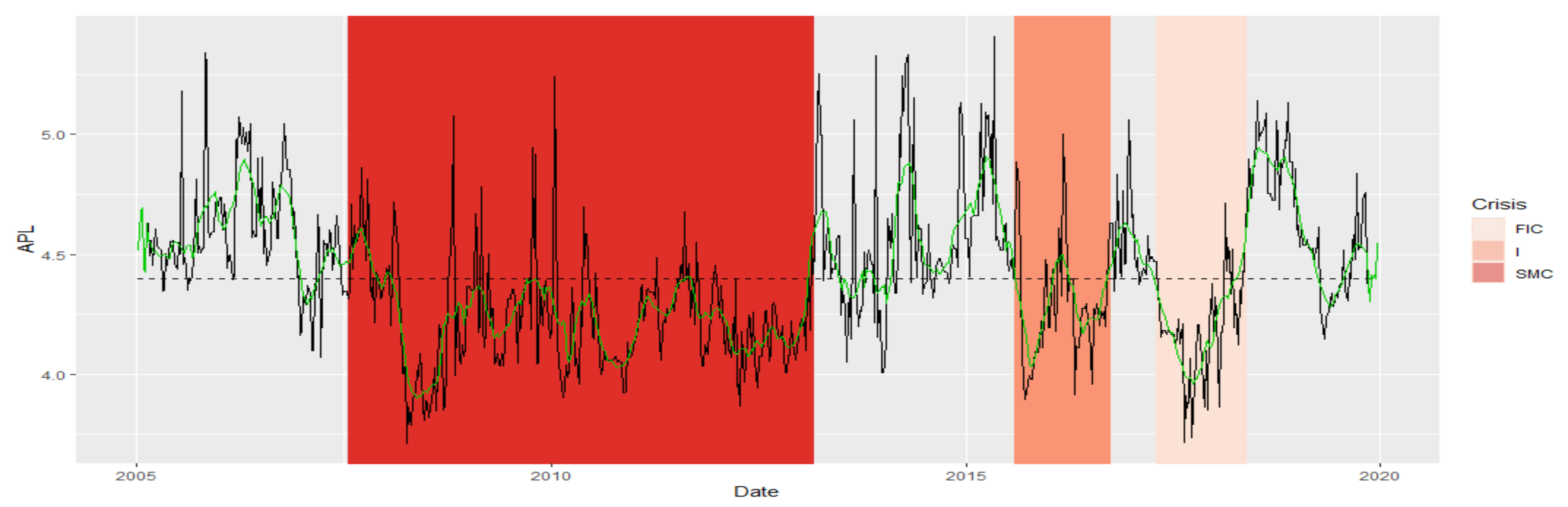
- Average Path Length (APL) [25]. For MST, it is an indicator that tells you the average number of steps between all possible pairs of vertices in the network. As it is an average number of steps, the network may well have several vertices separated by a large number of steps and many others lying close to each other, i.e., needing few steps. This indicator is a measure of the effectiveness of the information flow. It is seen in the literature as one of the strongest measures of MST structure. It distinguishes between easy-to-transition networks and those that are complex and inefficient. The structure of the network of interconnections between financial institutions is important for systemic risk. This indicator tells you whether the MST data have a structure that will be vulnerable to infection with adverse effects of negative financial events. Or, on the contrary, as a network of difficult and distant connections, it will slow down the flow of information.
- Network Diameter (Diameter) [23]. This is an MST indicator obtained as the length of the longest geodesic path between any two nodes. This distance is determined as the sum of the weights assigned to the edges connecting the vertices. If the Diameter shrinks, it means the distance between the vertices lying most apart is decreasing. This network structure favors the transfer of information.
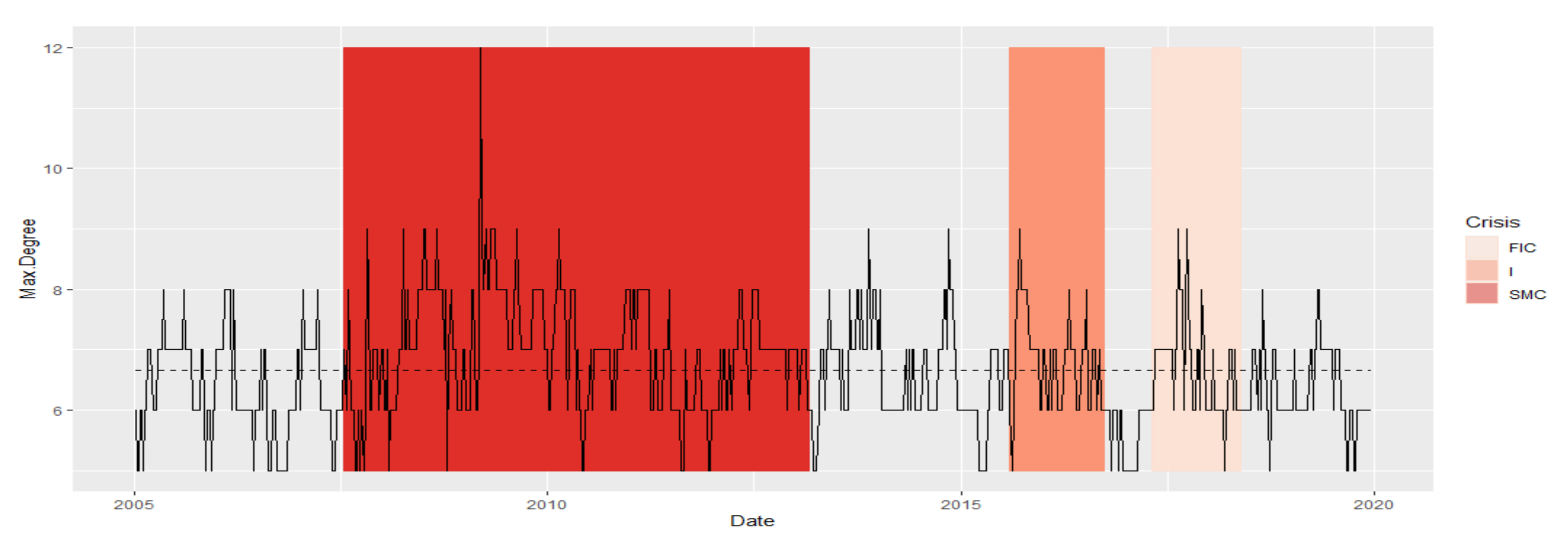
- Maximum Degree (Max.Degree) [25]. The degree of an MST vertex is the number of its connections to adjacent vertices. After determining the vertex that has the greatest number of such connections, this number is assigned to MST as the Maximum Degree. Any dynamic change of the Maximum Degree alters the structure of the network. The increase in Maximum Degree means that there is a vertex in the network that has numerous connections to other vertices. For systemic risk, the MST structure with a high Max.Degree offers the possibility of rapid shock contagion.
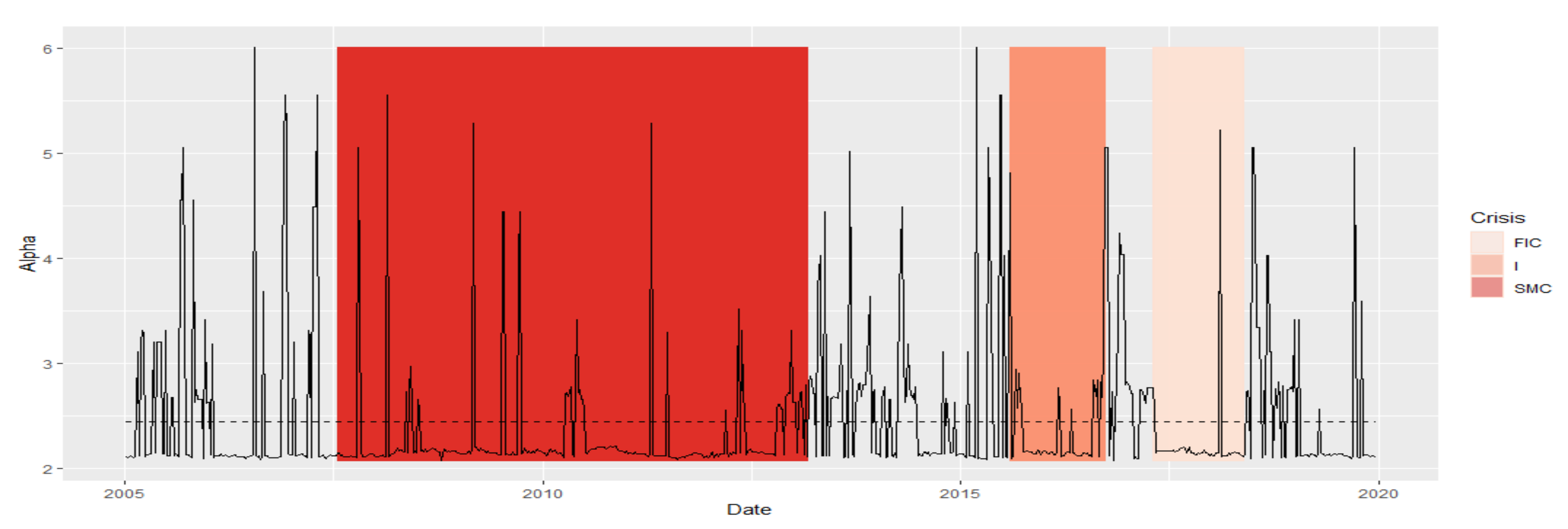
- Parameter “alpha” of the power law of the degree distribution [25]. This is a parameter of a power distribution of vertex degrees. For each MST, it can be checked whether the vertex distribution is consistent with the power distribution and has the form P (s) = C ∙ s ^ (−α), α > 0, for α, which is a parameter related to a given MST. If the α parameter belongs to the range (2,3), it means that the network structure is scale-free and has self-similarities, i.e., a repeating structure. When analyzing SR, such MSTs with hub nodes can promote the spread of negative financial information. Hub vertices, i.e., institutions that have numerous connections, are potentially systemically important institutions. If such an institution is threatened, the consequences of this situation could be felt by many related financial institutions.
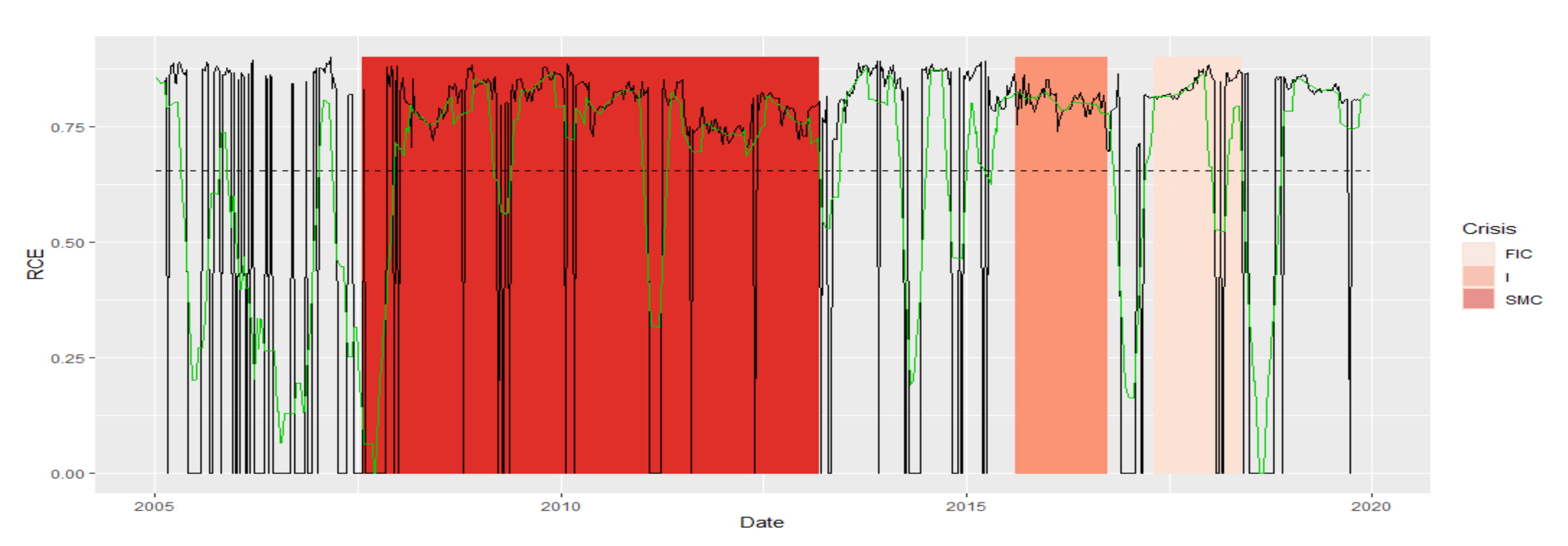
- Rich Club Effect (RCE) [22,23] specifies how the vertices are connected. The RCE for a fixed vertex degree k tells you how many times the vertices of degree k are connected to those of degree k or higher. RCE determines the stability of the network. The higher the RCE, the easier the information is conveyed. The structure of the MST is more compact for higher RCE, which potentially enables contagion and transferability of the negative effects of shocks in the financial market.
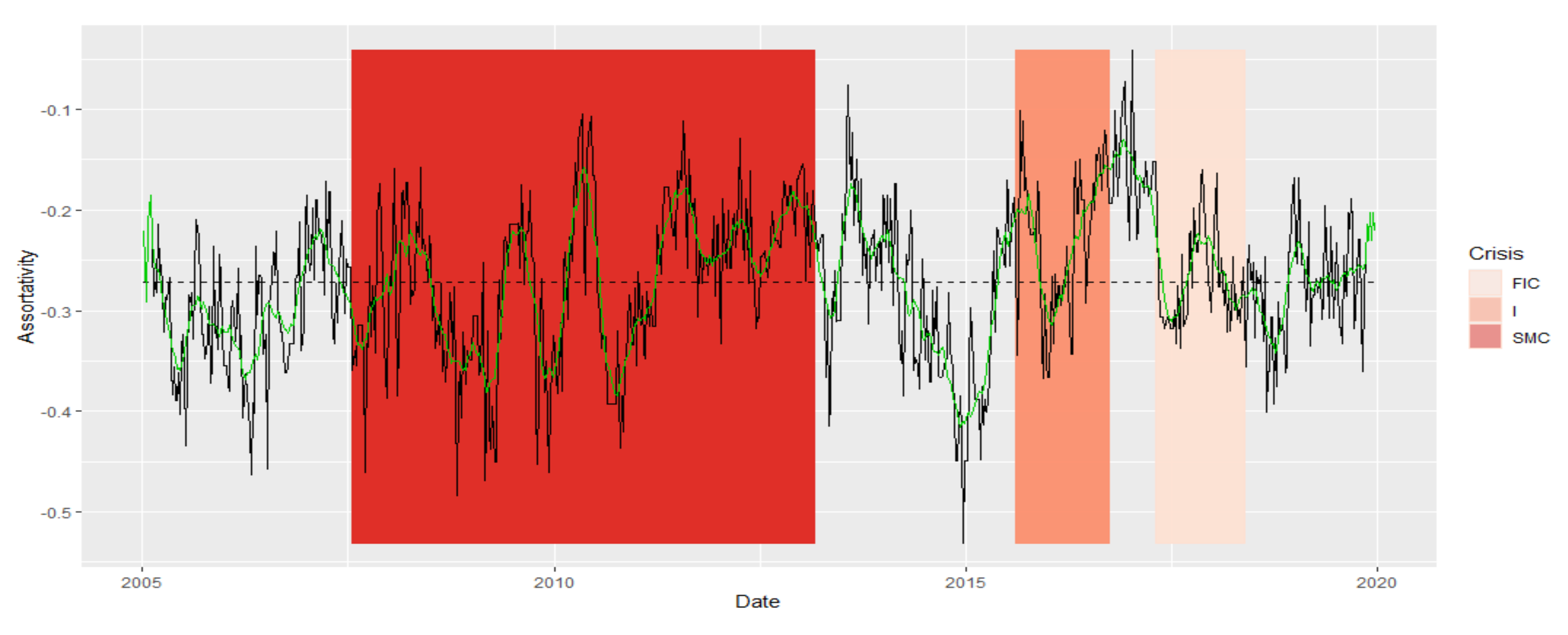
- Assortativity [24] evaluates the entire MST structure, how vertices in the network are generally linked one to another: whether the high-degree vertices connect with those that also have a high degree, or with low-degree ones. Assortativity, expressed with scalar ρ, takes values in the range (−1,1). Negative assortativity means that high-degree vertices merge into low-degree vertices. Positive assortativity means that high-degree vertices converge into high-degree vertices. Assortativity informs about the structure of the network and its dynamic behavior, as well as resistance to the random spread of the crisis.
2.3. Market Regimes under Study
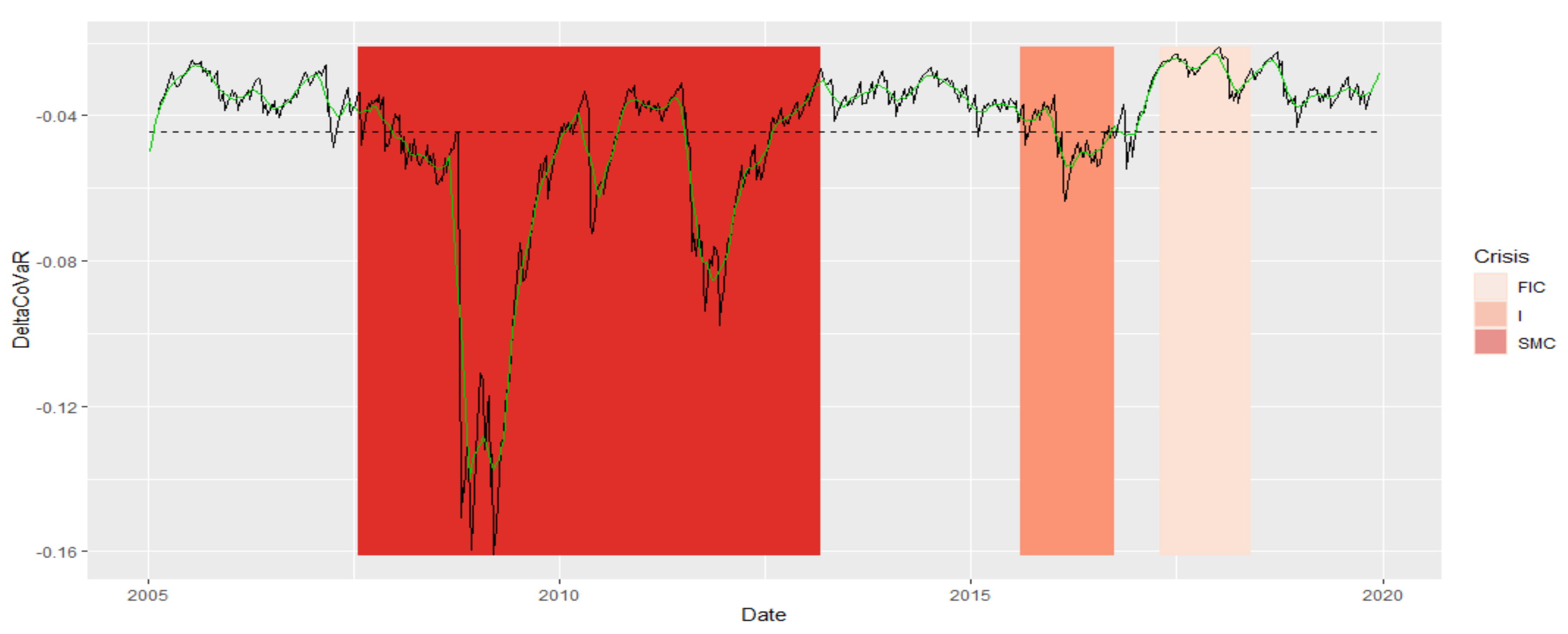
- Subprime Mortgage Crisis (SMC): the period of two subprime crises and excessive public debt, which began in 2008 and lasted until around 2013. This period in our time series stretches exactly between 8 February 2008 and 1 March 2013
- Immigrant (I): the period of crisis associated with the beginning of the migration crisis in Europe in 2015/2016. This period on our time series stretches exactly from 7 August 2015 to 23 September 2016
- France and Italy Crisis (FIC): crisis in the countries of the European Union related to the crisis in France associated with strikes, and in Italy due to the ever-growing public debt (which is now seven times higher than the debt in Greece), falling at the turn of 2017 and 2018. In our case, it is exactly the period from 21 April 2017 to 11 May 2018
- Normal (N), which is set in the remaining time intervals. It consists of four periods: (7 January 2005–1 February 2008), (8 March 2013–31 July 2015), (30 September 2016–14 April 2017), and (18 May 2018–20 December 2019).
2.4. Dynamic Time Warping Algorithm
- Boundary condition:
- Monotonicity condition:
- Step size condition: .
2.5. DeltaCoVaR Measure
3. Empirical Results and Discussion
3.1. MST’s Topological Indicators in the Determined Market Regimes
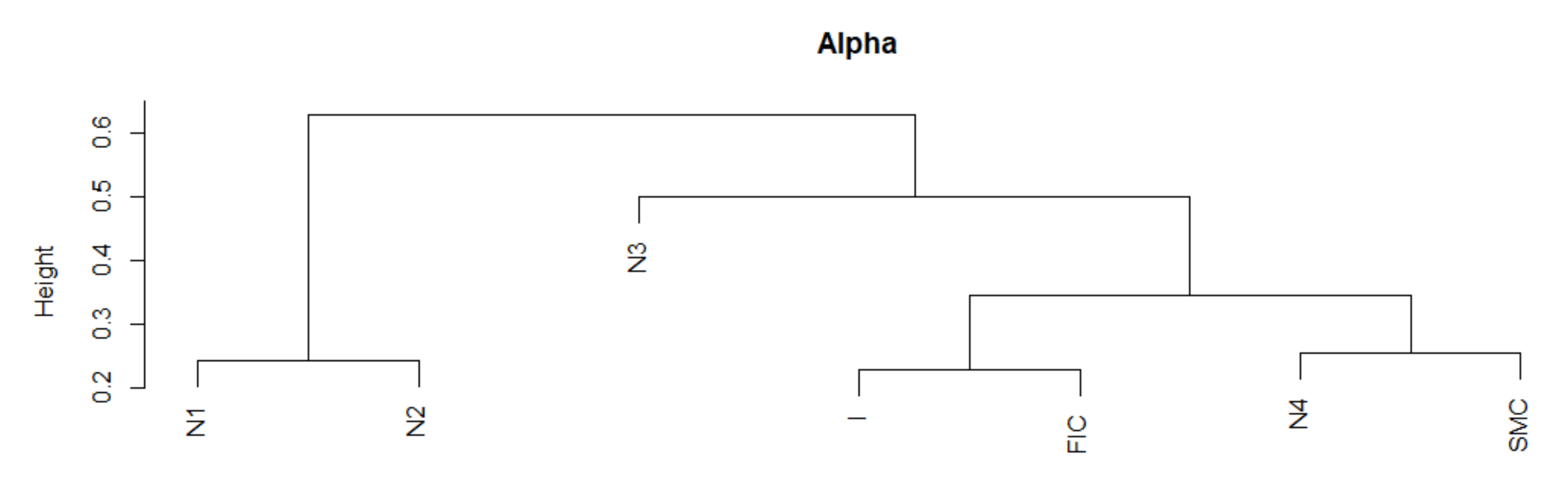
3.2. Analysis of the Similarity of Time Series of Topological Indicators Using the DTW Algorithm
3.3. Analysis of the Mean DeltaCoVaR Time Series
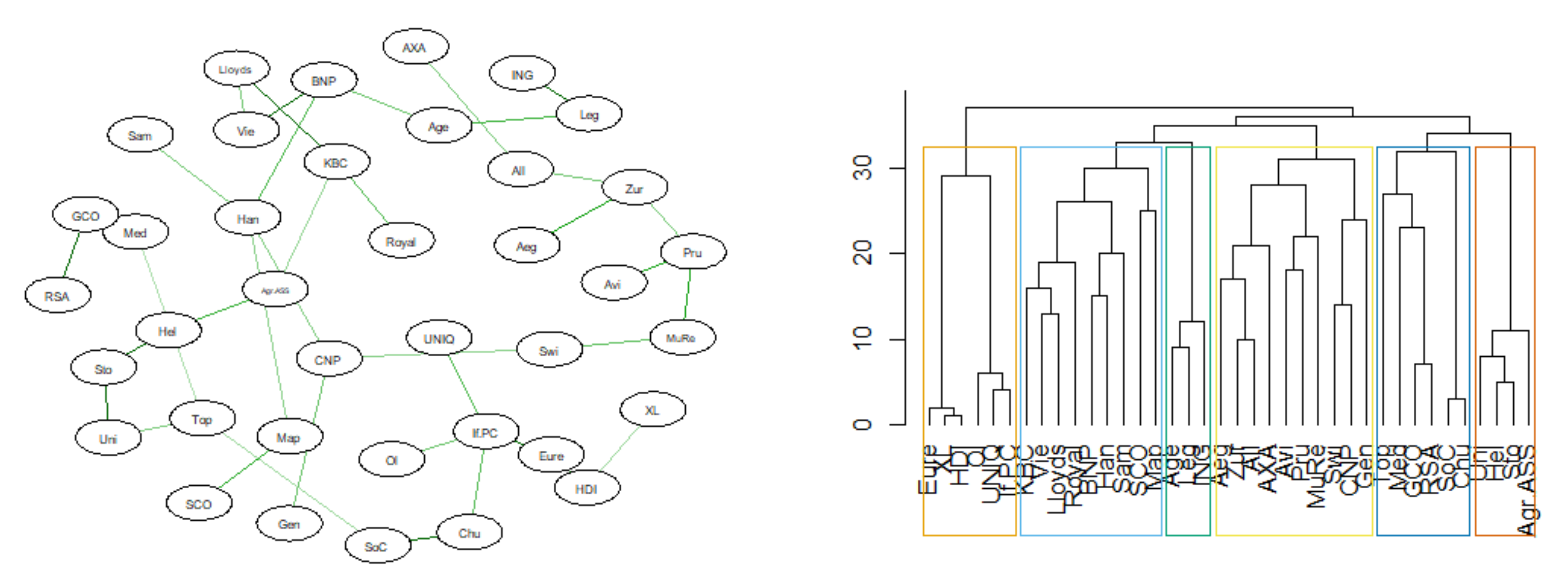
3.4. MST Based on DTW
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- EIOPA. Systemic Risk and Macroprudential Policy in Insurance; Publications Office of the EU: Luxembourg, 2019. [Google Scholar]
- Denkowska, A.; Wanat, S. A Tail Dependence-Based MST and Their Topological Indicators in Modeling Systemic Risk in the European Insurance Sector. Risks 2020, 8, 39. [Google Scholar] [CrossRef]
- Denkowska, A.; Wanat, S. A dynamic MST-deltaCoVaR model of systemic risk in the European insurance sector. Stat. Transit. New Ser. 2021, 22, 173–188. [Google Scholar] [CrossRef]
- Adrian, T.; Brunnermeier, M.K. CoVaR. Am. Econ. Rev. 2016, 106, 1705–1741. [Google Scholar] [CrossRef]
- Bierth, C.; Irresberger, F.; Weiß, G.N. Systemic risk of insurers around the globe. J. Bank. Finance 2015, 55, 232–245. [Google Scholar] [CrossRef]
- Brownlees, C.; Engle, R.F. SRISK: A Conditional Capital Shortfall Measure of Systemic Risk. Rev. Financial Stud. 2017, 30, 48–79. [Google Scholar] [CrossRef]
- Giglio, S.; Kelly, B.; Pruitt, S. Systemic risk and the macroeconomy: An empirical evaluation. J. Financial Econ. 2016, 119, 457–471. [Google Scholar] [CrossRef]
- Kanno, M. The network structure and systemic risk in the global non-life insurance market. Insur. Math. Econ. 2016, 67, 38–53. [Google Scholar] [CrossRef]
- Kaserer, C.; Klein, C. Supplementary Material to Systemic Risk in Financial Markets: How Systemically Important Are Insurers? J. Risk Insur. 2019, 86, 729–759. [Google Scholar] [CrossRef]
- Koijen, R.S.J.; Yogo, M. Shadow Insurance. Econometrica 2016, 84, 1265–1287. [Google Scholar] [CrossRef] [Green Version]
- Fan, Y.; Härdle, W.K.; Wang, W.; Zhu, L. Single-Index-Based CoVaR with Very High-Dimensional Covariates. J. Bus. Econ. Stat. 2017, 36, 212–226. [Google Scholar] [CrossRef] [Green Version]
- Hautsch, N.; Schaumburg, J.; Schienle, M. Financial Network Systemic Risk Contributions. Rev. Finance 2015, 19, 685–738. [Google Scholar] [CrossRef] [Green Version]
- Härdle, W.K.; Wang, W.; Yu, L. TENET: Tail-Event driven NETwork risk. J. Econ. 2016, 192, 499–513. [Google Scholar] [CrossRef]
- Bellman, R.; Kalaba, R. On adaptive control processes. IRE Trans. Autom. Control. 1959, 4, 1–9. [Google Scholar] [CrossRef]
- Sakoe, H.; Chiba, S. Dynamic programming algorithm optimization for spoken word recognition. IEEE Trans. Acoust. Speech Signal Process. 1978, 26, 43–49. [Google Scholar] [CrossRef] [Green Version]
- Cédras, C.; Shah, M. Motion-based recognition a survey. Image Vis. Comput. 1995, 13, 129–155. [Google Scholar] [CrossRef]
- Geiger, D.; Gupta, A.; Costa, L.A.; Vlontzos, J. Dynamic programming for detecting, tracking, and matching deformable contours. IEEE Trans. Pattern Anal. Mach. Intell. 1995, 17, 294–302. [Google Scholar] [CrossRef]
- Petitjean, F.; Ketterlin, A.; Gancarski, P. A global averaging method for dynamic time warping, with applications to clustering. Pattern Recognit. 2011, 44, 678–693. [Google Scholar] [CrossRef]
- Franses, P.H.; Wiemann, T. Intertemporal Similarity of Economic Time Series: An Application of Dynamic Time Warping. Comput. Econ. 2020, 56, 59–75. [Google Scholar] [CrossRef]
- Raihan, T. Predicting US recessions: A dynamic time warping exercise in economics. 2017; Unpublished work. [Google Scholar]
- Wang, G.-J.; Xie, C.; Han, F.; Sun, B. Similarity measure and topology evolution of foreign exchange markets using dynamic time warping method: Evidence from minimal spanning tree. Phys. A: Stat. Mech. Appl. 2012, 391, 4136–4146. [Google Scholar] [CrossRef]
- Colizza, V.; Flammini, A.; Serrano, M.A.; Vespignani, A. Detecting rich-club ordering in complex networks. Nat. Phys. 2006, 2, 110–115. [Google Scholar] [CrossRef]
- Li, W.; Hommel, U.; Paterlini, S. Network topology and systemic risk: Evidence from the Euro Stoxx market. Financ. Res. Lett. 2018, 27, 105–112. [Google Scholar] [CrossRef]
- Newman, M.E.J. Assortative Mixing in Networks. Phys. Rev. Lett. 2002, 89, 208701. [Google Scholar] [CrossRef] [Green Version]
- Wang, G.-J.; Xie, C.; Zhang, P.; Han, F.; Chen, S. Dynamics of Foreign Exchange Networks: A Time-Varying Copula Approach. Discret. Dyn. Nat. Soc. 2014, 2014, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Clauset, A.; Newman, M.E.J.; Moore, C. Finding community structure in very large networks. Phys. Rev. E 2004, 70, 066111. [Google Scholar] [CrossRef] [Green Version]



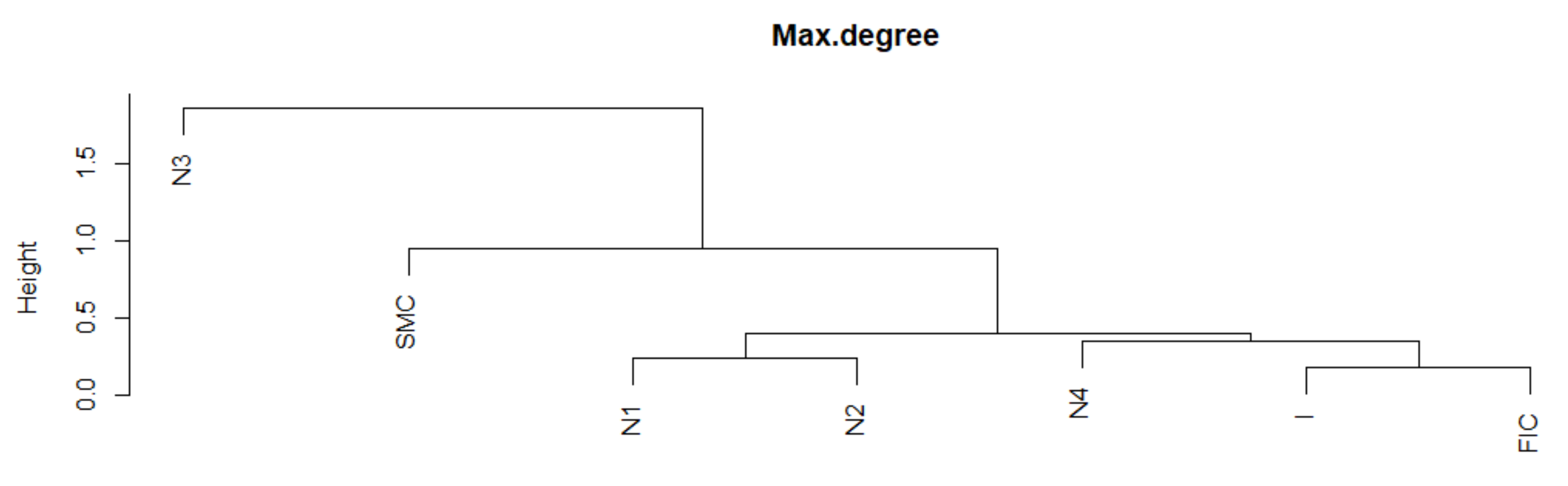




| APL | Diameter | Max.Deg | Alpha | RCE | Assortat. | Delta CoVaR | |
|---|---|---|---|---|---|---|---|
| N1-N2 | 0.1415 | 0.7691 | 0.2381 | 0.2429 | 0.2486 | 0.0356 | 0.0044 |
| N1-N3 | 0.1670 | 0.7311 | 1.2061 | 0.5678 | 0.3547 | 0.1221 | 0.0087 |
| N1-N4 | 0.1320 | 0.6459 | 0.3688 | 0.2839 | 0.3031 | 0.0353 | 0.0083 |
| N2-N3 | 0.1965 | 0.9689 | 1.2737 | 0.5480 | 0.1914 | 0.1199 | 0.0079 |
| N2-N4 | 0.1741 | 0.9364 | 0.3485 | 0.3119 | 0.0915 | 0.0402 | 0.0050 |
| N3-N4 | 0.1415 | 0.6348 | 1.1138 | 0.4948 | 0.1245 | 0.1129 | 0.0094 |
| N1-SMC | 0.2155 | 1.0845 | 0.6240 | 0.3328 | 0.3181 | 0.0348 | 0.0383 |
| N1-I | 0.1677 | 0.6190 | 0.3352 | 0.4661 | 0.4580 | 0.0538 | 0.0099 |
| N1-FIC | 0.2264 | 0.9463 | 0.3058 | 0.3995 | 0.3786 | 0.0444 | 0.0156 |
| N2-SMC | 0.2073 | 1.1236 | 0.6024 | 0.3600 | 0.0865 | 0.0396 | 0.0408 |
| N2-I | 0.1914 | 0.9087 | 0.2573 | 0.4595 | 0.3183 | 0.0544 | 0.0110 |
| N2-FIC | 0.2264 | 1.0082 | 0.2576 | 0.4092 | 0.1642 | 0.0510 | 0.0127 |
| N3-SMC | 0.2975 | 1.1755 | 1.5292 | 0.4380 | 0.1815 | 0.1118 | 0.0374 |
| N3-I | 0.2488 | 0.7529 | 1.2595 | 0.3047 | 0.2243 | 0.0893 | 0.0070 |
| N3-FIC | 0.2785 | 1.0607 | 1.2063 | 0.4293 | 0.0931 | 0.1024 | 0.0151 |
| N4-SMC | 0.2369 | 1.2986 | 0.8855 | 0.2541 | 0.0918 | 0.0374 | 0.0421 |
| N4-I | 0.1774 | 0.7061 | 0.3342 | 0.3600 | 0.2940 | 0.0456 | 0.0141 |
| N4-FIC | 0.2500 | 1.2132 | 0.2753 | 0.2658 | 0.1026 | 0.0340 | 0.0082 |
| SMC-I | 0.1520 | 0.9661 | 0.6336 | 0.2805 | 0.2996 | 0.0509 | 0.0338 |
| SMC-FIC | 0.1467 | 0.7658 | 0.6972 | 0.2686 | 0.1291 | 0.0478 | 0.0436 |
| I-FIC | 0.1391 | 0.8355 | 0.1803 | 0.2293 | 0.2182 | 0.0487 | 0.0195 |
| N | SMC | I | FIC | |
|---|---|---|---|---|
| APL | 7.1778 | 6.5021 | 8.6714 | 8.4211 |
| max.deg | 4.0000 | 7.0000 | 4.0000 | 4.0000 |
| alpha | 2.0284 | 3.6861 | 3.8064 | 3.8528 |
| RCE (k=2) | 0.4267 | 0.4410 | 0.2982 | 0.1428 |
| RCE (k=3) | 0.3410 | 0.0000 | 0.0000 | 0.0000 |
| diameter | 0.0124 | 0.0188 | 0.0178 | 0.0119 |
| assortativity | −0.3413 | −0.4137 | −0.2877 | −0.2982 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Denkowska, A.; Wanat, S. Dynamic Time Warping Algorithm in Modeling Systemic Risk in the European Insurance Sector. Entropy 2021, 23, 1022. https://doi.org/10.3390/e23081022
Denkowska A, Wanat S. Dynamic Time Warping Algorithm in Modeling Systemic Risk in the European Insurance Sector. Entropy. 2021; 23(8):1022. https://doi.org/10.3390/e23081022
Chicago/Turabian StyleDenkowska, Anna, and Stanisław Wanat. 2021. "Dynamic Time Warping Algorithm in Modeling Systemic Risk in the European Insurance Sector" Entropy 23, no. 8: 1022. https://doi.org/10.3390/e23081022
APA StyleDenkowska, A., & Wanat, S. (2021). Dynamic Time Warping Algorithm in Modeling Systemic Risk in the European Insurance Sector. Entropy, 23(8), 1022. https://doi.org/10.3390/e23081022






