1. Introduction
The idea of using simple, discrete, and finite models to understand complex phenomena is a fundamental part of statistical physics. In particular, this guiding idea has achieved particular success in the study of continuous phase transitions. For an infinite system, in the critical regime, the correlation length diverges, and the system becomes scale-invariant. The critical phenomena can then be described employing field theory in the long-wavelength limit, and their physical properties are governed by universal critical exponents [
1,
2,
3,
4,
5]. Two famous examples are continuous Landau Ginzburg-type phase transitions [
6,
7,
8,
9,
10], which are driven by topological defects (vortices). A simple model that exhibits many of these fascinating features is the so-called
q-state clock model, which is a discretized XY [
11,
12,
13] spin model defined on the square lattice. We recently solved this model exactly for a very small system [
14] and also on larger lattices up to square lattices 128 × 128 by Monte Carlo simulations, showing clearly the two-phase transitions and using two information theory approaches (mutability and diversity) and calculated in thermal equilibrium on the thermodynamic energy and magnetization variables as functions of temperature.
Moreover, the
q-state clock model is one of many magnetic models to mimic the thermodynamics of some materials, and it can be viewed as a classical Heisenberg spins model with very strong planar anisotropy or the already mentioned discrete XY model. In its simplest form it consists of a system of N spins,
at site
i, on a lattice where the spins can have
q equivalent possible orientations or
“stations” in two dimensions (2D), which can be written as
, where
. These spins are interacting with their nearest neighbors through an exchange energy
J, so the Hamiltonian of this system can be written as follows.
where the sum runs over all pairs of nearest neighbors
. If
the system is ferromagnetic since the fundamental state is that all spins are aligned. The case
corresponds to the well-known Ising model which will not be of much attention in the present paper.
A simulation in the canonical ensemble can be implemented to study properties as functions of temperature. One example is the magnetization that presents ferromagnetic ordering at low temperatures and paramagnetic disorder at very high temperatures. However, an intermediate phase arises for
, giving rise to two-phase transitions [
15,
16,
17,
18,
19,
20,
21]. The new ordering corresponds to the so-called Berezinskii-Kosterlitz-Thouless (BKT) phase where vortexes dominate ( BKT) [
22,
23]. Thus, the low critical temperature corresponds to the transition between a ferromagnetic phase (FP) to BKT, while the second transition at a higher critical temperature corresponds to the transition between the BKT phase to the usual disordered paramagnetic phase (PP). At values of
, this system only exhibits a single transition from an FP to a paramagnetic phase (PP). In this context, we highlight a particular work where through Monte Carlo simulations with nonconserved Glauber’s dynamics, the existence of two different transition temperatures for a finite
q-state clock model with
is confirmed [
24]. In that work, the transition temperatures are quantified using two different cumulants (the first transition temperature uses the Binder cumulant [
25,
26], while the second is characterized using a new cumulant defined by the authors).
The descent of the critical temperature for the FP to BKT phase transition is simple to understand: as
q grows, less energy is needed to change the next spin to the next possible station. If two adjacent spins differ in orientation in
the extra energy per pair of spins is only
which decreases as
. So as
q increases, the transition temperature FP to BKT decreases. The BKT phase at
is characterized by wave-like spin excitations and vortexes since their energies are very close to that of the ground state. Therefore when
the FP to BKT transition temperature
. The characterization of the different phases can be achieved by calculating the specific heat, or the 2D order parameter, which is the spin thermal average in the
X and
Y directions [
14,
27]. One of the main purposes of this work is to show that both phase transitions can also be characterized by appropriate short-range order parameters defined below, using simple spin correlations up to second and third nearest neighbors.
In the present paper, we want to get deeper into the vorticity reached by the BKT phase by two different means: On the one hand, we fully invoke diversity as the most sensitive tool provided by information theory to achieve this goal (mutability and Shannon entropy agree with these results but produce less sharp transition curves). On the other hand, we will define new and more appropriate parameters to recognize the way vortexes appear and disappear, establishing the way their presence marks both transitions.
This article is organized in the following way: Next Section describes the system.
Section 3 covers the methodology from different points of view, including the definition of the new short-range order parameters.
Section 4 is devoted to the presentation of the new results and their discussion.
Section 5 includes the main conclusions of this paper.
2. System
Let us consider a square lattice
with one magnetic unit or spin at each site
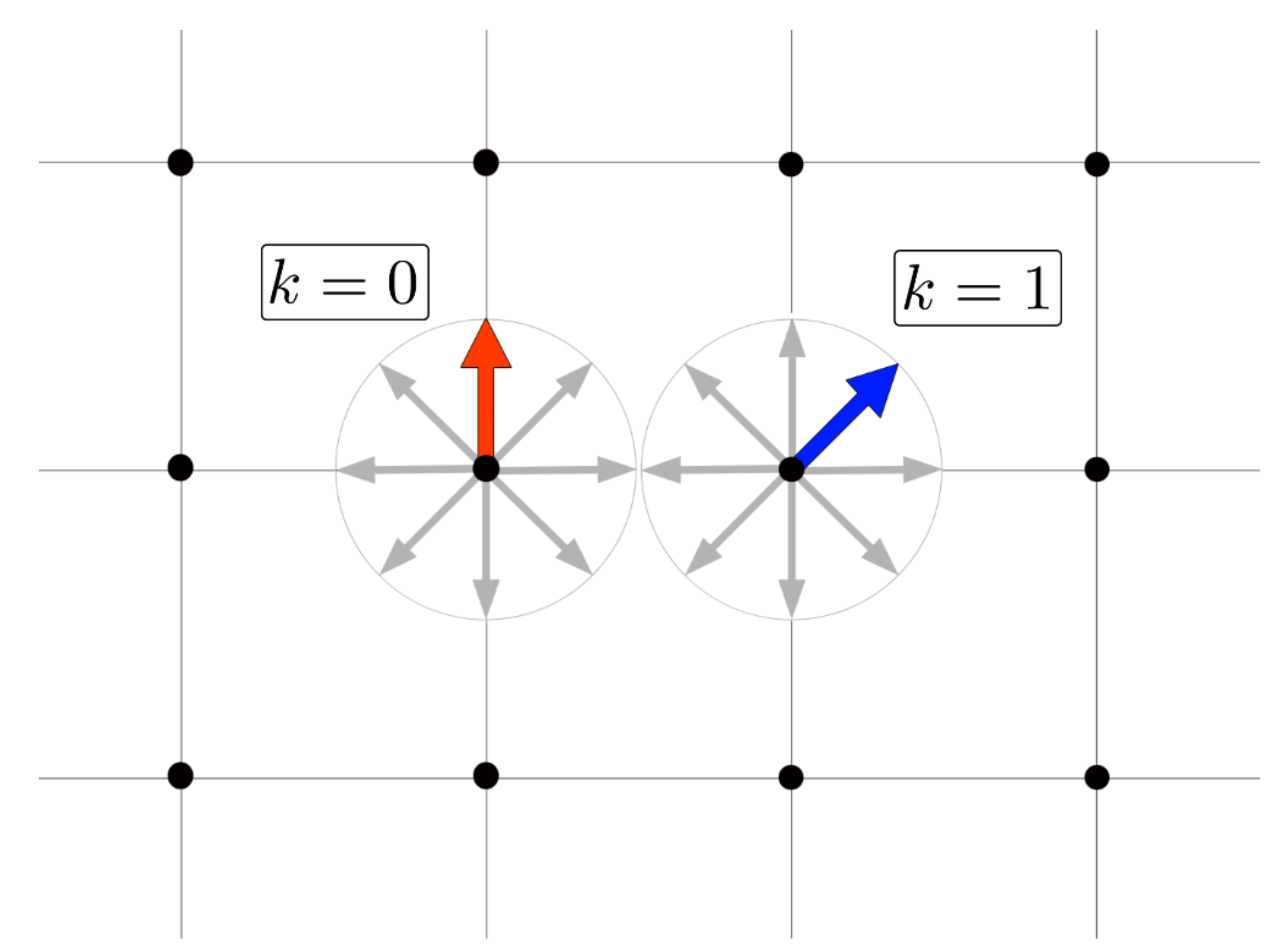
i. These spins lay on the plane of the lattice and have
q fixed possible orientations or stations at angles
with
(see
Figure 1).
The Hamiltonian defining this interaction is given by Equation (
1) where we express energy in units of
J (
unit of energy); temperature can also be expressed in the same scale (Boltzmann constant is dimensionless and equal the unity).
The lattice average of the spin configuration, equivalent to the magnetization per site
m, is given by the following expression:
where
with
is the value of the spin at site
j at a given time
t, and
is the total number of spins. In this particular case,
is a vector of two components,
The normalized absolute magnetization is defined by the following relation.
where
is the number of configurations used to perform thermal averages for state properties.
This form of looking at the magnetization will recognize long-range magnetic correlations that include the BKT phase. However, if we want to detect the ergodicity breaking associated with the short-range ordering, we have to look at the magnetization along the natural q directions of the system. Let us define as the normalized magnetization along the k-th direction only, namely, it presents the fraction of spins pointing along the k-th direction. If we start from a very low temperature, then the phase will be ferromagnetic along just one of these directions, say, while the magnetization along the oher directions vanish. Namely, in the limit , for , while otherwise. We say, is the dominant direction.
As T first increases, some spins deviate from the direction, and slightly weakens in favor of other directions. As T continues to increase, the dominant direction may shift to another different from , and the spontaneous magnetization direction of the system will be different. Thus, for instance, if the system was floating in the presence of an external weak magnetic field, it will now realign its direction according to its new magnetization axis. Let us define the dominant magnetization axis D at a given temperature T as the one that presents the highest fraction of spins pointing along the direction defined by this axis. Namely, among all the q directions at the time of observation, represents the largest number of spins pointing in the direction at a given temperature.
4. Results and Discussion
The internal energy of the system can be obtained from MC simulations, as depicted in the methodology presented above. Then, its temperature derivative leads us to the specific heat
, whose results for different
q values can be appreciated, for instance, Ref. [
14]. A clear maximum is observed in the
curves for
, changing to a maximum and a shoulder for
. A phase diagram presented in the same previous reference clarifies that this can be thought of as one phase transition originating in the loss of the FP to a PP for
and to a BKT phase for
; the critical temperature associated to this phase transition decreases monotonously towards zero as
. The second transition arises from the loss of the BKT into a PP, and its critical temperature is rather independent of
q at nearly 1.1. Such results are also confirmed by the changes in magnetization for the same MC simulations.
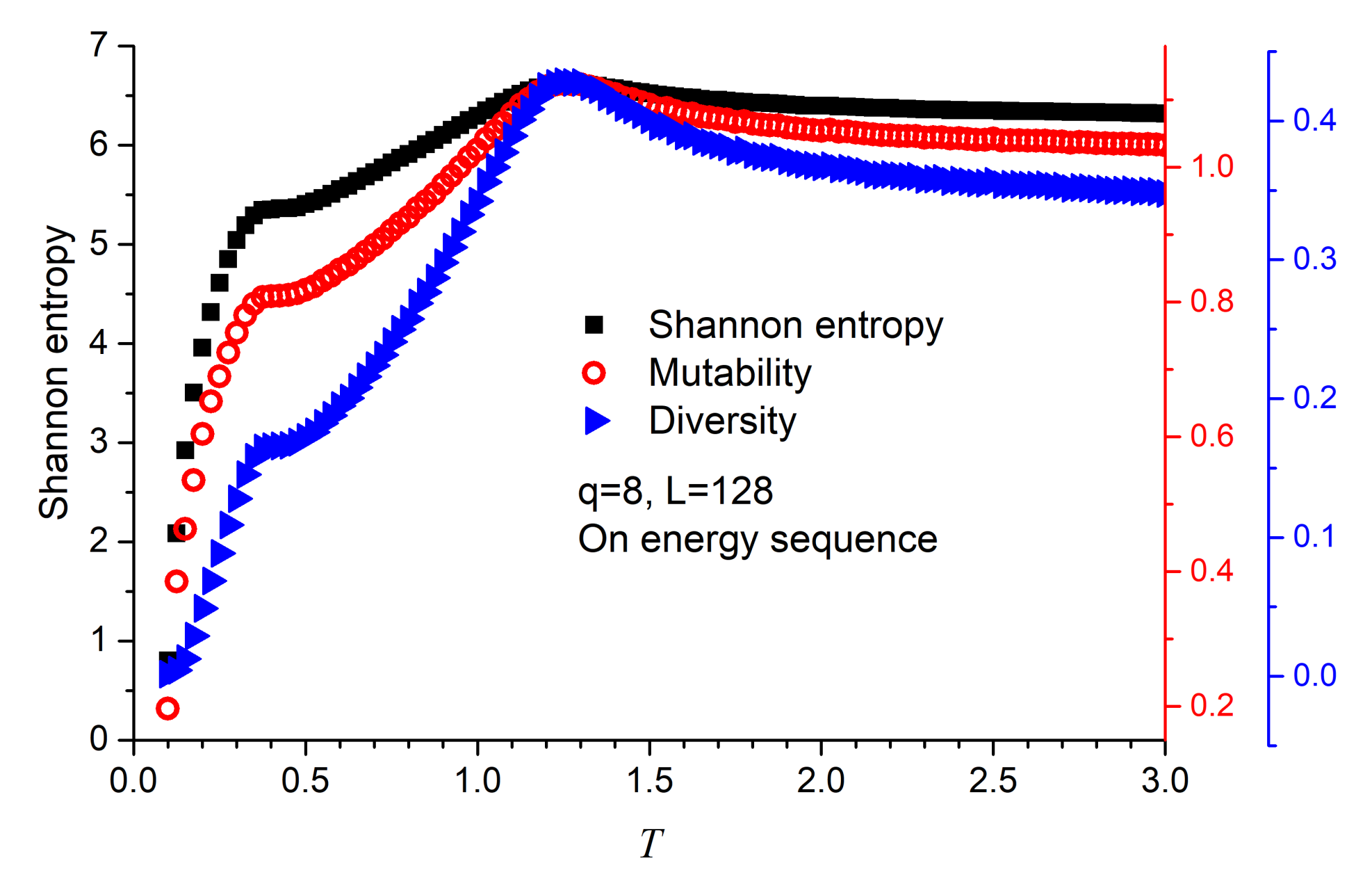
These previous results can also be obtained through information theory which is now complemented by including Shannon entropy as shown in
Figure 4 for
in a lattice with
(no significant differences are obtained for other
L values). It is not surprising that these three curves (as well as specific heat or magnetic susceptibility) maximize at nearly the same temperature. It is clear that any sequence of data representing an observable of a system will be altered near the critical temperatures. The recognition of this alteration can be obtained in different ways. In the present case, if a count of frequencies is obtained for the different values visited when measuring the magnetization we would obtain a distribution. Suppose a magnetization histogram is constructed with this information; then the normalized visits to any of these values will allow to sample the probability of visiting that value; this leads directly to the Shannon entropy according to Equation (
6); the span of the values visited will lead to the diversity (given by Equation (
4)); the relative size of the compressed file with respect to the original file containig the magnetization series will yield the mutability. It should be noticed that Shannon entropy and diversity pay no attention to time while mutability bears an indirect reference to time [
29,
34]: the sooner a value repeats itself in the series the lighter the compressed file results.
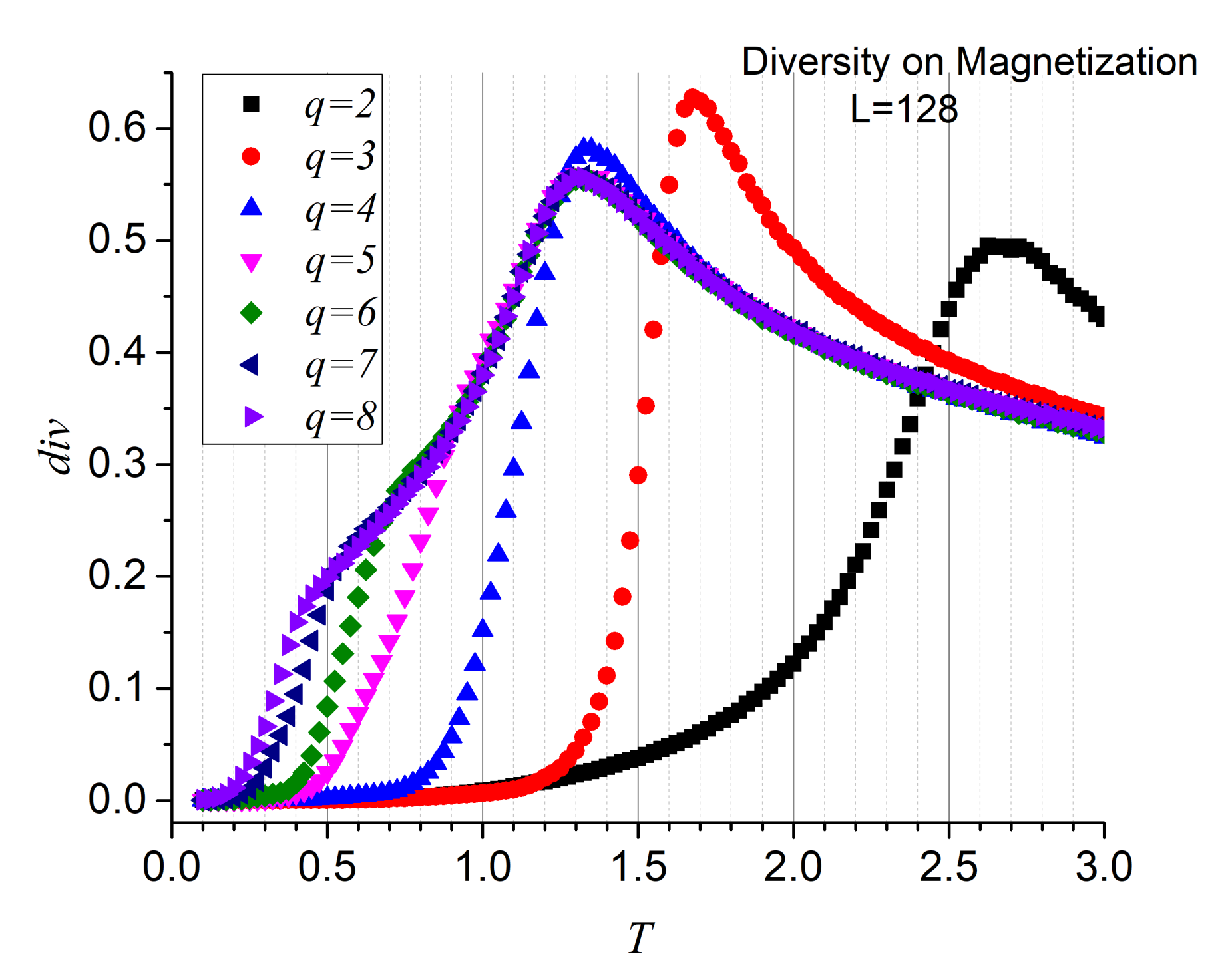
Although the three functions maximize at the precise temperatures, it is the diversity that reports the second maximum more sharply. For this reason, we stick to diversity only from now on.
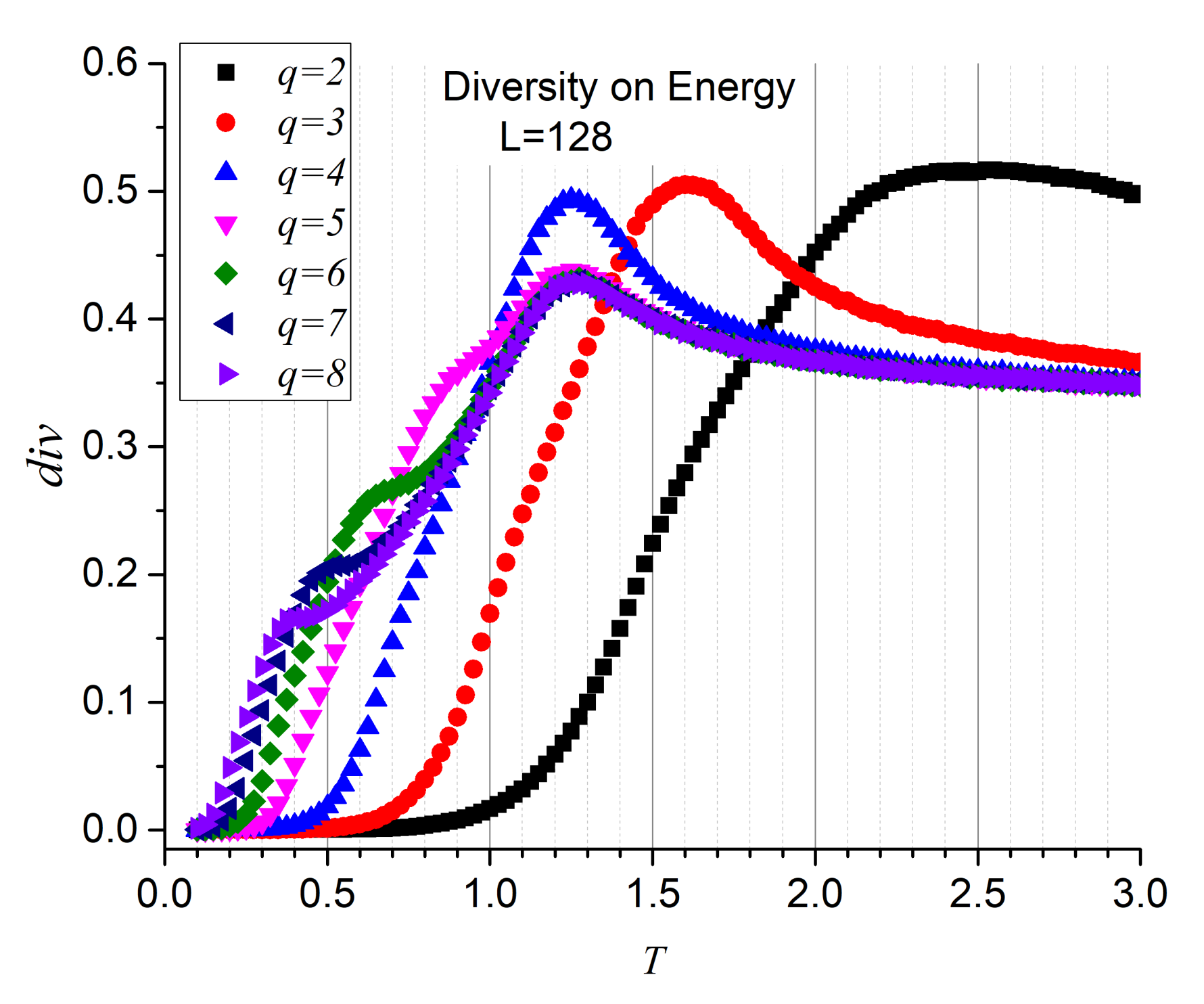
Figure 5 render the diversity results for the energy series for
, confirming both transitions and values of the critical temperatures. Additionally,
Figure 6 reports the diversity results for the magnetization series, confirming that the origin of these transitions is of magnetic nature. These are significant results since they fully incorporate information analysis as a tool for recognizing the FP- BKT-PP transitions.
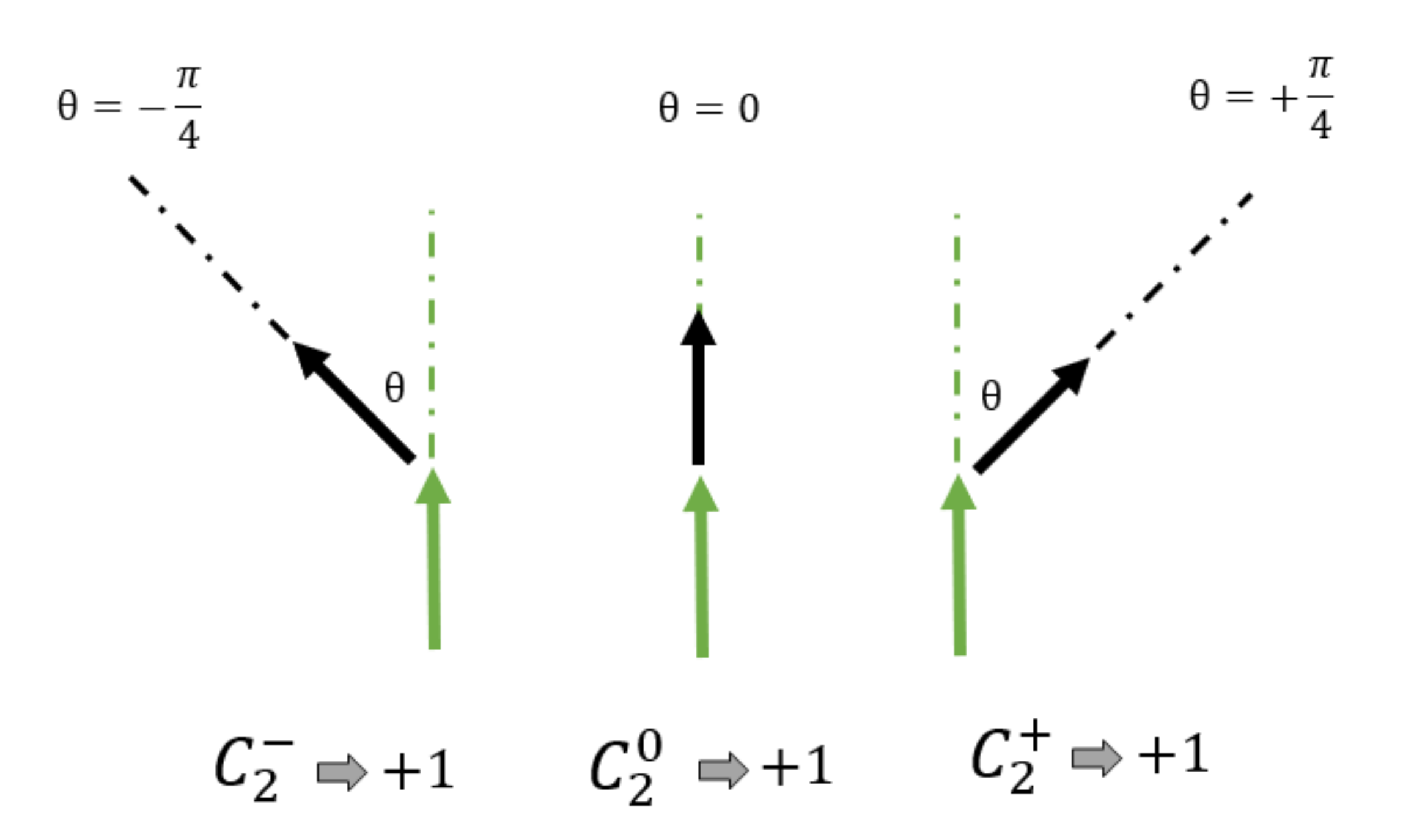
In spite of the recognition of the transition phases, there are no reports on the exact nature by which the BKT phase appears, evolves, and later disappears with temperature. It is only the fluctuations of energy and magnetization that reveals the change of state as a gross feature. We now turn our attention to the new parameters defined by Equation (
7) and
Figure 2 and
Figure 3 to better characterize the short-range order implied by the BKT phase. When applicable, we will prefer the case
to illustrate the vortex state since it is a system where the BKT phase is clearly present and the eight orientations for the clock model are rather intuitive at
angles between them.
Figure 7 presents the variations of
parameters as functions of temperature; a change in the curvature of the decaying magnetization in the form of a slight “swelling” can be appreciated. The lower curve with open symbols gives the average value
defined in Equation (
9) that presents a broad maximum at
(the same temperature at which
presents the commented swelling). The inset presents separate results for
and
showing that they give almost identical results (as they should since there is no anisotropy). The interpretation of these curves is direct: the system is initiated as ferromagnetic, so
and
are both zero; slightly over
some spins randomly get enough energy to orient their magnetization to the next station at either side (
or
) and parameters
and
begin to grow; the growth reaches maximum pace at around
, and the abundance of these parameters tends to maximize near
. From there on, energy is high enough, so excitations to larger angles are also possible, and the two-spin vortex parameters slowly decrease to their asymptotic limit for huge temperatures, which is typical for two-spin parameters at any angle, namely
(0.125 in the scale of
Figure 7).
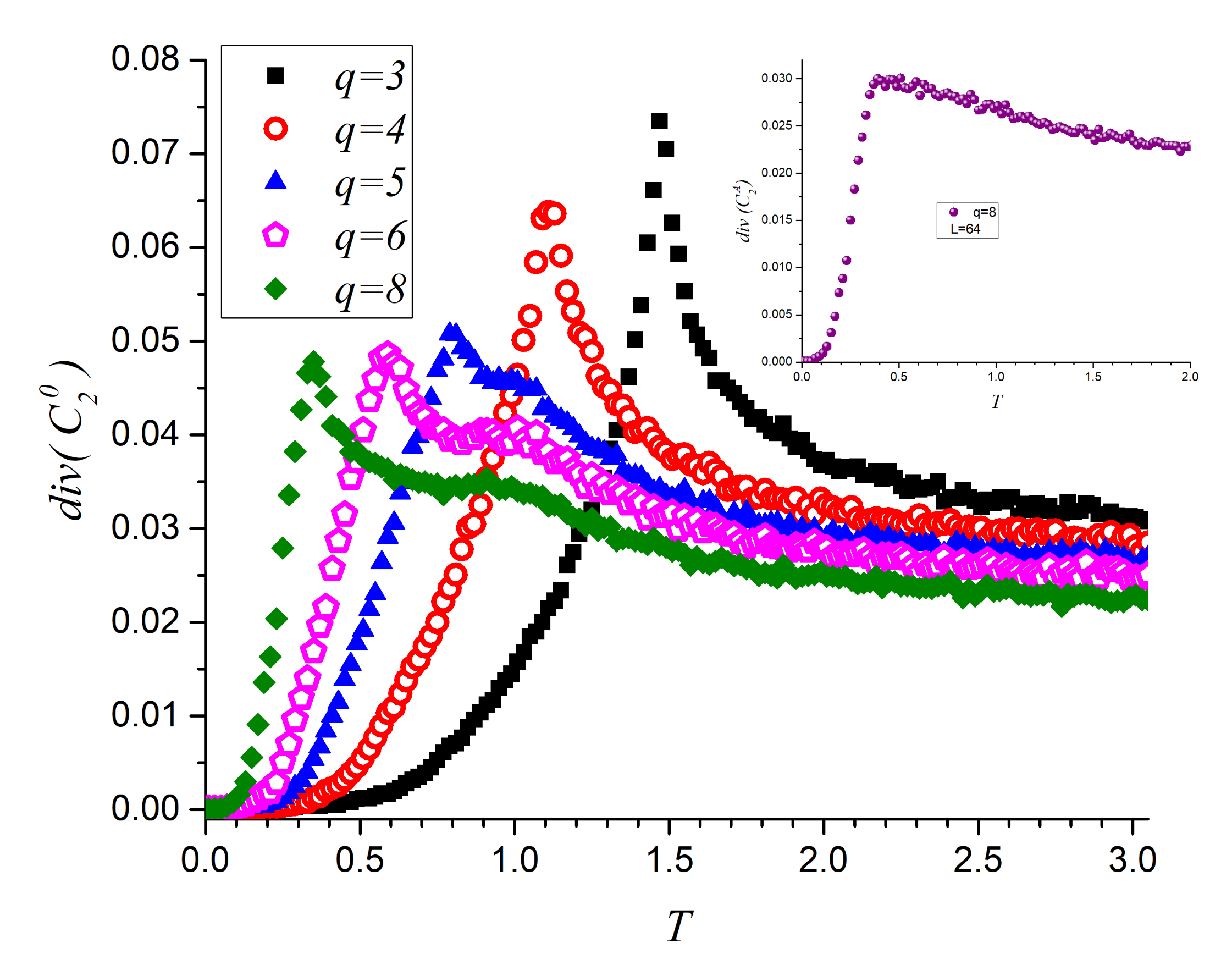
The information content in the
series is reported through the diversity of
in
Figure 8 for
, 4, 5, 6 and 8 which confirm previous findings by this additional method. Namely, for
just one peak is found just above
; this maximum decreases to
for
, while for
,
and
the low temperature peak keeps on moving to lower temperatures while the high temperature peak sticks around
. All of this in correspondence with previous gross feature results (
Figure 5 in particular). The inset of
Figure 8 reports on the average diversity of the curling two-spin parameters (
) that maximizes nearly at
in agreement with the greatest slope in the inset of
Figure 7.
Figure 9 presents the descent of
parameter as functions of temperature in a way similar to
. The inset presents the diversity of
that maximizes at the point of the more pronounced descent of the parameter itself (main figure). Parameters
and
(not shown) behave similarly to the corresponding two-spin parameters
and
, except that their curves maximize as they approach
since spins need to be freer by effect of temperature to articulate a series of two consecutive
(
) angles. The inset reports the diversity of
maximizing at the same temperature
did in the inset of
Figure 7 evidencing that they both represent ferromagnetic alignment. The inset of
Figure 9 presents an additional disctintive feature: a slight broad swelling near
can be seen for
evidencing the disappearance of three-spin correlations; this effect will appear again in a different way after the next paragraph.
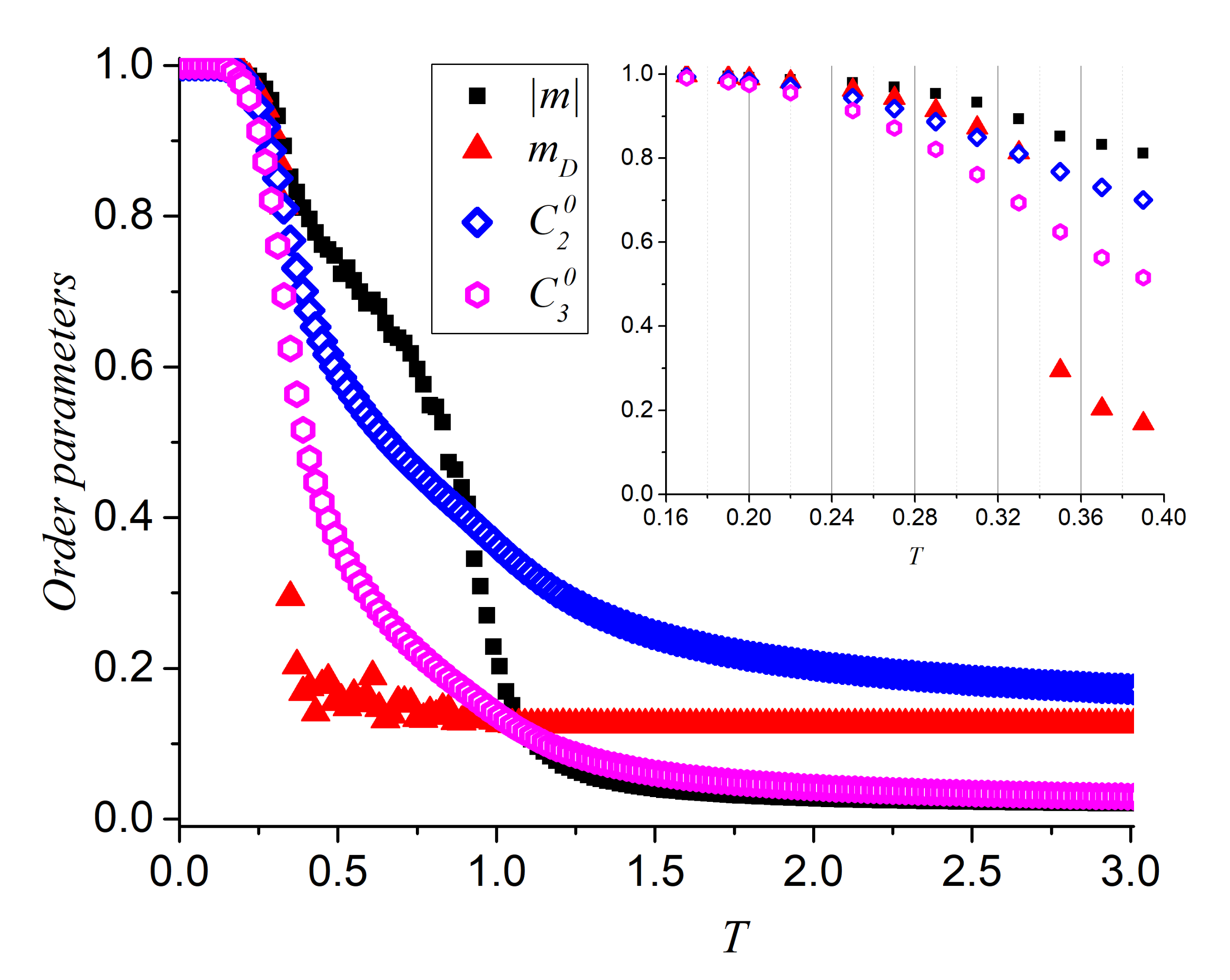
The descents of
and
resemble a bit like the magnetization curves for these systems. In
Figure 10 we do this comparison for
. The four parameters presented in this figure measure similar properties but with subtle differences:
measures the way in which the pairing of two parallel spins is gradually lost tending to its asymptotic value
;
measures the way in which the pairing of three parallel spins is lost at lower temperatures than previous case tending to its asymptotic value of
(first spin is a pivot and second and third spins have independents probabilities
to point along the curling direction). The absolute magnetization curve given by Equation (
2) changes twice its slope evidencing the two changes of phase and tending asymptotically to zero. On the other hand,
measures the way the magnetization loses its dominant direction originated in the spontaneous ergodicity breaking associated to the FP- BKT phase transition only, as defined at the end of
Section 2. Thus, this figure offers a complete picture of the magnetization evolution of the system as
T increases: at low-temperature, ergodicity is broken in favor of a ferromagnetic ordering along one dominant direction; then the FP is lost as drastically shown by the abrupt descent of
; at T increases the absolute magnetization,
and
point to the presence of short magnetic ordering, with ergodicity recovering with the increase of
T; At a temperature in which the slightest short-range interaction is exceeded by the thermal fluctuations (this critical temperature is unique) the PP is finally reached and ergodicity is fully recovered. We observe in the low temperature range that the decrease of the ferromagnetic spin-spin correlation occurs first for
, then
and finally the extended order parameters, i.e., the dominant magnetization and the absolute magnetization.
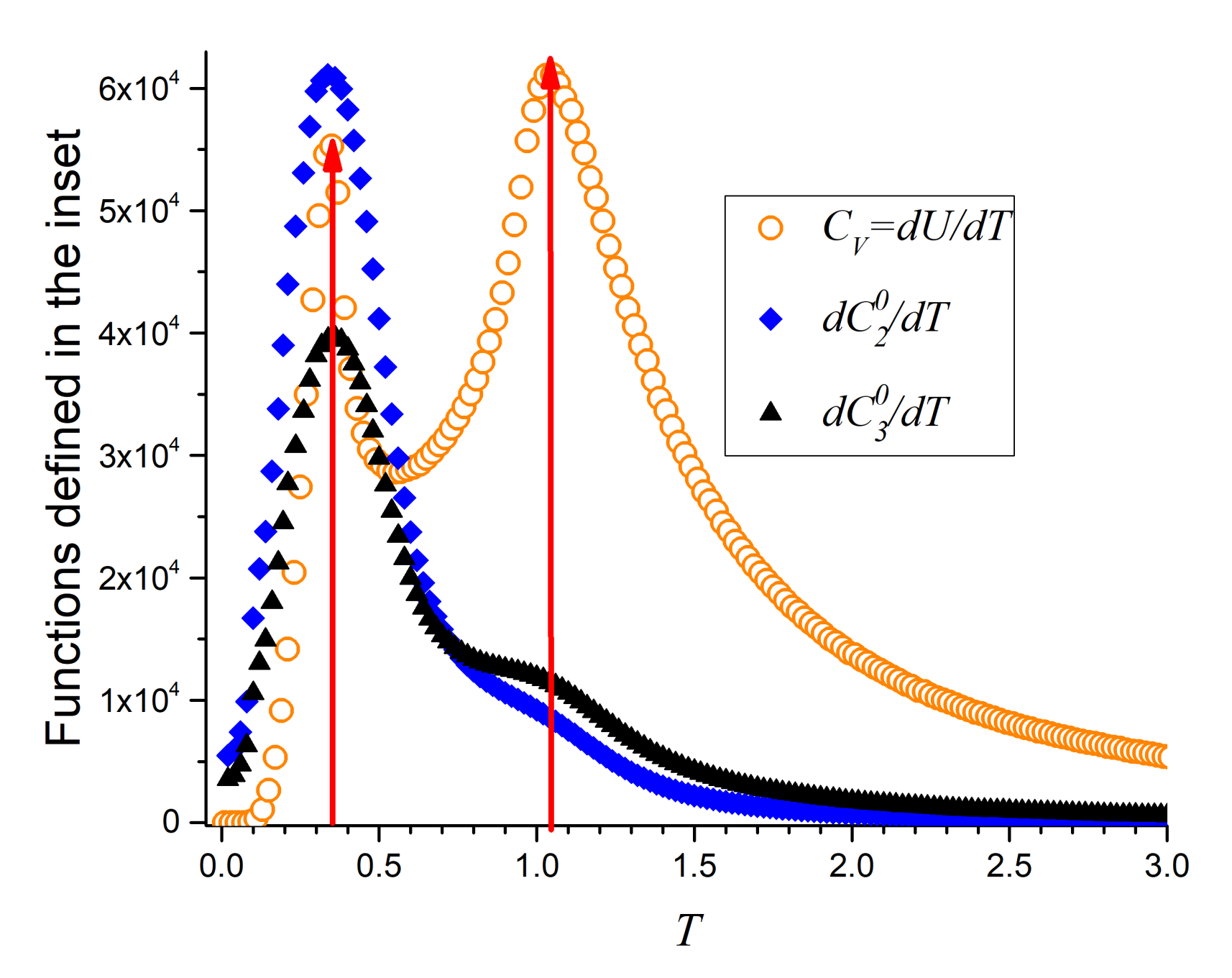
If careful attention is paid to
Figure 7 and
Figure 9 it can be noticed that
and
present changes of curvature. This is better analyzed by taking the temperature derivatives of these curves which are presented in
Figure 11, where they are compared to the specific heat of the same particular system (
). It is clear that the derivatives of the spin parameters showing ferromagnetic alignments maximize at both transitions thus providing an additional argument and measurements to define these magnetic transitions. The low temperature maximum is more pronounced and agrees perfectly with the corresponding maximum of the specific heat. In the case of the highest transition temperature, the temperature derivative of
shows a larger broad maximum than the temperature derivative of
in consonance with the light swelling shown by the diversity of
in the inset of
Figure 9.
5. Conclusions
Information content of the series corresponding to the classical variables internal energy and magnetization recognize the different phase transitions present in the clock model. Among the three investigated information theory techniques (Shannon entropy, mutability, and diversity), it is diversity that provides the sharpest curves with appropriate contrast to better recognize the transitions.
The new parameters defined here following the curling lines of the vortexes give information on the short-range ordering achieved by the system. Thus, the ferromagnetic phase is first lost to two-spin vortex parameters at just under , which is then complemented by the less frequent three-spin parameters with two consecutive twists of . The complete BKT phase receives contributions from all possible n-spin vortex parameters rendering a composed critical temperature around for the BKT-PP transition.
Diversity of the time series confirms both transitions for
and just one transition for
in perfect agreement with the phase transitions already reported by reference [
14].
parameters are more sensitive than parameters since the former actually measure the formation of three-spin vortexes, while the former arise from the loss of the original ferromagnetic phase.
All q-clock systems have a similar critical temperature for the BKT-PP phase transition since this is mainly due to the dissociation of correlation in the interaction of neighboring spins, thus affecting the and parameters, which are at the bases of more complex n-spin parameters.
Temperature derivatives of the new parameters are in perfect agreement with the temperature derivative of the internal energy (specific heat) further validating the new parameters as describing the phenomenon which can now be also explained in terms of short-range ordering. Finally, we can conclude that the spin-spin ferromagnetic correlation at first-nearest neighbors is able to recognize the two phase transitions, FP to BKT and BKT to PP, confirming the same transition temperatures of the q-state clock model for .