Anisotropic Strange Star in 5D Einstein-Gauss-Bonnet Gravity
Abstract
1. Introduction
2. Basic Field Equations for Einstein-Gauss-Bonnet (EGB) Gravity
3. Anisotropic Solution for Strange Star Model in 5D Einstein-Gauss-Bonnet Gravity
4. Boundary Conditions
5. Physical Analysis of the Obtained Solution
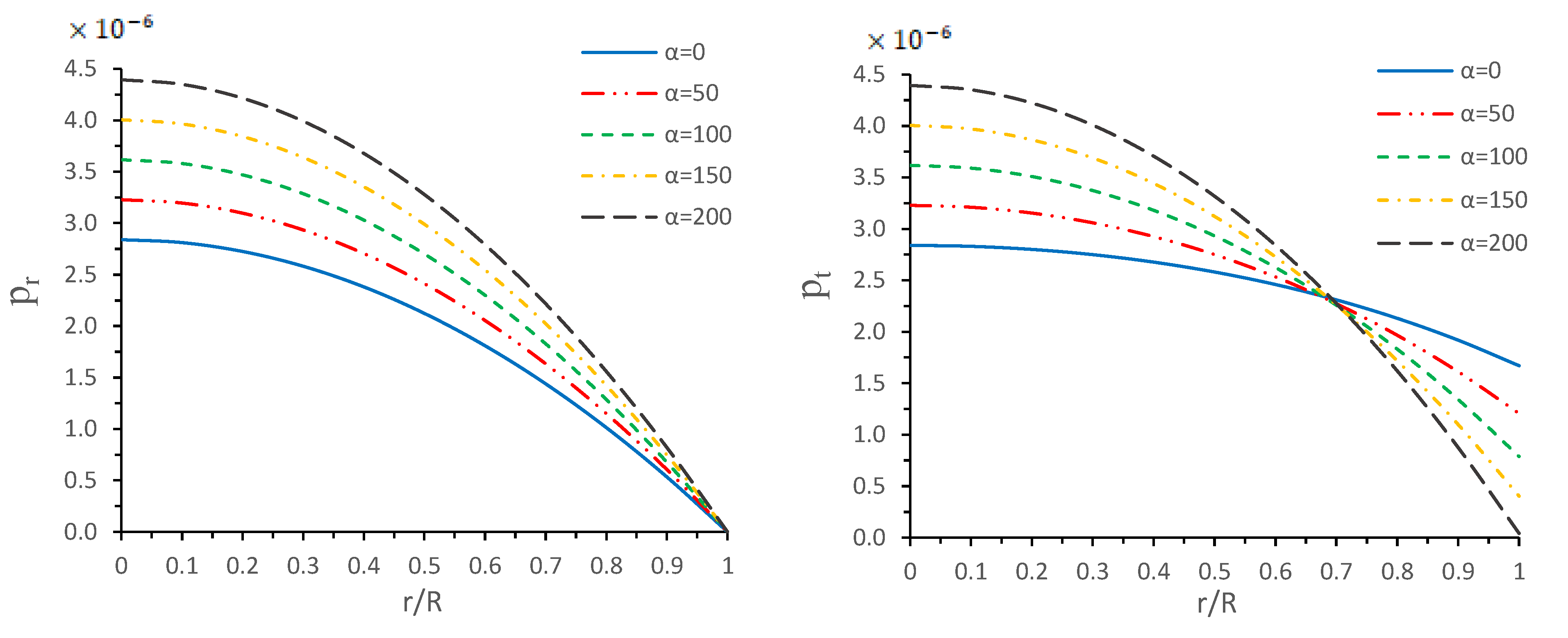
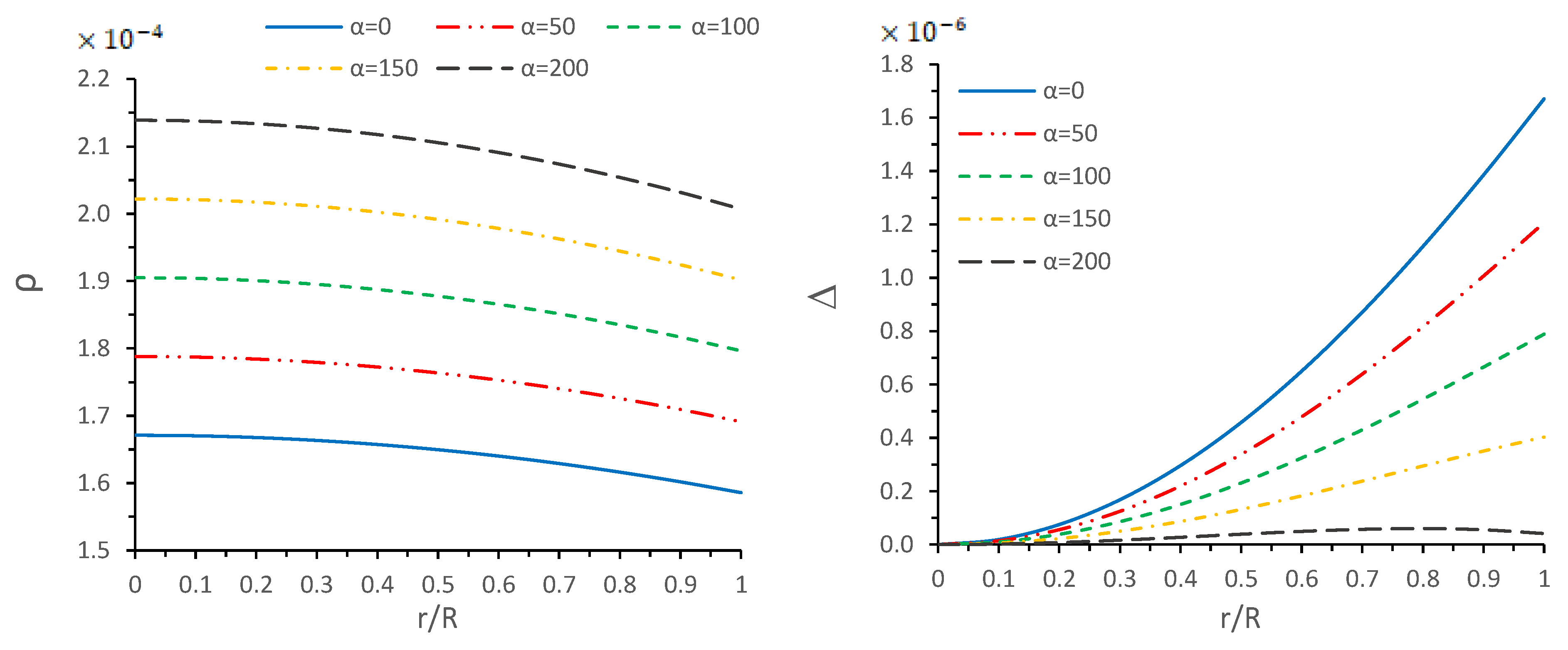
5.1. Regularity Conditions
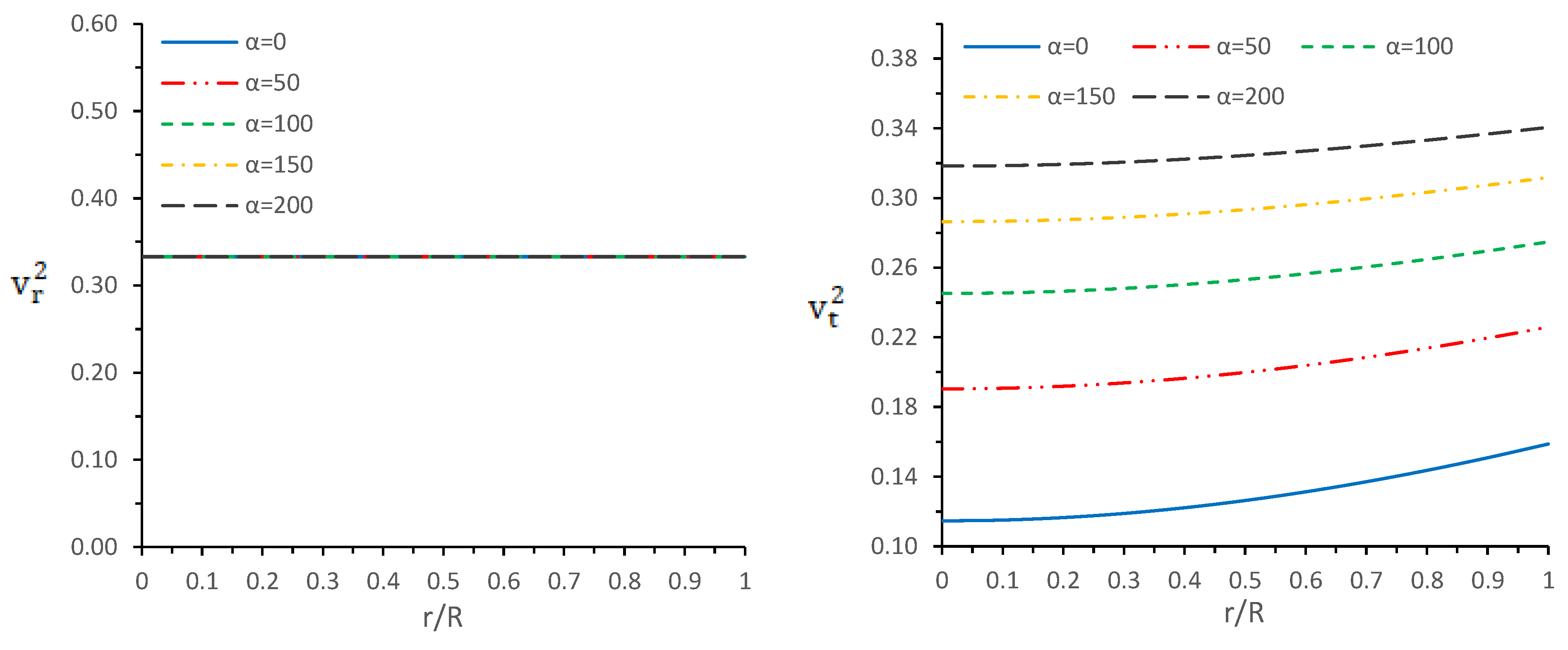
5.2. Causality
5.3. Stability of Anisotropic Compact Objects via Cracking
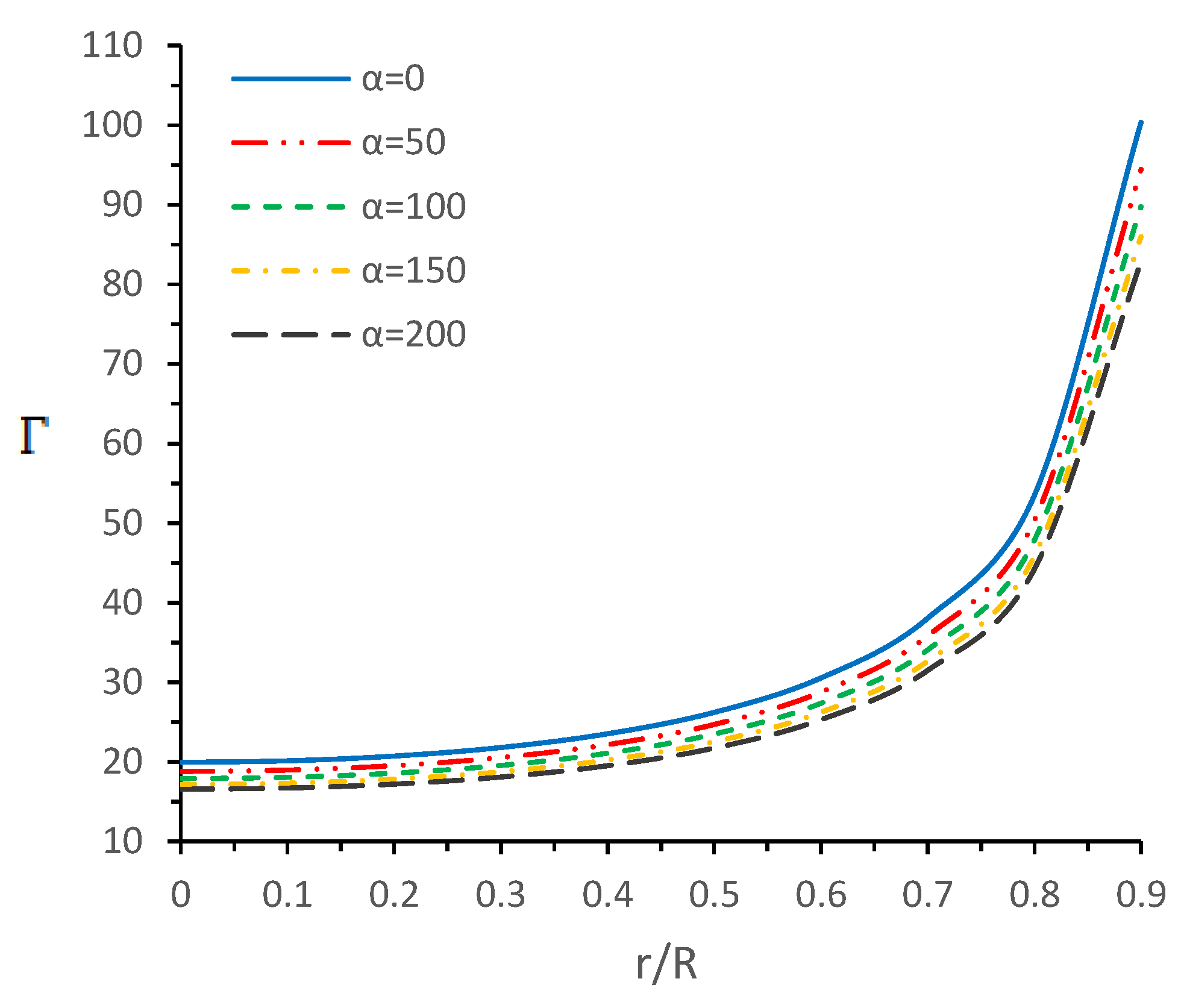
5.4. The Stability Criterion and the Adiabatic Indices
5.5. Hydrostatic Equilibrium via Modified TOV Equation
5.6. Mass-Radius Relationship
5.7. Maximum Mass and Fitting of the Radius for Known Compact Objects via Curve
6. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Complexity for Self-Gravitating Fluid Distributions under the Static Spherically Symmetric Spacetime
References
- Bicak, J. Einstein equations: Exact solutions. Encycl. Math. Phys. 2006, 2, 165. [Google Scholar]
- Delgaty, M.S.R.; Lake, K. Physical Acceptability of Isolated, Static, Spherically Symmetric, Perfect Fluid Solutions of Einstein’s Equations. Comput. Phys. Commun. 1998, 115, 395. [Google Scholar] [CrossRef]
- Tolman, R.C. Static Solutions of Einstein’s Field Equations for Spheres of Fluid. Phys. Phys. Rev. D 1939, 55, 364. [Google Scholar] [CrossRef]
- Oppenheimer, J.R.; Volkoff, G. On Massive Neutron Cores. Phys. Rev. 1939, 55, 374–381. [Google Scholar] [CrossRef]
- Schwarzschild, K. Uber das Gravitationsfeld einer Kugel aus inkompressibler Flussigkeit nach der Einsteinschen Theorie. Math. Phys. Tech. 1939, 55, 364–373. [Google Scholar]
- Chandrasekhar, S. The Maximum mass of ideal white dwarfs. Astrophys. J. 1931, 74, 81–82. [Google Scholar] [CrossRef]
- Bhar, P.; Rahaman, F.; Ray, S.; Chatterjee, V. Possibility of higher-dimensional anisotropic compact star. Eur. Phys. J. C 2015, 75, 190. [Google Scholar] [CrossRef]
- Jhingan, S.; Ghosh, S.G. Inhomogeneous dust collapse in 5D Einstein-Gauss-Bonnet gravity. Phys. Rev. D 2010, 81, 024010. [Google Scholar] [CrossRef]
- Myers, R.C.; Simons, J.Z. Black-hole thermodynamics in Lovelock gravity. Phys. Rev. D 1988, 38, 2434. [Google Scholar] [CrossRef]
- Torii, T.; Maeda, H. Spacetime structure of static solutions in Gauss-Bonnet gravity: Neutral case. Phys. Rev. D 2005, 71, 124002. [Google Scholar] [CrossRef]
- Boulware, D.G.; Deser, S. String-generated gravity models. Phys. Rev. Lett. 1985, 55, 2656. [Google Scholar] [CrossRef] [PubMed]
- Tangherlini, F.R. Source of the Schwarzschild field. Il Nuovo Cimento (1955–1965) 1963, 636, 153–174. [Google Scholar] [CrossRef]
- Myers, R.C.; Perry, M.J. Black holes in higher dimensional space-times. Ann. Phys. 1986, 172, 304. [Google Scholar] [CrossRef]
- Maeda, H. Final fate of spherically symmetric gravitational collapse of a dust cloud in Einstein-Gauss-Bonnet gravity. Phys. Rev. D 2006, 73, 104004. [Google Scholar] [CrossRef]
- Dadhich, N.K.; Molina, A.; Khugaev, A. Uniform density static fluid sphere in Einstein-Gauss-Bonnet gravity and its universality. Phys. Rev. D 2010, 81, 104026. [Google Scholar] [CrossRef]
- Hansraj, S.; Chilambwe, B.; Maharaj, S.D. Exact EGB models for spherical static perfect fluids. Eur. Phys. J. C. 2015, 75, 277. [Google Scholar] [CrossRef]
- Bhar, P.; Govender, M.; Sharma, R. A comparative study between EGB gravity and GTR by modeling compact stars. Eur. Phys. J. C 2017, 77, 109. [Google Scholar] [CrossRef]
- Manuel, M.; Kasmaei, H.D. Mathematical Modeling of Strange Stars in 5-D Einstein-Gauss-Bonnet Gravity. Appl. Phys. 2021, 4, 18–35. [Google Scholar]
- De Martino, I.; De Laurentis, M.; Capozziello, S. Tracing the cosmic history by Gauss-Bonnet gravity. Phys. Rev. D 2020, 102, 063508. [Google Scholar] [CrossRef]
- Alimohammadi, M.; Ghalee, A. Remarks on generalized Gauss-Bonnet dark energy. Phys. Rev. D 2009, 79, 063006. [Google Scholar] [CrossRef]
- Böhmer, C.G.; Lobo, F.S. Stability of the Einstein static universe in modified Gauss-Bonnet gravity. Phys. Rev. D 2009, 79, 067504. [Google Scholar] [CrossRef]
- Cognola, G.; Elizalde, E.; Nojiri, S.; Odintsov, S.D.; Zerbini, S. String-inspired Gauss-Bonnet gravity reconstructed from the universe expansion history and yielding the transition from matter dominance to dark energy. Phys. Rev. D 2007, 75, 086002. [Google Scholar] [CrossRef]
- Granda, L.N. Dark energy from scalar field with gauss–bonnet and non-minimal kinetic coupling. Mod. Phys. Lett. A 2012, 27, 1250018. [Google Scholar] [CrossRef]
- Ivanov, M.M.; Toporensky, A.V. Cosmological dynamics of fourth-order gravity with a Gauss-Bonnet term. Gravit. Cosmol. 2012, 18, 43–53. [Google Scholar] [CrossRef][Green Version]
- Li, B.; Barrow, J.D.; Mota, D.F. Cosmology of modified Gauss-Bonnet gravity. Phys. Rev. D 2007, 76, 044027. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Modified Gauss–Bonnet theory as gravitational alternative for dark energy. Phys. Lett. B 2005, 631, 1–6. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Sasaki, M. Gauss-Bonnet dark energy. Phys. Rev. D 2005, 71, 123509. [Google Scholar] [CrossRef]
- Astashenok, A.V.; Capozziello, S.; Odintsov, S.D. Nonperturbative models of quark stars in f(R) gravity. Phys. Lett. B 2015, 742, 160–166. [Google Scholar] [CrossRef]
- Astashenok, A.V.; Capozziello, S.; Odintsov, S.D.; Oikonomou, V.K. Causal limit of neutron star maximum mass in f(R) gravity in view of GW190814. Phys. Lett. B 2021, 816, 136222. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K.; Fronimos, F.P. Rectifying Einstein-Gauss-Bonnet inflation in view of GW170817. Nucl. Phys. B 2020, 958, 115135. [Google Scholar] [CrossRef]
- Bowers, R.L.; Liang, E.P.T. Anisotropic spheres in general relativity. Astrophys. J. 1974, 188, 657. [Google Scholar] [CrossRef]
- Herrera, L.; Santos, N.O. Local anisotropy in self gravitating systems. Phys. Rep. 1997, 286, 53. [Google Scholar] [CrossRef]
- Harko, T.; Mak, M.K. Anisotropic relativistic stellar models. Ann. Phys. 2002, 11, 3. [Google Scholar] [CrossRef]
- Usov, V.V. Electric fields at the quark surface of strange stars in the color-flavor locked phase. Phys. Rev. D 2004, 70, 067301. [Google Scholar] [CrossRef]
- Sokolov, A.I. Phase transitions in a superfluid neutron liquid. Sov. Phys. JETP 1980, 52, 575–576. [Google Scholar]
- Esculpi, M.; Malaver, M.; Aloma, E. A Comparative Analysis of the Adiabatic Stability of Anisotropic Spherically Symmetric solutions in General Relativity. Gen. Relat. Grav. 2007, 39, 633–652. [Google Scholar] [CrossRef]
- Cosenza, M.; Herrera, L.; Esculpi, M.; Witten, L. Evolution of radiating anisotropic spheres in general relativity. Phys. Rev. D 1982, 25, 2527–2535. [Google Scholar] [CrossRef]
- Herrera, L. Cracking of self-gravitating compact objects. Phys. Lett. A 1992, 165, 206–210. [Google Scholar] [CrossRef]
- Herrera, L.; Nunez, L. Modeling ‘hydrodynamic phase transitions’ in a radiating spherically symmetric distribution of matter. Astrophys. J. 1989, 339, 339–353. [Google Scholar] [CrossRef]
- Herrera, L.; Ruggeri, G.J.; Witten, L. Adiabatic Contraction of Anisotropic Spheres in General Relativity. Astrophys. J. 1979, 234, 1094–1099. [Google Scholar] [CrossRef]
- Herrera, L.; Jimenez, L.; Leal, L.; Ponce de Leon, J.; Esculpi, M.; Galina, V. Anisotropic fluids and conformal motions in general relativity. J. Math. Phys. 1984, 25, 3274. [Google Scholar] [CrossRef]
- Malaver, M. Quark Star Model with Charge Distributions. Open Sci. J. Mod. Phys. 2014, 1, 6–11. [Google Scholar]
- Malaver, M. Strange Quark Star Model with Quadratic Equation of State. Front. Math. Appl. 2014, 1, 9–15. [Google Scholar]
- Malaver, M. Charged anisotropic models in a modified Tolman IV space time. World Sci. News 2018, 101, 31–43. [Google Scholar]
- Malaver, M. Charged stellar model with a prescribed form of metric function y(x) in a Tolman VII spacetime. World Sci. News 2018, 108, 41–52. [Google Scholar]
- Malaver, M. Classes of relativistic stars with quadratic equation of state. World Sci. News 2016, 57, 70–80. [Google Scholar]
- Sunzu, J.; Danford, P. New exact models for anisotropic matter with electric field. Pramana J. Phys. 2017, 89, 44. [Google Scholar] [CrossRef]
- Bhar, P.; Murad, M.H.; Pant, N. Relativistic anisotropic stellar models with Tolman VII spacetime. Astrophys. Space Sci. 2015, 359, 13. [Google Scholar] [CrossRef]
- Sunzu, J.M.; Maharaj, S.D.; Ray, S. Quark star model with charged anisotropic matter. Astrophys. Space Sci. 2014, 354, 517–524. [Google Scholar] [CrossRef]
- Feroze, T.; Siddiqui, A. Charged anisotropic matter with quadratic equation of state. Gen. Rel. Grav. 2011, 43, 1025–1035. [Google Scholar] [CrossRef]
- Feroze, T.; Siddiqui, A. Some Exact Solutions of the Einstein-Maxwell Equations with a Quadratic Equation of State. J. Korean Phys. Soc. 2014, 65, 944–947. [Google Scholar] [CrossRef]
- Malaver, M. Some new models of anisotropic compact stars with quadratic equation of state. World Sci. News 2018, 109, 180–194. [Google Scholar]
- Malaver, M. Charged anisotropic matter with modified Tolman IV potential. Open Sci. J. Mod. Phys. 2015, 2, 65–71. [Google Scholar]
- Gross, D.J. Twenty five years of asymptotic freedom. Nucl. Phys. B Proc. Suppl. 1999, 74, 426–446. [Google Scholar] [CrossRef]
- Maeda, H.; Dadhich, N. Matter without matter: Novel Kaluza-Klein spacetime in Einstein-Gauss-Bonnet gravity. Phys. Rev. D 2007, 75, 044007. [Google Scholar] [CrossRef]
- Xu, W.; Wang, C.Y.; Zhu, B. Effects of Gauss-Bonnet term on the phase transition of a Reissner-Nordström-AdS black hole in (3 + 1) dimensions. Phys. Rev. D 2019, 99, 044010. [Google Scholar] [CrossRef]
- Wu, C.H.; Hu, Y.P.; Xu, H. Hawking evaporation of Einstein-Gauss-Bonnet AdS black holes in D ⩾ 4 dimensions. Eur. Phys. J. C 2021, 81, 351. [Google Scholar] [CrossRef]
- Lovelock, D. The four-dimensionality of space and the Einstein tensor. J. Math. Phys. 1972, 13, 874. [Google Scholar] [CrossRef]
- Wright, M. Buchdahl’s inequality in five dimensional Gauss-Bonnet gravity. Gen. Relativ. Gravit. 2016, 48, 93. [Google Scholar] [CrossRef]
- Maurya, S.K.; Banerjee, A.; Hansraj, S. Role of pressure anisotropy on relativistic compact stars. Phys. Rev. D 2018, 97, 044022. [Google Scholar] [CrossRef]
- Maurya, S.K.; Banerjee, A.; Jasim, M.K.; Kumar, J.; Prasad, A.K.; Pradhan, A. Anisotropic compact stars in the Buchdahl model: A comprehensive study. Phys. Rev. D 2019, 99, 044029. [Google Scholar] [CrossRef]
- Deb, D.; Ketov, S.V.; Maurya, S.K.; Khlopov, M.; Moraes, P.H.R.S.; Ray, S. Exploring physical features of anisotropic strange stars beyond standard maximum mass limit in f(R, T) gravity. Mon. Not. R. Astron. Soc. 2019, 485, 5652. [Google Scholar] [CrossRef]
- Shamir, M.F.; Malik, A. Behavior of Anisotropic Compact Stars in f(R, ϕ) Gravity. Commun. Theor. Phys. 2019, 71, 599. [Google Scholar] [CrossRef]
- Maurya, S.K.; Errehymy, A.; Deb, D.; Tello-Ortiz, F.; Daoud, M. Study of anisotropic strange stars in f(R, T) gravity: An embedding approach under the simplest linear functional of the matter-geometry coupling. Phys. Rev. D. 2019, 100, 044014. [Google Scholar] [CrossRef]
- Maurya, S.K.; Maharaj, S.D.; Kumar, J.; Prasad, A.K. Effect of pressure anisotropy on Buchdahl-type relativistic compact stars. Gen. Relat. Gravit. 2019, 51, 86. [Google Scholar] [CrossRef]
- Shamir, M.F.; Naz, T. Compact Stars with Modified Gauss–Bonnet Tolman–Oppenheimer–Volkoff Equation. J. Exp. Theor. Phys. 2019, 128, 871. [Google Scholar] [CrossRef]
- Maurya, S.K.; Banerjee, A.; Tello-Ortiz, F. Buchdahl model in f (R, T) gravity: A comparative study with standard Einstein’s gravity. Phys. Dark Universe 2020, 27, 100438. [Google Scholar] [CrossRef]
- Maurya, S.K.; Tello-Ortiz, F. Anisotropic fluid spheres in the framework of f (R, T) gravity theory. Ann. Phys. 2020, 414, 168070. [Google Scholar] [CrossRef]
- Maurya, S.K.; Singh, K.N.; Errehymy, A.; Daoud, M. Anisotropic stars in f(G, T) gravity under class I space-time. Eur. Phys. J. Plus. 2020, 135, 824. [Google Scholar] [CrossRef]
- Javed, M.; Mustafa, G.; Shamir, M.F. Anisotropic spheres in f (R, G) gravity with Tolman-Kuchowicz spacetime. New Astron. 2021, 84, 101518. [Google Scholar] [CrossRef]
- Mustafa, G.; Tie-Cheng, X.; Shamir, M.F.; Javed, M. Embedding class one solutions of anisotropic fluid spheres in modified f() gravity. Eur. Phys. J. Plus. 2021, 136, 166. [Google Scholar] [CrossRef]
- Mustafa, G.; Tie-Cheng, X.; Ahmad, M.; Shamir, M.F. Anisotropic spheres via embedding approach in R+βR2 gravity with matter coupling. Phys. Dark Universe 2021, 31, 100747. [Google Scholar] [CrossRef]
- Mustafa, G.; Shamir, M.F.; Ahmad, M. Ahmad M. Bardeen stellar structures with Karmarkar condition. Phys. Dark Universe 2020, 30, 100652. [Google Scholar] [CrossRef]
- Mustafa, G.; Shamir, M.F.; Tie-Cheng, X. Physically viable solutions of anisotropic spheres in f(,) gravity satisfying the Karmarkar condition. Phys. Rev. D 2020, 101, 104013. [Google Scholar] [CrossRef]
- Rej, P.; Bhar, P.; Govender, M. Charged compact star in f(R, T) gravity in Tolman–Kuchowicz spacetime. Eur. Phys. J. C 2021, 81, 316. [Google Scholar] [CrossRef]
- Biswas, S.; Shee, D.; Guha, B.K.; Ray, S. Anisotropic strange star with Tolman–Kuchowicz metric under f(R, T) gravity. Eur. Phys. J. C 2020, 80, 175. [Google Scholar] [CrossRef]
- Demorest, P.B.; Pennucci, T.; Ransom, S.M.; Roberts, M.S.E.; Hessels, J.W.T. A two-solar-mass neutron star measured using Shapiro delay. Nature 2010, 467, 1081. [Google Scholar] [CrossRef]
- DiPrisco, A.; Fuenmayor, E.; Herrera, L.; Varela, V. Tidal forces and fragmentation of self-gravitating compact objects. Phys. Lett. A 1994, 195, 23–26. [Google Scholar] [CrossRef]
- DiPrisco, A.; Herrera, L.; Varela, V. Cracking of homogeneous self-gravitating compact objects induced by fluctuations of local anisotropy. Gen. Rel. Grav. 1997, 29, 1239. [Google Scholar] [CrossRef]
- Abreu, H.; Hernandez, H.; Nunez, L.A. Sound speeds, cracking and the stability of self-gravitating anisotropic compact objects. Class. Quantum Grav. 2007, 24, 4631–4645. [Google Scholar] [CrossRef]
- Chandrasekhar, S. The Dynamical Instability of Gaseous Masses Approaching the Schwarzschild Limit in General Relativity. Astrophys. J. 1964, 140, 417. [Google Scholar] [CrossRef]
- Merafina, M.; Ruffini, R. Systems of selfgravitating classical particles with a cutoff in their distribution function. Astron. Astrophys. 1989, 221, 4. [Google Scholar]
- Moustakidis, C.C. The stability of relativistic stars and the role of the adiabatic index. Gen. Relativ. Gravit. 2017, 49, 68. [Google Scholar] [CrossRef]
- Chan, R.; Kichenassamy, S.; Denmat, G.L.; Santos, N.O. Heat flow and dynamical instability in spherical collapse. Mon. Not. R. Astron. Soc. 1989, 239, 91. [Google Scholar] [CrossRef]
- Haensel, P.; Potekhin, A.Y.; Yakovlev, D.G. Neutron Stars 1: Equation of State and Structure; Springer: New York, NY, USA, 2007. [Google Scholar]
- Buchdahl, H.A. General relativistic fluid spheres. Phys. Rev. 1959, 116, 1027. [Google Scholar] [CrossRef]
- Straumann, N. General Relativity and Relativistic Astrophysics; Springer: Berlin/Heidelberg, Germany, 1984; Volume 43. [Google Scholar]
- Ivanov, B.V. Maximum bounds on the surface redshift of anisotropic stars. Phys. Rev. D 2002, 65, 104011. [Google Scholar] [CrossRef]
- Lopez-Ruiz, R.; Mancini, H.L.; Calbet, X. A statistical measure of complexity. Phys. Lett. A 1995, 209, 321. [Google Scholar] [CrossRef]
- Catalan, R.G.; Garay, J.; Lopez-Ruiz, R. Features of the extension of a statistical measure of complexity to continuous systems. Phys. Rev. E 2002, 66, 011102. [Google Scholar]
- Sañudo, J.; Pacheco, A.F. Complexity and white-dwarf structure. Phys. Lett. A 2009, 373, 807. [Google Scholar] [CrossRef]
- Chatzisavvas, K.C.H.; Psonis, V.P.; Panos, C.P.; Moustakidis, C.C. Complexity and neutron star structure. Phys. Lett. A 2009, 373, 3901. [Google Scholar] [CrossRef]
- De Avellar, M.G.B.; Horvath, J.E. Entropy, complexity and disequilibrium in compact stars. Phys. Lett. A 2012, 376, 1085. [Google Scholar] [CrossRef]
- De Souza, R.A.; de Avellar, M.G.B.; Horvath, J.E. Statistical measure of complexity in compact stars with global charge neutrality. In Proceedings of the Compact Stars in the QCD Phase Diagram III (CSQCD III), Guarujá, Brazil, 12–15 December 2012; arXiv: 1308.3519. Available online: http://www.astro.iag.usp.br/foton/CSQCD3 (accessed on 28 June 2021).
- De Avellar, M.G.B.; de Souza, R.A.; Horvath, J.E.; Paret, D.M. Information theoretical methods as discerning quantifiers of the equations of state of neutron stars. Phys. Lett. A 2014, 378, 3481. [Google Scholar] [CrossRef]
- Herrera, L. New definition of complexity for self-gravitating fluid distributions: The spherically symmetric, static case. Phys. Rev. D 2018, 97, 044010. [Google Scholar] [CrossRef]

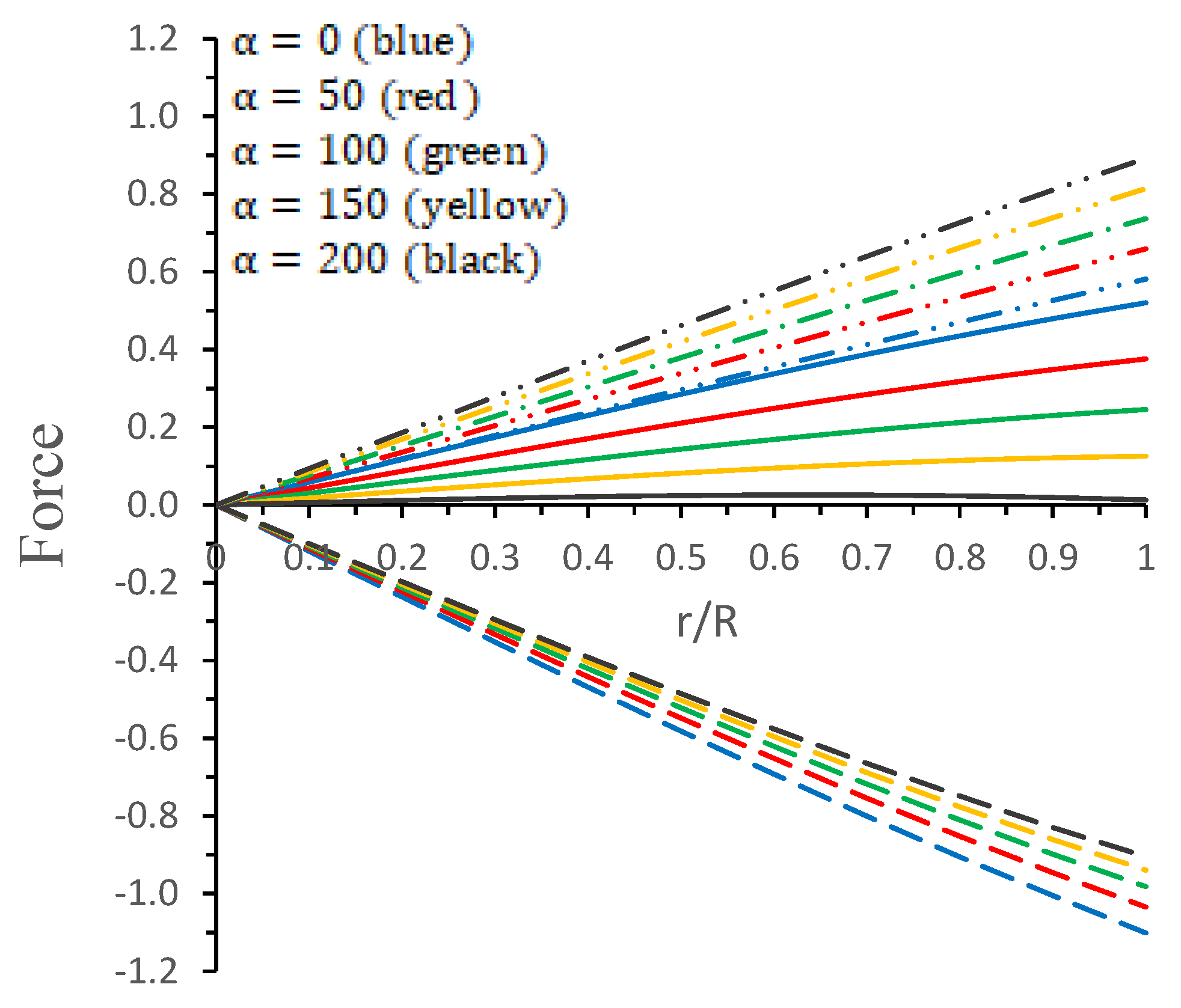
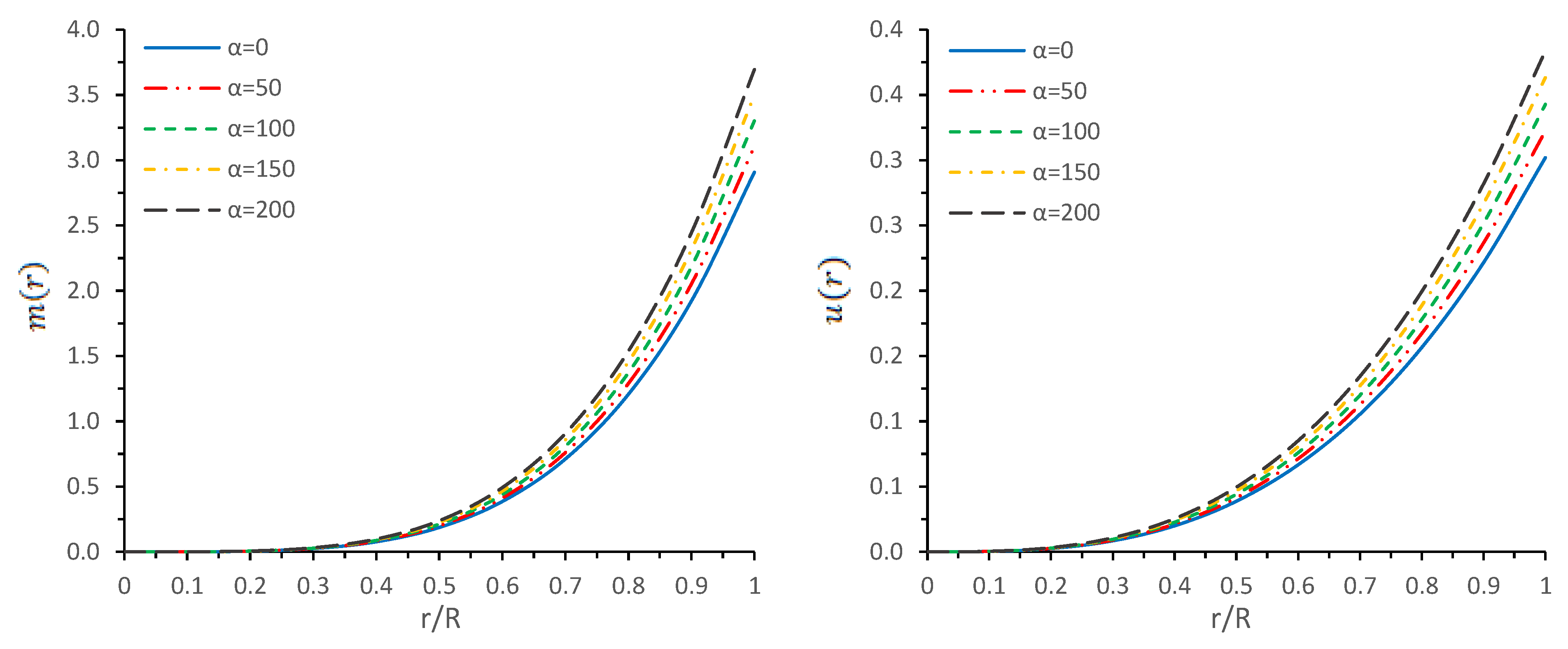
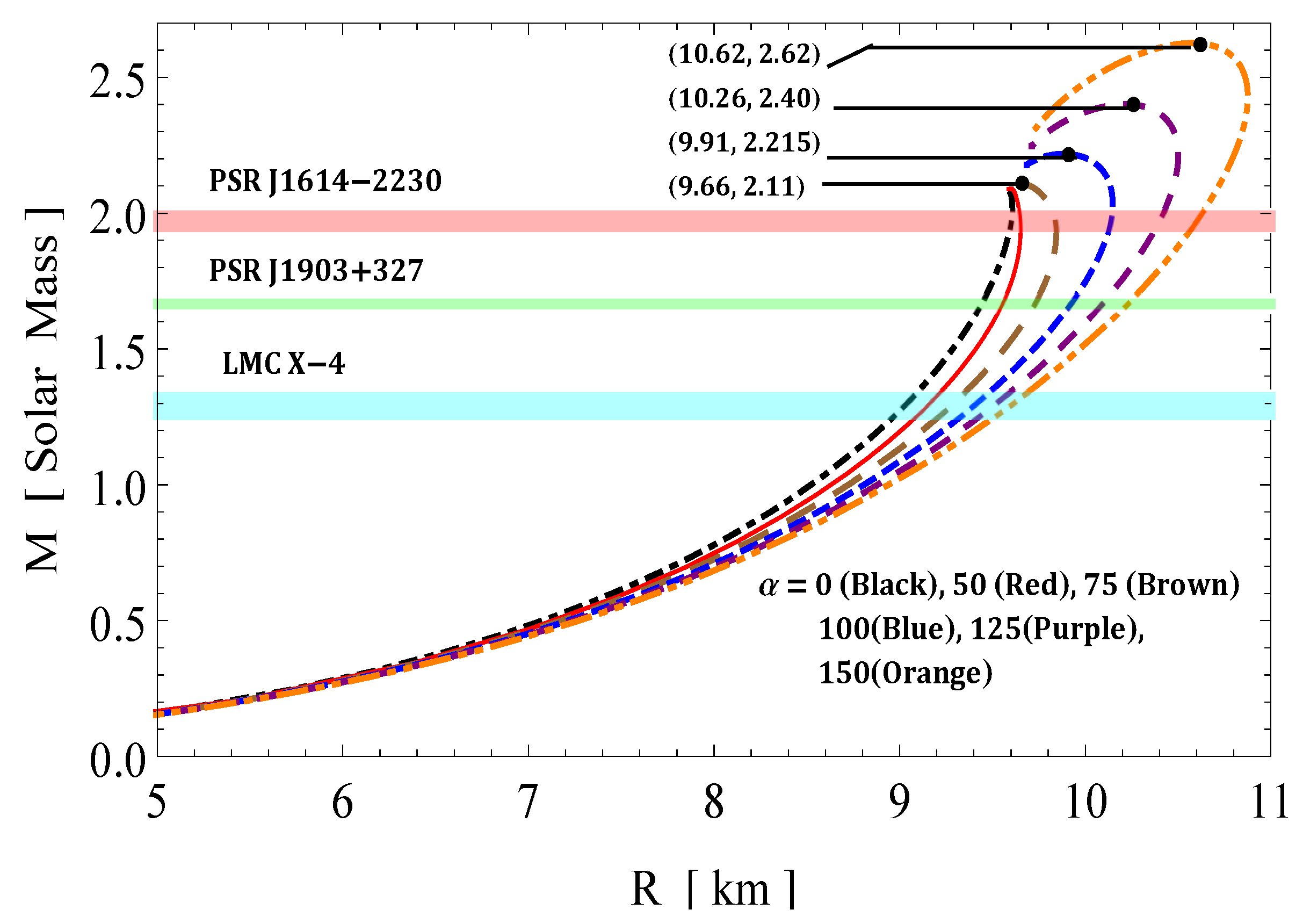
| Surface | Central Density | Surface Density | Central Pressure | ||||||
|---|---|---|---|---|---|---|---|---|---|
| (km−2) | Red-Shift () | () in g/cm3 | () in g/cm3 | () in dyne/cm2 | km−2 | ||||
| 0 | 1.97 | 0.30 | 0.589 | 19.928 | 1.606 | 0.00099542 | |||
| 50 | 2.10 | 0.32 | 0.677 | 18.776 | 1.625 | 0.0010615 | |||
| 100 | 2.24 | 0.34 | 0.783 | 17.872 | 1.643 | 0.0011276 | |||
| 150 | 2.37 | 0.36 | 0.911 | 17.143 | 1.662 | 0.0011937 | |||
| 200 | 2.5 | 0.38 | 1.072 | 16.54 | 1.680 | 0.0012598 |
| Objects | Predicted R km | ||||||
|---|---|---|---|---|---|---|---|
| 0 | 50 | 75 | 100 | 125 | 150 | ||
| PSR J1614-2230 | 1.97 ± 0.04 | ||||||
| PSR J1903+327 | 1.667 ± 0.021 | ||||||
| LMC X-4 | 1.29 ± 0.05 | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jasim, M.K.; Maurya, S.K.; Singh, K.N.; Nag, R. Anisotropic Strange Star in 5D Einstein-Gauss-Bonnet Gravity. Entropy 2021, 23, 1015. https://doi.org/10.3390/e23081015
Jasim MK, Maurya SK, Singh KN, Nag R. Anisotropic Strange Star in 5D Einstein-Gauss-Bonnet Gravity. Entropy. 2021; 23(8):1015. https://doi.org/10.3390/e23081015
Chicago/Turabian StyleJasim, Mahmood Khalid, Sunil Kumar Maurya, Ksh. Newton Singh, and Riju Nag. 2021. "Anisotropic Strange Star in 5D Einstein-Gauss-Bonnet Gravity" Entropy 23, no. 8: 1015. https://doi.org/10.3390/e23081015
APA StyleJasim, M. K., Maurya, S. K., Singh, K. N., & Nag, R. (2021). Anisotropic Strange Star in 5D Einstein-Gauss-Bonnet Gravity. Entropy, 23(8), 1015. https://doi.org/10.3390/e23081015






