Randomized Oblivious Transfer for Secure Multiparty Computation in the Quantum Setting
Abstract
:1. Introduction
Our Contribution
- A quantum protocol based on the UC construction by Unruh [28] and augmented with an additional subroutine to enforce randomized outputs.
2. Background
3. Protocols
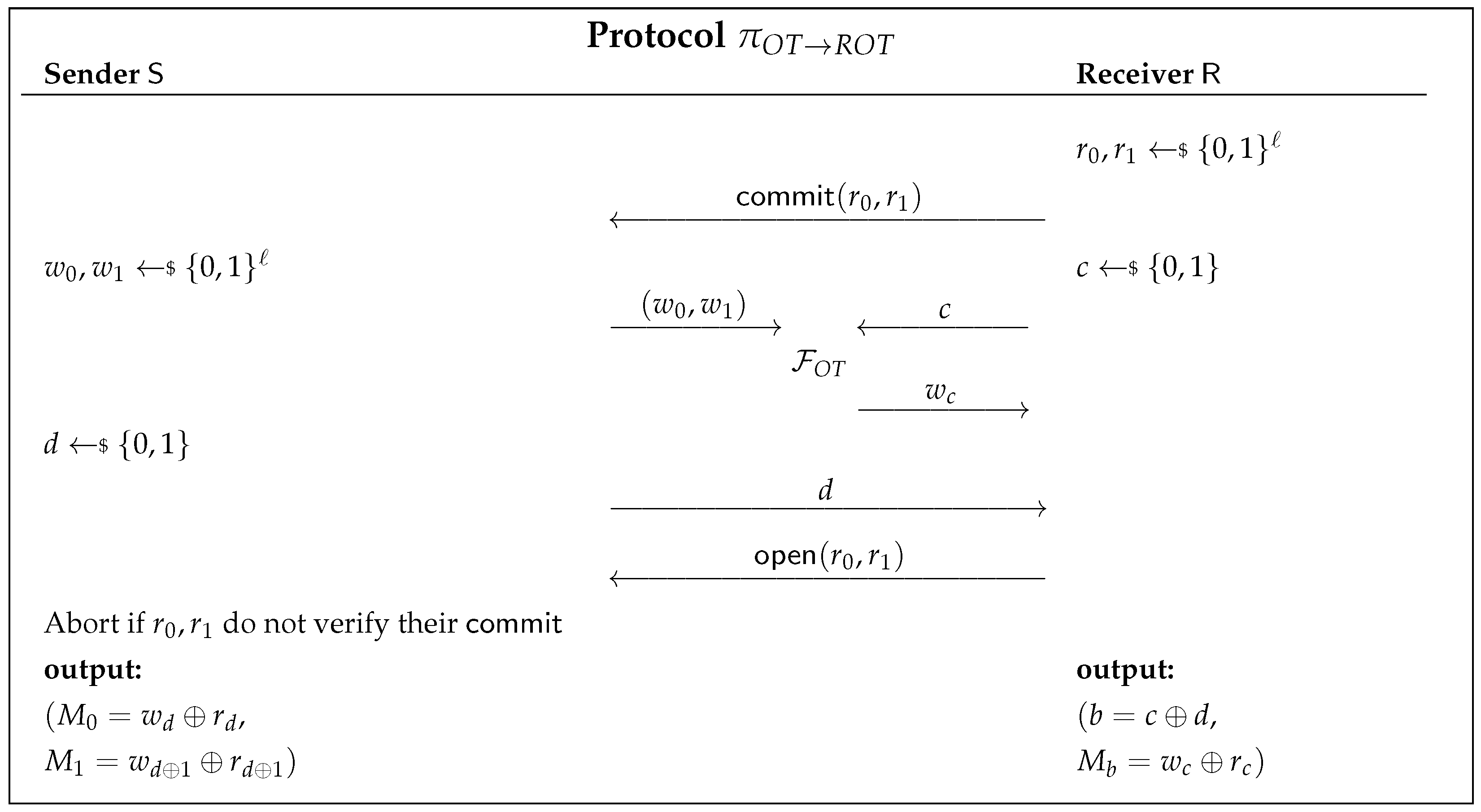
3.1. Generating an UC-Secure Random OT
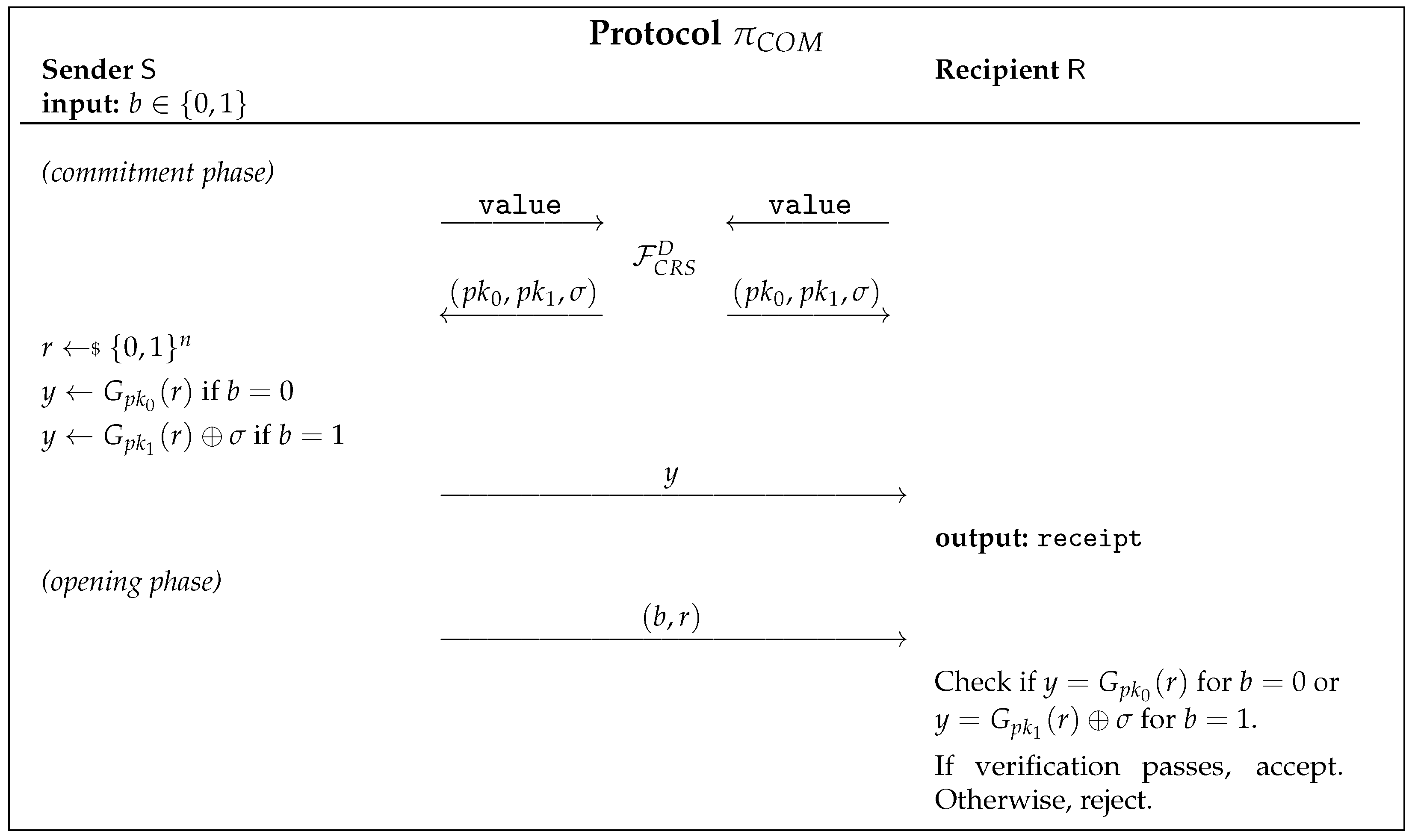
3.2. UC-Secure Commitment Scheme
3.3. UC-Secure Quantum OT Protocol
3.4. Post-Quantum UC-Secure ROT Protocol
4. Security
4.1. Quantum-UC Security of the Quantum ROT Protocol
- Corrupted Sender. In this case, simulates the view of the sender, effectively controlling the inputs to and the input bit to . In order to do so, we start by replacing by a commitment functionality , which allows the receiver to cheat. In the commit phase, expects a message commit instead of (commit, x); in the open phase, expects a message (open, x) instead of open, which is then sent to the sender. We now change the receiver’s implementation to match with the new functionality; that is, when committing to message m, the receiver stores that message and later gives it to when opening the commitment.
- Corrupted Receiver. Now, simulates the view of the receiver, controlling the input messages to . The simulator starts by receiving from . After receiving the commitment message, extracts the strings and the bit c from observing the receiver’s call to and , respectively. It then computes and and samples ; afterwards, send to and d to . When replies with open , it checks if the values received match the original commitments and aborts if they do not.
- Both/None parties corrupted. When both parties are corrupted, internally runs , which generates the messages for both parties.When the adversary does not corrupt any party, the simulator does not have an input from the ideal functionality . As such, runs the honest receiver and the honest sender, executing the needed algorithms when a dummy party is called in the ideal execution. The simulator forwards the messages of the honestly simulated protocol to .
- Sample values and commit to values .
- Sample bit and run the OT protocol with the choice bit c.
- Open the commitment to values .
- Send commit to .
- Sample bit send c to .
- Send (open, ) to , where and .
- Sample strings and run the OT protocol with .
- Sample bit d and send it to
- Check if the received values verify their commitment.
- Sample string and compute ; afterwards, send () to .
- Compute and send it to .
- Check if the received values verify their commit.
4.2. Quantum-UC Security of the Post-Quantum ROT Protocol
- Corrupted Sender. The simulator simulates the view of the sender, meaning that it controls the communication with as well as the inputs of and . As in the proof of security for , we will be replacing by the functionality and changing the receiver’s implementation to match .
- Corrupted Receiver. In this case, simulates the view of the receiver, controlling the communication with . The simulator starts by receiving from . It computes as an honest sender; after receiving as well as the receipt of the commitment, it computes honestly, for , and sends to . After receiving the reply from , if the test passed, extracts c from observing the call made to and comparing to and . Finally, it computes and , samples and sends to . At the end, it checks if match the initial commitment, aborting if they do not.
- Both/None parties corrupted. Here, both cases work as in the previous UC security proof. When both parties are corrupted, the adversary is ran internally by . When neither of the parties are corrupted, runs the honest receiver and sender, sending all the messages between them to .
- Sample bit and strings .Generate RLWE sample and, if , compute .Send and commit to values .
- Compute and run the NIZK protocol with .
- Open the commitment to values .
- Sample bit .Generate RLWE samples and program to return .Send to and send commit to .
- Compute , for , and send to .
- Send (open,) to , where and .
- Generate RLWE sample .
- Compute . Compute and , for .Send .
- Run the NIZK protocol and check if the test passes; abort if it does not.Sample and . Send ().
- Check if the received values verify their commitment; abort if they do not.
- Generate RLWE sample .
- Compute . Compute and , for .Send .
- Check if the received answer from is 1; abort if it is not.Send , where , , and .
- Check if the received values verify their commitment; abort if they do not.
5. Conclusions
- Further optimization of the commitment scheme to reduce the number of CRS calls and PRNG computations per committed bit in the context of a string commitment scheme.
- The implementation of both protocols and a comparison of their performance, taking available (quantum) technologies into account. This poses a challenge, as the limitations of quantum technologies are much less known than traditional computational power and communication.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rabin, M.O. How To Exchange Secrets with Oblivious Transfer. IACR Cryptol. ePrint Arch. 2005, 2005, 187, Originally published as: Technical Report TR-81, Aiken Computation Lab, Harvard University, Cambridge, MA, USA, 1981. [Google Scholar]
- Ishai, Y.; Prabhakaran, M.; Sahai, A. Founding Cryptography on Oblivious Transfer—Efficiently. In Proceedings of the Advances in Cryptology—CRYPTO 2008, Santa Barbara, CA, USA, 17–21 August 2008; Wagner, D., Ed.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 572–591. [Google Scholar]
- Kilian, J. Founding Cryptography on Oblivious Transfer. In Proceedings of the Twentieth Annual ACM Symposium on Theory of Computing, Chicago, IL, USA, 4–6 May 1988; Association for Computing Machinery: New York, NY, USA, 1988; pp. 20–31. [Google Scholar] [CrossRef]
- Goldreich, O.; Micali, S.; Wigderson, A. How to play any mental game, or a completeness theorem for protocols with honest majority. In Providing Sound Foundations for Cryptography: On the Work of Shafi Goldwasser and Silvio Micali; Association for Computing Machinery: New York, NY, USA, 2019; pp. 307–328. [Google Scholar]
- Blum, M. Coin flipping by telephone a protocol for solving impossible problems. ACM SIGACT News 1983, 15, 23–27. [Google Scholar] [CrossRef]
- Cramer, R.; Damgård, I.; Maurer, U. General secure multi-party computation from any linear secret-sharing scheme. In Proceedings of the Advances in Cryptology—EUROCRYPT 2000, Bruges, Belgium, 14–18 May 2000; Springer: Berlin/Heidelberg, Germany, 2000; pp. 316–334. [Google Scholar]
- Lindell, Y.; Pinkas, B. Secure two-party computation via cut-and-choose oblivious transfer. J. Cryptol. 2012, 25, 680–722. [Google Scholar] [CrossRef] [Green Version]
- Even, S.; Goldreich, O.; Lempel, A. A randomized protocol for signing contracts. Commun. ACM 1985, 28, 637–647. [Google Scholar] [CrossRef]
- Crépeau, C. Equivalence between two flavours of oblivious transfers. In Proceedings of the Advances in Cryptology—CRYPTO ’87, Santa Barbara, CA, USA, 16–20 August 1987; Springer: Berlin/Heidelberg, Germany, 1987; pp. 350–354. [Google Scholar]
- Yao, A.C. Protocols for secure computations. In Proceedings of the 23rd Annual Symposium on Foundations of Computer Science (SFCS 1982), Chicago, IL, USA, 3–5 November 1982; IEEE Computer Society: Washington, DC, USA, 1982; pp. 160–164. [Google Scholar] [CrossRef]
- Goldreich, O.; Micali, S.; Wigderson, A. How to Play ANY Mental Game. In Proceedings of the Nineteenth Annual ACM Symposium on Theory of Computing, New York, NY, USA, 25–27 May 1987; Association for Computing Machinery: New York, NY, USA, 1987; pp. 218–229. [Google Scholar] [CrossRef]
- Ishai, Y.; Kilian, J.; Nissim, K.; Petrank, E. Extending Oblivious Transfers Efficiently. In Proceedings of the Advances in Cryptology—CRYPTO 2003, Santa Barbara, CA, USA, 17–21 August 2003; Boneh, D., Ed.; Springer: Berlin/Heidelberg, Germany, 2003; pp. 145–161. [Google Scholar]
- Orrù, M.; Orsini, E.; Scholl, P. Actively Secure 1-out-of-N OT Extension with Application to Private Set Intersection. In Proceedings of the Topics in Cryptology—CT-RSA 2017, San Francisco, CA, USA, 14–17 February 2017; Handschuh, H., Ed.; Springer International Publishing: Cham, Switzerland, 2017; pp. 381–396. [Google Scholar]
- Pinkas, B.; Rosulek, M.; Trieu, N.; Yanai, A. Spot-light: Lightweight private set intersection from sparse ot extension. In Proceedings of the Advances in Cryptology—CRYPTO 2019, Santa Barbara, CA, USA, 18–22 August 2019; Springer International Publishing: Cham, Switzerland, 2019; pp. 401–431. [Google Scholar]
- Shor, P.W. Algorithms for Quantum Computation: Discrete Logarithms and Factoring. In Proceedings of the 35th Annual Symposium on Foundations of Computer Science, Santa Fe, NM, USA, 20–22 November 1994; IEEE Computer Society: Washington, DC, USA, 1994; pp. 124–134. [Google Scholar] [CrossRef]
- Lyubashevsky, V.; Peikert, C.; Regev, O. On Ideal Lattices and Learning with Errors over Rings. In Proceedings of the Advances in Cryptology—EUROCRYPT 2010, French Riviera, France, 30 May–3 June 2010; Gilbert, H., Ed.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 1–23. [Google Scholar]
- Regev, O. On Lattices, Learning with Errors, Random Linear Codes, and Cryptography. In Proceedings of the Thirty-Seventh Annual ACM Symposium on Theory of Computing, Baltimore, MD, USA, 22–24 May 2005; Association for Computing Machinery: New York, NY, USA, 2005; pp. 84–93. [Google Scholar] [CrossRef]
- Broadbent, A.; Schaffner, C. Quantum cryptography beyond quantum key distribution. Des. Codes Cryptogr. 2015, 78, 351–382. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Renner, R.; Gisin, N.; Kraus, B. Information-theoretic security proof for quantum-key-distribution protocols. Phys. Rev. A 2005, 72, 012332. [Google Scholar] [CrossRef] [Green Version]
- Shenoy-Hejamadi, A.; Pathak, A.; Radhakrishna, S. Quantum Cryptography: Key Distribution and Beyond. Quanta 2017, 6, 1. [Google Scholar] [CrossRef] [Green Version]
- Lo, H.K.; Chau, H.F. Is Quantum Bit Commitment Really Possible? Phys. Rev. Lett. 1997, 78, 3410–3413. [Google Scholar] [CrossRef] [Green Version]
- Mayers, D. Unconditionally Secure Quantum Bit Commitment is Impossible. Phys. Rev. Lett. 1997, 78, 3414–3417. [Google Scholar] [CrossRef] [Green Version]
- Erven, C.; Ng, N.; Gigov, N.; Laflamme, R.; Wehner, S.; Weihs, G. An experimental implementation of oblivious transfer in the noisy storage model. Nat. Commun. 2014, 5, 3418. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Furrer, F.; Gehring, T.; Schaffner, C.; Pacher, C.; Schnabel, R.; Wehner, S. Continuous-Variable Protocol for Oblivious Transfer in the Noisy-Storage Model. Nat. Commun. 2018, 9, 1450. [Google Scholar] [CrossRef] [PubMed]
- Ng, N.H.Y.; Joshi, S.K.; Chen Ming, C.; Kurtsiefer, C.; Wehner, S. Experimental implementation of bit commitment in the noisy-storage model. Nat. Commun. 2012, 3, 1326. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qiang, X.; Zhou, X.; Aungskunsiri, K.; Cable, H.; O’Brien, J.L. Quantum processing by remote quantum control. Quantum Sci. Technol. 2017, 2, 045002. [Google Scholar] [CrossRef] [Green Version]
- Long, G.L.; Liu, X.S. Theoretically efficient high-capacity quantum-key-distribution scheme. Phys. Rev. A 2002, 65, 032302. [Google Scholar] [CrossRef] [Green Version]
- Unruh, D. Universally Composable Quantum Multi-party Computation. In Proceedings of the Advances in Cryptology—EUROCRYPT 2010, French Riviera, France, 30 May–3 June 2010; Gilbert, H., Ed.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 486–505. [Google Scholar]
- Branco, P.; Ding, J.; Goulão, M.; Mateus, P. A Framework for Universally Composable Oblivious Transfer from One-Round Key-Exchange. In Proceedings of the IMA International Conference on Cryptography and Coding, Oxford, UK, 15–17 December 2019; Albrecht, M., Ed.; Springer International Publishing: Cham, Switzerland, 2019; pp. 78–101. [Google Scholar]
- Branco, P.; Fiolhais, L.; Goulão, M.; Martins, P.; Mateus, P.; Sousa, L. ROTed: Random Oblivious Transfer for Embedded Devices. IACR Transactions of Cryptographic Hardware and Embedded Systems. Available online: https://eprint.iacr.org/2021/935 (accessed on 7 June 2021).
- Applebaum, B.; Cash, D.; Peikert, C.; Sahai, A. Fast Cryptographic Primitives and Circular-Secure Encryption Based on Hard Learning Problems. In Proceedings of the Advances in Cryptology—CRYPTO 2009, Santa Barbara, CA, USA, 16–20 August 2009; Halevi, S., Ed.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 595–618. [Google Scholar]
- Canetti, R. Universally Composable Security: A New Paradigm for Cryptographic Protocols. In Proceedings of the 42nd IEEE Symposium on Foundations of Computer Science, Las Vegas, NV, USA, 14–17 October 2001; IEEE Computer Society: Washington, DC, USA, 2001; p. 136. [Google Scholar]
- Canetti, R.; Fischlin, M. Universally Composable Commitments. In Proceedings of the Advances in Cryptology—CRYPTO 2001, Santa Barbara, CA, USA, 19–23 August 2001; Kilian, J., Ed.; Springer: Berlin/Heidelberg, Germany, 2001; pp. 19–40. [Google Scholar]
- Ding, J.; Xie, X.; Lin, X. A Simple Provably Secure Key Exchange Scheme Based on the Learning with Errors Problem. Cryptology ePrint Archive, Report 2012/688. 2012. Available online: https://eprint.iacr.org/2012/688 (accessed on 7 June 2021).
- Canetti, R.; Sarkar, P.; Wang, X. Triply Adaptive UC NIZK. Cryptology ePrint Archive, Report 2020/1212. 2020. Available online: https://eprint.iacr.org/2020/1212 (accessed on 7 June 2021).





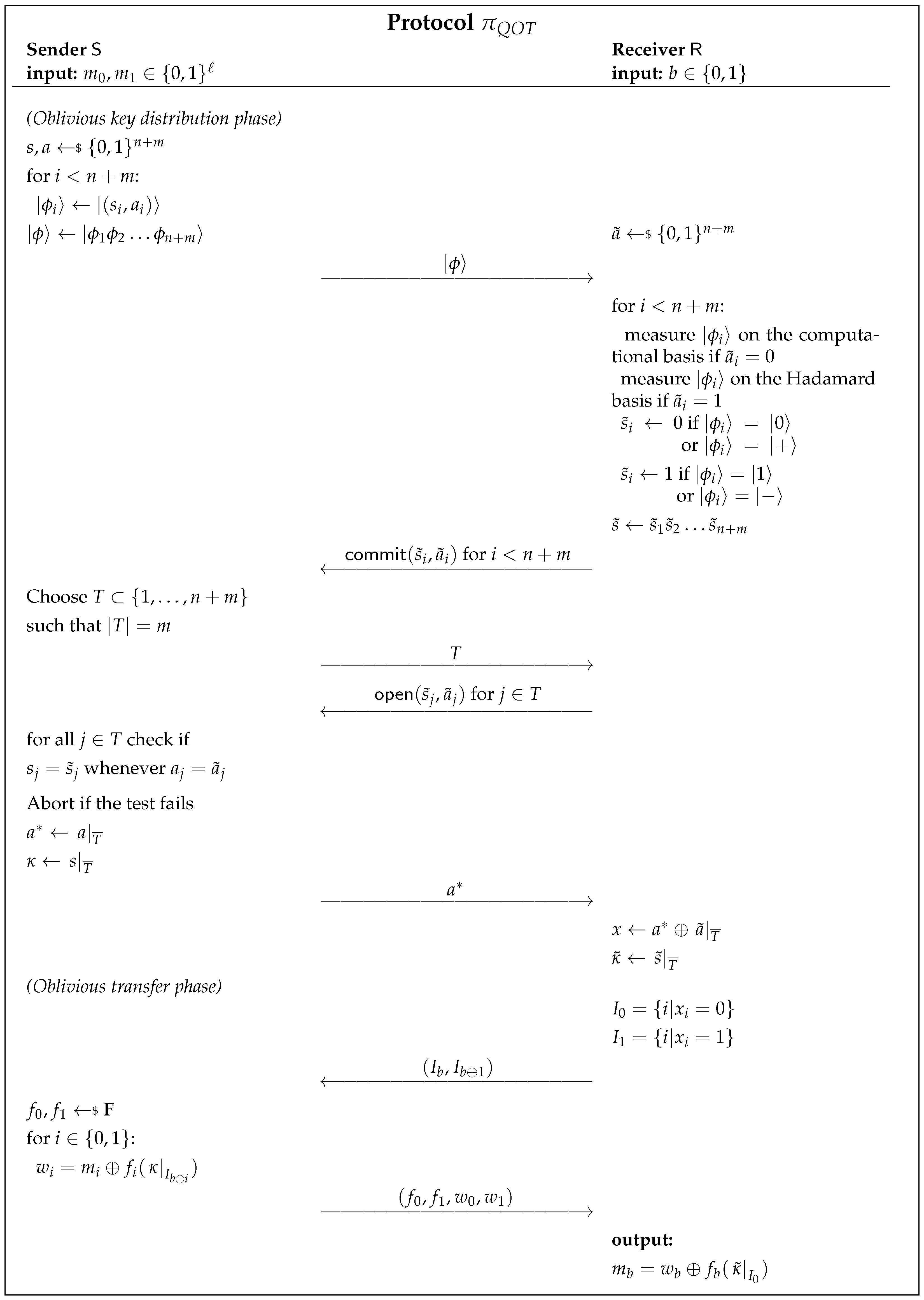

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Costa, B.; Branco, P.; Goulão, M.; Lemus, M.; Mateus, P. Randomized Oblivious Transfer for Secure Multiparty Computation in the Quantum Setting. Entropy 2021, 23, 1001. https://doi.org/10.3390/e23081001
Costa B, Branco P, Goulão M, Lemus M, Mateus P. Randomized Oblivious Transfer for Secure Multiparty Computation in the Quantum Setting. Entropy. 2021; 23(8):1001. https://doi.org/10.3390/e23081001
Chicago/Turabian StyleCosta, Bruno, Pedro Branco, Manuel Goulão, Mariano Lemus, and Paulo Mateus. 2021. "Randomized Oblivious Transfer for Secure Multiparty Computation in the Quantum Setting" Entropy 23, no. 8: 1001. https://doi.org/10.3390/e23081001
APA StyleCosta, B., Branco, P., Goulão, M., Lemus, M., & Mateus, P. (2021). Randomized Oblivious Transfer for Secure Multiparty Computation in the Quantum Setting. Entropy, 23(8), 1001. https://doi.org/10.3390/e23081001





