Confined Quantum Hard Spheres
Abstract
1. Introduction
2. Method
3. Results
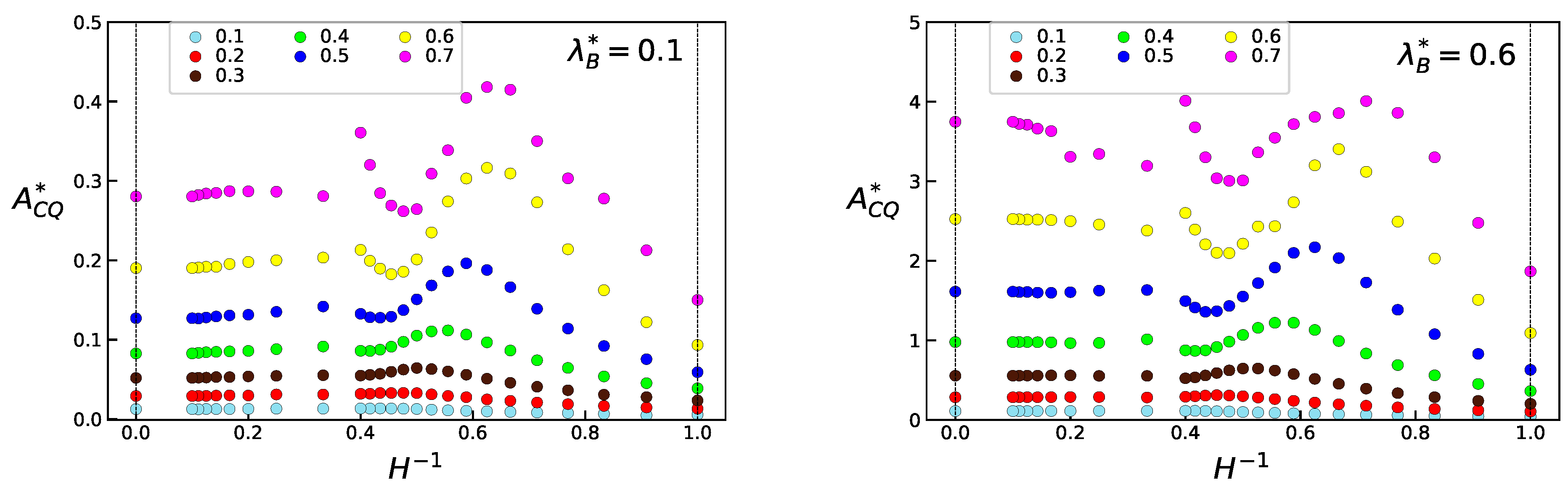
3.1. Confined QHS Global Behaviour
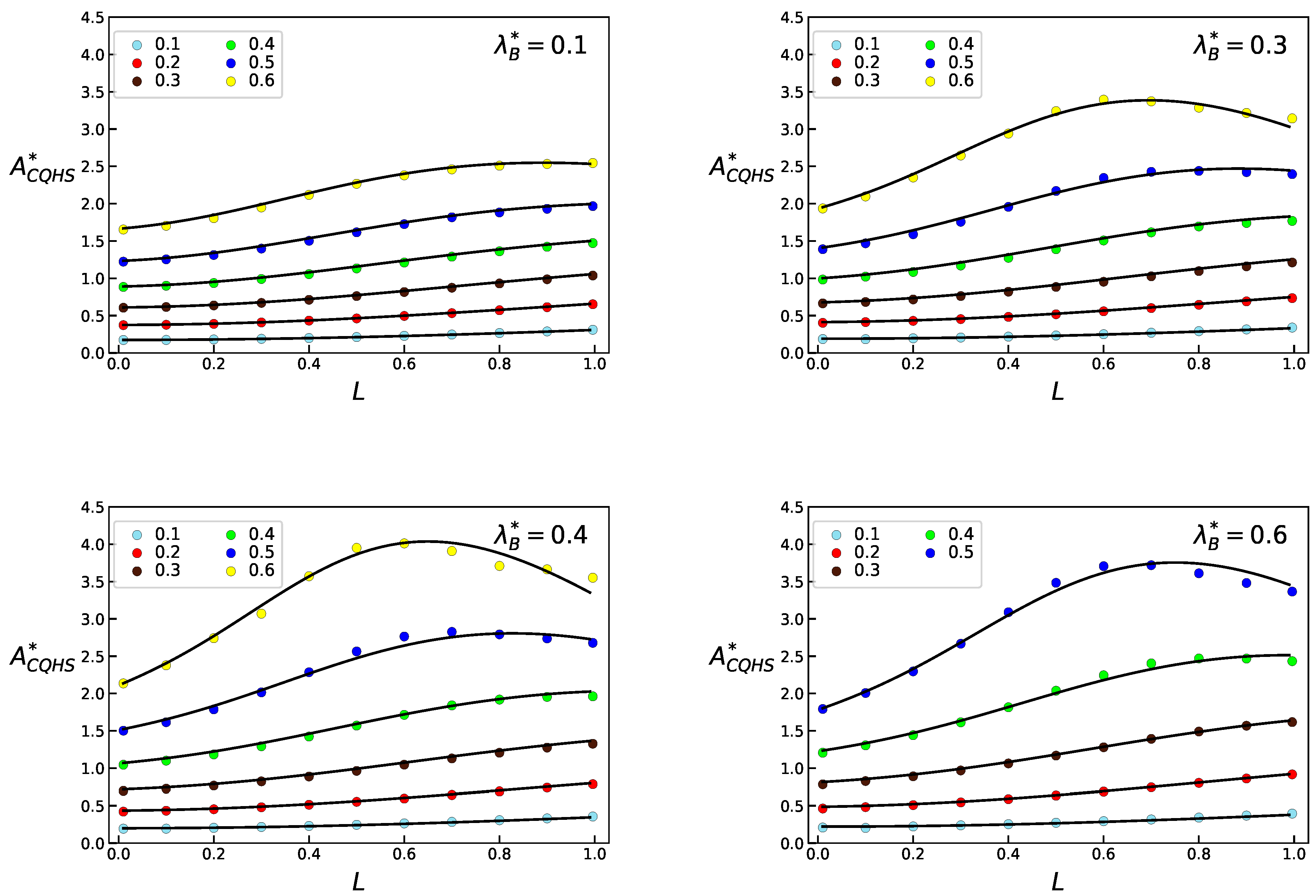
3.2. Equation of State for Extreme Confinement
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Neek-Amal, M.; Lohrasebi, A.; Mousaei, M.; Shayeganfar, F.; Radha, B.; Peeters, F.M. Fast water flow through graphene nanocapillaries: A continuum model approach involving the microscopic structure of confined water. Appl. Phys. Lett. 2018, 113, 083101. [Google Scholar] [CrossRef]
- Hu, S.; Gopinadhan, K.; Rakowski, A.; Neek-Amal, M.; Heine, T.; Grigorieva, I.V.; Haigh, S.J.; Peeters, F.M.; Geim, A.K.; Lozada-Hidalgo, M. Transport of hydrogen isotopes through interlayer spacing in van der Waals crystals. Nat. Nanotechnol. 2018, 13, 468–472. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Panagiotopoulos, A.Z.; Debenedetti, P. Finite-size scaling study of the vapor-liquid critical properties of confined fluids: Crossover from three dimensions to two dimensions. J. Chem. Phys. 2010, 132, 144107. [Google Scholar] [CrossRef]
- Das, C.K.; Singh, J.K. Effect of confinement on the solid-liquid coexistence of Lennard-Jones Fluid. J. Chem. Phys. 2013, 139, 174706. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, M.; Löwen, H. Phase diagram of hard spheres confined between two parallel plates. Phys. Rev. E 1997, 55, 7228–7241. [Google Scholar] [CrossRef]
- Liu, K.S.; Kalos, M.H.; Chester, G.V. Quantum hard spheres in a channel. Phys. Rev. A 1974, 10, 303–308. [Google Scholar] [CrossRef]
- Trejos, V.M.; Martínez, A.; Gil-Villegas, A. Computer simulation of liquid-vapor coexistence of confined quantum fluids. J. Chem. Phys. 2013, 139, 184505. [Google Scholar] [CrossRef]
- Wigner, E. On the quantum correction for thermodynamic equilibrium. Phys. Rev. 1932, 40, 749–759. [Google Scholar] [CrossRef]
- Kirkwood, J.G. Quantum statistics of almost classical assemblies. Phys. Rev. 1933, 44, 31–37. [Google Scholar] [CrossRef]
- Dai, W.-S.; Xie, M. Interacting quantum gases in confined space; Two- and three-dimensional equations of state. J. Math. Phys. 2007, 48, 123302. [Google Scholar] [CrossRef]
- Del Río, F.; Martina, E.; Leiva, M. Generalized Bernoulli construction. A heuristic approach to the equation of state. Am. J. Phys. 1974, 42, 1083–1086. [Google Scholar] [CrossRef]
- Del Río, F.; Trigueros, M.; Martina, E. On the generalized Bernoulli construction. II. Extension to two and three dimensions. Am. J. Phys. 1976, 44, 36–40. [Google Scholar] [CrossRef]
- Gil-Villegas, A.; del Río, F.; Vega, C. Thermodynamics of fluids obtained by mapping the collision properties. Phys. Rev. E 1996, 53, 2326–2336. [Google Scholar] [CrossRef]
- Dai, W.-S.; Xie, M. Quantum statistics of ideal gases in confined space. Phys. Lett. A 2003, 311, 340–346. [Google Scholar] [CrossRef][Green Version]
- Dai, W.-S.; Xie, M. Geometry effects in confined space. Phys. Rev. E 2004, 70, 016103. [Google Scholar] [CrossRef]
- Yoon, B.-J.; Scheraga, H.A. Monte Carlo simulation of the hard-sphere fluid with quantum correction and estimate of its free energy. J. Chem. Phys. 1988, 88, 3923–3933. [Google Scholar] [CrossRef]
- Franosch, T.; Lang, S.; Schilling, R. Fluids in extreme confinement. Phys. Rev. Lett. 2012, 109, 240601. [Google Scholar] [CrossRef]
- Slater, J.C. The Quantum Theory of the equation of state. Phys. Rev. 1931, 38, 237–242. [Google Scholar] [CrossRef]
- Gibson, W.G. Quantum corrections to the properties of a dense fluid with non-analytic intermolecular potential function. I. The general case. Mol. Phys. 1975, 30, 1–11. [Google Scholar] [CrossRef]
- Gibson, W.G. Quantum corrections to the properties of a dense fluid with non-analytic intermolecular potential function. II. Hard spheres. Mol. Phys. 1975, 30, 13–30. [Google Scholar] [CrossRef]
- Zwanzig, R.W. High-temperature equation of state by a perturbation method. I. Non-polar gases. J. Chem. Phys. 1954, 22, 1420–1426. [Google Scholar] [CrossRef]
- Gibson, W.G. Quantum corrections to the equation of state for nonanalytical potentials. Phys. Rev. A 1972, 5, 862–867. [Google Scholar] [CrossRef]
- Hooper, M.A.; Nordholm, S. Generalized van der Waals theory X. Interface profiles and surface tension of simple quantum fluids. Mol. Phys. 1982, 47, 329–345. [Google Scholar] [CrossRef]
- Nordholm, S.; Greberg, H.; Penfold, R. On the statistical mechanical equations of state for simple fluids: Effective hard spheres and quantum corrections. Fluid Phase Eq. 1993, 90, 307–332. [Google Scholar] [CrossRef]
- Runge, K.J.; Chester, G.V. Solid-fluid transition of quantum hard spheres at finite temperatures. Phys. Rev. B 1998, 38, 135–162. [Google Scholar] [CrossRef] [PubMed]
- Chandler, D.; Wolynes, P.G. Exploiting the isomorphism between quantum theory and classical statistical mechanics of polyatomic fluids. J. Chem. Phys. 1981, 74, 4078–4095. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Carnahan, N.F.; Starling, K.E. Equation of state for nonattractive rigid spheres. J. Chem. Phys. 1969, 51, 635–636. [Google Scholar] [CrossRef]
- Henderson, D. A simple equation of state for hard discs. Mol. Phys. 1975, 30, 971–972. [Google Scholar]
- Gloor, G.J.; Jackson, G.; Blas, F.J.; de Miguel, E. Test-area simulation method for the direct determination of the interfacial tension of systems with continuous or discontinuous potentials. J. Chem. Phys. 2005, 123, 134703. [Google Scholar] [CrossRef]
- Serna, C.; Gil-Villegas, A. Molecular thermodynamics of quantum square-well fluids using a path-integral perturbation theory. Mol. Phys. 2016, 114, 2700–2716. [Google Scholar] [CrossRef]
- Contreras, S.; Serna, C.; Gil-Villegas, A. Wertheim Model for Quantum Associating Hard Spheres. J. Chem. Eng. Dat 2020, 65, 5933–5937. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Contreras, S.; Gil-Villegas, A. Confined Quantum Hard Spheres. Entropy 2021, 23, 775. https://doi.org/10.3390/e23060775
Contreras S, Gil-Villegas A. Confined Quantum Hard Spheres. Entropy. 2021; 23(6):775. https://doi.org/10.3390/e23060775
Chicago/Turabian StyleContreras, Sergio, and Alejandro Gil-Villegas. 2021. "Confined Quantum Hard Spheres" Entropy 23, no. 6: 775. https://doi.org/10.3390/e23060775
APA StyleContreras, S., & Gil-Villegas, A. (2021). Confined Quantum Hard Spheres. Entropy, 23(6), 775. https://doi.org/10.3390/e23060775





