Two Chebyshev Spectral Methods for Solving Normal Modes in Atmospheric Acoustics
Abstract
1. Introduction
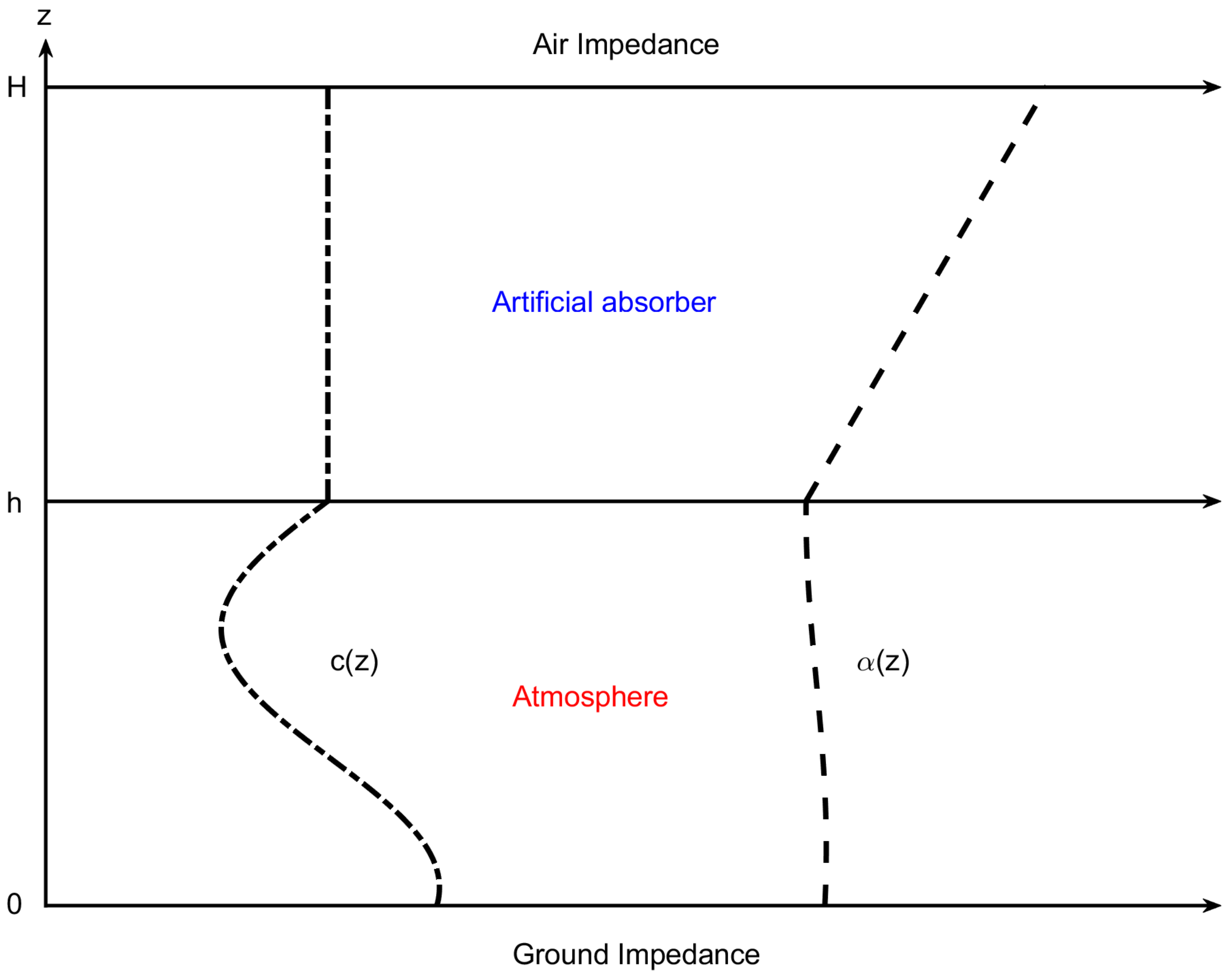
2. Atmospheric Normal Modes
3. Discretized Atmospheric Normal Modes by Two Spectral Methods
3.1. Discretized Atmospheric Normal Modes by Chebyshev-Tau Spectral Method
3.2. Discretized Atmospheric Normal Modes by Chebyshev-Collocation Spectral Method
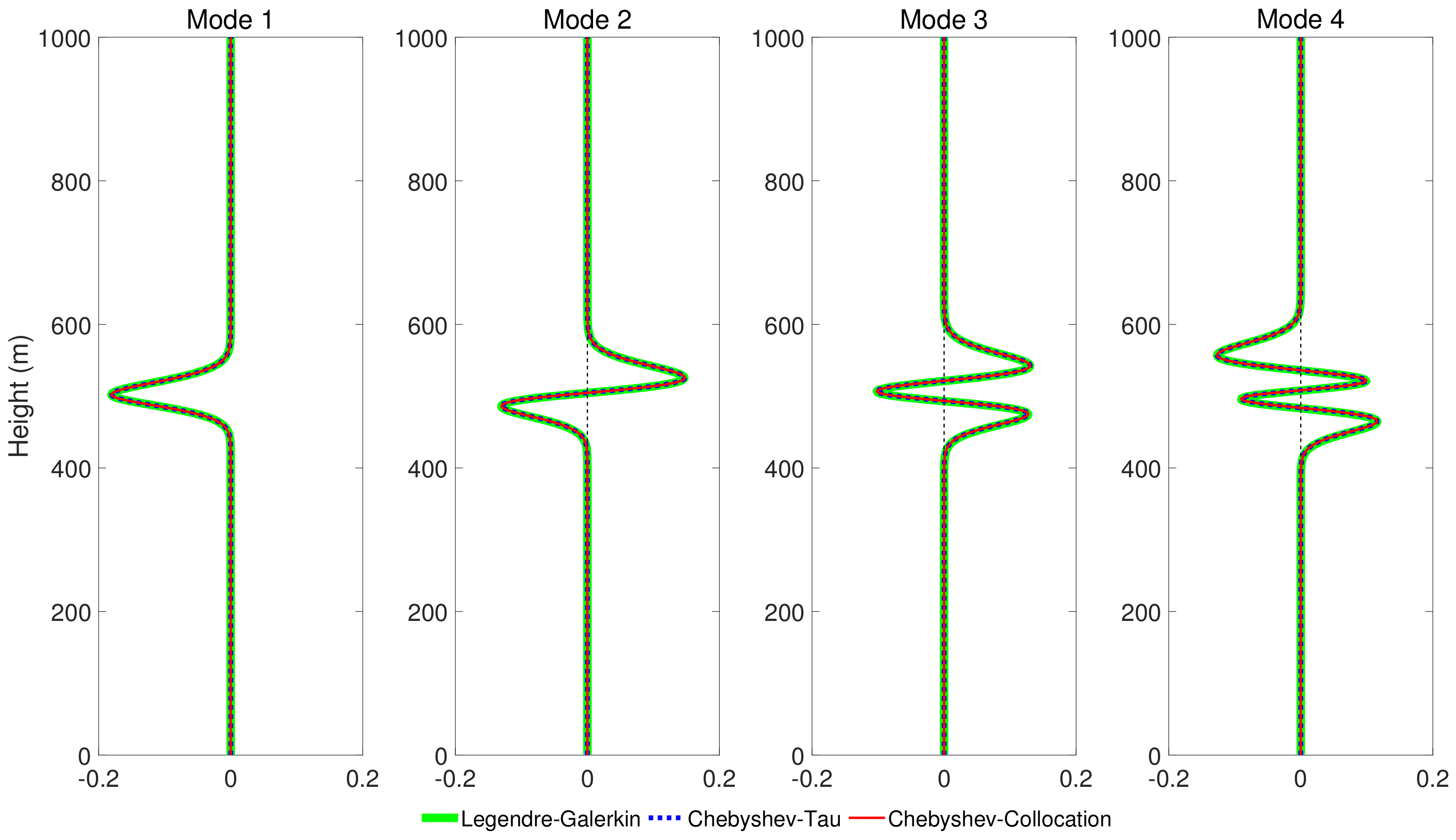
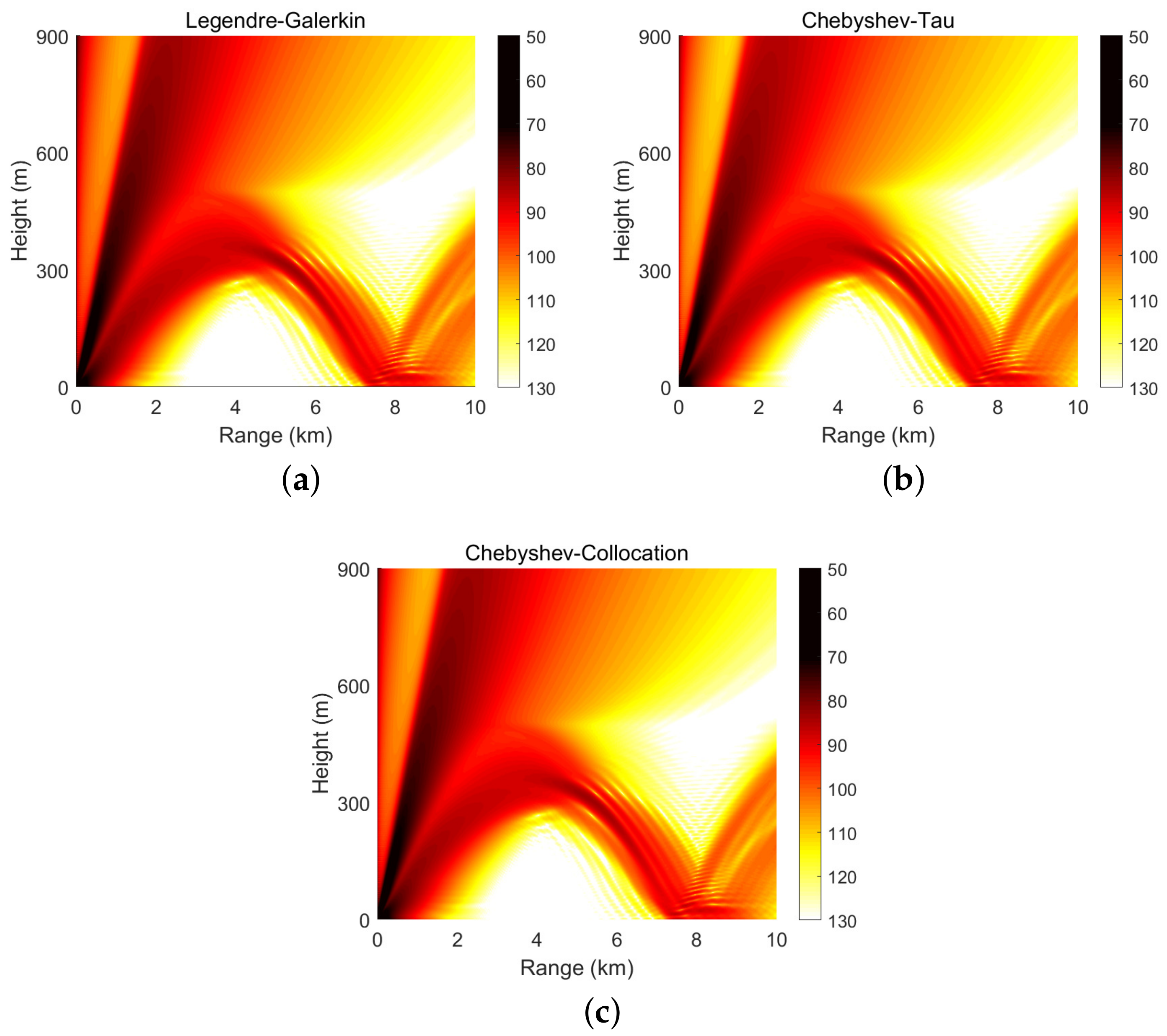
4. Numerical Experiment and Analysis
4.1. Downwind Case
4.2. Upwind Case
5. Discussion of Computational Speed
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Salomons, E.M. Computational Atmospheric Acoustics; Springer Science Business Media: Dordrecht, The Netherlands, 2001. [Google Scholar]
- Yang, X. Computational Atmospheric Acoustics; Science Press: Beijing, China, 2015. [Google Scholar]
- Gilbert, K.; White, M. Application of the parabolic equation to sound propagation in a refracting atmosphere. J. Acoust. Soc. Am. 1989, 85, 630–637. [Google Scholar]
- Gilbert, K.E.; Di, X. A fast Green’s function method for one-way sound propagation in the atmosphere. J. Acoust. Soc. Am. 1993, 94, 2343–2352. [Google Scholar] [CrossRef]
- Jensen, F.B.; Kuperman, W.A.; Porter, M.B.; Schmidt, H. Computational Ocean Acoustics; Springer: New York, NY, USA, 2011. [Google Scholar]
- Gilbert, R.; Lee, S.W.; Kuester, E.; Chang, D.C.; Richards, W.F.; Gilbert, R.; Bong, N. A fast-field program for sound propagation in a layered atmosphere above an impedance ground. J. Acoust. Soc. Am. 1985, 77, 345. [Google Scholar]
- Porter, M.B. Scooter: A Finite Element FFP Code. 2010. Available online: https://oalib-acoustics.org/AcousticsToolbox/index_at.html (accessed on 2 June 2021).
- Pierce, A.D. Acoustics: An Introduction to Its Physical Principles and Applications; American Institute of Physics: New York, NY, USA, 1991. [Google Scholar]
- Waxler, R. An eigenfunction expansion for low-frequency acoustic propagation in a downward-refracting stratified medium over a complex impedance plane. J. Acoust. Soc. Am. 2002, 111, 2352. [Google Scholar] [CrossRef]
- Waxler, R. A vertical eigenfunction expansion for the propagation of sound in a downward-refracting atmosphere over a complex impedance plane. J. Acoust. Soc. Am. 2002, 112, 2540. [Google Scholar] [CrossRef] [PubMed]
- Dzieciuch, M. A Matlab Code for Computing Normal Modes Based on Chebyshev Approximations. 1993. Available online: https://oalib-acoustics.org/Modes/aw (accessed on 2 June 2021).
- Evans, R.B. A Legendre-Galerkin Technique for Differential Eigenvalue Problems with Complex and Discontinuous Coefficients, Arising in Underwater Acoustics. 2016. Available online: https://oalib-acoustics.org/Modes/rimLG/ (accessed on 2 June 2021).
- Tu, H.; Wang, Y.; Liu, W.; Ma, X.; Xiao, W.; Lan, Q. A Chebyshev Spectral Method for Normal Mode and Parabolic Equation Models in Underwater Acoustics. Math. Probl. Eng. 2020, 2020, 1–12. [Google Scholar] [CrossRef]
- Tu, H.; Wang, Y.; Lan, Q.; Liu, W.; Xiao, W.; Ma, S. A Chebyshev-Tau spectral method for normal modes of underwater sound propagation with a layered marine environment. J. Sound Vib. 2020, 2020, 1–16. [Google Scholar] [CrossRef]
- Tu, H. A Chebyshev-Tau Spectral Method for Normal Modes of Underwater Sound Propagation with a Layered Marine Environment in Matlab and Fortran. 2021. Available online: https://oalib-acoustics.org/Modes/NM-CT (accessed on 2 June 2021).
- Tu, H.; Wang, Y.; Lan, Q.; Liu, W.; Xiao, W.; Ma, S. Applying a Legendre collocation method based on domain decomposition to calculate underwater sound propagation in a horizontally stratified environment. J. Sound Vib. (under review).
- Wang, Y.; Tu, H.; Liu, W.; Xiao, W.; Lan, Q. Application of Chebyshev collocation method to solve parabolic equation model of underwater acoustic propagation. Acoust. Aust. 2021, 2021, 1–12. [Google Scholar] [CrossRef]
- Tu, H.; Wang, Y.; Ma, X.; Zhu, X. Applying Chebyshev-Tau spectral method to solve the parabolic equation model of wide-angle rational approximation in ocean acoustics. J. Theor. Comput. Acoust. (under review).
- Gottlieb, D.; Orszag, S.A. Numerical Analysis of Spectral Methods, Theory and Applications; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1977. [Google Scholar] [CrossRef]
- Boyd, J.P. Chebyshev and Fourier Spectral Methods, 2nd ed.; Dover: New York, NY, USA, 2001. [Google Scholar]
- Canuto, C.; Hussaini, M.Y.; Quarteroni, A.; Zang, T.A. Spectral Methods Fundamentals in Single Domains; Spring: Berlin, Germany, 2006. [Google Scholar] [CrossRef]
- Jie, S.; Tao, T.; Lilian, W. Spectral Methods Algorithms, Analysis and Applications; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Evans, R.B.; Di, X.; Gilbert, K.E. (Eds.) A Legendre-Galerkin Technique for Finding Atmospheric Acoustic Normal Modes; Acoustical Society of America: Boston, MA, USA, 2017; Volume 30. [Google Scholar]
- Evans, R.B.; Di, X.; Gilbert, K.E. A Legendre-Galerkin spectral method for constructing atmospheric acoustic normal modes. J. Acoust. Soc. Am. 2018, 143, 3595–3601. [Google Scholar] [CrossRef] [PubMed]
- Evans, R.B. The Convergence of the Legendre–Galerkin Spectral Method for Constructing Atmospheric Acoustic Normal Modes. J. Theor. Comput. Acoust. 2020, 28, 2050002. [Google Scholar] [CrossRef]
- Sabatini, R.; Cristini, P. A Multi-Domain Collocation Method for the Accurate Computation of Normal Modes in Open Oceanic and Atmospheric Waveguides. Acta Acust. United Acust. 2019, 105, 464–474. [Google Scholar] [CrossRef]
- Tisseur, F. Backward error and condition of polynomial eigenvalue problems. Linear Algebra Appl. 2000, 309, 339–361. [Google Scholar] [CrossRef]
- Francoise, T.; Meerbergen, K. The quadratic eigenvalue problem. Siam Rev. 2001, 43, 235–286. [Google Scholar]
- Pierre, D.J.; Tisseur, F. Perturbation theory for homogeneous polynomial eigenvalue problems. Linear Algebra Appl. 2003, 358, 71–94. [Google Scholar]
- Pichon, A.L.; Hauchecorne, E.B.A. Infrasound Monitoring for Atmospheric Studies, Challenges in Middle Atmosphere Dynamiacs and Societal Benefits; Springer Nature: Cham, Switzerland, 2019. [Google Scholar]
- Anderson, P.J.; Loizou, G. A Jacobi Type Method for Complex Symmetric Matrices. Numer. Math. 1976, 25, 347–363. [Google Scholar] [CrossRef]






| Height (m) | Sound Speed (m/s) | Attenuation (dB/Wavelength) |
|---|---|---|
| 2000 | 344.0 | 2.50 |
| 1500 | 344.0 | 0.10 |
| 900 | 344.0 | 0.01 |
| 700 | 344.0 | 0.00 |
| 500 | 341.5 | 0.00 |
| 100 | 349.0 | 0.00 |
| 0 | 345.0 | 0.00 |
| Height (m) | Sound Speed (m/s) | Attenuation (dB/Wavelength) |
|---|---|---|
| 2000 | 346.0 | 1.00 |
| 1500 | 346.0 | 0.10 |
| 1200 | 346.0 | 0.01 |
| 900 | 346.0 | 0.00 |
| 500 | 348.0 | 0.00 |
| 350 | 344.0 | 0.00 |
| 100 | 340.0 | 0.00 |
| 0 | 344.0 | 0.00 |
| Experiment | Part of Program | aaLG | aaLG-M | AtmosCTSM | AtmosCCSM |
|---|---|---|---|---|---|
| 1. discretize | 105.344 | 104.691 | 0.522 | 0.468 | |
| 2. solve eigenvalues | 2017.324 | 34.289 | 34.091 | 34.331 | |
| 3. normal modes | 35.587 | 35.292 | 0.867 | 0.237 | |
| 4. synthesis | 10.021 | 8.714 | 0.518 | 0.421 | |
| Total | 2138.276 | 182.986 | 35.998 | 35.184 | |
| 1. discretize | 125.429 | 123.892 | 0.482 | 0.361 | |
| 2. solve eigenvalues | 2039.324 | 36.119 | 34.886 | 34.017 | |
| 3. normal modes | 36.501 | 38.181 | 0.911 | 0.334 | |
| 4. synthesis | 11.669 | 10.648 | 0.806 | 0.616 | |
| Total | 2212.923 | 208.840 | 37.085 | 35.328 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Tu, H.; Liu, W.; Xiao, W.; Lan, Q. Two Chebyshev Spectral Methods for Solving Normal Modes in Atmospheric Acoustics. Entropy 2021, 23, 705. https://doi.org/10.3390/e23060705
Wang Y, Tu H, Liu W, Xiao W, Lan Q. Two Chebyshev Spectral Methods for Solving Normal Modes in Atmospheric Acoustics. Entropy. 2021; 23(6):705. https://doi.org/10.3390/e23060705
Chicago/Turabian StyleWang, Yongxian, Houwang Tu, Wei Liu, Wenbin Xiao, and Qiang Lan. 2021. "Two Chebyshev Spectral Methods for Solving Normal Modes in Atmospheric Acoustics" Entropy 23, no. 6: 705. https://doi.org/10.3390/e23060705
APA StyleWang, Y., Tu, H., Liu, W., Xiao, W., & Lan, Q. (2021). Two Chebyshev Spectral Methods for Solving Normal Modes in Atmospheric Acoustics. Entropy, 23(6), 705. https://doi.org/10.3390/e23060705






