1. Introduction
In addition to the omnipresent noise, many complex systems are governed by dynamical equations that involve some sort of memory or time delay. The latter may stem from delayed response in the communication between (active) constituents, retardation effects due to finite signal transmission times, or maturation times in population growth. Another common source of delay is the presence of feedback loops, which typically involve a delay due to the time lag between feeding a signal and receiving the response [
1,
2,
3,
4,
5,
6,
7]. Feedback is a widespread mechanism in nature, encountered in various biological systems (such as gene regulatory networks [
8,
9,
10,
11,
12,
13,
14], the cell metabolism [
15,
16], or the chemotactal motion of bacteria [
17,
18,
19]); and is further implemented in numerous artificial systems (such as robots [
5], autonomously driving cars [
20], or quantum devices [
21,
22]). Recent experiments on small-scale, fluctuating systems successfully apply feedback control involving video microscopy and co-moving laser traps to create virtual potentials [
23,
24] or realize arbitrary interactions between colloidal particles [
25,
26]. Such experiments give rise to a stochastic motion with time delay of the feedback-controlled colloidal particles [
2,
23,
24,
25,
26,
27,
28,
29].
As a most simple way to mathematically describe stochastic motion with time delay, we will consider the overdamped Langevin equation
with a noise term
, an external potential
V, and a linear delay force,
, where
K defines the distribution of the delay. The delay distribution depends on the details of the underlying (feedback) mechanism. For example, in biological systems, the delay often has a rather broad distribution [
11,
30,
31], while in control theory, a delta-distributed delay is more common,
, giving rise to a single delay time,
. The prime physical example motivating this paper is a colloidal particle under time-delayed feedback control, where the delay distribution is, in principle, externally tunable by the involved computer.
From a practical point of view, delay is often unwanted, as it may destroy the system’s stability [
32,
33,
34,
35,
36,
37,
38] or induce chaos [
39,
40]. It furthermore dramatically increases the difficulty of the mathematical description, as the combination of delay and noise yields non-Markovian stochastic processes with infinite-dimensionality [
31,
32,
37,
38,
41], that are, moreover, automatically far from thermal equilibrium [
42,
43]. At the same time, it is known that delay can also be beneficial, for example, it can stabilize period solutions [
3,
44,
45,
46] or induce coherent oscillations [
43,
47], which is why delay is sometimes intentionally implemented, see [
45,
48,
49]. Furthermore, it has recently been shown that delay may yield intriguing thermodynamic behavior. For example, a delay force acting on a colloid can induce a net heat flow from the heat bath to the colloid, i.e., a reduction of the medium entropy [
43,
50]. This refrigeration effect, called feedback cooling, is closely related to feedback cooling and “entropy pumping” in Markovian inertial systems with velocity-dependent feedback [
51,
52,
53,
54,
55,
56] (specifically, the delay force has a comparable effect as a velocity-dependent force, and both induce entropy pumping, see [
43,
57]). While these effects are, in principle, known, we are still only at the beginning of a full understanding of the impact of delay on stochastic dynamics. Given the omnipresence of time delay in many fluctuating systems, deepening our theoretical understanding seems indeed crucial.
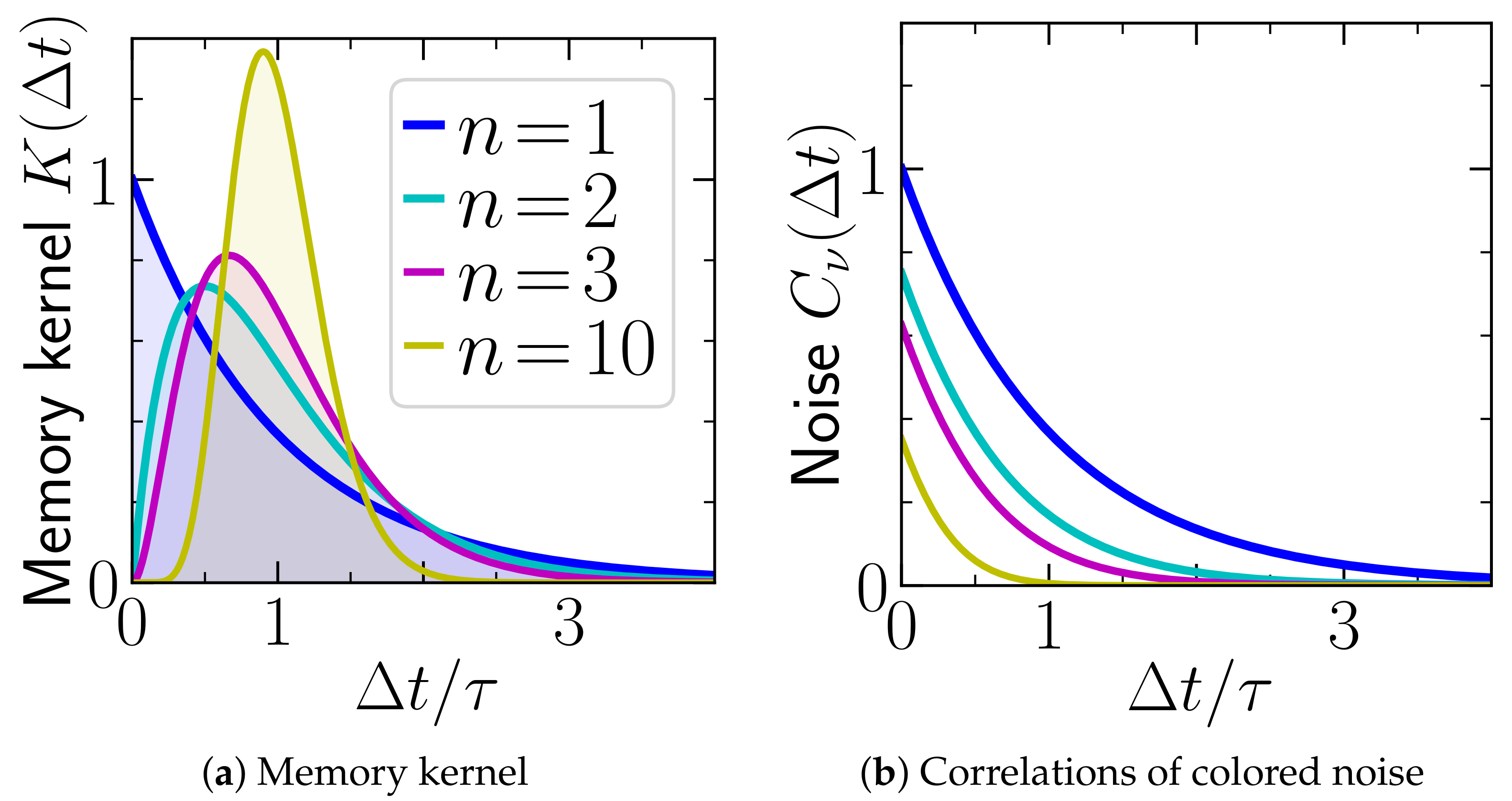
In this paper, we discuss the influence of the distribution of the delay (i.e., the functional form of
K in Equation (
1)) on dynamical and thermodynamical properties in the overdamped case. In contrast to algebraically decaying delay distributions, we here focus on “short-ranged” ones that eventually decay exponentially fast in the long time limit, which are more important in the context of feedback and naturally arise in biological systems. For a recent discussion of other kernels and corresponding stability issues, see [
58]. Specifically, we will perform a linear stability analysis (around local extrema of an external potential) and study how the stability boundaries shift when we change nothing but the distribution of the delay while keeping the mean delay time and the weight of the kernel constant. Gamma-distributed delays turn out to be particularly suitable to study these questions. They are versatile (including single-exponential, and delta-distributed delay, as well as distributions with a pronounced maximum of finite width), and, at the same time, are embeddable in a higher-dimensional Markovian system. We will exploit both properties in this paper. As a prominent example for thermodynamic behavior induced by delay, we will further consider how the distribution of delay influences the aforementioned “negative dissipation”. We also study the impact of colored noise. Lastly, we discuss the total entropy production and the thermodynamic efficiency for a specific realization of a feedback controller involving non-reciprocal interactions between some linear, stochastic internal degrees of freedom (which we interpret as the “memory cells”) and gives rise to a delay force with Gamma-distributed delay.
3. Stability for Different n
Let us now turn to the dynamics of
. A prominent property of systems with delay are delay-induced oscillations (which can generally not occur in first order ODEs, but arise in first order DDEs [
33]). In linear systems, they are either damped, such that a stable steady state is reached in the limit
, or their amplitude increases with time yielding instability. Here we explore whether, for a given
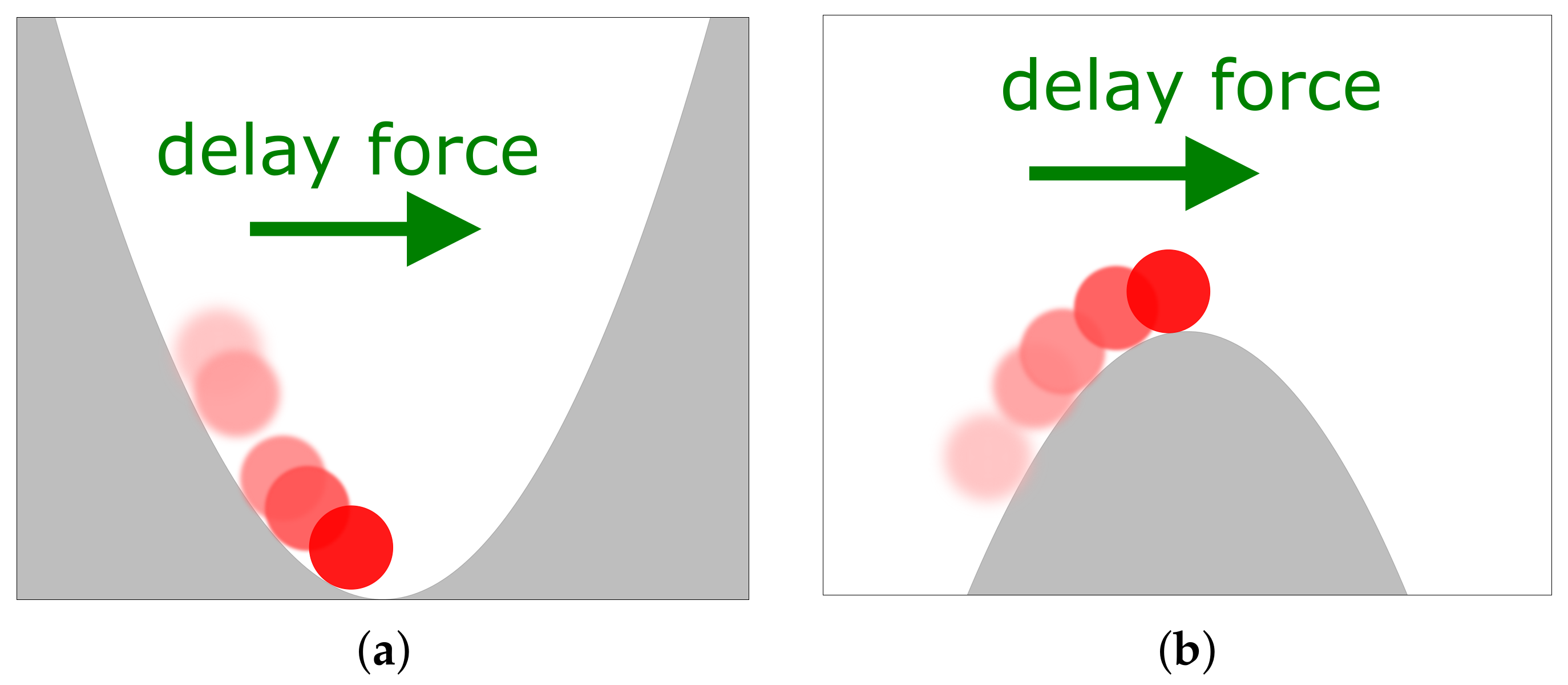
,
k,
and
n, the system reaches a stable steady state (for more mathematical discussions of noise-free systems with Gamma-distributed delay, see [
65,
66]). For a stochastic system (
2) with a general potential
V, the following analysis determines the linear stability of the fixed points. As an illustration, imagine the task to stabilize a particle on a parabolic mountain (when
) by means of a delayed feedback force (
Figure 1). As we now show, the system’s stability significantly depends on the distribution of the delay, even if the feedback gain and mean delay time stay the same.
Determining the stability of the noisy process
amounts to checking whether the moments stay finite or diverge as
. In the here considered examples, the steady state probability density is Gaussian [
32,
67] (with zero mean due to the system’s symmetry). Thus, we need to consider the second moment,
. A calculation of the latter for different
n is provided in
Appendix B. For
, this yields cumbersome integral expressions. Interestingly, we found that the stability boundaries, however, do not depend on the temperatures
and
. We conclude that the type of noise or the presence of noise at all does not have any impact on the linear stability of the system. This includes, in particular, the colored noise and the related additional memory.
Owing to these insights, we here discuss a simpler route to check the stability based on the noise-free case (
), where (5) reduces to
This linear matrix equation has solutions of the form , such that the stability boundaries can be simply determined by calculating the real part of the largest eigenvalue of the coupling matrix , called . If , the system is unstable, while it is stable if .
Due to the sparseness of
, this strategy allows to determine the stability boundaries up to very large values of
n. However, it is still limited to finite
n. To determine to stability in the limit
, we consider directly the noise-free delay Equation (
9), that is
This equation can also be solved by an exponential ansatz
, yielding the transcendental equation [
68,
69]
In the trivial cases
and
, the solutions are
and
, respectively, immediately giving some stability boundaries. Further, if
, a solution is
. In general, the solutions of Equation (
16) read [
68,
69]
with the infinitely many branches of the Lambert-W function
,
. The branch
has the highest real part. Thus, the stability of the DDE changes at
.
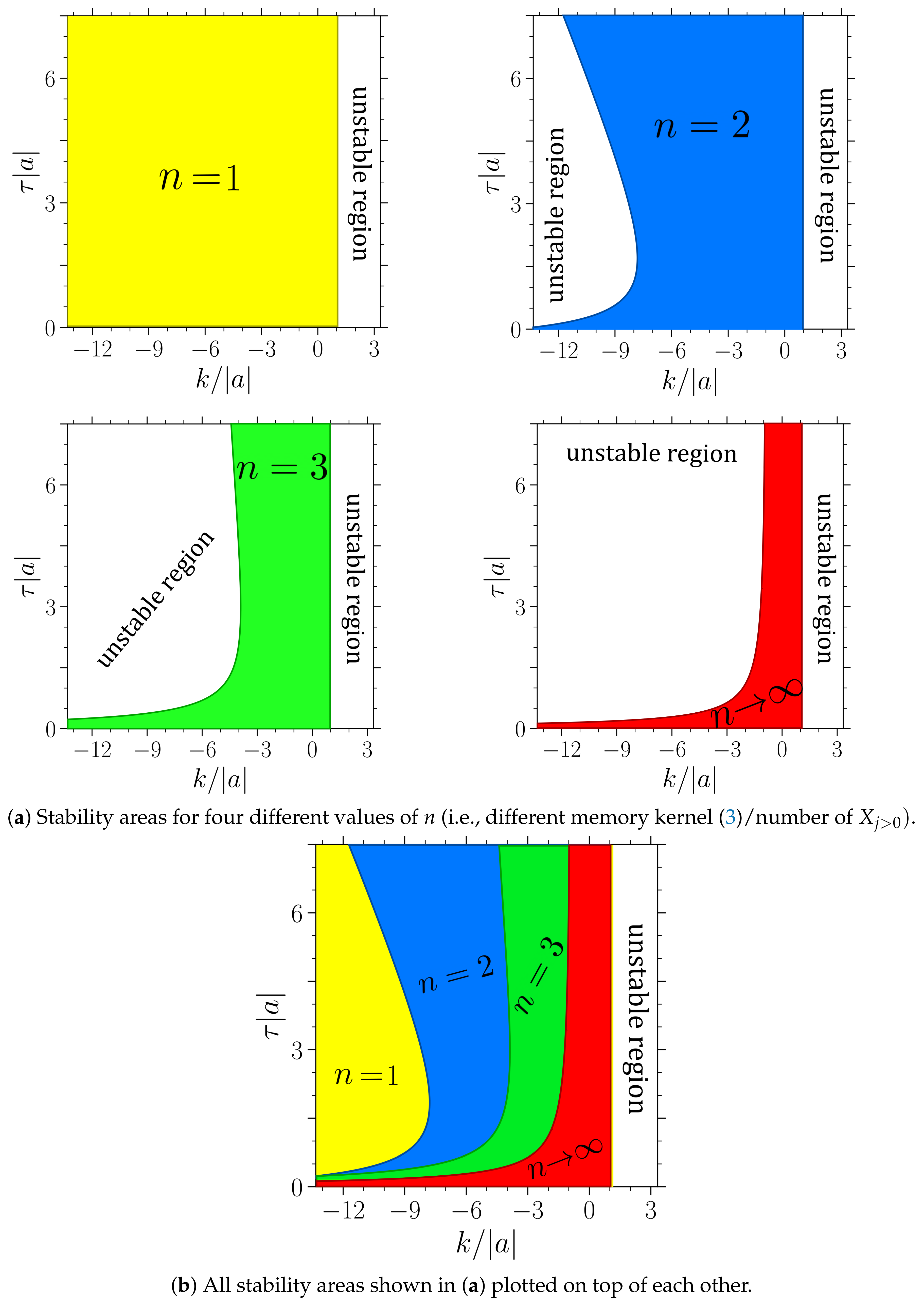
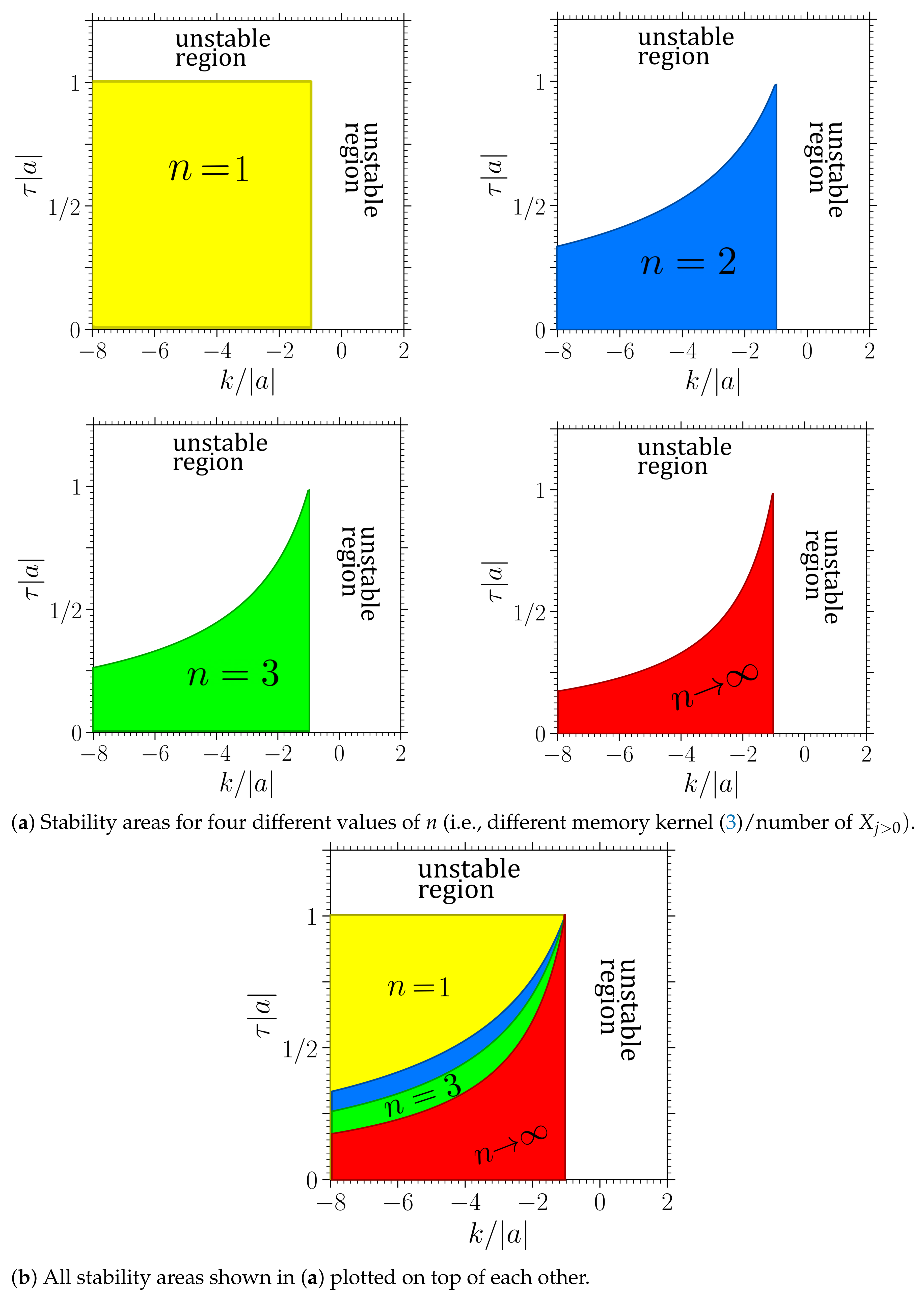
Figure 4 and
Figure 5 show the stability boundaries for various
n of the deterministic system with
and
, respectively, in the plane spanned by the feedback gain
k and mean delay time
(given in units of
and
, respectively). Note that the figures hold for arbitrary values of
and
, respectively. The parameter
can be scaled out from the noise-free Langevin equation upon rescaling the time by
. The system in
Figure 4 (where
) corresponds to a colloidal particle in a harmonic trap, which is as expected stable in the absence of delay force (
or
). In contrast, the system displayed in
Figure 5 (where
) without delay force corresponds to a colloidal particle in a reversed trap, i.e., on a “parabolic mountain”, which is not stable, consistent with our expectation. However, in the presence of delayed feedback, stable and unstable regions emerge for both signs of
a and for all values of
n.
Figure 4 and
Figure 5 reveal that there is a critical
k value of
above which the system is generally unstable for all
n. To get an intuitive understanding for this critical value, we assume for a moment that the particle would for
all past times
stand still, i.e.,
. Under this assumption
because
, such that Equation (
2) reduces to
irrespective of the value of
n (including finite
n and
), and irrespective of the values of
k,
a and
. Now, it becomes clear that the system is generally unstable if
, and that
is a critical value (for all
n).
We now focus on the regions below , where the system with is stable, but may be destabilized by the delay. In this region, we make several interesting observations.
Most prominently, the system with exponentially distributed delay (
) has the
largest stable area for positive and negative
. Further, the stability region of every
, includes the whole
region, while the reverse is never found. This means, the system generally becomes less stable as the delay distribution gets more localized around the delay time
. This trend (which has also been found in the mathematical analysis of corresponding deterministic systems [
65]) is very robust, and also holds for higher
n (e.g.,
) and other
. To achieve stability, it appears to be beneficial to take into account a “larger fraction of the past”. Thus, if the aim of a controller was to stabilize
at a given location, the feedback with exponential delay would be the most effective and robust one.
Another remarkable aspect is the behavior for large mean delay times,
. Only if
(“particle on the parabolic mountain”), increasing the mean delay time seems to generally destabilize the system. Then there even exists a maximal
value of
, where the system is unstable for all
n and
k, see
Figure 5. For
(“particle in the trap”), the behavior is very different. Here, an increased mean delay time can be both, disadvantageous or advantageous for stability (depending on
n and
k). Interestingly, for
n values
, we observe a
reentrant behavior: by increasing the mean delay time, the linear stability is destroyed, but by further increasing
, the system becomes stable again. We suspect that this behavior is a consequence of an interplay with an internal timescale, specifically, the relaxation time within the parabolic potential well, which is of order
. (Note that this estimate stems from solving just the conservative part on the right hand side of the LE
. Strictly speaking, in the presence of the delay force, all timescales may be shifted, including the relaxation times.). If the mean delay time matches this internal timescale, the delay-induced oscillations might be resonantly enhanced, destroying the stability. However, this reentrant behavior is not observed for
and
.
4. Delay-Induced Heat Flow
Let us now turn to a thermodynamic consideration of the systems. To this end, we utilize and extend results from Ref. [
57], where we have explored the connection between coupling topology
and the thermodynamic properties for generic linear systems of the type (5). We note that more general coupling topologies also allow to model other physical systems, as active particles [
57]. Here we will focus on the topology Equation (
5b), which yields the Gamma-distributed delay distributions. We will further give two special cases our main attention: the case of isothermal conditions, i.e., system and controller have the same temperature
(red symbols in the
Figure 6 and the figures below), and the case of a “perfect” (noise-less) controller, i.e.,
(black symbols in
Figure 6).
In steady state, the mean Shannon entropy of the system, i.e.,
[
70] is, per se, conserved (because
). However, nonequilibrium steady states are typically characterized by an entropy flow between system and its bath associated with heat flow. We therefore start by studying the magnitude and sign of the steady-state mean heat flow
between
and its bath induced by the delay force, which is proportional to the medium entropy production rate
. According to the framework by Sekimoto [
71], the stochastic heat
flowing from
to its bath, i.e., the
dissipation of
per infinitesimal time step
is given by [
71]
Note that we define the heat such that
indicates energy transfer from the particle to the bath (different from [
71]). The heat flux (
19) is independent of the question whether the non-Markovian (
2) or the Markovian description (5) is employed. We will thus exploit the latter, allowing us to handle the system analytically in the case of linear forces. We are particularly interested in the
mean heat production or dissipation rate, and find from Equations (5) and (
19)
Further, in the steady state,
-correlations vanish, since
, such that the mean heat production can be expressed based on the positional correlations only
From Equation (
21), analytical expressions for
can be derived for any
n, as outlined in
Appendix B. Noteworthy, the steady-state heat production rate equals the work applied to the system by the external delay force [
70,
71]. Using the closed-form expressions
,
from [
57,
72], one finds from Equation (
21) for the case
From this expression, we see that the heat flow rate diverges at both previously determined stability boundaries
, or
. This shows that, in the unstable regions, the transient dynamics is accompanied by a medium entropy production rate that is unboundedly growing with time. Analogous behavior at the stability boundaries is also found for
. Within the stable regions, we can further simplify Equation (
22) and find
From Equation (
23), one immediately sees that for
the heat flow between
and its bath vanishes when the condition for the FDR (
7) is fulfilled, consistent with the expectation that the system then reaches equilibrium.
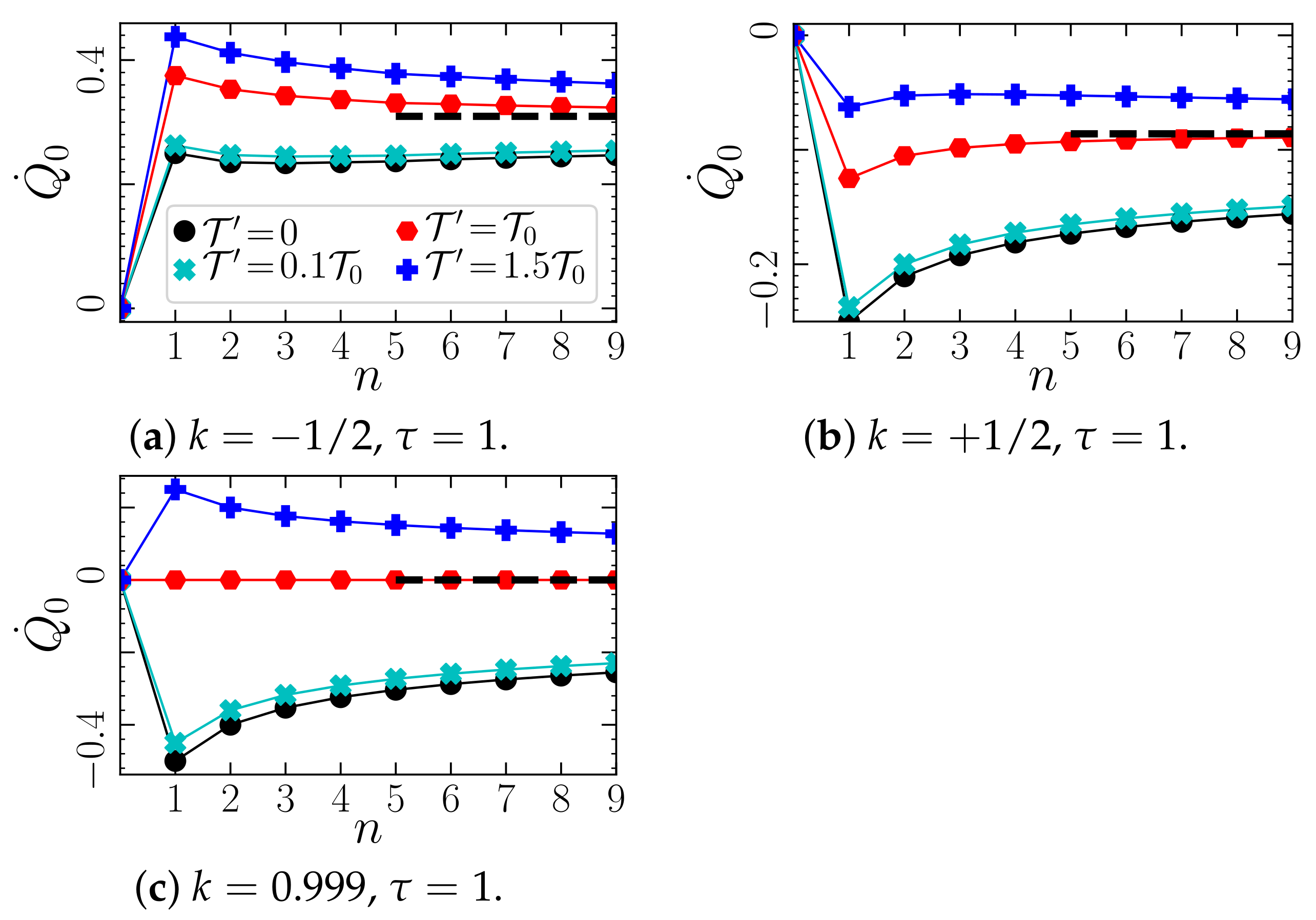
Let us now discuss the general behavior for different
n, i.e., different delay distributions.
Figure 6 shows analytical results for the mean heat rate as functions of
n, for three different values of the feedback gain
k. We here mainly focus on the case
, such that we can consider both negative and
positive k (in stable regions). Note that, in experiments with optical traps, usually the case
is of more practical relevance. First, we notice that the net heat flow of
is generally nonzero, even if the temperature of
and all
is the same (red symbols), showing that the systems considered here are out of equilibrium. An exception is the case
and
, where the medium entropy production rate vanishes. For this special case, the FDR is approximately fulfilled for
(but violated for
[
57]). Further, we find that the magnitude of the induced heat flow is generally maximal for
, and decreases for larger
n. Thus, the exponentially decaying delay generally yields the highest entropy flow between system and bath.
Another observation from
Figure 6 is that for
, the heat flow from the colloid to the bath is negative (
), corresponding to medium entropy
reduction. This means that we have a steady state in which the delay force consistently extracts energy from the heat bath, i.e., feedback cooling. A Markovian external force could not have this impact on the stochastic system (as follows from the second law of thermodynamics). Importantly, this phenomenon also occurs when the “controller”
has the same temperature as the colloid, i.e., isothermal conditions (
Figure 6c), or even if the controller is hotter (then the heat flow is “reversed”) (
Figure 6b). From Equation (
23) follows for the case
the following condition to find feedback cooling and medium entropy reduction
On the level of the Markovian “supersystem” (colloid plus controller), the negative heat flow can be explained by the involved non-reciprocal couplings [
57]. Using the non-Markovian model alone, the explanation is more subtle. An extensive discussion of the origin of the heat flow, which is connected to non-trivial information flow from the colloidal system to the controller appearing in the generalized second law for the controlled system, is provided in [
57]. As an example for a nonlinear system, we have further numerically explored the heat flow in a bistable potential
; and again found regimes where a delay force induces a negative heat flow (for all values of
n).
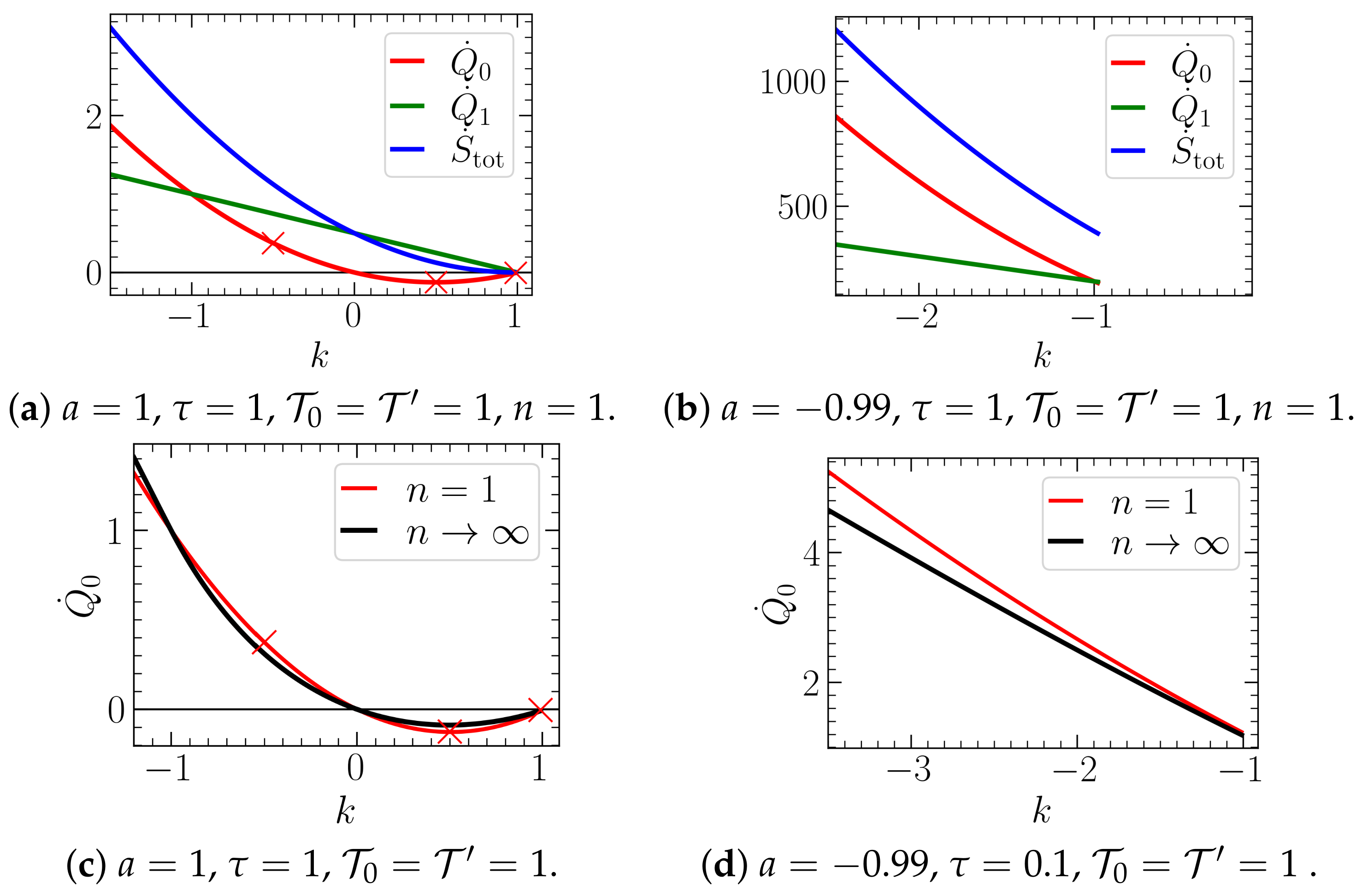
In
Figure 7, we display the heat flow
as a function of
k, for positive and negative
a, for the systems with
and
. We observe that feedback cooling is only possible for
. The reason is that only in this case, stable parameter regimes with
exist, for all
n (see
Section 3). Further, we observe that the heat flow
displays very similar behavior in the systems with
and
for all considered values of
k and
.
Concerning the connection to the stability analysis presented in the previous section, we note that the parameter combination considered in
Figure 6c corresponds for all
n almost to the stability boundary
(see
Figure 4 for a comparable case); i.e., slight increase of
k would result in an unstable dynamics. In that case, the heat rate diverges due to the divergence of correlations entering Equation (
21). However, when approaching this boundary from the left, the heat rate does not exhibit any noticeable difference compared to the parameter settings in the middle of the stability region. On the contrary, if the stability boundary at
is approached, we notice very high values of the heat rate, see
Figure 7b for an example.
Let us now consider the limit
. Recall that in this limit the colored noise
vanishes, while the delay distribution becomes a delta-distribution around
[see Equation (
9)]. We have intensely studied the heat flow in such a system in [
43], for linear and nonlinear systems. The data in
Figure 6 indeed seems to converge to the result from [
43] (given in
Appendix D) as
n increases (as follows from the reasoning in
Section 2.3). We expect the convergence to be more obvious in a regime of
n larger than the regime that we can study on the bases of our analytical solutions. Preliminary numerical simulation results confirm this expectation, but we have not studied this question rigorously yet, and feel that it is beyond the scope of this manuscript. Remarkably, the approach is fastest for isothermal conditions
. In fact, for this specific case, the heat flow behaves very similar to the the heat flow in the limit
for all
k values, see
Figure 7c. To us, the reason for this fastest convergence for
is not clear and represents an interesting perspective of future research.
Finally, we consider the impact of the colored noise
, which in our model stems from the noise terms
in Equation (5) and, thus, from a finite controller temperature, or from controller errors (depending on the interpretation).
Figure 6 shows that the heat flow of
generally increases with the magnitude of the colored noise,
. Thus, this additional noise generally yields an additional
positive contribution to the heat dissipated by the colloid into its heat bath (irrespective of the sign of the heat flow induced by the delay force). This trend persists (not shown here) when we employ the alternative interpretation of the noises associated to
(see
Section 2.4), i.e., when we set
.
Taken together, we conclude that, if the aim of the controller was to cool down the surrounding fluid (like a microscopic refrigerator), the feedback with exponential delay () and without controller errors () would be the most effective one.
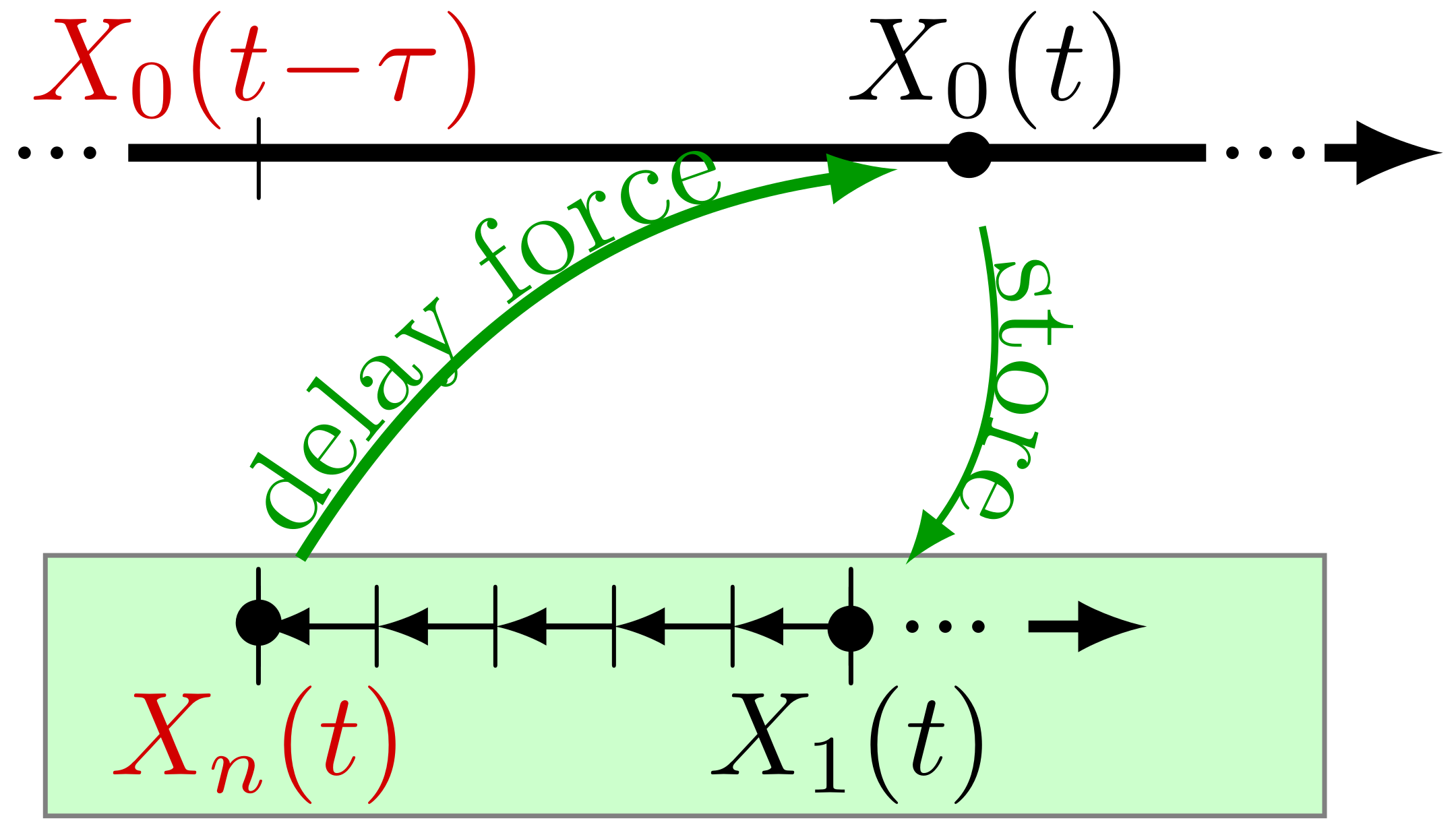
5. The Total Entropy Production
Recent literature for (underdamped) systems with
discrete delay [
42,
50,
73] has pointed out strategies (and related difficulties) in calculating measures of irreversibility based on the non-Markovian dynamics of
alone. Here, we rather focus on the total entropy production of the supersystem consisting of particle plus controller, assuming that all variables in Equation (5) are physical. In other words, we from now on interpret the
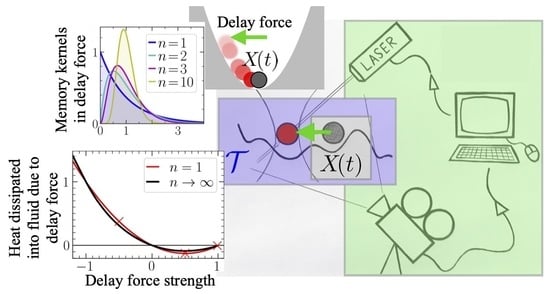
as the internal degrees of freedom of the controller, which are non-reciprocally coupled among each other and generate a time-delayed feedback force on the particle
(as illustrated in
Figure 3). A main goal of the subsequent analysis is to explore how the total entropy production depends on
n and thus, on the sharpness of the delay distribution.
To calculate the dissipated energy of the total supersystem (particle plus controller), we employ the standard formalism from stochastic thermodynamics [
70,
74]. The total EP along a fluctuating trajectory
is given by
involving the multivariate joint Shannon entropy
of the
-point joint probability density function (pdf)
, and the path probabilities
and
for forward and backward process.
conditioned on the starting point
, is essentially the exponential of the Onsager–Machlup action, stated in
Appendix C. We assume that
are even under time-reversal, like positions, which is more suitable when
model memory cells (odd parity would imply information storage in particle velocities). This assumption implies
where
can be identified as the heat flow from
to its bath (
20). In the steady state,
. Applying the analogous steps as between Equations (
20) and (
21), we find that the ensemble average of the EP (
25) reads
with
from (
21). The nonnegativity of
follows by construction from Equation (
25), see [
70]. Equation (
27) yields analytical expressions for the total EP for any
n, see
Appendix B. For
(which was also discussed in [
72]), this yields a particularly simple closed-form expression, which diverges in the unstable regions (
, or
), and in the stable region reads
The mean EP (
27) has a contribution stemming from the dissipation of
to its bath,
, and a contribution from the
, i.e., the dissipation of the additional d.o.f.,
. This second contribution can be considered as the “entropic cost” of the memory [
42,
50,
73] (where the “memory” arises in the form of colored noise and distributed delay). It should be emphasized, however, that memory is not unequivocally connected to EP. For example, the
case with parameters such that FDR is fulfilled, also has memory in the process
, but no EP, see Equation (
29). From Equation (
29), one immediately sees that the EP vanishes if,
and only if, the condition for the FDR (
7) is fulfilled. In all other cases, the process (5) has entropic cost.
Note that the total EP is also positive for isothermal conditions
(red symbols) where no temperature gradients are present in the system. The EP is closely connected with the non-reciprocal couplings between the
, which are non-conservative interactions [
57]. We further note that the total EP is positive even in the cases where we detected the reversed heat flow, showing that the second law of thermodynamics holds for the supersystem (“the colloidal system plus the controller”), as expected. In
Figure 7, we further show for the case
, as a function of
k, both heat flows (
and
) and the total entropy production, which grows like
(as also can be seen from Equation (
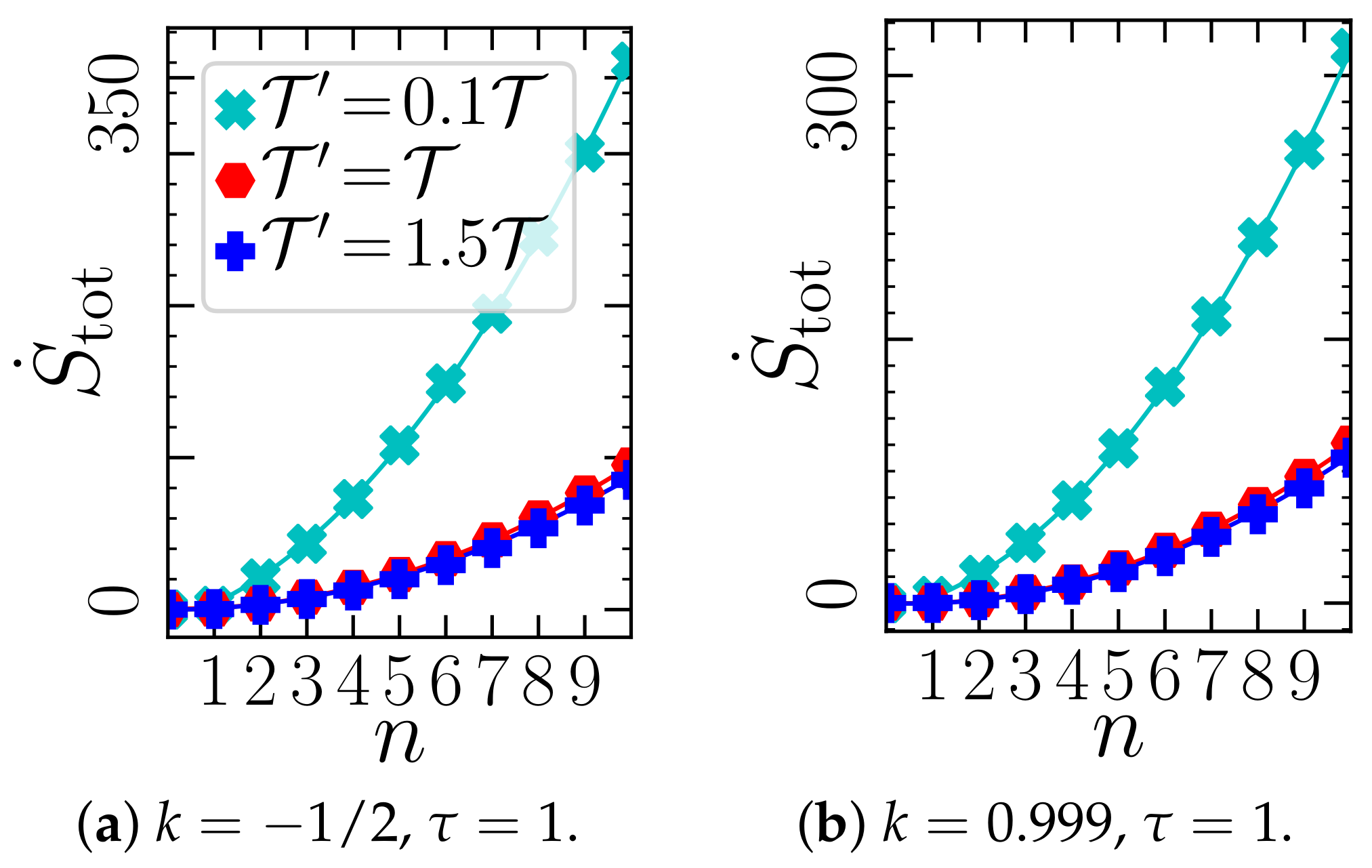
29)).
Now we discuss the dependency on
n. The left panels of
Figure 8 show that, in sharp contrast to the
saturating at large
n, the total EP generally increases with
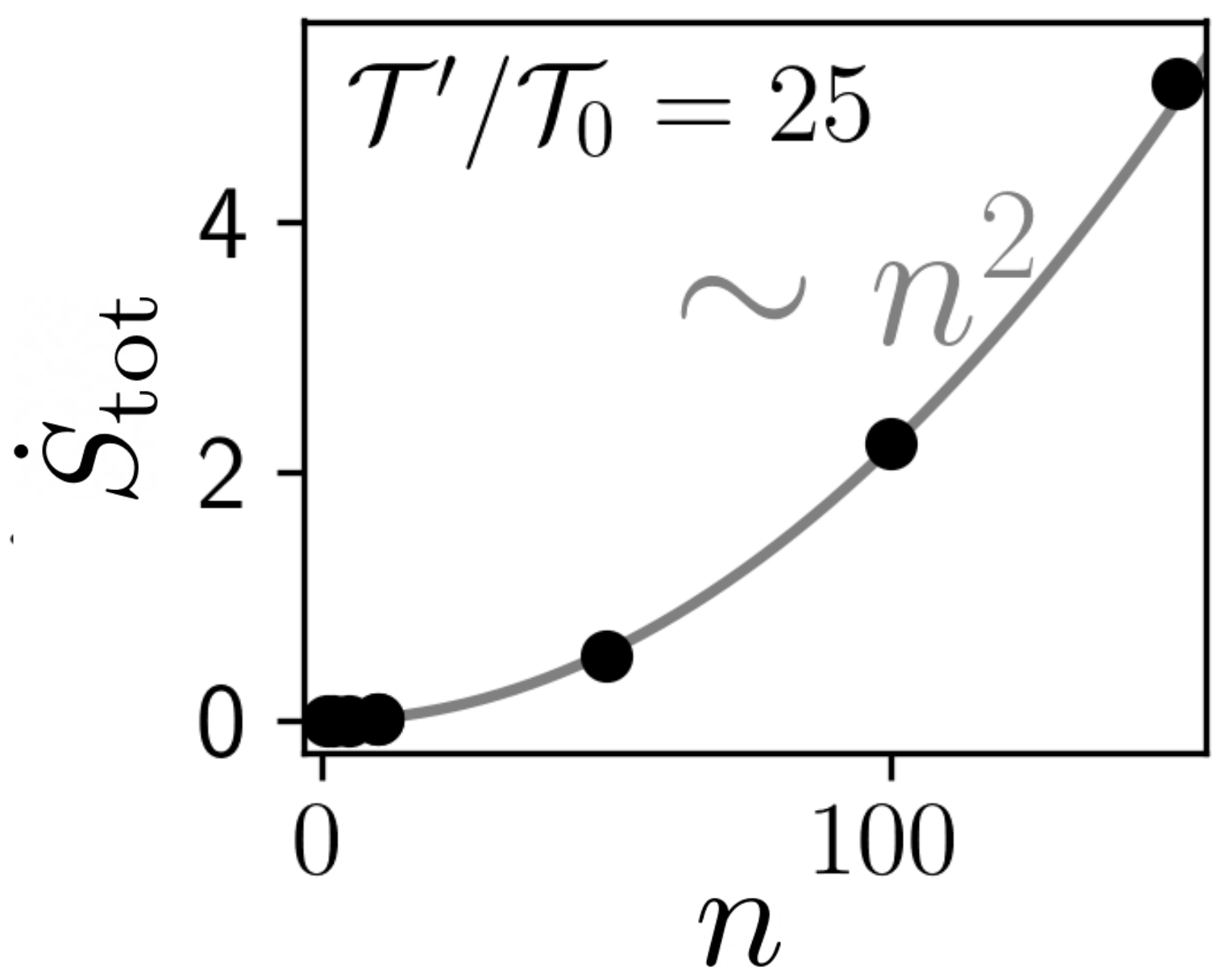
n, specifically we observe a
quadratic increase. This observation is robust against the details of the system, like
a,
k,
. In fact, it even holds for
nonlinear systems, as exemplarily shown in
Figure 9 for a bistable system. We further note that the
dependence persists within in the aforementioned alternative interpretation (see
Section 2.4), when we scale the heat baths of
with
n, i.e.,
(not shown here). The observed
dependency implies a divergent EP. Taking the perspective that the
model a memory device, where each memory cell contributes to EP, a divergent total EP is indeed expected due to the infinite system size. From an information-theoretical perspective, it is indeed also not surprising, as for
the controller stores a full stochastic trajectory, which has, due to the white noise, infinitely many jumps at each time interval, giving it an infinite information content.
The total EP also diverges if
goes to zero, corresponding to the cases of vanishing controller errors. Thus, an infinite precision has an infinite cost. This is in accordance with the result from [
75], whose limit of “precise and infinitely fast” control corresponds in our time-continuous model to the limit
. (Mathematically, the divergence of the entropy production rate as
, can simply be seen as a consequence of the definition
, where one should note that the heat fluxes themselves do not vanish in this limit).
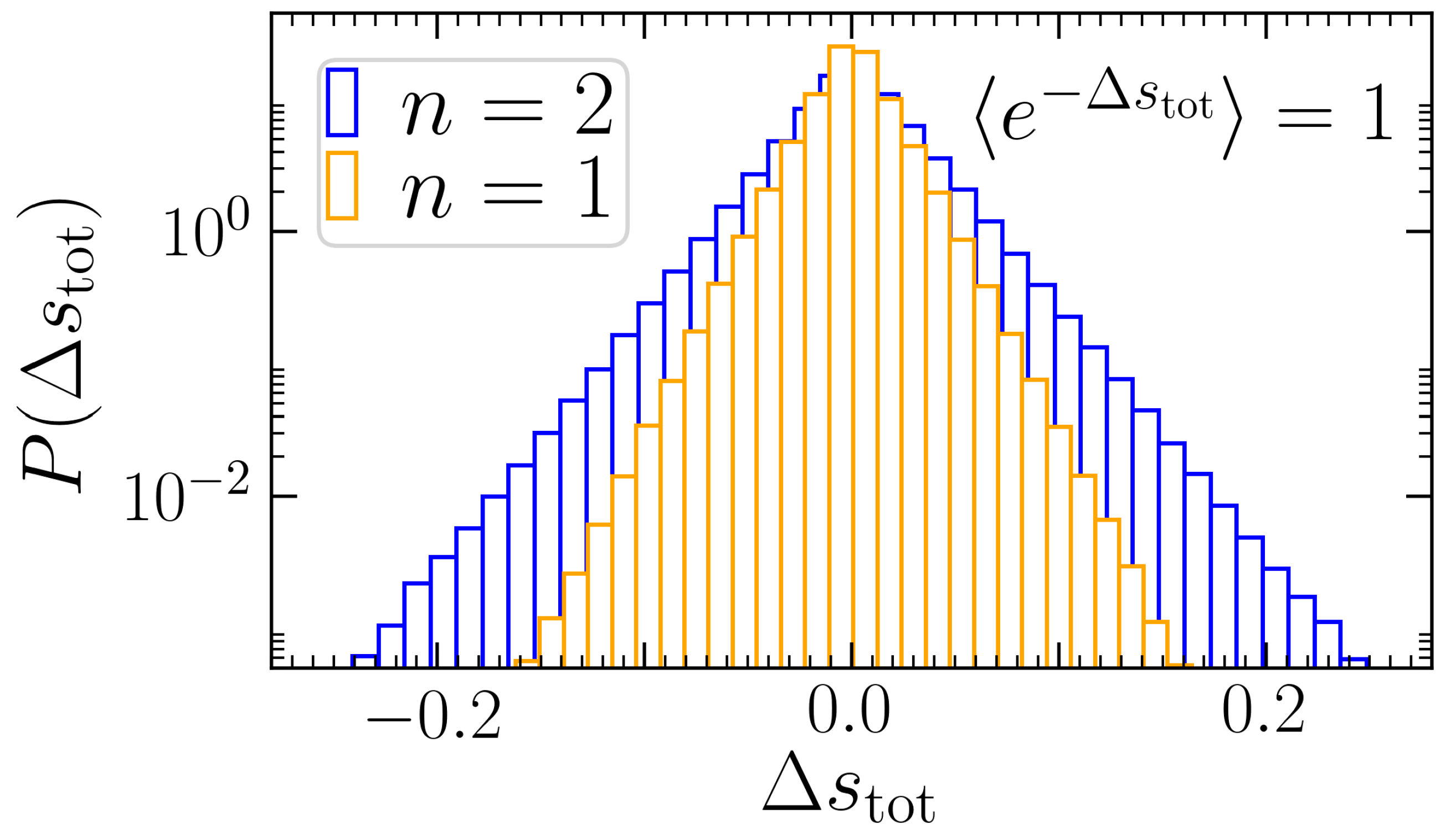
Lastly, let us briefly comment on the total EP fluctuations (discussed in
Appendix E). The characteristics of the entropy distributions are found to be very similar for exponential vs. non-monotonic delay distributions (specifically,
Figure A1 shows
). In both cases, they exhibit exponentially decaying tails and fulfilling an integral fluctuation theorem.
6. Conclusions
In this work, we have studied single-particle stochastic systems under the impact of a linear delay force. We have focused on the question how the distribution of the delay affects the stability and entropy production of the stochastic system.
To this end, we have considered a one-variable Langevin equation for
with white and colored noise, conservative forces stemming from an external potential, and a linear delay force that involves a Gamma-distributed delay. Gamma-distributions turn out to be particularly suitable to study these questions, because they are versatile and moreover allow for a finite representation in the form of a set of
Markovian first-order differential equation (involving
n “auxiliary variables”). This set of equations resembles a unidirectionally coupled ring network of length
[
41]. We note that for a general functional form of the delay distribution, a finite-dimensional representation is not guaranteed. By exploiting the Markovian representation of the dynamics, we could find analytical results for ensemble-averaged quantities in the long-time limit, where the non-Markovian process reaches a steady state.
We have found that the distribution of the delay has a tremendous impact on the linear stability, even if mean delay time and weight of delay distribution remain unchanged. Interestingly, the regime of parameter where the system is stable is smallest in the case of a delta-distributed delay, while the exponentially decaying delay represents the type of delay with the largest stability region. Another remarkable observation is that for delay distributions with a peak of nonzero width around the mean delay time, we observe a reentrant behavior by varying the mean delay time. In particular, upon increasing the mean delay time, a system may become unstable, while an even further increase of delay time stabilizes the system again. This reentrant behavior is however not observed for delta-distributed or exponentially decaying delay. While in this paper, we have discussed the linear stability of
fixed points of (nonlinear) time-delay processes, it would further be very interesting, as a next step, to systematically consider the stability regions of different dynamical regimes of nonlinear delay systems (e.g., for different
n). For example, nonlinear delay systems may exhibit bifurcations where stable periodic orbits emerge, associated with rich dynamical phenomena such as coherence resonance and stochastic resonance [
43,
58]. In fact, our preliminary numerical studies show that the coherence resonance regime that we have described in [
43] for
also exists for finite values of
n.
Studying the heat flow of in the stable parameter regions, we found that for all types of delay distribution, the mean steady-state heat rate can be positive or negative. Negative heat flow implies that the delay force continuously cools down the heat bath by extracting energy from it and thereby reduces the medium entropy production. This points out the fundamentally different character of a delay force and a Markovian drive, which can never on average extract energy as stated by the second law. We have shown that the exponentially decaying delay yields the largest magnitude of heat flow, i.e., extracts the most energy from the heat bath.
Last, we have considered the total entropy production of all variables in the Markovian representation of the process. This entropy production is only meaningful if we interpret the “auxiliary variables” as actual physical processes. However, this consideration offered an interesting new perspective on the feedback cooling. First, this phenomenon can be traced back to the involved non-reciprocal couplings [
57]. Second, it is not due to (hidden) temperature gradients. Specifically, one might have argued that a “colder feedback controller” is expected to extract energy from a system it is coupled to. However, here we have clearly shown that also an isothermal “controller” may extract energy. We found that the total entropy production increases quadratically with
n, implying that the controller with
, which yields exponentially decaying delay, has the lowest entropic cost. Taken together, the exponentially decaying delay force is the one with the largest linear stability region, which may extract the most energy from the bath, and has, at the same time, the lowest entropic cost, making it the most “robust” and “efficient” one.
The special case of discrete delay with white noise emerges as the limit
in our approach. We find that the heat exchange of the system of interest,
, approaches a known result from the literature [
43]. On the contrary, the total entropy production diverges, suggesting that the cost of storing an infinite amount of information is unbounded.
While we have here mostly looked at linear systems, our numerical investigations demonstrate that the main effects can also be found in nonlinear systems.
A particular interesting application of our results concerns the approximation of discrete delay processes by finite numbers of
n. Indeed, if a non-Markovian process with a single delay time of type (Equation (
A16)) is the original process, one may consider the
n-dimensional Markovian process with small numbers of
n as an approximation to the latter (which becomes exact as
). One generally expects that, the smaller
n, the “worse” this approximation. Our results confirm this expectation. However, they moreover show that the approximation can be improved upon setting
. Furthermore,
Figure 7c,d demonstrates that this approximation is actually already surprisingly good, even for
, in terms of heat flow (and, thus, average applied work by the feedback). This is somewhat surprising, given that heat and work are “sensitive” to dynamical aspects, as they depend on two-time correlation functions. Our results thus demonstrate a powerful way to approximate the discrete delay case by a very low-dimensional representation.
As a physical application for our theoretical considerations, we have here considered a colloidal particle under time-delayed feedback control, which is, in principle, experimentally realizable with optical feedback. More generally, our results carry over to other real-world systems, describable by delayed Langevin equations. Possible applications include the dynamics (and associated thermodynamics) of tracer particles in nonequilibrium viscoelastic environments [
76], active environments [
77], or granular media [
78]. It will further be interesting to think about the physical implications of the negative heat flow reported here in other systems.
By generalizing the coupling matrix in the Markovian representation, one could use the approach presented here to further analyze more complicated delay distributions (e.g., multi-peaked ones, oscillatory delay), broadening the range of applications. We have undertaken first steps in this direction in [
79], where we studied correlation functions and the nonequilibrium dynamics of systems similar to the one considered here, with up to two auxiliary variables. Further, several conclusions are indeed expected to carry over to other types of (non-Gamma) delay distributions. Indeed we have numerically observed that the
-dynamics essentially remains the same upon moderate variations of the delay distribution. An exception represent delay distributions that are not “short-ranged", like algebraically decaying delay distributions. These are, moreover known to yield anomalous diffusion, which might also result in interesting thermodynamic behavior and non-trivial stability bounds, representing a worthwhile perspective of future research.
Lastly, various interesting open questions concerning the thermodynamic analysis remain. For example, we have here only considered the EP of the Markovian supersystem, but we have not discussed irreversibility measures based on the non-Markovian dynamics of
alone. Thermodynamic notions of systems with discrete delay were indeed recently also discussed by Rosinberg, Munakata and Tarjus [
42,
50,
73]. They introduced such a framework of irreversibility measures based solely on the non-Markovian dynamics of
, focusing on the case of underdamped motion. In this context, one may for example investigate if, upon marginalization of the total entropy production calculated here, an effective irreversibility measure for the delay process, similar to [
80], can be constructed.
Next, while we have so far mostly focused on the mean values, one could further explore the distributions. The mean value of the heat flow considered here is equivalent to the mean work performed on the system. For Markovian systems, the fluctuations of the work are known to fulfill useful fluctuation theorems such as the Jarzynski relation. It would be interesting to discuss generalization of such work fluctuations theorems to non-Markovian systems, taking the approach presented here as a possible starting point. For non-Makovian systems that fulfill FDR, such generalizations have indeed been carried out successfully in the past: see [
81,
82]. Similarly, this approach might also be useful to investigate thermodynamic uncertainty [
83,
84] relations in non-Markovian systems [
85,
86].