Entropy Production in Exactly Solvable Systems
Abstract
1. Introduction
2. Brief Review of Entropy Production
3. Systems
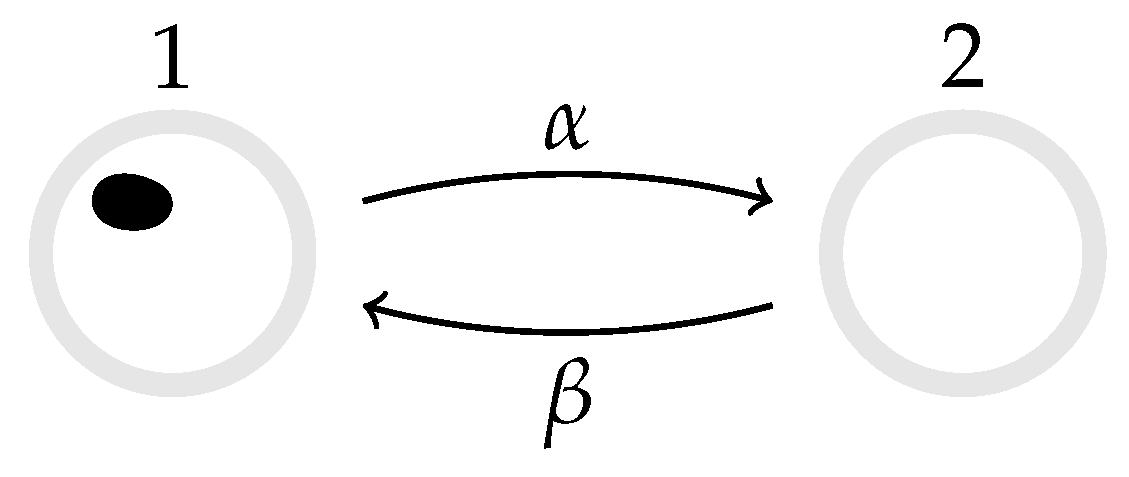
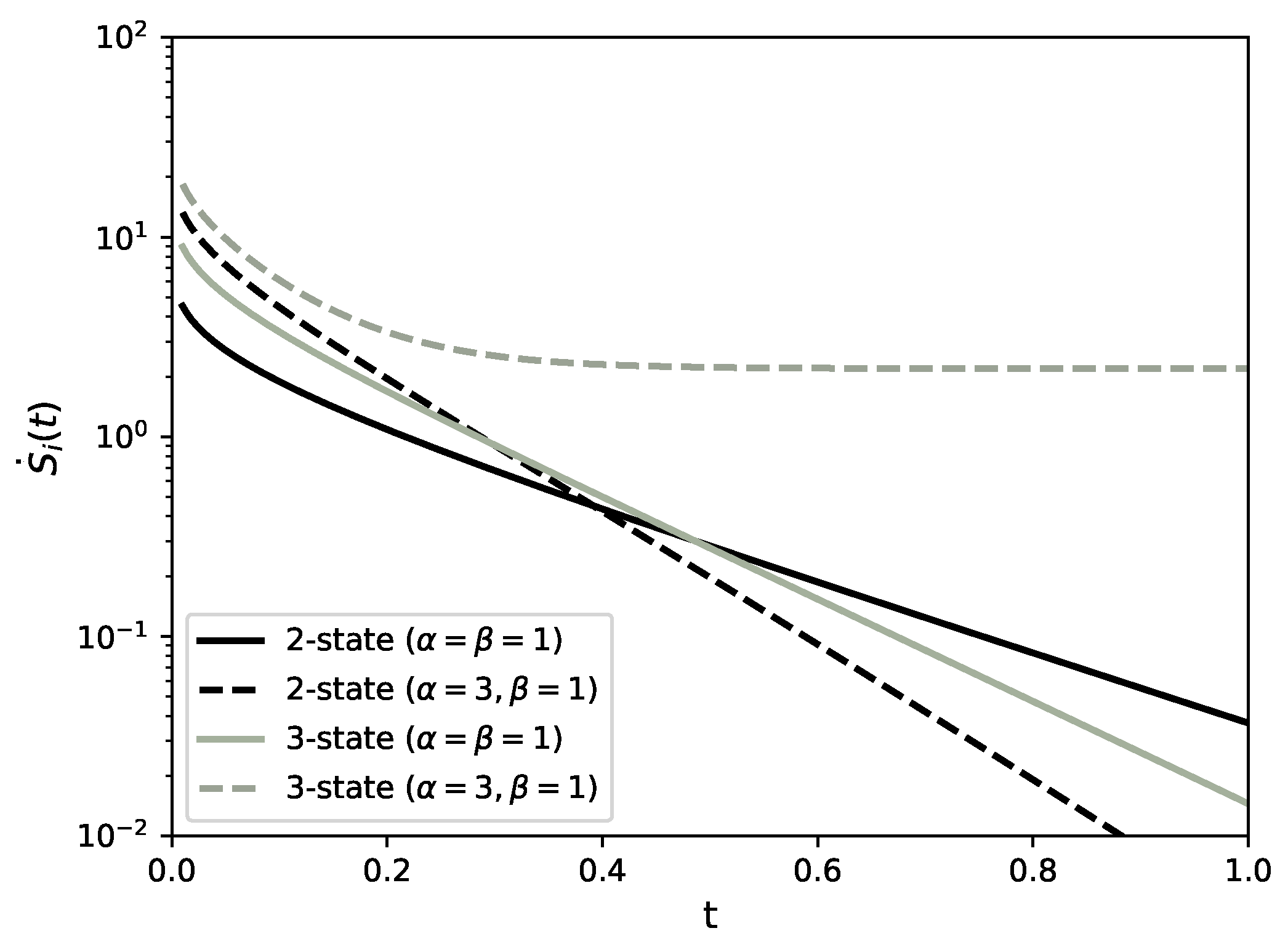
3.1. Two-State Markov Process
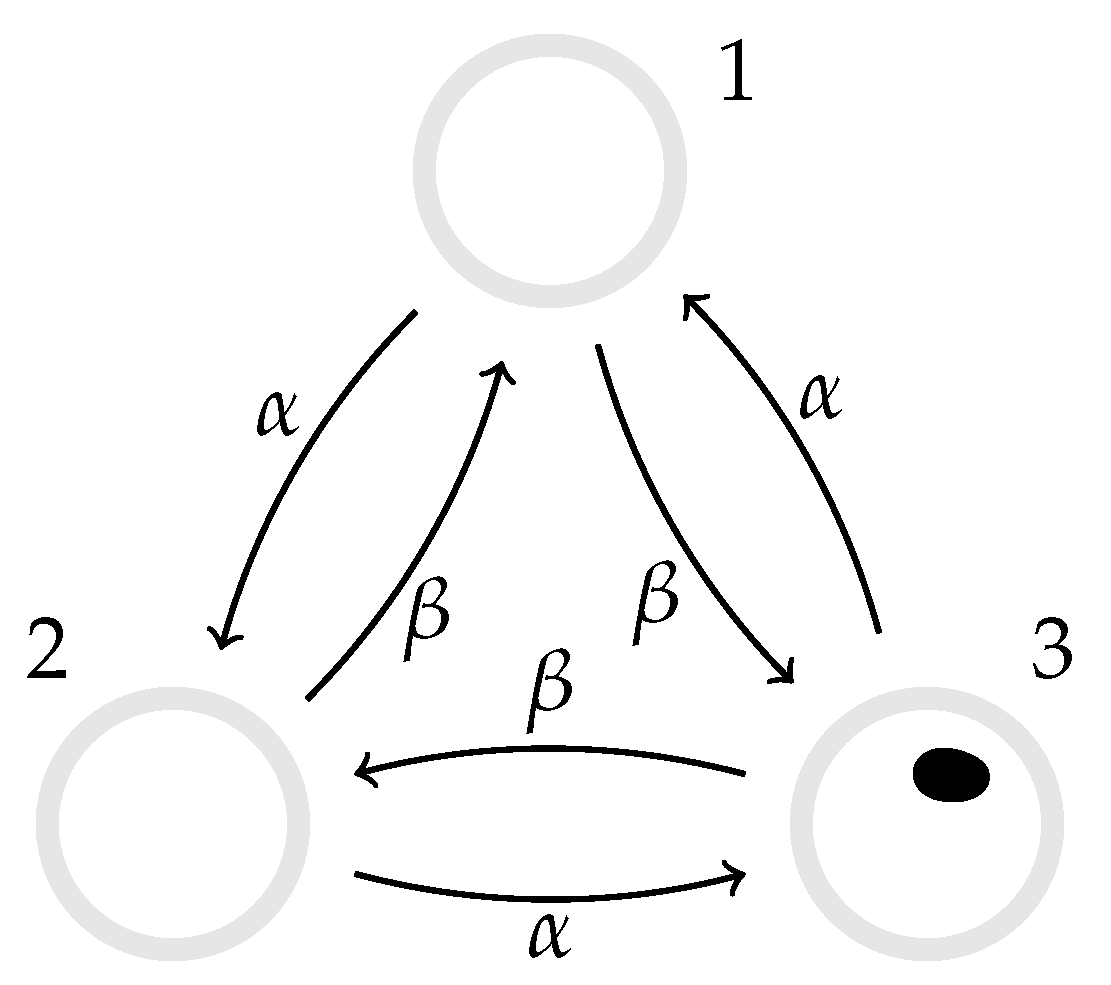
3.2. Three-State Markov Process
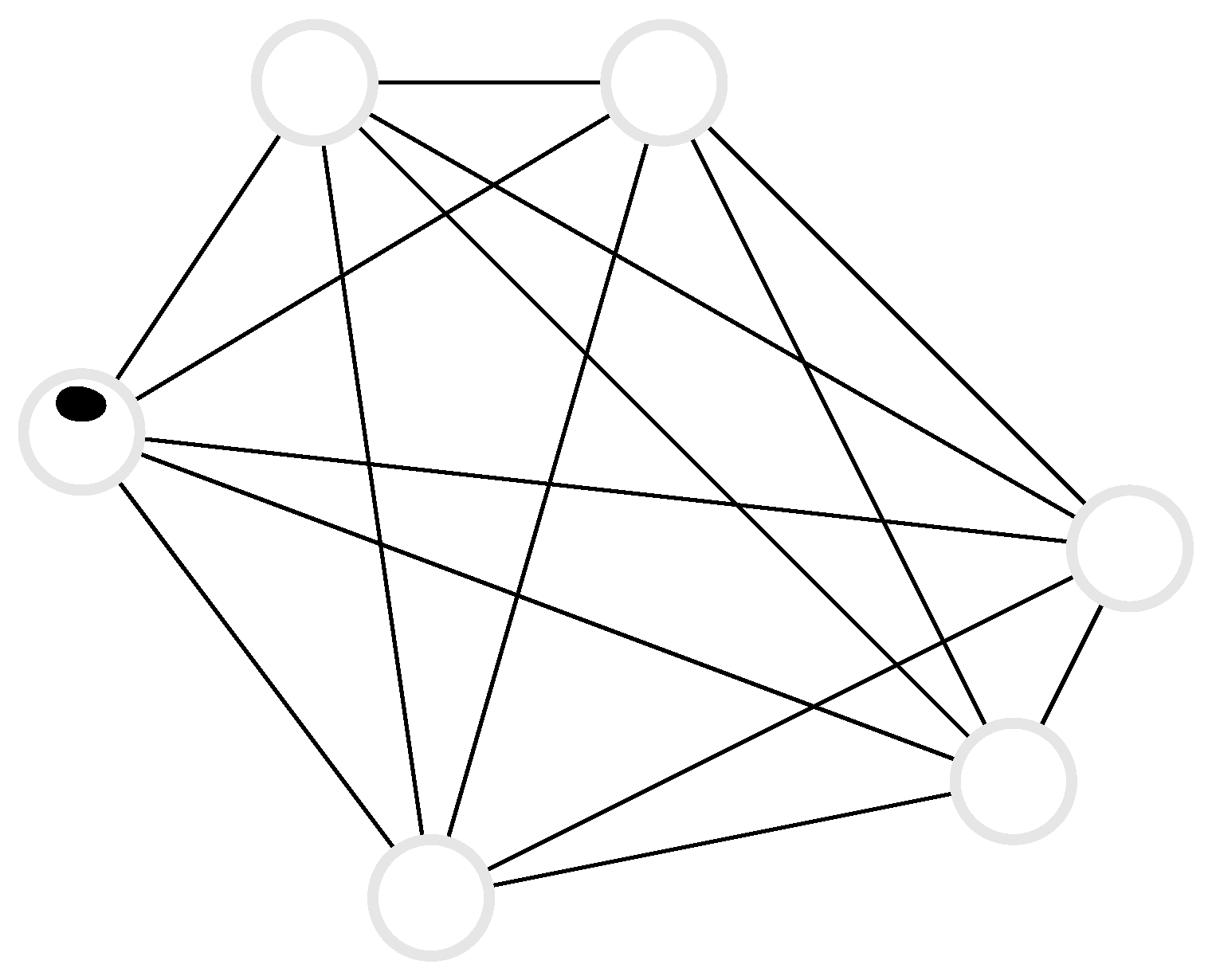
3.3. Random Walk on a Complete Graph
3.4. N Independent, Distinguishable Markov Processes
3.5. N Independent, Indistinguishable Two-State Markov Processes
3.6. N Independent, Indistinguishable d-State Processes
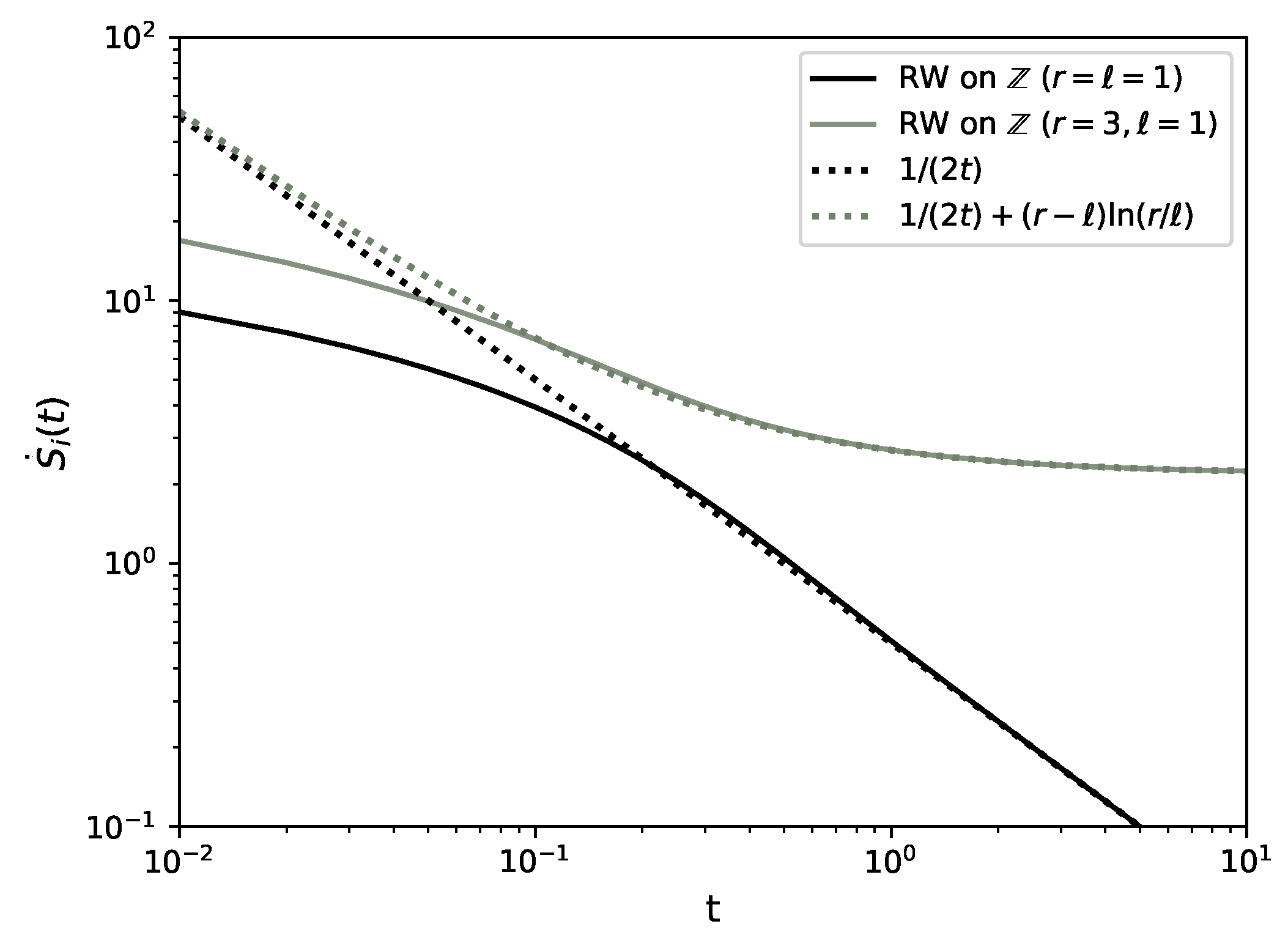
3.7. Random Walk on a Lattice
3.8. Random Walk on a Ring Lattice
3.9. Driven Brownian Particle
3.10. Driven Brownian Particle in a Harmonic Potential
3.11. Driven Brownian Particle on a Ring with Potential
3.12. Run-and-Tumble Motion with Diffusion on A ring
3.13. Switching Diffusion Process on a Ring
4. Discussion and Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Seifert, U. Stochastic thermodynamics, fluctuation theorems, and molecular machines. Rep. Prog. Phys. 2012, 75, 126001. [Google Scholar] [CrossRef] [PubMed]
- Jiang, D.Q.; Qian, M.; Qian, M.P. Mathematical Theory of Nonequilibrium Steady States: On the Frontier of Probability and Dynamical Systems; Lecture notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Seifert, U. Stochastic thermodynamics: From principles to the cost of precision. Physica A 2018, 504, 176–191. [Google Scholar] [CrossRef]
- Barato, A.C.; Hartich, D.; Seifert, U. Efficiency of cellular information processing. New J. Phys. 2014, 16, 103024. [Google Scholar] [CrossRef]
- Lan, G.; Tu, Y. Information processing in bacteria: Memory, computation, and statistical physics: A key issues review. Rep. Prog. Phys. 2016, 79, 052601. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.; Wang, H.; Ouyang, Q.; Tu, Y. The free-energy cost of accurate biochemical oscillations. Nat. Phys. 2015, 11, 772–778. [Google Scholar] [CrossRef]
- Schmiedl, T.; Seifert, U. Stochastic thermodynamics of chemical reaction networks. J. Chem. Phys. 2007, 126, 044101. [Google Scholar] [CrossRef]
- Pietzonka, P.; Fodor, É.; Lohrmann, C.; Cates, M.E.; Seifert, U. Autonomous Engines Driven by Active Matter: Energetics and Design Principles. Phys. Rev. X 2019, 9, 041032. [Google Scholar] [CrossRef]
- Schnakenberg, J. Network theory of microscopic and macroscopic behavior of master equation systems. Rev. Mod. Phys. 1976, 48, 571–585. [Google Scholar] [CrossRef]
- Maes, C. The Fluctuation Theorem as a Gibbs Property. J. Stat. Phys. 1999, 95, 367–392. [Google Scholar] [CrossRef]
- Gaspard, P. Time-Reversed Dynamical Entropy and Irreversibility in Markovian Random Processes. J. Stat. Phys. 2004, 117, 599–615. [Google Scholar] [CrossRef]
- Seifert, U. Entropy production along a stochastic trajectory and an integral fluctuation theorem. Phys. Rev. Let. 2005, 95, 040602. [Google Scholar] [CrossRef] [PubMed]
- Nardini, C.; Fodor, É.; Tjhung, E.; van Wijland, F.; Tailleur, J.; Cates, M.E. Entropy Production in Field Theories without Time-Reversal Symmetry: Quantifying the Non-Equilibrium Character of Active Matter. Phys. Rev. X 2017, 7, 021007. [Google Scholar] [CrossRef]
- Landi, G.T.; Tomé, T.; de Oliveira, M.J. Entropy production in linear Langevin systems. J. Phys. A Math. Theor. 2013, 46, 395001. [Google Scholar] [CrossRef]
- Munakata, T.; Rosinberg, M.L. Entropy production and fluctuation theorems for Langevin processes under continuous non-Markovian feedback control. Phys. Rev. Lett. 2014, 112, 180601. [Google Scholar] [CrossRef]
- Loos, S.A.M.; Klapp, S.H.L. Heat flow due to time-delayed feedback. Sci. Rep. 2019, 9, 2491. [Google Scholar] [CrossRef]
- Ouldridge, T.E.; Brittain, R.A.; Wolde, P.R.T. The power of being explicit: Demystifying work, heat, and free energy in the physics of computation. In The Energetics of Computing in Life and Machines; Wolpert, D.H., Ed.; SFI Press: Santa Fe, NM, USA, 2018. [Google Scholar]
- Rodenfels, J.; Neugebauer, K.M.; Howard, J. Heat Oscillations Driven by the Embryonic Cell Cycle Reveal the Energetic Costs of Signaling. Dev. Cell 2019, 48, 646–658. [Google Scholar] [CrossRef]
- Song, Y.; Park, J.O.; Tanner, L.; Nagano, Y.; Rabinowitz, J.D.; Shvartsman, S.Y. Energy budget of Drosophila embryogenesis. Curr. Biol. 2019, 29, R566–R567. [Google Scholar] [CrossRef]
- Horowitz, J.M.; Gingrich, T.R. Thermodynamic uncertainty relations constrain non-equilibrium fluctuations. Nat. Phys. 2020, 16, 15–20. [Google Scholar] [CrossRef]
- Dorosz, S.; Pleimling, M. Entropy production in the nonequilibrium steady states of interacting many-body systems. Phys. Rev. E 2011, 83, 031107. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Esposito, M.; Van den Broeck, C. Three faces of the second law. I. Master equation formulation. Phys. Rev. E 2010, 82, 011143. [Google Scholar] [CrossRef]
- Lebowitz, J.L.; Spohn, H. A Gallavotti–Cohen-Type Symmetry in the Large Deviation Functional for Stochastic Dynamics. J. Stat. Phys. 1999, 95, 333–365. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On Information and Sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Diana, G.; Esposito, M. Mutual entropy production in bipartite systems. J. Stat. Mech. Theory Exp. 2014, 2014, P04010. [Google Scholar] [CrossRef]
- Roldán, E.; Neri, I.; Dörpinghaus, M.; Meyr, H.; Jülicher, F. Decision Making in the Arrow of Time. Phys. Rev. Lett. 2015, 115, 250602. [Google Scholar] [CrossRef]
- Wissel, C. Manifolds of equivalent path integral solutions of the Fokker-Planck equation. Z. Phys. B Condens. Matter 1979, 35, 185–191. [Google Scholar] [CrossRef]
- Pavliotis, G.A. Stochastic Processes and Applications—Diffusion Processes, the Fokker-Planck and Langevin Equations; Springer: New York, NY, USA, 2014. [Google Scholar]
- Wang, J. Landscape and flux theory of non-equilibrium dynamical systems with application to biology. Adv. Phys. 2015, 64, 1–137. [Google Scholar]
- Seifert, U. Lecture Notes: Soft Matter. From Synthetic to Biological Materials. 39th IFF Spring School, Institut of Solid State Research, Jülich. 2008. Available online: https://www.itp2.uni-stuttgart.de/dokumente/b5_seifert_web.pdf (accessed on 2 November 2020).
- Pietzonka, P.; Seifert, U. Entropy production of active particles and for particles in active baths. J. Phys. A Math. Theor. 2017, 51, 01LT01. [Google Scholar]
- Onsager, L.; Machlup, S. Fluctuations and Irreversible Processes. Phys. Rev. 1953, 91, 1505–1512. [Google Scholar]
- Täuber, U.C. Critical Dynamics: A Field Theory Approach to Equilibrium and Non-Equilibrium Scaling Behavior; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar] [CrossRef]
- Cugliandolo, L.F.; Lecomte, V. Rules of calculus in the path integral representation of white noise Langevin equations: The Onsager–Machlup approach. J. Phys. A Math. Theor. 2017, 50, 345001. [Google Scholar] [CrossRef]
- Fodor, É.; Nardini, C.; Cates, M.E.; Tailleur, J.; Visco, P.; van Wijland, F. How far from equilibrium is active matter? Phys. Rev. Lett. 2016, 117, 038103. [Google Scholar] [CrossRef]
- Caprini, L.; Marconi, U.M.B.; Puglisi, A.; Vulpiani, A. The entropy production of Ornstein–Uhlenbeck active particles: A path integral method for correlations. J. Stat. Mech. Theory Exp. 2019, 2019, 053203. [Google Scholar] [CrossRef]
- Lesne, A. Shannon entropy: A rigorous notion at the crossroads between probability, information theory, dynamical systems and statistical physics. Math. Struct. Comput. Sci. 2014, 24, e240311. [Google Scholar] [CrossRef]
- Zhang, X.J.; Qian, H.; Qian, M. Stochastic theory of nonequilibrium steady states and its applications. Part I. Phys. Rep. 2012, 510, 1–86. [Google Scholar] [CrossRef]
- Herpich, T.; Cossetto, T.; Falasco, G.; Esposito, M. Stochastic thermodynamics of all-to-all interacting many-body systems. New J. Phys. 2020, 22, 063005. [Google Scholar] [CrossRef]
- Lacoste, D.; Lau, A.W.; Mallick, K. Fluctuation theorem and large deviation function for a solvable model of a molecular motor. Phys. Rev. E 2008, 78, 011915. [Google Scholar] [CrossRef]
- Magnus, W.; Oberhettinger, F.; Soni, R.P. Formulas and Theorems for the Special Functions of Mathematical Physics; Springer: Berlin, Germany, 1966. [Google Scholar]
- Galassi, M.; Davies, J.; Theiler, J.; Gough, B.; Jungman, G.; Alken, P.; Booth, M.; Rossi, F. GNU Scientific Library Reference Manual, 3rd ed.; Network Theory Ltd., 2009; p. 592. Available online: https://www.gnu.org/software/gsl/ (accessed on 27 October 2020).
- Van den Broeck, C.; Esposito, M. Three faces of the second law. II. Fokker-Planck formulation. Phys. Rev. E 2010, 82, 011144. [Google Scholar] [CrossRef]
- Risken, H.; Frank, T. The Fokker-Planck Equation—Methods of Solution and Applications; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Maes, C.; Redig, F.; Moffaert, A.V. On the definition of entropy production, via examples. J. Math. Phys. 2000, 41, 1528–1554. [Google Scholar] [CrossRef]
- Spinney, R.E.; Ford, I.J. Entropy production in full phase space for continuous stochastic dynamics. Phys. Rev. E 2012, 85, 051113. [Google Scholar] [CrossRef]
- Andrieux, D.; Gaspard, P.; Ciliberto, S.; Garnier, N.; Joubaud, S.; Petrosyan, A. Thermodynamic time asymmetry in non-equilibrium fluctuations. J. Stat. Mech. Theory Exp. 2008, 2008, 01002. [Google Scholar] [CrossRef]
- Reimann, P.; Van den Broeck, C.; Linke, H.; Hänggi, P.; Rubi, J.M.; Pérez-Madrid, A. Giant Acceleration of Free Diffusion by Use of Tilted Periodic Potentials. Phys. Rev. Lett. 2001, 87, 010602. [Google Scholar] [CrossRef]
- Pigolotti, S.; Neri, I.; Roldán, É.; Jülicher, F. Generic properties of stochastic entropy production. Phys. Rev. Lett. 2017, 119, 140604. [Google Scholar] [CrossRef]
- Neri, I.; Roldán, É.; Pigolotti, S.; Jülicher, F. Integral fluctuation relations for entropy production at stopping times. J. Stat. Mech. Theory Exp. 2019, 2019, 104006. [Google Scholar] [CrossRef]
- Horsthemke, W.; Lefever, R. Noise-Induced Transitions-Theory and Applications in Physics, Chemistry, and Biology; Springer: Berlin/Heidelberg, Germany, 1984. [Google Scholar]
- Schnitzer, M.J. Theory of continuum random walks and application to chemotaxis. Phys. Rev. E 1993, 48, 2553–2568. [Google Scholar] [CrossRef]
- Yang, S.X.; Ge, H. Decomposition of the entropy production rate and nonequilibrium thermodynamics of switching diffusion processes. Phys. Rev. E 2018, 98, 012418. [Google Scholar] [CrossRef]
- Doi, M. Second quantization representation for classical many-particle system. J. Phys. A Math. Gen. 1976, 9, 1465–1477. [Google Scholar] [CrossRef]
- Peliti, L. Path integral approach to birth-death processes on a lattice. J. Phys. 1985, 46, 1469–1483. [Google Scholar] [CrossRef]
- Täuber, U.C.; Howard, M.; Vollmayr-Lee, B.P. Applications of field-theoretic renormalization group methods to reaction-diffusion problems. J. Phys. A Math. Gen. 2005, 38, R79–R131. [Google Scholar] [CrossRef]
- Smith, E.; Krishnamurthy, S. Path-reversal, Doi-Peliti generating functionals, and dualities between dynamics and inference for stochastic processes. arXiv 2018, arXiv:1806.02001. [Google Scholar]
- Bordeu, I.; Amarteifio, S.; Garcia-Millan, R.; Walter, B.; Wei, N.; Pruessner, G. Volume explored by a branching random walk on general graphs. Sci. Rep. 2019, 9, 15590. [Google Scholar] [CrossRef]
- Lazarescu, A.; Cossetto, T.; Falasco, G.; Esposito, M. Large deviations and dynamical phase transitions in stochastic chemical networks. J. Chem. Phys. 2019, 151, 064117. [Google Scholar] [CrossRef]
- Pausch, J.; Pruessner, G. Is actin filament and microtubule growth reaction-or diffusion-limited? J. Stat. Mech. Theory Exp. 2019, 2019, 053501. [Google Scholar] [CrossRef]
- Garcia-Millan, R. The concealed voter model is in the voter model universality class. J. Stat. Mech. 2020, 2020, 053201. [Google Scholar] [CrossRef]
- Garcia-Millan, R.; Pruessner, G. Run-and-tumble motion: Field theory and entropy production. 2020; To be published. [Google Scholar]
- Yiu, K.T. Entropy Production and Time Reversal. Master’s Thesis, Imperial College London, London, UK, 2017. [Google Scholar]

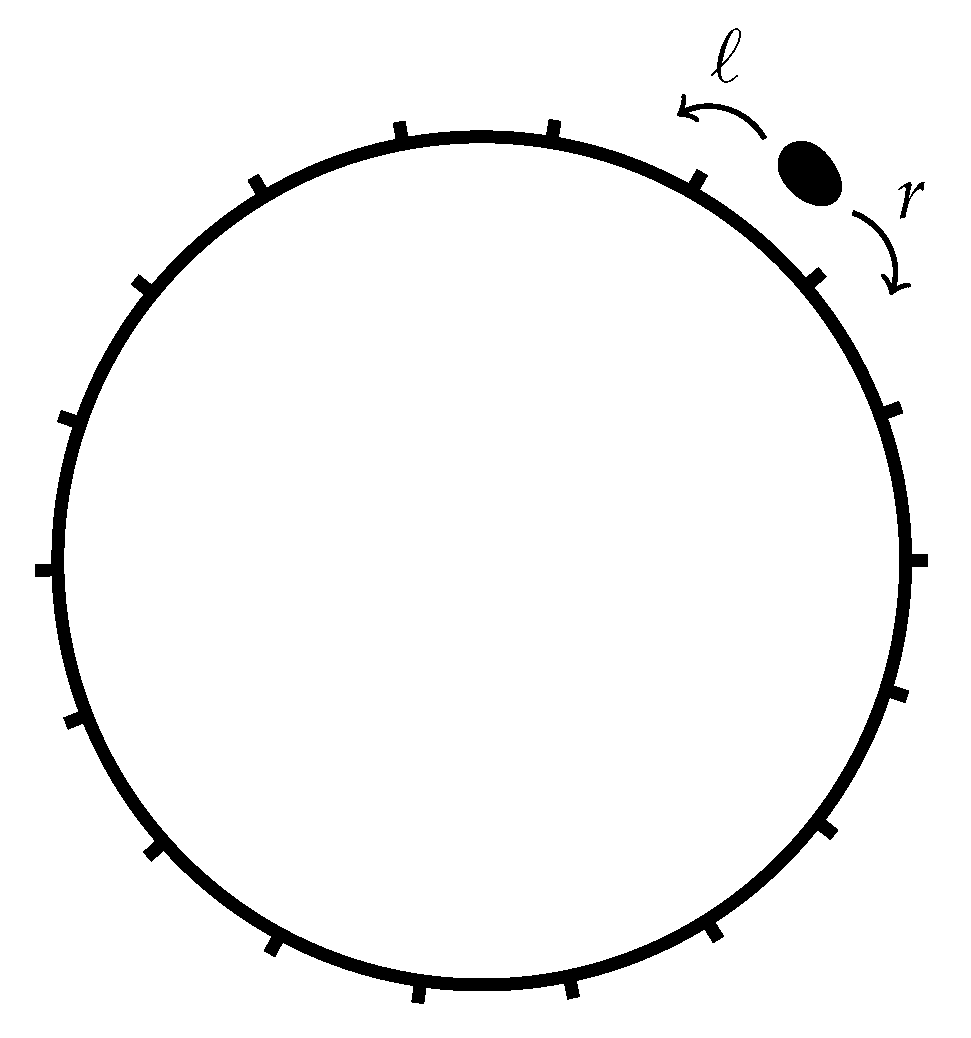



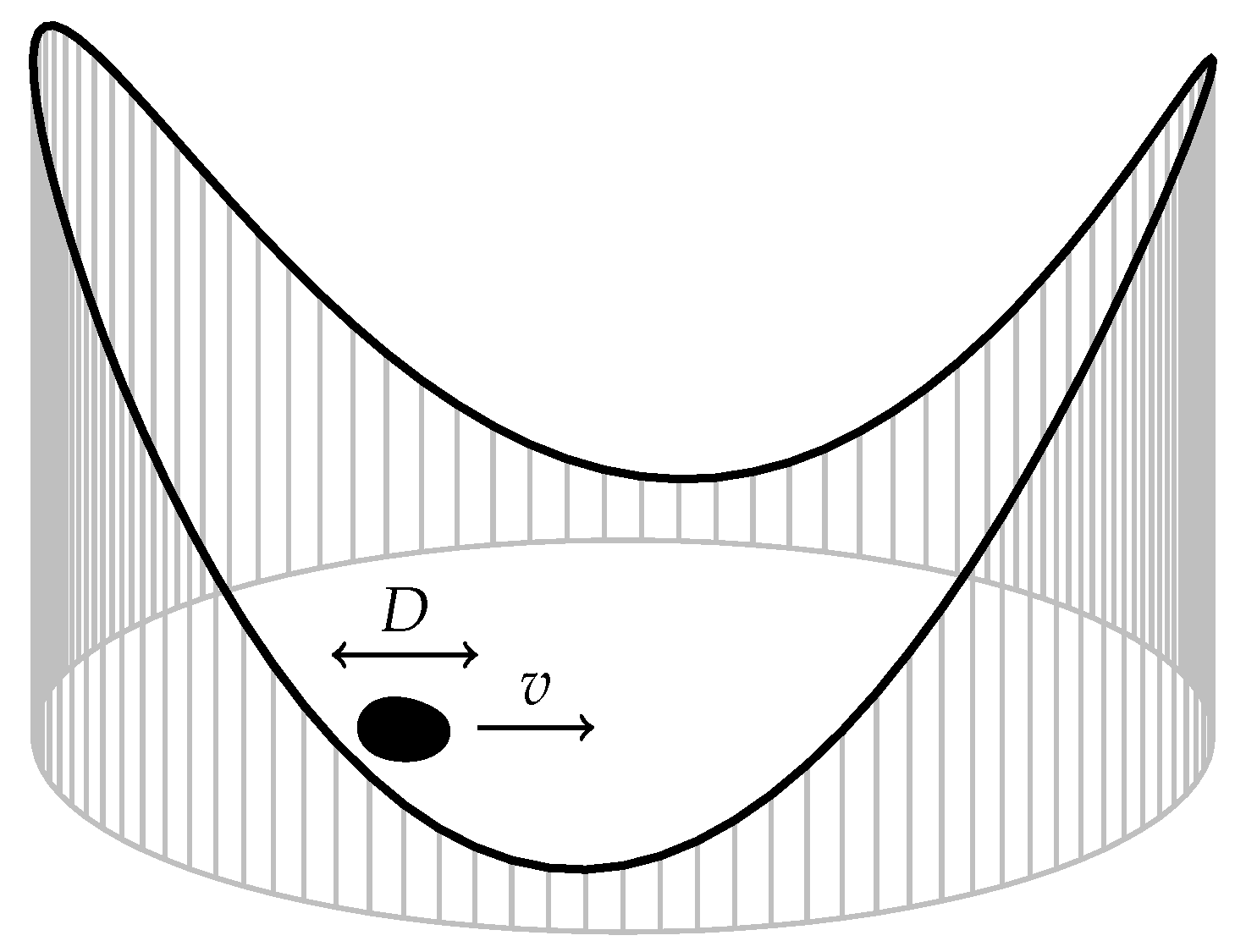
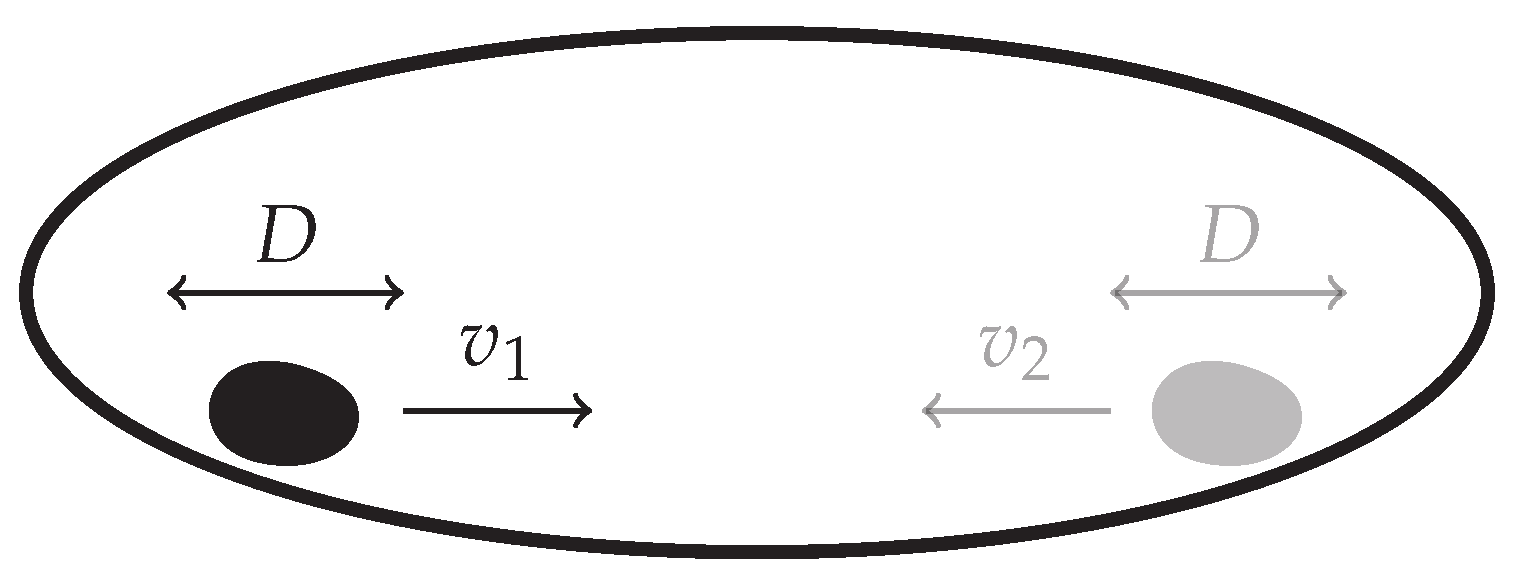
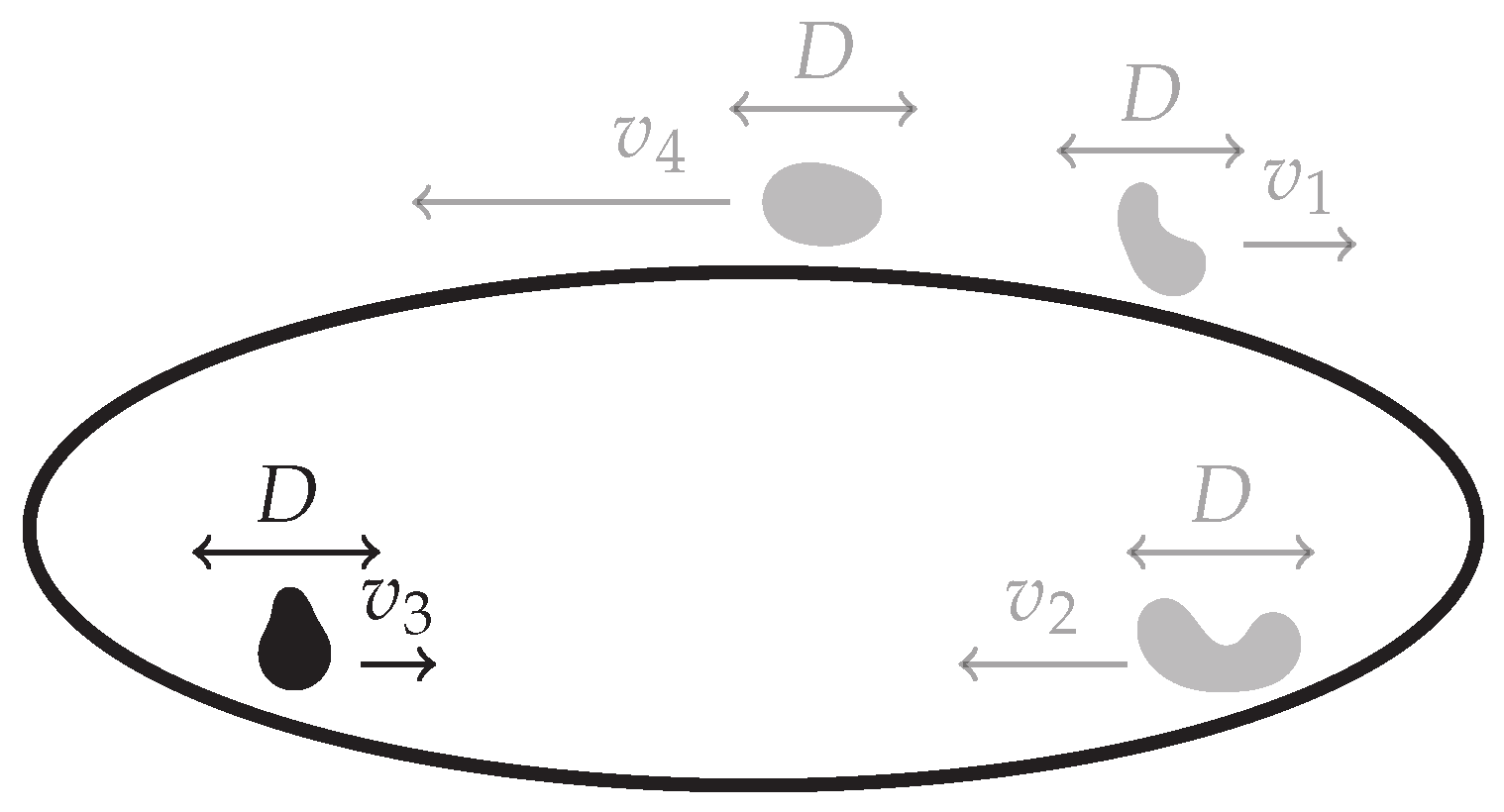
| Section | System | |
|---|---|---|
| Section 3.1 | Two-state Markov process | (37) |
| Section 3.2 | Three-state Markov process | (41) |
| Section 3.3 | Random walk on a complete graph | (44), (45) |
| Section 3.4 | N independent, distinguishable Markov processes | (52) |
| Section 3.5 | N independent, indistinguishable two-state Markov processes | (55b) |
| Section 3.6 | N independent, indistinguishable d-state processes | (68) |
| Section 3.7 | Random Walk on a lattice | (82) |
| Section 3.8 | Random Walk on a ring lattice | (87), (89) |
| Section 3.9 | Driven Brownian particle | (94) |
| Section 3.10 | Driven Brownian particle in a harmonic potential | (100) |
| Section 3.11 | Driven Brownian particle on a ring with potential | (113d) |
| Section 3.12 | Run-and-tumble motion with diffusion on a ring | (121) |
| Section 3.13 | Switching diffusion process on a ring | (128) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cocconi, L.; Garcia-Millan, R.; Zhen, Z.; Buturca, B.; Pruessner, G. Entropy Production in Exactly Solvable Systems. Entropy 2020, 22, 1252. https://doi.org/10.3390/e22111252
Cocconi L, Garcia-Millan R, Zhen Z, Buturca B, Pruessner G. Entropy Production in Exactly Solvable Systems. Entropy. 2020; 22(11):1252. https://doi.org/10.3390/e22111252
Chicago/Turabian StyleCocconi, Luca, Rosalba Garcia-Millan, Zigan Zhen, Bianca Buturca, and Gunnar Pruessner. 2020. "Entropy Production in Exactly Solvable Systems" Entropy 22, no. 11: 1252. https://doi.org/10.3390/e22111252
APA StyleCocconi, L., Garcia-Millan, R., Zhen, Z., Buturca, B., & Pruessner, G. (2020). Entropy Production in Exactly Solvable Systems. Entropy, 22(11), 1252. https://doi.org/10.3390/e22111252





