Stochastic Thermodynamics of a Piezoelectric Energy Harvester Model
Abstract
1. Introduction
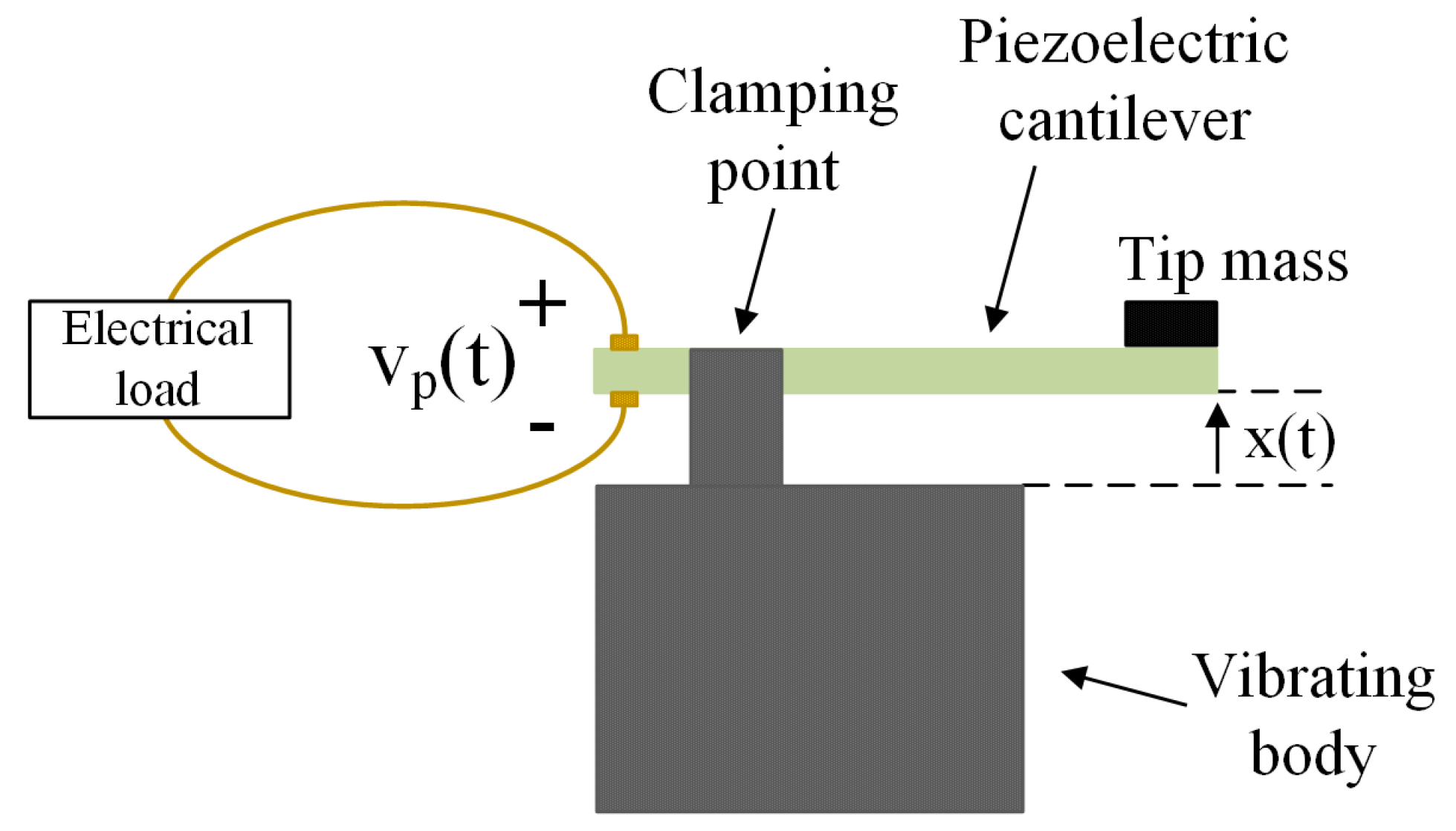
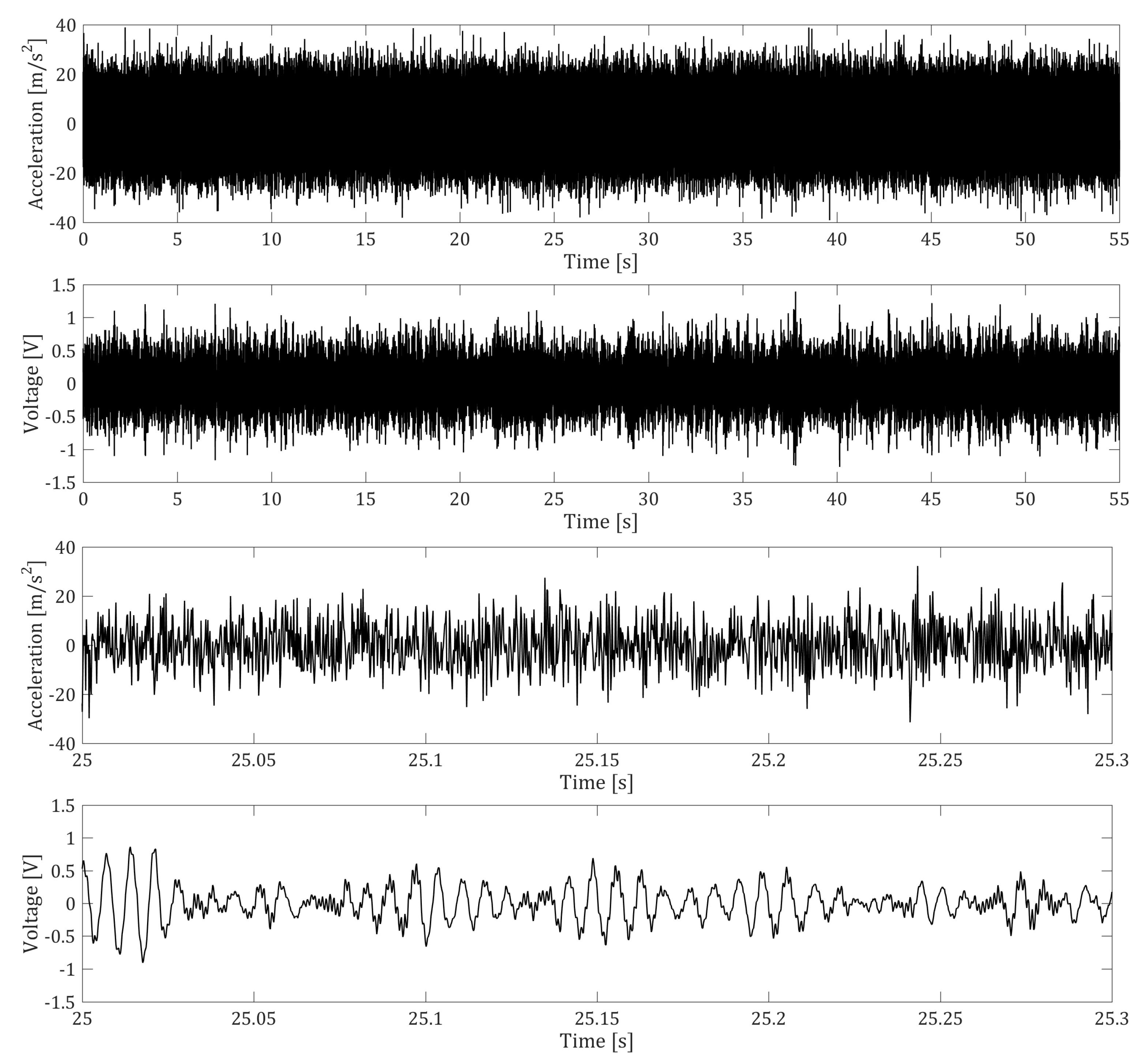
2. Experimental Setup
3. Theoretical Model
3.1. Average Values
3.2. Fitting the Model to Experimental Data
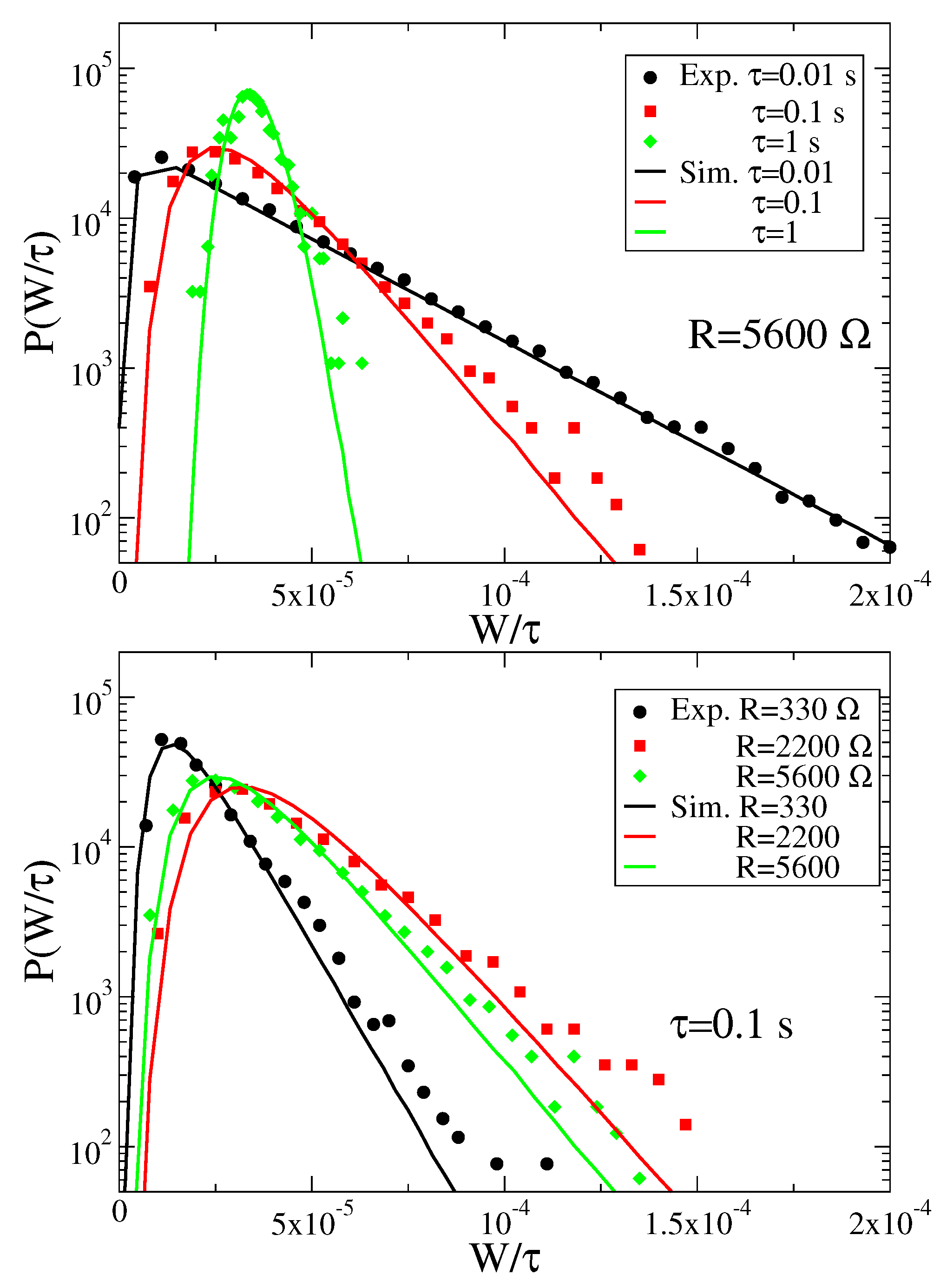
3.3. Stochastic Energetics
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Puglisi, A.; Sarracino, A.; Vulpiani, A. Thermodynamics and Statistical Mechanics of Small Systems. Entropy 2018, 20, 392. [Google Scholar] [CrossRef]
- Seifert, U. Stochastic thermodynamics, fluctuation theorems and molecular machines. Rep. Prog. Phys. 2012, 75, 126001. [Google Scholar] [CrossRef] [PubMed]
- Marconi, U.M.B.; Puglisi, A.; Rondoni, L.; Vulpiani, A. Fluctuation-dissipation: Response theory in statistical physics. Phys. Rep. 2008, 461, 111. [Google Scholar] [CrossRef]
- Jepps, O.G.; Rondoni, L. Deterministic thermostats, theories of nonequilibrium systems and parallels with the ergodic condition. J. Phys. A Math. Theor. 2010, 43, 133001. [Google Scholar] [CrossRef]
- Gallavotti, G.; Cohen, E.G.D. Dynamical ensembles in stationary states. J. Stat. Phys. 1995, 80, 931. [Google Scholar] [CrossRef]
- Evans, D.J.; Cohen, E.G.D.; Morriss, G.P. Probability of second law violations in shearing steady flows. Phys. Rev. Lett. 1993, 71, 2401. [Google Scholar] [CrossRef]
- Searles, D.J.; Rondoni, L.; Evans, D.J. The steady state fluctuation relation for the dissipation function. J. Stat. Phys. 2007, 128, 1337. [Google Scholar] [CrossRef]
- Rondoni, L. Deterministic thermostats, fluctuation relations. In Dynamics of Dissipation, Lecture Notes in Physics 597; Garbaczewski, P., Olkiewicz, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Maes, C. The fluctuation theorem as a Gibbs property. J. Stat. Phys. 1999, 95, 367. [Google Scholar] [CrossRef]
- Baiesi, M.; Maes, C. An update on the nonequilibrium linear response. New J. Phys. 2013, 15, 013004. [Google Scholar] [CrossRef]
- Puglisi, A.; Sarracino, A.; Vulpiani, A. Temperature in and out of equilibrium: A review of concepts, tools and attempts. Phys. Rep. 2017, 709, 1–60. [Google Scholar] [CrossRef]
- Jarzynski, C. Nonequilibrium equality for free energy differences. Phys. Rev. Lett. 1997, 78, 2690. [Google Scholar] [CrossRef]
- Crooks, G.E. Path ensemble averages in systems driven far from equilibrium. Phys. Rev. E 2000, 61, 2361. [Google Scholar] [CrossRef]
- Hatano, T.; Sasa, S. Steady-state thermodynamics of Langevin systems. Phys. Rev. Lett. 2001, 86, 3463. [Google Scholar] [CrossRef]
- Barato, A.C.; Seifert, U. Thermodynamic Uncertainty Relation for Biomolecular Processes. Phys. Rev. Lett. 2015, 114, 158101. [Google Scholar] [CrossRef]
- Farago, J. Injected Power Fluctuations in Langevin Equation. J. Stat. Phys. 2002, 107, 781. [Google Scholar] [CrossRef]
- Baiesi, M.; Jacobs, T.; Maes, C.; Skantzos, N.S. Fluctuation symmetries for work and heat. Phys. Rev. E 2006, 74, 021111. [Google Scholar] [CrossRef] [PubMed]
- Kwon, C.; Noh, J.D.; Park, H. Nonequilibrium fluctuations for linear diffusion dynamics. Phys. Rev. E 2011, 83, 061145. [Google Scholar] [CrossRef] [PubMed]
- Kwon, C.; Noh, J.D.; Park, H. Work fluctuations in a time-dependent harmonic potential: Rigorous results beyond the overdamped limit. Phys. Rev. E 2013, 88, 062102. [Google Scholar] [CrossRef]
- Holubec, V.; Dierl, M.; Einax, M.; Maass, P.; Chvosta, P.; Ryabov, A. Asymptotics of work distribution for a Brownian particle in a time-dependent anharmonic potential. Phys. Scr. 2015, T165, 014024. [Google Scholar] [CrossRef]
- Xiao, B.; Li, R. Work fluctuation and its optimal extraction with time dependent harmonic potential from a non-Markovian bath. Phys. A Stat. Mech. Its Appl. 2019, 516, 161–171. [Google Scholar] [CrossRef]
- Paraguassú, P.V.; Morgado, W.A.M. The heat distribution in a logarithm potential. J. Stat. Mech. Theory Exp. 2021, 2021, 023205. [Google Scholar] [CrossRef]
- Pal, A.; Sabhapandit, S. Work fluctuations for a Brownian particle driven by a correlated external random force. Phys. Rev. E 2014, 90, 052116. [Google Scholar] [CrossRef] [PubMed]
- Salazar, D.S.P. Work distribution in thermal processes. Phys. Rev. E 2020, 101, 030101. [Google Scholar] [CrossRef]
- Albay, J.A.C.; Kwon, C.; Lai, P.Y.; Jun, Y. Work relation in instantaneous-equilibrium transition of forward and reverse processes. New J. Phys. 2020, 22, 123049. [Google Scholar] [CrossRef]
- Rosinberg, M.L.; Tarjus, G.; Munakata, T. Heat fluctuations for underdamped Langevin dynamics. EPL Europhys. Lett. 2016, 113, 10007. [Google Scholar] [CrossRef]
- Crisanti, A.; Sarracino, A.; Zannetti, M. Heat fluctuations of Brownian oscillators in nonstationary processes: Fluctuation theorem and condensation transition. Phys. Rev. E 2017, 95, 052138. [Google Scholar] [CrossRef]
- Corberi, F.; Sarracino, A. Probability distributions with singularities. Entropy 2018, 21, 312. [Google Scholar] [CrossRef]
- Ciliberto, S.; Laroche, C. An experimental test of the Gallavotti-Cohen fluctuation theorem. J. Phys. IV 1998, 8, 215. [Google Scholar] [CrossRef]
- Garnier, N.; Ciliberto, S. Nonequilibrium fluctuations in a resistor. Phys. Rev. E 2005, 71, 060101. [Google Scholar] [CrossRef]
- Douarche, F.; Joubaud, S.; Garnier, N.B.; Petrosyan, A.; Ciliberto, S. Work fluctuation theorems for harmonic oscillators. Phys. Rev. Lett. 2006, 97, 140603. [Google Scholar] [CrossRef] [PubMed]
- Douarche, F.; Ciliberto, S.; Petrosyan, A.; Rabbiosi, I. An experimental test of the Jarzynski equality in a mechanical experiment. Europhys. Lett. 2005, 70, 593. [Google Scholar] [CrossRef]
- Reimann, P. Brownian motors: Noisy transport far from equilibrium. Phys. Rep. 2002, 361, 57. [Google Scholar] [CrossRef]
- Gnoli, A.; Petri, A.; Dalton, F.; Gradenigo, G.; Pontuale, G.; Sarracino, A.; Puglisi, A. Brownian Ratchet in a Thermal Bath Driven by Coulomb Friction. Phys. Rev. Lett. 2013, 110, 120601. [Google Scholar] [CrossRef]
- Gnoli, A.; Sarracino, A.; Petri, A.; Puglisi, A. Non-equilibrium fluctuations in frictional granular motor: Experiments and kinetic theory. Phys. Rev. E. 2013, 87, 052209. [Google Scholar] [CrossRef]
- Di Leonardo, R.; Angelani, L.; Dell’Arciprete, D.; Ruocco, G.; Iebba, V.; Schippa, S.; Conte, M.P.; Mecarini, F.; De Angelis, F.; Di Fabrizio, E. Bacterial ratchet motors. Proc. Natl. Acad. Sci. USA 2010, 107, 9541–9545. [Google Scholar] [CrossRef]
- Kim, H.S.; Kim, J.H.; Kim, J. A review of piezoelectric energy harvesting based on vibration. Int. J. Precis. Eng. Manuf. 2011, 12, 1129. [Google Scholar] [CrossRef]
- Du, S.; Jia, Y.; Zhao, C.; Amaratunga, G.A.J.; Seshia, A.A. A Passive Design Scheme to Increase the Rectified Power of Piezoelectric Energy Harvesters. IEEE Trans. Ind. Electron. 2018, 65, 7095. [Google Scholar] [CrossRef]
- Costanzo, L.; Schiavo, A.L.; Vitelli, M. Active Interface for Piezoelectric Harvesters Based on Multi-Variable Maximum Power Point Tracking. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 2503. [Google Scholar] [CrossRef]
- Brenes, A.; Morel, A.; Juillard, J.; Lefeuvre, E.; Badel, A. Maximum power point of piezoelectric energy harvesters: A review of optimality condition for electrical tuning. Smart Mater. Struct. 2020, 29, 033001. [Google Scholar] [CrossRef]
- Costanzo, L.; Vitelli, M. Tuning Techniques for Piezoelectric and Electromagnetic Vibration Energy Harvesters. Energies 2020, 13, 527. [Google Scholar] [CrossRef]
- Halvorsen, E. Energy harvesters driven by broadband random vibrations. J. Microelectromechanical Syst. 2008, 17, 1061. [Google Scholar] [CrossRef]
- Costanzo, L.; Schiavo, A.L.; Vitelli, M. Power Extracted From Piezoelectric Harvesters Driven by Non-Sinusoidal Vibrations. IEEE Trans. Circuits Syst. I Regul. Pap. 2019, 66, 1291. [Google Scholar] [CrossRef]
- Quaranta, G.; Trentadue, F.; Maruccio, C.; Marano, G.C. Analysis of piezoelectric energy harvester under modulated and filtered white Gaussian noise. Mech. Sys. Signal Proc. 2018, 104, 134. [Google Scholar] [CrossRef]
- Cryns, J.W.; Hatchell, B.K.; Santiago-Rojas, E.; Silvers, K.L. Experimental Analysis of a Piezoelectric Energy Harvesting System for Harmonic, Random, and Sine on Random Vibration. Adv. Acoust. Vib. 2013, 10, 241025. [Google Scholar] [CrossRef][Green Version]
- Risken, H. The Fokker–Planck Equation: Methods of Solution and Applications; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Sekimoto, K. Stochastic Energetics; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- van Zon, R.; Cohen, E.G.D. Extension of the Fluctuation Theorem. Phys. Rev. Lett. 2003, 91, 110601. [Google Scholar] [CrossRef]
- Gammaitoni, L.; Neri, I.; Vocca, H. Nonilinear oscillators for vibration energy harvesting. Appl. Phys. Lett. 2009, 94, 164102. [Google Scholar] [CrossRef]
- Cottone, F.; Vocca, H.; Gammaitoni, L. Nonlinear Energy Harvesting. Phys. Rev. Lett. 2009, 102, 080601. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Costanzo, L.; Lo Schiavo, A.; Sarracino, A.; Vitelli, M. Stochastic Thermodynamics of a Piezoelectric Energy Harvester Model. Entropy 2021, 23, 677. https://doi.org/10.3390/e23060677
Costanzo L, Lo Schiavo A, Sarracino A, Vitelli M. Stochastic Thermodynamics of a Piezoelectric Energy Harvester Model. Entropy. 2021; 23(6):677. https://doi.org/10.3390/e23060677
Chicago/Turabian StyleCostanzo, Luigi, Alessandro Lo Schiavo, Alessandro Sarracino, and Massimo Vitelli. 2021. "Stochastic Thermodynamics of a Piezoelectric Energy Harvester Model" Entropy 23, no. 6: 677. https://doi.org/10.3390/e23060677
APA StyleCostanzo, L., Lo Schiavo, A., Sarracino, A., & Vitelli, M. (2021). Stochastic Thermodynamics of a Piezoelectric Energy Harvester Model. Entropy, 23(6), 677. https://doi.org/10.3390/e23060677








