Count Data Time Series Modelling in Julia—The CountTimeSeries.jl Package and Applications
Abstract
1. Introduction
2. The CountTimeSeries Package
2.1. INGARCH Framework
2.2. INARMA Framework
2.3. Package Structure
3. Application: COVID-19
3.1. Model
3.2. Implementation
3.3. Results
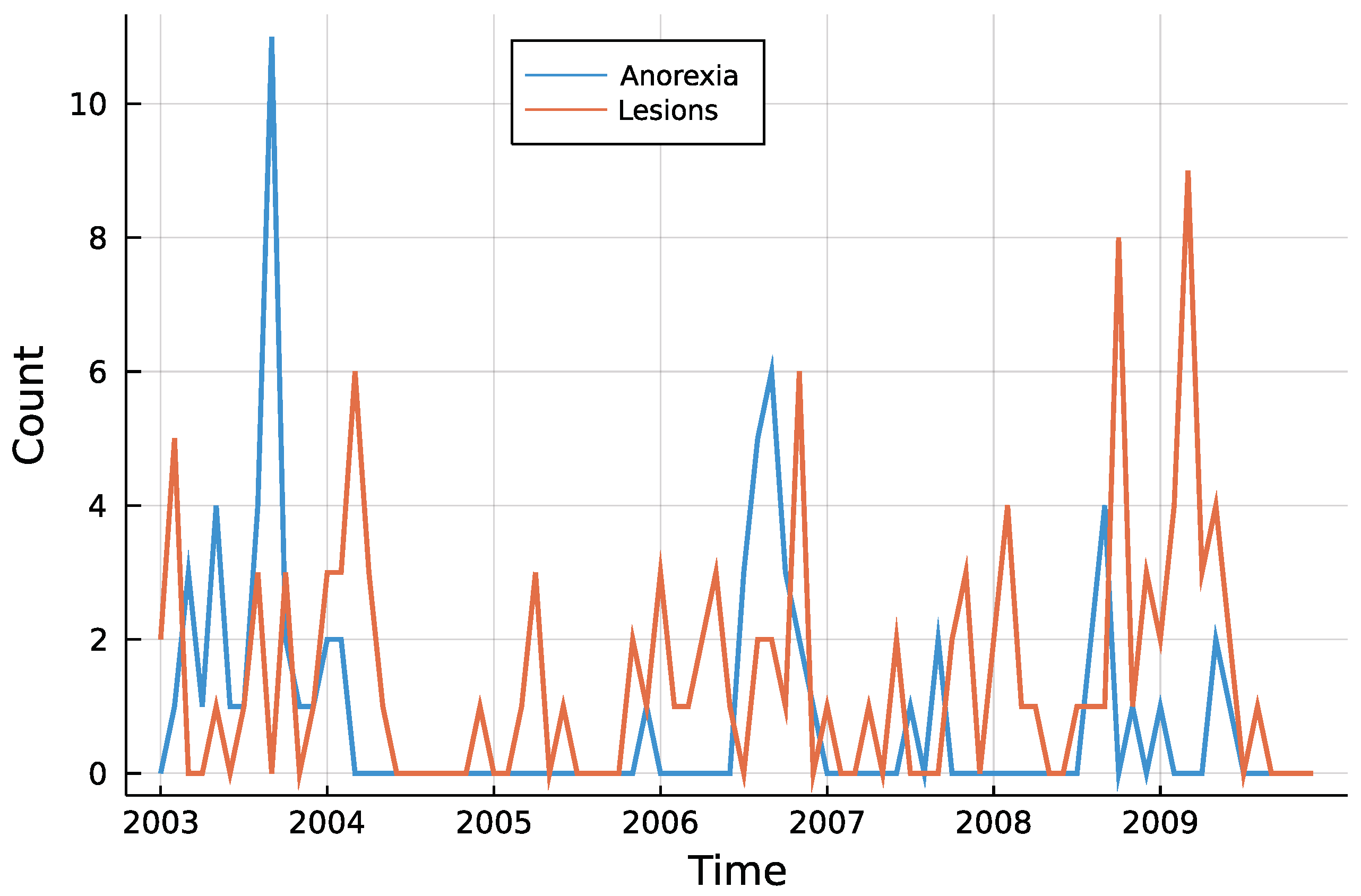
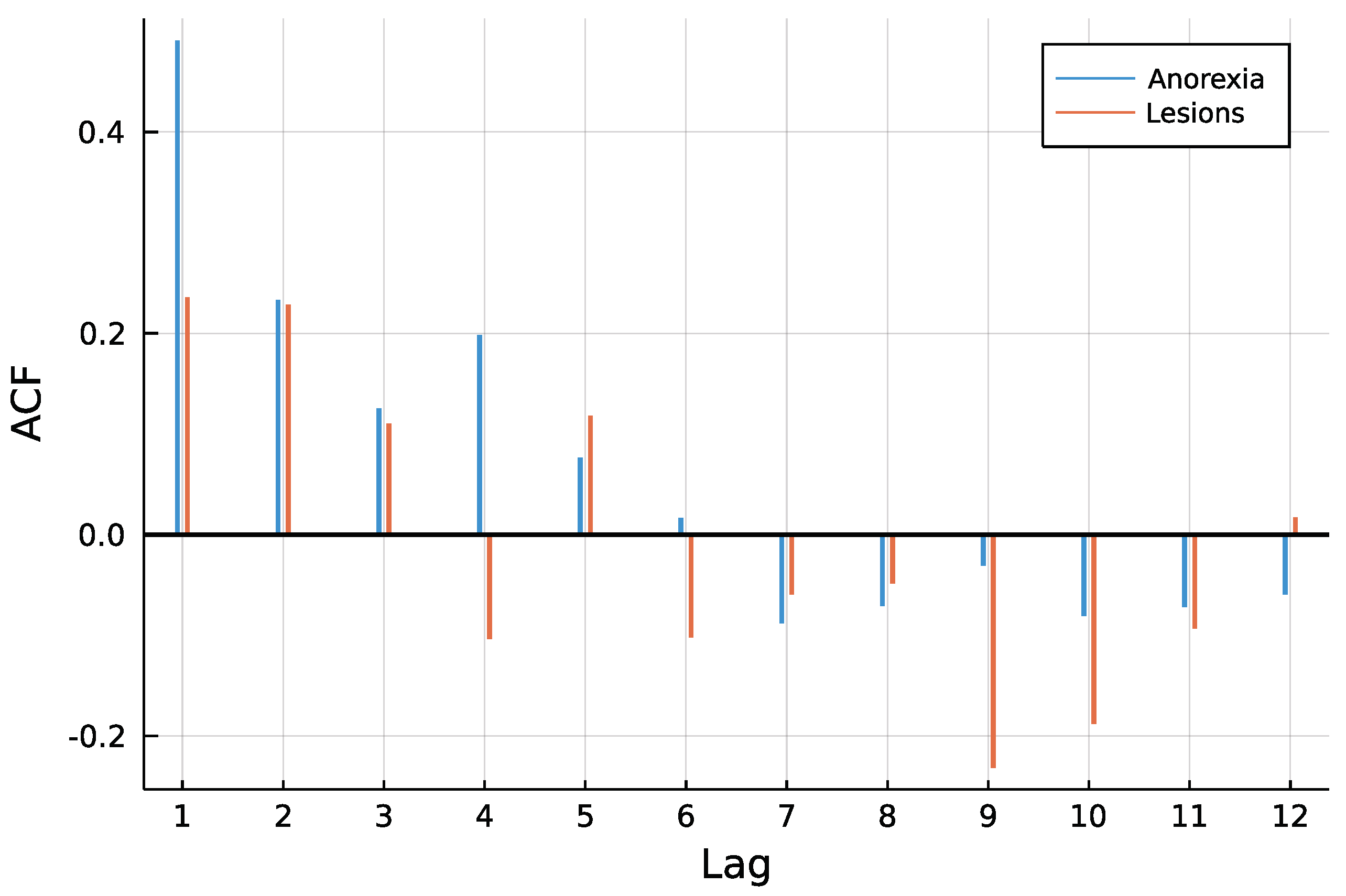
4. Application: Animal Health in New Zealand
4.1. Model and Implementation
4.2. Results
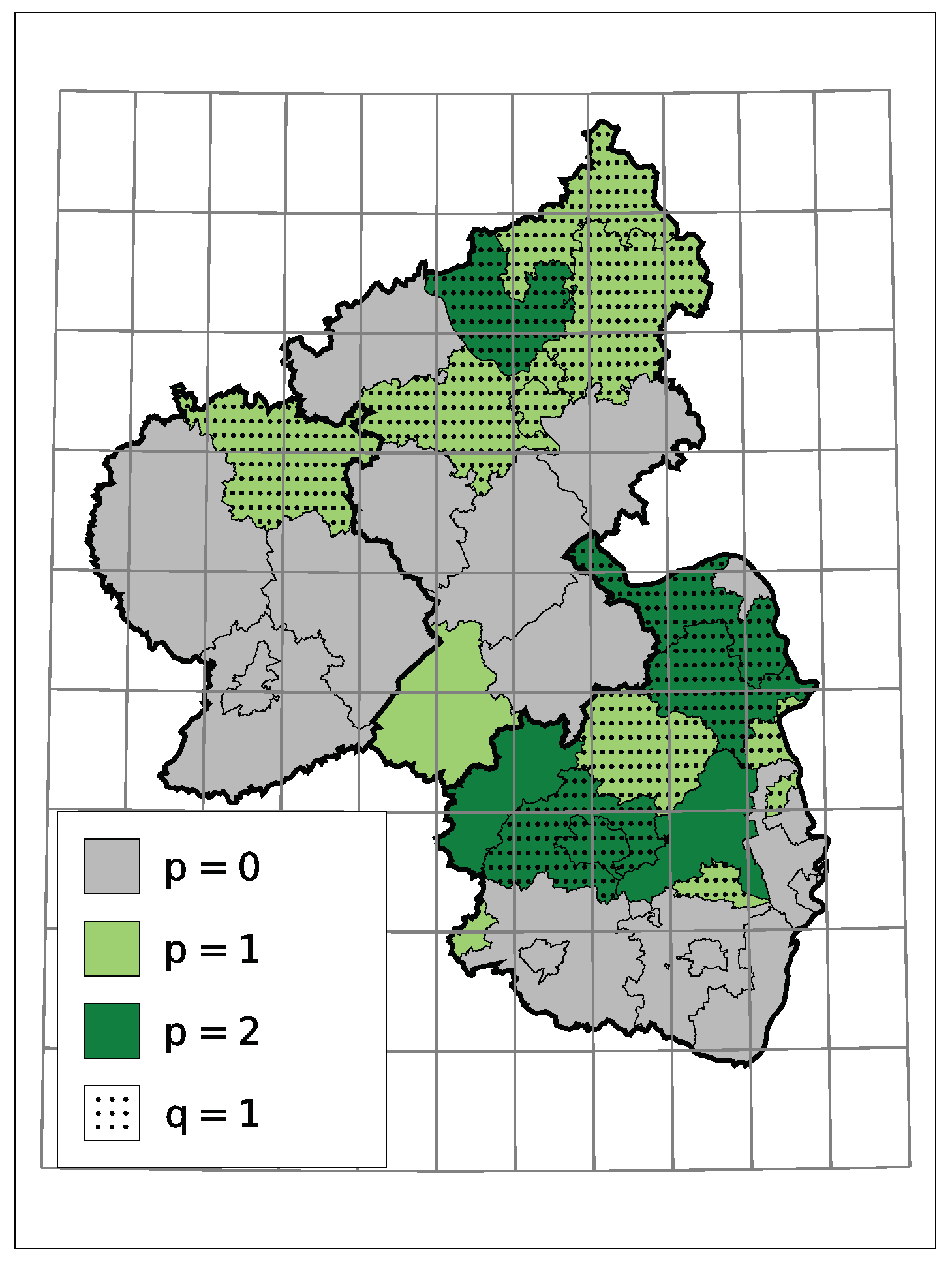
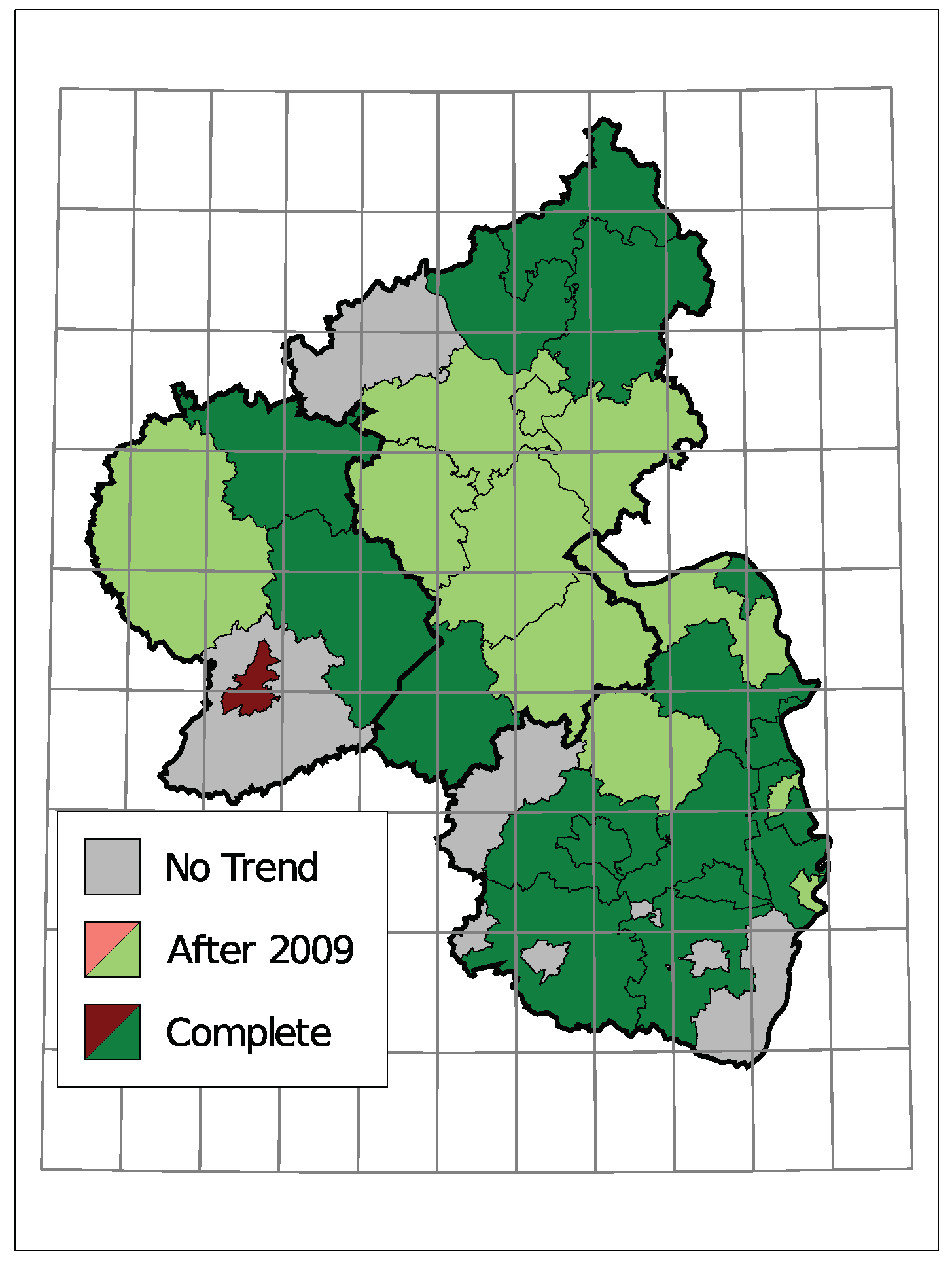
5. Application: Corporate Insolvencies in Rhineland-Palatinate
5.1. Models and Implementation
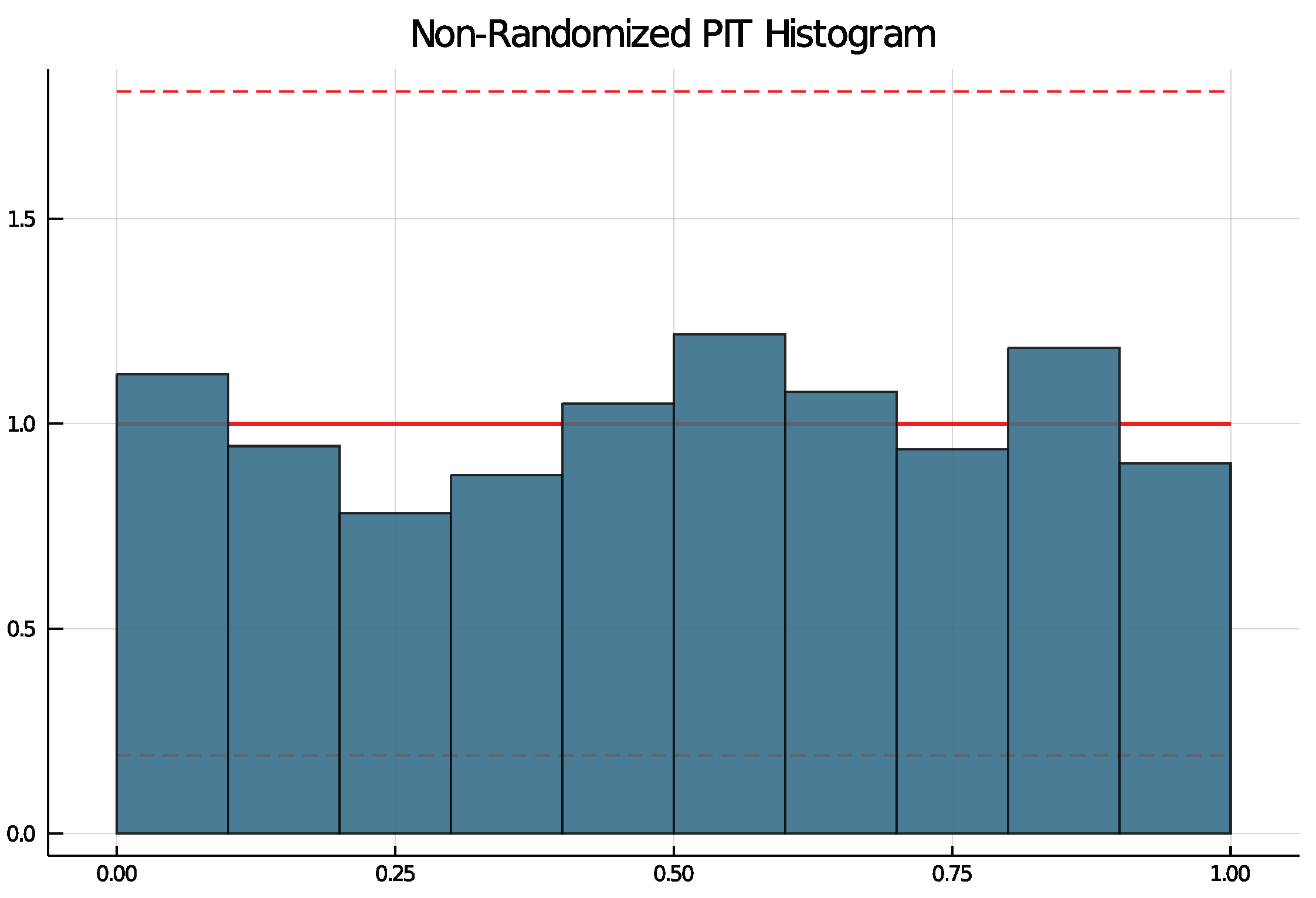
5.2. Results
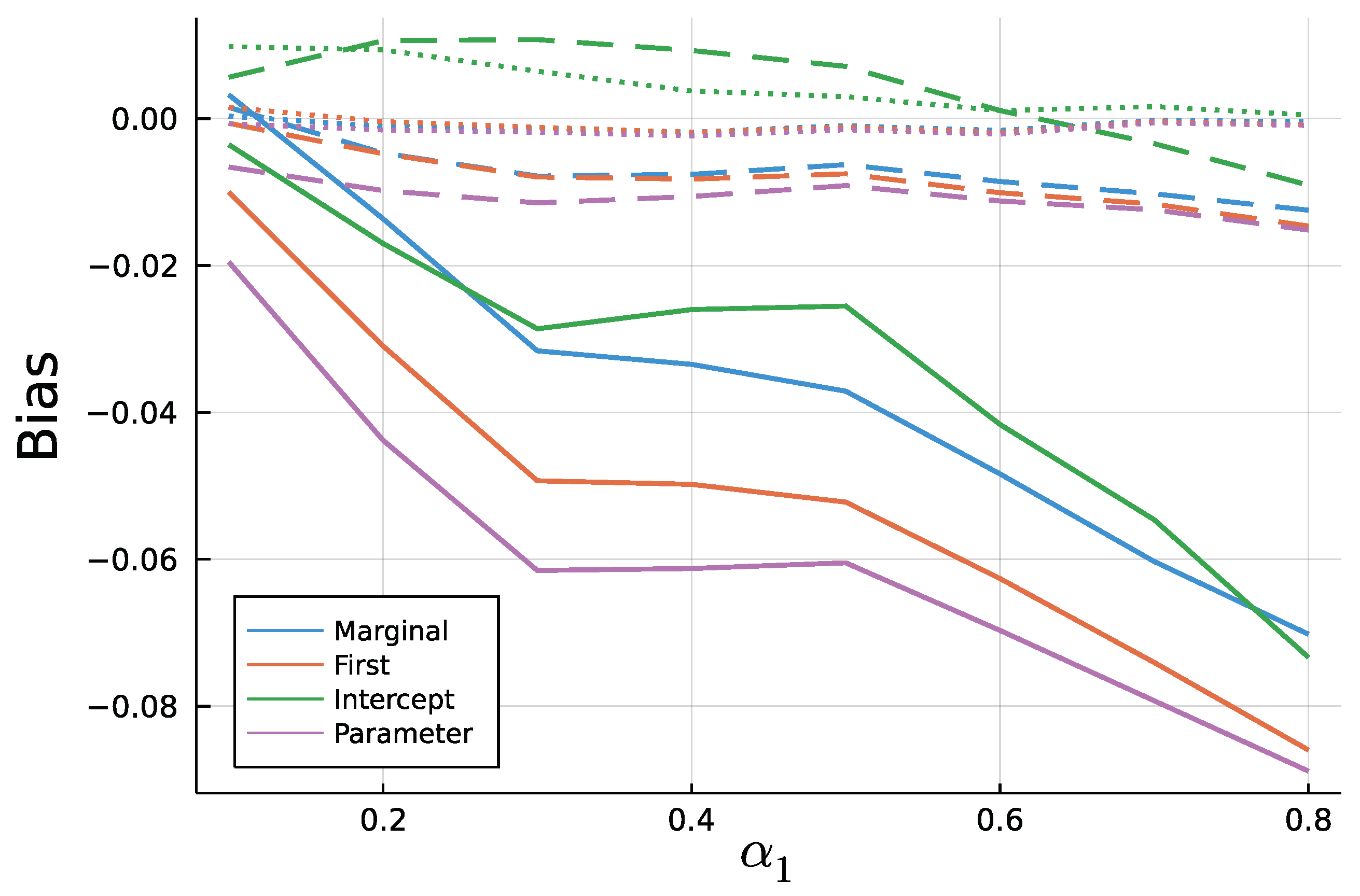
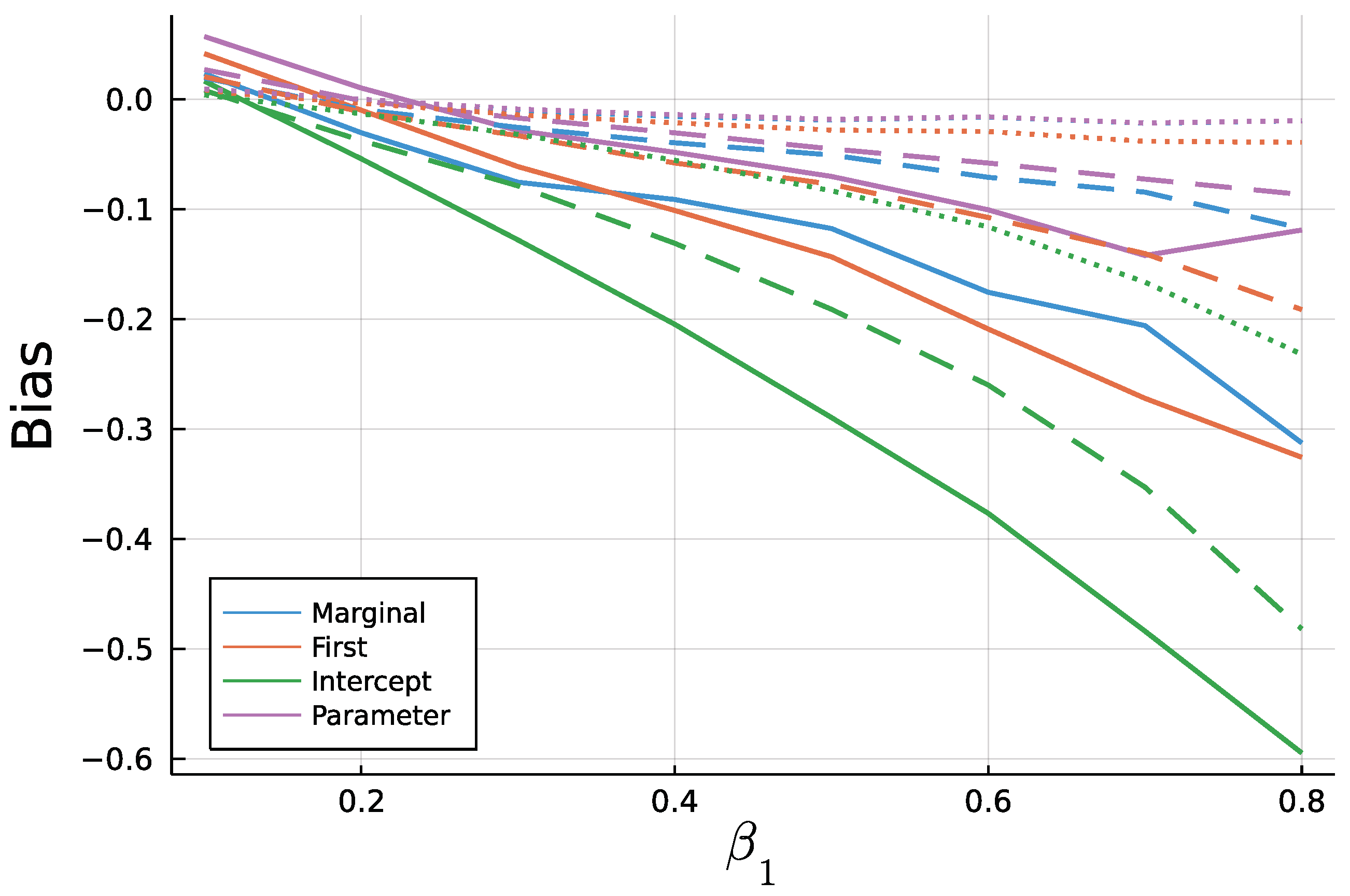
6. Simulation Study: Finite Sample ML—Estimation
6.1. Study and Implementation
6.2. Results
7. Discussion and Outlook
Supplementary Materials
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

| Model | AIC | |||||
|---|---|---|---|---|---|---|
| Anorexia | Pois-INAR(1) | 0.511 | 0.385 | - | - | 225.05 |
| (0.087) | (0.073) | - | - | |||
| Pois-INAR(2) | 0.450 | 0.353 | 0.098 | - | 224.70 | |
| (0.088) | (0.078) | (0.072) | - | |||
| NB-INAR(1) | 0.579 | 0.304 | - | 0.194 | 181.64 | |
| (0.173) | (0.078) | - | (0.011) | |||
| NB-INAR(2) | 0.545 | 0.220 | 0.118 | 0.139 | 180.37 | |
| (0.188) | (0.096) | (0.078) | (0.059) | |||
| Lesions | Pois-INAR(1) | 1.172 | 0.173 | - | - | 294.77 |
| (0.146) | (0.068) | - | - | |||
| Pois-INAR(2) | 0.976 | 0.145 | 0.132 | - | 292.17 | |
| (0.153) | (0.068) | (0.067) | - | |||
| NB-INAR(1) | 1.236 | 0.128 | - | 0.839 | 268.59 | |
| (0.217) | (0.076) | - | (0.006) | |||
| NB-INAR(2) | 1.017 | 0.084 | 0.164 | 0.608 | 265.85 | |
| (0.214) | (0.076) | (0.075) | (0.248) |
| District | Mean | Var | Model | Trend |
|---|---|---|---|---|
| Ahrweiler | 3.11 | 3.39 | Pois IID | No |
| Altenkirchen | 3.03 | 5.34 | NB-INGARCH(1, 1) | Yes |
| Alzey-Worms | 2.76 | 4.61 | NB-INGARCH(2, 1) | Yes |
| Bad Dürckheim | 1.88 | 2.57 | NB INARCH(2) | Yes |
| Bad Kreuznach | 4.94 | 5.90 | Pois IID | Partly |
| Bernkastell-Wittlich | 3.25 | 4.58 | Pois IID | Yes |
| Birkenfeld | 2.29 | 3.22 | NB-INARCH(1) | Yes |
| Cochem-Zell | 1.29 | 1.72 | NB IID | Partly |
| Donnersbergkreis | 1.38 | 1.86 | P-INGARCH(1, 1) | Partly |
| Eifelkr. Bitburg-Prüm | 2.03 | 3.28 | NB-IID | Partly |
| Frankenthal, kfr. S. | 0.96 | 1.29 | P-INGARCH(1, 1) | Partly |
| Gemersheim | 1.71 | 1.93 | Pois IID | No |
| Kaiserslautern, kfr. S. | 2.95 | 4.59 | P-INGARCH(2, 1) | Yes |
| Kaiserslautern | 2.73 | 6.03 | NB-INGARCH(2, 1) | Yes |
| Koblenz | 3.49 | 4.79 | P-INGARCH(1, 1) | Partly |
| Kusel | 1.27 | 1.53 | P-INARCH(2) | No |
| Landau i.d.P | 0.83 | 0.91 | Pois IID | No |
| Ludwigshafen | 3.06 | 4.73 | NB IID | Yes |
| Mainz | 4.90 | 10.62 | NB IID | Yes |
| Mainz-Bingen | 4.55 | 8.21 | P-INGARCH(2, 1) | Partly |
| Mayen-Koblenz | 5.24 | 6.67 | NB-INGARCH(1, 1) | Partly |
| Neustadt a.d.W. | 1.06 | 1.23 | P-INGARCH(1, 1) | Yes |
| Neuwied | 6.73 | 11.84 | P-INGARCH(2, 1) | Yes |
| Pirmasens | 0.94 | 0.91 | Pois IID | No |
| Rhein-Hunsrück-Kreis | 2.56 | 3.07 | Pois IID | Partly |
| Rhein-Lahn-Kreis | 2.88 | 3.83 | Pois IID | Partly |
| Rhein-Pfalz-Kreis | 2.40 | 2.82 | Pois IID | Yes |
| Speyer | 1.01 | 1.04 | Pois IID | Partly |
| Südliche Weinstraße | 1.76 | 1.98 | Pois IID | Yes |
| Südwestpfalz | 1.61 | 1.87 | Pois IID | Yes |
| Trier, kfr. S. | 1.87 | 1.85 | Pois IID | Yes |
| Trier-Saarburg | 1.46 | 1.90 | NB IID | No |
| Vulkaneifel | 1.41 | 1.70 | P-INGARCH(1, 1) | Yes |
| Westerwald | 5.30 | 8.66 | NB-INGARCH(1, 1) | Yes |
| Worms | 2.94 | 8.88 | NB-INGARCH(1, 1) | Yes |
| Zweibrücken | 0.88 | 1.13 | P-INARCH(1) | No |

References
- Alzaid, A.; Al-Osh, M. First-Order Integer-Valued Autoregressive (INAR(1)) Process: Distributional and Regression Properties. Stat. Neerl. 1988, 41, 53–60. [Google Scholar] [CrossRef]
- Ferland, R.; Latour, A.; Oraichi, D. Integer-Valued GARCH Process. J. Time Ser. Anal. 2006, 27, 923–942. [Google Scholar] [CrossRef]
- Bezanson, J.; Karpinski, S.; Shah, V.B.; Edelman, A. Julia: A Fast Dynamic Language for Technical Computing. arXiv 2012, arXiv:1209.5145. [Google Scholar]
- Liboschik, T.; Fried, R.; Fokianos, K.; Probst, P. tscount: Analysis of Count Time Series, R Package Version 1.4.1; Available online: https://cran.r-project.org/web/packages/tscount/index.html (accessed on 16 March 2021).
- Weiß, C.H.; Feld, M.H.J.M.; Mamode Khan, N.; Sunecher, Y. INARMA Modeling of Count Time Series. Stats 2019, 2, 284–320. [Google Scholar] [CrossRef]
- Harte, D. HiddenMarkov: Hidden Markov Models; R Package Version 1.8-11; Statistics Research Associates: Wellington, New Zealand, 2017. [Google Scholar]
- Himmelmann, L. HMM: HMM—Hidden Markov Models, R Package Version 1.0; Available online: https://cran.r-project.org/web/packages/HMM/index.html (accessed on 16 March 2021).
- Jackman, S. pscl: Classes and Methods for R Developed in the Political Science Computational Laboratory; R Package Version 1.5.5. Available online: https://github.com/atahk/pscl/ (accessed on 16 March 2021).
- Zeileis, A.; Kleiber, C.; Jackman, S. Regression Models for Count Data in R. J. Stat. Softw. 2008, 27, 1–25. [Google Scholar] [CrossRef]
- Mouchet, M. HMMBase—A Lightweight and Efficient Hidden Markov Model Abstraction. 2020. Available online: https://github.com/maxmouchet/HMMBase.jl (accessed on 16 March 2021).
- Weiß, C.H.; Feld, M. On the performance of information criteria for model identification of count time Series. Stud. Nonlinear Dyn. Econom. 2019, 24. [Google Scholar] [CrossRef]
- Liboschik, T.; Kerschke, P.; Fokianos, K.; Fried, R. Modelling interventions in INGARCH processes. Int. J. Comput. Math. 2016, 93, 640–657. [Google Scholar] [CrossRef]
- Aghababaei Jazi, M.; Jones, G.; Lai, C.D. First-order integer valued AR processes with zero inflated poisson innovations. J. Time Ser. Anal. 2012, 33, 954–963. [Google Scholar] [CrossRef]
- Czado, C.; Gneiting, T.; Held, L. Predictive Model Assessment for Count Data. Biometrics 2009, 65, 1254–1261. [Google Scholar] [CrossRef] [PubMed]
- RKI. Robert-Koch-Institut: SurvStat@RKI 2.0. 2021. Available online: https://survstat.rki.de/ (accessed on 16 March 2021).
- NPGEO. RKI COVID19. 2021. Available online: https://npgeo-corona-npgeo-de.hub.arcgis.com/datasets/dd4580c810204019a7b8eb3e0b329dd6_0 (accessed on 16 March 2021).
- World Health Organization. Transmission of SARS-CoV-2: Implications for Infection Prevention Precautions. 2020. Available online: https://www.who.int/news-room/commentaries/detail/transmission-of-sars-cov-2-implications-for-infection-prevention-precautions (accessed on 7 May 2021).
- Christou, V.; Fokianos, K. Quasi-Likelihood Inference for Negative Binomial Time Series Models. J. Time Ser. Anal. 2014, 35, 55–78. [Google Scholar] [CrossRef]
- Mohammadpour, M.; Bakouch, H.; Shirozhan, M. Poisson-Lindley INAR(1) model with applications. Braz. J. Probab. Stat. 2018, 32, 262–280. [Google Scholar] [CrossRef]
- Schweer, S.; Weiß, C.H. Compound Poisson INAR(1) processes: Stochastic properties and testing for overdispersion. Comput. Stat. Data Anal. 2014, 77, 267–284. [Google Scholar] [CrossRef]
- Röhl, K.H.; Vogt, G. Unternehmensinsolvenzen in Deutschland. 2019. Available online: https://www.iwkoeln.de/studien/iw-trends/beitrag/klaus-heiner-roehl-unternehmensinsolvenzen-in-deutschland-trendwende-voraus-449151.html (accessed on 16 March 2021).
- Li, Q.; Chen, H.; Zhu, F. Robust Estimation for Poisson Integer-Valued GARCH Models Using a New Hybrid Loss. J. Syst. Sci. Complex. 2021. [Google Scholar] [CrossRef]
- Xiong, L.; Zhu, F. Minimum Density Power Divergence Estimator for Negative Binomial Integer-Valued GARCH Models. Commun. Math. Stat. 2021. [Google Scholar] [CrossRef]
- Weiß, C.H. Stationary count time series models. WIREs Comput. Stat. 2021, 13. [Google Scholar] [CrossRef]
- Möller, T.; Weiß, C.; Kim, H.Y.; Sirchenko, A. Modeling Zero Inflation in Count Data Time Series with Bounded Support. Methodol. Comput. Appl. Probab. 2018, 20. [Google Scholar] [CrossRef]
- Quoreshi, A.M.M.S. Bivariate Time Series Modeling of Financial Count Data. Commun. Stat. Theory Methods 2006, 35, 1343–1358. [Google Scholar] [CrossRef]
- Eurostat. GISCO: Geographische Informationen und Karten. 2021. Available online: https://ec.europa.eu/eurostat/de/web/gisco/geodata/reference-data/administrative-units-statistical-units/nuts (accessed on 16 March 2021).

| Criterion | Model | Prediction Horizon | ||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||
| RMSPE | Poisson | 29.53 | 30.18 | 30.11 | 30.14 | 28.81 | 28.07 | 27.86 |
| Quasi-Poisson | 29.53 | 30.07 | 30.04 | 29.98 | 28.59 | 27.89 | 27.71 | |
| Negative Binomial | 30.95 | 31.14 | 30.89 | 30.86 | 30.38 | 29.68 | 30.09 | |
| MedAPE | Poisson | 10.14 | 10.39 | 10.19 | 10.27 | 10.38 | 10.20 | 10.03 |
| Quasi-Poisson | 10.07 | 10.22 | 10.26 | 10.12 | 10.28 | 9.96 | 9.69 | |
| Negative Binomial | 12.55 | 12.43 | 12.19 | 12.05 | 11.71 | 11.97 | 11.75 | |
| Inside PI | Poisson | 46.5 | 46.5 | 46.5 | 48.5 | 50.5 | 49.5 | 49.5 |
| Quasi-Poisson | 97.0 | 97.0 | 97.0 | 97.0 | 97.0 | 97.0 | 97.0 | |
| Negative Binomial | 98.0 | 98.0 | 99.0 | 99.0 | 99.0 | 99.0 | 99.0 | |
| (Quasi-)Poisson | NegativeBinomial | |||||
|---|---|---|---|---|---|---|
| Estimate | Std. Err. | Conf. Interval | Estimate | Std. Err. | Conf. Interval | |
| −0.159 | 0.049 | (−0.254,−0.063) | −0.540 | 0.107 | (−0.749,−0.330) | |
| 0.041 | 0.018 | (0.006, 0.077) | 0.115 | 0.063 | (−0.010,0.239) | |
| 0.122 | 0.022 | (0.079, 0.165) | 0.088 | 0.080 | (−0.068, 0.245) | |
| 0.053 | 0.030 | (−0.006, 0.112) | 0.005 | 0.100 | (−0.190, 0.200) | |
| −0.032 | 0.015 | (−0.061,−0.003) | −0.034 | 0.057 | (−0.146, 0.078) | |
| 0.221 | 0.027 | (0.168, 0.274) | 0.252 | 0.076 | (0.103, 0.401) | |
| 0.314 | 0.029 | (0.257, 0.370) | 0.356 | 0.078 | (0.203, 0.509) | |
| 0.149 | 0.024 | (0.102, 0.196) | 0.194 | 0.084 | (0.030, 0.359) | |
| 0.265 | 0.024 | (0.218, 0.312) | 0.317 | 0.074 | (0.172, 0.463) | |
| 1.405 | 1.516 | 0.164 | (1.195, 1.837) | |||
| Model | AIC | ||||||
|---|---|---|---|---|---|---|---|
| Anorexia | Pois-INAR(1) | 2.215 | 0.338 | - | - | 0.669 | 183.00 |
| (0.428) | (0.074) | - | - | (0.069) | |||
| Pois-INAR(2) | 2.692 | 0.249 | 0.118 | - | 0.752 | 179.85 | |
| (0.536) | (0.090) | (0.070) | - | (0.061) | |||
| NB-INAR(1) | 1.642 | 0.310 | - | 1.278 | 0.424 | 182.25 | |
| (0.831) | (0.077) | - | (1.766) | (0.283) | |||
| NB-INAR(2) | 2.363 | 0.225 | 0.120 | 2.668 | 0.630 | 179.94 | |
| (0.794) | (0.093) | (0.073) | (3.561) | (0.178) | |||
| Lesions | Pois-INAR(1) | 2.042 | 0.175 | - | - | 0.372 | 276.26 |
| (0.278) | (0.071) | - | - | (0.077) | |||
| Pois-INAR(2) | 2.055 | 0.110 | 0.176 | - | 0.464 | 271.32 | |
| (0.333) | (0.073) | (0.073) | - | (0.089) | |||
| NB-INAR(1) | 1.344 | 0.130 | - | 1.018 | 0.047 | 270.60 | |
| (0.599) | (0.077) | - | (1.081) | (0.242) | |||
| NB-INAR(2) | 1.252 | 0.084 | 0.166 | 0.920 | 0.103 | 267.76 | |
| (0.754) | (0.076) | (0.075) | (1.218) | (0.313) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stapper, M. Count Data Time Series Modelling in Julia—The CountTimeSeries.jl Package and Applications. Entropy 2021, 23, 666. https://doi.org/10.3390/e23060666
Stapper M. Count Data Time Series Modelling in Julia—The CountTimeSeries.jl Package and Applications. Entropy. 2021; 23(6):666. https://doi.org/10.3390/e23060666
Chicago/Turabian StyleStapper, Manuel. 2021. "Count Data Time Series Modelling in Julia—The CountTimeSeries.jl Package and Applications" Entropy 23, no. 6: 666. https://doi.org/10.3390/e23060666
APA StyleStapper, M. (2021). Count Data Time Series Modelling in Julia—The CountTimeSeries.jl Package and Applications. Entropy, 23(6), 666. https://doi.org/10.3390/e23060666






