Abstract
Decentralized partially observable Markov decision process (DEC-POMDP) models sequential decision making problems by a team of agents. Since the planning of DEC-POMDP can be interpreted as the maximum likelihood estimation for the latent variable model, DEC-POMDP can be solved by the EM algorithm. However, in EM for DEC-POMDP, the forward–backward algorithm needs to be calculated up to the infinite horizon, which impairs the computational efficiency. In this paper, we propose the Bellman EM algorithm (BEM) and the modified Bellman EM algorithm (MBEM) by introducing the forward and backward Bellman equations into EM. BEM can be more efficient than EM because BEM calculates the forward and backward Bellman equations instead of the forward–backward algorithm up to the infinite horizon. However, BEM cannot always be more efficient than EM when the size of problems is large because BEM calculates an inverse matrix. We circumvent this shortcoming in MBEM by calculating the forward and backward Bellman equations without the inverse matrix. Our numerical experiments demonstrate that the convergence of MBEM is faster than that of EM.
1. Introduction
Markov decision process (MDP) models sequential decision making problems and has been used for planning and reinforcement learning [1,2,3,4]. MDP consists of an environment and an agent. The agent observes the state of the environment and controls it by taking actions. The planning of MDP is to find the optimal control policy maximizing the objective function, which is typically solved by the Bellman equation-based algorithms such as value iteration and policy iteration [1,2,3,4].
Decentralized partially observable MDP (DEC-POMDP) is an extension of MDP to a multiagent and partially observable setting, which models sequential decision making problems by a team of agents [5,6,7]. DEC-POMDP consists of an environment and multiple agents, and the agents cannot observe the state of the environment and the actions of the other agents completely. The agents infer the environmental state and the other agents’ actions from their observation histories and control them by taking actions. The planning of DEC-POMDP is to find not only the optimal control policy but also the optimal inference policy for each agent, which maximize the objective function [5,6,7]. Applications of DEC-POMDP include planetary exploration by a team of rovers [8], target tracking by a team of sensors [9], and information transmission by a team of devices [10]. Since the agents cannot observe the environmental state and the other agents’ actions completely, it is difficult to extend the Bellman equation-based algorithms for MDP to DEC-POMDP straightforwardly [11,12,13,14,15].
DEC-POMDP can be solved using control as inference [16,17]. Control as inference is a framework to interpret a control problem as an inference problem by introducing auxiliary variables [18,19,20,21,22]. Although control as inference has several variants, Toussaint and Storkey showed that the planning of MDP can be interpreted as the maximum likelihood estimation for a latent variable model [18]. Thus, the planning of MDP can be solved by EM algorithm, which is the typical algorithm for the maximum likelihood estimation of latent variable models [23]. Since the EM algorithm is more general than the Bellman equation-based algorithms, it can be straightforwardly extended to POMDP [24,25] and DEC-POMDP [16,17]. The computational efficiency of the EM algorithm for DEC-POMDP is comparable to that of other algorithms for DEC-POMDP [16,17,26,27,28], and the extensions to the average reward setting and to the reinforcement learning setting have been studied [29,30,31].
However, the EM algorithm for DEC-POMDP is not efficient enough to be applied to real-world problems, which often have a large number of agents or a large size of an environment. Therefore, there are several studies in which improvement of the computational efficiency of the EM algorithm for DEC-POMDP was attempted [26,27]. Because these studies achieve improvements by restricting possible interactions between agents, their applicability is limited. Therefore, it is desirable to have improvement in the efficiency for more general DEC-POMDP problems.
In order to improve the computational efficiency of EM algorithm for general DEC-POMDP problems, there are two problems that need to be resolved. The first problem is the forward–backward algorithm up to the infinite horizon. The EM algorithm for DEC-POMDP uses the forward–backward algorithm, which has also been used in EM algorithm for hidden Markov models [23]. However, in the EM algorithm for DEC-POMDP, the forward–backward algorithm needs to be calculated up to the infinite horizon, which impairs the computational efficiency [32,33]. The second problem is the Bellman equation. The EM algorithm for DEC-POMDP does not use the Bellman equation, which plays a central role in the the planning and in the reinforcement learning for MDP [1,2,3,4]. Therefore, the EM algorithm for DEC-POMDP cannot use the advanced techniques based on the Bellman equation, which makes it possible to solve large-size problems [34,35,36].
In some previous studies, resolution of these problems was attempted by replacing the forward–backward algorithm up to the infinite horizon with the Bellman equation [32,33]. However, in these studies, the computational efficiency could not be improved completely. For example, Song et al. replaced the forward–backward algorithm with the Bellman equation and showed that their algorithm is more efficient than EM and other DEC-POMDP algorithms by the numerical experiments [32]. However, since a parameter dependency is overlooked in [32], their algorithm may not find the optimal policy under a general situation (see Appendix D for more details). Moreover, Kumar et al. showed that the forward–backward algorithm can be replaced by linear programming with the Bellman equation as a constraint [33]. However, their algorithm may be less efficient than the EM algorithm when the size of problems is large. Therefore, previous studies have not yet completely improved the computational efficiency of EM algorithm for DEC-POMDP.
In this paper, we propose more efficient algorithms for DEC-POMDP than EM algorithm by introducing the forward and backward Bellman equations into it. The backward Bellman equation corresponds to the traditional Bellman equation, which has been used in previous studies [32,33]. In contrast, the forward Bellman equation has not yet been used for the planning of DEC-POMDP explicitly. This equation is similar to that recently proposed in the offline reinforcement learning of MDP [37,38,39]. In the offline reinforcement learning of MDP, the forward Bellman equation is used to correct the difference between the data sampling policy and the policy to be evaluated. In the planning of DEC-POMDP, the forward Bellman equation plays the important role in inferring the environmental state.
We propose the Bellman EM algorithm (BEM) and the modified Bellman EM algorithm (MBEM) by replacing the forward–backward algorithm with the forward and backward Bellman equations. They are different in terms of how to solve the forward and backward Bellman equations. BEM solves the forward and backward Bellman equations by calculating an inverse matrix. BEM can be more efficient than EM because BEM does not calculate the forward–backward algorithm up to the infinite horizon. However, since BEM calculates the inverse matrix, it cannot always be more efficient than EM when the size of problems is large, which is the same problem as [33]. Actually, BEM is essentially the same as [33]. In the linear programming problem of [33], the number of variables is equal to that of constraints, which enables us to solve it only from the constraints without the optimization. Therefore, the algorithm in [33] becomes equivalent to BEM, and they suffers from the same problem as BEM.
This problem is addressed by MBEM. MBEM solves the forward and backward Bellman equations by applying the forward and backward Bellman operators to the arbitrary initial functions infinite times. Although MBEM needs to calculate the forward and backward Bellman operators infinite times, which is the same problem with EM, MBEM can evaluate approximation errors more tightly owing to the contractibility of these operators. It can also utilize the information of the previous iteration owing to the arbitrariness of the initial functions. These properties enable MBEM to be more efficient than EM. Moreover, MBEM resolves the drawback of BEM because MBEM does not calculate the inverse matrix. Therefore, MBEM can be more efficient than EM even when the size of problems is large. Our numerical experiments demonstrate that the convergence of MBEM is faster than that of EM regardless of the size of problems.
The paper is organized as follows: In Section 2, DEC-POMDP is formulated. In Section 3, the EM algorithm for DEC-POMDP, which was proposed in [16], is briefly reviewed. In Section 4, the forward and backward Bellman equations are derived, and the Bellman EM algorithm (BEM) is proposed. In Section 5, the forward and backward Bellman operators are defined, and the modified Bellman EM algorithm (MBEM) is proposed. In Section 6, EM, BEM, and MBEM are summarized and compared. In Section 7, the performances of EM, BEM, and MBEM are compared through the numerical experiment. In Section 8, this paper is concluded, and future works are discussed.
2. DEC-POMDP
DEC-POMDP consists of an environment and N agents (Figure 1 and Figure 2a) [7,16]. is the state of the environment at time t. , , and are the observation, the memory, and the action available to the agent , respectively. , , , and are finite sets. , , and are the joint observation, the joint memory, and the joint action of the N agents, respectively.
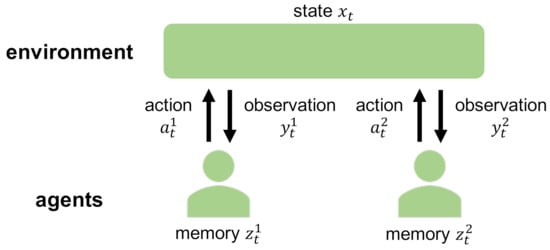
Figure 1.
Schematic diagram of DEC-POMDP. DEC-POMDP consists of an environment and N agents ( in this figure). is the state of the environment at time t. , , and are the observation, the memory, and the action available to the agent , respectively. The agents update their memories based on their observations, and take their actions based on their memories to control the environmental state. The planning of DEC-POMDP is to find their optimal memory updates and action selections that maximize the objective function.
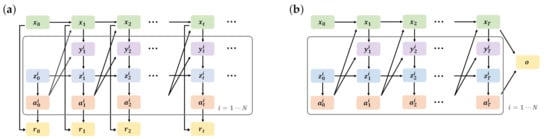
Figure 2.
Dynamic Bayesian networks of DEC-POMDP (a) and the latent variable model for the time horizon (b). is the state of the environment at time t. , , and are the observation, the memory, and the action available to the agent , respectively. (a) is the reward, which is generated at each time. (b) is the optimal variable, which is generated only at the time horizon T.
The time evolution of the environmental state is given by the initial state probability and the state transition probability . Thus, agents can control the environmental state by taking appropriate actions . The agent i cannot observe the environmental state and the joint action completely, and obtains the observation instead of them. Thus, the observation obeys the observation probability . The agent i updates its memory from to based on the observation . Thus, the memory obeys the initial memory probability and the memory transition probability . The agent i takes the action based on the memory by following the action probability . The reward function defines the amount of reward that is obtained at each step depending on the state of the environment and the joint action taken by the agents.
The objective function in the planning of DEC-POMDP is given by the expected return, which is the expected discounted cumulative reward:
is the policy, where , , and . is the discount factor, which decreases the weight of the future reward. The closer is to 1, the closer the weight of the future reward is to that of the current reward.
The planning of DEC-POMDP is to find the policy that maximizes the expected return as follows:
In other words, the planning of DEC-POMDP is to find how to take the action and how to update the memory for each agent to maximize the expected return.
3. EM Algorithm for DEC-POMDP
In this section, we explain the EM algorithm for DEC-POMDP, which was proposed in [16].
3.1. Control as Inference
In this subsection, we show that the planning of DEC-POMDP can be interpreted as the maximum likelihood estimation for a latent variable model (Figure 2b).
We introduce two auxiliary random variables: the time horizon and the optimal variable . These variables obey the following probabilities:
where and are the maximum and the minimum value of the reward function , respectively. Thus, is satisfied.
By introducing these variables, DEC-POMDP changes from Figure 2a to Figure 2b. While Figure 2a considers the infinite time horizon, Figure 2b considers the finite time horizon T, which obeys Equation (3). Moreover, while the reward is generated at each time in Figure 2a, the optimal variable o is generated only at the time horizon T in Figure 2b.
Theorem 1
Proof.
See Appendix A.1. □
Therefore, the planning of DEC-POMDP is equivalent to the maximum likelihood estimation for the latent variable model as follows:
Intuitively, while the planning of DEC-POMDP is to find the policy which maximizes the reward, the maximum likelihood estimation for the latent variable model is to find the policy which maximizes the probability of the optimal variable. Since the probability of the optimal variable is proportional to the reward, the planning of DEC-POMDP is equivalent to the maximum likelihood estimation for the latent variable model.
3.2. EM Algorithm
Since the planning of DEC-POMDP can be interpreted as the maximum likelihood estimation for the latent variable model, it can be solved by the EM algorithm [16]. EM algorithm is the typical algorithm for the maximum likelihood estimation of latent variable models, which iterates two steps, E step and M step [23].
In the E step, we calculate the Q function, which is defined as follows:
where is the current estimator of the optimal policy.
In the M step, we update to by maximizing the Q function as follows:
Since each iteration between the E step and the M step monotonically increases the likelihood , we can find that locally maximizes the likelihood .
3.3. M Step
Proposition 1
([16]). In the EM algorithm for DEC-POMDP, Equation (8) can be calculated as follows:
. and are defined in the same way. and are defined as follows:
where , and .
Proof.
See Appendix A.2. □
quantifies the frequency of the state x and the memory z, which is called the frequency function in this paper. quantifies the probability of when the initial state and memory are x and z, respectively. Since the probability of is proportional to the reward, is called the value function in this paper. Actually, corresponds to the value function [33].
3.4. E Step
and need to be obtained to calculate Equations (9)–(11). In [16], and are calculated by the forward–backward algorithm, which has been used in EM algorithm for the hidden Markov model [23].
In [16], the forward probability and the backward probability are defined as follows:
It is easy to calculate and as follows:
Moreover, and are easily calculated from and :
where
Equations (18) and (19) are called the forward and backward equations, respectively. Using Equations (16)–(19), and can be efficiently calculated from to , which is called the forward–backward algorithm [23].
By calculating the forward–backward algorithm from to , and can be obtained as follows [16]:
However, and cannot be calculated exactly by this approach because it is practically impossible to calculate the forward–backward algorithm until . Therefore, the forward–backward algorithm needs to be terminated at , where is finite. In this case, and are approximated as follows:
needs to be large enough to reduce the approximation errors. In the previous study, a heuristic termination condition was proposed as follows [16]:
where . However, the relation between and the approximation errors is unclear in Equation (25). We propose a new termination condition to guarantee the approximation errors as follows:
Proposition 2.
We set an acceptable error bound . If
is satisfied, then
are satisfied.
Proof.
See Appendix A.3. □
3.5. Summary
In summary, the EM algorithm for DEC-POMDP is given by Algorithm 1. In the E step, we calculate and from to by the forward–backward algorithm. In M step, we update to using Equations (9)–(11). The time complexities of the E step and the M step are and , respectively. Note that , and and are defined in the same way. The EM algorithm for DEC-POMDP is less efficient when the discount factor is closer to 1 or the acceptable error bound is smaller because needs to be larger in these cases.
| Algorithm 1 EM algorithm for DEC-POMDP |
4. Bellman EM Algorithm
In the EM algorithm for DEC-POMDP, and are calculated from to to obtain and . However, needs to be large to reduce the approximation errors of and , which impairs the computational efficiency of the EM algorithm for DEC-POMDP [32,33]. In this section, we calculate and directly without calculating and to resolve the drawback of EM.
4.1. Forward and Backward Bellman Equations
The following equations are useful to obtain and directly:
Theorem 2.
and satisfy the following equations:
Equations (29) and (30) are called the forward Bellman equation and the backward Bellman equation, respectively.
Proof.
See Appendix B.1. □
Note that the direction of time is different between Equations (29) and (30). In Equation (29), and are earlier state and memory than x and z, respectively. In Equation (30), and are later state and memory than x and z, respectively.
The backward Bellman Equation (30) corresponds to the traditional Bellman equation, which has been used in other algorithms for DEC-POMDP [11,12,13,14]. In contrast, the forward Bellman equation, which is introduced in this paper, is similar to that recently proposed in the offline reinforcement learning [37,38,39].
Since the forward and backward Bellman equations are linear equations, they can be solved exactly as follows:
where
Therefore, we can obtain and from the forward and backward Bellman equations.
4.2. Bellman EM Algorithm (BEM)
The forward–backward algorithm from to in the EM algorithm for DEC-POMDP can be replaced by the forward and backward Bellman equations. In this paper, the EM algorithm for DEC-POMDP that uses the forward and backward Bellman equations instead of the forward–backward algorithm from to is called the Bellman EM algorithm (BEM).
4.3. Comparison of EM and BEM
BEM is summarized as Algorithm 2. The M step in Algorithm 2 is almost the same as that in Algorithm 1—only the E step is different. While the time complexity of the E step in EM is , that in BEM is .
| Algorithm 2 Bellman EM algorithm (BEM) |
BEM can calculate and exactly. Moreover, BEM can be more efficient than EM when the discount factor is close to 1 or the acceptable error bound is small because needs to be large enough in these cases. However, when the size of the state space or that of the joint memory space is large, BEM cannot always be more efficient than EM because BEM needs to calculate the inverse matrix . To circumvent this shortcoming, we propose a new algorithm, the modified Bellman EM algorithm (MBEM), to obtain and without calculating the inverse matrix.
5. Modified Bellman EM Algorithm
5.1. Forward and Backward Bellman Operators
We define the forward and backward Bellman operators as follows:
where . From the forward and backward Bellman equations, and satisfy the following equations:
Thus, and are the fixed points of and , respectively. and have the following useful property:
Proposition 3.
and are contractive operators as follows:
where .
Proof.
See Appendix C.1. □
Note that the norm is different between Equations (37) and (38). It is caused by the difference of the time direction between and . While and are earlier state and memory than x and z, respectively, in the forward Bellman operator , and are later state and memory than x and z, respectively, in the backward Bellman operator .
We obtain and using Equations (35)–(38), as follows:
Proposition 4.
where .
Proof.
See Appendix C.2. □
Therefore, it is shown that and can be calculated by applying the forward and backward Bellman operators, and , to arbitrary initial functions, and , infinite times.
5.2. Modified Bellman EM Algorithm (MBEM)
The calculation of the forward and backward Bellman equations in BEM can be replaced by that of the forward and backward Bellman operators. In this paper, BEM that uses the forward and backward Bellman operators instead of the forward and backward Bellman equations is called modified Bellman EM algorithm (MBEM).
5.3. Comparison of EM, BEM, and MBEM
Since MBEM does not need the inverse matrix, MBEM can be more efficient than BEM when the size of the state space and that of the joint memory space are large. Thus, MBEM resolves the drawback of BEM.
On the other hand, MBEM has the same problem as EM. MBEM calculates and infinite times to obtain and . However, since it is practically impossible to calculate and infinite times, the calculation of and needs to be terminated after times, where is finite. In this case, and are approximated as follows:
needs to be large enough to reduce the approximation errors of and , which impairs the computational efficiency of MBEM. Thus, MBEM can potentially suffer from the same problem as EM. However, we can theoretically show that MBEM is more efficient than EM by comparing and under the condition that the approximation errors of and are smaller than the acceptable error bound .
When and , Equations (41) and (42) can be calculated as follows:
which are the same with Equations (23) and (24), respectively. Thus, in this case, , and the computational efficiency of MBEM is the same as that of EM. However, MBEM has two useful properties that EM does not have, and therefore, MBEM can be more efficient than EM. In the following, we explain these properties in more detail.
The first property of MBEM is the contractibility of the forward and backward Bellman operators, and . From the contractibility of the Bellman operators, is determined adaptively as follows:
Proposition 5.
We set an acceptable error bound . If
are satisfied, then
are satisfied.
Proof.
See Appendix C.3. □
is always constant for every E step, . Thus, even if the approximation errors of and are smaller than when , the forward–backward algorithm cannot be terminated until because the approximation errors of and cannot be evaluated in the forward–backward algorithm.
is adaptively determined depending on and . Thus, if and are close enough to and , the E step of MBEM can be terminated because the approximation errors of and can be evaluated owing to the contractibility of the forward and backward Bellman operators.
Indeed, when and , MBEM is more efficient than EM as follows:
Proposition 6.
When and , is satisfied.
Proof.
See Appendix C.4. □
The second property of MBEM is the arbitrariness of the initial functions, and . In MBEM, the initial functions, and , converge to the fixed points, and , by applying the forward and backward Bellman operators, and , times. Therefore, if the initial functions, and , are close to the fixed points, and , can be reduced. Then, the problem is what kind of the initial functions are close to the fixed points.
We suggest that and are set as the initial functions, and . In most cases, is close to . When is close to , it is expected that and are close to and . Therefore, by setting and as the initial functions and , respectively, is expected to be reduced. Hence, MBEM can be more efficient than EM because MBEM can utilize the results of the previous iteration, and , by this arbitrariness of the initial functions.
However, it is unclear how small can be compared to by setting and as the initial functions and . Therefore, numerical evaluations are needed. Moreover, in the first iteration, we cannot use the results of the previous iteration, and . Therefore, in the first iteration, we set and because these initial functions guarantee from Proposition 6.
MBEM is summarized as Algorithm 3. The M step of Algorithm 3 is exactly the same as that of Algorithms 1 and 2, and only the E step is different. The time complexity of the E step in MBEM is . MBEM does not use the inverse matrix, which resolves the drawback of BEM. Moreover, MBEM can reduce by the contractibility of the Bellman operators and the arbitrariness of the initial functions, which can resolve the drawback of EM.
| Algorithm 3 Modified Bellman EM algorithm (MBEM) |
6. Summary of EM, BEM, and MBEM
EM, BEM, and MBEM are summarized as in Table 1. The M step is exactly the same among these algorithms, and only the E step is different:

Table 1.
Summary of EM, BEM, and MBEM.
- EM obtains and by calculating the forward–backward algorithm up to . needs to be large enough to reduce the approximation errors of and , which impairs the computational efficiency.
- BEM obtains and by solving the forward and backward Bellman equations. BEM can be more efficient than EM because BEM calculates the forward and backward Bellman equations instead of the forward–backward algorithm up to . However, BEM cannot always be more efficient than EM when the size of the state or that of the memory is large because BEM calculates an inverse matrix to solve the forward and backward Bellman equations.
- MBEM obtains and by applying the forward and backward Bellman operators, and , to the initial functions, and , times. Since MBEM does not need to calculate the inverse matrix, MBEM may be more efficient than EM even when the size of problems is large, which resolves the drawback of BEM. Although needs to be large enough to reduce the approximation errors of and , which is the same problem as EM, MBEM can evaluate the approximation errors more tightly owing to the contractibility of and , and can utilize the results of the previous iteration, and , as the initial functions, and . These properties enable MBEM to be more efficient than EM.
7. Numerical Experiment
In this section, we compare the performance of EM, BEM, and MBEM using numerical experiments of four benchmarks for DEC-POMDP: broadcast [40], recycling robot [15], wireless network [27], and box pushing [41]. Detailed settings such as the state transition probability, the observation probability, and the reward function are described at http://masplan.org/problem_domains, accessed on 22 June 2020. We implement EM, BEM, and MBEM in C++.
Figure 3 shows the experimental results. In all the experiments, we set the number of agent , the discount factor , the upper bound of the approximation error , and the size of the memory available to the ith agent . The size of the state , the action , and the observation are different for each problem, which are shown on each panel. We note that the size of the state is small in the broadcast (a,e,i) and the recycling robot (b,f,j), whereas it is large in the wireless network (c,g,k) and the box pushing (d,h,l).
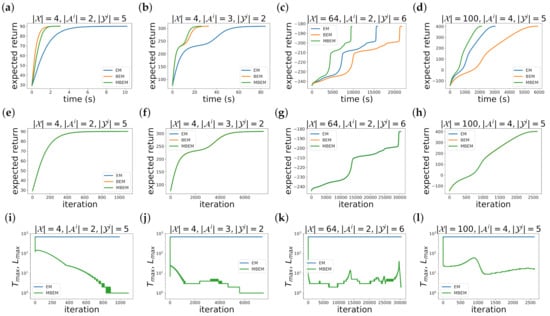
Figure 3.
Experimental results of four benchmarks for DEC-POMDP: (a,e,i) broadcast; (b,f,j) recycling robot; (c,g,k) wireless network; (d,h,l) box pushing. (a–d) The expected return as a function of the computational time. (e–h) The expected return as a function of the iteration k. (i–l) and as functions of the iteration k. In all the experiments, we set the number of agent , the discount factor , the upper bound of the approximation error , and the size of the memory available to the ith agent . The size of the state , the action , and the observation are different for each problem, which are shown on each panel.
While the expected return with respect to the computational time is different between the algorithms (a–d), that with respect to the iteration k is almost the same (e–h). This is because the M step of these algorithms is exactly the same. Therefore, the difference of the computational time is caused by the computational time of the E step.
The convergence of BEM is faster than that of EM in the small state size problems, i.e., Figure 3a,b. This is because EM calculates the forward–backward algorithm from to , where is large. On the other hand, the convergence of BEM is slower than that of EM in the large state size problems, i.e., Figure 3c,d. This is because BEM calculates the inverse matrix.
The convergence of MBEM is faster than that of EM in all the experiments in Figure 3a–d. This is because is smaller than as shown in Figure 3i–l. While EM requires about 1000 calculations of the forward–backward algorithm to guarantee that the approximation error of and is smaller than , MBEM requires only about 10 calculations of the forward and backward Bellman operators. Thus, MBEM is more efficient than EM. The reason why is smaller than is that MBEM can utilize the results of the previous iteration, and , as the initial functions, and . It is shown from and in the first iteration. In the first iteration , is almost the same with because and cannot be used as the initial functions and in the first iteration. On the other hand, in the subsequent iterations , is much smaller than because MBEM can utilize the results of the previous iteration, and , the initial functions and .
8. Conclusions and Future Works
In this paper, we propose the Bellman EM algorithm (BEM) and the modified Bellman EM algorithm (MBEM) by introducing the forward and backward Bellman equations into the EM algorithm for DEC-POMDP. BEM can be more efficient than EM because BEM does not calculate the forward–backward algorithm up to the infinite horizon. However, BEM cannot always be more efficient than EM when the size of the state or that of the memory is large because BEM calculates the inverse matrix. MBEM can be more efficient than EM regardless of the size of problems because MBEM does not calculate the inverse matrix. Although MBEM needs to calculate the forward and backward Bellman operators infinite times, MBEM can evaluate the approximation errors more tightly owing to the contractibility of these operators, and can utilize the results of the previous iteration owing to the arbitrariness of initial functions, which enables MBEM to be more efficient than EM. We verified this theoretical evaluation by the numerical experiment, which demonstrates that the convergence of MBEM is much faster than that of EM regardless of the size of problems.
Our algorithms still leave room for further improvements that deal with the real-world problems, which often have a large discrete or continuous state space. Some of them may be addressed by the advanced techniques of the Bellman equations [1,2,3,4]. For example, MBEM may be accelerated by the Gauss–Seidel method [2]. The convergence rate of the E step of MBEM is given by the discount factor , which is the same as that of EM. However, the Gauss–Seidel method modifies the Bellman operators, which allows the convergence rate of MBEM to be smaller than the discount factor . Therefore, even if and are not close to and , MBEM may be more efficient than EM by the Gauss–Seidel method. Moreover, in DEC-POMDP with a large discrete or continuous state space, and cannot be expressed exactly because it requires a large space complexity. This problem may be resolved by the value function approximation [34,35,36]. The value function approximation approximates and using parametric models such as neural networks. The problem is how to find the optimal approximate parameters. The value function approximation finds them by the Bellman equation. Therefore, the potential extensions of our algorithms may lead to the applications to the real-world DEC-POMDP problems.
Author Contributions
Conceptualization, T.T., T.J.K.; Formal analysis, T.T., T.J.K.; Funding acquisition, T.J.K.; Writing—original draft, T.T., T.J.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by JSPS KAKENHI Grant Number 19H05799 and by JST CREST Grant Number JPMJCR2011.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We would like to thank the lab members for a fruitful discussion.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Proof in Section 3
Appendix A.1. Proof of Theorem 1
can be calculated as follows:
where and .
Appendix A.2. Proof of Proposition 1
In order to prove Proposition 1, we calculate . It can be calculated as follows:
where
C is a constant independent of .
Proposition A1
([16]). , , and are calculated as follows:
and are defined by Equations (12) and (13).
Proof.
Firstly, we prove Equation (A6). can be calculated as follows:
Since , we have
Since , -4.6cm0cm
can be calculated as follows:
Therefore, Equation (A6) is proved.
Secondly, we prove Equation (A7). can be calculated as follows:
Since , we have
Since ,
Therefore, Equation (A7) is proved.
Finally, we prove Equation (A8). can be calculated as follows:
Therefore, Equation (A8) is proved. □
Appendix A.3. Proof of Proposition 2
Appendix B. Proof in Section 4
Proof of Theorem 2
can be calculated as follows:
Therefore, Equation (29) is proved. Equation (30) can be proved in the same way.
Appendix C. Proof in Section 5
Appendix C.1. Proof of Proposition 3
The left-hand side of Equation (37) can be calculated as follows:
where , , and . Equation (38) can be proved in the same way.
Appendix C.2. Proof of Proposition 4
Appendix C.3. Proof of Proposition 5
From the definition of the norm,
The right-hand side can be calculated as follows:
From this inequality, we have
Therefore, if is satisfied,
holds. Equation (48) is proved in the same way.
Appendix C.4. Proof of Proposition 6
When and , the termination conditions of MBEM can be calculated as follows:
The calculation of is omitted because it is the same as that of . If
is satisfied,
holds. Thus, satisfies
is defined by . From Proposition 2, the minimum is given by the following equation:
Therefore, holds.
Appendix D. A Note on the Algorithm Proposed by Song et al.
In this section, we show that a parameter dependency is overlooked in the algorithm of [32]. We outline the derivation of the algorithm in [32] and discuss the parameter dependency. Since we use the notation in this paper, it is recommended to read the full paper before reading this section.
Firstly, we calculate the expected return to derive the algorithm in [32]. Since [32] considers the case where , we also consider the same case in this section. The expected return can be calculated as follows:
is the value function, which is defined as follows:
Equation (A36) can be rewritten as:
where
Maximizing is equivalent to maximizing , and can be calculated as follows:
where
By the Jensen’s inequality, Equation (A41) can be calculated as follows:
is satisfied when .
Then, is defined as follows:
In this case, the following proposition holds:
Proposition A2
([32]). .
Therefore, since Equation (A46) monotonically increases , we can find , which locally maximizes . This is the algorithm in [32].
Then, the problem is how to calculate Equation (A46). It cannot be calculated analytically because dependency of is too complex. However, ref. [32] overlooked the parameter dependency of and , and therefore, it calculated Equation (A46) as follows:
However, Equations (A47) and (A48) do not correspond to Equation (A46), and therefore, the algorithm as a whole may not always provide the optimal policy.
References
- Bertsekas, D.P. Dynamic Programming and Optimal Control: Vol. 1; Athena Scientific: Belmont, MA, USA, 2000. [Google Scholar]
- Puterman, M.L. Markov Decision Processes: Discrete Stochastic Dynamic Programming; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Introduction to Reinforcement Learning; MIT Press: Cambridge, MA, USA, 1998; Volume 135. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Kochenderfer, M.J. Decision Making under Uncertainty: Theory and Application; MIT Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Oliehoek, F. Value-Based Planning for Teams of Agents in Stochastic Partially Observable Environments; Amsterdam University Press: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Oliehoek, F.A.; Amato, C. A Concise Introduction to Decentralized POMDPs; Springer: Berlin/Heidelberg, Germany, 2016; Volume 1. [Google Scholar]
- Becker, R.; Zilberstein, S.; Lesser, V.; Goldman, C.V. Solving transition independent decentralized Markov decision processes. J. Artif. Intell. Res. 2004, 22, 423–455. [Google Scholar] [CrossRef]
- Nair, R.; Varakantham, P.; Tambe, M.; Yokoo, M. Networked distributed POMDPs: A synthesis of distributed constraint optimization and POMDPs. In Proceedings of the AAAI’05: Proceedings of the 20th National Conference on Artificial Intelligence, Pittsburgh, PA, USA, 9–13 July 2005; pp. 133–139. [Google Scholar]
- Bernstein, D.S.; Givan, R.; Immerman, N.; Zilberstein, S. The complexity of decentralized control of Markov decision processes. Math. Oper. Res. 2002, 27, 819–840. [Google Scholar] [CrossRef]
- Bernstein, D.S.; Hansen, E.A.; Zilberstein, S. Bounded policy iteration for decentralized POMDPs. In Proceedings of the Nineteenth International Joint Conference on Artificial Intelligence (IJCAI), Edinburgh, UK, 30 July–5 August 2005; pp. 52–57. [Google Scholar]
- Bernstein, D.S.; Amato, C.; Hansen, E.A.; Zilberstein, S. Policy iteration for decentralized control of Markov decision processes. J. Artif. Intell. Res. 2009, 34, 89–132. [Google Scholar] [CrossRef][Green Version]
- Amato, C.; Bernstein, D.S.; Zilberstein, S. Optimizing fixed-size stochastic controllers for POMDPs and decentralized POMDPs. Auton. Agents Multi-Agent Syst. 2010, 21, 293–320. [Google Scholar] [CrossRef]
- Amato, C.; Bonet, B.; Zilberstein, S. Finite-state controllers based on mealy machines for centralized and decentralized pomdps. In Proceedings of the AAAI Conference on Artificial Intelligence, Atlanta, GA, USA, 11–15 July 2010. [Google Scholar]
- Amato, C.; Bernstein, D.S.; Zilberstein, S. Optimizing memory-bounded controllers for decentralized POMDPs. arXiv 2012, arXiv:1206.5258. [Google Scholar]
- Kumar, A.; Zilberstein, S. Anytime planning for decentralized POMDPs using expectation maximization. In Proceedings of the 26th Conference on Uncertainty in Artificial Intelligence, Catalina Island, CA, USA, 8–11 July 2010; pp. 294–301. [Google Scholar]
- Kumar, A.; Zilberstein, S.; Toussaint, M. Probabilistic inference techniques for scalable multiagent decision making. J. Artif. Intell. Res. 2015, 53, 223–270. [Google Scholar] [CrossRef][Green Version]
- Toussaint, M.; Storkey, A. Probabilistic inference for solving discrete and continuous state Markov Decision Processes. In Proceedings of the 23rd International Conference on Machine Learning, Pittsburgh, PA, USA, 25–29 June 2006; pp. 945–952. [Google Scholar]
- Todorov, E. General duality between optimal control and estimation. In Proceedings of the 47th IEEE Conference on Decision and Control, Cancun, Mexico, 9–11 December 2008; pp. 4286–4292. [Google Scholar]
- Kappen, H.J.; Gómez, V.; Opper, M. Optimal control as a graphical model inference problem. Mach. Learn. 2012, 87, 159–182. [Google Scholar] [CrossRef]
- Levine, S. Reinforcement learning and control as probabilistic inference: Tutorial and review. arXiv 2018, arXiv:1805.00909. [Google Scholar]
- Sun, X.; Bischl, B. Tutorial and survey on probabilistic graphical model and variational inference in deep reinforcement learning. In Proceedings of the IEEE Symposium Series on Computational Intelligence (SSCI), Xiamen, China, 6–9 December 2019; pp. 110–119. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Toussaint, M.; Harmeling, S.; Storkey, A. Probabilistic Inference for Solving (PO) MDPs; Technical Report; Technical Report EDI-INF-RR-0934; School of Informatics, University of Edinburgh: Edinburgh, UK, 2006. [Google Scholar]
- Toussaint, M.; Charlin, L.; Poupart, P. Hierarchical POMDP Controller Optimization by Likelihood Maximization. UAI 2008, 24, 562–570. [Google Scholar]
- Kumar, A.; Zilberstein, S.; Toussaint, M. Scalable multiagent planning using probabilistic inference. In Proceedings of the 22nd International Joint Conference on Artificial Intelligence, Barcelona, Spain, 16–22 July 2011. [Google Scholar]
- Pajarinen, J.; Peltonen, J. Efficient planning for factored infinite-horizon DEC-POMDPs. In Proceedings of the Twenty-Second International Joint Conference on Artificial Intelligence, Barcelona, Spain, 16–22 July 2011; Volume 22, p. 325. [Google Scholar]
- Pajarinen, J.; Peltonen, J. Periodic finite state controllers for efficient POMDP and DEC-POMDP planning. Adv. Neural Inf. Process. Syst. 2011, 24, 2636–2644. [Google Scholar]
- Pajarinen, J.; Peltonen, J. Expectation maximization for average reward decentralized POMDPs. In Joint European Conference on Machine Learning and Knowledge Discovery in Databases, Proceedings of the European Conference, ECML PKDD 2013, Prague, Czech Republic, 23–27 September 2013; Springer: Berlin/Heidelberg, Germany, 2013; pp. 129–144. [Google Scholar]
- Wu, F.; Zilberstein, S.; Jennings, N.R. Monte-Carlo expectation maximization for decentralized POMDPs. In Proceedings of the Twenty-Third International Joint Conference on Artificial Intelligence, Beijing, China, 3–9 August 2013. [Google Scholar]
- Liu, M.; Amato, C.; Anesta, E.; Griffith, J.; How, J. Learning for decentralized control of multiagent systems in large, partially-observable stochastic environments. In Proceedings of the AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016; Volume 30. [Google Scholar]
- Song, Z.; Liao, X.; Carin, L. Solving DEC-POMDPs by Expectation Maximization of Value Function. In Proceedings of the AAAI Spring Symposia, Palo Alto, CA, USA, 21–23 March 2016. [Google Scholar]
- Kumar, A.; Mostafa, H.; Zilberstein, S. Dual formulations for optimizing Dec-POMDP controllers. In Proceedings of the AAAI, Phoenix, AZ, USA, 12–17 February 2016. [Google Scholar]
- Bertsekas, D.P. Approximate policy iteration: A survey and some new methods. J. Control. Theory Appl. 2011, 9, 310–335. [Google Scholar] [CrossRef]
- Liu, D.R.; Li, H.L.; Wang, D. Feature selection and feature learning for high-dimensional batch reinforcement learning: A survey. Int. J. Autom. Comput. 2015, 12, 229–242. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Hallak, A.; Mannor, S. Consistent on-line off-policy evaluation. In Proceedings of the International Conference on Machine Learning, PMLR, Sydney, Australia, 6–11 August 2017; pp. 1372–1383. [Google Scholar]
- Gelada, C.; Bellemare, M.G. Off-policy deep reinforcement learning by bootstrapping the covariate shift. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 3647–3655. [Google Scholar]
- Levine, S.; Kumar, A.; Tucker, G.; Fu, J. Offline reinforcement learning: Tutorial, review, and perspectives on open problems. arXiv 2020, arXiv:2005.01643. [Google Scholar]
- Hansen, E.A.; Bernstein, D.S.; Zilberstein, S. Dynamic programming for partially observable stochastic games. In Proceedings of the AAAI, Palo Alto, CA, USA, 22–24 March 2004; Volume 4, pp. 709–715. [Google Scholar]
- Seuken, S.; Zilberstein, S. Improved memory-bounded dynamic programming for decentralized POMDPs. arXiv 2012, arXiv:1206.5295. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).