Genomic Intelligence as Über Bio-Cybersecurity: The Gödel Sentence in Immuno-Cognitive Systems
Abstract
1. Introduction
2. G-T-P Conditions and Major Evolutionary Developments in Immuno-Cognitive Systems
| G-T-P Conditions | Adaptive Immune System (AIS) | Brain/Neuronal System | |
|---|---|---|---|
| 1 | G-T-P Encoded Genomic Basal Information in Fixed Finite Language, Recursive Function Operations on Codes for Online Machine Executions: Self–Ref (Self-Reference) and Self-Assembly | ||
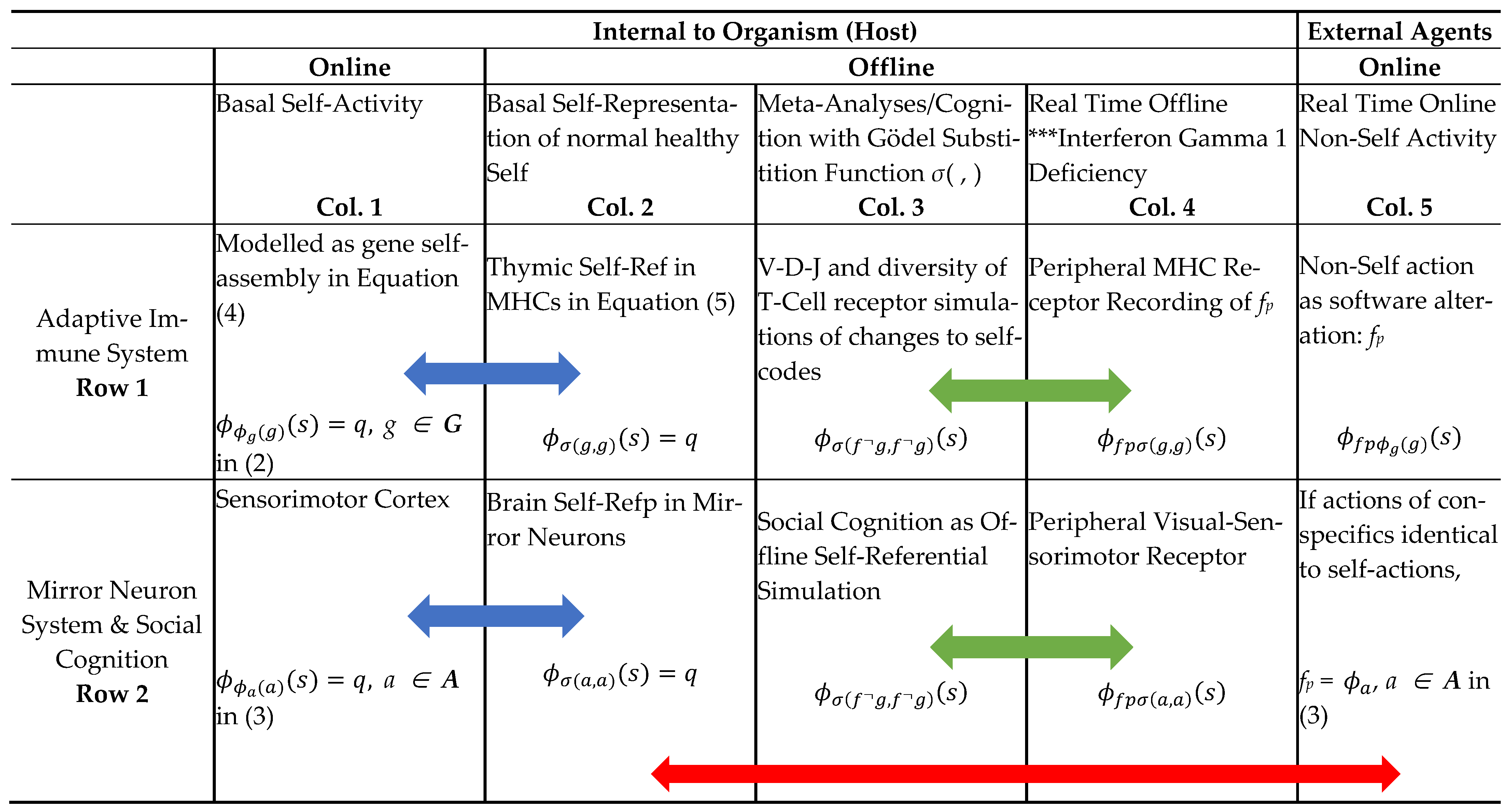
| (1a) Section 2.1 and Section 2.2 | Unique identifiers aka Gödel numbers (gns) from smallest unit of programs/algorithms based on encoded information, Equations (2) and (3) Notation: Set G for gene codes in Equation (2); Set A for self-actions in Equation (3) |
| Unique identifiers for single neurons and neuron-neuron interaction [82,83,84] |
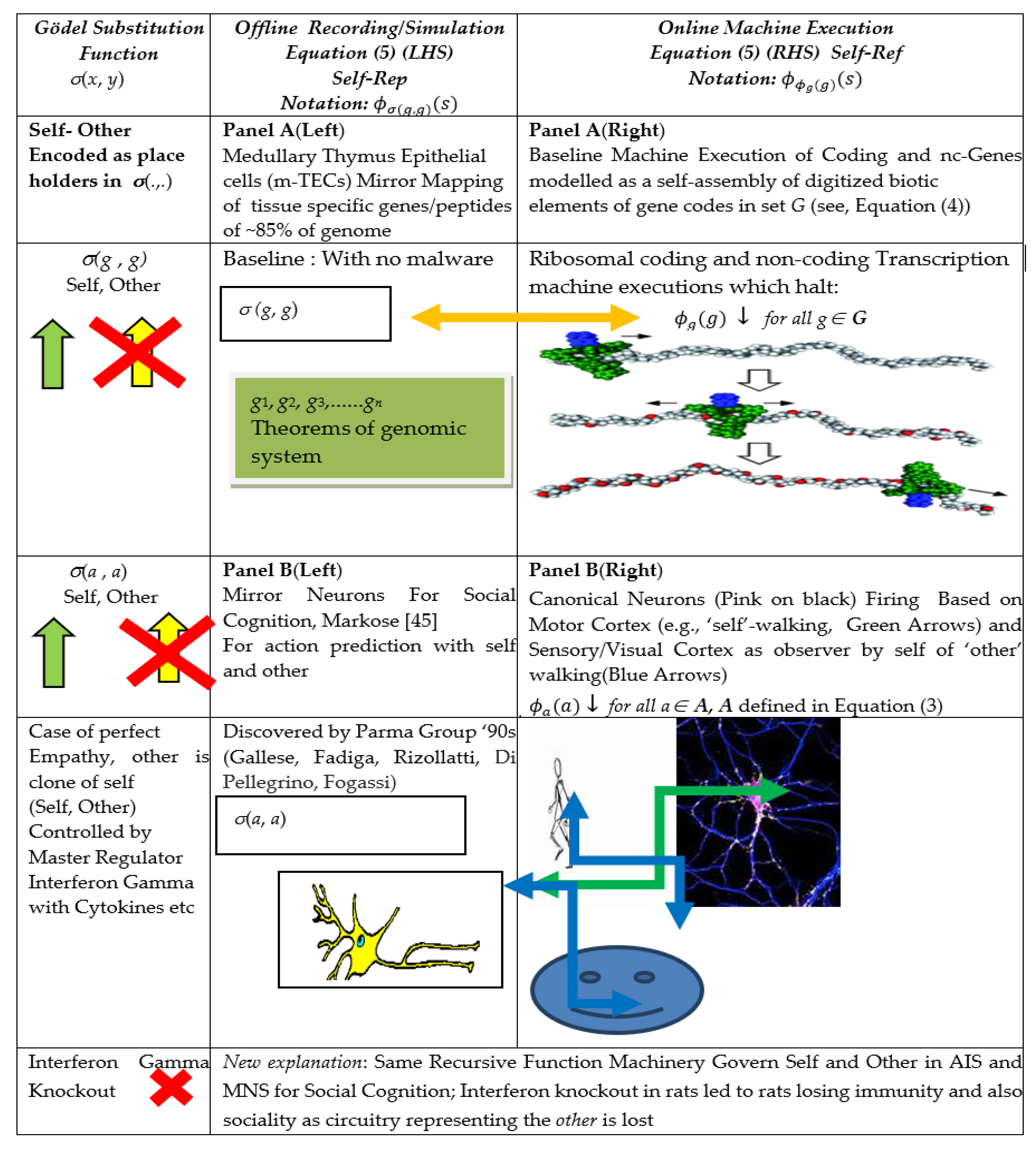
| (1b) Section 2.2 | Self–Ref (Online): Diag(x) = , Online halting (↓) self-assembly program x instructs machine ϕ to run code x as its input Equations (4) and (7) [17] | Online Basal Ribosomal and RNA Machine Execution of gene codes as 3D Self Assembly of digitized materials of morphology and regulatory networks Diag(g) = ↓, g ∊ G. [85] (p. 30) and [4,5,86] | Online Basal Self-Actions with Canonical Neurons Firing in Sensorimotor Cortex Diag(a) = ↓, a ∊ A. [52] |
| 2 | G.T.P Offline Mirror Systems with One-One Mapping of Online Machine Execution in AIS of Gene Codes and Self Action in MNS: Self–Rep (Self-Representation): Rogers [16], (pp. 202–204) | ||
| (2a) Section 2.3 |
|
|
|
| (2b) |
|
| |
| 3 | G-T-P Formal System of the Other and Novel Hostile Other, Fixed Point of Gödel Liar/Negation as Gödel Sentence (See Section 3) | ||
| (3a) |
|
| |
| (3b) |
|
|
|
2.1. G-T-P Condition (1): Encoding and Recursive Function Operations on Codes
Unique Biotic Identifiers and Gödel Numbers
2.2. G.T-P Gödel Numbering of Basal Information in Gene Codes and Sensorimotor Cortex
Online Self-Assembly/Self-Ref Machinery
2.3. G-T-P Mirror/Meta Condition 2 and Evidence from Genomic Evolution of Self-Rep
3. G-T-P Bio-Informatics for V(D)J Recombination and T-Cell Training for Non-Self Antigen Detection
3.1. Horizon Scanning and Astronomic Numbers in AIS
- In having mirrored/expressed ~85% of gene codes in m-TECs, the V(D)J recombinations generate putative clones of non-self antigens in relation to these gene codes.
- This provides “an anticipatory system of defense” [87] of prodigious capacity. Ref [88] state that the capacity of the AIS for “somatic generation of immune recognition motifs of a system of practically unlimited (open-ended) information capacity” with orders of magnitude of “αβT cell receptors to be around 1015 to 1020 with such levels of diversity in a single individual that exceeds the size of the entire germline genome by several orders of magnitude.” [62] gives an even higher number for the V(D)J generated “individual antigen receptors computed to be approximately 1030”.
- Ref [102] (Chapter 8) ask the following question in the context of Bio-Inspired Computing and Cyber Security:
“Any paradigm for computer security that is based on the differentiation of self from non-self must imply some operational definition of self that represents normal and benign operation. It is clear that a good definition is matched to the signature of the threat being defended against, and hence the designer must be able to answer the question, “How would I know my system were under attack?”(Ibid, p. 263)
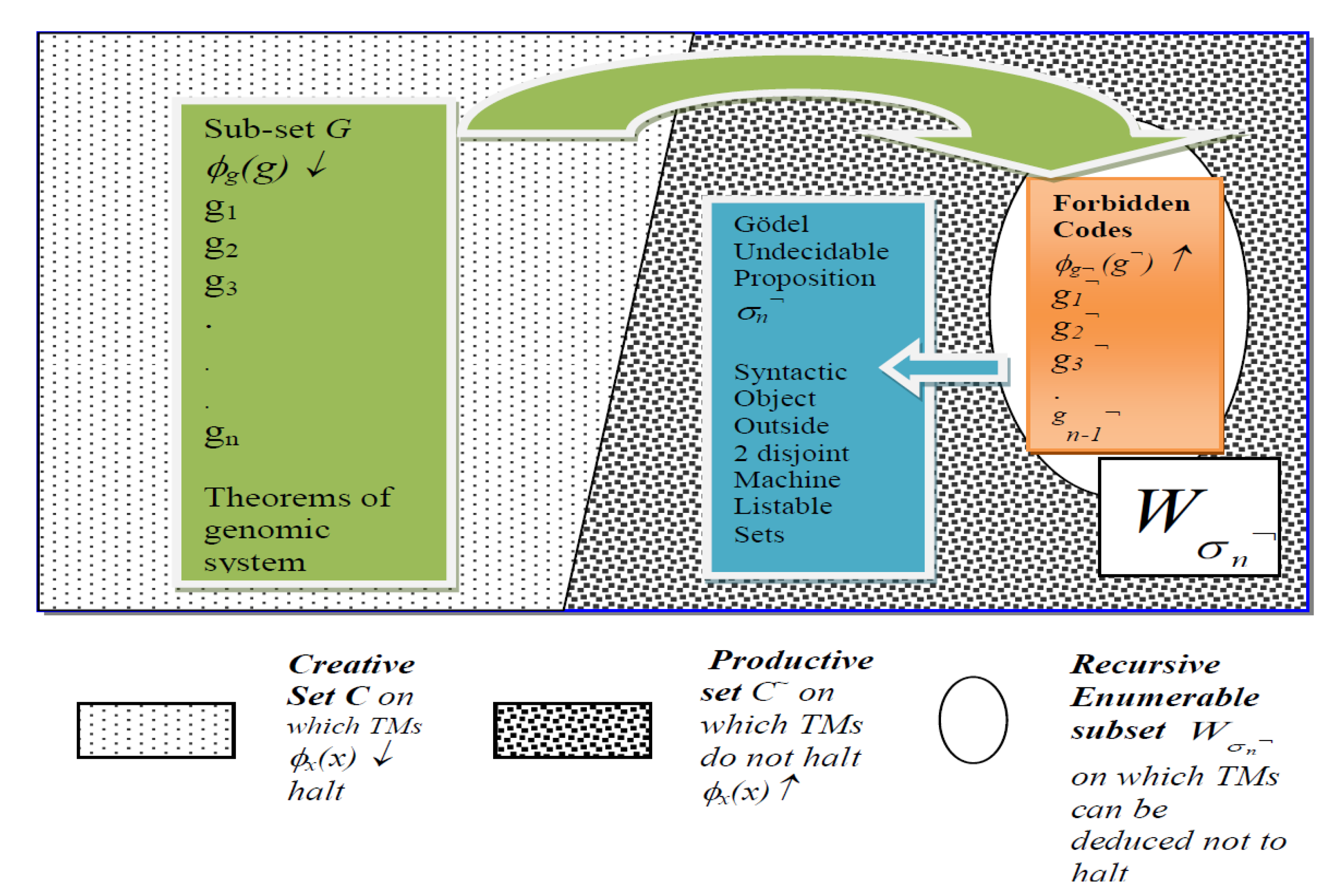
3.2. Halting Self-Assembly Gene Codes and Forbidden Codes of Antigens in G-T-P Formal System
3.3. Information Processing in G-T-P Meta Systems for V(D)J: Positive Selection of T Cell Receptors

- (i)
- A change in the program;
- (ii)
- A change in its input;
- (iii)
- A change in both program and input.
- σ(g, f◦g): Implying change in input of the basal Diag(g) = .
- σ(f◦g, g): Implying change in program of the basal which is no longer a Diag(.) operation.
- σ(f◦g, f◦g): Implying a change in both program and input for Diag(g) and transforming it to Diag(f◦g).
3.3.1. Positive Selection of T Cell Receptor (TCR) Motifs {σ(g, f◦g), σ(f◦g, g), σ(f◦g, f◦g)}
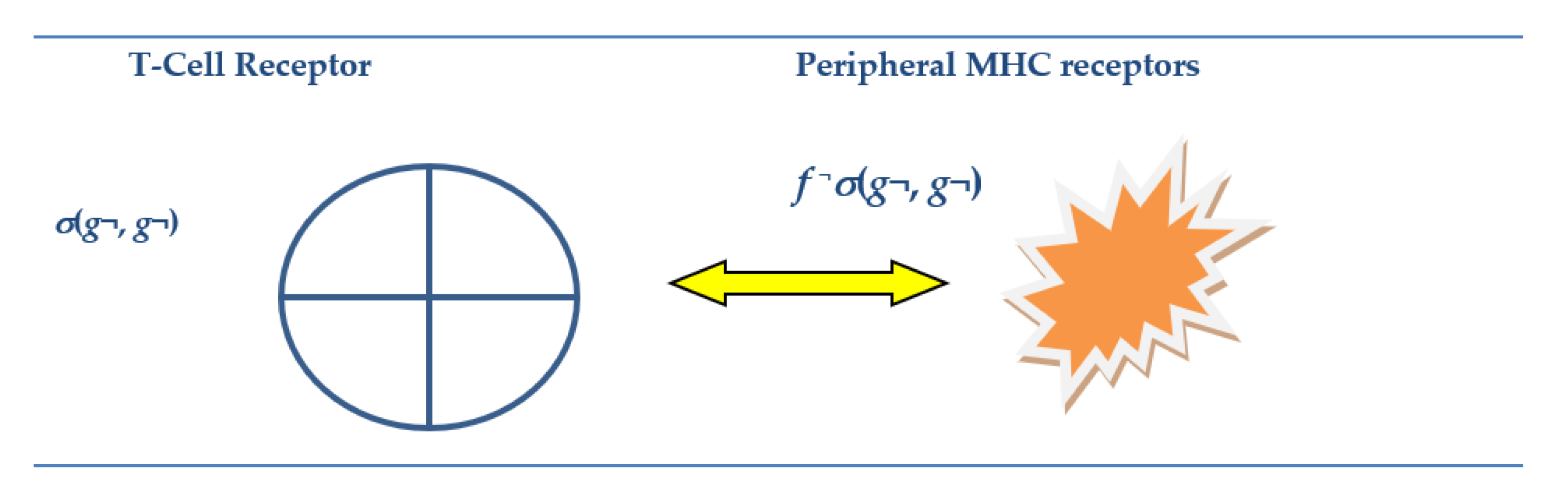
3.3.2. Synchrony in Anticipatory T-Cell Receptors Clone of Tissue Specific Attacker with Peripheral MHC Record of Same in Online Attack
3.3.3. Negative Selection of T-Cells
3.3.4. Dangerous V(D)J Codes and Successful Non-Self Antigen Attacks
3.3.5. Negative Selection of Dangerous T-Cells Receptors with Motifs: σ(gn¬, gn) in (10)
3.4. Precision Engineered Novel Antibodies Made Possible Only by Gödel Sentence σ(gn¬, gn¬)
3.5. G-T-P Bioinformatics for COVID-19 Pathology and Recovery
4. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References and Notes
- Hood, L.; Galas, D.J. The digital code of DNA. Nat. Cell Biol. 2003, 421, 444–448. [Google Scholar] [CrossRef]
- Ben-Jacob, E. Bacterial wisdom, Gödel’s theorem and creative genomic webs. Phys. A Stat. Mech. Appl. 1998, 248, 57–76. [Google Scholar] [CrossRef]
- Brenner, S. Turing centenary: Life’s code script. Nature 2012, 482, 461. [Google Scholar] [CrossRef]
- Danchin, A. From chemical metabolism to life: The origin of the genetic coding process. Beilstein J. Org. Chem. 2017, 13, 1119–1135. [Google Scholar] [CrossRef] [PubMed]
- Danchin, A. Bacteria as computers making computers. FEMS Microbiol. Rev. 2008, 33, 3–26. [Google Scholar] [CrossRef] [PubMed]
- Nurse, P. Life, logic and information. Nat. Cell Biol. 2008, 454, 424–426. [Google Scholar] [CrossRef]
- In dealing with the biotic implications of digital information storage of the genome, Ref [6] refers to the need to develop a framework that can catalogue and identify the cellular biochemistry which implements specific computational functions. The aim is to identify what Nurse [6] calls segments of “logic modules” that conduct operations within cells and provide a mapping between the cellular chemistry toolkit with the logic tool-kit.
- Ramakrishnan, V. Ribosome structure and the mechanism of translation. Cell 2002, 108, 557–572. [Google Scholar] [CrossRef]
- Shapiro, E. A mechanical Turing machine: Blueprint for a biomolecular computer. Interface Focus 2012, 2, 497–503. [Google Scholar] [CrossRef]
- Varghese, S.; Elemans, J.A.A.W.; Rowan, A.E.; Nolte, R.J.M. Molecular computing: Paths to chemical Turing machines. Chem. Sci. 2015, 6, 6050–6058. [Google Scholar] [CrossRef]
- Kunkel, T.A. Evolving views of DNA replication (in)fidelity. Cold Spring Harb. Symp. Quant. Biol. 2009, 74, 91–101. [Google Scholar] [CrossRef]
- Kunkel, T.A.; Erie, D.A. Eukaryotic Mismatch Repair in Relation to DNA Replication. Ann. Rev. Genetic. 2015, 49, 291–313. [Google Scholar] [CrossRef]
- Shapiro, J.A. How life changes itself: The Read–Write (RW) genome. Phys. Life Rev. 2013, 10, 287–323. [Google Scholar] [CrossRef]
- McClintock, B. The significance of responses of the genome to challenge. Science 1984, 226, 792–801. [Google Scholar] [CrossRef]
- In this paper, the terms computation and recursive function will be used interchangeably as in the respective titles of the two well-known textbooks [16,17], which cover identical content of operations on encoded information based on a finite alphabet. Computation or recursive functions include all elementary arithmetic, logical operations and also functions obtained from substitution, iteration and recursion. In the latter, functions call on themselves and use inputs that are outputs from previous computations.
- Rogers, H. Theory of Recursive Functions and Effective Computability; McGraw-Hill: New York, NY, USA, 1967. [Google Scholar]
- Cutland, N.J. Computability: An Introduction to Recursive Function Theory; Cambridge University Press: Cambridge, UK, 1980. [Google Scholar]
- McClintock [14] described the genome “as a highly sensitive organ of the cell, monitoring genomic activities and correcting common errors, sensing the unusual and unexpected events, and responding to them, often by restructuring the genome”.
- Feschotte, C.; Pritham, E.J. DNA Transposons and the Evolution of Eukaryotic Genomes. Annu. Rev. Genet. 2007, 41, 331–368. [Google Scholar] [CrossRef]
- Dyson, F. Origins of Life; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Dyson, G. Review on “Is Life Analog or Digital”, Edge. 2001. Available online: https://www.edge.org/conversation/freeman_dyson-is-life-analog-or-digital (accessed on 5 February 2019).
- Forterre, P. The origin of viruses and their possible roles in major evolutionary transitions. Virus Res. 2006, 117, 5–16. [Google Scholar] [CrossRef]
- Zimmer, C. Did DNA Come From Viruses? Science 2006, 312, 870–872. [Google Scholar] [CrossRef] [PubMed]
- Fedoroff, N.V. Transposable elements, epigenetics and genome evolution. Science 2012, 338, 758–767. [Google Scholar] [CrossRef]
- “It is becoming increasingly difficult to escape the conclusion that eukaryotic genome evolution is driven from within (italics added) by the stronger winds (with perhaps occasional gale force gusts) of transposon activity. The ability to evoke rapid genome restructuring is at the heart of eukaryotic evolvability—the capacity of organisms with larger and larger genomes to maintain evolutionary flexibility” Fedoroff [24].
- Shapiro, J.A. Living Organisms Author Their Read-Write Genomes in Evolution. Biology 2017, 6, 42. [Google Scholar] [CrossRef]
- Amaral, P.D.P.; Dinger, M.; Mercer, T.R.; Mattick, J.S. The Eukaryotic Genome as an RNA Machine. Science 2008, 319, 1787–1789. [Google Scholar] [CrossRef] [PubMed]
- Mattick, J.S.; Mehler, M.F. RNA editing, DNA recoding and the evolution of human cognition. Trends Neurosci. 2008, 31, 227–233. [Google Scholar] [CrossRef] [PubMed]
- Chang, W.-L.; Vasilakos, A. Molecular Computing: Towards a Novel Computing Architecture for Complex Problem Solving; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Loscri, V.; Marchal, C.; Mitton, N.; Fortino, G.; Vasilakos, A.V. Security and Privacy in Molecular Communication and Networking: Opportunities and Challenges. IEEE Trans. NanoBioscience 2014, 13, 198–207. [Google Scholar] [CrossRef]
- Bradley, R.W.; Wang, B. Designer cell signal processing circuits for biotechnology. New Biotechnol. 2015, 32, 635–643. [Google Scholar] [CrossRef] [PubMed]
- Istrail, S.; De-Leon, S.B.-T.; Davidson, E.H. The regulatory genome and the computer. Dev. Biol. 2007, 310, 187–195. [Google Scholar] [CrossRef]
- This includes Neil Dalchau, Sara-Jane Dunn and others at Biological Computation research group at Microsoft Research Cambridge.
- “Biological research is in crisis, we are drowning in a sea of data and thirsting for some theoretical framework with which to understand it”, Brenner [3].
- Gödel, K. On Formally Undecidable Propositions of Principia Mathematica and Related Systems; Croom Helm: London, UK, 1931; (Translation in English in Gödel’s Theorem in Focus; Shanker, S.G., Ed., 1988). [Google Scholar]
- Turing, A.M. On computable numbers, with an application to the Entscheidungsproblem. Proc. Lond. Math. Soc. 1963, 42, 230–265. [Google Scholar] [CrossRef]
- Post, E. Recursively Enumerable Sets of Positive Integers and Their Decision Problems. Bull. Am. Math. Soc. 1944, 50, 284–316. [Google Scholar] [CrossRef]
- Smullyan, R. Theory of Formal Systems; Princeton University Press: Princeton, NJ, USA, 1961. [Google Scholar]
- Markose, S.M. The Digital Origins of Intelligence: How We Became Smart and Protean. Keynote Talk at 2019 Bio-Inspired ICT (BICT) Conference; Carnegie Mellon University: Pittsburgh, PA, USA, 2019; Available online: http://bionetics2019.eai-conferences.org/keynotes/ (accessed on 2 August 2020).
- Hofstader, D. Gödel, Escher, Bach: An Eternal Golden Braid; Basic Books Inc.: New York, NY, USA, 1999. [Google Scholar]
- The monikers Self-Ref and Self-Rep have been taken from [40]. The acronym Diag (.) for the Self-Ref recursive function, as will be seen, denotes 2-place diagonal matrix entries.
- Marion, J.-Y. Viruses in Turing’s Garden. Available online: https://hal.inria.fr/hal-00762918/ (accessed on 9 December 2019).
- Marion, J.-Y. From Turing machines to computer viruses. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2012, 370, 3319–3339. [Google Scholar] [CrossRef][Green Version]
- Markose, S.M. Novelty production and evolvability in digital genomic agents: Logical foundations and policy design implications of complex adaptive systems. In Complex Systems in the Social and Behavioral Sciences: Theory, Method and Application; Elliot, E., Douglas Kiel, L., Eds.; Michigan University Press: Ann Arbor, MI, USA, 2020. [Google Scholar]
- Markose, S.M. Complex Type 4 Structure Changing Dynamics of Digital Agents: Nash Equilibria of a Game with Arms Race in Innovations. J Dynam. Game. 2017, 4, 255–284. [Google Scholar] [CrossRef]
- Tsuda, I. Logic Dynamics for Deductive Inference Its Stability and Neural Basis. In Chaos, Information Processing and Paradoxical Games: The Legacy of John S Nicolis; Gregoire, N., Vasileios, B., Eds.; World Scientific Publishing: London, UK, 2014; Chapter 17. [Google Scholar]
- Fadiga, L.; Fogassi, L.; Pavesi, G.; Rizzolatti, G. Motor Facilitation during Action Observation: A Magnetic Stimulation study. J. Neurophysiol. 1995, 73, 2608–2611. [Google Scholar] [CrossRef]
- Gallese, V.; Fadiga, L.; Fogassi, L.; Rizzolatti, G. Action recognition in the premotor cortex. Brain 2009, 66, 557–560. [Google Scholar] [CrossRef] [PubMed]
- Rizzolatti, G.; Fadiga, L.; Gallese, V.; Fogassi, L. Premotor cortex and the recognition of motor actions. Cogn. Brain Res. 1996, 3, 131–141. [Google Scholar] [CrossRef]
- Ramachandran, V.S. Mirror Neurons and imitation learning as the driving force behind the great leap forward in human evolution. EDGE Con-versation. Available online: https://www.edge.org/conversation/mirror-neurons-and-imitation-learning-as-the-driving-force-behind-the-great-leap-forward-in-human-evolution (accessed on 29 March 2021).
- Ramachandran [50] describes this as follows: “It’s as if anytime you want to make a judgement about someone else’s movements you have to run a VR (virtual reality) simulation of the corresponding movements in your own brain and without mirror neurons you cannot do this”.
- Fagg, A.; Arbib, M. Modelling parietal-premotor interactions in primate control of grasping. Neural Netw. 1998, 11, 1277–1303. [Google Scholar] [CrossRef]
- Marion [43] makes a distinction between a benign viral software which simply prints/copies itself with the host code embedded in it without changing it. The malign viral software, in contrast, as will be shown, changes the host code to produce the opposite of what the original code produced.
- Prokopenko, M.; Harré, M.; Lizier, J.; Boschetti, F.; Peppas, P.; Kauffman, S. Self-referential basis of undecidable dynamics: From the Liar paradox and the halting problem to the edge of chaos. Phys. Life Rev. 2019, 31, 134–156. Available online: https://www.ncbi.nlm.nih.gov/pubmed/30655222 (accessed on 9 July 2020). [CrossRef] [PubMed]
- Naeem, M.; Prasad, G.; Watson, D.R.; Kelso, J.S. Electrophysiological signatures of intentional social coordination in the 10–12Hz range. NeuroImage 2012, 59, 1795–1803. [Google Scholar] [CrossRef] [PubMed]
- Tognoli, E.; Lagarde, J.; De Guzman, G.; Kelso, S. The phi Complex as the Neuromarker of Human Social Coordination. Proc. Natl. Acad. Sci. USA 2007, 104, 8190–8195. [Google Scholar] [CrossRef]
- Janeway, C.A.; Travers, P.; Walport, M.; Shlomchik, M.J. Immunobiology, 6th ed.; Garland Science: Oxon, UK, 2005. [Google Scholar]
- Analog defence strategies rely chiefly on protective barriers, toxic molecules, raising temperature, and phagocytic cells that ingest and destroy invading microorganisms (microbes) and larger parasites (such as worms).
- Kyewski, B.; Klein, L. A central role for central tolerance. Annu. Rev. Immunol. 2006, 24, 571–606. [Google Scholar] [CrossRef]
- Danan-Gotthold, M.; Guyon, C.; Giraud Levanon, E.; Abramson, J. Extensive RNA editing and splicing increase immune self-representation diversity in medullary thymic epithelial cells. Genome Biol. 2016, 17, 219. [Google Scholar] [CrossRef]
- Kapitonov, V.V.; Jurka, J. RAG1 core and V(D)J recombination signal sequences were derived from Transib transposons. PLoS Biol. 2005, 3, e181. [Google Scholar]
- Greenen, V. The thymus and the science of self. Semin. Immunopathol. 2021, 1–10. [Google Scholar] [CrossRef]
- Filiano, A.; Xu, Y.; Tustiton, N.; Marsh, R.; Baker, W.; Smirnov, I.; Overall, C.; Gadani, S.; Turner, S.; Weng, Z.; et al. Unexpected role of interferon-γ in regulating neuronal connectivity and social behaviour. Nature 2016, 535, 425–429. [Google Scholar] [CrossRef]
- Cohen, I. The cognitive paradigm and the immunological homunculus. Immunol. Today 1992, 13, 490–494. [Google Scholar] [CrossRef]
- Nataf, S. Autoimmunity as a Driving Force of Cognitive Evolution. Front. Neurosci. 2017, 11, 582. [Google Scholar] [CrossRef]
- Kipnis, J. Multifaceted interactions between adaptive immunity and the central nervous system. Science 2016, 353, 766–771. [Google Scholar] [CrossRef]
- Kipnis, J.; Gadani, S.; Derecki, N.C. Pro-cognitive properties of T cells. Nat. Rev. Immunol. 2012, 12, 663–669. [Google Scholar] [CrossRef]
- Lopes, P. Why are behavioural and immune traits linked? Horm. Behav. 2017, 88, 52–59. [Google Scholar] [CrossRef] [PubMed]
- Northoff, G.; Heinzel, A.; de Greck, M.; Bermpohl, F.; Dobrowolny, H.; Panksepp, J. Self-referential processing in our brain—A meta-analysis of imaging studies on the self. NeuroImage 2006, 31, 440–457. [Google Scholar] [CrossRef]
- Miller, W.B. Biological information systems: Evolution as cognition-based information management. Prog. Biophys. Mol. Biol. 2018, 134, 1–26. [Google Scholar] [CrossRef] [PubMed]
- Sánchez-Ramón, S.; Faure, F. Self and the Brain. The Immune Metaphor. Front Psychiatry. 2020, 11, 540676. [Google Scholar] [CrossRef]
- Morimoto, K.; Nakajima, K. Role of the Immune System in the Development of the Central Nervous System. Front. Neurosci. 2019, 13, 916. [Google Scholar] [CrossRef] [PubMed]
- Shatz, C.J. MHC Class I: An unexpected role in neuronal plasticity. Neuron 2009, 64, 40–45. [Google Scholar] [CrossRef] [PubMed]
- Lazarczyk, M.; Kemmler, J.; Eyford, B.; Short, J.A.; Varghese, M.; Sowa, A.; Dickstein, D.R.; Yuk, F.J.; Puri, R.; Biron, K.E.; et al. Major Histocompatibility Complex class I proteins are critical for maintaining neuronal structural complexity in the aging brain. Sci. Rep. 2016, 6, 26199. [Google Scholar] [CrossRef]
- Nelson, P.A.; Sage, J.R.; Wood, S.C.; Davenport, C.M.; Anagnostaras, S.G.; Boulanger, L.M. MHC class I immune proteins are critical for hippocampus-dependent memory and gate NMDAR-dependent hippocampal long-term depression. Learn. Mem. 2013, 20, 505–517. [Google Scholar] [CrossRef]
- Carignano, A.; Dachau, N. A theory for how the antigen presentation profile influences the timing of T-cell detection. biRxiv 2018. [Google Scholar] [CrossRef]
- I am grateful to an anonymous referee for pointing this out. Papers (see [78,79]) that use the Gödel formalism, which predates recursive function theory, generates the Gödel [35] sentence that typically takes the form: PA ͰA ↔ ¬Prov(A). Here, A effectively says of itself that it is not provable (¬Prov(A)), with this undecidable proposition being a theorem (Ͱ) in the formal system of Peano Arithmetic (PA).
- Laforte, G.; Hayes, P.J.; Ford, K.M. Why Gödel’s theorem cannot refute computationalism. Artif. Intell. 1998, 104, 265–286. [Google Scholar] [CrossRef][Green Version]
- Raatikainen, P. Gödel’s Incompleteness Theorems. Stanf. Encycl. Philos. 2015. [Google Scholar]
- Burnet, F.M. A reassessment of the forbidden clone hypothesis of autoimmune disease. Aust. J. Exp. Biol. Med Sci. 1972, 50, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Derbinski, J.; Schulte, A.; Kyewski, B.; Klein, L. Promiscuous gene expression in medullary thymic epithelial cells mirrors the peripheral self. Nat. Immunol. 2001, 2, 1032–1039. [Google Scholar] [CrossRef] [PubMed]
- Brickner, D.G.; Ahmed, S.; Meldi, L.; Thompson, A.; Light, W.; Young, M.; Hickman, T.L.; Chu, F.; Fabre, E.; Brickner, J.H. Transcription Factor Binding to a DNA Zip Code Controls Interchromosomal Clustering at the Nuclear Periphery. Dev. Cell 2012, 22, 1234–1246. [Google Scholar] [CrossRef]
- Lefebvre, J.L.; Kostadinov, D.; Chen, W.V.; Maniatis, T.; Sanes, J.R. Protocadherins mediate dendritic self-avoidance in the mammalian nervous system. Nat. Cell Biol. 2012, 488, 517–521. [Google Scholar] [CrossRef]
- Wu, Q.; Maniatis, T. A striking organization of a large family of human neural cadherin-like cell adhesion genes. Cell 1999, 97, 779–790. [Google Scholar] [CrossRef]
- Gershenfeld, N. How to Make Anything: The Digital Fabrication Revolution. In Fourth Industrial Revolution, the Davos Reader; Rose, G., Ed.; 2012; Available online: https://www.foreignaffairs.com/system/files/c0040.pdf (accessed on 19 January 2016).
- Hardy, N.; Westoff, E. Folding and Self-assembly of Biological Macromolecules. World Sci. 2004. [Google Scholar]
- Flajnik, M.F.; Kasahara, M. Origin and evolution of the adaptive immune system: Genetic events and selective pressures. Nat. Rev. Genet. 2009, 11, 47–59. [Google Scholar] [CrossRef] [PubMed]
- Müller, V.; De Boer, R.J.; Bonhoeffer, S.; Szathmáry, E. An evolutionary perspective on the systems of adaptive immunity. Biol. Rev. 2018, 93, 505–528. [Google Scholar] [CrossRef] [PubMed]
- Gallese, V.; Sinigaglia, C. What is so special about embodied simulation? Trends Cogn. Sci. 2011, 15, 512–519. [Google Scholar] [CrossRef]
- Wu, Y.; Zheng, Z.; Jiang, Y.; Chess, L.; Jiang, H. The specificity of T cell regulation that enables self-nonself discrimination in the periphery. Proc. Natl. Acad. Sci. USA 2008, 106, 534–539. [Google Scholar] [CrossRef] [PubMed]
- Brouwer, P.; Rosen, L.B.; Zhang, Q.; Michailidis, E.; Hoffmann, H.-H.; Zhang, Y.; Dorgham, K.; Philippot, Q.; Rosain, J.; Béziat, V. Auto-antibodies against type I IFNs in patients with life-threatening COVID-19. Science 2020, 370, eabd4585. [Google Scholar] [CrossRef]
- Kaneko, N.; Kuo, H.-H.; Boucau, J.; Farmer, J.R.; Allard-Chamard, H.; Mahajan, V.S.; Piechocka-Trocha, A.; Lefteri, K.; Osborn, M.; Bals, J. Loss of Bcl-6-expressing T follicular helper cells and germinal centers in COVID-19. Cell 2020, 183, 143–157.e13. [Google Scholar] [CrossRef]
- Zhang, Q.; Bastard, P.; Liu, Z.; Le Pen, J.; Moncada-Velez, M.; Chen, J.; Ogishi, M.; Sabli, I.K.D.; Hodeib, S.; Korol, C.; et al. Inborn errors of type I IFN immunity in patients with life-threatening COVID-19. Science 2020, 370, eabd4570. [Google Scholar] [CrossRef]
- The first limitative result on functions computable by T.Ms is that at most there can only be a countable number of these with the cardinality of ℵ being denoted by ℵ0, while from Cantor we know that the set of all number theoretic functions have cardinality of 2ℵ0. Hence, not all number theoretic functions are computable (see [17]).
- Ref [10] states “The resemblance of the Turing machine to naturally occurring molecular machineries that are capable of processing information, such as the ribosome and processive DNA (and RNA) polymerase enzymes, is striking and has recently motivated researchers to start programs on the development of biomolecular computers”.
- Since at least the 1990s, there has been an intense study of the biochemistry of life processes that are deemed to be driven by a self-assembly of biotic macromolecules with mechanistic features [86,97]. The shift in focus from the autonomous nature of this self-assembly to a program for self-assembly in the key transcription and translation processes [85], such that a gene code is viewed as a program that can both build the machine that can be instructed by the same program to read and run/execute it is also present in [5].
- Steven, A.; Baumeister, W.; Johnson, L.N.; Perham, R.N. Molecular Biology of Assemblies and Machines; Garland Science: Oxon, UK, 2016. [Google Scholar]
- Hartford, C.; Lal, A. When long non-coding becomes protein coding. Mol. Cell Biol. 2000, 40, 1–11. [Google Scholar] [CrossRef]
- Note, analog measurements of state variables, such as chemical concentration, temperature, etc., have to be converted into digital code in order for this to be processed by a digital agent.
- Fitch, T. Toward a computational framework for cognitive biology: Unifying approaches from cognitive neuroscience and compara-tive Cognition. Phys. Life Rev. 2014, 11, 329–364. [Google Scholar]
- Markose [44], contrasts Fitch [100] Bayesian model of cognition and intelligence with the G-T-P one. The main drawback of the Bayesian model, as with extant decision models, is that they are incapable of a constructive procedure for novelty production. Bayesian inference is statistical and is a far cry from inference by embodied offline simulation in the G-T-P cognitive system.
- Wooley, J.; Lin, H. Catalyzing Inquiry at the Interface of Computing and Biology; John, C., Wooley, J.C., Herbert, S., Lin, H.S., Eds.; The National Academies Press: Washington, DC, USA, 2005. [Google Scholar]
- In standard game theory, the strategies are constrained to lie in a fixed set, such as G or A, and the system is closed and complete with no possibility for exiting from a fixed repertoire and produce novelty (see [44,45]). Some of the G-T-P formalism used here for novelty production in digital systems was first mentioned in Markose [104] and given a detailed derivation in the context of generating novelty production as a Nash equilibrium of a game in [45].
- Markose, S.M. Novelty in complex adaptive systems (CAS) dynamics: A computational theory of actor innovation. Phys. A Stat. Mech. its Appl. 2004, 344, 41–49. [Google Scholar] [CrossRef]
- Note that a machine listable set or recursively enumerable set , is the domain of the function, viz. the y as inputs, on which ↓ for , where ℵ is the set of integers. Thus, . The archetypical set C contains the domain of halting functions of Diag(x) operations and hence set C contains the g.ns of those recursively enumerable sets, Wx, that contain their own indexes (see [17] (p. 123) and [16] (p.62)): C = . The complement of C, denoted by C¬, represents the “anti-diagonal” set, which is different from every listable set Wx for all : C¬ = . A set A is creative if it is recursively enumerable and its complement ℵ–A is not recursively enumerable such that for any Wn ⊂ ℵ–A, there is a recursive function f(n) ℵ–A–Wn. The complement set of A is said to be productive. Thus, set C is creative and C¬ is productive, see also [45].
- Note when focusing exclusively on non-self antigens, a subscript p is used in fp¬!.
- It is well known that, by what is called the SMN Theorem or the Parameterization Theorem [16,17]), new g.ns for recursive operations on extant g.ns can be mechanically generated.
- However, it is well known that only V(D)J motifs that the mTEC selection process can deal with as those self-represented in the Thymic MHC viz. g G*, G* ⊂ G as given in Equation (7). Hence, at the negative selection process TCRs, especially, for example, when there is deficiency of the autoimmune regulator AIRE, restricted gene codes do not get “Self-Repped” in the m-TECs for the training of the T-cell receptors [60]. So, TCRs with motifs σ(f◦g, g) for g ∉ G* in (7) can cause auto-immune disease.
- Michael Lotz, in his Bio-Inspired ICT (BICT) 2019 Keynote, apocryphally called “Know yourself, know the enemy”, stated that, while almost 99.9% of genes are the same for humans, only 6% of T-cell repertoires of different humans are the same. Hence, while the V(D)J realizations of some can combat new pathogens because they succeeded in cloning the code for this in the T-cells, others may not due to the random generation of codes in T-cell receptors and hence, without the anticipatory capacity to identify the novel non-self antigen when it strikes a tissue online, they succumb to them.
- Rogers Fixed point Theorem [16] (Section 11.2) states that any total computable function, fp¬!, for the case in question, has as its fixed point an index given by an integer v such that (s) (s), viz. either both sides are defined and are equal or else both sides are undefined. This index for the fixed point for a total computable function f can be obtained constructively. The first part of the proof is already satisfied with the index function σ(.) in the Self-Rep Theorem in (5) for the program for the partial computable function Diag(gn) = . The next step is to assign the index gn¬ to fp¬!Diag(gn) which leads to the function with a TCR motif of σ(gn¬, gn) as in Equations (10) and (11). The final step is to substitute gn¬ into fp¬! Diag(gn) to get fp¬! Diag(gn¬), which is the function . Then, assign v as the index for = Diag(gn¬) = σ(gn¬, gn), which yields (s) (s).
- On updating Equation (11) with the Liar/Malware strategy gn¬ in the place holder for the other, and assuming v = = Diag(gn¬) = σ(gn¬, gn) is a halting computation then we have a contradiction: = = = ¬. The last two terms follow from Equation (11) when gn¬ is substituted for in ¬.
- It is beyond the scope of this paper to give the detailed recursive function based bioinformatics behind the somatic hyper mutations [113] on B-cells that follow from this point in the host adaptive immune system. The same is the case on how retrotransposon activity can change the germline.
- Noia, J.M.; Neuberger, M.S. Molecular mechanisms of antibody somatic hypermutation. Annu. Rev. Biochem. 2007, 76, 1–22. [Google Scholar] [CrossRef] [PubMed]
- There is evidence that it is Type 1 Interferon gamma factor that is needed for this (see [91,93]).
- Bastard, P.J.M.; Caniels, T.G.; Van Der Straten, K.; Snitselaar, J.L.; Aldon, Y.; Bangaru, S.; Torres, J.L.; Okba, N.M.A.; Claireaux, M.; Kerster, G.; et al. Potent neutralizing antibodies from COVID-19 patients define multiple targets of vulnerability. Science 2020, 369, 643–650. [Google Scholar] [CrossRef]
- Lankenau, D.-H. Two RNA Worlds: Toward the Origin of Replication, Genes, Recombination, and Repair. In Origins of Life: The Primal Self-Organization, 1st ed.; Egel, R., Lankenau, D.-H., Mulkidjanian, A.Y., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2011; pp. 225–286. [Google Scholar]
- Walker, S.I.; Davies, P.C.W. The algorithmic origins of life. J. R. Soc. Interface 2013, 10, 20120869. [Google Scholar] [CrossRef] [PubMed]
- See [78] for an analysis that that the Gödel sentence does not imply the anti-computationalism sometimes ascribed to it. My position is that few have recognized that the mirror systems of the AIS and the MNS and the prodigious capacity for novelty production is the consequence of a code based genomic intelligence that has G-T-P recursive machinery at its core.
- Dawkins, R. The Extended Phenotype Oxford; Oxford University Press: Oxford, UK, 1989. [Google Scholar]
- Byrne, R.; Whiten, A. Machiavellian Intelligence: Social Expertise and the Evolution of Intellect in Monkeys, Apes, and Humans; Oxford University Press: Oxford, UK, 1988. [Google Scholar]
- Markose, S.M. Computability and Evolutionary Complexity: Markets as Complex Adaptive Systems (CAS). Econ. J. 2005, 115, F159–F192. [Google Scholar] [CrossRef]
- Binmore, K. Modelling Rational Players: Part I. Econ. Philos. 1987, 3, 179–214. [Google Scholar] [CrossRef]
- Ref [124] succinctly state this: “in a Nash equilibrium nobody is surprised about what others actually do, or what others believe, because strategies and beliefs are synchronized, presumably due to introspection, communication or learning”.
- Bhatt, M.; Camerer, C.F. Self-referential thinking and equilibrium as states of mind in games: FMRI evidence. Games Econ. Behav. 2005, 52, 424–459. [Google Scholar] [CrossRef]
- Mattick, J.S. The central role of RNA in human development and cognition. FEBS Lett. 2011, 585, 1600–1616. [Google Scholar] [CrossRef]
- Massey, S.E.; Mishra, B. Origin of biomolecular games: Deception and molecular evolution. J. R. Soc. Interface 2018, 15, 20180429. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Markose, S.M. Genomic Intelligence as Über Bio-Cybersecurity: The Gödel Sentence in Immuno-Cognitive Systems. Entropy 2021, 23, 405. https://doi.org/10.3390/e23040405
Markose SM. Genomic Intelligence as Über Bio-Cybersecurity: The Gödel Sentence in Immuno-Cognitive Systems. Entropy. 2021; 23(4):405. https://doi.org/10.3390/e23040405
Chicago/Turabian StyleMarkose, Sheri M. 2021. "Genomic Intelligence as Über Bio-Cybersecurity: The Gödel Sentence in Immuno-Cognitive Systems" Entropy 23, no. 4: 405. https://doi.org/10.3390/e23040405
APA StyleMarkose, S. M. (2021). Genomic Intelligence as Über Bio-Cybersecurity: The Gödel Sentence in Immuno-Cognitive Systems. Entropy, 23(4), 405. https://doi.org/10.3390/e23040405






