Abstract
We investigate the possibility of phantom crossing in the dark energy sector and the solution for the Hubble tension between early and late universe observations. We use robust combinations of different cosmological observations, namely the Cosmic Microwave Background (CMB), local measurement of Hubble constant (), Baryon Acoustic Oscillation (BAO) and SnIa for this purpose. For a combination of CMB+BAO data that is related to early universe physics, phantom crossing in the dark energy sector was confirmed at a 95% confidence level and we obtained the constraint km/s/Mpc at a 68% confidence level, which is in perfect agreement with the local measurement by Riess et al. We show that constraints from different combinations of data are consistent with each other and all of them are consistent with phantom crossing in the dark energy sector. For the combination of all data considered, we obtained the constraint km/s/Mpc at a 68% confidence level and the phantom crossing happening at the scale factor at a 68% confidence level.
1. Introduction
The observed phenomenon of cosmic acceleration [1,2] brought revolutionary change in our understanding of the cosmos. To explain the alleged accelerated expansion within the regime of General Relativity, it is essential to introduce some unknown source in the energy budget of the universe. This exotic source of energy is dubbed as dark energy. Different prescriptions from different branches of theoretical physics regarding the physical entity of dark energy are available in the literature (see [3] and references therein). The energy density of a vacuum [4,5,6], scalar fields’ energy density [7], or some unknown fluid [8,9] can be candidates for dark energy. However, none of these are beyond ambiguity. The unprecedented technical developments in cosmological observations in the recent years, like the observation of Cosmic Microwave Background (CMB) by Planck [10], the extended Supernova Cosmology Project [11], the observation of baryon distribution in the universe by the Baryon Oscillation Spectroscopic Survey (BOSS) [12], multi-wavelength observation of the large-scale structure of the universe by the Sloan Digital Sky Survey (SDSS) [13], etc., have ensured very precise constraints on cosmological models.
Depending on the nature of the dark energy equation of state, the time varying dark energy models are classified into two sections, namely phantom dark energy () and non-phantom dark energy (). The phantom barrier is delineated by , which represents the cosmological constant or the vacuum dark energy. The prime motivation of the present work is to check whether cosmological observations allow a dark energy to have a transition from phantom to non-phantom or vice versa. The theoretical background of phantom crossing dark energy are discussed in [14,15,16,17,18,19,20], in the composite scalar field model in [21,22,23], and in the context of Horndeski’s Theory [24,25]. Some recent studies regarding the observational aspects of phantom crossing dark energy are referred to in [26,27,28,29]. A recent model independent reconstruction of a dark energy equation state by Zhao et al. [30,31] shows that a combination of cosmological data including CMB data from Planck observations points towards possible phantom crossing in a dark energy equation of state. Similar results have been obtained by Capozziello et al. [32] with only low-redshift data. Moreover, reconstruction procedures for the dark energy density [29] as well as Hubble parameter [33] also exhibited phantom crossing in the dark energy sector.
Another serious issue of dark energy reconstruction is the disagreement of the local measurement of the Hubble parameter with the value estimated from the CMB. The local measurements suggest a higher value of the present Hubble parameter () compared to the value estimated for the standard model composed by a cosmological constant with cold dark matter (CDM) from the CMB likelihood. The latest measurement of , reported by the SH0ES collaboration, is km/s/Mpc at a 68% confidence level (CL) [34] and the value estimated by Planck for CDM is km/s/Mpc at a 68% CL [35]. The tension is now at a 4.4 level. There are many attempts to alleviate the issue in the literature (see for an incomplete list of works Refs. [36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78] and the recent overview in [79,80]). It has been recently discussed [81,82] that a transition in absolute magnitude for SnIa can also explain the apparent tension between the local and CMB measurements of the Hubble parameter . Such variation in in SnIa can be related to the apparent variation of the normalized Newtonian constant .
An important aspect of the present reconstruction is, therefore, to investigate whether a phantom crossing in dark energy evolution can alleviate the present Hubble tension. The present reconstruction is purely phenomenological based on the parametrization of the dark energy density. There is no assumption about the physical entity of dark energy from any theoretical background apart from that it has a phantom crossing at some stage during its evolution. The dark energy density is parametrized using a Taylor series expansion truncated at a certain order. The coefficients of the series expansion are constrained using observational data with a statistical approach. We have assumed that the components in the energy budget, namely the matter, dark energy and radiation, are independently conserved. In the following sections, we discuss the present reconstruction, the observational constraints and finally conclude with overall remarks on the results.
2. Reconstruction of the Model
One can parametrize the phantom crossing behavior in the dark energy either through its equation of state or directly through its energy density . On the one hand, different observables are directly related to the Hubble parameter rather than the equation of state of the dark energy fluid. If one parametrizes dark energy with , the dark energy contribution in involves the integration of over the redshift interval, whereas parametrizing dark energy with contributes directly to . Hence is the simpler and more direct way to parametrize the dark energy contribution in . Hence we chose to model the dark energy behavior.
Let us write the energy conservation equation for the dark energy fluid: . It is straightforward to see that for (non-phantom models), decreases with the scale factor, whereas for (phantom models) increases with the scale factor. For , is constant and that is the "Cosmological Constant". Hence, for any phantom crossing, dark energy density should pass through an extremum at some redshift where changes its sign. We perform a Taylor series expansion of around this extremum at :
Here we normalize the present day scale factor . As we have assumed that has an extrema at , we have ignored the first order derivative term in the Taylor expansion. We also restricted ourselves up to the third order in the Taylor expansion. Allowing higher-order terms will involve more parameters in the model that may not be tightly constrained with present data. One should also note that there can be a second extrema in depending on the values of and . With this, the Hubble parameter can be written as:
Finally we will have:
and the dark energy equation of state:
One can easily rewrite the above expression for to show that it represents a Pade series of order (3,3), which has a better convergence radius. Additionally, for early times (), the equation of state shows the Cosmological Constant behavior for the dark energy. This confirms that the dark energy equation of state is well behaved at an early time without any convergence issues. It is also not difficult to verify that adding higher-order terms in does not change the behavior at an early time. We should add that the different terms in the expression for can be generated by non-canonical scalar fields with Lagrangian with different values of n, as shown in [83].
A set of model parameters are introduced through the present reconstruction. Clearly the present model mimics the CDM for . The is the scale factor, where the has an extrema. If is constrained to be (we fix for the present day scale factor), it is a signature of transition in the nature of dark energy. In our subsequent analysis, we assume a spatially flat universe, i.e., . We allow the dark energy density to become negative, as considered by other works (see for example [29,33,84,85]).
3. Methodology
In order to constrain the Dark Energy models’ parameters, we make use of some of the most recent cosmological measurements available. These will be:
- CMB: we consider the temperature and polarization CMB angular power spectra of the Planck legacy release of 2018 plikTTTEEE+lowl+lowE [35,86] as a baseline (Note that there is an alternative likelihood for the Planck data, CamSpec [87], but they are consistent, as stated clearly from the Planck collaboration).
- R19: we adopt the gaussian prior km/s/Mpc at a 68% CL on the Hubble constant as measured by the SH0ES collaboration in [34].
- BAO: we add the Baryon Acoustic Oscillation (BAO) measurements 6dFGS [88], SDSS MGS [89], and BOSS DR12 [90], as adopted by the Planck collaboration in [35] (Note that there is an updated version of the BAO data [91], but we prefer to keep the combination used in the literature, for a better comparison).
- Pantheon: we make use of the luminosity distance data of 1048 type Ia Supernovae from the Pantheon catalog [92].
- Lensing: we consider the 2018 CMB lensing reconstruction power spectrum data, obtained with a CMB trispectrum analysis in [93].
We adopt as a baseline a nine-dimensional parameter space, i.e., we vary the following cosmological parameters: the baryon energy density , the cold dark matter energy density , the ratio of the sound horizon at decoupling to the angular diameter distance to last scattering , the optical depth to reionization , the amplitude and the spectral index of the primordial scalar perturbations and , and, finally, the three parameters assumed in our expansion of the in Equation (1), i.e., , and . We impose flat uniform priors on these parameters, as reported in Table 1.

Table 1.
Flat priors for the cosmological parameters.
To analyze the data and extract the constraints on these cosmological parameters, we used our modified version of the publicly available Monte Carlo Markov Chain package CosmoMC [94]. This is equipped with a convergence diagnostic based on the Gelman and Rubin statistic [95], assuming , and implements an efficient sampling of the posterior distribution using the fast/slow parameter decorrelations [96]. CosmoMC includes support for the 2018 Planck data release [86] (see http://cosmologist.info/cosmomc/). Finally, since for point , the present model becomes the CDM one, as was already mentioned before, and the likelihood has a singular nature as becomes redundant in this case, we switch back to the unmodified CosmoMC code for the analysis of this point, to avoid problems.
4. Observational Constraints
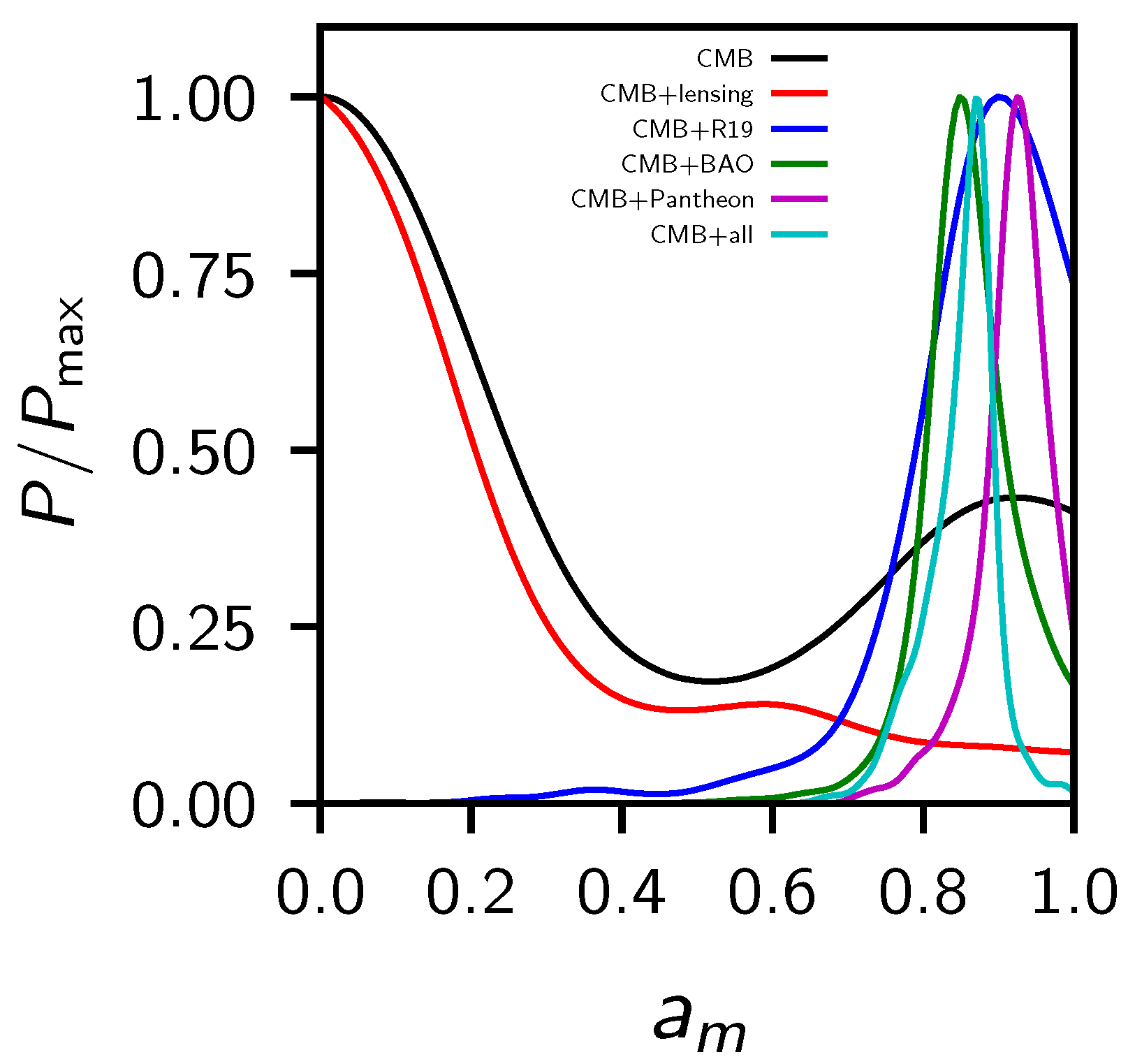
In Table 2 we show the constraints at a 68% CL for the cosmological parameters explored in this paper, for different dataset combinations. In Figure 1 we show instead the 2D contour plots and 1D posterior distribution on some of the most interesting parameters. We are not showing the CMB-only constraints because they are bimodal in , i.e., CMB alone is not able to distinguish which is its best value in fitting the data, but we need additional probes to break the degeneracy. Eventually, we found that CMB+lensing prefers one of the two peaks, while all the other combinations (+BAO, +Pantheon and +R19) prefer the other peak (see Figure 2). Finally, in Table 3 we compare the of the best fit of the data for the standard CDM model and the phantom crossing. We can see that in all the combinations of data considered here, the phantom crossing model improved the with respect to the standard model.

Table 2.
68% confidence level (CL) constraints on the cosmological parameters for the different dataset combinations explored in this work. CMB+all refers to Planck+lensing+BAO+R19+Pantheon.
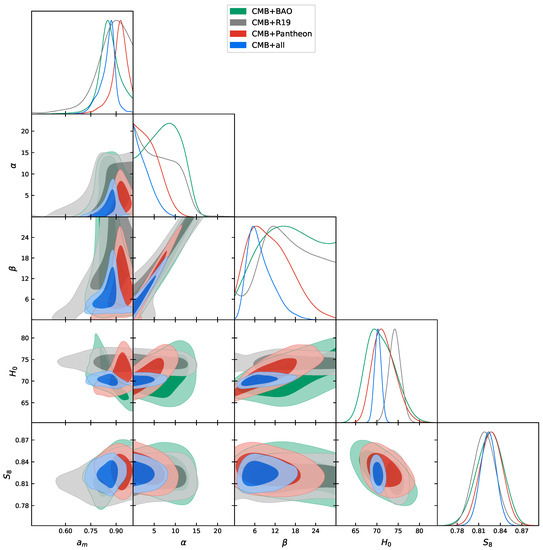
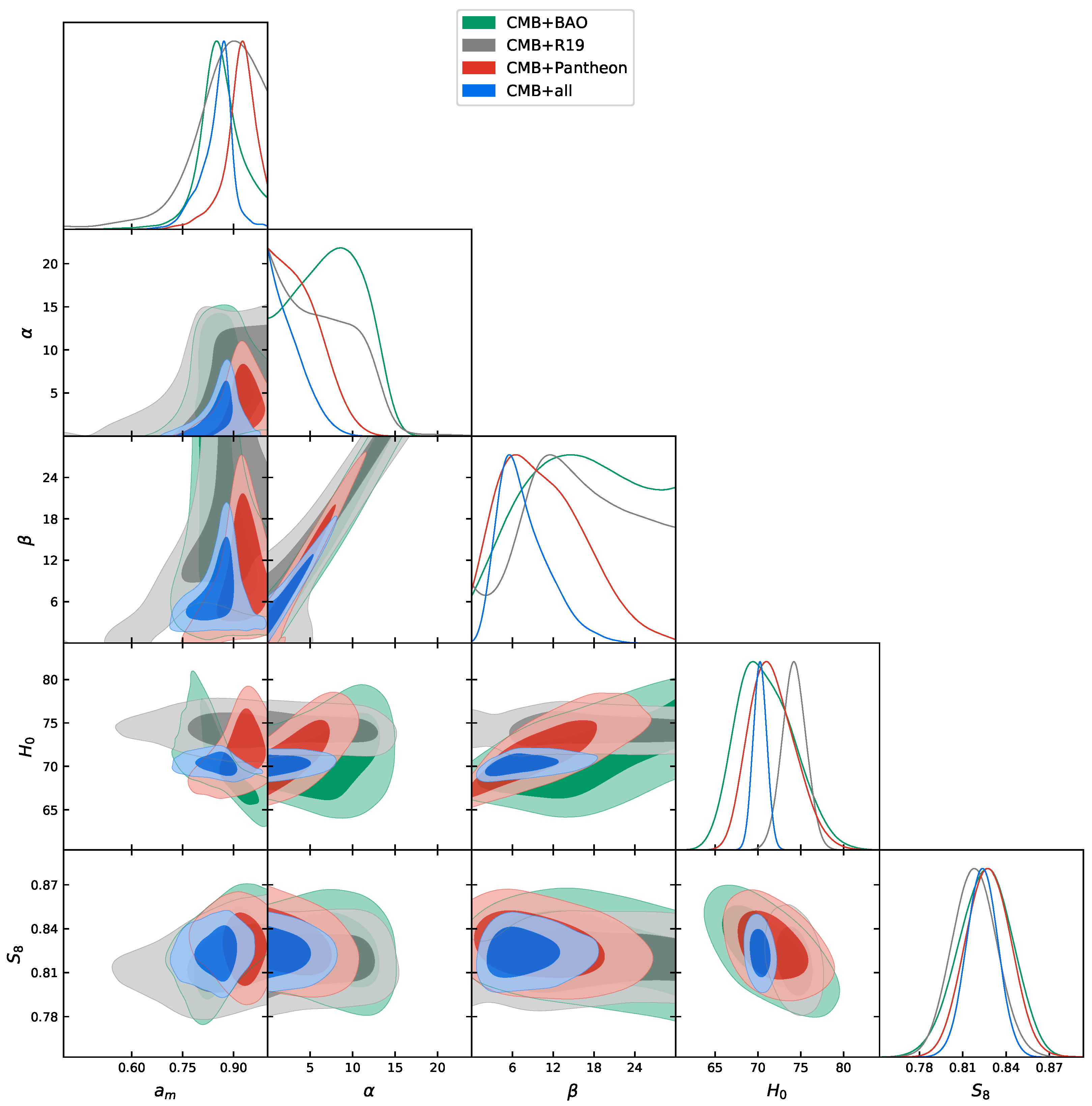
Figure 1.
Triangular plot showing 2D and 1D posterior distributions of some interesting parameters considered in this work. Planck+all refers to Planck+lensing+BAO+R19+Pantheon. CMB: Cosmic Microwave Background; BAO: Baryon Acoustic Oscillation.
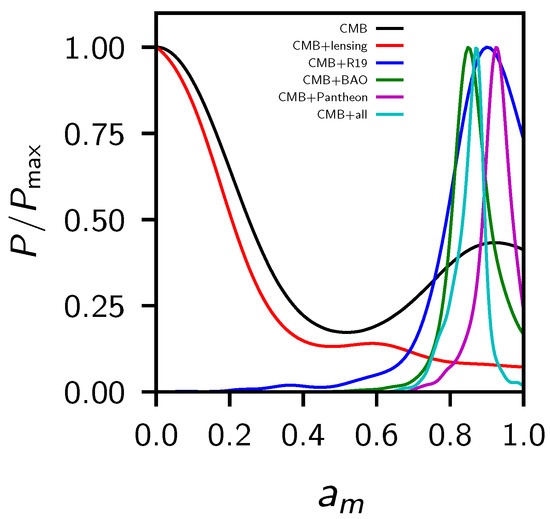
Figure 2.
1D posterior distribution of for the different dataset combinations explored in this work. CMB+all refers to Planck+lensing+BAO+R19+Pantheon.

Table 3.
s comparison between CDM and Phantom Crossing for the different dataset combinations explored in this work. CMB+all refers to Planck+lensing+BAO+R19+Pantheon.
Comparing the constraints on the cosmological parameters reported in Table 2 for our scenario with those reported by the Planck collaboration in [35] for a wCDM model, we can see that they are completely in agreement for the CMB+lensing dataset combination (second column). This happens because the scale factor of the transition is consistent with zero, so in agreement with a phantom dark energy as preferred by Planck in the wCDM model. Moreover, both and are consistent with 0, i.e., a cosmological constant, within one standard deviation. For CMB+lensing we found that the Hubble constant parameter is almost unconstrained ( km/s/Mpc at a 95% CL), and at a 68% CL is completely in agreement within one standard deviation with the combination of the cosmic shear data KiDS+VIKING-450+DES-Y1 [97], whereas the tension on is at in a CDM context.
Since the CMB and R19 are in agreement now within two standard deviations, we can combine them safely together. The results we obtained for the joint analysis CMB+R19 are reported in the third column of Table 2. Here we see that while is still consistent with zero within , we now have at a 68% CL and at a 68% CL, i.e., consistent with 1.
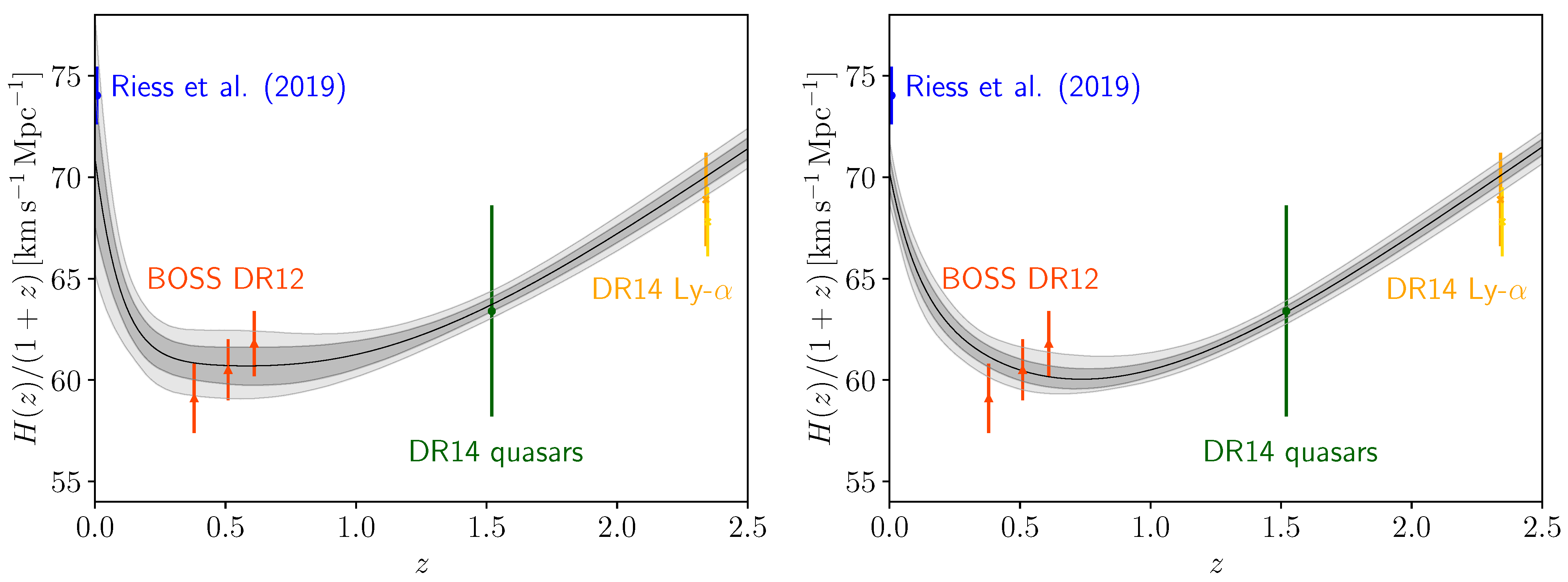
An interesting result is the one obtained combining CMB and BAO together, which is shown in the forth column of Table 2. Here we can see that contrary to many other cosmological scenarios, including a CDM model of which our parametrization is an extension, CMB+BAO gave km/s/Mpc at a 68% CL. This large Hubble constant value is now perfectly consistent within one standard deviation with the R19 measurement, while all other cosmological parameters are almost unchanged if compared with a wCDM scenario for the same CMB+BAO data combination. This increase of the parameter is due to its positive correlation with and , and negative correlation with , as can be seen in Figure 1. For the CMB+BAO case we have in fact an indication that all these three parameters are different from the expected values at more than . In particular we find, at a 68% CL, , and . Therefore, in this case there is an indication at more than for a transition in the dark energy density. The constraint on the present day equation of state is at a 95% CL, ruling out the cosmological constant at about 2. Given that both CMB and BAO are related to early universe physics, this shows that a phantom crossing in dark energy sectors alleviates the tension between the early and late universe determinations of the parameter . In the left panel of Figure 3, we show the behavior of the expansion rate of the universe for this dataset combination. We can see an excellent agreement with all the latest measurements. This agreement finds confirmation in the (see Table 3), where we show that the phantom crossing model improved the with respect to the standard CDM model, not only for the Planck+BAO combination, but also for the BAO data alone.
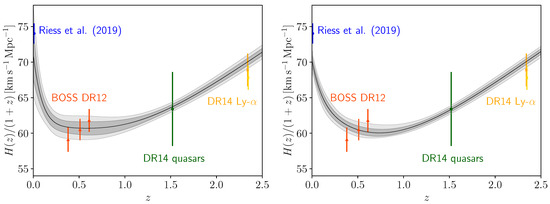
Figure 3.
Behavior of for the combinations CMB+BAO (on the left) and CMB+all (on the right). Observational data points of local measurement of by Riess et al. [34], BOSS DR12 [90], BOSS DR14 quasars [98], and BOSS DR14 Ly- [99,100] are also shown.
The same interesting larger value of the Hubble constant persists even if we combine CMB and Pantheon data. In this case, as we show in the fifth column of Table 2, km/s/Mpc at a 68% CL, i.e., consistent with R19. As can be seen in Figure 1, it is the positive correlation between and and that shifts the Hubble constant towards higher values, whereas, on the contrary with respect to the CMB+BAO combination, in this case there is a positive correlation also between and . For the dark energy parameters of our model we found for CMB+Pantheon, at a 68% CL, and , i.e., different from the expected value in a CDM model at more than , while is consistent with zero.
Given a preference for all data combinations of a large , we can conclude that this indication is robust irrespective to the combination of data analyzed here. For this reason we combine them all together because they are no more in tension. In fact, even the Planck+lensing dataset combination resulted in km/s/Mpc at a 95% CL, i.e., in perfect agreement with R19. The joint result, i.e., CMB+lensing+BAO+Pantheon+R19, is displayed in the last column of Table 2, where we see km/s/Mpc at a 68% CL, reducing the tension with R19 at standard deviations. In the right panel of Figure 3, we show the behavior of the expansion rate of the universe for this combination. Also in this case, we can see a good agreement with all of the latest measurements of BAO. However, even if for this dataset combination we have a slightly lower at a 68% CL, the tension with the cosmic shear data KiDS+VIKING-450+DES-Y1 [97] is still at . For the joint case we found, at a 68% CL, and , i.e., they are different from the expected value in a CDM scenario at more than because they are highly non-gaussian, while at a 68% CL is consistent with zero. Therefore, a robust indication at more than for a transition in the dark energy density is suggested by the data. The constraint on the present day equation of state is at a 95% CL, ruling out the cosmological constant at more than 2. Finally, if we look at the in Table 3, we can see that the Phantom Crossing model improves significantly the total we had for the standard CDM model.
From the constraints on in Table 3 for different data combinations, especially for the CMB+BAO combination, we can say that our results agree with BAO data, as well as a larger value, even if we do not change as constrained by Planck for CDM. This may be due to non-monotonic dark energy evolution in late time.
It is also not difficult to check that for the constrained parameter space can become negative for some redshifts and this is consistent with earlier results by [29,33,84,85]. A negative at some earlier time may help reduce the Hubble tension.
Additionally, to perform a model comparison, we computed the Bayesian evidence and we show the results in Table 4. This allowed us to quantify which model fits the data better between CDM and phantom crossing. We used the publicly available cosmological code MCEvidence (https://github.com/yabebalFantaye/MCEvidence [101,102]). We assumed that for negative (positive) values of the Bayes factor , the CDM (phantom crossing) is the preferred model. To interpret the results, we referred to the revised Jeffreys scale by Kass and Raftery as in Reference [103]. Therefore, we will have for weak evidence, for definite evidence, for strong evidence, and for very strong evidence for one model versus the second one. Looking at Table 4 we can see that we have very strong evidence for the phantom crossing for CMB+R19, while the CDM model is preferred for all other dataset combinations.

Table 4.
The table shows the values of calculated for the phantom crossing model with respect to the CDM scenario. The negative value in indicates that there is a preference for CDM against the phantom crossing model, while a positive value indicates a preference for phantom crossing.
5. Conclusions
In this work, we considered a dark energy behavior with phantom crossing and confronted it with different observational data including the latest CMB data from Planck. We did not consider any specific theoretical setup involving fields but rather we approached it in a general way where we assumed that the dark energy density should have an extrema at a particular scale factor for phantom crossing. If , this crossing happens before the present day. We Taylor expanded the dark energy density around this extrema and checked whether the observational data are consistent with . We found that a combination of observational data including that from Planck is indeed consistent with , confirming the presence of phantom crossing. Moreover, the phantom crossing also helps to alleviate the tension between low and high redshift observations. The CMB+BAO combination, which represents early universe physics, gave the constraint km/s/Mpc at a 68% CL for the model with phantom crossing, which is fully in agreement with the local measurement of by R19. Moreover, constraints on different parameters including for different combinations of data were found to be consistent with each other, which allowed us to combine all the data. For the combination of all data, the phantom crossing was observed at more than and the constraint on was km/s/Mpc at a 68% CL, which is in tension with R19 at standard deviations—much lower than the present tension with CDM and many other dark energy models, suggesting a substantial alleviation of the Hubble tension with phantom crossing. Finally, as seen in Table 3, the phantom crossing model fit better than CDM the full dataset combination, improving the .
Author Contributions
Conceptualization, A.M. and A.A.S.; methodology, E.D.V.; formal analysis, E.D.V.; writing—original draft preparation, E.D.V., A.M. and A.A.S.; writing—review and editing, E.D.V., A.M. and A.A.S. All authors have read and agreed to the published version of the manuscript.
Funding
E.D.V. acknowledges the support of the Addison–Wheeler Fellowship awarded by the Institute of Advanced Study at Durham University. A.M. acknowledges the financial support from the Science and Engineering Research Board (SERB), Department of Science and Technology, Government of India as a National Post-Doctoral Fellow (NPDF, File no. PDF/2018/001859). A.A.S. acknowledges funding from DST-SERB, Govt. of India, under the project NO. MTR/20l9/000599. The authors also thank Ruchika for computational help.
Data Availability Statement
All the datasets used are publicly available and a description can be found in the methodology section.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E. Measurements of Ω and Λ from 42 high redshift supernovae. Astrophys. J. 1999, 517, 565. [Google Scholar] [CrossRef]
- Bamba, K.; Capozziello, S.; Nojiri, S.I.; Odintsov, S.D. Dark energy cosmology: The equivalent description via different theoretical models and cosmography tests. Astrophys. Space Sci. 2012, 342, 155–228. [Google Scholar] [CrossRef]
- Carroll, S.M. The cosmological constant. Living Rev. Rel. 2001, 4, 1–56. [Google Scholar] [CrossRef]
- Peebles, P.J.E.; Ratra, B. The cosmological constant and dark energy. Rev. Mod. Phys. 2003, 75, 559. [Google Scholar] [CrossRef]
- Padmanabhan, T. Cosmological constant—the weight of the vacuum. Phys. Rep. 2003, 380, 235–320. [Google Scholar] [CrossRef]
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. Int. J. Mod. Phys. D 2006, 15, 1753–1935. [Google Scholar] [CrossRef]
- Kamenshchik, A.; Moschella, U.; Pasquier, V. An alternative to quintessence. Phys. Lett. B 2001, 511, 265–268. [Google Scholar] [CrossRef]
- Bento, M.; Bertolami, O.; Sen, A.A. Generalized Chaplygin gas, accelerated expansion, and dark-energy-matter unification. Phys. Rev. D 2002, 66, 043507. [Google Scholar] [CrossRef]
- Akrami, Y.; Arroja, F.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.; Barreiro, R.; Bartolo, N.; Basak, S. Planck 2018 results. I. Overview and the cosmological legacy of Planck. arXiv 2018, arXiv:1807.06205. [Google Scholar]
- Suzuki, N.; Rubin, D.; Lidman, C.; Aldering, G.; Amanullah, R.; Barbary, K.; Barrientos, L.; Botyanszki, J.; Brodwin, M.; Connolly, N. The Hubble Space Telescope cluster supernova survey. V. Improving the dark-energy constraints above z> 1 and building an early-type-hosted supernova sample. Astrophys. J. 2012, 746, 85. [Google Scholar] [CrossRef]
- Dawson, K.S.; Schlegel, D.J.; Ahn, C.P.; Anderson, S.F.; Aubourg, É.; Bailey, S.; Barkhouser, R.H.; Bautista, J.E.; Beifiori, A.; Berlind, A.A. The Baryon oscillation spectroscopic survey of SDSS-III. Astron. J. 2012, 145, 10. [Google Scholar] [CrossRef]
- Alam, S.; Albareti, F.D.; Prieto, C.A.; Anders, F.; Anderson, S.F.; Anderton, T.; Andrews, B.H.; Armengaud, E.; Aubourg, É.; Bailey, S. The eleventh and twelfth data releases of the Sloan Digital Sky Survey: Final data from SDSS-III. Astrophys. J. Suppl. Ser. 2015, 219, 12. [Google Scholar] [CrossRef]
- Vikman, A. Can dark energy evolve to the phantom? Phys. Rev. D 2005, 71, 023515. [Google Scholar] [CrossRef]
- Nojiri, S.I.; Odintsov, S.D. Inhomogeneous equation of state of the universe: Phantom era, future singularity, and crossing the phantom barrier. Phys. Rev. D 2005, 72, 023003. [Google Scholar] [CrossRef]
- Nojiri, S.I.; Odintsov, S.D. Unifying phantom inflation with late-time acceleration: Scalar phantom–non-phantom transition model and generalized holographic dark energy. Gen. Relativ. Gravit. 2006, 38, 1285–1304. [Google Scholar] [CrossRef]
- Nojiri, S.I.; Odintsov, S.D. The oscillating dark energy: Future singularity and coincidence problem. Phys. Lett. B 2006, 637, 139–148. [Google Scholar] [CrossRef]
- Bamba, K.; Geng, C.-Q.; Nojiri, S.I.; Odintsov, S.D. Crossing of the phantom divide in modified gravity. Phys. Rev. D 2009, 79, 083014. [Google Scholar] [CrossRef]
- Jaime, L.G.; Jaber, M.; Escamilla-Rivera, C. New parametrized equation of state for dark energy surveys. Phys. Rev. D 2018, 98, 083530. [Google Scholar] [CrossRef]
- Saridakis, E.N. Phantom crossing and quintessence limit in extended nonlinear massive gravity. Class. Quantum Gravity 2013, 30, 075003. [Google Scholar] [CrossRef]
- Chimento, L.P.; Forte, M.; Lazkoz, R.; Richarte, M.G. Internal space structure generalization of the quintom cosmological scenario. Phys. Rev. D 2009, 79, 043502. [Google Scholar] [CrossRef]
- Hu, W. Crossing the phantom divide: Dark energy internal degrees of freedom. Phys. Rev. D 2005, 71, 047301. [Google Scholar] [CrossRef]
- Wei, H.; Cai, R.-G. A note on crossing the phantom divide in hybrid dark energy model. Phys. Lett. B 2006, 634, 9–13. [Google Scholar] [CrossRef]
- Deffayet, C.; Pujolas, O.; Sawicki, I.; Vikman, A. Imperfect dark energy from kinetic gravity braiding. J. Cosmol. Astropart. Phys. 2010, 2010, 026. [Google Scholar] [CrossRef]
- Matsumoto, J. Phantom crossing dark energy in Horndeski’s theory. Phys. Rev. D 2018, 97, 123538. [Google Scholar] [CrossRef]
- Nesseris, S.; Perivolaropoulos, L. Crossing the phantom divide: Theoretical implications and observational status. J. Cosmol. Astropart. Phys. 2007, 2007, 018. [Google Scholar] [CrossRef]
- Fang, W.; Hu, W.; Lewis, A. Crossing the phantom divide with parametrized post-Friedmann dark energy. Phys. Rev. D 2008, 78, 087303. [Google Scholar] [CrossRef]
- Shafer, D.L.; Huterer, D. Chasing the phantom: A closer look at Type Ia supernovae and the dark energy equation of state. Phys. Rev. D 2014, 89, 063510. [Google Scholar] [CrossRef]
- Wang, Y.; Pogosian, L.; Zhao, G.-B.; Zucca, A. Evolution of dark energy reconstructed from the latest observations. Astrophys. J. Lett. 2018, 869, L8. [Google Scholar] [CrossRef]
- Zhao, G.-B.; Crittenden, R.G.; Pogosian, L.; Zhang, X. Examining the evidence for dynamical dark energy. Phys. Rev. Lett. 2012, 109, 171301. [Google Scholar] [CrossRef]
- Zhao, G.-B.; Raveri, M.; Pogosian, L.; Wang, Y.; Crittenden, R.G.; Handley, W.J.; Percival, W.J.; Beutler, F.; Brinkmann, J.; Chuang, C.-H. Dynamical dark energy in light of the latest observations. Nat. Astron. 2017, 1, 627–632. [Google Scholar] [CrossRef]
- Capozziello, S.; Sen, A.A. Model-independent constraints on dark energy evolution from low-redshift observations. Mon. Not. R. Astron. Soc. 2019, 484, 4484–4494. [Google Scholar] [CrossRef]
- Dutta, K.; Roy, A.; Sen, A.A.; Sheikh-Jabbari, M. Beyond ΛCDM with low and high redshift data: Implications for dark energy. Gen. Relativ. Gravit. 2020, 52, 1–16. [Google Scholar] [CrossRef]
- Riess, A.G.; Casertano, S.; Yuan, W.; Macri, L.M.; Scolnic, D. Large Magellanic Cloud Cepheid standards provide a 1% foundation for the determination of the Hubble constant and stronger evidence for physics beyond ΛCDM. Astrophys. J. 2019, 876, 85. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.; Barreiro, R.; Bartolo, N.; Basak, S. Planck 2018 results-VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar]
- Di Valentino, E.; Melchiorri, A.; Silk, J. Reconciling Planck with the local value of H0 in extended parameter space. Phys. Lett. B 2016, 761, 242–246. [Google Scholar] [CrossRef]
- Bernal, J.L.; Verde, L.; Riess, A.G. The trouble with H0. J. Cosmol. Astropart. Phys. 2016, 2016, 19. [Google Scholar] [CrossRef]
- Kumar, S.; Nunes, R.C. Probing the interaction between dark matter and dark energy in the presence of massive neutrinos. Phys. Rev. D 2016, 94, 123511. [Google Scholar] [CrossRef]
- Kumar, S.; Nunes, R.C. Echo of interactions in the dark sector. Phys. Rev. D 2017, 96, 103511. [Google Scholar] [CrossRef]
- Di Valentino, E.; Melchiorri, A.; Mena, O. Can interacting dark energy solve the H 0 tension? Phys. Rev. D 2017, 96, 043503. [Google Scholar] [CrossRef]
- Di Valentino, E.; Bœhm, C.; Hivon, E.; Bouchet, F.R. Reducing the H0 and σ8 tensions with Dark Matter-neutrino interactions. Phys. Rev. D 2018, 97, 043513. [Google Scholar] [CrossRef]
- Di Valentino, E.; Linder, E.V.; Melchiorri, A. Vacuum phase transition solves the H0 tension. Phys. Rev. D 2018, 97, 043528. [Google Scholar] [CrossRef]
- Di Valentino, E.; Melchiorri, A.; Linder, E.V.; Silk, J. Constraining dark energy dynamics in extended parameter space. Phys. Rev. D 2017, 96, 023523. [Google Scholar] [CrossRef]
- Solà, J.; Gómez-Valent, A.; de Cruz Pérez, J. The H0 tension in light of vacuum dynamics in the Universe. Phys. Lett. B 2017, 774, 317–324. [Google Scholar] [CrossRef]
- Nunes, R.C. Structure formation in f(T) gravity and a solution for H0 tension. J. Cosmol. Astropart. Phys. 2018, 2018, 052. [Google Scholar] [CrossRef]
- Yang, W.; Pan, S.; Di Valentino, E.; Nunes, R.C.; Vagnozzi, S.; Mota, D.F. Tale of stable interacting dark energy, observational signatures, and the H0 tension. J. Cosmol. Astropart. Phys. 2018, 2018, 019. [Google Scholar] [CrossRef]
- Yang, W.; Mukherjee, A.; Di Valentino, E.; Pan, S. Interacting dark energy with time varying equation of state and the H0 tension. Phys. Rev. D 2018, 98, 123527. [Google Scholar] [CrossRef]
- Yang, W.; Pan, S.; Di Valentino, E.; Saridakis, E.N.; Chakraborty, S. Observational constraints on one-parameter dynamical dark-energy parametrizations and the H0 tension. Phys. Rev. D 2019, 99, 043543. [Google Scholar] [CrossRef]
- Poulin, V.; Smith, T.L.; Karwal, T.; Kamionkowski, M. Early dark energy can resolve the Hubble tension. Phys. Rev. Lett. 2019, 122, 221301. [Google Scholar] [CrossRef]
- Mörtsell, E.; Dhawan, S. Does the Hubble constant tension call for new physics? J. Cosmol. Astropart. Phys. 2018, 2018, 025. [Google Scholar] [CrossRef]
- Martinelli, M.; Hogg, N.B.; Peirone, S.; Bruni, M.; Wands, D. Constraints on the interacting vacuum–geodesic CDM scenario. Mon. Not. R. Astron. Soc. 2019, 488, 3423–3438. [Google Scholar] [CrossRef]
- Vattis, K.; Koushiappas, S.M.; Loeb, A. Dark matter decaying in the late Universe can relieve the H0 tension. Phys. Rev. D 2019, 99, 121302. [Google Scholar] [CrossRef]
- Kumar, S.; Nunes, R.C.; Yadav, S.K. Dark sector interaction: A remedy of the tensions between CMB and LSS data. Eur. Phys. J. C 2019, 79, 1–5. [Google Scholar] [CrossRef]
- Agrawal, P.; Cyr-Racine, F.-Y.; Pinner, D.; Randall, L. Rock’n’Roll Solutions to the Hubble Tension. arXiv 2019, arXiv:1904.01016. [Google Scholar]
- Yang, W.; Pan, S.; Di Valentino, E.; Paliathanasis, A.; Lu, J. Challenging bulk viscous unified scenarios with cosmological observations. Phys. Rev. D 2019, 100, 103518. [Google Scholar] [CrossRef]
- Yang, W.; Mena, O.; Pan, S.; Di Valentino, E. Dark sectors with dynamical coupling. Phys. Rev. D 2019, 100, 083509. [Google Scholar] [CrossRef]
- Di Valentino, E.; Ferreira, R.Z.; Visinelli, L.; Danielsson, U. Late time transitions in the quintessence field and the H0 tension. Phys. Dark Universe 2019, 26, 100385. [Google Scholar] [CrossRef]
- Pan, S.; Yang, W.; Di Valentino, E.; Saridakis, E.N.; Chakraborty, S. Interacting scenarios with dynamical dark energy: Observational constraints and alleviation of the H0 tension. Phys. Rev. D 2019, 100, 103520. [Google Scholar] [CrossRef]
- Martinelli, M.; Tutusaus, I. CMB tensions with low-redshift H0 and S8 measurements: Impact of a redshift-dependent type-Ia supernovae intrinsic luminosity. Symmetry 2019, 11, 986. [Google Scholar] [CrossRef]
- Pan, S.; Yang, W.; Di Valentino, E.; Shafieloo, A.; Chakraborty, S. Reconciling H0 tension in a six parameter space? J. Cosmol. Astropart. Phys. 2020, 2020, 62. [Google Scholar] [CrossRef]
- Di Valentino, E.; Melchiorri, A.; Silk, J. Cosmological constraints in extended parameter space from the Planck 2018 Legacy release. J. Cosmol. Astropart. Phys. 2020, 2020, 013. [Google Scholar] [CrossRef]
- Di Valentino, E.; Melchiorri, A.; Mena, O.; Vagnozzi, S. Interacting dark energy in the early 2020s: A promising solution to the H0 and cosmic shear tensions. Phys. Dark Universe 2020, 30, 100666. [Google Scholar] [CrossRef]
- Di Valentino, E.; Melchiorri, A.; Mena, O.; Vagnozzi, S. Nonminimal dark sector physics and cosmological tensions. Phys. Rev. D 2020, 101, 063502. [Google Scholar] [CrossRef]
- Colgain, E.O.; Yavartanoo, H. Testing the Swampland: H0 tension. Phys. Lett. B 2019, 797, 134907. [Google Scholar] [CrossRef]
- Alcaniz, J.; Bernal, N.; Masiero, A.; Queiroz, F.S. Light dark matter: A common solution to the lithium and H0 problems. Phys. Lett. B 2021, 812, 136008. [Google Scholar] [CrossRef]
- Pan, S.; Yang, W.; Singha, C.; Saridakis, E.N. Observational constraints on sign-changeable interaction models and alleviation of the H0 tension. Phys. Rev. D 2019, 100, 083539. [Google Scholar] [CrossRef]
- Berghaus, K.V.; Karwal, T. Thermal friction as a solution to the Hubble tension. Phys. Rev. D 2020, 101, 83537. [Google Scholar] [CrossRef]
- Knox, L.; Millea, M. Hubble constant hunter’s guide. Phys. Rev. D 2020, 101, 043533. [Google Scholar] [CrossRef]
- Pandey, K.L.; Karwal, T.; Das, S. Alleviating the H0 and σ8 anomalies with a decaying dark matter model. J. Cosmol. Astropart. Phys. 2020, 2020, 026. [Google Scholar] [CrossRef]
- Adhikari, S.; Huterer, D. Super-CMB fluctuations and the Hubble tension. Phys. Dark Universe 2020, 28, 100539. [Google Scholar] [CrossRef]
- Hart, L.; Chluba, J. Updated fundamental constant constraints from Planck 2018 data and possible relations to the Hubble tension. Mon. Not. R. Astron. Soc. 2020, 493, 3255–3263. [Google Scholar] [CrossRef]
- Liao, K.; Shafieloo, A.; Keeley, R.E.; Linder, E.V. Determining model-independent H0 and consistency tests. Astrophys. J. Lett. 2020, 895, L29. [Google Scholar] [CrossRef]
- Benevento, G.; Hu, W.; Raveri, M. Can late dark energy transitions raise the Hubble constant? Phys. Rev. D 2020, 101, 103517. [Google Scholar] [CrossRef]
- Vagnozzi, S. New physics in light of the H0 tension: An alternative view. Phys. Rev. D 2020, 102, 023518. [Google Scholar] [CrossRef]
- Chudaykin, A.; Gorbunov, D.; Nedelko, N. Combined analysis of Planck and SPTPol data favors the early dark energy models. J. Cosmol. Astropart. Phys. 2020, 2020, 013. [Google Scholar] [CrossRef]
- Alestas, G.; Kazantzidis, L.; Perivolaropoulos, L. H0 tension, phantom dark energy, and cosmological parameter degeneracies. Phys. Rev. D 2020, 101, 123516. [Google Scholar] [CrossRef]
- Wang, D.; Mota, D. Can f(T) gravity resolve the H0 tension? Phys. Rev. D 2020, 102, 063530. [Google Scholar] [CrossRef]
- Blinov, N.; Marques-Tavares, G. Interacting radiation after Planck and its implications for the Hubble Tension. J. Cosmol. Astropart. Phys. 2020, 2020, 029. [Google Scholar] [CrossRef]
- Di Valentino, E.; Anchordoqui, L.A.; Ali-Haimoud, Y.; Amendola, L.; Arendse, N.; Asgari, M.; Ballardini, M.; Battistelli, E.; Benetti, M.; Birrer, S. Cosmology intertwined II: The Hubble constant tension. arXiv 2020, arXiv:2008.11284. [Google Scholar]
- Di Valentino, E.; Mena, O.; Pan, S.; Visinelli, L.; Yang, W.; Melchiorri, A.; Mota, D.F.; Riess, A.G.; Silk, J. In the Realm of the Hubble tension—A Review of Solutions. arXiv 2021, arXiv:2103.01183. [Google Scholar]
- Alestas, G.; Kazantzidis, L.; Perivolaropoulos, L. A w-M phantom transition at zt < 0.1 as a resolution of the Hubble tension. arXiv 2020, arXiv:2012.13932. [Google Scholar]
- Camarena, D.; Marra, V. Hockey-stick dark energy is not a solution to the H0 crisis. arXiv 2021, arXiv:2101.08641. [Google Scholar]
- Sen, A. Deviation from ΛCDM: Pressure parametrization. Phys. Rev. D 2008, 77, 043508. [Google Scholar] [CrossRef]
- Delubac, T.; Bautista, J.E.; Rich, J.; Kirkby, D.; Bailey, S.; Font-Ribera, A.; Slosar, A.; Lee, K.-G.; Pieri, M.M.; Hamilton, J.-C. Baryon acoustic oscillations in the Lyα forest of BOSS DR11 quasars. Astron. Astrophys. 2015, 574, A59. [Google Scholar] [CrossRef]
- Poulin, V.; Boddy, K.K.; Bird, S.; Kamionkowski, M. Implications of an extended dark energy cosmology with massive neutrinos for cosmological tensions. Phys. Rev. D 2018, 97, 123504. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.; Bartolo, N.; Basak, S. Planck 2018 results-V. CMB power spectra and likelihoods. Astron. Astrophys. 2020, 641, A5. [Google Scholar]
- Efstathiou, G.; Gratton, S. A detailed description of the CamSpec likelihood pipeline and a reanalysis of the Planck high frequency maps. arXiv 2019, arXiv:1910.00483. [Google Scholar]
- Beutler, F.; Blake, C.; Colless, M.; Jones, D.H.; Staveley-Smith, L.; Campbell, L.; Parker, Q.; Saunders, W.; Watson, F. The 6dF Galaxy Survey: Baryon acoustic oscillations and the local Hubble constant. Mon. Not. R. Astron. Soc. 2011, 416, 3017–3032. [Google Scholar] [CrossRef]
- Ross, A.J.; Samushia, L.; Howlett, C.; Percival, W.J.; Burden, A.; Manera, M. The clustering of the SDSS DR7 main Galaxy sample–I. A 4 per cent distance measure at z = 0.15. Mon. Not. R. Astron. Soc. 2015, 449, 835–847. [Google Scholar] [CrossRef]
- Alam, S.; Ata, M.; Bailey, S.; Beutler, F.; Bizyaev, D.; Blazek, J.A.; Bolton, A.S.; Brownstein, J.R.; Burden, A.; Chuang, C.-H. The clustering of galaxies in the completed SDSS-III Baryon Oscillation Spectroscopic Survey: Cosmological analysis of the DR12 galaxy sample. Mon. Not. R. Astron. Soc. 2017, 470, 2617–2652. [Google Scholar] [CrossRef]
- de Mattia, A.; Ruhlmann-Kleider, V.; Raichoor, A.; Ross, A.J.; Tamone, A.; Zhao, C.; Alam, S.; Avila, S.; Burtin, E.; Bautista, J. The Completed SDSS-IV extended Baryon Oscillation Spectroscopic Survey: Measurement of the BAO and growth rate of structure of the emission line galaxy sample from the anisotropic power spectrum between redshift 0.6 and 1.1. Mon. Not. R. Astron. Soc. 2021, 501, 5616–5645. [Google Scholar]
- Scolnic, D.M.; Jones, D.; Rest, A.; Pan, Y.; Chornock, R.; Foley, R.; Huber, M.; Kessler, R.; Narayan, G.; Riess, A. The complete light-curve sample of spectroscopically confirmed SNe Ia from Pan-STARRS1 and cosmological constraints from the combined pantheon sample. Astrophys. J. 2018, 859, 101. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.; Bartolo, N.; Basak, S. Planck 2018 results-VIII. Gravitational lensing. Astron. Astrophys. 2020, 641, A8. [Google Scholar]
- Lewis, A.; Bridle, S. Cosmological parameters from CMB and other data: A Monte Carlo approach. Phys. Rev. D 2002, 66, 103511. [Google Scholar] [CrossRef]
- Gelman, A.; Rubin, D.B. Inference from iterative simulation using multiple sequences. Stat. Sci. 1992, 7, 457–472. [Google Scholar] [CrossRef]
- Lewis, A. Efficient sampling of fast and slow cosmological parameters. Phys. Rev. D 2013, 87, 103529. [Google Scholar] [CrossRef]
- Asgari, M.; Tröster, T.; Heymans, C.; Hildebrandt, H.; van den Busch, J.L.; Wright, A.H.; Choi, A.; Erben, T.; Joachimi, B.; Joudaki, S. KiDS+ VIKING-450 and DES-Y1 combined: Mitigating baryon feedback uncertainty with COSEBIs. Astron. Astrophys. 2020, 634, A127. [Google Scholar] [CrossRef]
- Zarrouk, P.; Burtin, E.; Gil-Marín, H.; Ross, A.J.; Tojeiro, R.; Pâris, I.; Dawson, K.S.; Myers, A.D.; Percival, W.J.; Chuang, C.-H. The clustering of the SDSS-IV extended Baryon Oscillation Spectroscopic Survey DR14 quasar sample: Measurement of the growth rate of structure from the anisotropic correlation function between redshift 0.8 and 2.2. Mon. Not. R. Astron. Soc. 2018, 477, 1639–1663. [Google Scholar] [CrossRef]
- de Sainte Agathe, V.; Balland, C.; Des Bourboux, H.D.M.; Blomqvist, M.; Guy, J.; Rich, J.; Font-Ribera, A.; Pieri, M.M.; Bautista, J.E.; Dawson, K. Baryon acoustic oscillations at z = 2.34 from the correlations of Lyα absorption in eBOSS DR14. Astron. Astrophys. 2019, 629, A85. [Google Scholar] [CrossRef]
- Blomqvist, M.; Des Bourboux, H.D.M.; de Sainte Agathe, V.; Rich, J.; Balland, C.; Bautista, J.E.; Dawson, K.; Font-Ribera, A.; Guy, J.; Le Goff, J.-M. Baryon acoustic oscillations from the cross-correlation of Lyα absorption and quasars in eBOSS DR14. Astron. Astrophys. 2019, 629, A86. [Google Scholar] [CrossRef]
- Heavens, A.; Fantaye, Y.; Sellentin, E.; Eggers, H.; Hosenie, Z.; Kroon, S.; Mootoovaloo, A. No evidence for extensions to the standard cosmological model. Phys. Rev. Lett. 2017, 119, 101301. [Google Scholar] [CrossRef] [PubMed]
- Heavens, A.; Fantaye, Y.; Mootoovaloo, A.; Eggers, H.; Hosenie, Z.; Kroon, S.; Sellentin, E. Marginal Likelihoods from Monte Carlo Markov Chains. arXiv 2017, arXiv:1704.03472. [Google Scholar]
- Kass, R.; Raftery, A. Bayes factor and model uncertainty. J. Am. Stat. Assoc. 1995, 90, 773–795. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).