Mechanism Integrated Information
Abstract
1. Introduction
2. Axioms and Postulates
3. Theory
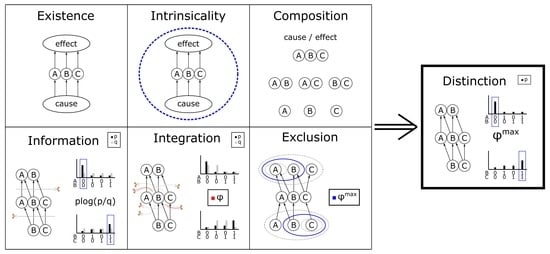
3.1. Mechanism Integrated Information
3.1.1. Existence
3.1.2. Intrinsicality
3.1.3. Information
3.1.4. Integration
3.1.5. Exclusion
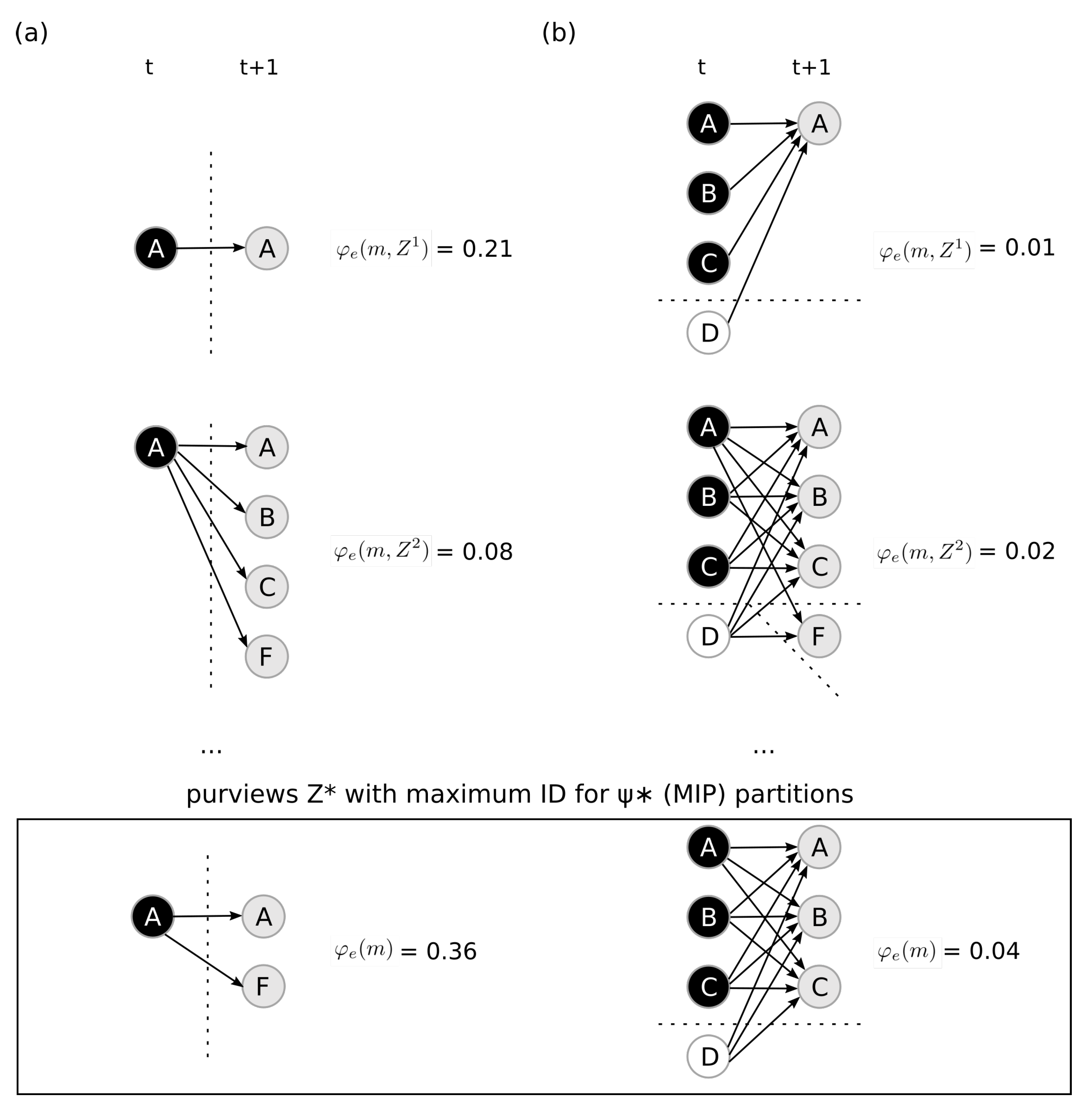
3.2. Disintegrating Partitions
3.3. Intrinsic Difference (ID)
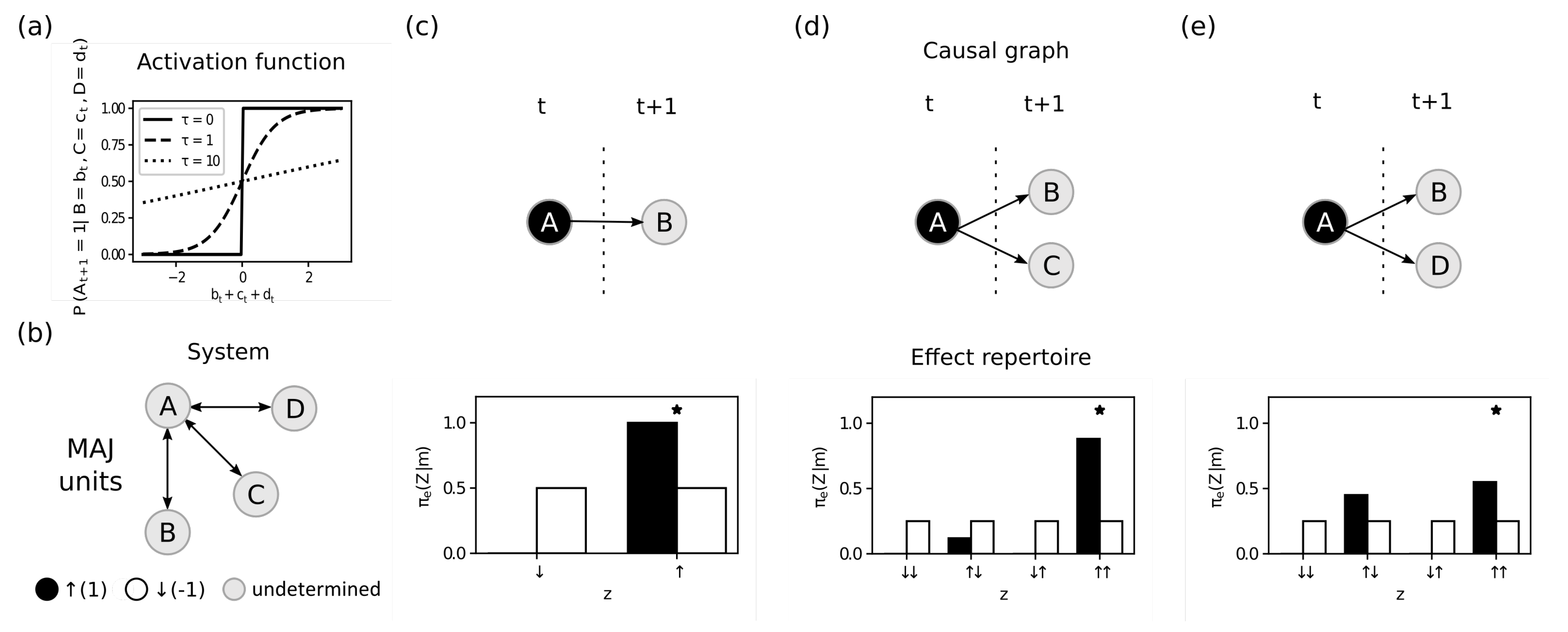
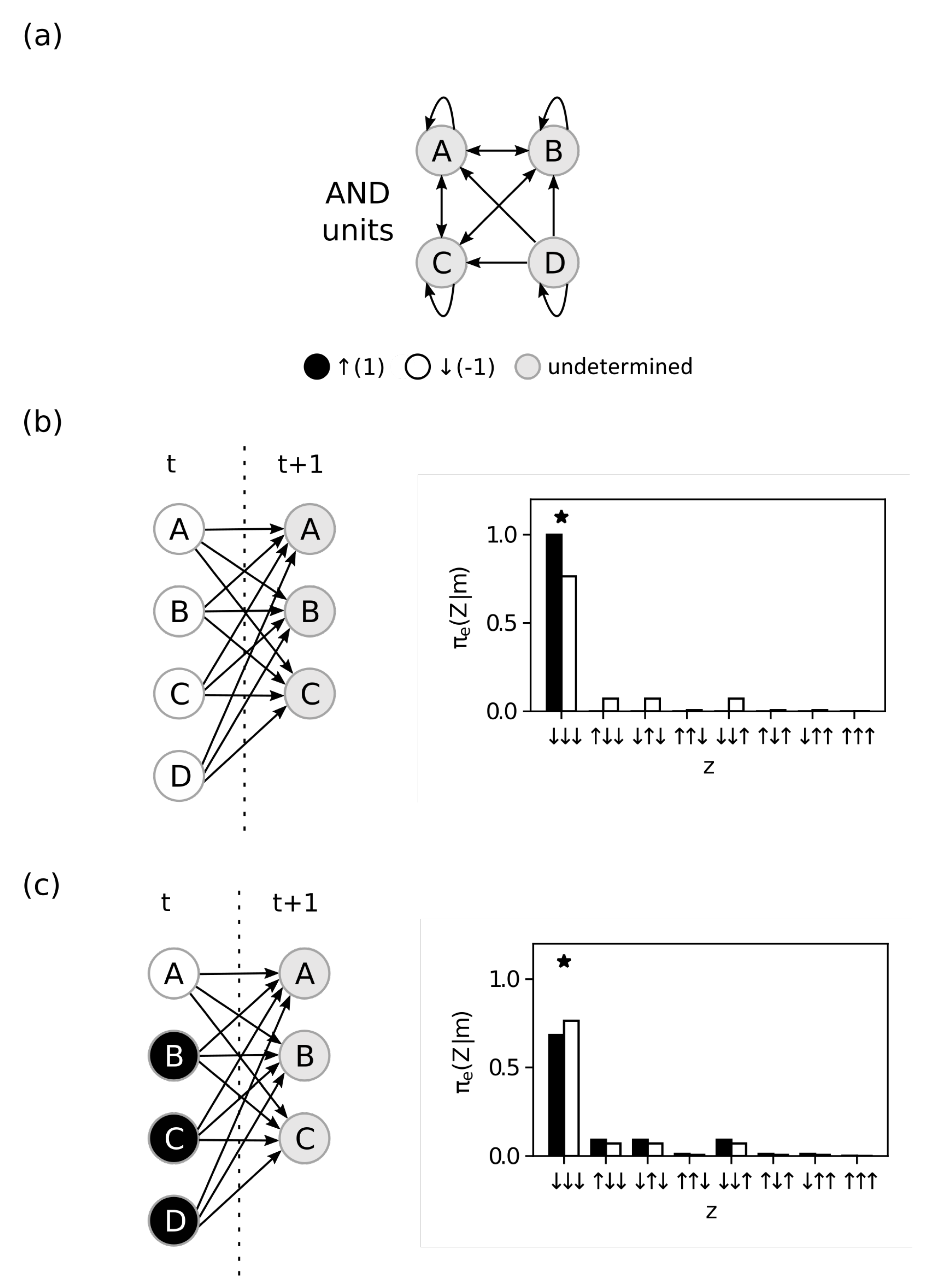
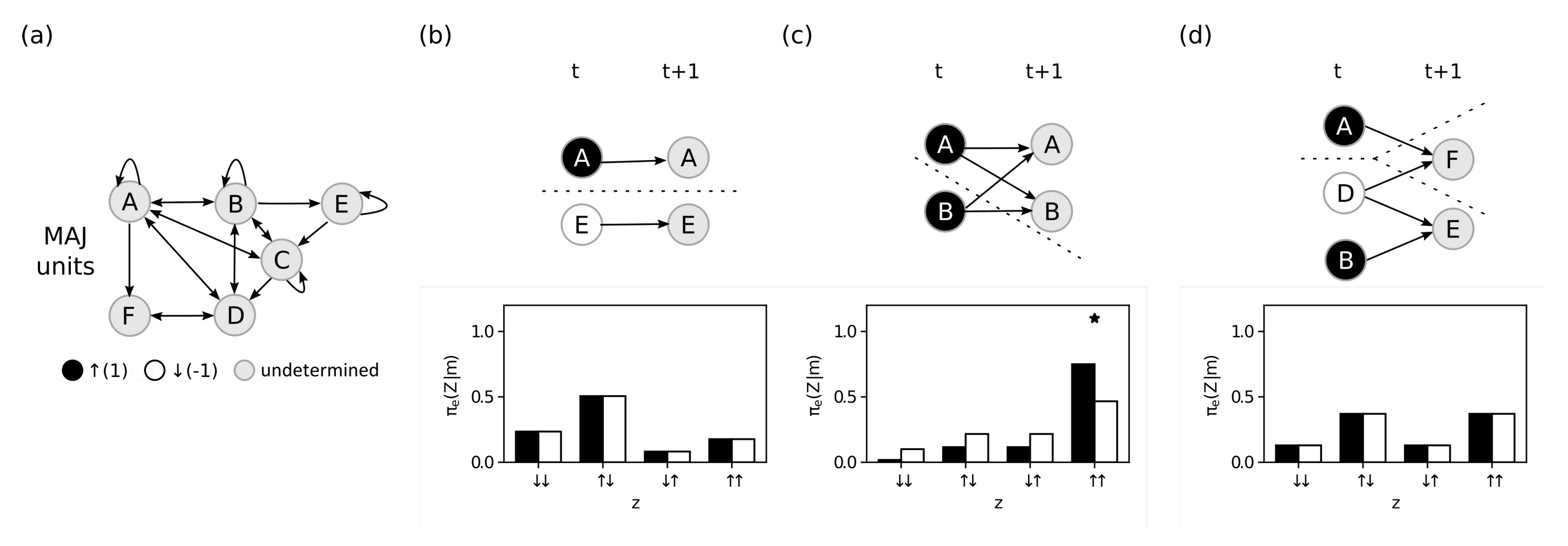
4. Methods and Results
4.1. Intrinsic Information
4.2. Integrated Information
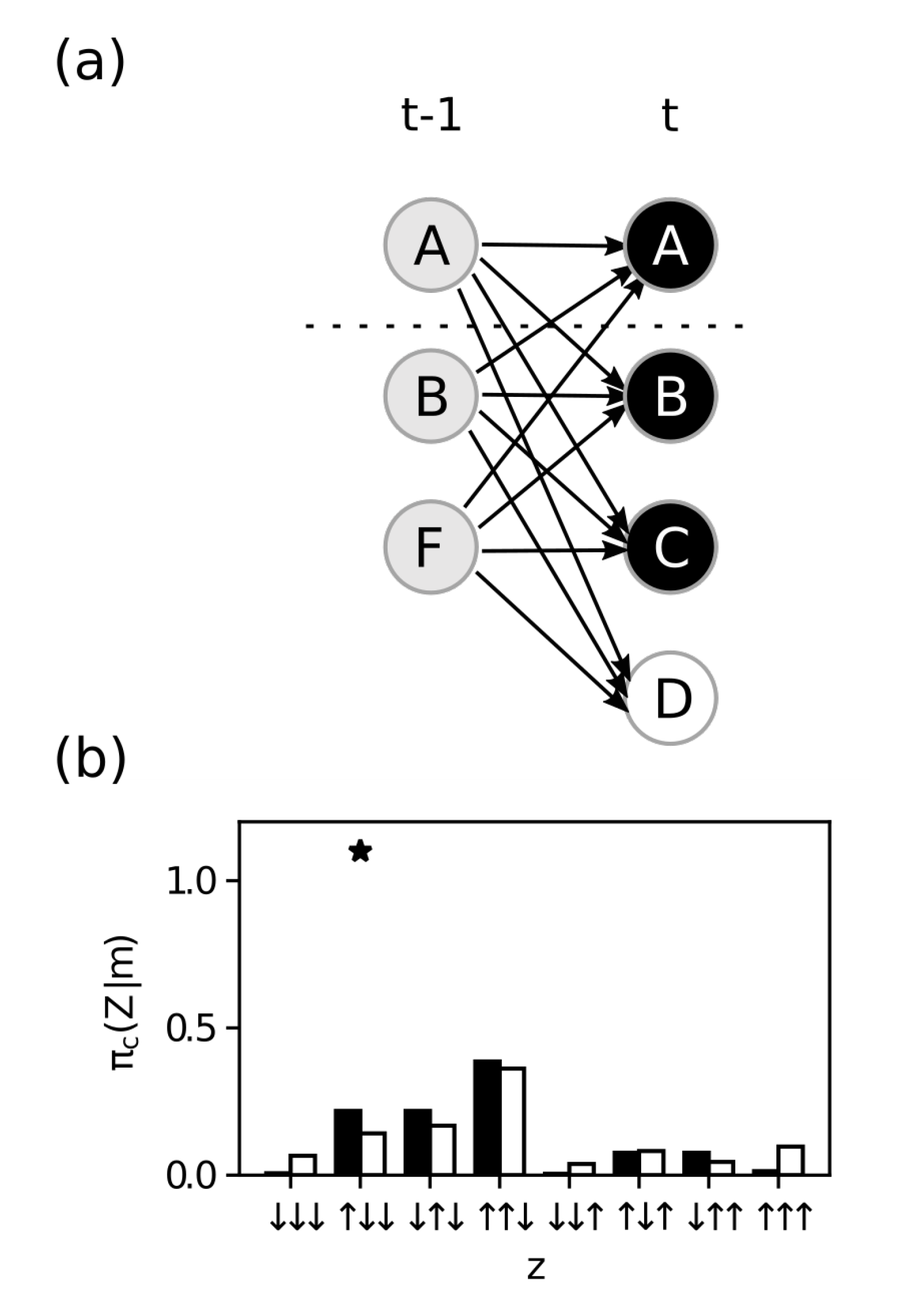
4.3. Maximal Integrated Information
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Cause and Effect Repertoires
Appendix A.1. Causal Marginalization
Appendix A.2. Partitioned Repertoires
Appendix B. Full Statement and Proof of Theorem 1
- Property I: Causality. Let . The difference is defined as , such that
- Property II: Intrinsicality. Let and . Then(a) expansion:(b) dilution:where and from Property I .
- Property III: Specificity. The difference must be state-specific, meaning there exists such that for all we have , where , and . More precisely, we definewhere f is continuous on K, analytic on and is analytic on J.
- AS1:
- such that is a strict maximum in Equation (A11),
- AS2:
- such that in Equation (A14),
- AS3:
- is never a strict maximum in Equation (A15),
- AS4:
- .
Appendix C. Comparison between ID and EMD

References
- Albantakis, L. Integrated information theory. In Beyond Neural Correlates of Consciousness; Overgaard, M., Mogensen, J., Kirkeby-Hinrup, A., Eds.; Routledge: London, UK, 2020; pp. 87–103. [Google Scholar]
- Tononi, G.; Boly, M.; Massimini, M.; Koch, C. Integrated information theory: From consciousness to its physical substrate. Nat. Rev. Neurosci. 2016, 17, 450–461. [Google Scholar] [CrossRef] [PubMed]
- Oizumi, M.; Albantakis, L.; Tononi, G. From the Phenomenology to the Mechanisms of Consciousness: Integrated Information Theory 3. 0. PLoS Comput Biol 2014, 10, e1003588. [Google Scholar] [CrossRef] [PubMed]
- Balduzzi, D.; Tononi, G. Integrated information in discrete dynamical systems: Motivation and theoretical framework. PLoS Comput. Biol. 2008, 4, e1000091. [Google Scholar] [CrossRef] [PubMed]
- Barbosa, L.; Marshall, W.; Streipert, S.; Albantakis, L.; Tononi, G. A measure for intrinsic information. Sci. Rep. 2020, 10, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Tononi, G. The Integrated Information Theory of Consciousness. In The Blackwell Companion to Consciousness; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2017; pp. 243–256. [Google Scholar]
- Albantakis, L.; Marshall, W.; Hoel, E.; Tononi, G. What caused what? A quantitative account of actual causation using dynamical causal networks. Entropy 2019, 21, 459. [Google Scholar]
- Tononi, G. Consciousness as integrated information: A provisional manifesto. Biol. Bull. 2008, 215, 216–242. [Google Scholar] [CrossRef] [PubMed]
- Marshall, W.; Albantakis, L.; Tononi, G. Black-boxing and cause-effect power. PLoS Comput. Biol. 2018, 14, e1006114. [Google Scholar] [CrossRef] [PubMed]
- Haun, A.; Tononi, G. Why Does Space Feel the Way it Does? Towards a Principled Account of Spatial Experience. Entropy 2019, 21, 1160. [Google Scholar]
- Albantakis, L.; Tononi, G. The Intrinsic Cause-Effect Power of Discrete Dynamical Systems—From Elementary Cellular Automata to Adapting Animats. Entropy 2015, 17, 5472–5502. [Google Scholar] [CrossRef]
- Albantakis, L.; Tononi, G. Causal Composition: Structural Differences among Dynamically Equivalent Systems. Entropy 2019, 21, 989. [Google Scholar] [CrossRef]
- Marshall, W.; Gomez-Ramirez, J.; Tononi, G. Integrated Information and State Differentiation. Conscious. Res. 2016, 7, 926. [Google Scholar]
- Gomez, J.D.; Mayner, W.G.P.; Beheler-Amass, M.; Tononi, G.; Albantakis, L. Computing Integrated Information (Φ) in Discrete Dynamical Systems with Multi-Valued Elements. Entropy 2021, 23, 6. [Google Scholar] [CrossRef] [PubMed]
- Csiszár, I. Axiomatic Characterizations of Information Measures. Entropy 2008, 10, 261–273. [Google Scholar] [CrossRef]
- Tononi, G. An information integration theory of consciousness. BMC Neurosci. 2004, 5, 42. [Google Scholar] [CrossRef] [PubMed]
- Kyumin, M. Exclusion and Underdetermined Qualia. Entropy 2019, 21, 405. [Google Scholar]
- Pearl, J. Causality; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Janzing, D.; Balduzzi, D.; Grosse-Wentrup, M.; Schölkopf, B. Quantifying causal influences. Ann. Stat. 2013, 41, 2324–2358. [Google Scholar] [CrossRef]
- Ebanks, B.; Sahoo, P.; Sander, W. Characterizations of Information Measures; World Scientific: Singapore, 1998. [Google Scholar]
- Krantz, S.G.; Parks, H.R. A Primer of Real Analytic Functions, 2nd ed.; Birkhäuser Advanced Texts Basler Lehrbücher; Birkhäuser: Basel, Switzerland, 2002. [Google Scholar]
- Aczél, J. Lectures on Functional Equations and Their Applications; Dover Publications: Mineola, NY, USA, 2006. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barbosa, L.S.; Marshall, W.; Albantakis, L.; Tononi, G. Mechanism Integrated Information. Entropy 2021, 23, 362. https://doi.org/10.3390/e23030362
Barbosa LS, Marshall W, Albantakis L, Tononi G. Mechanism Integrated Information. Entropy. 2021; 23(3):362. https://doi.org/10.3390/e23030362
Chicago/Turabian StyleBarbosa, Leonardo S., William Marshall, Larissa Albantakis, and Giulio Tononi. 2021. "Mechanism Integrated Information" Entropy 23, no. 3: 362. https://doi.org/10.3390/e23030362
APA StyleBarbosa, L. S., Marshall, W., Albantakis, L., & Tononi, G. (2021). Mechanism Integrated Information. Entropy, 23(3), 362. https://doi.org/10.3390/e23030362