Computing Integrated Information (Φ) in Discrete Dynamical Systems with Multi-Valued Elements
Abstract
1. Introduction
2. Theory and Pyphi Implementation
- Existence: the system must have cause-effect power—it must be able to take and make a difference.
- Intrinsicality: the system must have cause-effect power upon itself.
- Composition: the system must be composed of parts that have cause-effect power within the whole.
- Information: the system’s cause-effect power must be specific.
- Integration: the system’s cause-effect power must not be reducible to that of its parts.
- Exclusion: the system must specify a maximum of intrinsic cause-effect power.
3. Results
3.1. Comparison of Random Systems with Varying Numbers of Elements and States
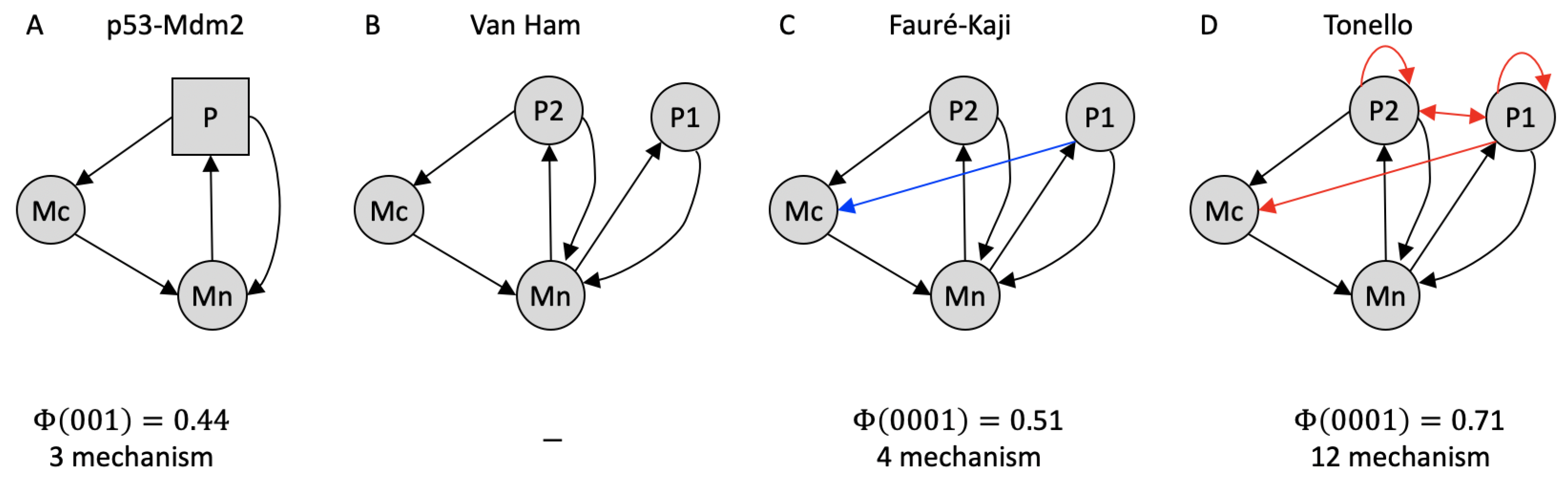
3.2. Model of Biological Example Systems with Non-Binary Elements
4. Discussion
5. Methods
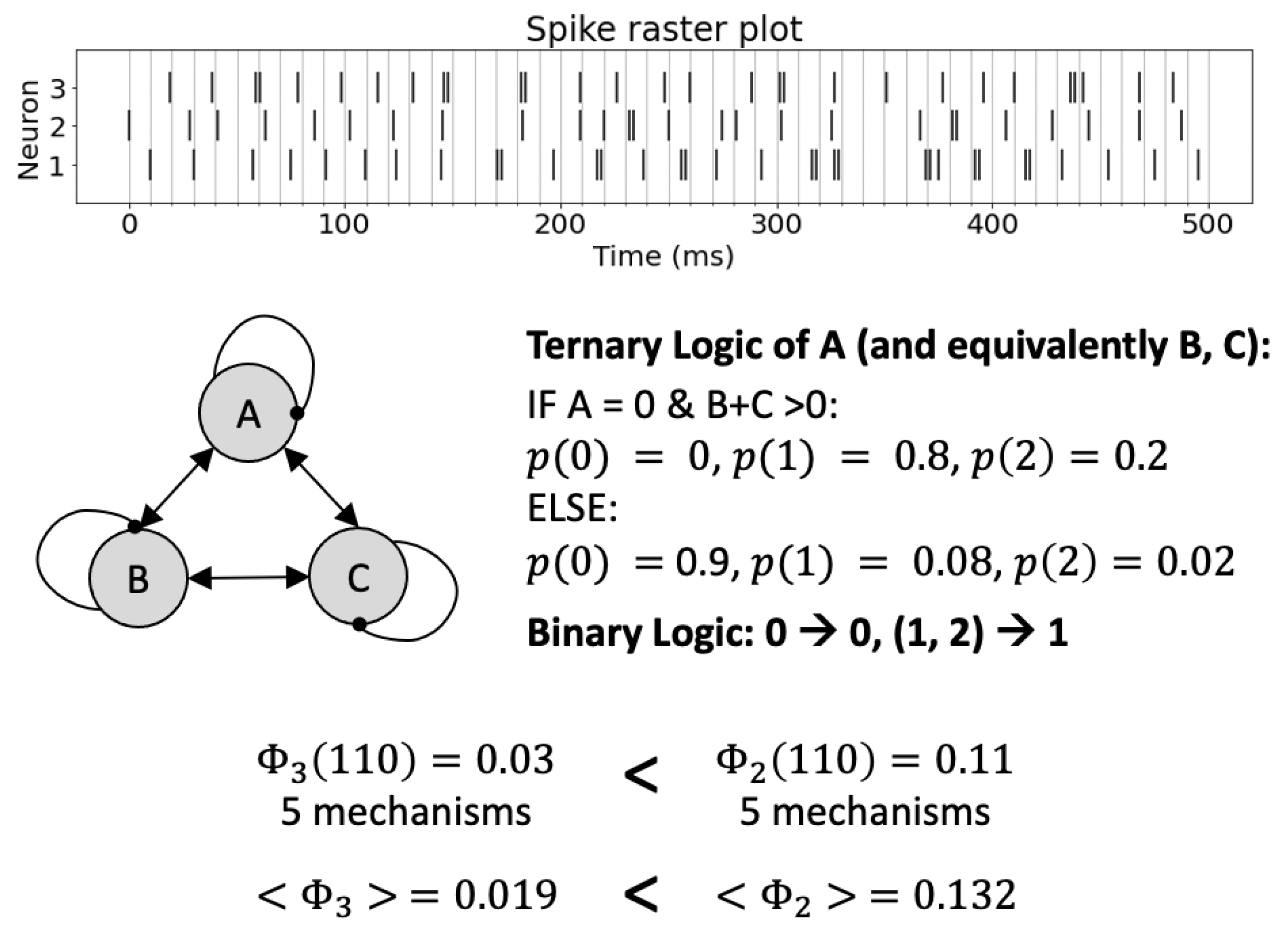
5.1. Non-Binary Implementation
5.2. Settings
5.3. Overview of the Algorithm in Pseudocode
| Algorithm 1. Python-like Pseudocode describing the functions used in the extended non-binary PyPhi. |
    |
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Thomas, R.; D’Ari, R. Biological Feedback; CRC Press: Boca Raton, FL, USA, 1990. [Google Scholar]
- Abou-Jaoudé, W.; Traynard, P.; Monteiro, P.T.; Saez-Rodriguez, J.; Helikar, T.; Thieffry, D.; Chaouiya, C. Logical Modeling and Dynamical Analysis of Cellular Networks. Front. Genet. 2016, 7, 94. [Google Scholar] [CrossRef] [PubMed]
- Thomas, R. Boolean formalization of genetic control circuits. J. Theor. Biol. 1973, 42, 563–585. [Google Scholar] [CrossRef]
- Thomas, R. Regulatory networks seen as asynchronous automata: A logical description. J. Theor. Biol. 1991, 153, 1–23. [Google Scholar] [CrossRef]
- Didier, G.; Remy, E.; Chaouiya, C. Mapping multivalued onto Boolean dynamics. J. Theor. Biol. 2011, 270, 177–184. [Google Scholar] [CrossRef][Green Version]
- Dayan, P.; Abbott, L.F. Theoretical Neuroscience—Computational and Mathematical Modeling of Neural Systems; MIT Press: Cambridge, MA, USA, 2000; pp. 1689–1699. [Google Scholar] [CrossRef]
- Hindmarsh, J.L.; Rose, R.M. A model of neuronal bursting using three coupled first order differential equations. Proc. R. Soc. London. Ser. Contain. Pap. Biol. Character. R. Soc. 1984, 221, 87–102. [Google Scholar]
- Aizenberg, I.N.; Naum, N.; Aizenberg, J.V. Multiple-Valued Threshold Logic and Multi-Valued Neurons. In Multi-Valued and Universal Binary Neurons; Springer: Berlin/Heidelberg, Germany, 2000; pp. 25–80. [Google Scholar]
- Prados, D.; Kak, S. Non-binary neural networks. In Advances in Computing and Control; Springer: Berlin/Heidelberg, Germany, 2006; pp. 97–104. [Google Scholar] [CrossRef]
- Hoel, E.P.; Albantakis, L.; Tononi, G. Quantifying causal emergence shows that macro can beat micro. Proc. Nalt. Acad. Sci. USA 2013, 110, 19790–19795. [Google Scholar] [CrossRef]
- Van Ham, P. How to Deal with Variables with More Than Two Levels; Springer: Berlin/Heidelberg, Germany, 1979; pp. 326–343. [Google Scholar] [CrossRef]
- Fauré, A.; Kaji, S. A circuit-preserving mapping from multilevel to Boolean dynamics. J. Theor. Biol. 2018, 440, 71–79. [Google Scholar] [CrossRef]
- Tonello, E. On the conversion of multivalued to Boolean dynamics. Discret. Appl. Math. 2019, 259, 193–204. [Google Scholar] [CrossRef]
- Oizumi, M.; Albantakis, L.; Tononi, G. From the Phenomenology to the Mechanisms of Consciousness: Integrated Information Theory 3.0. PLoS Comput. Biol. 2014, 10, e1003588. [Google Scholar] [CrossRef]
- Albantakis, L.; Marshall, W.; Hoel, E.; Tononi, G. What caused what? A quantitative account of actual causation using dynamical causal networks. Entropy 2019, 21, 459. [Google Scholar] [CrossRef]
- Albantakis, L.; Tononi, G. Causal Composition: Structural Differences among Dynamically Equivalent Systems. Entropy 2019, 21, 989. [Google Scholar] [CrossRef]
- Tononi, G. An information integration theory of consciousness. BMC Neurosci. 2004, 5, 42. [Google Scholar] [CrossRef] [PubMed]
- Tononi, G. Integrated information theory. Scholarpedia 2015, 10, 4164. [Google Scholar] [CrossRef]
- Tononi, G.; Boly, M.; Massimini, M.; Koch, C. Integrated information theory: From consciousness to its physical substrate. Nat. Rev. Neurosci. 2016, 17, 450–461. [Google Scholar] [CrossRef] [PubMed]
- Albantakis, L. Integrated information theory. In Beyond Neural Correlates of Consciousness; Overgaard, M., Mogensen, J., Kirkeby-Hinrup, A., Eds.; Routledge: Oxford, UK, 2020; pp. 87–103. [Google Scholar] [CrossRef]
- Albantakis, L. A Tale of Two Animats: What Does It Take to Have Goals? Springer: Berlin/Heidelberg, Germany, 2018; pp. 5–15. [Google Scholar] [CrossRef][Green Version]
- Marshall, W.; Kim, H.; Walker, S.I.; Tononi, G.; Albantakis, L. How causal analysis can reveal autonomy in models of biological systems. Philos. Trans. Ser. Math. Phys. Eng. Sci. 2017, 375, 20160358. [Google Scholar] [CrossRef] [PubMed]
- Marshall, W.; Gomez-Ramirez, J.; Tononi, G. Integrated Information and State Differentiation. Front. Psychol. 2016, 7, 926. [Google Scholar] [CrossRef] [PubMed]
- Albantakis, L.; Tononi, G. The Intrinsic Cause-Effect Power of Discrete Dynamical Systems—From Elementary Cellular Automata to Adapting Animats. Entropy 2015, 17, 5472–5502. [Google Scholar] [CrossRef]
- Aguilera, M. Scaling Behaviour and Critical Phase Transitions in Integrated Information Theory. Entropy 2019, 21, 1198. [Google Scholar] [CrossRef]
- Popiel, N.J.; Khajehabdollahi, S.; Abeyasinghe, P.M.; Riganello, F.; Nichols, E.S.; Owen, A.M.; Soddu, A. The Emergence of Integrated Information, Complexity, and ‘Consciousness’ at Criticality. Entropy 2020, 22, 339. [Google Scholar] [CrossRef]
- Albantakis, L.; Hintze, A.; Koch, C.; Adami, C.; Tononi, G. Evolution of Integrated Causal Structures in Animats Exposed to Environments of Increasing Complexity. PLoS Comput. Biol. 2014, 10, e1003966. [Google Scholar] [CrossRef]
- Oizumi, M.; Amari, S.i.; Yanagawa, T.; Fujii, N.; Tsuchiya, N. Measuring Integrated Information from the Decoding Perspective. PLoS Comput. Biol. 2016, 12, e1004654. [Google Scholar] [CrossRef] [PubMed]
- Hoel, E.P.; Albantakis, L.; Marshall, W.; Tononi, G. Can the macro beat the micro? Integrated information across spatiotemporal scales. Neurosci. Conscious. 2016, 2016. [Google Scholar] [CrossRef] [PubMed]
- Marshall, W.; Albantakis, L.; Tononi, G. Black-boxing and cause-effect power. PLoS Comput. Biol. 2018, 14, e1006114. [Google Scholar] [CrossRef]
- Mayner, W.G.; Marshall, W.; Albantakis, L.; Findlay, G.; Marchman, R.; Tononi, G. PyPhi: A toolbox for integrated information theory. PLoS Comput. Biol. 2018, 14, e1006343. [Google Scholar] [CrossRef] [PubMed]
- Haun, A.; Tononi, G. Why Does Space Feel the Way it Does? Towards a Principled Account of Spatial Experience. Entropy 2019, 21, 1160. [Google Scholar] [CrossRef]
- Nilsen, A.S.; Juel, B.E.; Marshall, W.; Storm, J.F. Evaluating Approximations and Heuristic Measures of Integrated Information. Entropy 2019, 21, 525. [Google Scholar] [CrossRef]
- Tononi, G.; Sporns, O. Measuring information integration. BMC Neurosci. 2003, 4, 1–20. [Google Scholar] [CrossRef]
- Abou-Jaoudé, W.; Ouattara, D.A.; Kaufman, M. From structure to dynamics: Frequency tuning in the p53–Mdm2 network: I. Logical approach. J. Theor. Biol. 2009, 258, 561–577. [Google Scholar] [CrossRef]
- Langton, C. Studying artificial life with cellular automata. Phys. Nonlinear Phenom. 1986, 22, 120–149. [Google Scholar] [CrossRef]
- Ermentrout, G.B.; Edelstein-Keshet, L. Cellular automata approaches to biological modeling. J. Theor. Biol. 1993, 160, 97–133. [Google Scholar] [CrossRef]
- Gottwald, S. Many-Valued Logic And Fuzzy Set Theory; Springer: Berlin/Heidelberg, Germany, 1999; pp. 5–89. [Google Scholar] [CrossRef]
- Cintula, P.; Hájek, P.; Noguera, C. Handbook of Mathematical Fuzzy Logic (in 2 Volumes); College Publications: London, UK, 2011. [Google Scholar]
- Israeli, N.; Goldenfeld, N. Coarse-graining of cellular automata, emergence, and the predictability of complex systems. Phys. Rev. E 2006, 73, 026203. [Google Scholar] [CrossRef] [PubMed]
- Hanson, J.R.; Walker, S.I. Integrated Information Theory and Isomorphic Feed-Forward Philosophical Zombies. Entropy 2019, 21, 1073. [Google Scholar] [CrossRef]
- Barbosa, L.S.; Marshall, W.; Streipert, S.; Albantakis, L.; Tononi, G. A measure for intrinsic information. Sci. Rep. 2020, 10, 18803. [Google Scholar] [CrossRef]
- Krohn, S.; Ostwald, D. Computing integrated information. Neurosci. Conscious. 2017, 2017. [Google Scholar] [CrossRef] [PubMed]
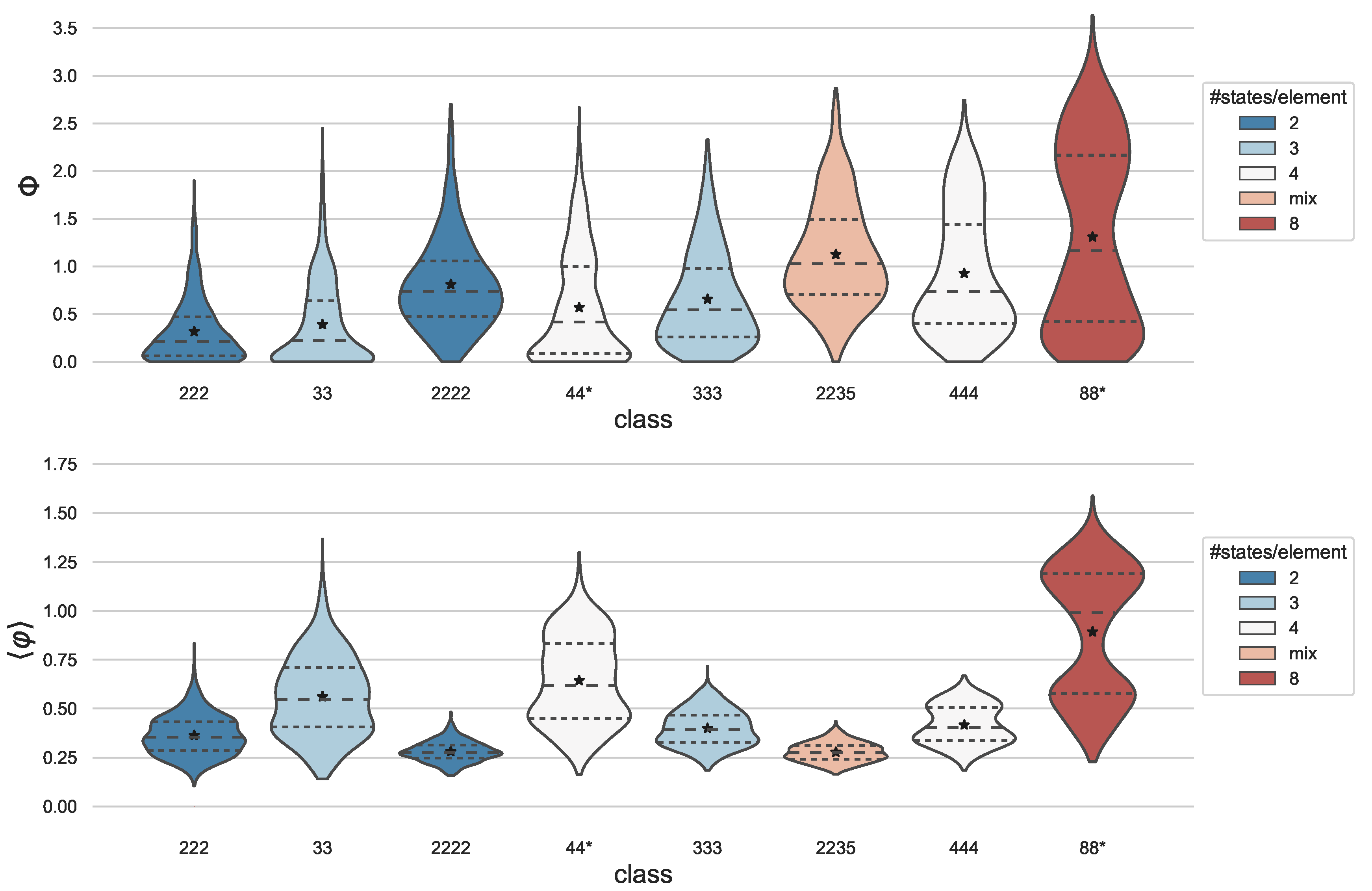
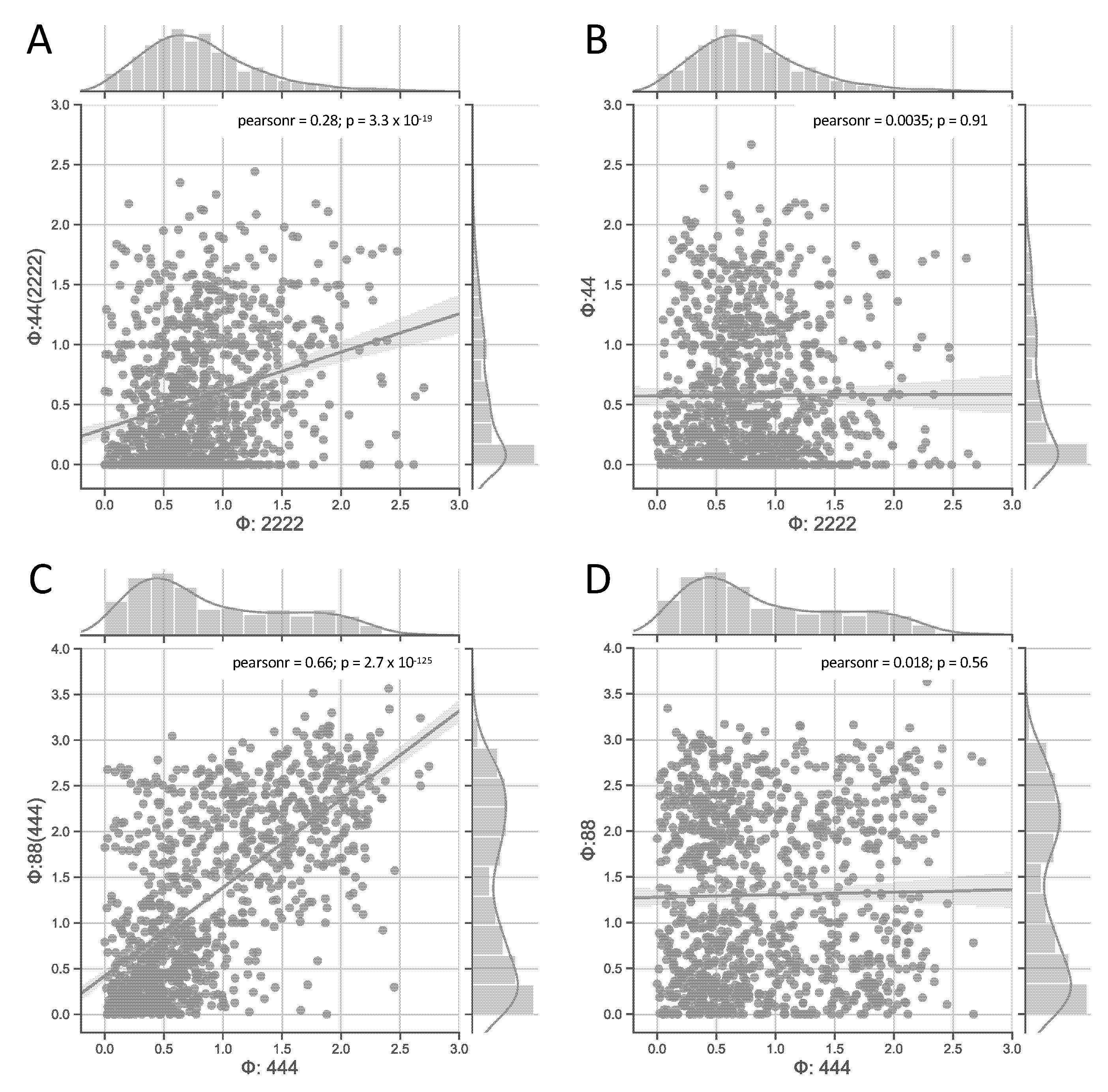

| Class | 222 | 33 | 2222 | 44(2222) | 44 | 333 | 2235 | 444 | 88(444) | 88 |
|---|---|---|---|---|---|---|---|---|---|---|
| #Nodes | 3 | 2 | 4 | 2 | 2 | 3 | 4 | 3 | 2 | 2 |
| #States (total) | 8 | 9 | 16 | 16 | 16 | 27 | 60 | 64 | 64 | 64 |
| Class | 222 | 33 | 2222 | 44* | 333 | 2235 | 444 | 88* |
|---|---|---|---|---|---|---|---|---|
| (max. #distinctions) | (7) | (3) | (15) | (3) | (7) | (15) | (7) | (3) |
| 〈#distinctions〉 | 5.35 | 2.71 | 13.81 | 2.91 | 7. | 14.95 | 7. | 3. |
| % of max | 76% | 90% | 92% | 97% | 100% | 100% | 100% | 100% |
| Multi-Valued | Binary | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Van Ham | Fauré & Kaji | Tonello | ||||||||||||||||||||
| t | t+1 | t | t+1 | t+1 | t+1 | |||||||||||||||||
| P | Mc | Mn | P | Mc | Mn | P1 | P2 | Mc | Mn | P1 | P2 | Mc | Mn | P1 | P2 | Mc | Mn | P1 | P2 | Mc | Mn | |
| 0 | 0 | 0 | 2 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | = | 1 | 0 | 0 | 1 | ||||
| 1 | 0 | 0 | 2 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | = | = | |||||||
| 0 | 1 | 0 | 0 | - | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | ||||||||||
| 2 | 0 | 0 | 2 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | = | = | |||||||
| 0 | 1 | 0 | 2 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | = | 1 | 0 | 0 | 1 | ||||
| 1 | 1 | 0 | 2 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | = | = | |||||||
| 0 | 1 | 1 | 0 | - | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | ||||||||||
| 2 | 1 | 0 | 2 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | = | = | |||||||
| 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | = | = | |||||||
| 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | = | = | |||||||
| 0 | 1 | 0 | 1 | - | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||||||||
| 2 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | = | 1 | 0 | 1 | 0 | ||||
| 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | = | = | |||||||
| 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | = | = | |||||||
| 0 | 1 | 1 | 1 | - | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | ||||||||||
| 2 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | = | 1 | 0 | 1 | 1 | ||||
| Class | 32 | 43 | 332 | |
|---|---|---|---|---|
| Fauré-Kaji | r | 0.56 | 0.35 | 0.29 |
| method | p-value | ≈0 | <0.001 | <0.005 |
| Tonello | r | 0.24 | 0.18 | 0.15 |
| method | p-value | 0.015 | 0.08 | 0.14 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gomez, J.D.; Mayner, W.G.P.; Beheler-Amass, M.; Tononi, G.; Albantakis, L. Computing Integrated Information (Φ) in Discrete Dynamical Systems with Multi-Valued Elements. Entropy 2021, 23, 6. https://doi.org/10.3390/e23010006
Gomez JD, Mayner WGP, Beheler-Amass M, Tononi G, Albantakis L. Computing Integrated Information (Φ) in Discrete Dynamical Systems with Multi-Valued Elements. Entropy. 2021; 23(1):6. https://doi.org/10.3390/e23010006
Chicago/Turabian StyleGomez, Juan D., William G. P. Mayner, Maggie Beheler-Amass, Giulio Tononi, and Larissa Albantakis. 2021. "Computing Integrated Information (Φ) in Discrete Dynamical Systems with Multi-Valued Elements" Entropy 23, no. 1: 6. https://doi.org/10.3390/e23010006
APA StyleGomez, J. D., Mayner, W. G. P., Beheler-Amass, M., Tononi, G., & Albantakis, L. (2021). Computing Integrated Information (Φ) in Discrete Dynamical Systems with Multi-Valued Elements. Entropy, 23(1), 6. https://doi.org/10.3390/e23010006





