Discrete Versions of Jensen–Fisher, Fisher and Bayes–Fisher Information Measures of Finite Mixture Distributions
Abstract
1. Introduction
2. Discrete Version of Jensen-Fisher Information
- (i)
- If is log-concave, then
- (ii)
- If is log-convex, then
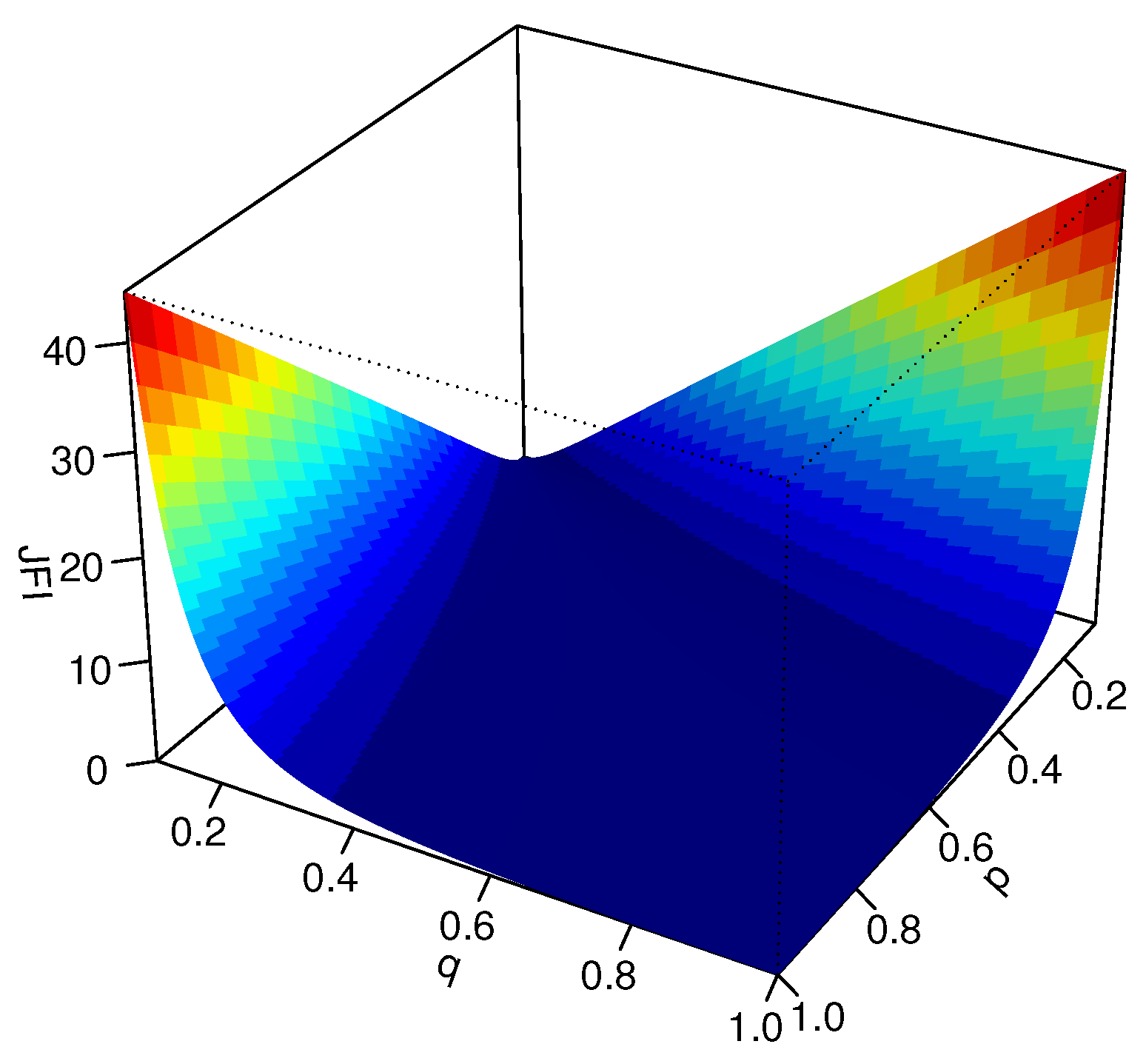
2.1. Discrete Jensen–Fisher Information Based on Two Probability Mass Functions P and Q
2.2. Discrete Jensen–Fisher Information Based on n Probability Mass Functions
3. Fisher Information of a Finite Mixture Probability Mass Function
4. Bayes–Fisher Information of a Finite Mixture Probability Mass Function
- (i)
- The Bayes–Fisher information for , under prior with PMF , is
- (ii)
- The Bayes-Fisher information for parameter , under prior with PMF , is
5. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Fisher, R.A. Tests of significance in harmonic analysis. Proc. R. Soc. Lond. A Math. Phys. Sci. 1929, 125, 54–59. [Google Scholar]
- Zegers, P. Fisher information properties. Entropy 2015, 17, 4918–4939. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Stepanov, A. On the Fisher information in record data. Stat. Probab. Lett. 2006, 76, 537–545. [Google Scholar] [CrossRef]
- Lin, J. Divergence measures based on the Shannon entropy. IEEE Trans. Inf. Theory 1991, 37, 145–151. [Google Scholar] [CrossRef]
- Sánchez-Moreno, P.; Zarzo, A.; Dehesa, J.S. Jensen divergence based on Fisher’s information. J. Phys. A Math. Theor. 2012, 45, 125305. [Google Scholar] [CrossRef]
- Mehrali, Y.; Asadi, M.; Kharazmi, O. A Jensen-Gini measure of divergence with application in parameter estimation. Metron 2018, 76, 115–131. [Google Scholar] [CrossRef]
- Martin, M.T.; Pennini, F.; Plastino, A. Fisher’s information and the analysis of complex signals. Phys. Lett. A 1999, 256, 173–180. [Google Scholar] [CrossRef]
- Ramírez-Pacheco, J.; Torres-Román, D.; Rizo-Dominguez, L.; Trejo-Sanchez, J.; Manzano-Pinzón, F. Wavelet Fisher’s information measure of 1/fα signals. Entropy 2011, 13, 1648–1663. [Google Scholar] [CrossRef]
- Ramírez-Pacheco, J.; Torres-Román, D.; Argaez-Xool, J.; Rizo-Dominguez, L.; Trejo-Sanchez, J.; Manzano-Pinzón, F. Wavelet q-Fisher information for scaling signal analysis. Entropy 2012, 14, 1478–1500. [Google Scholar] [CrossRef]
- Johnson, O. Information Theory and the Central Limit Theorem; World Scientific Publishers: Singapore, 2004. [Google Scholar]
- Contreras-Reyes, J.E.; Cortés, D.D. Bounds on Rényi and Shannon entropies for finite mixtures of multivariate skew-normal distributions: Application to swordfish (Xiphias gladius linnaeus). Entropy 2017, 18, 382. [Google Scholar] [CrossRef]
- Abid, S.H.; Quaez, U.J.; Contreras-Reyes, J.E. An information-theoretic approach for multivariate skew-t distributions and applications. Mathematics 2021, 9, 146. [Google Scholar] [CrossRef]
- Kolchinsky, A.; Tracey, B.D. Estimating mixture entropy with pairwise distances. Entropy 2017, 19, 361. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Broniatowski, M. Minimum divergence estimators, Maximum likelihood and the generalized bootstrap. Entropy 2021, 23, 185. [Google Scholar] [CrossRef] [PubMed]
- Cover, T.; Thomas, J. Elements of Information Theory; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kharazmi, O.; Balakrishnan, N. Discrete Versions of Jensen–Fisher, Fisher and Bayes–Fisher Information Measures of Finite Mixture Distributions. Entropy 2021, 23, 363. https://doi.org/10.3390/e23030363
Kharazmi O, Balakrishnan N. Discrete Versions of Jensen–Fisher, Fisher and Bayes–Fisher Information Measures of Finite Mixture Distributions. Entropy. 2021; 23(3):363. https://doi.org/10.3390/e23030363
Chicago/Turabian StyleKharazmi, Omid, and Narayanaswamy Balakrishnan. 2021. "Discrete Versions of Jensen–Fisher, Fisher and Bayes–Fisher Information Measures of Finite Mixture Distributions" Entropy 23, no. 3: 363. https://doi.org/10.3390/e23030363
APA StyleKharazmi, O., & Balakrishnan, N. (2021). Discrete Versions of Jensen–Fisher, Fisher and Bayes–Fisher Information Measures of Finite Mixture Distributions. Entropy, 23(3), 363. https://doi.org/10.3390/e23030363






