Higher Dimensional Rotating Black Hole Solutions in Quadratic f(R) Gravitational Theory and the Conserved Quantities
Abstract
1. Introduction
2. Basics of Gravitational Theory
3. Rotating Black Hole Solutions
4. Total Conserved Charge
5. Regularization with Relocalization for the Conserved Charge
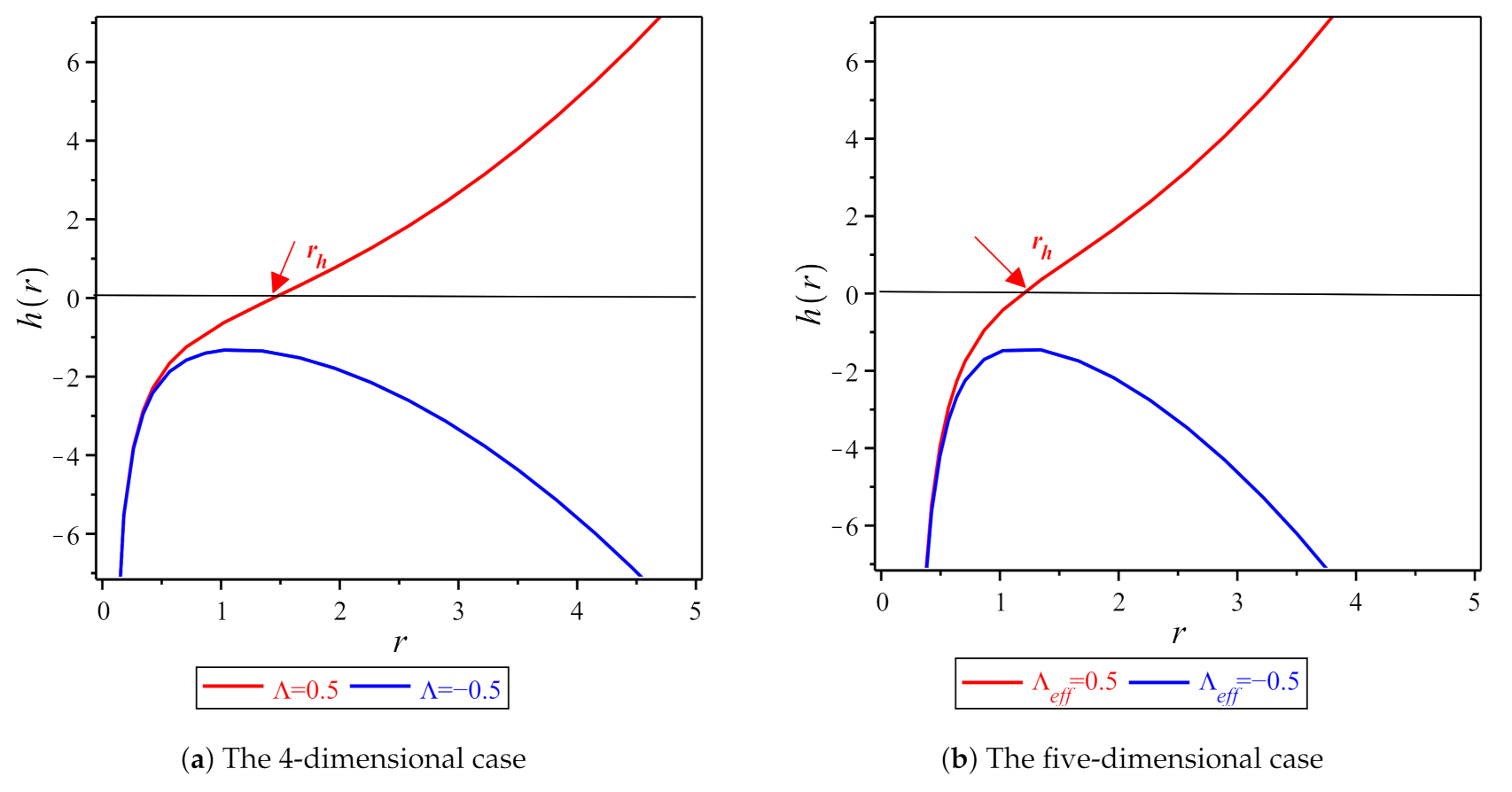
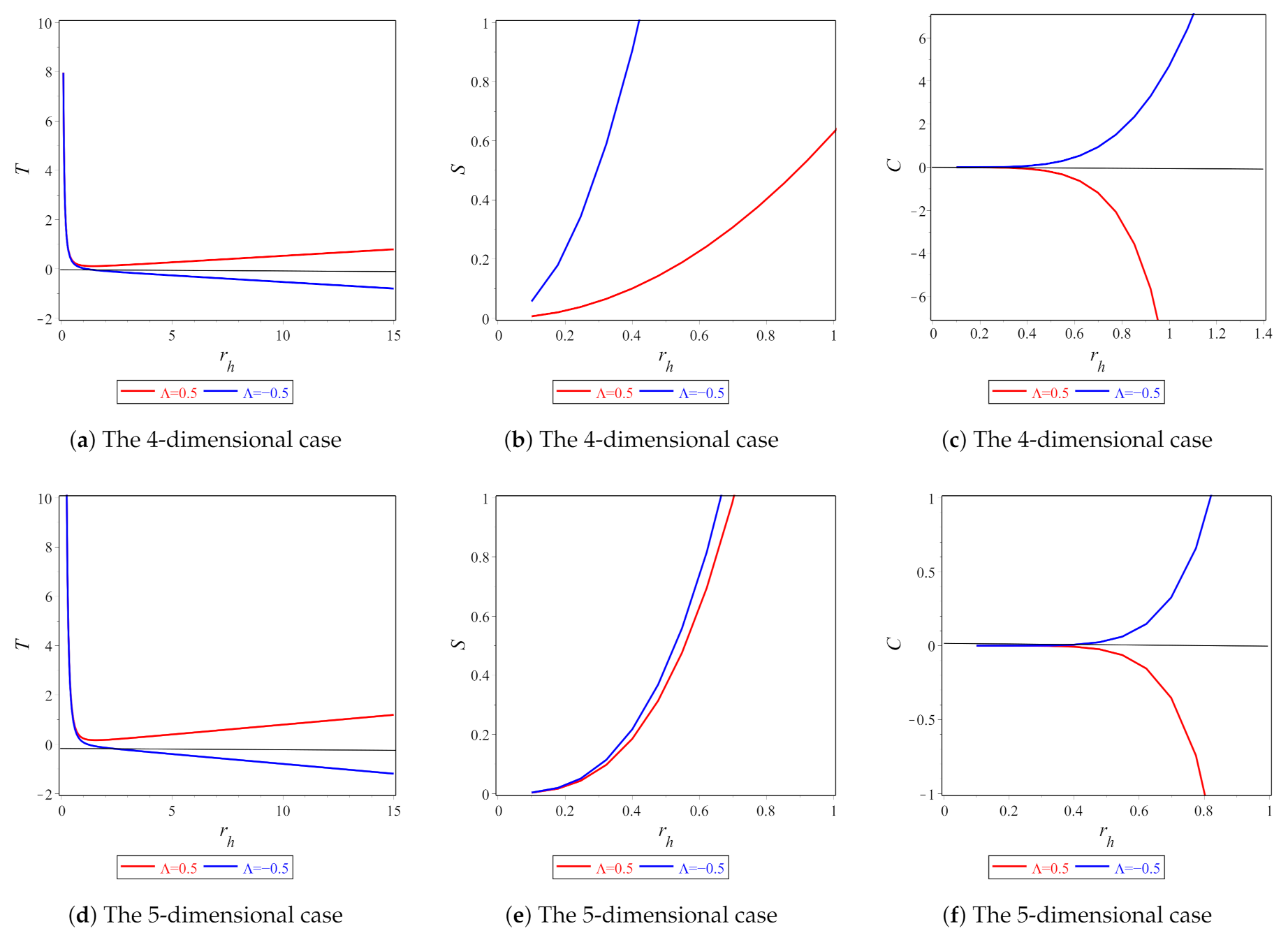
6. Thermodynamics for Black Holes
7. Summary and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Symbols Used in the Calculations of Conserved Quantities
Appendix B. Non-Zero Components for the Christoffel Symbols of the Second Kind and Ricci Curvature Tensor
References
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gillil, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Omega and Lambda from 42 high redshift supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Armitage-Caplan, C.; Arnaud, M.; Ashdown, M.; Atrio-Barandela, F.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; et al. Planck 2013 results. XVI. Cosmological parameters. Astron. Astrophys. 2014, 571, A16. [Google Scholar] [CrossRef]
- Spergel, D.N.; Bean, R.; Doré, O.; Nolta, M.R.; Bennett, C.L.; Dunkley, J.; Hinshaw, G.; Jarosik, N.E.; Komatsu, E.; Page, L.; et al. Wilkinson Microwave Anisotropy Probe (WMAP) three year results: Implications for cosmology. Astrophys. J. Suppl. 2007, 170, 377. [Google Scholar] [CrossRef]
- Jain, B.; Taylor, A. Cross-correlation tomography: Measuring dark energy evolution with weak lensing. Phys. Rev. Lett. 2003, 91, 141302. [Google Scholar] [CrossRef] [PubMed]
- Cole, S.; Percival, W.J.; Peacock, J.A.; Norberg, P.; Baugh, C.M.; Frenk, C.S.; Baldry, I.; Bland-Hawthorn, J.; Bridges, T.; Cannon, R.; et al. The 2dF Galaxy Redshift Survey: Power-spectrum analysis of the final dataset and cosmological implications. Mon. Not. Roy. Astron. Soc. 2005, 362, 505–534. [Google Scholar] [CrossRef]
- Eisenstein, D.J.; Zehavi, I.; Hogg, D.W.; Scoccimarro, R.; Blanton, M.R.; Nichol, R.C.; Scranton, R.; Seo, H.J.; Tegmark, M.; Zheng, Z.; et al. Detection of the Baryon Acoustic Peak in the Large-Scale Correlation Function of SDSS Luminous Red Galaxies. Astrophys. J. 2005, 633, 560–574. [Google Scholar] [CrossRef]
- Percival, W.J.; Reid, B.A.; Eisenstein, D.J.; Bahcall, N.A.; Budavari, T.; Frieman, J.A.; Fukugita, M.; Gunn, J.E.; Ivezić, Ž.; Knapp, G.R.; et al. Baryon acoustic oscillations in the Sloan Digital Sky Survey Data Release 7 galaxy sample. Mon. Not. Roy. Astron. Soc. 2010, 401, 2148–2168. [Google Scholar] [CrossRef]
- Padmanabhan, N.; Xu, X.; Eisenstein, D.J.; Scalzo, R.; Cuesta, A.J.; Mehta, K.T.; Kazin, E. A 2 per cent distance to z=0.35 by reconstructing baryon acoustic oscillations - I. Methods and application to the Sloan Digital Sky Survey. Mon. Not. Roy. Astron. Soc. 2012, 427, 2132–2145. [Google Scholar] [CrossRef]
- Blake, C.; Kazin, E.A.; Beutler, F.; Davis, T.M.; Parkinson, D.; Brough, S.; Colless, M.; Contreras, C.; Couch, W.; Croom, S.; et al. The WiggleZ Dark Energy Survey: Mapping the distance-redshift relation with baryon acoustic oscillations. Mon. Not. Roy. Astron. Soc. 2011, 418, 1707–1724. [Google Scholar] [CrossRef]
- Manera, M.; Scoccimarro, R.; Percival, W.J.; Samushia, L.; McBride, C.K.; Ross, A.J.; Sheth, R.K.; White, M.; Reid, B.A.; Sánchez, A.G.; et al. The clustering of galaxies in the SDSS-III Baryon Oscillation Spectroscopic Survey: A large sample of mock galaxy catalogues. Mon. Not. Roy. Astron. Soc. 2013, 428, 1036–1054. [Google Scholar] [CrossRef]
- Simon, J.; Verde, L.; Jimenez, R. Constraints on the redshift dependence of the dark energy potential. Phys. Rev. D 2005, 71, 123001. [Google Scholar] [CrossRef]
- Stern, D.; Jimenez, R.; Verde, L.; Kamionkowski, M.; Stanford, S.A. Cosmic Chronometers: Constraining the Equation of State of Dark Energy. I: H(z) Measurements. JCAP 2010, 1002, 8. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, H.; Yuan, S.; Zhang, T.J.; Sun, Y.C. Four new observational H(z) data from luminous red galaxies in the Sloan Digital Sky Survey data release seven. Res. Astron. Astrophys. 2014, 14, 1221–1233. [Google Scholar] [CrossRef]
- Blake, C.; Glazebrook, K.; Davis, T.M.; Brough, S.; Colless, M.; Contreras, C.; Couch, W.; Croom, S.; Drinkwater, M.J.; Forster, K.; et al. The WiggleZ Dark Energy Survey: Measuring the cosmic expansion history using the Alcock-Paczynski test and distant supernovae. Mon. Not. Roy. Astron. Soc. 2011, 418, 1725–1735. [Google Scholar] [CrossRef]
- Chuang, C.H.; Wang, Y. Modeling the Anisotropic Two-Point Galaxy Correlation Function on Small Scales and Improved Measurements of H(z), DA(z), and β(z) from the Sloan Digital Sky Survey DR7 Luminous Red Galaxies. Mon. Not. Roy. Astron. Soc. 2013, 435, 255–262. [Google Scholar] [CrossRef]
- Moresco, M.; Cimatti, A.; Jimenez, R.; Pozzetti, L.; Zamorani, G.; Bolzonella, M.; Dunlop, J.; Lamareille, F.; Mignoli, M.; Pearce, H.; et al. Improved constraints on the expansion rate of the Universe up to z 1.1 from the spectroscopic evolution of cosmic chronometers. JCAP 2012, 1208, 6. [Google Scholar] [CrossRef]
- Hawkins, E.; Maddox, S.; Cole, S.; Lahav, O.; Madgwick, D.S.; Norberg, P.; Peacock, J.A.; Baldry, I.K.; Baugh, C.M.; Bland-Hawthorn, J.; et al. The 2dF Galaxy Redshift Survey: Correlation functions, peculiar velocities and the matter density of the Universe. Mon. Not. R. Astron. Soc. 2003, 346, 78–96. [Google Scholar] [CrossRef]
- Tegmark, M.; Strauss, M.A.; Blanton, M.R.; Abazajian, K.; Dodelson, S.; Sandvik, H.; Wang, X.; Weinberg, D.H.; Zehavi, I.; Bahcall, N.A.; et al. Cosmological parameters from SDSS and WMAP. Phys. Rev. D 2004, 69, 103501. [Google Scholar] [CrossRef]
- Weinberg, S. The cosmological constant problem. Rev. Mod. Phys. 1989, 61, 1–23. [Google Scholar] [CrossRef]
- Nashed, G.G.L.; Bamba, K. Spherically symmetric charged black hole in conformal teleparallel equivalent of general relativity. JCAP 2018, 1809, 20. [Google Scholar] [CrossRef]
- Ferraro, R.; Fiorini, F. Modified teleparallel gravity: Inflation without an inflaton. Phys. Rev. D 2007, 75, 084031. [Google Scholar] [CrossRef]
- Ferraro, R.; Fiorini, F. Born-Infeld gravity in Weitzenböck spacetime. Phys. Rev. D 2008, 78, 124019. [Google Scholar] [CrossRef]
- Bengochea, G.R.; Ferraro, R. Dark torsion as the cosmic speed-up. Phys. Rev. D 2009, 79, 124019. [Google Scholar] [CrossRef]
- Li, B.; Sotiriou, T.P.; Barrow, J.D. Large-scale structure in f(T) gravity. Phys. Rev. D 2011, 83, 104017. [Google Scholar] [CrossRef]
- Nashed, G.L. FRW in quadratic form of f(T) gravitational theories. Gen. Rel. Grav. 2015, 47, 75. [Google Scholar] [CrossRef]
- Li, B.; Sotiriou, T.P.; Barrow, J.D. f(T) gravity and local Lorentz invariance. Phys. Rev. D 2011, 83, 064035. [Google Scholar] [CrossRef]
- Nashed, G.G.L. A special exact spherically symmetric solution in f(T) gravity theories. Gen. Rel. Grav. 2013, 45, 1887–1899. [Google Scholar] [CrossRef]
- Awad, A.; Nashed, G. Generalized teleparallel cosmology and initial singularity crossing. JCAP 2017, 1702, 46. [Google Scholar] [CrossRef]
- Nashed, G.G.L. Spherically symmetric charged-dS solution in f(T) gravity theories. Phys. Rev. 2013, D88, 104034. [Google Scholar] [CrossRef]
- Awad, A.M.; Capozziello, S.; Nashed, G.G.L. D-dimensional charged Anti-de-Sitter black holes in f(T) gravity. JHEP 2017, 7, 136. [Google Scholar] [CrossRef]
- Nashed, G.G.L.; El Hanafy, W. Analytic rotating black hole solutions in N-dimensional f(T) gravity. Eur. Phys. J. 2017, 77, 90. [Google Scholar] [CrossRef]
- Capozziello, S.; Gonzalez, P.A.; Saridakis, E.N.; Vasquez, Y. Exact charged black-hole solutions in D-dimensional f(T) gravity: Torsion vs. curvature analysis. J. High Energy Phys. 2013, 2, 39. [Google Scholar] [CrossRef]
- Kallosh, R.; Quevedo, F.; Uranga, A.M. String Theory Realizations of the Nilpotent Goldstino. J. High Energy Phys. 2015, 12, 39. [Google Scholar] [CrossRef]
- Hendi, S.H.; Dehghani, A. Thermodynamics of third-order Lovelock-AdS black holes in the presence of Born-Infeld type nonlinear electrodynamics. Phys. Rev. D 2015, 91, 064045. [Google Scholar] [CrossRef]
- Kofinas, G.; Papantonopoulos, E.; Saridakis, E.N. Modified Brans–Dicke cosmology with matter-scalar field interaction. Class. Quant. Grav. 2016, 33, 155004. [Google Scholar] [CrossRef]
- Guth, A.H. Inflationary universe: A possible solution to the horizon and flatness problems. Phys. Rev. D 1981, 23, 347–356. [Google Scholar] [CrossRef]
- Pogosian, L.; Silvestri, A. Pattern of growth in viable f(R) cosmologies. Phys. Rev. D 2008, 77, 23503. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: From f(R) theory to Lorentz non-invariant models. Phys. Rept. 2011, 505, 59–144. [Google Scholar] [CrossRef]
- Capozziello, S.; De Laurentis, M. Extended Theories of Gravity. Phys. Rept. 2011, 509, 167–321. [Google Scholar] [CrossRef]
- Faraoni, V.; Capozziello, S. Beyond Einstein Gravity; Springer: Dordrecht, The Netherlands, 2011; Volume 170. [Google Scholar] [CrossRef]
- Bamba, K.; Odintsov, S.D. Inflationary cosmology in modified gravity theories. Symmetry 2015, 7, 220–240. [Google Scholar] [CrossRef]
- Cai, Y.F.; Capozziello, S.; De Laurentis, M.; Saridakis, E.N. f(T) teleparallel gravity and cosmology. Rept. Prog. Phys. 2016, 79, 106901. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Modified Gravity Theories on a Nutshell: Inflation, Bounce and Late-time Evolution. Phys. Rept. 2017, 692, 1–104. [Google Scholar] [CrossRef]
- Bamba, K.; Capozziello, S.; Nojiri, S.; Odintsov, S.D. Dark energy cosmology: The equivalent description via different theoretical models and cosmography tests. Astrophys. Space Sci. 2012, 342, 155–228. [Google Scholar] [CrossRef]
- Artymowski, M.; Lalak, Z. Inflation and dark energy from f(R) gravity. J. Cosmol. Astropart. Phys. 2014, 1409, 36. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. Singular inflationary universe from F(R) gravity. Phys. Rev. D 2015, 92, 124024. [Google Scholar] [CrossRef]
- Motohashi, H.; Starobinsky, A.A. Constant-roll inflation: Confrontation with recent observational data. EPL 2017, 117, 39001. [Google Scholar] [CrossRef]
- Huang, Q.G. A polynomial f(R) inflation model. J. Cosmol. Astropart. Phys. 2014, 1402, 35. [Google Scholar] [CrossRef]
- Addazi, A.; Khlopov, M.Y. Dark matter and inflation in R + ζR2 supergravity. Phys. Lett. 2017, B766, 17–22. [Google Scholar] [CrossRef]
- Koyama, K. Cosmological Tests of Modified Gravity. Rept. Prog. Phys. 2016, 79, 46902. [Google Scholar] [CrossRef]
- Utiyama, R.; DeWitt, B.S. Renormalization of a classical gravitational field interacting with quantized matter fields. J. Math. Phys. 1962, 3, 608–618. [Google Scholar] [CrossRef]
- Barrow, J.D.; Cotsakis, S. Chaotic Behaviour in higher-order gravity theories. Phys. Lett. B 1989, 232, 172–176. [Google Scholar] [CrossRef]
- Clifton, T.; Barrow, J.D. Further exact cosmological solutions to higher-order gravity theories. Class. Quant. Grav. 2006, 23, 2951. [Google Scholar] [CrossRef]
- Middleton, J.; Barrow, J.D. Stability of an isotropic cosmological singularity in higher-order gravity. Phys. Rev. D 2008, 77, 103523. [Google Scholar] [CrossRef]
- Sk, N.; Sanyal, A.K. On the equivalence between different canonical forms of F(R) theory of gravity. Int. J. Mod. Phys. 2018, D27, 1850085. [Google Scholar] [CrossRef]
- Starobinsky, A.A. A New Type of Isotropic Cosmological Models without Singularity. Adv. Ser. Astrophys. Cosmol. 1987, 3, 130–133. [Google Scholar] [CrossRef]
- Starobinskii, A.A. The Perturbation Spectrum Evolving from a Nonsingular Initially De-Sitter Cosmology and the Microwave Background Anisotropy. Sov. Astron. Lett. 1983, 9, 302–304. [Google Scholar]
- Sotiriou, T.P.; Faraoni, V. f(R) theories of gravity. Rev. Mod. Phys. 2010, 82, 451–497. [Google Scholar] [CrossRef]
- De Felice, A.; Tsujikawa, S. f(R) theories. Living Rev. Rel. 2010, 13, 3. [Google Scholar] [CrossRef]
- Guo, J.Q.; Wang, D.; Frolov, A.V. Spherical collapse in f(R) gravity and the Belinskii-Khalatnikov-Lifshitz conjecture. Phys. Rev. D 2014, 90, 024017. [Google Scholar] [CrossRef]
- Clifton, T. Spherically Symmetric Solutions to Fourth-Order Theories of Gravity. Class. Quant. Grav. 2006, 23, 7445. [Google Scholar] [CrossRef]
- Sebastiani, L.; Zerbini, S. Static Spherically Symmetric Solutions in F(R) Gravity. Eur. Phys. J. 2011, C71, 1591. [Google Scholar] [CrossRef]
- Nashed, G.G.L.; Capozziello, S. Charged spherically symmetric black holes in f(R) gravity and their stability analysis. Phys. Rev. 2019, D99, 104018. [Google Scholar] [CrossRef]
- Chakrabarti, S.; Banerjee, N. Gravitational collapse in f (R) gravity for a spherically symmetric spacetime admitting a homothetic Killing vector. Eur. Phys. J. Plus 2016, 131, 144. [Google Scholar] [CrossRef]
- Zhang, C.Y.; Tang, Z.Y.; Wang, B. Gravitational collapse of massless scalar field in f(R) gravity. Phys. Rev. D 2016, 94, 104013. [Google Scholar] [CrossRef]
- De la Cruz-Dombriz, A.; Dobado, A.; Maroto, A.L. Black holes in f(R) theories. Phys. Rev. D 2009, 80, 124011. [Google Scholar] [CrossRef]
- Nashed, G.G.L. Higher Dimensional Charged Black Hole Solutions in f(R) Gravitational Theories. Adv. High Energy Phys. 2018, 2018, 7323574. [Google Scholar] [CrossRef]
- Moon, T.; Myung, Y.S.; Son, E.J. f(R) black holes. Gen. Rel. Grav. 2011, 43, 3079–3098. [Google Scholar] [CrossRef]
- Nashed, G.G.L. Spherically symmetric charged black holes in f(R) gravitational theories. Eur. Phys. J. Plus 2018, 133, 18. [Google Scholar] [CrossRef]
- Rodrigues, M.E.; Junior, E.L.B.; Marques, G.T.; Zanchin, V.T. Regular black holes in f(R) gravity coupled to nonlinear electrodynamics. Phys. Rev. D 2016, 94, 024062. [Google Scholar] [CrossRef]
- Nashed, G.G.L. Rotating charged black hole spacetimes in quadratic f(R) gravitational theories. Int. J. Mod. Phys. D 2018, 27, 1850074. [Google Scholar] [CrossRef]
- Cañate, P.; Jaime, L.G.; Salgado, M. Spherically symmetric black holes in f(R) gravity: Is geometric scalar hair supported? Class. Quant. Grav. 2016, 33, 155005. [Google Scholar] [CrossRef]
- Moon, T.; Myung, Y.S. Stability of Schwarzschild black hole in f(R) gravity with the dynamical Chern-Simons term. Phys. Rev. 2011, D84, 104029. [Google Scholar] [CrossRef]
- Ayon-Beato, E.; Garbarz, A.; Giribet, G.; Hassaine, M. Analytic Lifshitz black holes in higher dimensions. J. High Energy Phys. 2010, 4, 30. [Google Scholar] [CrossRef]
- Hendi, S.H.; Eslam Panah, B.; Mousavi, S.M. Some exact solutions of F(R) gravity with charged (a)dS black hole interpretation. Gen. Rel. Grav. 2012, 44, 835–853. [Google Scholar] [CrossRef]
- Hendi, S.H.; Eslam Panah, B.; Saffari, R. Exact solutions of three-dimensional black holes: Einstein gravity versus F(R) gravity. Int. J. Mod. Phys. 2014, D23, 1450088. [Google Scholar] [CrossRef]
- Cao, Z.; Galaviz, P.; Li, L.F. Binary black hole mergers in f(R) theory. Phys. Rev. D 2013, 87, 104029. [Google Scholar] [CrossRef]
- Addazi, A. (Anti)evaporation of Dyonic Black Holes in string-inspired dilaton f(R)-gravity. Int. J. Mod. Phys. 2017, A32, 1750102. [Google Scholar] [CrossRef]
- Fan, Z.Y.; Lü, H. Thermodynamical first laws of black holes in quadratically-extended gravities. Phys. Rev. D 2015, 91, 064009. [Google Scholar] [CrossRef]
- Akbar, M.; Cai, R.G. Thermodynamic Behavior of Field Equations for f(R) Gravity. Phys. Lett. 2007, B648, 243–248. [Google Scholar] [CrossRef]
- Faraoni, V. Black hole entropy in scalar-tensor and f(R) gravity: An Overview. Entropy 2010, 12, 1246. [Google Scholar] [CrossRef]
- Ortaggio, M. Higher dimensional black holes in external magnetic fields. J. High Energy Phys. 2005, 5, 48. [Google Scholar] [CrossRef]
- Tangherlini, F.R. Schwarzschild field inn dimensions and the dimensionality of space problem. Il Nuovo C. (1955–1965) 1963, 27, 636–651. [Google Scholar] [CrossRef]
- Myers, R.C.; Perry, M.J. Black holes in higher dimensional space-times. Ann. Phys. 1986, 172, 304–347. [Google Scholar] [CrossRef]
- Emparan, R.; Reall, H.S. A Rotating black ring solution in five-dimensions. Phys. Rev. Lett. 2002, 88, 101101. [Google Scholar] [CrossRef]
- Emparan, R. Rotating circular strings, and infinite nonuniqueness of black rings. J. High Energy Phys. 2004, 3, 64. [Google Scholar] [CrossRef]
- Horne, J.H.; Horowitz, G.T. Exact black string solutions in three-dimensions. Nucl. Phys. 1992, B368, 444–462. [Google Scholar] [CrossRef]
- Cisterna, A.; Oliva, J. Exact black strings and p-branes in general relativity. Class. Quant. Grav. 2018, 35, 35012. [Google Scholar] [CrossRef]
- Sheykhi, A.; Salarpour, S.; Bahrampour, Y. Rotating black strings in f(R)-Maxwell theory. Phys. Scr. 2013, 87, 45004. [Google Scholar] [CrossRef]
- Sheykhi, A. Higher-dimensional charged f(R) black holes. Phys. Rev. D 2012, 86, 024013. [Google Scholar] [CrossRef]
- Hendi, S.H.; Sheykhi, A. Charged rotating black string in gravitating nonlinear electromagnetic fields. Phys. Rev. D 2013, 88, 044044. [Google Scholar] [CrossRef]
- Kobayashi, T.; Maeda, K.I. Relativistic stars in f(R) gravity, and absence thereof. Phys. Rev. D 2008, 78, 064019. [Google Scholar] [CrossRef]
- Kobayashi, T.; Maeda, K.I. Can higher curvature corrections cure the singularity problem in f(R) gravity? Phys. Rev. D 2009, 79, 24009. [Google Scholar] [CrossRef]
- Nashed, G.G.L.; El Hanafy, W.; Odintsov, S.D.; Oikonomou, V.K. Thermodynamical correspondence of f(R) gravity in the Jordan and Einstein frames. Int. J. Mod. Phys. D 2020, 29, 2050090. [Google Scholar] [CrossRef]
- Elizalde, E.; Nashed, G.G.L.; Nojiri, S.; Odintsov, S.D. Spherically symmetric black holes with electric and magnetic charge in extended gravity: Physical properties, causal structure, and stability analysis in Einstein’s and Jordan’s frames. Eur. Phys. J. C 2020, 80, 109. [Google Scholar] [CrossRef]
- Nashed, G.G.L.; Saridakis, E.N. New rotating black holes in nonlinear Maxwell f(R) gravity. Phys. Rev. D 2020, 102, 124072. [Google Scholar] [CrossRef]
- Cognola, G.; Elizalde, E.; Nojiri, S.; Odintsov, S.D.; Zerbini, S. One-loop f(R) gravity in de Sitter universe. J. Cosmol. Astropart. Phys. 2005, 5, 10. [Google Scholar] [CrossRef]
- Koivisto, T.; Kurki-Suonio, H. Cosmological perturbations in the palatini formulation of modified gravity. Class. Quant. Grav. 2006, 23, 2355–2369. [Google Scholar] [CrossRef]
- Nashed, G.G.L.; Saridakis, E.N. Rotating AdS black holes in Maxwell-f(T) gravity. Class. Quant. Grav. 2019, 36, 135005. [Google Scholar] [CrossRef]
- Bahamonde, S.; Odintsov, S.D.; Oikonomou, V.K.; Tretyakov, P.V. Deceleration versus acceleration universe in different frames of F(R) gravity. Phys. Lett. 2017, 766, 225–230. [Google Scholar] [CrossRef]
- Bahamonde, S.; Odintsov, S.D.; Oikonomou, V.K.; Wright, M. Correspondence of F(R) Gravity Singularities in Jordan and Einstein Frames. Ann. Phys. 2016, 373, 96–114. [Google Scholar] [CrossRef]
- Lemos, J.P.S. Cylindrical black hole in general relativity. Phys. Lett. 1995, B353, 46–51. [Google Scholar] [CrossRef]
- Awad, A.M. Higher dimensional charged rotating solutions in (A)dS space-times. Class. Quant. Grav. 2003, 20, 2827–2834. [Google Scholar] [CrossRef]
- Stachel, J. Globally stationary but locally static space-times: A gravitational analog of the Aharonov-Bohm effect. Phys. Rev. 1982, 26, 1281–1290. [Google Scholar] [CrossRef]
- Obukhov, Y.N.; Rubilar, G.F. Invariant conserved currents in gravity theories with local Lorentz and diffeomorphism symmetry. Phys. Rev. D 2006, 74, 64002. [Google Scholar] [CrossRef]
- Kopczynski, W. Variational principles for gravity and fluids. Ann. Phys. 1990, 203, 308–338. [Google Scholar] [CrossRef]
- Komar, A. Asymptotic Covariant Conservation Laws for Gravitational Radiation. Phys. Rev. 1962, 127, 1411–1418. [Google Scholar] [CrossRef]
- Shirafuji, T.; Nashed, G.G.L.; Kobayashi, Y. Equivalence principle in the new general relativity. Prog. Theor. Phys. 1996, 96, 933–948. [Google Scholar] [CrossRef][Green Version]
- Komar, A. Covariant Conservation Laws in General Relativity. Phys. Rev. 1959, 113, 934–936. [Google Scholar] [CrossRef]
- Ashtekar, A. Angular Momentum of Isolated Systems in General Relativity. In Cosmology and Gravitation: Spin, Torsion, Rotation, and Supergravity; Bergmann, P.G., De Sabbata, V., Eds.; Springer: Boston, MA, USA, 1980; pp. 435–448. [Google Scholar] [CrossRef]
- Obukhov, Y.N.; Rubilar, G.F. Invariant conserved currents in gravity theories: Diffeomorphisms and local gauge symmetries. Phys. Rev. D 2007, 76, 124030. [Google Scholar] [CrossRef]
- Nashed, G.G.L. Energy and momentum of a spherically symmetric dilaton frame as regularized by teleparallel gravity. Ann. Phys. 2011, 523, 450–458. [Google Scholar] [CrossRef]
- Obukhov, Y.N.; Rubilar, G.F. Invariant conserved currents for gravity. Phys. Lett. 2008, B660, 240–246. [Google Scholar] [CrossRef]
- Awad, A.; Chamblin, A. A Bestiary of higher dimensional Taub—NUT AdS space-times. Class. Quant. Grav. 2002, 19, 2051–2062. [Google Scholar] [CrossRef]
- Sheykhi, A. Thermodynamics of apparent horizon and modified Friedmann equations. Eur. Phys. J. 2010, C69, 265–269. [Google Scholar] [CrossRef]
- Hendi, S.H.; Sheykhi, A.; Dehghani, M.H. Thermodynamics of higher dimensional topological charged AdS black branes in dilaton gravity. Eur. Phys. J. 2010, C70, 703–712. [Google Scholar] [CrossRef]
- Sheykhi, A.; Dehghani, M.H.; Hendi, S.H. Thermodynamic instability of charged dilaton black holes in AdS spaces. Phys. Rev. D 2010, 81, 84040. [Google Scholar] [CrossRef]
- Davies, P.C.W. Thermodynamics of Black Holes. Proc. Roy. Soc. Lond. 1977, 353, 499–521. [Google Scholar] [CrossRef]
- Babichev, E.O.; Dokuchaev, V.I.; Eroshenko, Y.N. Black holes in the presence of dark energy. Phys. Usp. 2013, 56, 1155–1175, Erratum in 2013, 189, 1257. [Google Scholar] [CrossRef]
- Saridakis, E.N.; Gonzalez-Diaz, P.F.; Siguenza, C.L. Unified dark energy thermodynamics: Varying w and the -1-crossing. Class. Quant. Grav. 2009, 26, 165003. [Google Scholar] [CrossRef]
- Brevik, I.; Nojiri, S.; Odintsov, S.D.; Vanzo, L. Entropy and universality of the Cardy-Verlinde formula in a dark energy universe. Phys. Rev. D 2004, 70, 043520. [Google Scholar] [CrossRef]
- Nunes, R.C.; Pan, S.; Saridakis, E.N.; Abreu, E.M.C. New observational constraints on f(R) gravity from cosmic chronometers. J. Cosmol. Astropart. Phys. 2017, 1701, 5. [Google Scholar] [CrossRef]
- Nashed, G.G.L. Stability of the vacuum nonsingular black hole. Chaos Solitons Fractals 2003, 15, 841. [Google Scholar] [CrossRef]
- Nouicer, K. Black holes thermodynamics to all order in the Planck length in extra dimensions. Class. Quant. Grav. 2007, 24, 5917–5934, Erratum in 2007, 24, 6435. [Google Scholar] [CrossRef]
- Dymnikova, I.; Korpusik, M. Thermodynamics of regular cosmological black holes with de Sitter interior. Gravit. Cosmol. 2011, 17, 35–37. [Google Scholar] [CrossRef]
- Chamblin, A.; Emparan, R.; Johnson, C.V.; Myers, R.C. Charged AdS black holes and catastrophic holography. Phys. Rev. 1999, D60, 64018. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nashed, G.G.L.; Bamba, K. Higher Dimensional Rotating Black Hole Solutions in Quadratic f(R) Gravitational Theory and the Conserved Quantities. Entropy 2021, 23, 358. https://doi.org/10.3390/e23030358
Nashed GGL, Bamba K. Higher Dimensional Rotating Black Hole Solutions in Quadratic f(R) Gravitational Theory and the Conserved Quantities. Entropy. 2021; 23(3):358. https://doi.org/10.3390/e23030358
Chicago/Turabian StyleNashed, Gamal G. L., and Kazuharu Bamba. 2021. "Higher Dimensional Rotating Black Hole Solutions in Quadratic f(R) Gravitational Theory and the Conserved Quantities" Entropy 23, no. 3: 358. https://doi.org/10.3390/e23030358
APA StyleNashed, G. G. L., & Bamba, K. (2021). Higher Dimensional Rotating Black Hole Solutions in Quadratic f(R) Gravitational Theory and the Conserved Quantities. Entropy, 23(3), 358. https://doi.org/10.3390/e23030358






